Two triangles are said to be similar if all the corresponding angles are congruent or all the corresponding sides ratios is proportional. We also have some similarity criterion theorems to prove that two triangles are similar to each other. One among those theorems is the AA Criterion of Similarity. The complete details about this Angle-Angle Similarity Criteria are provided below along with solved questions.
What is AA Similarity Criteria?
The AA criterion of similarity states that if the three angles of one triangle are equal to the three angles of the other triangle, then the two triangles are similar. It can also be stated as the equiangular triangles are similar.
The name of the theorem should be AAA(Angle-Angle-Angle) criterion, but it can be called as AA criterion as we require only two pairs of angles to be equal. So that the third pair will be automatically equal by the angle sum property of triangles.
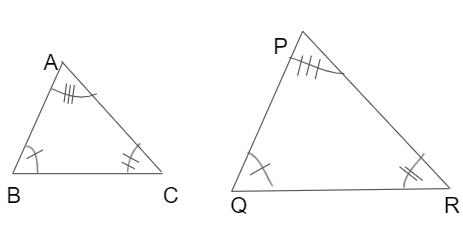
In ΔABC, ΔPQR
- ∠A = ∠P
- ∠C = ∠R
- ∠B = ∠Q
Using the AA criterion, ΔABC is similar to ΔPQR. So the corresponding sides are proportional.
\(\frac { AB }{ PQ } \) = \(\frac { BC }{ QR } \) = \(\frac { AC }{ PR } \)
More Related Articles:
AA Criterion of Similarity With Proof
Let us take two equiangular triangles ΔABC and ΔDEF
Given that,
∠A = ∠D, ∠B = ∠E and ∠C = ∠F
To prove: ΔABC ~ ΔDEF
Construction: Assume that AB > DE
- Take a point X on AB so that AX = DE
- Draw a line segment XY from X which is parallel to BC and meet AC at point Y.

Since XY ∥ BC,
So, ΔAXY ∼ ΔABC —– (i)
Now compare ΔAXY with ΔDEF
∠A = ∠D (given)
∠AXY = ∠E (XY ∥ BC)
AX = DE
By using ASA criterion, ΔAXY ∼ ΔDEF
ΔAXY ∼ ΔDEF —– (ii)
From (i) and (ii)
ΔDEF ∼ ΔABC.
Examples on Angle-Angle Criterion of Similarity
Example 1:
Show that both triangles are similar.
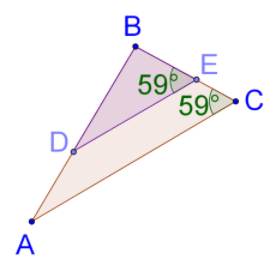
Solution:
Given two triangles are ΔABC, ΔBDE
∠E = 59°, ∠C = 59°
∠C = ∠E (Given)
∠B = ∠B (Common angle)
By using AA criterion of similarity, ΔABC ∼ ΔBDE.
Example 2:
In the two similar triangles PQR and XYZ, PM ⊥ QR and XN ⊥ YZ. Prove that \(\frac { PQ }{ XY } \) = \(\frac { PM }{ XN } \).
Solution:
Proof:
| Statement | Reason |
|---|---|
| In ∆PQM and ∆XYN, ∠PQM = ∠XYN ∠PMQ = ∠XNY = 90° |
Being similar triangles, they are equal. Given |
| ∆PQM ∼ ∆XYN | By AA criterion of similarity |
| \(\frac { PQ }{ XY } \) = \(\frac { PM }{ XN } \) | Corresponding sides of similar triangles are proportional. |
Example 3:
In a right-angled triangle, if a perpendicular is drawn from the right-angled vertex to the hypotenuse, the triangles on each side of it are similar to the whole triangle and to one another.
Solution:
Let XYZ be a right angle in which ∠YXZ = 90° and XM ⊥ YZ.
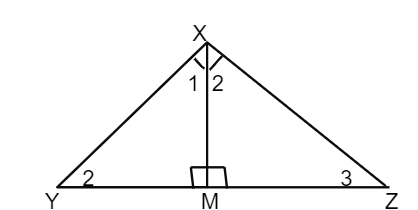
So, ∠XMY = ∠XMZ = 90°
To prove: ∆XYM ∼ ∆ZXM ∼ ∆ ZYX
Proof:
| Statement | Reason |
|---|---|
| In ∆XYM and ∆XYZ, ∠XMY = ∠YXZ = 90° ∠XYM = ∠XMZ |
Given Common angle |
| Therefore, ∆XYM ∼ ∆ZYX | By AA criterion of similarity |
| In ∆XYZ and ∆XMZ, ∠YXZ = ∠XMZ = 90° ∠XZY= ∠XZM |
Given Common angle |
| Therefore, ∆ZYX ∼ ∆ZXM | By AA criterion of similarity |
| Hence, ∆XYM ∼ ∆ZXM ∼ ∆ZYX (Proved) | From statements 2 and 4 |
Frequently Asked Question’s on AA Similarity Criteria
1. What is the difference between the AA and AAA similarity criterion?
According to AAA similarity criteria, if two triangles are equiangular, then they are similar. As per AA similarity, if two angles of the first triangle are equal to the two angles of another triangle, then they are similar.
2. What does AA similarity mean?
In two triangles, if two pairs of corresponding angles are congruent, then the triangleas are said to be similar.
3. Does the AA similarity criterion apply to quadrilaterals?
The AA similarity theorem does not apply to the quadrilaterals.