A quadrilateral is a closed polygon that has four sides, four vertices. We can use theorems related to the AA criterion of similarly to explore the concept quadrilateral. Have a look at the following sections to know about the theorems on the angle-angle similarly criterion and the solved questions.
Theorems on AA Criterion of Similarly on Quadrilateral
Here we will provide the prove related to the theorems on the AA criterion of similarly.
Theorem 1: In quadrilateral ABCD, AB ∥ CD and O is the point of intersection of two diagonals, such that OA × OD = OB × OC.
Given: ABCD is a quadrilateral, the side AB is parallel to CD.
Point O is the intersection of two diagonals.
To Prove: OA × OD = OB × OC
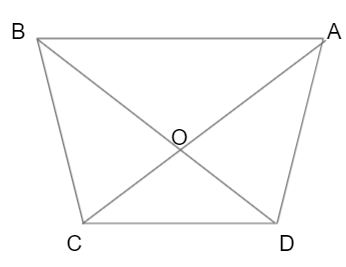
Proof:
| Statement | Reason |
|---|---|
| In ∆ABC, ∆BPC ∠ACB = ∠PCB ∠ABC = ∠BPC = 90° |
Vertically opposite angles are equal Alternate angles |
| ∆OAB ∼ ∆OCD | By AA criterion of similarity |
| Therefore, \(\frac { OA }{ OC } \) = \(\frac { OB }{ OD } \) | Corresponding sides of similar triangles are proportional |
Hence, OA × OD = OB × OC.
More Related Articles:
- Greater segment of the Hypotenuse is Equal to the Smaller Side of the Triangle
- Application of Basic Proportionality Theorem
- Converse of Basic Proportionality Theorem
Theorem 2: In quadrilateral PQRS, PQ ∥ RS. T is a point on PS. QT is joined and produced to meet RS produced at U, then \(\frac { PQ }{ SU } \) = \(\frac { PT }{ TS } \).
Given: PQRS is a quadrilateral, sides PQ and RS are parallel to each other. T is a point on the side PS.
Construction:
Let us take a quadrilateral PQRS, where PQ is parallel to RS.
Locate any point T on PS and join QT and extend it till U and U is a straight line extending from RS.
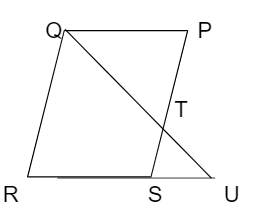
To Prove: \(\frac { PQ }{ SU } \) = \(\frac { PT }{ TS } \)
Proof:
| Statement | Reason |
|---|---|
| In ∆PQT and ∆SUT, ∠PTQ = ∠STU ∠QPT = ∠TSU |
Vertically opposite angles are equal Alternate angles are equal |
| ∆PQT ∼ ∆SUT | By AA criterion of similarity |
| Therefore, \(\frac { PQ }{ SU } \) = \(\frac { PT }{ TS } \) | Corresponding sides of similar triangles are proportional |
Hence, proved.
Questions on Quadrilateral AA Criterion of Similarly
Question 1:
In a quadrilateral PQRS, PQ is parallel to RS and the meeting point of diagonals. If OP = 20 cm, OR = 5 cm, OS = 6 cm, find OQ.
Solution:
Given that,
PQRS is a quadrilateral where PQ is parallel to RS
OP = 20 cm, OR = 5 cm, OS = 6 cm
According to the theorem on AA criterion on similarity on quadrilateral OP × OS = OQ × OR
20 x 6 = OQ x 5
120 = OQ x 5
OQ = 24
Therefore, OQ = 24 cm.
Question 2:
In quadrilateral ABCD, AB ∥ CD. P is a point on AD. BP is joined and produced to meet CD produced at U. If AB = 10 cm, DU = 5 cm, PD = 12 cm, find PA.
Solution:
Given that,
AB = 10 cm, DU = 5 cm, PD = 12 cm
ABCD is a quadrilateral, AB is parallel to CD
P is a point on AD. BP is joined and produced to meet CD produced at U
\(\frac { AB }{ DU } \) = \(\frac { AP }{ PD } \)
\(\frac { 10 }{ 5 } \) = \(\frac { AP }{ 12 } \)
2 = \(\frac { AP }{ 12 } \)
AP = 2 x 12 = 24
Frequently Asked Question’s
1. How to prove that two quadrilaterals are similar?
Two quadrilaterals are said to be similar quadrilaterals when the three corresponding angles are the same and two adjacent sides have equal ratios.
2. What is AA similarity criteria?
The AA criterion of similarity for triangles states that if all three angles of one triangle are equal to the corresponding three angles are equal, then the two triangles are similar.
3. What are the theorems related to AA criterion of similarly on quadrilaterals?
One theorem is any two sides of the quadrilateral are parallel, two diagonals are drawn. If the product of the diagonals meeting point to the two sides is equal to the product of the diagonals meeting point to other two sides.