Different Fractions can be represented on the number line. We have explained the step-by-step procedure on how to add and subtract fractions using a number line. Refer to the solved examples on adding and subtracting fractions on the fraction number line having both same and different denominators and learn the problem-solving approach used. 4th Grade Math students can utilize the article over here to get a deeper insight on the concept of Addition and Subtraction of Fractions on Fraction Number Line and learn them effectively.
Do Check,
How to Add Fractions using a Fraction Number Line?
Follow the step-by-step procedure to Add Fractions using a Fraction Number Line.
- Take the number line and divided it into equal parts.
- Divide the line into n equal parts where n is the denominator of the fraction.
- Take the first part of the fraction on a number line and add the second fraction to the first fraction.
- Then, take the last fraction as the final output of the addition of the fraction.
Examples on Addition of Fractions using a Number Line
Check out the below examples to add different fractions with the help of a number line.
Example 1.
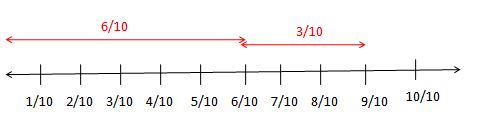
Calculate the sum of \(\frac { 6 }{ 10 } \) + \(\frac { 3 }{ 10 } \) on the fraction number line.
Solution:
Given fractions are \(\frac { 6 }{ 10 } \) + \(\frac { 3 }{ 10 } \)
The denominator is 10.
Take the number line and divide it into 10 equal parts.
First, take 6 parts out of 10 parts because the first fraction is \(\frac { 6 }{ 10 } \) on a number line.
Add 3 parts from the 6 out of 10 parts because the second fraction is \(\frac { 3 }{ 10 } \) on a number line.
\(\frac { 6 }{ 10 } +\frac { 3 }{ 10 } =\frac { 9 }{ 10 } \)
Finally, the final output is \(\frac { 9 }{ 10 } \).
Example 2.
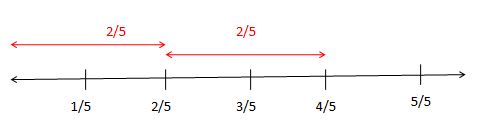
Calculate the sum of \(\frac { 2 }{ 5 } \) + \(\frac { 2 }{ 5 } \) on the fraction number line.
Solution:
Given fractions are \(\frac { 2 }{ 5 } \) + \(\frac { 2 }{ 5 } \)
The denominator is 5.
Take the number line and divide it into 5 equal parts.
First, take 2 parts out of 5 parts because the first fraction is \(\frac { 2 }{ 5 } \) on a number line.
Add 2 parts from the 2 out of 5 parts because the second fraction is \(\frac { 2 }{ 5 } \) on a number line.
\(\frac { 2 }{ 5 } +\frac { 2 }{ 5 } =\frac { 4 }{ 5 } \)
Finally, the final output is \(\frac { 4 }{ 5 } \).
Example 3.
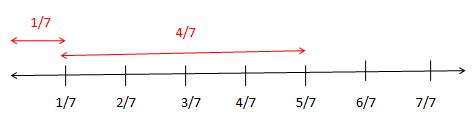
Calculate the sum of \(\frac { 1 }{ 7 } \) + \(\frac { 4 }{ 7 } \) on the fraction number line.
Solution:
Given fractions are \(\frac { 1 }{ 7 } \) + \(\frac { 4 }{ 7 } \)
The denominator is 7.
Take the number line and divide it into 7 equal parts.
First, take 1 part out of 7 parts because the first fraction is \(\frac { 1 }{ 7 } \) on a number line.
Add 4 parts from the first part out of 7 parts because the second fraction is \(\frac { 4 }{ 7 } \) on a number line.
\(\frac { 1 }{ 7 } +\frac { 4 }{ 7 } =\frac { 5 }{ 7 } \)
Finally, the final output is \(\frac { 5 }{ 7 } \).
How to Subtract Fractions using a Fraction Number Line?
The process of subtracting fractions using a Fraction Number Line is given below. All the steps will help you to solve the problems to subtract fractions.
- Take the number line and divided it into equal parts.
- Divide the line into n equal parts where n is the denominator of the fraction.
- Take the two numerator numbers on a number line.
- Then, subtract the small number from a large number.
- Finally, write the numerator and denominator to get the final answer.
Subtraction of Fractions using a Number Line Examples
Example 1.
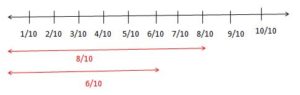
Find the difference between \(\frac { 8 }{ 10 } \) and \(\frac { 6 }{ 10 } \)
Solution:
Given fractions are \(\frac { 8 }{ 10 } \) – \(\frac { 6 }{ 10 } \)
The denominator is 10.
Take the number line and divide it into 10 equal parts.
Find out the numerators on a number line 8 and 6.
Subtract 6 from the 8 on a number line. Then, you will get 2.
So, \(\frac { 8 }{ 10 } – \frac { 6 }{ 10 } =\frac { 2 }{ 10 } \)
The remaining part on the number line after subtraction is \(\frac { 2 }{ 10 } \).
Finally, the final output is \(\frac { 2 }{ 10 } \).
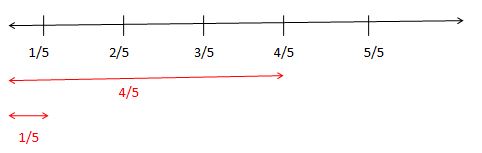
Example 2.
Find the difference between \(\frac { 4 }{ 5 } \) and \(\frac { 1 }{ 5 } \)
Solution:
Given fractions are \(\frac { 4 }{ 5 } \) – \(\frac { 1 }{ 5 } \)
The denominator is 10.
Take the number line and divide it into 5 equal parts.
Find out the numerators on a number line 4 and 1.
Subtract 1 from the 4 on a number line. Then, you will get 4 – 1 = 3.
So, \(\frac { 4 }{ 5 } – \frac { 1 }{ 5 } =\frac { 3 }{ 5 } \)
The remaining part on the number line after subtraction is \(\frac { 3 }{ 5 } \).
Finally, the final output is \(\frac { 3 }{ 5 } \).
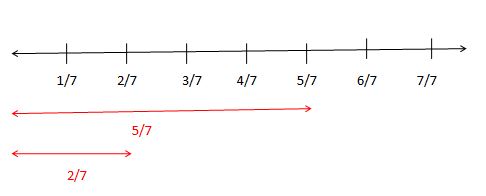
Example 3.
Find the difference between \(\frac { 5 }{ 7 } \) and \(\frac { 2 }{ 7 } \)
Solution:
Given fractions are \(\frac { 5 }{ 7 } \) – \(\frac { 2 }{ 7 } \)
The denominator is 7.
Take the number line and divide it into 7 equal parts.
Find out the numerators on a number line 5 and 2.
Subtract 2 from the 5 on a number line. Then, you will get 5 – 2 = 3.
So, \(\frac { 5 }{ 7 } – \frac { 2 }{ 7 } =\frac { 3 }{ 7 } \)
The remaining part on the number line after subtraction is \(\frac { 3 }{ 7 } \).
Finally, the final output is \(\frac { 3 }{ 7 } \).
FAQs on Adding and Subtracting Fractions on the Fraction Number Line
1. How do you represent a fraction on a number line? Give Example?
For example \(\frac { 3 }{ 5 } \) is the fraction, we can take it on a number line by dividing the number line into 5 parts and at third part it is represents as \(\frac { 3 }{ 5 } \).
2. Can I add or subtract fractions using a number line?
Yes, it is easier to represent the addition or subtractions of fractions using a number line.
3. What does \(\frac { 4 }{ 5 } \) mean?
\(\frac { 4 }{ 5 } \) means 4 out of 5 parts.
4. Can I add or subtract unlike fractions using a number line?
Yes, you can add or subtract unlike fractions using a number line.
