Adjacent Angles are the angles that have a common vertex and common arm. The other arms of the two adjacent angles present on the opposite sides of the common arm. The adjacent angles can be a supplementary angle or complementary angle when they share the common vertex and side. Find other concepts of Lines and Angles along with the adjacent angles on our website with a clear explanation.
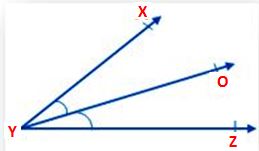
From the above figure, YO is the common arm and Y is the common vertex. The above figure shows a pair of adjacent angles. The Ray XY and ray YZ are present on the opposite sides of the common arm YO. Therefore, ∠XYO and ∠OYZ are adjacent angles.
∠XYZ and ∠XYO are not adjacent angles, because their other arms YZ and YO are not on the opposite sides of the common arm XY.
Adjacent Angle Example
If you take a wall clock, you can see a minute hand, second hand, and also an hour hand. The minute hand and second hand of the clock form one angle represented as ∠XYO and the hour hand form another angle with the second hand represented as∠OYZ. Both the angles i.e.∠XYO and ∠OYZ are present on the opposite sides of the common hand. Therefore, these two angles are adjacent angles.
Properties of Adjacent Angles
Check out the Properties of Adjacent Angles mentioned below as a part of your preparation. They are as such
- Adjacent Angles share the common vertex
- Angles do not overlap
- They share the common arm
- There is no common interior-point in Adjacent Angles.
- It may be complementary or supplementary angles.
- There should be a non-common arm on both sides of the common arm.
Adjacent Angles Solved Problems
1. Are the following angles adjacent? Give reasons.
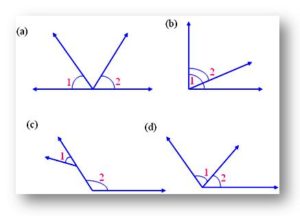
Solution:
(a) From figure a, ∠1, and ∠2 don’t have a common arm. Therefore, ∠1 and ∠2 are not adjacent angles.
(b) Adjacent angles will not overlap each other. From figure b, ∠1 and ∠2 interiors are overlapped. Therefore, ∠1 and ∠2 are not adjacent angles.
(c) Adjacent angles must have a common vertex. from figure c, ∠1, and ∠2 don’t have a common vertex. Therefore, ∠1 and ∠2 are not adjacent angles.
(d) From figure (d), ∠1 and ∠2 are adjacent angles. Because they have a common vertex, a common arm, and their interiors do not overlap.