As we already know a triangle is a three-sided polygon having three angles, vertices and sides. Isosceles Triangle is one of the types of triangles which has two sides of equal length. You have learned about the classification of triangles on the basis of their sides and got the different types of triangles. Check the isosceles triangle theorem statement and proof in the following section.
Angles Opposite to Equal Sides of an Isosceles Triangle are Equal
An isosceles triangle has two equal sides and two equal angles (base angle). When one of the angles of the isosceles triangle is 90°, then it is called the right isosceles triangle.
The first isosceles triangle theorem states that Angles Opposite to Equal Sides of an Isosceles Triangle are also Equal.
Proof: Consider an isosceles triangle ABC where AC = BC
We have to prove that the angles opposite to the sides AC, BC are equal, that is, ∠CAB = ∠CBA.
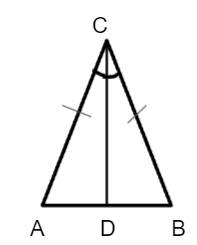
Draw an angle bisector from vertex C to the opposite side CD.
In ∆ACD and ∆BCD
AC = BC [Given]
∠ACD = ∠BCD [Angle bisector divides the angle into two equal parts]
CD = CD [Common side]
So, ∆ACD ≅∆BCD [By SAS congruence criterion]
Thus, ∠CAB = ∠CBA [By CPCT]
Hence proved, that the angles opposite to equal sides of an isosceles triangle are equal.
Note: The converse of this isosceles triangle theorem is also true i.e the sides opposite to equal angles of a triangle are also equal.
Do check:
- An Altitude of an Equilateral Triangle is also a Median
- Geometrical Property of Altitudes
- Geometry and Measurement
- Bisectors of the Angles of a Triangle Meet at a Point
Example Problems on Isosceles Triangle Theorem
Problem 1:
The perimeter of ∆ABC is 15 cm, ∠ABC = ∠ACB, and the length of base BC is 5 cm. Find the length of sides AB, AC.
Solution:
Given that,
BC = 5 cm
Perimeter of ∆ABC = 15 cm
∠ABC = ∠ACB, by applying the isosceles triangle thorem, the sides opposite to equal angles of a triangle are equal.
So, length of sides AB = AC
Let us take AB length as s
Perimeter of ∆ABC = AB + BC + CA
15 = x + 5 + x
15 = 2x + 5
15 – 5 = 2x
10 = 2x
x = 5
Therefore, the length of sides AB and AC are 5 cm, 5 cm respectively.
Problem 2:
If the area of an isosceles triangle is 120 sq cm, the base length is 10 cm. Find the other sides length, the height of the triangle.
Solution:
Given that,
The base length of triangle b = 10 cm
Area of an isosceles triangle = 120 sq cm
Let h be the height of the isosceles triangle
Area of an isosceles triangle A = ½bh
120 = ½ x 10 x h
120 = 5 x h
h = 120/5
h = 24
The height line is also called the angle bisector.
According to the isosceles triangle theorem, the sides opposite to equal angles of a triangle are equal.
Using the Pythagorean theorem, side² = ½base² + height²
side² = (½ x 10)² + 24²
= 25 + 576 = 601
side = 24.5
Therefore, the side length, height of the isosceles triangle are 24.5 cm, 24 cm.
FAQ’s on Isosceles Triangle Theorem
1. In which triangle angles opposite to equal sides are equal?
In an isosceles triangle, the angles opposite to equal sides are also equal.
2. Is opposite angles of a triangle equal?
The sides opposite to equal angles of a triangle are equal.
3. How many sides isosceles triangle are equal?
Two sides of an isosceles triangle are equal.