The area of trapezium is the region covered by the trapezium in 2-D geometry. A trapezium is a type of quadrilateral that consists of four sides, four angles, and a set of parallel lines. The Formula Area of Trapezium is used in the concept of Mensuration in order to measure the two-dimensional figures. Let us learn the basic properties of trapezium from this article. Read this article thoroughly to know how to calculate the area of the trapezium with the help of the example problems. Also, learn the derivation of the area of the trapezium from here.
Area of Trapezium Definition
The area of trapezium is the region covered by the trapezium in two-dimensional geometry. The area of trapezium is equal to the product of half of the sum of parallel sides and distance between the parallel sides. The area of trapezium is measured in square units.
Properties of Trapezium
The properties of a trapezium are as follows,
- The sum of the four angles is equal to 360 degrees.
- The trapezium consists of a set of parallel sides and a set of non-parallel sides.
- The diagonals of the trapezium bisect each other.
- All the sides of the trapezium are not equal.
Area of Trapezium Formula
The formula for Area of Trapezium can be found by the product of half of the sum of parallel lines and distance between the parallel sides.
- Area of Trapezium = 1/2 (a + b)h
Derivation of Area of Trapezium Formula
Area of trapezium = sum of the area of rectangles and area of the triangle.
That means,
Area of trapezium = area of rectangle + area of triangle 1 + area of triangle 2
A = a1h + bh/2 + ch/2
A = (2a1h + bh + ch)/2
Take h as common
A = (a1 + a1 + b + c)h/2
A = (a1 + (a1 + b + c)h/2
Let a2 = a1 + b + c
A = (a1 + a2)h/2
Solved Examples on Area of the Trapezium
1. ABCD is a trapezium in which AB||CD, AD⊥DC, AB = 10 cm, DC = 15 cm and BC = 7 cm. Find the area of the trapezium?
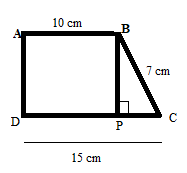
Solution:
Given,
AB = 10 cm
DC = 15 cm
BC = 7 cm
We know that,
Area of Trapezium = 1/2 (a + b)h
PC = DC – DP
PC = 15 cm – 10 cm
PC = 5 cm
Now area of trapezium = Area of rectangle ABPD + Area of ΔBPC
Area of ΔBPC
BC² = BP² + PC²
7² = BP² + 5²
BP² = 49 – 25
BP² = 24
BP = 4.89 cm
Now area of trapezium ABCD = Area of rectangle ABPD + Area of ΔBPC
Area of rectangle ABPD = 10 × 4.89 = 48.9 sq. cm
Area of ΔBPC = 1/2 (5) (7) = 17.5 sq. cm
Area of trapezium ABCD = 48.9 + 17.5 = 66.4 sq. cm
Thus the area of trapezium ABCD is 66.4 sq. cm
2. Given height equal to 10cm, sides equal to 6cm and 5cm. Find the area of the trapezium?
Solution:
Given,
Height = 10cm
a = 6cm
b = 5cm
We know that,
Area of Trapezium = 1/2 (a + b)h
A = 1/2 (6cm + 5cm) 10cm
A = 11cm × 5cm
A = 55 sq. cm
Therefore the area of the trapezium is 55 sq. cm.
3. The area of the trapezium is 81 sq. m, sides are 9m and 6m. Find the height of the trapezium.
Solution:
Given,
The area of the trapezium is 81 sq. m
a = 9m
b = 6m
We know that,
Area of Trapezium = 1/2 (a + b)h
81 = 1/2 (9m + 6m)h
162 = 15m × h
h = 162/15 = 10.8m
Therefore the height of the trapezium is 10.8 meters.
FAQs on Area of Trapezium
1. What is the area of a trapezium?
The area of trapezium is half of the product of the height and the sum of the parallel lines.
2. What is trapezium?
A trapezium is a geometrical shape that has four sides and one set of parallel lines. It consists of four vertices and four angles.
3. What is the area of the trapezium formula?
Formula for Area of trapezium = 1/2 (a + b)h