Are you confused about measuring the area using square paper? Here you can find more information on measuring the area using square paper. This topic includes the definition of the area, How to measure the area using square paper. You can also check the examples for a better understanding of the concept.
Do Refer:
Area – Definition
The area is defined as the amount of space occupied by the surface of an object. The area is measured in square units.
How to Measure the Area using Square Paper?
Here we will discuss how to measure the area using square paper. Take a square paper and draw any shape. We can determine the area covered by that shape by counting the no of squares. Steps to be followed for measuring the area are as follows
Step 1: Count the no of Full Squares
Step 2: Count the no of Half Squares also we know that two triangles make one square.
Step 3: If the square is more than half, consider it as 1.
Step 4: If the square is less than half, Don’t consider it. Thus we get the area of the figure.
Finding the Area using Square Paper Examples
Example 1:
Find the area of the below figure?
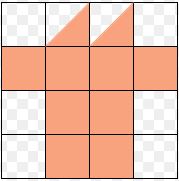
Solution:
No of squares=8
No of half squares=2
We know two half squares becomes one.
Total no of squares=8+1=9.
Therefore, the Area of the figure=9squnits.
Example 2:
Find the area of the below figure?
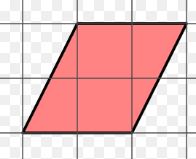
Solution:
since the first square is less than half don’t consider it.
The second one is full square.
The third one is more than half. So we have to consider it as one.
the fourth one is more than half. So we have to consider it as one.
The Fifth one is full square.
The sixth one is less than half. So don’t consider it.
No of Full squares=2
No of half squares=2 i.e. 1 square.
No of squares less than half is 2. So, we exclude the two squares.
Therefore, the total area of the figure is 2+1=3 sq units.
Example 3:
Find the area of the below figure?
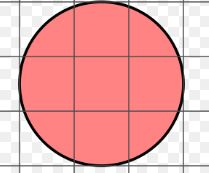
Solution:
No of Full squares=5
No of Half squares=4 i.e. 2 squares
Therefore, the total area of the figure is 5+2= 7 sq units.
Example 4:
Find the area of the below figure?
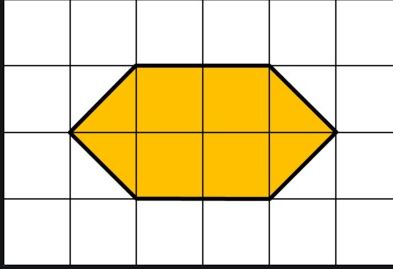
Solution:
Here no of Full squares=4
No of half squares=4 i.e. 2 squares
Therefore, the total area of the figure=4+2=6 sq units.
Example 5:
Measure the area of the below figure?
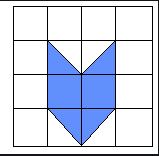
Solution:
No of Full squares=2
No of half squares=4 i.e. 2 squares
Therefore, the total area of the figure is 2+2=4 sq units.
Example 6.
Measure the area of the following figure?
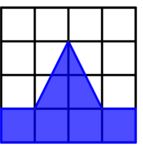
Solution:
No of Full squares=4
No of squares more than half=2
No of squares less than half=2. So don’t consider it.
Therefore, the total area of the figure is 4+2=6 sq units.
Example 7:
Measure the area of the figure below?

Solution:
Count the no of squares=25
Therefore, the total area of the figure is 25 sq units.
Example 8:
Measure the area of the below figure
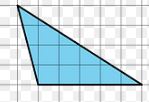
Solution:
No of full squares=5
No of half squares=2 i.e 1 square
No. of squares more than half should be considered as 1. There are 4 such squares
Therefore, the total area of the figure is 5+1+4=10 sq units
FAQs on Measuring the Area with Square Paper
1. Which will measure the surface covered by a two-dimensional object?
The area measures the surface covered by a two-dimensional object.
2. What is the Measurement of the area?
Square units are the measurement of the area.
3. Write the steps for measuring the area using square paper?
- Count the no. of Full Squares
- Count the no. of Half Squares also we know that two triangles make one square.
- If the square is more than half, consider it as 1.
- If the square is less than half, Don’t consider it. Thus we get the area of the figure.
