Download Go Math Grade 6 Answer Key Chapter 9 Independent and Dependent Variables pdf for free of cost. It is very important for the students to learn the fundamentals at the secondary level. In order to help you guys, we are providing the answers to all the questions in HMH Go Math Grade 6 Chapter 9 Solution Key Independent and Dependent Variables.
Go Math Grade 6 Answer Key Chapter 9 Independent and Dependent Variables
The Independent and Dependent Variables chapter consists of the topics like equations and tables, analyze relationships, graphs etc. It is essential for students to know the relationship between the graphs and tables in this chapter. You can know different methods of solving the problems by using Go Math Grade 6 Solution Key Chapter 9 Independent and Dependent Variables. All you have to do is to tap the below-given links.
Lesson 1: Independent and Dependent Variables
- Share and Show – Page No. 493
- Unlock the Problem – Page No. 494
- Independent and Dependent Variables – Page No. 495
- Lesson Check – Page No. 496
Lesson 2: Equations and Tables
- Share and Show – Page No. 499
- Cause and Effect – Page No. 500
- Equations and Tables – Page No. 501
- Lesson Check – Page No. 502
Lesson 3: Problem Solving • Analyze Relationships
- Share and Show – Page No. 505
- On Your Own – Page No. 506
- Problem Solving Analyze Relationships – Page No. 507
- Lesson Check – Page No. 508
Mid-Chapter Checkpoint
Lesson 4: Graph Relationships
- Share and Show – Page No. 513
- Problem Solving + Applications – Page No. 514
- Graph Relationships – Page No. 515
- Lesson Check – Page No. 516
Lesson 5: Equations and Graphs
- Share and Show – Page No. 519
- Problem Solving + Applications – Page No. 520
- Equations and Graphs – Page No. 521
- Lesson Check – Page No. 522
Chapter 9 Review/Test
- Chapter 9 Review/Test – Page No. 523
- Chapter 9 Review/Test – Page No. 524
- Chapter 9 Review/Test – Page No. 525
- Chapter 9 Review/Test – Page No. 526
- Chapter 9 Review/Test – Page No. 527
- Chapter 9 Review/Test – Page No. 528
Share and Show – Page No. 493
Identify the independent and dependent variables. Then write an equation to represent the relationship between them.
Question 1.
An online store lets customers have their name printed on any item they buy. The total cost c in dollars is the price of the item p in dollars plus $3.99 for the name.
Type below:
________________
Answer: c = p + $3.99
Explanation:
The independent variable is c, the price of the item because it is not going to depend on anything else.
The dependent variable is p because the total cost depends on how many items there are, whether your name is marked on it, etc.
The equation would be:
c = p + $3.99
Question 2.
A raft travels downriver at a rate of 6 miles per hour. The total distance d in miles that the raft travels is equal to the rate times the number of hours h.
Type below:
________________
Answer: d = 6 × h
Explanation:
Speed of the raft= 6 miles per hour
Total distance (d) of the raft = rate × number of hours h
The dependent variable is the number of hours h
The independent variable is distance d.
The equation would be:
d = 6 × h
Question 3.
Apples are on sale for $1.99 a pound. Sheila buys p pounds of apples for a total cost of c dollars.
Type below:
________________
Answer: c = p × $1.99
Explanation:
Apples are on sale for $1.99 a pound
p = pounds of apples
c = total cost of dollars
The equation would be:
c = p × $1.99
c is the independent variable.
p is the dependent variable.
On Your Own
Identify the independent and dependent variables. Then write an equation to represent the relationship between them.

Question 5.
Billy has $25. His father is going to give him more money. The total amount t Billy will have is equal to the amount m his father gives him plus the $25 Billy already has.
Type below:
________________
Answer: t = m + $25
Explanation:
Billy has $25. His father is going to give him more money.
The total amount t Billy will have is equal to the amount m his father gives him plus the $25 Billy already has.
The equation would be:
t = m + $25
t is the independent variable
m is the dependent variable.
Question 6.
Connect Symbols and Words Describe a situation that can be represented by the equation c = 12b.
Type below:
________________
Answer:
Melinda is making necklaces. She uses 12 beads for each necklace. The total number of beads b depends on the cost of the necklace c.
The equation is c = 12n
Question 7.
Belinda pays $4.25 for each glass she buys. The total cost c is equal to the price per glass times the number of glasses n plus $9.95 for shipping and handling. Write an equation and use it to find how much it will cost Belinda to buy 12 glasses.
Type below:
________________
Answer:
Belinda pays $4.25 for each glass she buys. The total cost c is equal to the price per glass times the number of glasses n plus $9.95 for shipping and handling.

The equation is: c = 4.25n + 9.95
Now we have to find the cost of 12 glasses.
c = 4.25(12) + 9.95
c = 60.95
It takes $60.95 to buy 12 glasses.
Unlock the Problem – Page No. 494
Question 8.
Benji decides to save $15 per week to buy a computer program. Write an equation that models the total amount t in dollars Benji will have saved in w weeks.
a. What does the variable t represent?
Type below:
________________
Answer: t represents the total amount in dollars Banji saved.
Question 8.
b. Which is the dependent variable? Which is the independent variable? How do you know?
Type below:
________________
Answer:
w is the dependent variable.
t is the independent variable.
w is dependent because it represents the number of weeks. So, we have to multiply 15 by w.
t is an independent variable because t determines the value of a dependent variable.
Question 8.
c. How can you find the total amount saved in w weeks?
Type below:
________________
Answer: We can find the total amount saved in w weeks by multiplying 15 with w.
Question 8.
d. Write an equation for the total amount that Benji will have saved.
Type below:
________________
Answer: t = 15w
Question 9.
Coach Diaz is buying hats for the baseball team. The total cost c is equal to the number of hats n that he buys times the sum of the price per hat h and a $2 charge per hat to have the team name printed on it. Write an equation that can be used to find the cost of the hats.
Type below:
________________
Answer: c = n + 2h
Explanation:
Coach Diaz is buying hats for the baseball team.
The total cost c is equal to the number of hats n that he buys times the sum of the price per hat h and a $2 charge per hat to have the team name printed on it.
c represents the total cost.
n is the number of hats
h is the price per hat.
The equation is c is equal to the number of hats plus price per hat and $2.
c = n + 2h
Question 10.
A steel cable that is \(\frac{1}{2}\) inch in diameter weighs 0.42 pound per foot. The total weight in pounds w is equal to 0.42 times of the number of feet f of steel cable. Choose the letter or equation that makes each sentence true.
The independent variable is ______________ .
The dependent variable is ______________ .
The equation that represents the relationship between the variables is ______________ .
Answer:
A steel cable that is \(\frac{1}{2}\) inch in diameter weighs 0.42 pound per foot.
The total weight in pounds w is equal to 0.42 times of the number of feet f of steel cable.
The equation would be:
w = 0.2f
f is the dependent variable
w is the dependent variable.
Independent and Dependent Variables – Page No. 495
Identify the independent and dependent variables. Then write an equation to represent the relationship between them.

Question 2.
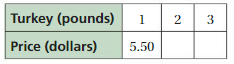
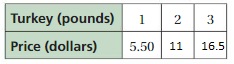
An online clothing store charges $6 for shipping, no matter the price of the items. The total cost c in dollars is the price of the items ordered p plus $6 for shipping.
Type below:
________________
Answer: c = p + 6
Explanation:
Given,
An online clothing store charges $6 for shipping, no matter the price of the items.
The total cost c in dollars is the price of the items ordered p plus $6 for shipping.
The equation would be:
c = p + $6
where c = cost in dollars
p is the price of items
The independent variable is c.
The dependent variable is p
Question 3.
Melinda is making necklaces. She uses 12 beads for each necklace. The total number of beads b depends on the number of necklaces n.
Type below:
________________
Answer: b = 12n
Explanation:
Melinda is making necklaces. She uses 12 beads for each necklace.
The total number of beads b depends on the number of necklaces n.
b = total number of beads
n = number of necklaces
The equation would be:
b = 12n
b is the independent variable
n is the dependent variable.
Problem Solving
Question 4.
Maria earns $45 for every lawn that she mows. Her earnings e in dollars depend on the number of lawns n that she mows. Write an equation that represents this situation.
Type below:
________________
Answer: e = 45n
Explanation:
Maria earns $45 for every lawn that she mows.
Her earnings e in dollars depend on the number of lawns n that she mows.
e = earnings in dollars
n = number of lawns
The equation would be:
e = 45n
e is the independent variable.
n is the dependent variable.

Question 6.
Write a situation in which one unknown is dependent on another unknown. Write an equation for your situation and identify the dependent and independent variables.
Type below:
________________
Answer:
Byron is playing a game. He earns 10 points for each question he answers correctly. His total score s equals the number of correct answers a time a.
Answer:
Dependent variable: s
Independent variable: a
Equation: s = 10a
Lesson Check – Page No. 496
Question 1.
There are 12 boys in a math class. The total number of students s depends on the number of girls in the class g. Write an equation that represents this situation.
Type below:
________________
Answer: s = 12 + g
Explanation:
There are 12 boys in a math class.
The total number of students s depends on the number of girls in class g.
The equation would be:
s = 12 + g
s is the independent variable.
g is the dependent variable.

Spiral Review
Question 3.
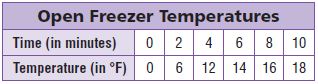
The formula F = \(\frac{9}{5}\)C + 32 gives the Fahrenheit temperature for a Celsius temperature of C degrees. Gwen measured a Celsius temperature of 35 degrees. What is this temperature in degrees Fahrenheit?
______ °F
Answer: 95 degrees
Explanation:
The formula F = \(\frac{9}{5}\)C + 32 gives the Fahrenheit temperature for a Celsius temperature of C degrees.
C = 35
F = 9C ÷ 5 + 32
F = 9(35) ÷ 5 + 32
F = 315 ÷ 5 + 32
F = 63 + 32
F = 95 degrees
Question 4.
Write an equation to represent this sentence. The difference of a number n and 1.8 is 2.
Type below:
________________
Answer: n – 1.8 = 2
Explanation:
The difference of a number n and 1.8 is 2.
The phrase difference is nothing but subtraction.
The equation would be:
n – 1.8 = 2

Question 6.
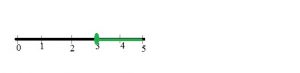
Graph x ≤ –4.5 on a number line.
Type below:
________________
Answer:
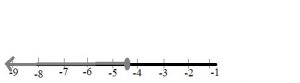
Share and Show – Page No. 499
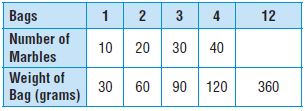
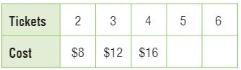
Use the equation to complete the table.
Question 1.
y = x + 3
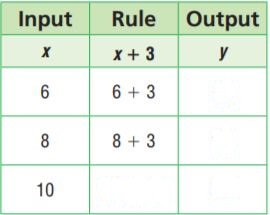
Type below:
________________
Answer:
Substitute the value of x in the above equation.
The equation is x + 3.
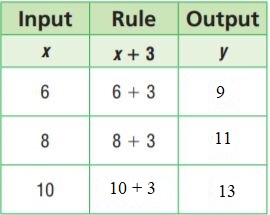
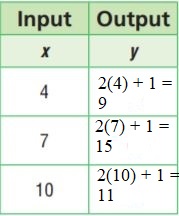
Question 2.
y = 2x + 1
Type below:
________________
Answer:
Substitute the value of x in the above equation.
The equation is y = 2x + 1
On Your Own
Write an equation for the relationship shown in the table. Then find the unknown value in the table.
Question 3.
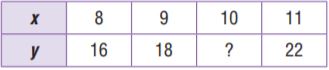
Type below:
________________
Answer:
The equation is y = 2x
The output is multiple of 2 and x
For x = 10
The output is y = 2x
y = 2 × 10 = 20
Question 4.
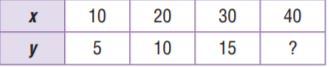
Type below:
________________
Answer:
y = x ÷ 2
The output is the quotient of x and 2.
The output for x = 40 is
y = 40 ÷ 2
y = 20
Question 5.
The table shows the current cost of buying apps for a cell phone. Next month, the price of each app will double. Write an equation you can use to find the total cost y of buying x apps next month.
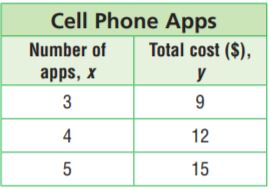
Type below:
________________
Answer: y = 3x
Explanation:
The equation is multiple of 3 and x.
The equation is y = 3x
Question 6.
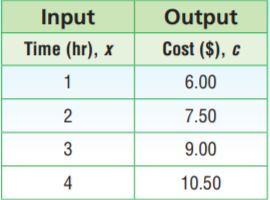
A beach resort charges $1.50 per hour plus $4.50 to rent a bicycle. The equation c = 1.50x + 4.50 gives the total cost c of renting a bicycle for x hours. Use numbers and words to explain how to find the cost c of renting a bicycle for 6 hours.
Type below:
________________
Answer:
A beach resort charges $1.50 per hour plus $4.50 to rent a bicycle.
The equation c = 1.50x + 4.50 gives the total cost c of renting a bicycle for x hours.
For x = 1
c = 1.50(1) + 4.50
c = 1.50 + 4.50
c = $6.00
For x = 2
c = 1.50(2) + 4.50
c = 3.00 + 4.50
c = $7.50
For x = 3
c = 1.50(3) + 4.50
c = 4.50 + 4.50
c = $9.00
For x = 4
c = 1.50(4) + 4.50
c = 6.00 + 4.50
c = $10.50
</aCause and Effect – Page No. 500
The reading skill cause and effect can help you understand how a change in one variable may cause a change in another variable.
In karate, a person’s skill level is often shown by the color of his or her belt. At Sara’s karate school, students must pass a test to move from one belt level to the next. Each test costs $23. Sara hopes to move up 3 belt levels this year. How will this affect her karate expenses?

Question 7.
Write an equation to show the relationship between cause and effect. Then use the equation to solve the problem.
Type below:
________________
Answer: y = 23x
Explanation:
Let x represent the number of belt levels Sara moves up and let y represent the increase in dollars in her karate expenses.
Write the equation:
y = 23x
Sara plans to move up 3 levels, so replace x with 3
y = 23 × 3
y = 69
So, if Sara moves up 3 belt levels this year, her karate expenses will increase by $69.
Write an equation to show the relationship between cause and effect. Then use the equation to solve the problem.
Question 8.
Classes at Tony’s karate school cost $29.50 per month. This year he plans to take 2 more months of classes than he did last year. How will this affect Tony’s karate expenses?
Type below:
________________
Answer:
The equation is y = 29.50x
where x is the number of additional classes
y is the increase in dollars in expenses.
Tony plans to take 2 more months of classes so his expenses will increase by y = 29.5 × 2 = $59

Equations and Tables – Page No. 501
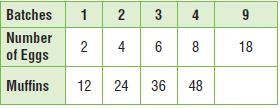
Use the equation to complete the table.
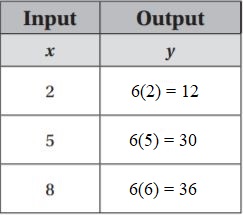
Question 1.
y = 6x
Type below:
________________
Answer:
The equation is y = 6x
Substitute the value of x in the above equation.
Question 2.
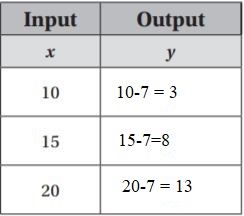
y = x − 7
Type below:
________________
Answer:
The equation is y = x – 7
Substitute the value of x in the equation.
Use the equation to get the output y.
Question 3.
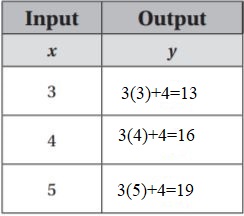
y = 3x + 4
Type below:
________________
Answer:
The equation is y = 3x + 4
Substitute the value of x in the above equation.
Use the equation to get the output y.
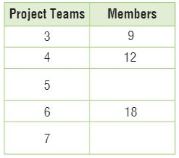
Write an equation for the relationship shown in the table. Then find the unknown value in the table.
Question 4.
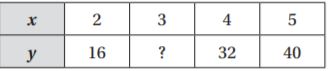
Type below:
________________
Answer: y = 8x
Explanation:
The equation is the multiple of 8.
The equation is y = 8x
Substitute x = 3 in the equation.
y = 8(3) = 24
Thus the unknown value is 24.
Question 5.
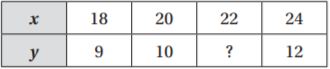
Type below:
________________
Answer: y = x ÷ 2
Explanation:
The equation is divisible by 2.
The equation is y = x ÷ 2
Substitute x = 22 in the equation.
y = x ÷ 2
y = 22 ÷ 2
y = 11
Therefore the unknown value is 11.
Problem Solving

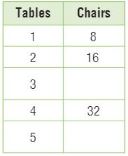
Question 7.
Write an equation for the relationship shown in the table. Then use the equation to find the estimated number of shrimp in a 5-pound bag.
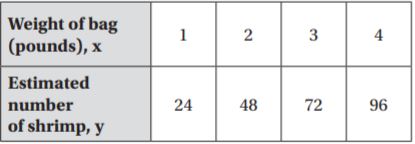
Type below:
________________
Answer: y = 24x
Explanation:
The equation is the multiple of 24.
The equation is y = 24x
Question 8.
Write a word problem that can be represented by a table and equation. Solve your problem and include the table and equation.
Type below:
________________
Answer:
Susie ran a race. She ran 5 miles an hour and the race took her x hours to complete.
y = 5x
Use the equation to get the output y.
Lesson Check – Page No. 502
Question 1.
Write an equation that represents the relationship shown in the table.
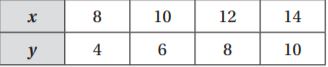
Type below:
________________
Answer: y = x – 4
Explanation:
The relationship between x and y is y = x – 4.
We get the output when we subtract 4 from x.
Question 2.
There is a one-time fee of $27 to join a gym. The monthly cost of using the gym is $18. Write an equation for the relationship that gives the total cost y in dollars of joining the gym and using it for x months.
Type below:
________________
Answer: y = 18x + 27
Explanation:
Given,
There is a one-time fee of $27 to join a gym. The monthly cost of using the gym is $18.
Here y represents the total coast in dollars of joining the gym.
x represents months.
So, the equation would be: y = 18x + 27
Spiral Review
Question 3.
Mindy wants to buy several books that each cost $10. She has a coupon for $6 off her total cost. Write an expression to represent her total cost in dollars for b books.
Type below:
________________
Answer: 10b – 6
Explanation:
Given,
Mindy wants to buy several books that each cost $10.
She has a coupon for $6 off her total cost.
b represents the total cost in dollars for b books.
So, the equation to represent the total cost is 10b – 6.
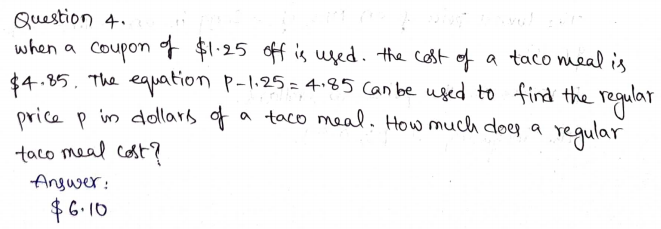

Question 5.
Which of the following are solutions to the inequality n > –7?
n = –7 n = –6.9 n = –7.2 n = –6\(\frac{1}{2}\)
Type below:
________________
Answer: n = -7
Explanation:
Substitute the value of n in the inequality.
n > –7
n = -7
-7 > -7
Thus -7 is the solution.
n = –6.9
-6.9 > -7
-6.9 is not the solution.
n = –7.2
-7.2 > -7
-7.2 is less than – 7
Thus -7.2 is not the solution.
n = –6\(\frac{1}{2}\)
–6\(\frac{1}{2}\) > -7
–6\(\frac{1}{2}\) is not the solution.
Question 6.
Marcus sold brownies at a bake sale. He sold d dollars worth of brownies. He spent $5.50 on materials, so his total profit p in dollars can be found by subtracting $5.50 from his earnings. Write an equation that represents this situation.
Type below:
________________
Answer: p = d – 5.50
Explanation:
Marcus sold brownies at a bake sale. He sold d dollars worth of brownies.
He spent $5.50 on materials, so his total profit p in dollars can be found by subtracting $5.50 from his earnings.
p represents the total profit in dollars.
d is the dollars worth of brownies.
The equation is p = d – 5.50
Share and Show – Page No. 505
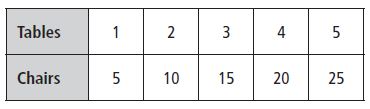
Question 1.
A soccer coach is ordering shirts for the players. The table shows the total cost based on the number of shirts ordered. How much will it cost the coach to order 18 shirts?
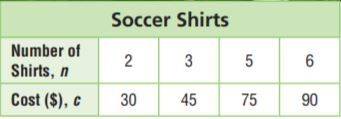
$ _______
Answer: 270
Explanation:
First, find a pattern and write an equation.
The cost is $15 multiplied by the number of shirts.
c = $15 × n
Next, use the equation to find the cost of 18 shirts.
c = $15 × n
c = $15 × 18
c = $270
So, the cost of 18 shirts is $270.
Question 2.
What if the coach spent $375 to purchase a number of shirts? Could you use the same equation to find how many shirts the coach bought? Explain.
Type below:
________________
Answer:
Yes, I could use the same equation.
I could substitute 375 for the variable c and solve for n.
Question 3.
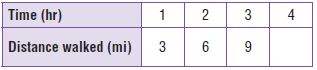
The table shows the number of miles the Carter family drove over time. If the pattern continues, will the Carter family have driven more than 400 miles in 8 hours? Explain.
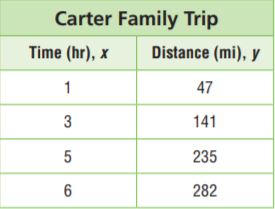
Type below:
________________
Answer: 376 miles
Explanation:
First, find a pattern and write an equation.
The distance is 47 miles multiplied by the number of hours.
y = 47 × x
Next, use the equations to find the distance for 8 hours.
y = 47x
y = 47 × 8
y = 376
So, the family will have driven 376 miles in 8 hours, which is less than 400 miles.

On Your Own – Page No. 506
Question 5.
A group of dancers practiced for 4 hours in March, 8 hours in April, 12 hours in May, and 16 hours in June. If the pattern continues, how many hours will they practice in November?
_______ hours
Answer: 36 hours
Explanation:
Given that, a group of dancers practiced for 4 hours in March, 8 hours in April, 12 hours in May, and 16 hours in June.
The equation would be h = 4m
m = 9
h = 4 × 9 = 36
Thus the group practiced 36 hours in the month of November.
Question 6.
The table shows the number of hours Jacob worked and the amount he earned each day.
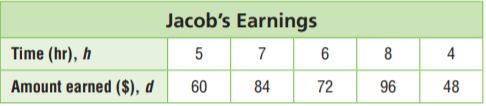
At the end of the week, he used his earnings to buy a new pair of skis. He had $218 left over. How much did the skis cost?
$ _______
Answer: 142
Explanation:
First, add the total amount he earned.
60 + 84 + 72 + 96 + 48 = 360
Jacob earned $360 for the week.
If he has $218 leftover, this means that the cost of the skis is 360 – 218 = 14
Therefore the cost of the skis is $142.
Question 7.
Pose a Problem Look back at Problem 6. Use the data in the table to write a new problem in which you could use the strategy to find a pattern. Then solve the problem.
Type below:
________________
Answer:
How much money would Jacob earn if he worked for 10 hours?
From the table, we can see that the pattern is that Jacob earns $12 per hour.
The equation is s = 12h
Where s is the total pay and h is the number of hours worked.
s = 12h
s = 12 × 10
s = 120
Thus Jacob earned $120 for 10 hours.
Question 8.
Draw Conclusions Marlon rode his bicycle 9 miles the first week, 18 miles the second week, and 27 miles the third week. If the pattern continues, will Marlon ride exactly 100 miles in a week at some point? Explain how you determined your answer.
Type below:
________________
Answer: No, Marlon will not ride exactly 100 miles in a week at some point.
Each number in the pattern is a multiple of 9 and 100 is not a multiple of 9.
Question 9.
A diving instructor ordered snorkels. The table shows the cost based on the number of snorkels ordered.
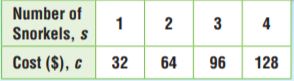
If the diving instructor spent $1,024, how many snorkels did he order? Use numbers and words to explain your answer.
_______ snorkels
Answer: 32
Explanation:
Use the table to find the equation.
c represents the cost based on the number of snorkels.
s represents the number of snorkels
The equation would be:
c = 32s
The diving instructor spent $1,024
c = 1024
1024 = 32s
s = 1024/32
s = 32
Thus the diving instructor gets 32 snorkels for $1024.
Problem Solving Analyze Relationships – Page No. 507
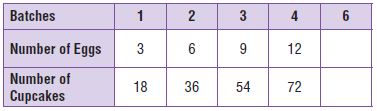
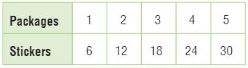
The table shows the number of cups of yogurt needed to make different amounts of a fruit smoothie. Use the table for 1–3.

Question 1.
Write an equation to represent the relationship.
Type below:
________________
Answer: c = 3b
Explanation:
c represents number of cups of yogurt
b represents the batches
From the table, we can observe that b is multiplied with 3 to get cups of yogurt.
So, the equation to find the number of cups of yogurt is c = 3b
Question 2.
How much yogurt is needed for 9 batches of smoothie?
_______ cups
Answer: 27
Explanation:
Given that there are 9 batches of smoothie.
By using the above equation we can find the number of cups.
c = 3b
c = 3 × 9 = 27 cups
Thus 27 cups of yogurt is need to make 9 batches of smoothie.
Question 3.
Jerry used 33 cups of yogurt to make smoothies. How many batches did he make?
_______ batches
Answer: 11 batches
Explanation:
Jerry used 33 cups of yogurt to make smoothies.
Use the equation to find the batches.
c = 3b
33 = 3b
b = 33/3
b = 11
Therefore jerry made 11 batches of smoothie.
The table shows the relationship between Winn’s age and his sister’s age. Use the table for 4–5.

Question 4.
Write an equation to represent the relationship.
Type below:
________________
Answer: s = w + 4
Explanation:
By using the table we can find the relationship between wine’s age and wine’s sister’s age.
Winn’s sister’s age will be the sum of Winn’s age and 4.
So, the equation is s = w + 4
Question 5.
When Winn is 14 years old, how old will his sister be?
_______ years old
Answer: 18
Explanation:
Use the equation s = w + 4
W = 14 years
s = 14 + 4
s = 18 years
Thus winn’s sister’s age is 18 years.
Question 6.
Write a problem for the table. Use a pattern and an equation to solve your problem.
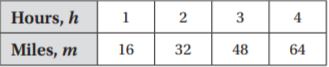
Type below:
________________
Answer: m = 16h
Explanation:
Jerry runs 16 miles per hour. How many miles he can run in 5 hours?
The equation is m = 16h
m = 16 × 5 = 80 miles
Therefore jerry runs 80 miles in 5 hours.
Lesson Check – Page No. 508
Question 1.
The table shows the total cost c in dollars of n gift baskets. What will be the cost of 9 gift baskets?

Answer: $108
Explanation:
By seeing the above we can say that the equation is
c = 12n
n = 9
Use the equation to find the cost of 9 gift baskets.
c = 12 × 9
c = $108
Thus the cost of 9 gift baskets is $108.
Question 2.
The table shows the number of minutes m that Tara has practiced after d days. If Tara has practiced for 70 minutes, how many days has she practiced?
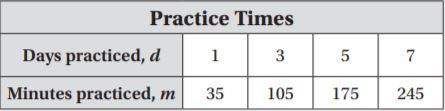
_______ days
Answer: 2 days
Explanation:
The table shows the number of minutes m that Tara has practiced after d days.
The equation would be
m = 35d
If Tara has practiced for 70 minutes
m = 70
Use the equation to find the number of days she practiced.
70 = 35d
d = 70/35
d = 2 days
Thus Tara has practiced 2 days.
Spiral Review
Question 3.
Soccer shirts cost $15 each, and soccer shorts cost $18 each. The expression 15n + 18n represents the total cost in dollars of n uniforms. Simplify the expression by combining like terms.
Type below:
________________
Answer: 33n
Explanation:
Soccer shirts cost $15 each, and soccer shorts cost $18 each.
The expression 15n + 18n represents the total cost in dollars of n uniforms.
Now combine the like terms.
15n + 18n = 33n
Question 4.
What is an equation that represents the relationship in the table?
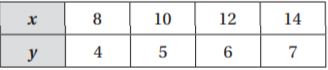
Type below:
________________
Answer: y = x ÷ 2
Explanation:
By seeing the above table we can find the relationship between x and y.
y is the quotient of x and 2.
We get the value of y when you divide x by 2.
The equation is y = x ÷ 2

Question 6.
Marisol plans to make 9 mini-sandwiches for every 2 people attending her party. Write a ratio that is equivalent to Marisol’s ratio.
Type below:
________________
Answer: 9:2
Explanation:
Given that, Marisol plans to make 9 mini-sandwiches for every 2 people attending her party.
The ratio will be 9:2
Now we need to write the equivalent ratio for the 9 sandwiches for every 2 people i.e, 9:2
We know that the equivalent ratio can be written as
9/2 × 3/3 = 27/6
9/2 × 5/5 = 45/6
Thus the equivalent fractions are 27/6 and 45/6.
Mid-Chapter Checkpoint – Vocabulary – Page No. 509
Choose the best term from the box to complete the sentence.

Question 1.
A(n) _____ has a value that determines the value of another quantity.
Type below:
________________
Answer: Independent variable
An Independent variable has a value that determines the value of another quantity.
Question 2.
A variable whose value is determined by the value of another quantity is called a(n) _____.
Type below:
________________
Answer: Dependent variable
A variable whose value is determined by the value of another quantity is called a Dependent variable.
Concepts and Skills
Identify the independent and dependent variables.

Write an equation for the relationship shown in the table. Then find the unknown value in the table.
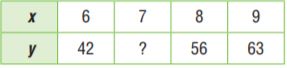
Question 5.
Type below:
________________
Answer: 49
Explanation:
The equation is y = 7x
x = 7
y = 7 × 7 = 49
Thus the unknown value y is 49.
Question 6.
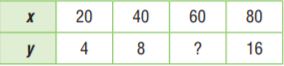
Type below:
________________
Answer: 12
Explanation:
The equation for the above table is
y = x ÷ 5
Use the equation to find the value of y where x = 60
y = 60 ÷ 5
y = 12
Thus the unknown value is 12.
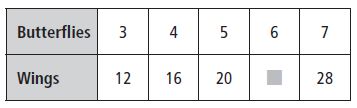
Write an equation that describes the pattern shown in the table.
Question 7.
The table shows how the number of pepperoni slices used depends on the number of pizzas made.
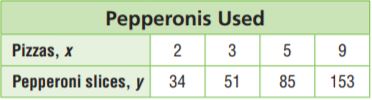
Type below:
_______________
Answer: y = 17x
Explanation:
The table shows how the number of pepperoni slices used depends on the number of pizzas made.
y is 17 times of x.
The equation for the above table is y = 17x
Question 8.
Brayden is training for a marathon. The table shows how the number of miles he runs depends on which week of training he is in.
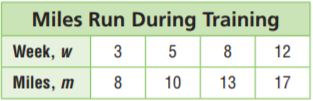
Type below:
________________
Answer: m = w + 5
Explanation:
Brayden is training for a marathon. The table shows how the number of miles he runs depends on which week of training he is in.
m is equal to the sum of w and 5.
Thus the equation is m = w + 5.
Page No. 510
Question 9.
The band has a total of 152 members. Some of the members are in the marching band, and the rest are in the concert band. Write an equation that models how many marching band members m there are if there are c concert band members.
Type below:
________________
Answer: m = 152 – c
Explanation:
Given,
The band has a total of 152 members. Some of the members are in the marching band, and the rest are in the concert band.
m is equal to the difference of 152 and c.
The equation is m = 152 – c

Question 11.
Amy volunteers at an animal shelter. She worked 10 hours in March, 12 hours in April, 14 hours in May, and 16 hours in June. If the pattern continues, how many hours will she work in December?
_______ hours
Answer: 28 hours
Explanation:
Amy volunteers at an animal shelter.
She worked 10 hours in March, 12 hours in April, 14 hours in May, and 16 hours in June.
As she started working from the march. December will be the 10th month.
Keep on adding 2 hours for each month you get 28 hours for December.
Thus she worked 28 hours in December.
Question 12.
Aaron wants to buy a new snowboard. The table shows the amount that he has saved. If the pattern in the table continues, how much will he have saved after 1 year?
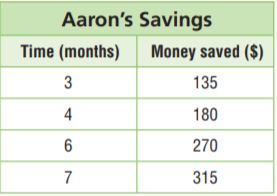
$ _______
Answer: $540
Explanation:
Aaron wants to buy a new snowboard. The table shows the amount that he has saved.
The equation will be s = 45m
s is the money saved
m is the number of months
1 year = 12 months
s = 45 × 12
s = 540
Thus he saved $540 after 1 year.
Share and Show – Page No. 513
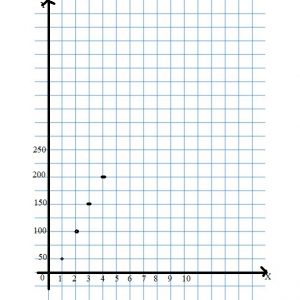
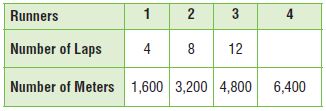
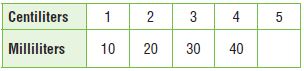
Graph the relationship represented by the table.
Question 1.
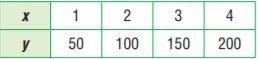
Type below:
________________
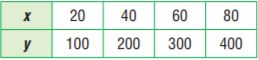
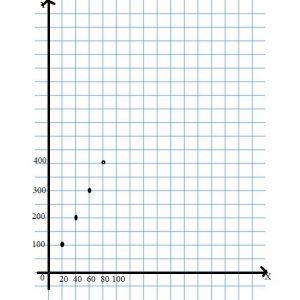
Answer: y = 50x
Question 2.
Type below:
________________
Answer: y = 5x
Graph the relationship represented by the table to find the unknown value of y.
Question 3.
Type below:
________________
Answer: 3
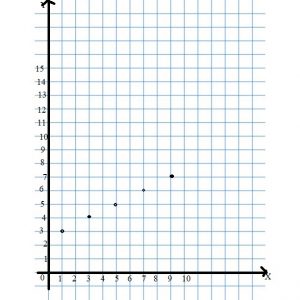
Question 4.
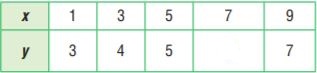
Type below:
________________
Answer: 6
On Your Own
Practice: Copy and Solve Graph the relationship represented by the table to find the unknown value of y.
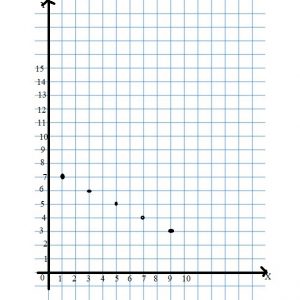
Question 5.
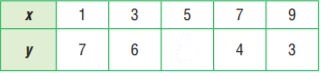
Type below:
________________
Answer: 5
Question 6.
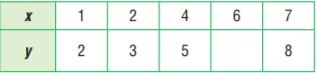
Type below:
________________
Answer: 7
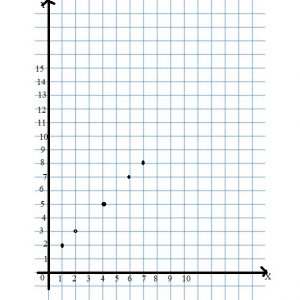
Problem Solving + Applications – Page No. 514
The table at the right shows the typical price of a popular brand of corn cereal over time. Use the table for 7–8.
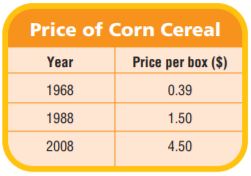
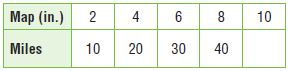
Question 7.
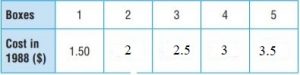
Use Graphs Complete the table below to show the cost of buying 1 to 5 boxes of corn cereal in 1988. Then graph the relationship on the coordinate plane at right.

Type below:
________________
Answer:
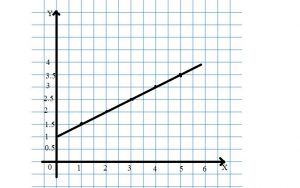
Question 8.
Suppose you graphed the cost of buying 1 to 5 boxes of corn cereal using the 1968 price and the 2008 price. Explain how those graphs would compare to the graph you made using the 1988 price.
Type below:
________________
Answer:
The points on both graphs would lie on a line, but the line for the 1968 costs would rise less steeply than the line for 1988 costs and the line for the 2008 costs would rise more steeply than the line for 1988 costs.

Question 10.
Graph the relationship represented by the table to find the unknown value of y.
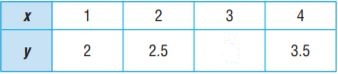
Type below:
________________
Answer: 3
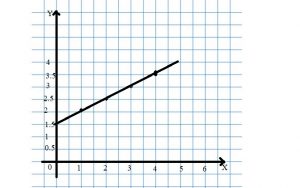
Graph Relationships – Page No. 515
Graph the relationship represented by the table.
Question 1.

Type below:
________________
Answer: y = 25x
Question 2.

Type below:
________________
Answer:
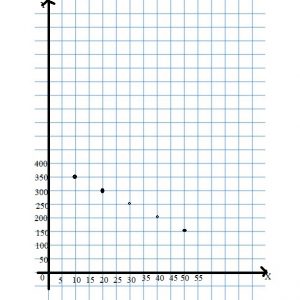
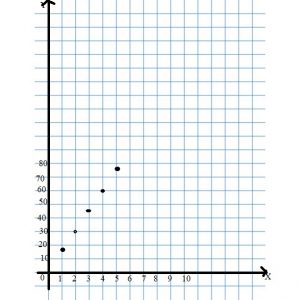
Graph the relationship represented by the table to find the unknown value of y.
Question 3.

Type below:
________________
Answer: 6
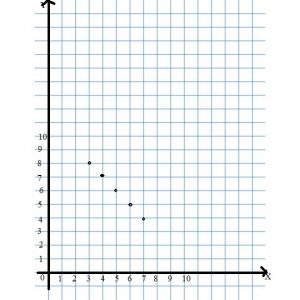
Question 4.

Type below:
________________
Answer: 2
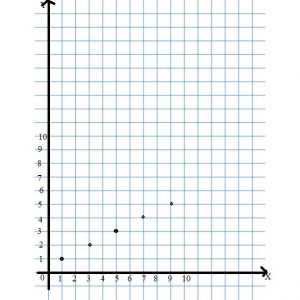
Problem Solving
Question 5.
Graph the relationship represented by the table.

Type below:
________________
Answer: y = 15x
Question 6.
Use the graph to find the cost of purchasing 5 DVDs.
$ ______
Answer:
The above graph shows that the cost of 5 DVDs is $75.
Question 7.
Both tables and graphs can be used to represent relationships between two variables. Explain how tables and graphs are similar and how they are different.
Type below:
________________
Answer:
Tables and graphs can be useful tools for helping people make decisions. However, they only provide part of a story. Inferences often have to be made from the data shown. As well as being able to identify clearly what the graph or table is telling us, it is important to identify what parts of the story are missing.
Lesson Check – Page No. 516
Question 1.
Mei wants to graph the relationship represented by the table. Write an ordered pair that is a point on the graph of the relationship.

Type below:
________________
Answer: y = 8x
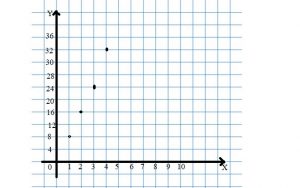
Question 2.
An online bookstore charges $2 to ship any book. Cole graphs the relationship that gives the total cost y in dollars to buy and ship a book that costs x dollars. Name an ordered pair that is a point on the graph of the relationship.
Type below:
________________
Answer:
An online bookstore charges $2 to ship any book.
Cole graphs the relationship that gives the total cost y in dollars to buy and ship a book that costs x dollars.
y = x + 2
x = 4
y = 4 + 2
y = 6
The ordered pair is (4,6)
Spiral Review
Question 3.
Write an expression that is equivalent to 6(g + 4).
Type below:
________________
Answer:
6(g + 4)
6 × g + 6 × 4
6g + 24

Question 5.
Graph n > –2 on a number line.
Type below:
________________
Answer:

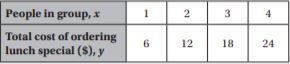
Question 6.
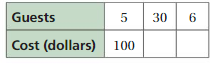
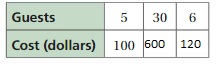
Sam is ordering lunch for the people in his office. The table shows the cost of lunch based on the number of people. How much will lunch cost for 35 people?

$ _____
Answer: 280
Explanation:
Sam is ordering lunch for the people in his office.
The table shows the cost of lunch based on the number of people.
The equation is c = 8n
c = 8 × 35
c = 280
Thus the lunch cost for 35 people is $280.
Share and Show – Page No. 519
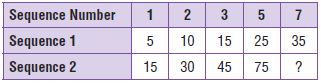
Graph the linear equation.
Question 1.
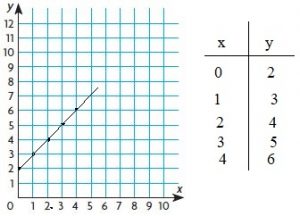
y = x + 2
Type below:
________________
Answer:
Question 2.
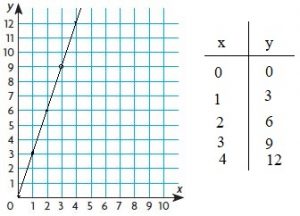
y = 3x
Type below:
________________
Answer:
Write the linear equation for the relationship shown by the graph.
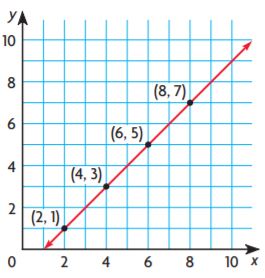
Question 3.
Type below:
________________
Answer: y = x – 1
Question 4.
Type below:
________________
On Your Own
Graph the linear equation.
Question 5.
y = x + 1
Type below:
________________
Answer:
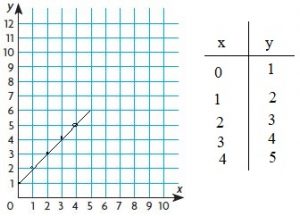
Question 6.
y = 2x − 1
Type below:
________________
Answer:
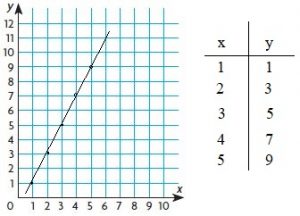
Question 7.
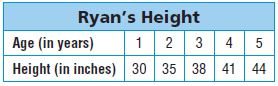
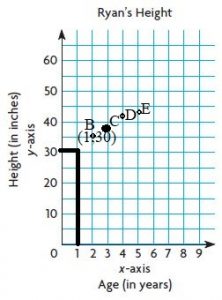
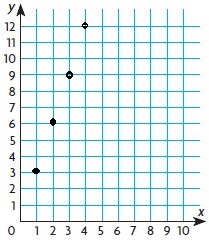
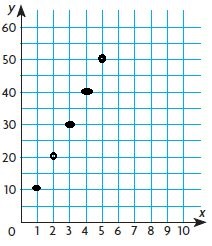
Identify Relationships The graph shows the number of loaves of bread y that Kareem bakes in x hours. Write the linear equation for the relationship shown by the graph.
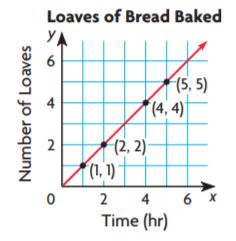
Type below:
________________
Answer:
The ordered pairs are (1,1), (2,2), (4,4), (5,5)
Look for a pattern among the pairs: each y value is the same as the corresponding x-value.
The equation is y = x
y = x
Problem Solving + Applications – Page No. 520
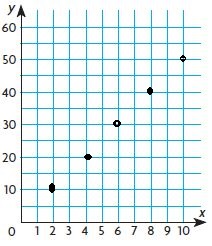
The graph shows the growth of a bamboo plant. Use the graph for 8–9.
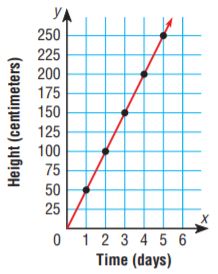
Question 8.
Write a linear equation for the relationship shown by the graph. Use your equation to predict the height of the bamboo plant after 7 days.
Type below:
________________
Answer:
Write the ordered pairs from the graph: (1,50), (2,100), (3,150), (4,200), (5,250).
Look for a pattern among the pairs: each y value is 50 times the corresponding x value.
The equation is y = 50x
For x = 7, the solution is y = 50 × 7 = 350.
So, the height of the bamboo plant after 7 days will be 350 centimeters.

Question 10.
Maria graphed the linear equation y = x + 3. Then she used her ruler to draw a vertical line through the point (4, 0). At what point do the two lines intersect?
Type below:
________________
Answer:
y = x + 3
y = 4 + 0 = 4
y = 4 + 3 = 7
The coordinate is (4, 7)
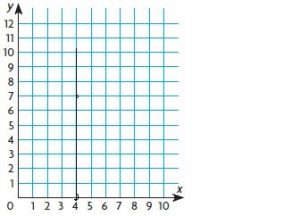
Question 11.
Antonio claims the linear equation for the relationship shown by the graph is y = \(\frac{1}{2}\)x + 2. Use numbers and words to support Antonio’s claim.
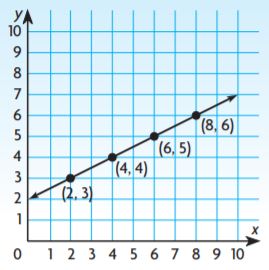
Type below:
________________
Answer:
The ordered pairs (2,3) and (6,5) on the line make the equation.
y = \(\frac{1}{2}\)x + 2
y = 1/2 × 2 + 2
y = 1 + 2 = 3
y = 1/2 × 6 + 2
y = 3 + 2 = 5
Equations and Graphs – Page No. 521
Graph the linear equation.
Question 1.
y = x − 3
Type below:
________________
Answer:
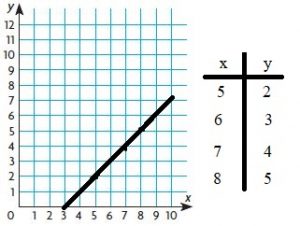
Question 2.
y = x ÷ 3
Type below:
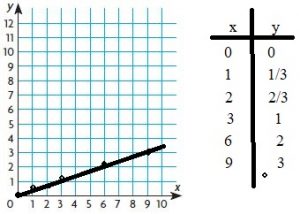
________________
Answer:
Write a linear equation for the relationship shown by the graph.
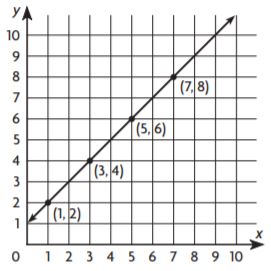
Question 3.
Type below:
________________
Answer:
By seeing the above graph we can say that the equation is
y = x + 1
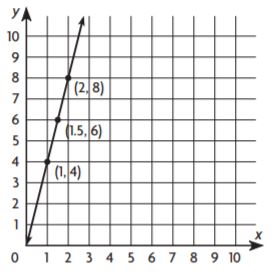
Question 4.
Type below:
________________
Answer:
The ordered pairs are (1,4), (1.5,6), (2,8)
By seeing the above pairs we can say that the equation is y = 4x
Problem Solving
Question 5.
Dee is driving at an average speed of 50 miles per hour. Write a linear equation for the relationship that gives the distance y in miles that Dee drives in x hours.
Type below:
________________
Answer: y = 50x
Explanation:
Dee is driving at an average speed of 50 miles per hour.
y represents the distance in miles
x is the number of hours.
y is equal to the product of 50 and x.
y = 50x
Question 6.
Graph the relationship from Exercise 5.
Type below:
________________
Answer:
Question 7.
Explain how to write a linear equation for a line on a graph.
Type below:
________________
Answer:
To write an equation in slope-intercept form, given a graph of that equation, pick two points on the line and use them to find the slope.
Lesson Check – Page No. 522
Question 1.
A balloon rises at a rate of 10 feet per second. What is the linear equation for the relationship that gives the height y in feet of the balloon after x seconds?
Type below:
________________
Answer: The linear equation for the relationship is y = 10x
Question 2.
Write the linear equation that is shown by the graph.
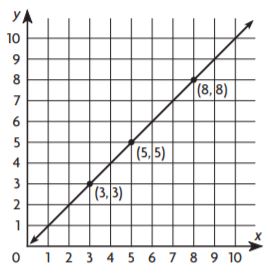
Type below:
________________
Answer:
Write the ordered pairs from the graph: (3,3), (5,5), (8,8)
Look for a pattern among the pairs: each y value is the same as the corresponding x-value.
The equation is y = x
Spiral Review

Question 4.
Which of the following are solutions of j ≥ 0.6?
j = 1 j = –0.6 j = \(\frac{3}{5}\) j = 0.12 j = 0.08
Type below:
________________
Answer: j = \(\frac{3}{5}\)
Explanation:
Substitute the values of j in the inequality.
j = 1
1 ≥ 0.6
1 is greater than 0.6 but not equal.
Thus 1 is not the solution of j ≥ 0.6.
j = –0.6
-0.6 ≥ 0.6
-0.6 is less than 0.6
Thus -0.6 is not the solution of j ≥ 0.6.
j = \(\frac{3}{5}\)
\(\frac{3}{5}\) ≥ 0.6
\(\frac{3}{5}\) = 0.6
0.6 ≥ 0.6
Thus \(\frac{3}{5}\) is the solution.
j = 0.12
0.12 ≥ 0.6
0.12 is less than 0.6.
Thus 0.12 is not the solution of j ≥ 0.6.
j = 0.08
0.08 ≥ 0.6
0.08 is less than 0.6.
Thus 0.08 is not the solution of j ≥ 0.6.
Question 5.
Red grapes cost $2.49 per pound. Write an equation that shows the relationship between the cost c in dollars and the number of pounds of grapes p.
Type below:
________________
Answer: c = 2.49p
Explanation:
Given,
Red grapes cost $2.49 per pound.
c is the cost in dollars.
p is the number of pounds of grapes.
The equation c is equal to the product of the number of pounds of grapes and $2.49
c = 2.49p
Chapter 9 Review/Test – Page No. 523
Question 1.
A box of peanut butter crackers contains 12 individual snacks. The total number of individual snacks s is equal to 12 times the number of boxes of crackers b.
The independent variable is _____.
The dependent variable is _____.
The equation that represents the relationship between the variables is _____.
Answer:
The independent variable is b.
The dependent variable is s.
The equation that represents the relationship between the variables is s = 12b.
Question 2.
A stationery store charges $8 to print logos on paper purchases. The total cost c is the price of the paper p plus $8 for printing the logo.
For numbers 2a–2d, select True or False for each statement.
2a. The total cost c depends on the price of the paper.
2b. c is the dependent variable.
2c. p is the independent variable.
2d. The equation that represents the relationship between the variables is c = 8p.
2a. ____________
2b. ____________
2c. ____________
2d. ____________
Answer:
2a. True
2b. True
2c. True
2d. False
Explanation:
2a. c represents the relationship between the two quantities.
So, the statement “The total cost c depends on the price of the paper” is true.
2b. c is the total cost so the statement “c is the dependent variable” is true.
2c. p represents the price to print logos
So, the statement “p is the independent variable” is true.
2d. The total cost c is the price of the paper p plus $8 for printing the logo.
The equation would be:
c = 8 + p
Thus the statement “The equation that represents the relationship between the variables is c = 8p” is false.
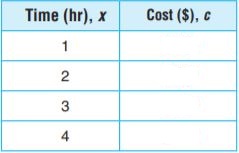
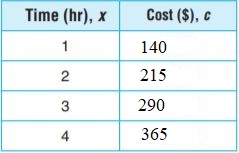
Question 3.
An electrician charges $75 an hour for labor and an initial fee of $65. The total cost c equals 75 times the number of hours x plus 65. Write an equation for the relationship and use the equation to complete the table.
Type below:
________________
Answer: c = 75x + 65
Substitute the value of x in the equation.
Page No. 524
Question 4.
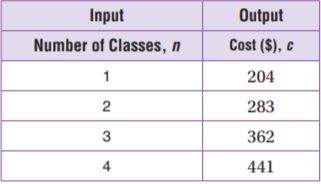
The community center offers classes in arts and crafts. There is a registration fee of $125 and each class costs $79. The total cost c in dollars equals 79 times the number of classes n plus 125.
For numbers 4a–4d, select True or False for each statement.
4a. The registration fee is $120.
4b. n is the independent variable.
4c. c is the dependent variable.
4d. The cost for 7 classes is $678.
4a. ____________
4b. ____________
4c. ____________
4d. ____________
Answer:
4a. False
4b. True
4c. True
4d. True
Explanation:
4a. The registration fee is $120.
The registration fee is $125, not $120.
So, the statement is false.
4b. n is the independent variable.
n represents the number of classes.
The statement is true.
4c. c is the dependent variable.
c depends on the registration fee.
Thus the statement is true.
4d. The cost for 7 classes is $678
79 × 7 + 125 = $678
Thus the statement is true.
Question 5.
Ms. Walsh is buying calculators for her class. The table shows the total cost based on the number of calculators purchased.

If Ms. Walsh spent a total of $525, how many calculators did she buy? Use numbers and words to explain your answer.
Type below:
________________
Answer:
She bought 35 calculators. I found a pattern and wrote the equation c = 15n.
Since I know that Mrs.Walsh spent a total of $525, I can substitute 525 for c and solve for n
525 = 15n
n = 35
Chapter 9 Review/Test – Page No. 525
Question 6.
The table shows the number of cups of lemonade that can be made from cups of lemon juice.

Mary Beth says the number of cups of lemon juice j depends on the number of cups of lemonade l. She says the equation j = 7l represents the relationship between the cups of lemon juice j and the cups of lemonade l. Is Mary Beth correct? Use words and numbers to explain why or why not.
Type below:
________________
Answer:
Mary Beth is not correct. The number of cups of lemonade l depends on the number of cups of lemon juice j.
So l is the dependent variable and j is the independent variable.
The equation showing the relationship is l = 7j
Question 7.
For numbers 7a–7d, choose Yes or No to indicate whether the points, when graphed, would lie on the same line.
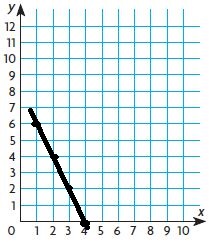
7a. (1, 6), (2, 4), (3, 2), (4, 0)
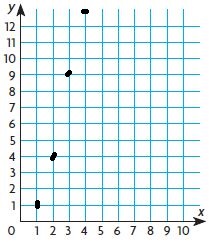
7b. (1, 1), (2, 4), (3, 9), (4, 16)
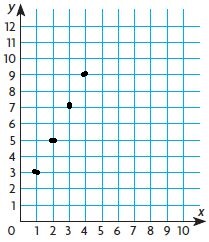
7c. (1, 3), (2, 5), (3, 7), (4, 9)
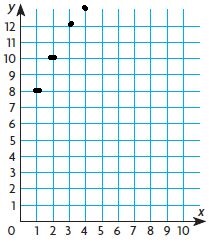
7d. (1, 8), (2, 10), (3, 12), (4, 14)
7a. ____________
7b. ____________
7c. ____________
7d. ____________
Answer:
7a. Yes
7b. No
7c. Yes
7d. Yes
Question 8.
Graph the relationship represented by the table to find the unknown value.

Type below:
________________
Answer: 10
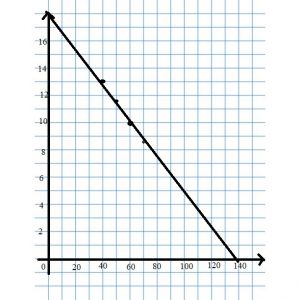
Chapter 9 Review/Test – Page No. 526
Question 9.
Graph the relationship represented by the table.

Type below:
________________
Answer:
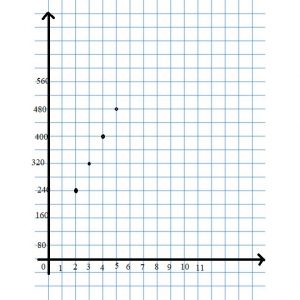
Question 10.
Miranda’s wages are $15 per hour. Write a linear equation that gives the wages w in dollars that Miranda earns in h hours.
Type below:
________________
Answer: w = 15h
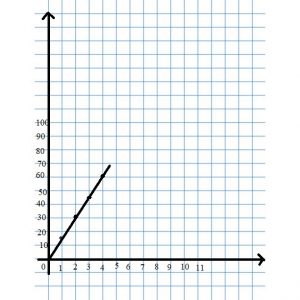
Question 11.
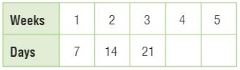
The table shows the number of miles m that Lucinda could walk in h hours.

Graph the relationship between hours h and miles m. Then write the equation that shows the relationship.
Type below:
________________
Answer: m = 4h
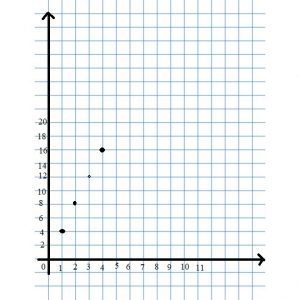
Chapter 9 Review/Test – Page No. 527

Question 13.
Lacy is staying at a hotel that costs $85 per night. The total cost c in dollars of Lacy’s stay is 85 times the number of nights n she stays.
For numbers, 13a–13d, select True or False for each statement.
13a. The number of nights n is dependent on the cost c.
13b. n is the independent variable.
13c. c is the dependent variable.
13d. The equation that represents the total cost is c = 85n.
13a. ____________
13b. ____________
13c. ____________
13d. ____________
Answer:
13a. False
13b. True
13c. True
13d. True
Explanation:
13a. The number of nights n is dependent on the cost c.
n is independent on the cost c.
So, the statement is false.
13b. n is the independent variable.
The statement is true.
13c. c is the dependent variable.
c is dependent because it depends on the cost c.
So, the statement is true.
13d. The equation that represents the total cost is c = 85n.
The equation is true.
Question 14.
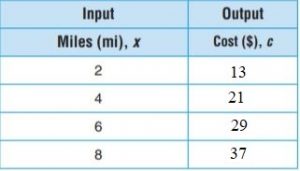
A taxi cab company charges an initial fee of $5 and then $4 per mile for a ride. Use the equation c = 4x + 5 to complete the table.
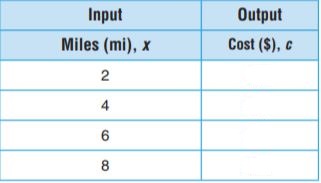
Type below:
________________
Answer:
Substitute the value of x in the equation.
We get,
Chapter 9 Review/Test – Page No. 528
Question 15.
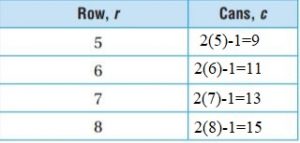
A grocery display of cans is arranged in the form of a pyramid with 1 can in the top row, 3 in the second row from the top, 5 in the third row, and 7 in the fourth row. The total number of cans c equals 2 times the row r minus 1. Use the equation c = 2r − 1 to complete the table.
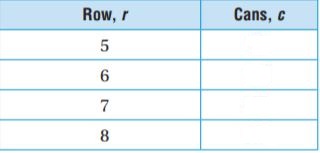
Type below:
________________
Answer:
A grocery display of cans is arranged in the form of a pyramid with 1 can in the top row, 3 in the second row from the top, 5 in the third row, and 7 in the fourth row.
c = 2r − 1
Substitute r in the equation.
Question 16.
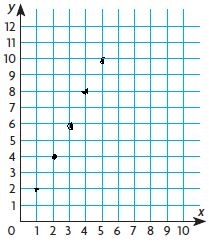
The graph shows the number of words Mason read in a given amount of minutes. If Mason continues to read at the same rate, how many words will he have read in 5 minutes?
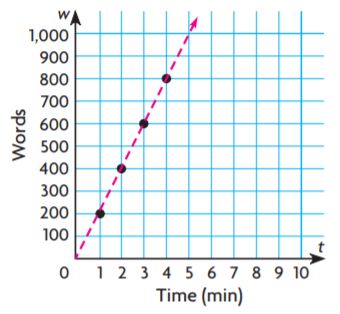
______ words
Answer: 1000 words
By seeing the above graph we can say that Mason can read 1000 words in 5 minutes.
Question 17.
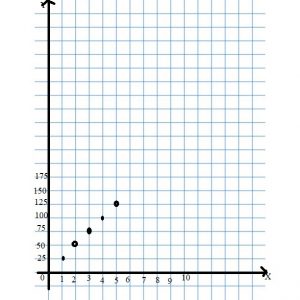
Casey claims the linear equation for the relationship shown by the graph is c = 25j. Use numbers and words to support Casey’s claim.
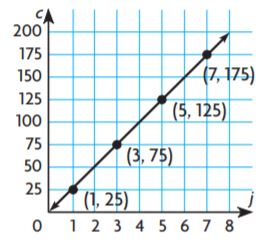
Type below:
________________
Answer: The ordered pairs (1,25), (3,75), (5,125) and (7,175) each make the equation c = 25j
Conclusion:
I wish the details prevailed in the Go Math Grade 6 Answer Key Chapter 9 is helpful for you. Share this pdf link with your friends and help them to overcome the difficulties. If you have any doubts regarding the solutions you can leave a comment in the comment section.
Must Read:

















































































































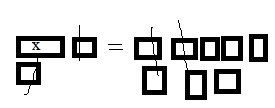
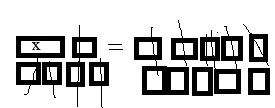

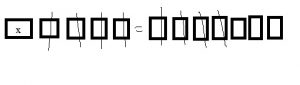
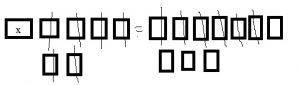












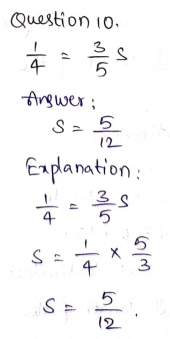































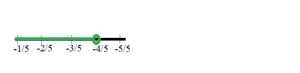


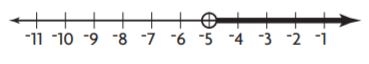
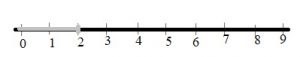






























































































































































































 cabinets of fiction books in the library.
cabinets of fiction books in the library.