In geometry, an isosceles triangle is a triangle that has two sides equal in measure. One of the theorems on the isosceles triangle states that if the provided two points on the isosceles triangle base are equidistant from the extremities of the base, then they are also equidistant from the vertex. Here we are giving detailed proof for the statement in the following sections of this page.
Points on the Isosceles Triangle Base are Equidistant From Vertex when Equidistant From Base Extremities
Here we will prove that if two points on the base of an isosceles triangle are equidistant from the extremities of the base, then they are equidistant from the vertex.
Consider ∆XYZ as an isosceles triangle and XY = XZ, M and N are the points on the base YZ so that YM = NZ
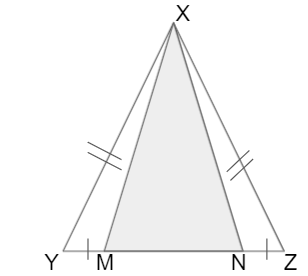
To prove: XM = XN
Proof:
| Statement | Reason |
|---|---|
| In ∆XYM and ∆XNZ, XY = XZ YM = NZ ∠XYM = ∠XZN |
Given Given Angles opposite to equal sides are equal |
| So, ∆XYM ≅ ∆XNZ | SAS Criterion |
| XM = XN | CPCTC |
Hence proved.
More Related Articles:
- Problems on Properties of Isosceles Triangles
- Lines Joining the Extremities of the Base of an Isosceles Triangle
- Angles Opposite to Equal Sides of an Isosceles Triangle are Equal
Example Questions on Isosceles Triangle Theorem
Question 1:
If the extremities of the base of an isosceles triangle are (2a, 0) and (0, a) and the equation of one side is x = 2a, find the area of the triangle?
Solution:
Let the vertices of triangle are A (2a, 0), B (0, a) and C (2a, t)
Given triangle is na isosceles triangle. So, AC = BC
√[(2a – 2a)² + (0 – t)²] = √[(0 – 2a)² + (a – t)²]
t = √(4a² + (a – t)²) = √(4a² + a² + t² – 2at)
t = \(\frac { 5a }{ 2 } \)
The coordinates of C are (2a, \(\frac { 5a }{ 2 } \))
The area of the triangle is = ±½| 2a \(\frac { 5a }{ 2 } \) 1|
|2a 0 1|
|0 a 1|
= \(\frac { 5a² }{ 2 } \) sq units
Question 2:
The extremities of the base of isosceles triangle △ABC are A(3, 2) and B (1, 4). If the equation of the side AC is x = 5 then find the slope of the side BC.
Solution:
Given that,
The base points of isosceles triangle △ABC are A(3, 2) and B(1, 4)
So, AC = BC
The equation of side AC is x = 5
Let us take the vertex C as (5, a)
Equate the equal sides i.e AC = BC
√(3 – 5)² + (2 – a)² = √(1 – 5)² + (4 – a)²
√(4 + 4 + a² – 4a) = √(16 + 16 + a² – 8a)
-4a + 8a = 32 – 8
4a = 24
a = 6
Therefore, the vertex C is (5, 6)
The slope of BC = \(\frac { 6 – 4 }{ 5 – 1 } \)
= \(\frac { 2 }{ 4 } \) = ½
FAQ’s on Base of an Isosceles Triangle
1. Is the base of an isosceles triangle the shortest side?
The angles opposite to the congruent sides measure 80 degrees each. So, the angle opposite to the base is 20 degrees. This means the base may be the smallest side of the triangle.
2. If the two points on the isosceles triangle base are equidistance from its base extremities, then what is the distance between those points to the other vertex.
It is a proven statement if any two points on the base of an isosceles triangle are equidistant from its base extremities, then the distance between points and opposite vertex is also equal.
3. What are the properties of an isosceles triangle?
An isosceles triangle has two equal sides. The angles opposite to the equal sides are equal. The altitude from the apex of the triangle divides it into two congruent triangles.