Are you confused about the concept of Perimeter? You have come to the right page which explains the perimeter concept, Definition of the Perimeter, How to find the Perimeter for Different Shapes. You can also check the solved examples for finding the perimeter of basic shapes explained step by step. Try to apply the knowledge to related problems and get the solutions easily.
Do Check:
Perimeter – Definition
Perimeter is an important attribute of the shape. Perimeter is defined as the boundary around the shape. It is also defined as the total length of the shape. i.e. total length of the sides of the shape. In day-to-day life, we can observe the perimeter for fencing the fields, fencing the backyards of the garden. The perimeter can be found for any shape whether it is regular or irregular.
Perimeter Formulas for Different Shapes
Now we will calculate the perimeter of basic shapes. We know the basic shapes such as rectangle, square, circle, triangle, pentagon, hexagon, etc.
Perimeter of a Square
In a square, all four sides are equal. Perimeter is the distance to the boundary of the shape.
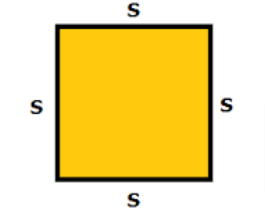
The perimeter of the squre=4s
where s is the length of the sides of the square.
Perimeter of a Rectangle
In a rectangle, opposite sides are equal and all angles are 900.
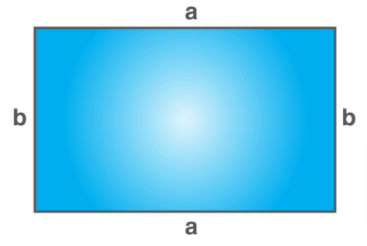
Perimeter of rectangle=2(a+b)
where a is the length and b is the width of the rectangle.
Perimeter of a Triangle
A Triangle has three sides. Irrespective of the type of the triangle be it scalene, isosceles, the equilateral perimeter of the triangle can be obtained by summation of all three sides length.
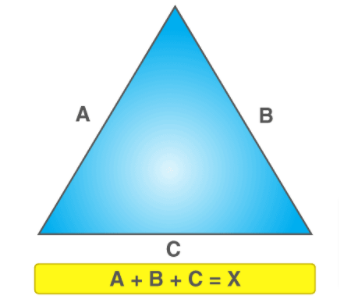
The perimeter of the triangle is a+b+c, where a, b, c are the three different sides of the triangle.
Perimeter of a Circle
In the case of the circle, circumference is the length of the boundary of the circle.
The Perimeter of the Circle=2πr
where r is the radius of the circle.
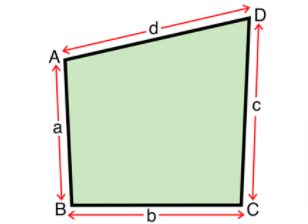
Perimeter of Quadrilateral
The Quadrilateral has four sides, four vertices, four corners. The perimeter of the quadrilateral is a+b+c+d where a,b,c,d are the sides of the quadrilateral.
Perimeter of the Pentagon
The Pentagon has five sides. The perimeter of the pentagon is 5*a where a is the length of the side of the pentagon.
Similarly, for Hexagon, the perimeter is 6*a
For octagon, the perimeter is 8*a
Example 1:
Find the perimeter of a square if the length of the side of the square is 9cm.
Solution:
length of the side=9
The perimeter of the square=4a=4*9=36
Therefore perimeter=36 sq cm.
Example 2:
The length and breadth of a rectangle are 9m and 8m. Find the perimeter of the rectangle?
Solution:
The length of the rectangle=9m
The breadth of the rectangle=8m
The perimeter of the rectangle=2(a+b)
=2(9+8)
=2(17)
=34m
Therefore perimeter of a rectangle=34m.
Example 3:
If the radius of the circle is 12cm. Find the circumference of the circle?
Solution:
The radius of the circle=12
Circumference of the circle=2πr
= 2*22/7*12
=75.42cm
Therefore circumference of the circle=75.42cm
Example 4:
If the length of sides of the triangle is 12m,11m,10m. Find the perimeter of the triangle.
Solution:
length of sides of triangle=12,11,10
Perimeter of triangle=a+b+c
=12+11+10
=33
Therefore Perimeter of triangle=33m.
Example 5:
If the square has an area of 225sq m. Find the perimeter of the square.
Solution:
Area of the square=225=side2=15*15
Perimeter of square=4a=4*15=60 sq m
Therefore, perimetre=60 sqm
FAQs On Basic Concept of Perimeter
1. What is the perimeter?
Perimeter is defined as the boundary around the shape.
2. What is the formula for the perimeter of the square?
The perimeter of the square is 4a where a is the side of the square.
3.What is the formula for the perimeter of the rectangle?
The perimeter of a rectangle is 2(a+b) where a,b are the length and breadth of the rectangle.
4. What is the formula for the circumference of the circle?
The circumference of the circle is 2πr.
5. What is the perimeter of the triangle?
The perimeter of the triangle is a+b+c where a, b, c are sides of the triangle.
