The basic proportionality theorem was invented by the famous mathematician, Thales, so it can also be called as Thales theorem. According to the mathematician, for any two equilateral triangles, the ratio of any two corresponding sides of the given triangles are equal. This basic proportionality theorem was proposed on this concept. To know more about the BPT, check the following sections.
Basic Proportionality Theorem Definition
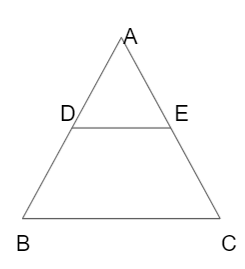
The basic proportionality theorem or Thales theorem states that the line drawn parallel to the one side of the triangle meets the other two sides at two points and divides the other two sides in equal proportion.
For example, in △ABC, DE is a line drawn parallel to the side BC, so that it joints the other two sides, AB and AC. According to basic proportionality theorem (BPT), it can be implied that \(\frac { AD }{ DB } \) = \(\frac { AE }{ EC } \).
More Related Articles:
Proof of Basic Proportionality Theorem
The proof for the basic proportionality theorem (BPT) is provided here.
Given: Let us take a triangle ΔABC. We draw a line DE parallel to the side BC of ΔABC and cut the sides AB and AC at points D and E, respectively.
Construction: Create the imaginary lines in the triangle where you can connect C, D and B and E. Draw DP perpendicular to AE and E perpendicular to AD.
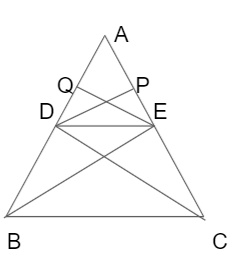
Proof:
Consider the triangles ΔADE, ΔBDE. Both triangles have an equal height EQ, on the same base BC.
So, \(\frac { Area of ΔADE }{ Area of ΔBDE } \) = \(\frac { ½ x AD x EQ }{ ½ x BD x EQ } \)
\(\frac { Area of ΔADE }{ Area of ΔBDE } \) = \(\frac { AD }{ BD } \)
Now, consider the triangles ΔCDE, ΔADE. Both triangles have an equal height DP, on the same base AC.
\(\frac { Area of ΔADE }{ Area of ΔCDE } \) = \(\frac { ½ x AE x DP }{ ½ x CE x DP } \)
\(\frac { Area of ΔADE }{ Area of ΔCDE } \) = \(\frac { AE }{ CE } \)
Both triangles ΔBDE, ΔCDE are between the same set of parallel lines.
So, Area of ΔBDE = Area of ΔCDE
Therefore, \(\frac { Area of ΔADE }{ Area of ΔBDE } \) = \(\frac { Area of ΔADE }{ Area of ΔCDE } \)
\(\frac { AD }{ BD } \) = \(\frac { AE }{ CE } \)
Hence, proved.
Therefore, the line DE drawn parallel to the side BC of the triangle divides the two sides AB, AC in equal proportion.
Examples of Basic Proportionality Theorem (BPT)
Example 1:
At a certain time of the day, a man, 10 feet tall, casts his shadow 14 feet long. Find the length of the shadow cast by a building 50 feet high, at the same time.
Solution:
Let the length of the shadow of the building be x.
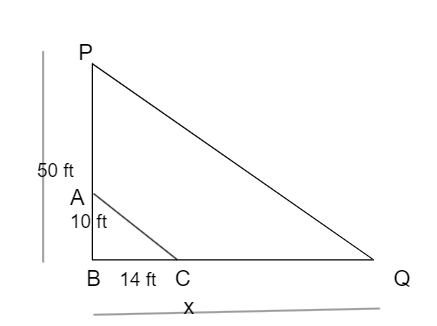
As source of light is sun, AB ∥ PQ and hence ∆BAC ∼ ∆BPQ
Therefore, \(\frac { Height of the man }{ Height of the building } \) = \(\frac { Length of the shadow cast by man }{ Length of shadow cast by the building } \)
\(\frac { 10 }{ 50 } \) = \(\frac { 14 }{ x } \)
x = 70 ft
Example 2:
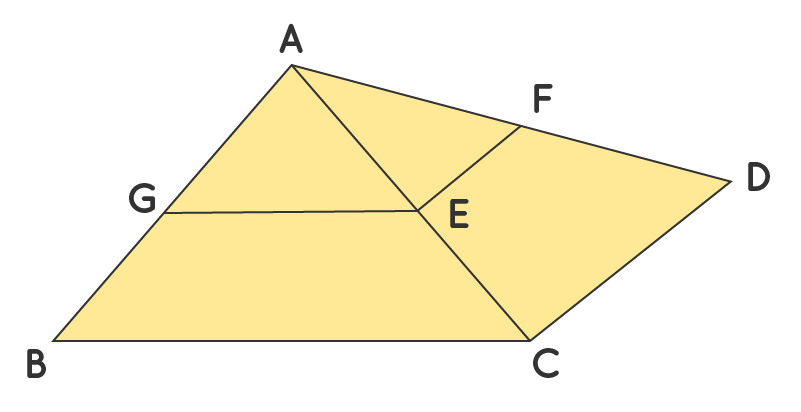
In the below figure GE//BC and EF//CD. Use basic proportionality theorem to prove AG/BG = AF/DF.
Solution:
In △ABC, we know that GE ∥ BC
Hence, \(\frac { AG }{ BG } \) = \(\frac { AE }{ CE } \)
Similarity, in △ACD we know that EF ∥ CD
So, by applying the basic proportionality theorem, \(\frac { AE }{ CE } \) = \(\frac { AF }{ DF } \)
From the above two statements, we can write that \(\frac { AG }{ BG } \) = \(\frac { AF }{ DF } \)
Hence, proved.
Example 3:
If in a ∆XYZ, P and Q are two points on XY and XZ respectively such that XP = 4 cm, PY = 3 cm, XQ = = 6 cm, QZ = 4.5 cm and ∠XPQ = 40° then find ∠XYZ.
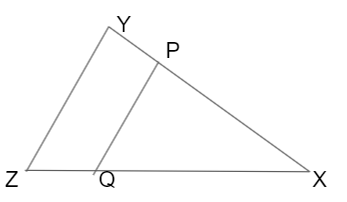
Solution:
Given that,
XP = 4 cm, PY = 3 cm, XQ = = 6 cm, QZ = 4.5 cm and ∠XPQ = 40°
Here, \(\frac { XP }{ PY } \) = \(\frac { 4 }{ 3 } \)
\(\frac { XQ }{ QZ } \) = \(\frac { 6 }{ 4.5 } \) = \(\frac { 4 }{ 3 } \)
Therefore, \(\frac { XP }{ PY } \) = \(\frac { XQ }{ QZ } \)
PQ ∥ YZ
Therefore, ∠XYZ = ∠XPQ = 40°
Frequently Asked Question’s on Thales Theorem
1. What is the basic proportionality theorem formula?
The formula of basic proportionality theorem for a triangle ABC with points D, E on AB, AC sides and DE ∥ BC is \(\frac { AD }{ DB } \) = \(\frac { AE }{ CE } \).
2. What are the applications of the basic proportionality theorem?
The basic proportionality theorem helps to find the lengths in which two sides of a triangle are divided by a line drawn parallel to the third side. And it has applications to find the relationship between two equiangular triangles.
3. What does Thales theorem state?
Thales theorem states that when a line is drawn parallel to one side of a triangle and intersect the other two sides, then the line divides the two sides in the same ratio.
4. What is the corollary of the BPT theorem?
According to the BPT theorem, if a line divides any two sides of a triangle in the same proportion, then the line is parallel to the third side.