Big Ideas Math Algebra 2 Answers Chapter 4 Polynomial Functions

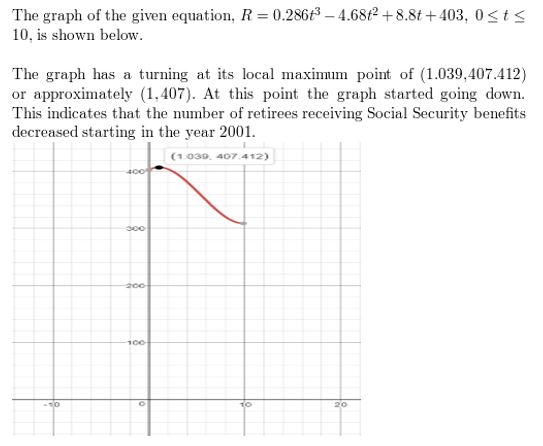
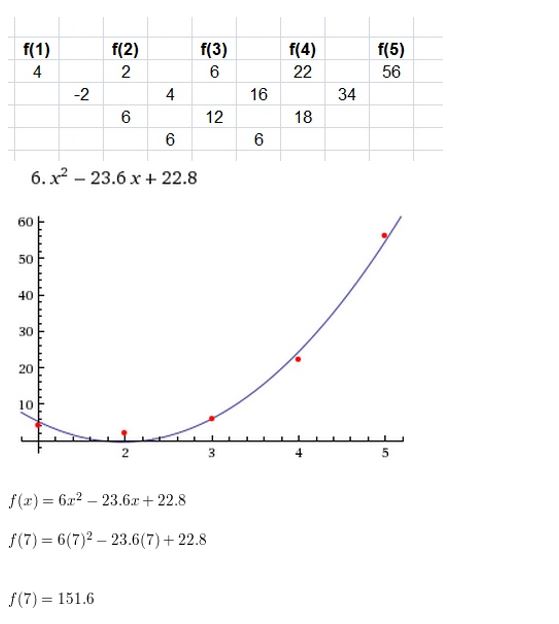
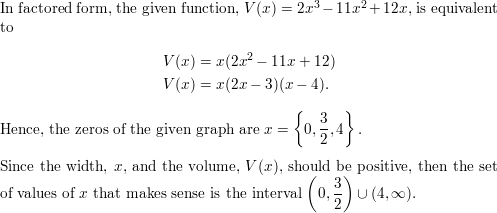View Big Ideas Math Algebra 2 Answers Chapter 4 Polynomial Functions with step by step explanation here. Students can find the easy methods to solve polynomial functions from this page. The solutions are prepared by the subject experts in a quick and simple manner that helps the students to score the highest marks in the exams. Our Chapter 4 Polynomial Functions BIM Algebra 2 Textbook Answers help the students to complete homework assignments in time and with accuracy.

Big Ideas Math Book Algebra 2 Answer Key Chapter 4 Polynomial Functions

It is not only important to score marks in the exams it is also necessary to understand the concept of the topic and know how it is applicable in the real life. Keeping this point in mind we have provided Big Ideas Math Textbook Algebra 2 Answers Chapter 4 Polynomial Functions with examples in detail. Math is a fun learning subject if you love to solve problems. Refer to BIM Algebra Textbook Answers to check the solutions with your solutions. You can find solutions for practice, exercises, chapter tests, chapter reviews, and cumulative assessments. Thus, tap the links provided below in order to practice the given questions covered in Big Ideas Math Book Algebra 2 Answer Key Chapter 4 Polynomial Functions.

• Polynomial Functions Maintaining Mathematical Proficiency – Page 155
• Polynomial Functions Mathematical Practices – Page 156
• Lesson 4.1 Graphing Polynomial Functions – Page (158-164)
• Graphing Polynomial Functions 4.1 Exercises – Page(162-164)
• Lesson 4.2 Adding, Subtracting, and Multiplying Polynomials – Page(166-172)
• Adding, Subtracting, and Multiplying Polynomials 4.2 Exercises – Page(170-172)
• Lesson 4.3 Dividing Polynomials – Page(174-178)
• Dividing Polynomials 4.3 Exercises – Page(177-178)
• Lesson 4.4 Factoring Polynomials – Page(180-186)
• Factoring Polynomials 4.4 Exercises – Page(184-186)
• Polynomial Functions Study Skills – Page 187
• Polynomial Functions 4.1 – 4.4 Quiz – Page 188
• Lesson 4.5 Solving Polynomial Equations – Page(190-196)
• Solving Polynomial Equations 4.5 Exercises – Page(194-196)
• Lesson 4.6 The Fundamental Theorem of Algebra – Page(198-204)
• The Fundamental Theorem of Algebra 4.6 Exercises – Page(202-204)
• Lesson 4.7 Transformations of Polynomial Functions – Page(206-210)
• Transformations of Polynomial Functions 4.7 Exercises – Page(209-210)
• Lesson 4.8 Analyzing Graphs of Polynomial Functions – Page(212-218)
• Analyzing Graphs of Polynomial Functions 4.8 Exercises – Page(216-218)
• Lesson 4.9 Modeling with Polynomial Functions – Page(220-224)
• Modeling with polynomial Functions 4.9 Exercises – Page(223-224)
• Polynomial Functions Performance Task – Page 225
• Polynomial Functions Chapter Review – Page(226-230)
• Polynomial Functions Chapter Test – Page 231
• Polynomial Functions Cumulative Assessment – Page(232-233)

Polynomial Functions Maintaining Mathematical Proficiency

Simplify the expression.

Question 1.
6x − 4x
Answer:
Given,
6x − 4x
Terms can be combined only if they have the exact same variable portion and combine like terms.
6x – 4x = 2x
So, the simplified expression is 2x.

Question 2.
12m − m − 7m + 3
Answer:
Given,
12m − m − 7m + 3
Terms can be combined only if they have the exact same variable portion and combine like terms.
(12m-m-7m)+3
=m(12 – 1 – 7) + 3
= 4m + 3
So, 12m − m − 7m + 3 = 4m + 3

Question 3.
3(y + 2) − 4y
Answer:
3(y + 2) − 4y
Terms can be combined only if they have the exact same variable portion and combine like terms.
3(y+2)-4y
= 3 × y + 3 × 2 – 4y
= 3y + 6 – 4y
= -y + 6
So, 3(y + 2) − 4y = -y + 6

Question 4.
9x − 4(2x − 1)
Answer:
Given,
9x − 4(2x − 1)
= 9x – 4 × 2x – 4 × -1 (since – × – = +)
Terms can be combined only if they have the exact same variable portion and combine like terms.
= 9x – 8x + 4
= x + 4
So, 9x − 4(2x − 1) = x + 4

Question 5.
−(z + 2) − 2(1 − z)
Answer:
Given,
−(z + 2) − 2(1 − z)
= -z – 2 – 2 + 2z (since – × – = +)
Terms can be combined only if they have the exact same variable portion and combine like terms.
=-z + 2z – 2 – 2
= z -4
So, −(z + 2) − 2(1 − z) = z – 4.

Question 6.
−x² + 5x + x²
Answer:
Given,
−x² + 5x + x²
Terms can be combined only if they have the exact same variable portion and combine like terms.
5x−x² + x²
= 5x
So, −x² + 5x + x² = 5x

Find the volume of the solid.

Question 7.
cube with side length 4 inches
Answer:
Given,

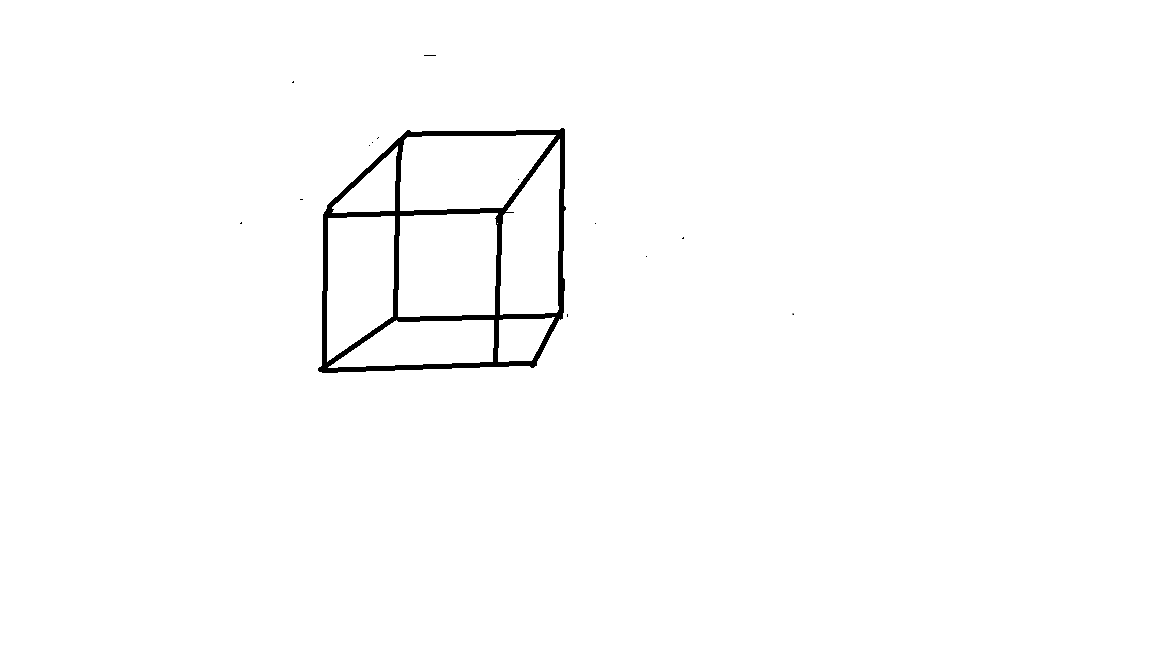
s = 4
We know that,
The volume of cube=s³
V =4 × 4 × 4=64 cu. inches
So, the volume of the solid is 64 cu. inches

Question 9.
rectangular prism with length 4 feet, width 2 feet, and height 6 feet
Answer:
Given,
length= 4 feet
width=2 feet
height= 6 feet
We know that,
volume of rectangular prism= length x width x height
Substitute the values in the formula
V = 4 × 2 × 6= 48 cubic feet
Thus the volume of the rectangular prism is 48 cu. feet.

Question 10.
right cylinder with radius 3 centimeters and height 5 centimeters
Answer:
Given that
Radius = 3 centimeters
Height = 5 centimeter
We know that,
Volume of a cylinder = area of base × height
V = π × r²× h
π = 3.14
V = 3.14 × 3 × 3 × 5=141.3 cubic centimeter

Question 11.
ABSTRACT REASONING Does doubling the volume of a cube have the same effect on the side length? Explain your reasoning
Answer:
If the side of the cube is doubled. The volume is 8 times larger.
Example: let’s use a cube that has a side length of 2 as an example.
The volume of that cube would be length x and width x height
V = 2 × 2 ×  2 = 8
If we double the edges to 4.
V = 4 × 4 × 4 = 64.
64/8=8
So, the volume increases by 8 times.

Polynomial Functions Mathematical Practices

Monitoring Progress

Use a graphing calculator to determine whether the function is continuous. Explain your reasoning.

Question 1.
f(x) = \(\frac{x^{2}-x}{x}\)
Answer:
Given,
f(x) = \(\frac{x^{2}-x}{x}\)
f(x) = x(x-1)/x
f(x) = x – 1
x = 0
f(0) = 0 – 1 = -1
f(1) = 1 – 1 = 0
f(2) = 2 – 1 = 1
f(3) = 3 – 1 = 2

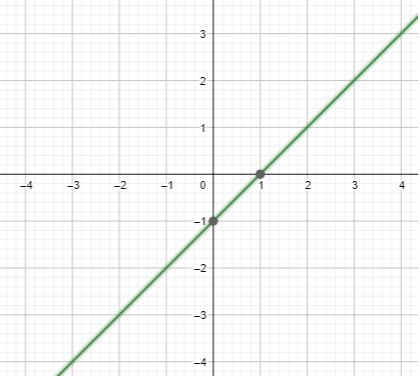
Question 2.
f(x) = x³ − 3
Answer:
Given,
f(x) = x³ − 3
f(0) = 0³ – 3 = -3
f(1) = 1³ – 3 = 1 – 3 = -2
f(2) = 2³ – 3 = 8 – 3 = 5
f(-1) = (-1)³ – 3 = -1 – 3 = -4
f(-2) = (-2)³ – 3 = -8 – 3 = -11

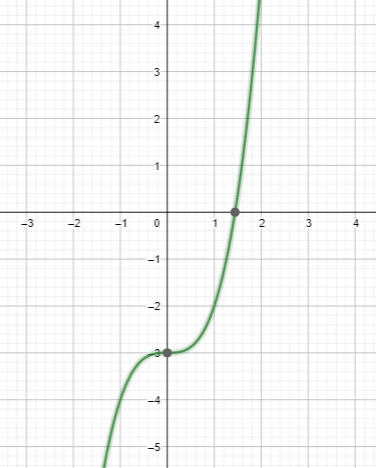
Question 3.
f(x) = \(\sqrt{x^{2}+1}\)
Answer:
Given,
f(x) = \(\sqrt{x^{2}+1}\)
f(0) = \(\sqrt{0^{2}+1}\) = 1
f(1) = \(\sqrt{1^{2}+1}\) = \(\sqrt{2}\)

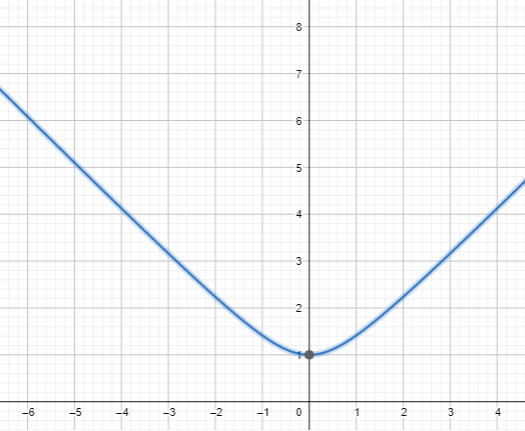
Question 4.
f(x) = | x + 2 |
Answer:
Given,
f(x) = | x + 2 |
f(0) = |0 + 2| = 2
f(1) = |1 + 2| = 3
f(-1) = |-1 + 2| = 1
f(-2) = |-2 + 2| = 0

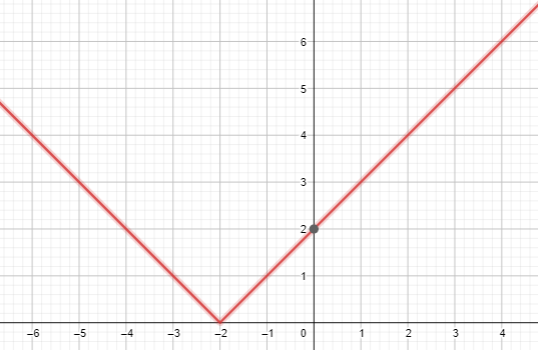
Question 5.
f(x) = \(\frac{1}{x}\)
Answer:
Given,
f(x) = \(\frac{1}{x}\)
f(0) = \(\frac{1}{x}\) = ∞
f(1) = \(\frac{1}{1}\) = 1
f(2) = \(\frac{1}{2}\) = 0.5
f(-1) = \(\frac{1}{-1}\) = -1
f(-2) = \(\frac{1}{-2}\) = -0.5

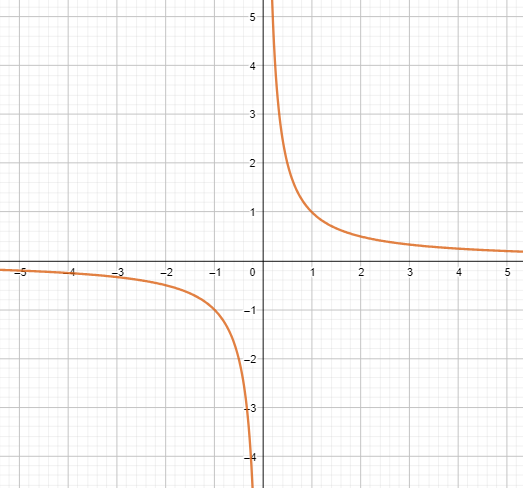
Question 6.
f(x) = \(\frac{1}{\sqrt{x^{2}-1}}\)
Answer:

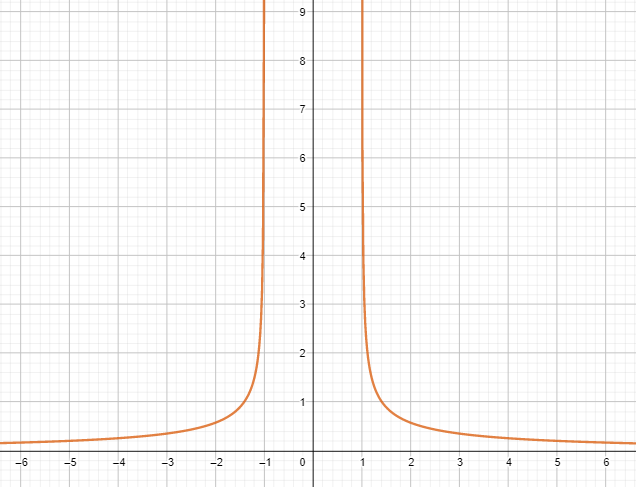
Question 7.
f(x) = x
Answer:
Given function is f(x) = x
f(0) = 0
f(1) = 1
f(2) = 2
f(-1) = -1
f(-2) = -2

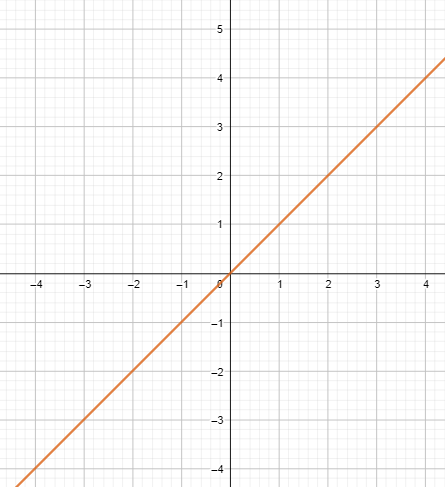
Question 8.
f(x) = 2x − 3
Answer:
Given,
f(x) = 2x − 3
f(0) = 2(0) – 3 = -3
f(1) = 2(1) – 3 = -1
f(-1) = 2(-1) – 3 = -5
f(2) = 2(2) – 3 = 1
f(-2) = 2(-2) – 3 = -7

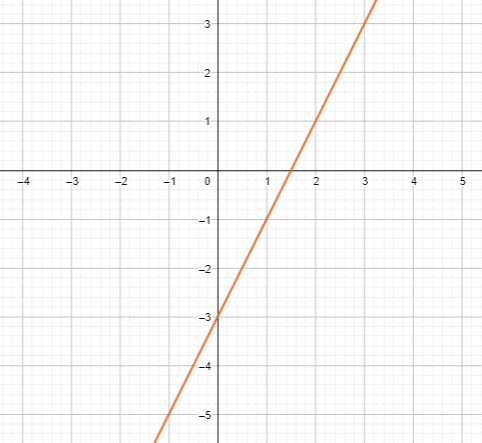
Question 9.
f(x) = \(\frac{x}{x}\)
Answer:
Given,
f(x) = \(\frac{x}{x}\)
f(1) = 1/1 = 1

Lesson 4.1 Graphing Polynomial Functions

Essential Question
What are some common characteristics of the graphs of cubic and quartic polynomial functions?
A polynomial function of the form
f(x) = a_nxⁿ + a_{n – 1}x^{n– 1} +. . .+ a₁x + a₀
where a_n ≠ 0, is cubic when n = 3 and quartic when n = 4.

EXPLORATION 1
Identifying Graphs of Polynomial Functions
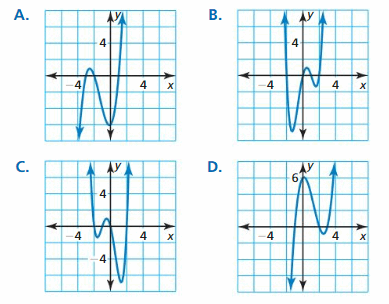
Work with a partner. Match each polynomial function with its graph. Explain your reasoning. Use a graphing calculator to verify your answers.
a. f(x) = x³ − x
b. f(x) = −x³ + x
c. f(x) = −x⁴ + 1
d. f(x) = x⁴
e. f(x) = x³
f. f(x) = x⁴ − x²

EXPLORATION 2
Identifying x-Intercepts of Polynomial Graphs
Work with a partner. Each of the polynomial graphs in Exploration 1 has x-intercept(s) of −1, 0, or 1. Identify the x-intercept(s) of each graph. Explain how you can verify your answers.

Communicate Your Answer

Question 3.
What are some common characteristics of the graphs of cubic and quartic polynomial functions?
Answer:
The polynomial functions with degree 2 are called quadratic functions and more have graphs that do not have sharp corners.
The characteristics of a graph of polynomial functions are.
A cubic function of form f(x) = ax³ + bx² + cx + d.
The polynomial function of degree 3 is a cubic function.
The cube function has 1 or 3 real numbers and 0 or 2 complex numbers.
The graph of the quadratic function is a plane curve which is a U-shaped curve called a parabola

Question 4.

Determine whether each statement is true or false. Justify your answer.
a. When the graph of a cubic polynomial function rises to the left, it falls to the right.
Answer:
The statement “When the graph of the cubic polynomial function rises to the left, it falls to the right” is true.

b. When the graph of a quartic polynomial function falls to the left, it rises to the right.
Answer:
The statement “When the graph of the quartic polynomial function falls to the left, it rises to the right” is false.

4.1 Lesson

Monitoring Progress

Decide whether the function is a polynomial function. If so, write it in standard form and state its degree, type, and leading coefficient.

Question 1.
f(x) = 7 − 1.6x² − 5x
Answer:
Given,
f(x) = 7 − 1.6x² − 5x
The standard form of polynomials has the exponents of the terms arranged in descending order.
The leading coefficient is the numerical factor of the terms with the highest degree. The highest degree in the given function is 2.
Hence the given function f(x) = 7 − 1.6x² − 5x has the  following characteristic
Standard form f (x) = -1.6x² -5x +7
Degree: 2
Type of function: quadratic
Leading coefficient: -1.6

Question 2.
p(x) =x+ 2x^-2 + 9.5
Answer:
Given,
p(x) =x+ 2x^-2 + 9.5
The given function is not a polynomial function because the term 2x^-2 has an exponent that is not a whole number.

Question 3.
q(x) = x³ − 6x + 3x⁴
Answer:
The standard form of polynomials has the exponents of the terms arranged in descending order.
The degree of a polynomial is the highest exponent of a term. The leading coefficient is the numerical factor of the terms with the highest degree. The highest degree of the function is 4.
The given function q(x) = x³ − 6x + 3x⁴  has the  following characteristic
Standard form : q(x) = 3x⁴ + x³ – 6x
Highest Degree: 4
Type of function: quadratic
Leading coefficient: 3

Evaluate the function for the given value of x.

Question 4.
f(x) = −x³ + 3x² + 9; x = 4
Answer:
Given,
f(x) = −x³ + 3x² + 9
substitute for x
f(4) =−x³ + 3x² + 9
⇒-(4)³+ 3(4)² +9
⇒-(64)+ 3(16) +9
⇒-64 + 48 + 9 = -7
So, f(x) = −x³ + 3x² + 9 when x = 4 is -7.

Question 5.
f(x) = 3x⁵ − x⁴ − 6x + 10; x = −2
Answer:
Given,
f(x) = 3x⁵ − x⁴ − 6x + 10
Substitute x = -2 in the given equation
f(-2) = 3(-2)⁵-(-2)⁴-6(-2)+10
Simplify the expression
⇒ 3(-32)-16+12+10
⇒ -96 -16 +12 +10
⇒ -90
So, f(x) = 3x⁵ − x⁴ − 6x + 10 when x = -2 is -90.

Question 6.
Describe the end behavior of the graph of f(x) = 0.25x³ − x² − 1.
Answer:

Graph the polynomial Function

Question 7.
f(x) = x⁴ + x² − 3
Answer:

Question 8.
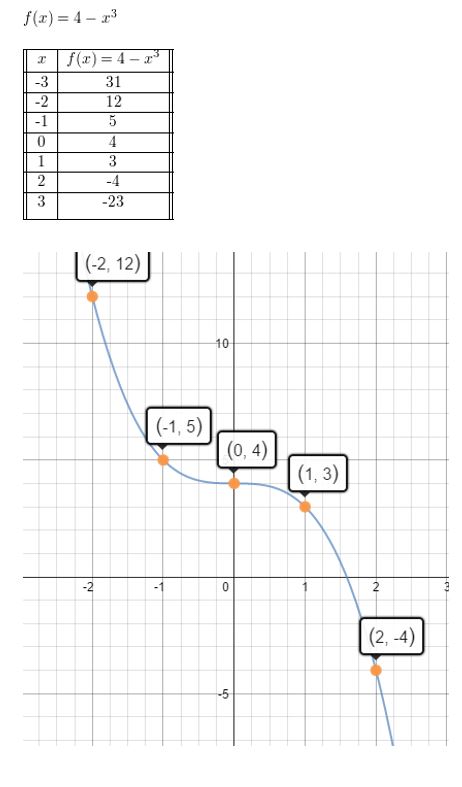
f(x) = 4 − x^3
Answer:

Question 9.
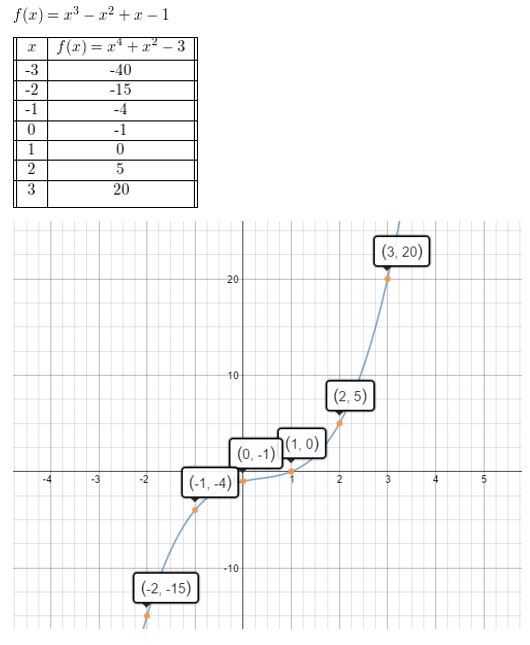
f(x) = x³ − x² + x − 1
Answer:

Question 10.
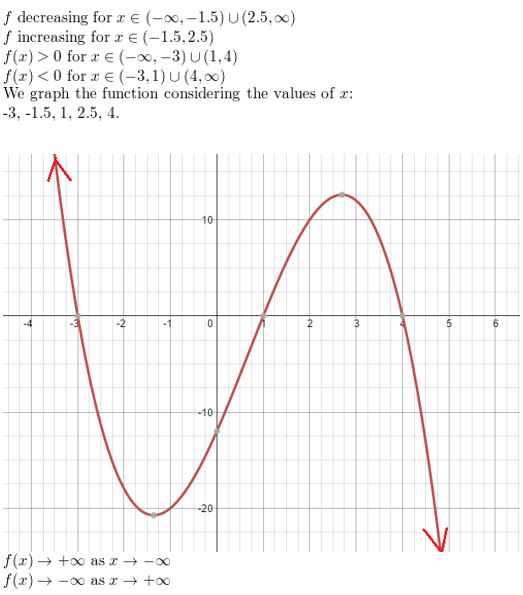
Sketch a graph of the polynomial function f having these characteristics.

• f is decreasing when x < −1.5 and x > 2.5; f is increasing when −1.5 < x < 2.5.
• f(x) > 0 when x < −3 and 1 < x < 4; f(x) < 0 when −3 < x < 1 and x > 4.
  Answer:
  
  

Use the graph to describe the degree and leading coefficient of f.

Question 11.
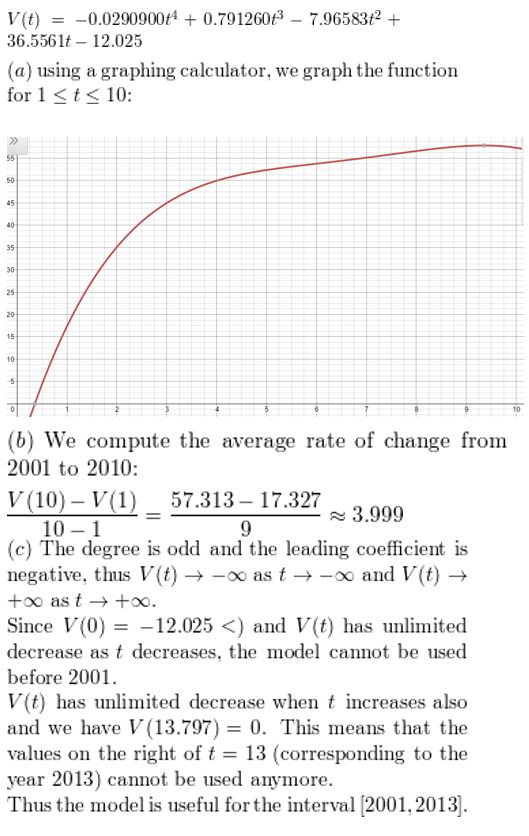
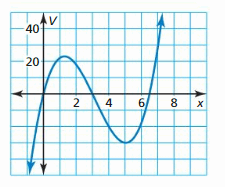
WHAT IF? Repeat Example 6 using the alternative model for electric vehicles of
V(t) = −0.0290900t⁴ + 0.791260t³ − 7.96583t² + 36.5561t − 12.025.

Graphing Polynomial Functions 4.1 Exercises

Vocabulary and Core Concept Check

Question 1.
WRITING Explain what is meant by the end behavior of a polynomial function.
Answer: The end behavior of a polynomial function describes the behavior of the graph of the polynomial function as x value approach ∞ or -∞.

Question 2.
WHICH ONE DOESN’T BELONG? Which function does not belong with the other three? Explain your reasoning.

Answer:

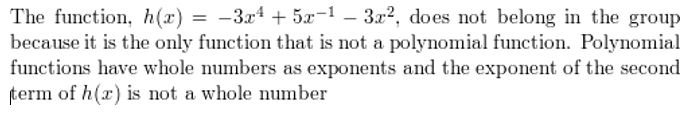
Monitoring Progress and Modeling with Mathematics

In Exercises 3–8, decide whether the function is a polynomial function. If so, write it in standard form and state its degree, type, and leading coefficient.

Question 3.
f(x) = −3x + 5x³ − 6x² + 2
Answer:

Question 4.
p(x) = \(\frac{1}{2}\)x² + 3x − 4x³ + 6x⁴ − 1
Answer:

Question 5.
f(x) = 9x⁴ + 8x³ − 6x^-2 + 2x
Answer:

Question 6.
g(x) = \(\sqrt{3}\) − 12x + 13x²
Answer:

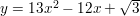
The polynomial is a quadratic function
Degree: 2
Type: quadratic
leading coefficient: 13

Question 7.
h(x) = \(\frac{5}{3}\)x² − \(\sqrt{7}\)x⁴ + 8x³ − \(\frac{1}{2}\) + x
Answer:

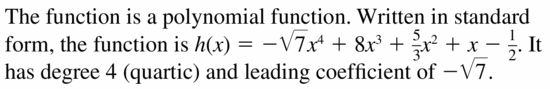
Question 8.
h(x) = 3x⁴ + 2x − \(\frac{5}{x}\) + 9x³ − 7
Answer:
The polynomial is a quadratic function.
Standard form: 3x⁴ + 9x³ + 2x − \(\frac{5}{x}\) − 7
Degree: 4
Type: Quadratic
Coefficient: 4

ERROR ANALYSIS In Exercises 9 and 10, describe and correct the error in analyzing the function.

Question 9.
f(x) = 8x³ − 7x⁴ − 9x − 3x² + 11

Answer:

Question 10.
f(x) = 2x⁴ + 4x – 9\(\sqrt{x}\) + 3x² – 8

Answer:

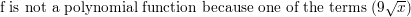
Question 11.
h(x) = −3x⁴ + 2x³ − 12x − 6; x = −2
Answer:

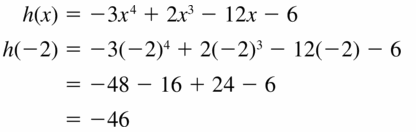
Question 12.
f(x) = 7x⁴ − 10x² + 14x − 26; x = −7
Answer:
Given,
f(x) = 7x⁴ − 10x² + 14x − 26
Substitute x = -7 in the given function
f(-7) = 7(-7)⁴– 10(-7)² + 14(-7) – 26
Simplify the expression
= 7(2401) – 10(49)- 98-26
= 16807- 490- 98- 26
= 16,193
So, f(x) = 7x⁴ − 10x² + 14x − 26 when x = −7 is 16,193

Question 13.
g(x) = x⁶ − 64x⁴ + x² − 7x − 51; x = 8
Answer:

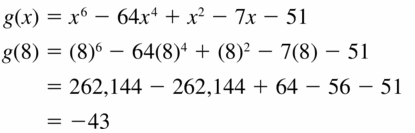
Question 14.
g(x) = −x³ + 3x² + 5x + 1; x = −12
Answer:
Given,
g(x) = −x³ + 3x² + 5x + 1
put x = -12
g(-12) =(-12 )³+ 3(-12) ²+ 5(-12 ) + 1
= 1728 + 3(144) – 60 +1
= 1728 + 432 – 60 +1
= 2101
So, g(x) = −x³ + 3x² + 5x + 1 when x = −12 is 2101.

Question 15.
p(x) = 2x³ + 4x² + 6x + 7; x = \(\frac{1}{2}\)
Answer:

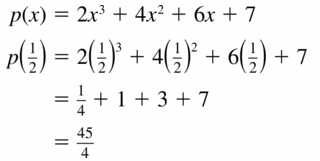
Question 16.
h(x) = 5x³ − 3x² + 2x + 4; x = −12
Answer:
Given polynomial
h(x) = 5x³ − 3x² + 2x + 4
put x = -12
h(-12) = 5(-12)³ – 3(-12)² + 2(-12) + 4
= 5(-1728) – 3 (144) – 24 + 4
Simplify the expression
= -8640 – 432 – 24 + 4
= -9092
So, h(x) = 5x³ − 3x² + 2x + 4 when x = −12 is -9092.

In Exercises 17–20, describe the end behavior of the graph of the function.

Question 17.
h(x) = −5x⁴ + 7x³ − 6x² + 9x + 2
Answer:

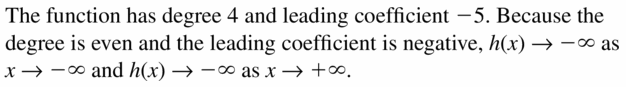
Question 18.
g(x) = 7x⁷ + 12x⁵ − 6x³ − 2x − 18
Answer:
Given polynomial is g(x) = 7x⁷ + 12x⁵ − 6x³ − 2x − 18
The given function has a degree of 7 and a leading coefficient of 7. Because the  degree is odd and leading coefficient  is positive g(x)->-∞ as x ->-∞  and  g(x)->+∞ as x->+∞

Question 19.
f(x) = −2x⁴ + 12x⁸ + 17 + 15x²
Answer:

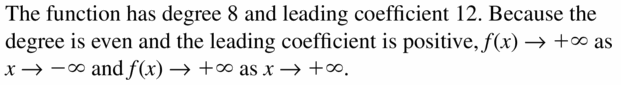
Question 20.
f(x) = 11 − 18x² − 5x⁵ − 12x⁴ − 2x
Answer:
Given polynomial is  f(x)= − 5x⁵ − 12x⁴− 18x²− 2x + 11
The highest exponent is 5, then the polynomial is of odd degree.
Hence the end behaviors are the opposite. With the negative leading coefficient
Then   f(x) ─> ∞ as x ─>-∞
f(x)─>-∞ as  x ─>+∞

In Exercises 21 and 22, describe the degree and leading coefficient of the polynomial function using the graph.

Question 21.

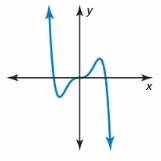
Answer:

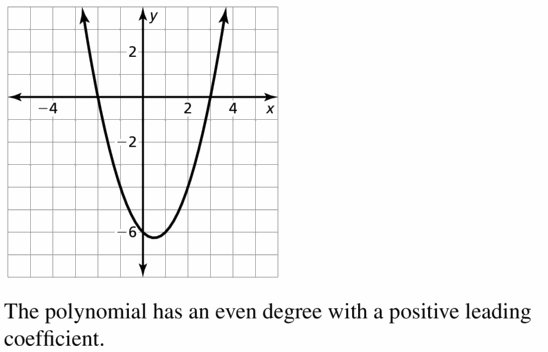
Question 22.

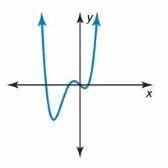
Answer:
The degree of the polynomial is even since one side goes up and the other goes up.
The leading coefficient is positive since the left side goes up and the right side goes up.

Question 23.
USING STRUCTURE Determine whether the function is a polynomial function. If so, write it in standard form and state its degree, type, and leading coefficient.
f(x) = 5x³x + \(\frac{5}{2}\)x³ − 9x⁴ + \(\sqrt{2}\)x² + 4x − 1 − x^-5x⁵ − 4
Answer:

Question 24.
WRITING Let f(x) = 13. State the degree, type, and leading coefficient. Describe the end behavior of the function. Explain your reasoning.
Answer:

In Exercises 25–32, graph the polynomial function.

Question 25.
p(x) = 3 − x⁴
Answer:

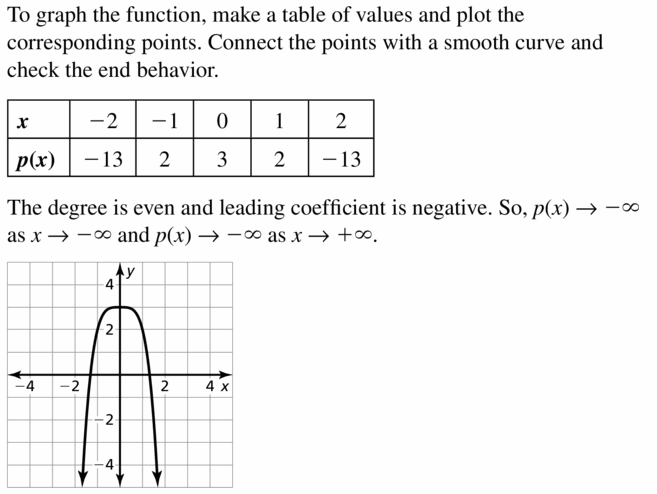
Question 26.
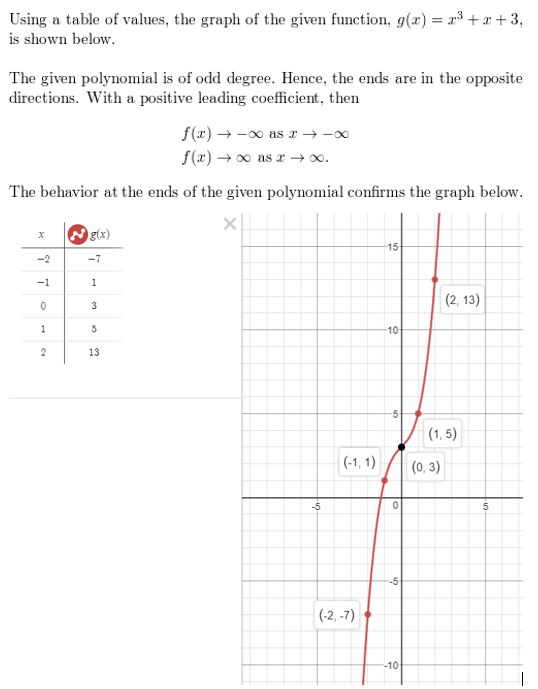
g(x) = x³ + x + 3
Answer:

Question 27.
f(x) = 4x − 9 − x³
Answer:

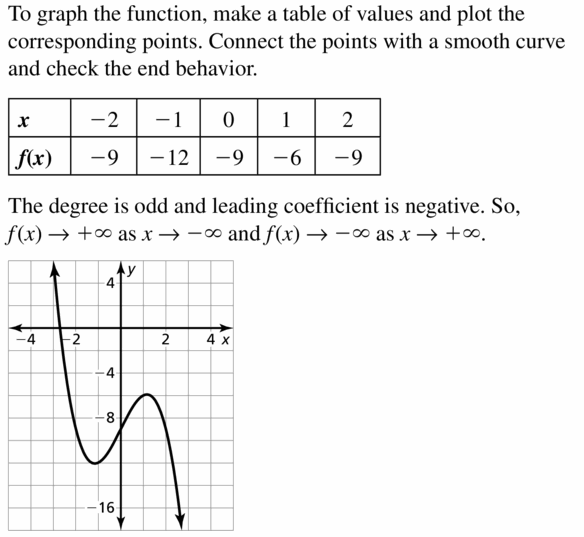
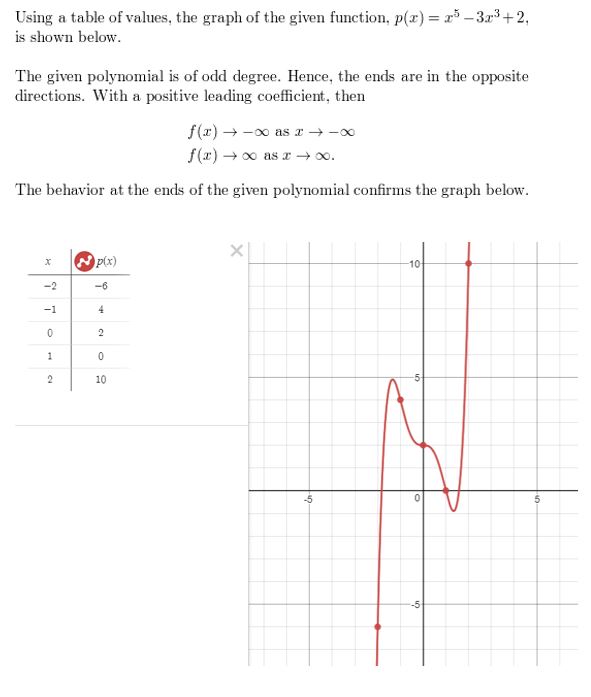
Question 28.
p(x) = x⁵ − 3x³ + 2
Answer:

Question 29.
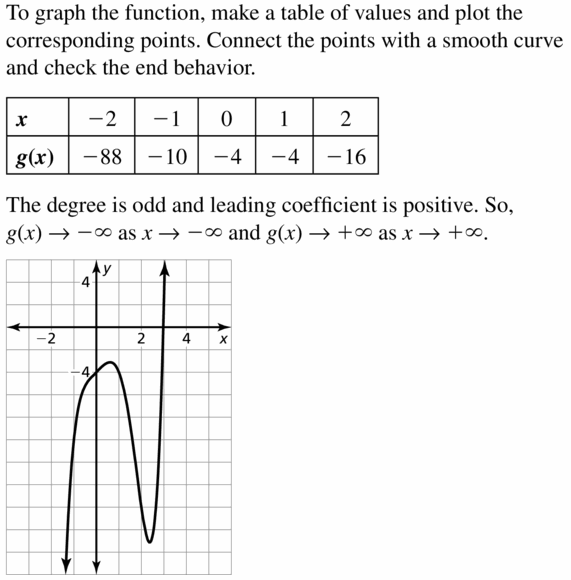
h(x) = x⁴ − 2x³ + 3x
Answer:

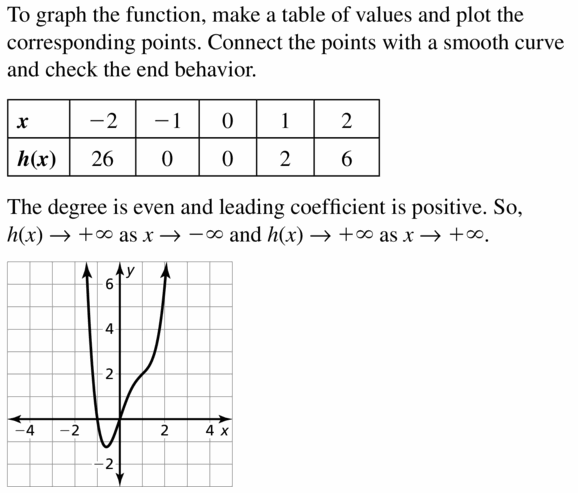
Question 30.
h(x) = 5 + 3x² − x⁴
Answer:

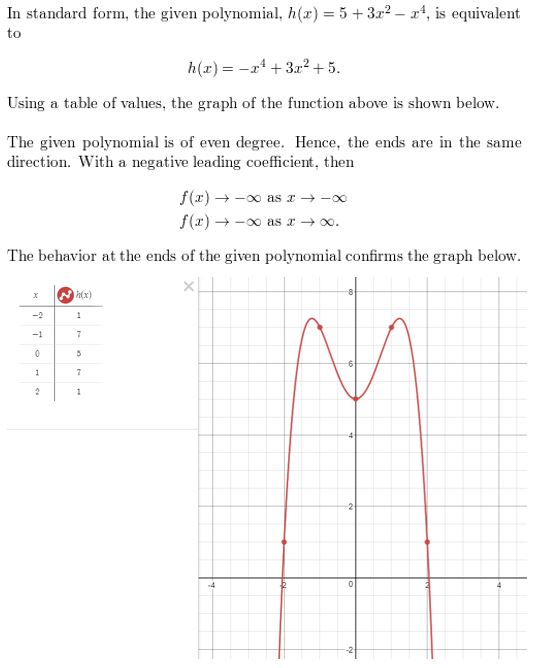
Question 31.
g(x) = x⁵ − 3x⁴ + 2x − 4
Answer:

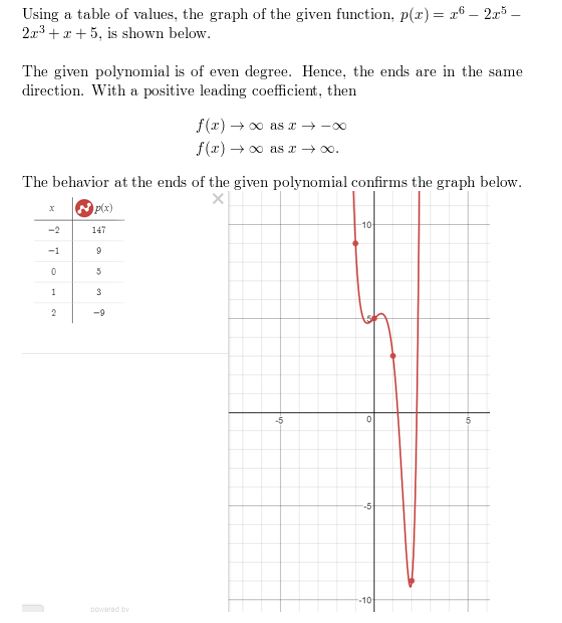
Question 32.
p(x) = x⁶ − 2x⁵ − 2x³ + x + 5
Answer:

ANALYZING RELATIONSHIPS In Exercises 33–36, describe the x-values for which
(a) f is increasing or decreasing,
(b) f(x) > 0, and
(c) f(x) < 0.

Question 33.

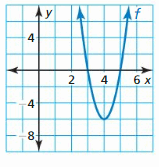
Answer:

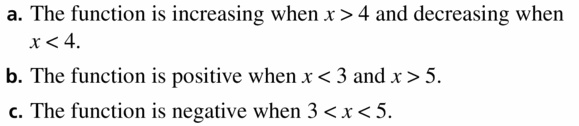
Question 34.

Answer:

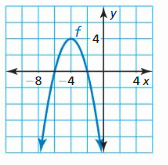
Question 35.

Answer:

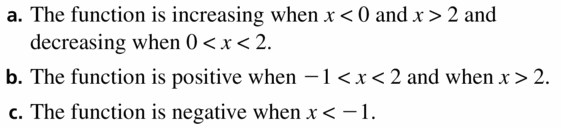
Question 36.

Answer:

In Exercises 37–40, sketch a graph of the polynomial function f having the given characteristics. Use the graph to describe the degree and leading coefficient of the function f.

Question 37.

• f is increasing when x > 0.5; f is decreasing when x < 0.5.
• f(x) > 0 when x < −2 and x > 3; f(x) < 0 when −2 < x < 3.

Answer:

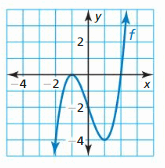
Question 38.

• f is increasing when −2 < x < 3;f is decreasing when x < −2 and x > 3.
• f(x) > 0 when x < −4 and 1 < x < 5; f(x) < 0 when −4 < x < 1 and x > 5.

Answer:

Question 39.

• f is increasing when −2 < x < 0 and x > 2;f is decreasing when x < −2 and 0 < x < 2.
• f(x) > 0 when x < −3, −1 < x < 1, and x > 3; f(x) < 0 when −3 < x < −1 and 1 < x < 3.

Answer:

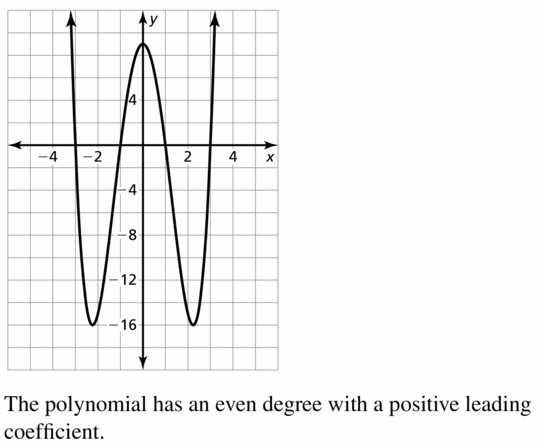
Question 40.

• f is increasing when x < −1 and x > 1;f is decreasing when −1 < x < 1.
• f(x) > 0 when −1.5 < x < 0 and x > 1.5; f(x) < 0 when x < −1.5 and 0 < x < 1.5.

Answer:

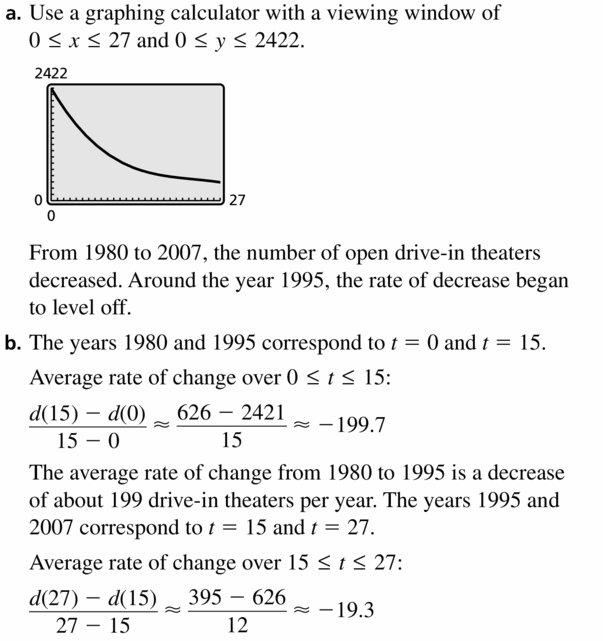
Question 41.
MODELING WITH MATHEMATICS From 1980 to 2007 the number of drive-in theaters in the United States can be modeled by the function
d(t) = −0.141t³ + 9.64t² − 232.5t + 2421
where d(t) is the number of open theaters and t is the number of years after 1980.
a. Use a graphing calculator to graph the function for the interval 0 ≤ t ≤ 27. Describe the behavior of the graph on this interval.
b. What is the average rate of change in the number of drive-in movie theaters from 1980 to 1995 and from 1995 to 2007? Interpret the average rates of change.
c. Do you think this model can be used for years before 1980 or after 2007? Explain.

Answer:

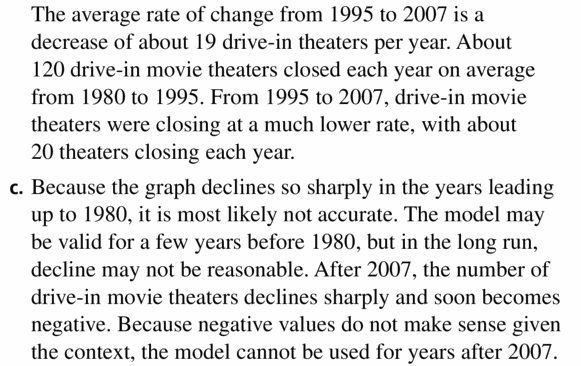
Question 42.
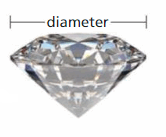
PROBLEM SOLVING The weight of an ideal round-cut diamond can be modeled by
w = 0.00583d³ − 0.0125d² + 0.022d − 0.01
where w is the weight of the diamond (in carats) and d is the diameter (in millimeters). According to the model, what is the weight of a diamond with a diameter of 12 millimeters?

Answer:
Given,
w = 0.00583d³ − 0.0125d² + 0.022d − 0.01
put d = 12 in the function.

Question 43.
ABSTRACT REASONING Suppose f(x) → ∞ as x → −∞ and f(x) →−∞ as x → ∞. Describe the end behavior of g(x) = −f(x). Justify your answer.
Answer:

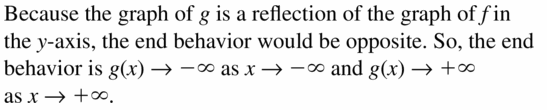
Question 44.
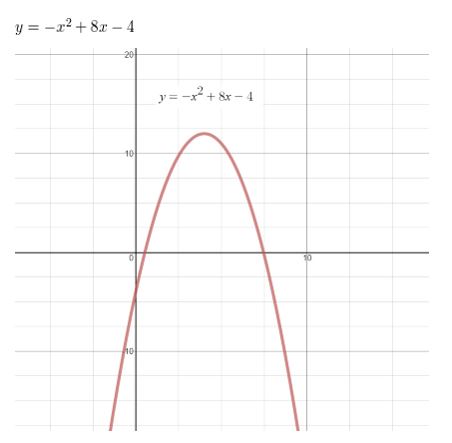
THOUGHT PROVOKING Write an even degree polynomial function such that the end behavior of f is given by f(x) → −∞ as x → −∞ and f(x) → −∞ as x → ∞. Justify your answer by drawing the graph of your function.
Answer:

Question 45.
USING TOOLS When using a graphing calculator to graph a polynomial function, explain how you know when the viewing window is appropriate.
Answer: The viewing window is appropriate when all of the high and low points are visible and the end behavior can be determined.

Question 46.
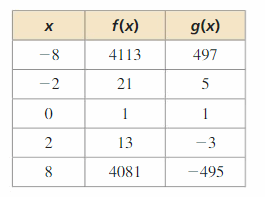
MAKING AN ARGUMENT Your friend uses the table to speculate that the function f is an even degree polynomial and the function g is an odd degree polynomial. Is your friend correct? Explain your reasoning.

Answer:

Question 47.
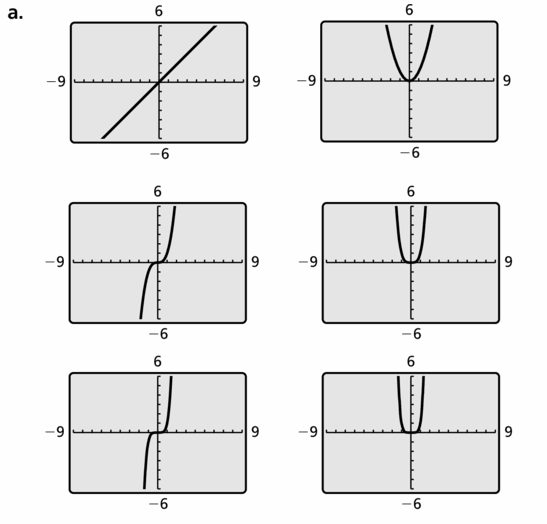
DRAWING CONCLUSIONS The graph of a function is symmetric with respect to the y-axis if for each point (a, b) on the graph, (−a, b) is also a point on the graph. The graph of a function is symmetric with respect to the origin if for each point (a, b) on the graph, (−a, −b) is also a point on the graph.
a. Use a graphing calculator to graph the function y = xⁿ when n = 1, 2, 3, 4, 5, and 6. In each case, identify the symmetry of the graph.
b. Predict what symmetry the graphs of y = x¹⁰ and y = x¹¹ each have. Explain your reasoning and then confirm your predictions by graphing.
Answer:

Question 48.
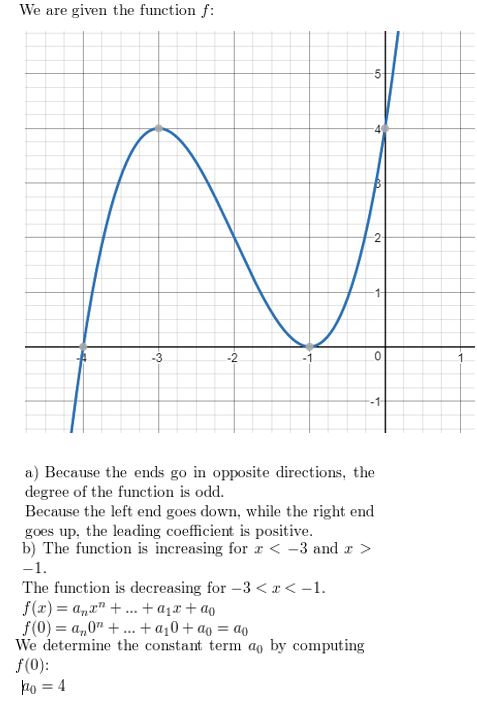
HOW DO YOU SEE IT? The graph of a polynomial function is shown.

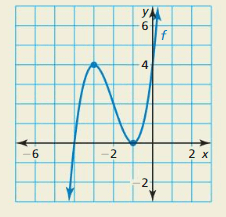
a. Describe the degree and leading coefficient of f.
b. Describe the intervals where the function is increasing and decreasing.
c. What is the constant term of the polynomial function?
Answer:

Question 49.
REASONING A cubic polynomial function f has a leading coefficient of 2 and a constant term of −5. When f(1) = 0 and f(2) = 3, what is f(−5)? Explain your reasoning.
Answer:

Question 50.
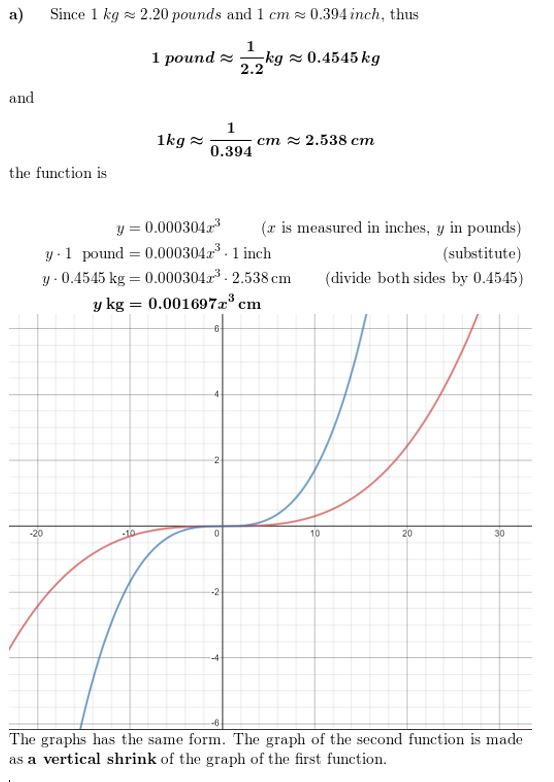
CRITICAL THINKING The weight y (in pounds) of a rainbow trout can be modeled by y = 0.000304x³, where x is the length (in inches) of the trout.
a. Write a function that relates the weight y and length x of a rainbow trout when y is measured in kilograms and x is measured in centimeters. Use the fact that 1 kilogram ≈ 2.20 pounds and 1 centimeter ≈ 0.394 inch.
b. Graph the original function and the function from part (a) in the same coordinate plane. What type of transformation can you apply to the graph of y = 0.000304x³ to produce the graph from part (a)?

Answer:

Maintaining Mathematical Proficiency

Simplify the expression. (Skills Review Handbook)

Question 51.
xy + x² + 2xy + y² − 3x²
Answer:
Given,
xy + x² + 2xy + y² − 3x²

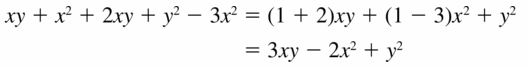
Question 52.
2h³g + 3hg³ + 7h²g² + 5h³g+ 2hg³
Answer:
Given,
2h³g + 3hg³ + 7h²g² + 5h³g+ 2hg³
Use the factoring method to simplify the expression.
h³g(2 + 5) + hg³(3 + 2) + 7h²g²
7h³g + 5hg³ + 7h²g²
So, 2h³g + 3hg³ + 7h²g² + 5h³g+ 2hg³ = 7h³g + 5hg³ + 7h²g²

Question 53.
−wk + 3kz − 2kw + 9zk − kw
Answer:

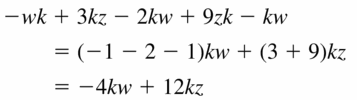
Question 54.
a²(m − 7a³) − m(a² − 10)
Answer:
Given,
a²(m − 7a³) − m(a² − 10)
((a²) •(m-(7•(a³))))-m•(a²-10)
((a²) • (m – 7a³)) – m • (a² – 10)
a² • (m – 7a³) –  m • (a² – 10)
= 10m – 7a⁵
So, a²(m − 7a³) − m(a² − 10) = 10m – 7a⁵

Question 55.
3x(xy − 4) + 3(4xy + 3) − xy(x²y − 1)
Answer:

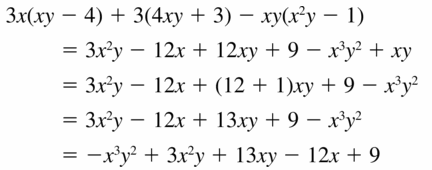
Question 56.
cv(9 − 3c) + 2c(v − 4c) + 6c
Answer:

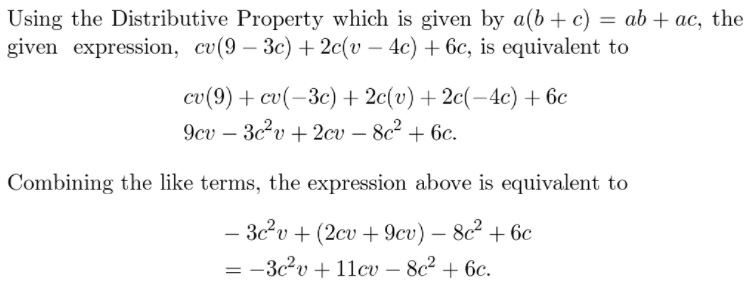
Lesson 4.2 Adding, Subtracting, and Multiplying Polynomials

Essential Question
How can you cube a binomial?

EXPLORATION 1
Cubing Binomials
Work with a partner. Find each product. Show your steps.

Answer:
a. (x + 1)³ = (x + 1)(x + 1)²
= (x + 1)(x² + 1 + 2x)
= x³ + x² + x + 1 + 2x² + 2x
= x³ + 3x² + 3x + 1

b. (a + b)³ = (a + b)(a + b)²
= (a + b)(a² + b² + 2ab)
= a³ + b³ + 2a²b + 2ab²

c. (x – 1)³ = (x – 1)(x – 1)²
= (x – 1)(x² + 1 – 2x)
= x³ + x² + x – 1 – 2x² + 2x
= x³ – x² + 3x – 1

d. (a – b)³ = (a – b)(a – b)²
= (a – b)(a² + b² – 2ab)
= a³ – b³ – 2a²b + 2ab²

EXPLORATION 2
Generalizing Patterns for Cubing a Binomial
Work with a partner.

a. Use the results of Exploration 1 to describe a pattern for the coefficients of the terms when you expand the cube of a binomial. How is your pattern related to Pascal’s Triangle, shown at the right?
b. Use the results of Exploration 1 to describe a pattern for the exponents of the terms in the expansion of a cube of a binomial.

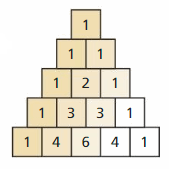
c. Explain how you can use the patterns you described in parts (a) and (b) to find the product (2x − 3)³. Then find this product.

Communicate Your Answer

Question 3.
How can you cube a binomial?
Answer:
First, write the cube of the binomial in the form of multiplication.
For example (p + q)³ = (p + q) (p + q) (p + q)
Next, multiply the first two binomials and remain the third one as same.
Then multiply the remaining binomial by the third term.

Question 4.
Find each product.
a. (x + 2)³
b. (x − 2)³
c. (2x − 3)³
d. (x − 3)³
e. (−2x + 3)³
f. (3x − 5)³

Answer:
a. (x + 2)³
This is in the form of (a + b)³ = a³ + b³ + 2a²b + 2ab²
(x + 2)³ = (x)³ + (2)³ + 3(x)²(2) + 3(x)(2)²
= x³ + 8 + 6x² + 12x
= x³ + 6x² + 12x + 8
b. (x – 2)³
This is in the form of (a – b)³ = a³ – b³ – 2a²b + 2ab²
(x – 2)³ = (x)³ – (2)³ – 3(x)²(2) + 3(x)(2)²
= x³ – 8 – 6x² + 12x
= x³ – 6x² + 12x – 8
c. (2x − 3)³
This is in the form of (a – b)³ = a³ – b³ – 2a²b + 2ab²
(2x − 3)³ = (2x)³ – (3)³ – 3(2x)²(3) + 3(2x)(3)²
= 8x³ – 27 – 36x² + 54x
= 8x³ – 36x² + 54x – 27
d. (x – 3)³
This is in the form of (a – b)³ = a³ – b³ – 2a²b + 2ab²
(x – 3)³ = (x)³ – (3)³ – 3(x)²(3) + 3(x)(3)²
= x³ – 27 – 9x² + 27x
= x³ – 9x² + 27x – 27
e. (−2x + 3)³
This is in the form of (a + b)³ = a³ + b³ + 2a²b + 2ab²
(−2x + 3)³ = (-2x)³ + (3)³ + 3(-2x)²(3) + 3(-2x)(3)²
= -8x³ + 27 – 36x² – 54x
= -8x³ – 36x² – 54x + 27
f. (3x − 5)³
This is in the form of (a – b)³ = a³ – b³ – 2a²b + 2ab²
(3x − 5)³ = (3x)³ – (5)³ – 3(3x)²(5) + 3(3x)(5)²
= 27x³ – 125 -135x² + 225x
= 27x³ -135x² + 225x – 125

4.2 Lesson

Monitoring Progress

Find the sum or difference.

Question 1.
(2x² − 6x + 5) + (7x² − x − 9)
Answer:
Given,
(2x² − 6x + 5) + (7x² − x − 9)
Removing the  grouping symbols and combining the like terms, the given expression is
(2x² − 6x + 5) + (7x² − x − 9) = 2x² − 6x + 5 + 7x² − x − 9
= (2x² + 7x²) + ( − 6x − x)+( 5-9)
= 9x² – 7x – 4
So, the sum of (2x² − 6x + 5) + (7x² − x − 9) = 9x² – 7x – 4

Question 2.
(3t³ + 8t² − t − 4) − (5t³ − t² + 17)
Answer:
Given,
(3t³ + 8t² − t − 4) − (5t³ − t² + 17)
=3t³ + 8t² -t – 4 – 5t³ + t² -17
= -2t³+ 9t² -t -21
Thus (3t³ + 8t² − t − 4) − (5t³ − t² + 17) = -2t³+ 9t² -t -21

Find the product.

Question 3.
(4x² + x − 5)(2x + 1)
Answer:
Given,
(4x² + x − 5)(2x + 1)
Multiply both the polynomials
=4x²(2x+1) + x(2x+1) – 5(2x+1)
=8x³+ 4x²+ 2x²+ x- 10x – 5
= 8x³+ 6x²– 9x – 5
So, the product of (4x² + x − 5)(2x + 1) = 8x³+ 6x²– 9x – 5

Question 4.
(y − 2)(5y² + 3y − 1)
Answer:
(y − 2)(5y² + 3y − 1)
Multiply both the polynomials
=(y – 2) 5y²+ (y – 2) 3y – 1(y – 2)
= 5y³-10y²+3y³-6y-y+2
= 5y³-7y²-7y+2
So, the product of (y − 2)(5y² + 3y − 1) = 5y³-7y²-7y+2

Question 5.
(m − 2)(m − 1)(m + 3)
Answer:
Given,
(m − 2)(m − 1)(m + 3)
find the product of the polynomials
= (m² – m – 2m + 2)(m + 3)
=(m² – 3m + 2)(m + 3)
=(m² – 3m + 2)m+(m² – 3m + 2)3
=m³ – 3m² + 2m + 3m²– 9m + 6
=m³ – 7m +6
So, the product of (m − 2)(m − 1)(m + 3) = m³ – 7m +6

Question 6.
(3t − 2)(3t + 2)
Answer:
(3t − 2)(3t + 2)
Use the formula: a²-b²= (a+ b) (a-b)
(3t − 2)(3t + 2) = (3t)²-(2)²
= 9t²-4
So, the product of (3t − 2)(3t + 2) = 9t² – 4

Question 7.
(5a + 2)²
Answer:
(5a + 2)²
This is in the form of (a + b)² = (a² + b² + 2ab)
=(5a)²+2. 5a .2+2²
=25a²+20a+4
So, the product of (5a + 2)² = 25a²+20a+4

Question 8.
(x y − 3)³
Answer:
(xy-3)³
(a-b)³=a³-3a² b +3a b ²-b³
= (x y)³-3(x y)².3+3. xy.3²-3³
= x³y³– 9x ²y²+27xy-27
So, the product of (x y − 3)³ = x³y³– 9x ²y²+27xy-27

Question 9.
(a) Prove the polynomial identity for the cube of a binomial representing a difference: (a − b)³ = a³ − 3a²b + 3ab² − b³.
(b) Use the cube of a binomial in part (a) to calculate 9³.
Answer:
(a) . (a-b)³ =a³– 3a ²b+3ab²-b³
= (a-b)³ =(a-b)(a-b)(a-b)
= (a²-2ab+b²)(a-b)
= a³-a ²b-2a ²b+2ab² +ab ²-b³
= a ³-3a ²b+3ab ²– b³

(b). 9³=(10-1)³=10³-3.10².1+3.10.1²-1³
= 1000-300+30-1
= 729

Question 10.
Use Pascal’s Triangle to expand
(a) (z + 3)⁴
Answer:
(z + 3)⁴ = (z)⁴ + (3)⁴ + 6z²(3)² + 4z(3)³
= z⁴ + 81 + 54z² + 12z³ + 108z

(b) (2t − 1)⁵
Answer:
1(2t)⁵ + 5(2t)⁴(-1) + 10(2t)³ (-1) + 10(2t)²(-1) + 5(2t)(-1)⁴ + 1(-1)
= (2t)⁵ – 5(2t)⁴ + 10(2t)³ – 10(2t)² + 5(2t) – 1
= 32t⁵ – 80t⁴ + 80t³ – 40t² + 10t – 1

Adding, Subtracting, and Multiplying Polynomials 4.2 Exercises

Vocabulary and Core Concept Check

Question 1.
WRITING Describe three different methods to expand (x + 3)³.
Answer:

Question 2.
WRITING Is (a + b)(a − b) = a² − b² an identity? Explain your reasoning.
Answer:
(a + b) (a – b)
a(a – b) + b(a – b)
a² – ab + ab – b²
= a² – b²
This is called standard algebraic identity called a difference of squares.

Monitoring Progress and Modeling with Mathematics

In Exercises 3–8, find the sum.

Question 3.
(3x² + 4x − 1) + (−2x² − 3x + 2)
Answer:

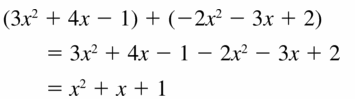
Question 4.
(−5x² + 4x − 2) + (−8x² + 2x + 1)
Answer:

Question 5.
(12x⁵ − 3x⁴ + 2x − 5) + (8x⁴ − 3x³ + 4x + 1)
Answer:

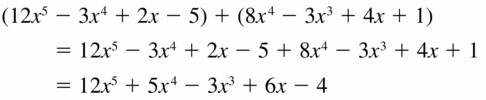
Question 6.
(8x⁴ + 2x² − 1) + (3x³ − 5x² + 7x + 1)
Answer:

Question 7.
(7x⁶ + 2x⁵ − 3x² + 9x) + (5x⁵ + 8x³ − 6x² + 2x − 5)
Answer:

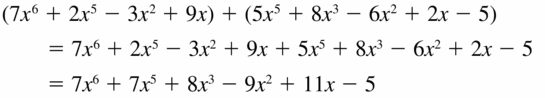
Question 8.
(9x⁴ − 3x³ + 4x² + 5x + 7) + (11x⁴ − 4x² − 11x − 9)
Answer:

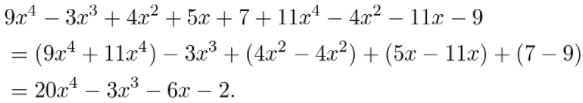
In Exercises 9–14, find the difference.

Question 9.
(3x³ − 2x² + 4x − 8) − (5x³ + 12x² − 3x − 4)
Answer:

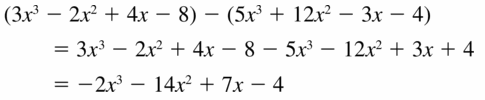
Question 10.
(7x⁴ − 9x³ − 4x² + 5x + 6) − (2x⁴ + 3x³ − x² + x − 4)
Answer:

Question 11.
(5x⁶ − 2x⁴ + 9x³ + 2x − 4) − (7x⁵ − 8x⁴ + 2x− 11)
Answer:

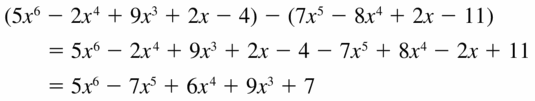
Question 12.
(4x⁵ − 7x³ − 9x² + 18) − (14x⁵ − 8x⁴ + 11x² + x)
Answer:

Question 13.
(8x⁵ + 6x³ − 2x² + 10x) − (9x⁵ − x³ − 13x² + 4)
Answer:

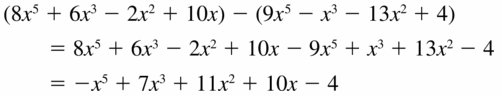
Question 14.
(11x⁴ − 9x² + 3x + 11) − (2x⁴ + 6x³ + 2x − 9)
Answer:

Question 15.
MODELING WITH MATHEMATICS During a recent period of time, the numbers (in thousands) of males Mand females F that attend degree-granting institutions in the United States can be modeled by
M = 19.7t² + 310.5t + 7539.6
F = 28t² + 368t + 10127.8

where t is time in years. Write a polynomial to model the total number of people attending degree-granting institutions. Interpret its constant term.
Answer:

Question 16.
MODELING WITH MATHEMATICS A farmer plants a garden that contains corn and pumpkins. The total area (in square feet) of the garden is modeled by the expression 2x² + 5x + 4. The area of the corn is modeled by the expression x² − 3x + 2. Write an expression that models the area of the pumpkins.
Answer:

In Exercises 17–24, find the product.

Question 17.
7x³(5x² + 3x + 1)
Answer:

Question 18.
−4x⁵(11x³ + 2x² + 9x + 1)
Answer:

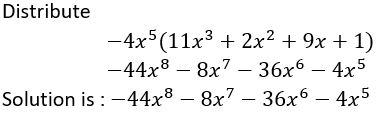
Question 19.
(5x² − 4x + 6)(−2x + 3)
Answer:

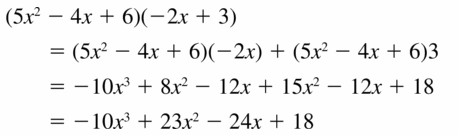
Question 20.
(−x − 3)(2x² + 5x + 8)
Answer:

Question 21.
(x² − 2x − 4)(x² − 3x − 5)
Answer:

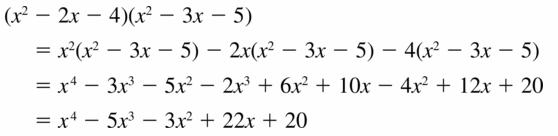
Question 22.
(3x² + x − 2)(−4x² − 2x − 1)
Answer:

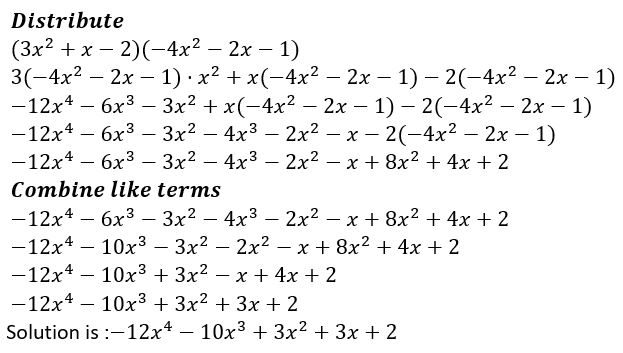
Question 23.
(3x³ − 9x + 7)(x² − 2x + 1)
Answer:

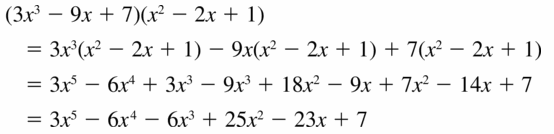
Question 24.
(4x² − 8x − 2)(x⁴ + 3x² + 4x)
Answer:

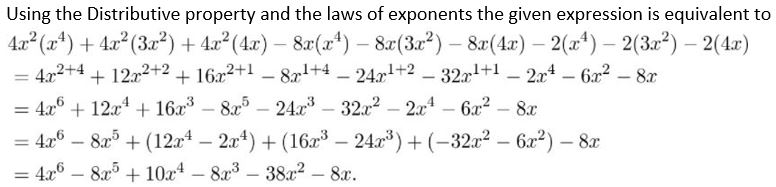
ERROR ANALYSIS In Exercises 25 and 26, describe and correct the error in performing the operation.

Question 25.

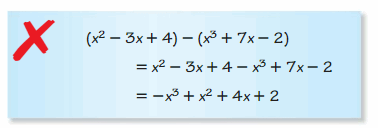
Answer:

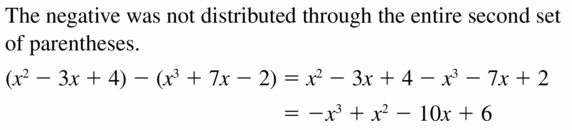
Question 26.

Answer:

In Exercises 27–32, find the product of the binomials.

Question 27.
(x − 3)(x + 2)(x + 4)
Answer:

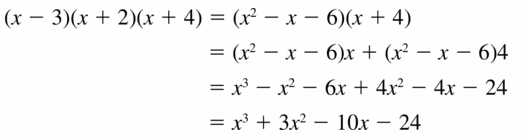
Question 28.
(x − 5)(x + 2)(x − 6)
Answer:

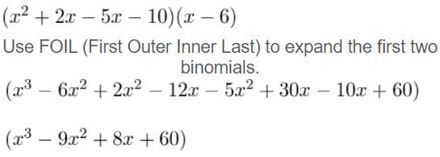
Question 29.
(x − 2)(3x + 1)(4x − 3)
Answer:

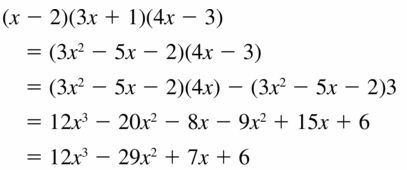
Question 30.
(2x + 5)(x − 2)(3x + 4)
Answer:

Question 31.
(3x − 4)(5 − 2x)(4x + 1)
Answer:

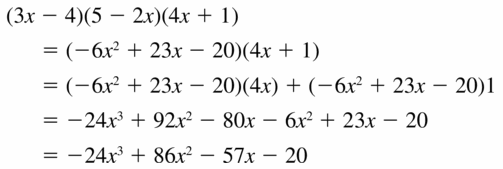
Question 32.
(4 − 5x)(1 − 2x)(3x + 2)
Answer:

Question 33.
REASONING Prove the polynomial identity (a + b)(a − b) = a² − b². Then give an example of two whole numbers greater than 10 that can be multiplied using mental math and the given identity. Justify your answers.
Answer:

Question 34.
NUMBER SENSE You have been asked to order textbooks for your class. You need to order 29 textbooks that cost $31 each. Explain how you can use the polynomial identity (a + b)(a − b) = a² − b² and mental math to find the total cost of the textbooks.

Answer:

In Exercises 35–42, find the product.

Question 35.
(x − 9)(x + 9)
Answer:

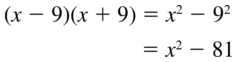
Question 36.
(m + 6)²
Answer:

Question 37.
(3c − 5)²
Answer:

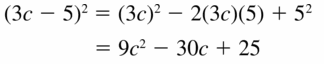
Question 38.
(2y − 5)(2y + 5)
Answer:

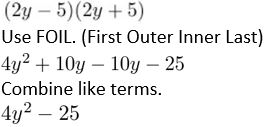
Question 39.
(7h + 4)²
Answer:

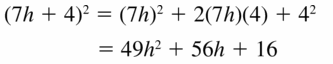
Question 40.
(9g − 4)²
Answer:

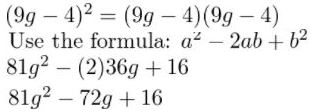
Question 41.
(2k + 6)³
Answer:

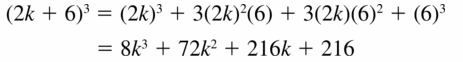
Question 42.
(4n − 3)³
Answer:

In Exercises 43–48, use Pascal’s Triangle to expand the binomial.

Question 43.
(2t + 4)³
Answer:

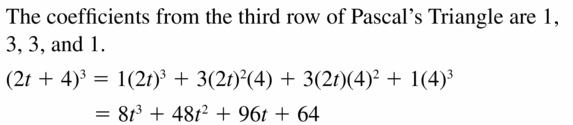
Question 44.
(6m + 2)²
Answer:

Question 45.
(2q − 3)⁴
Answer:

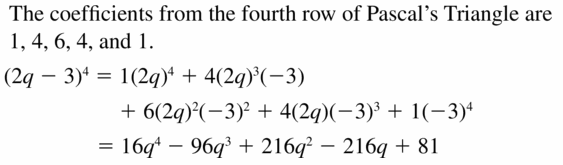
Question 46.
(g + 2)⁵
Answer:

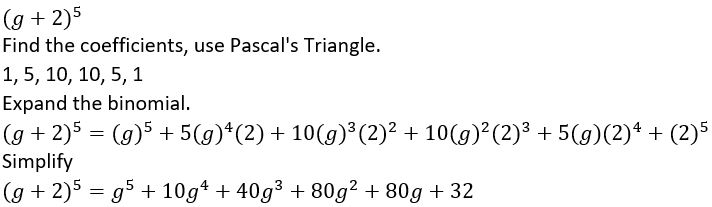
Question 47.
(yz + 1)⁵
Answer:

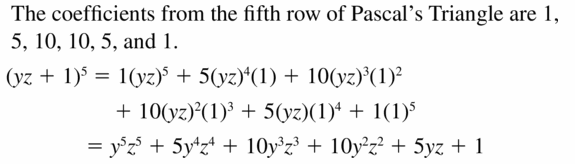
Question 48.
(np − 1)⁴
Answer:

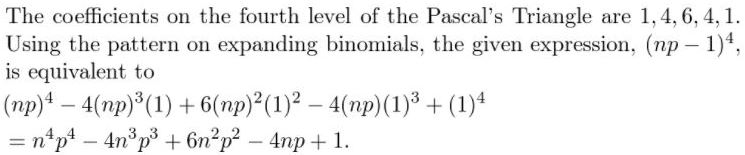
Question 49.
COMPARING METHODS Find the product of the expression (a² + 4b²)²(3a² − b²)² using two different methods. Which method do you prefer? Explain.
Answer:

Question 50.
THOUGHT PROVOKING Adjoin one or more polygons to the rectangle to form a single new polygon whose perimeter is double that of the rectangle. Find the perimeter of the new polygon.

Answer:

MATHEMATICAL CONNECTIONS In Exercises 51 and 52, write an expression for the volume of the figure as a polynomial in standard form.

Question 51.

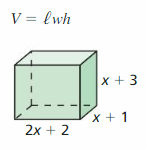
Answer:

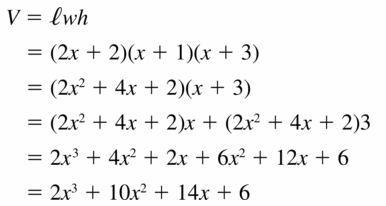
Question 52.

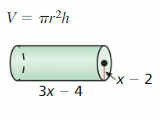
Answer:

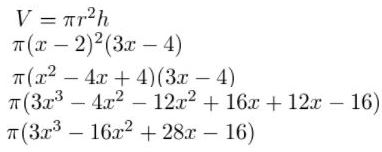
Question 53.
MODELING WITH MATHEMATICS Two people make three deposits into their bank accounts earning the same simple interest rate r.

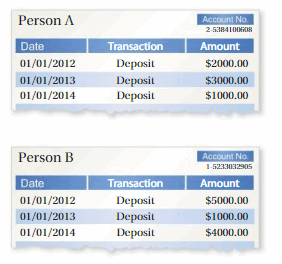
Person A’s account is worth 2000(1 + r)³ + 3000(1 + r)² + 1000(1 + r) on January 1, 2015.
a. Write a polynomial for the value of Person B’s account on January 1, 2015.
b. Write the total value of the two accounts as a polynomial in standard form. Then interpret the coefficients of the polynomial.
c. Suppose their interest rate is 0.05. What is the total value of the two accounts on January 1, 2015?
Answer:

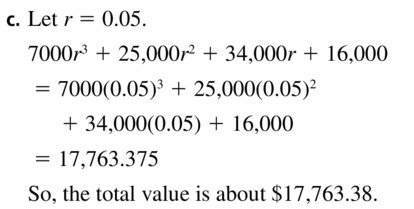
Question 54.
PROBLEM SOLVING
The sphere is centered in the cube. Find an expression for the volume of the cube outside the sphere.

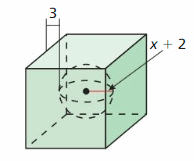
Answer:

Question 55.
MAKING AN ARGUMENT Your friend claims the sum of two binomials is always a binomial and the product of two binomials is always a trinomial. Is your friend correct? Explain your reasoning.
Answer:

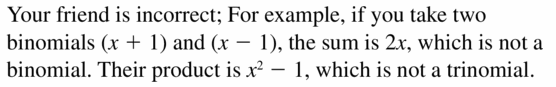
Question 56.
HOW DO YOU SEE IT? You make a tin box by cutting x-inch-by-x-inch pieces of tin off the corners of a rectangle and folding up each side. The plan for your box is shown.

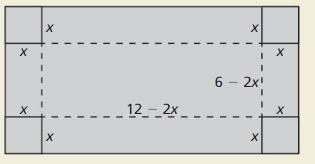
a. What are the dimensions of the original piece of tin?
b. Write a function that represents the volume of the box. Without multiplying, determine its degree.
Answer:

USING TOOLS In Exercises 57–60, use a graphing calculator to make a conjecture about whether the two functions are equivalent. Explain your reasoning.

Question 57.
f(x) = (2x − 3)³; g(x) = 8x³ − 36x² + 54x − 27
Answer:

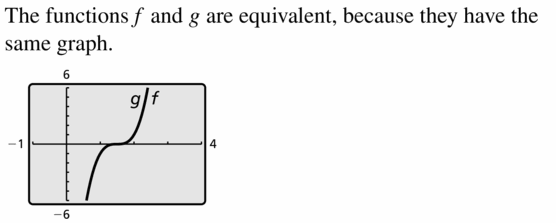
Question 58.
f(x) = (x + 2)⁵;
g(x) = x⁵ + 10x⁴ + 40x³ + 80x² + 64x
Answer:
Two Functions are not equal.

Question 59.
f(x) = (−x − 3)⁴;
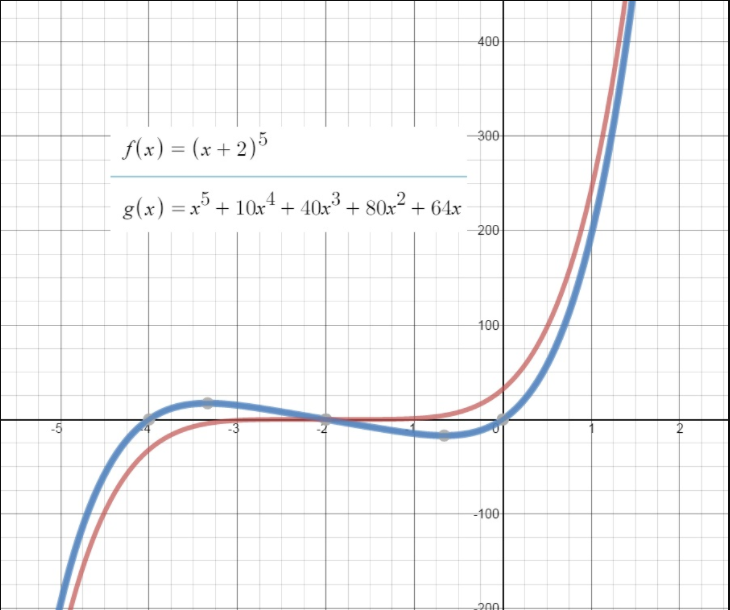
g(x) = x⁴ + 12x³ + 54x² + 108x + 80
Answer:

Question 60.
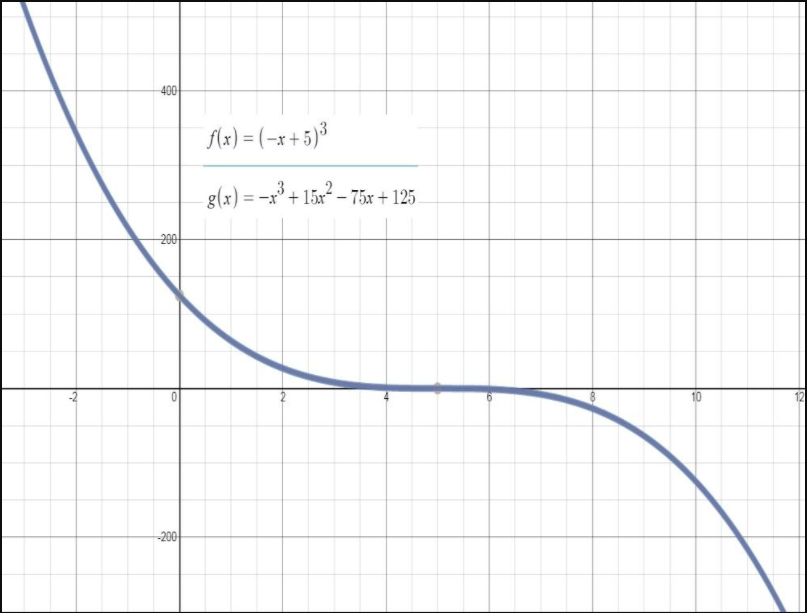
f(x) = (−x + 5)³; g(x) = −x³ + 15x² − 75x + 125
Answer:
They are Equal

Question 61.
REASONING Copy Pascal’s Triangle and add rows for n = 6, 7, 8, 9, and 10. Use the new rows to expand (x + 3)⁷ and (x − 5)⁹.
Answer:

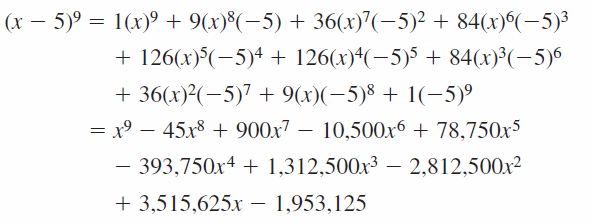
Question 62.
ABSTRACT REASONING You are given the function f(x) = (x + a)(x + b)(x + c)(x + d). When f(x) is written in standard form, show that the coefficient of x³ is the sum of a, b, c, and d, and the constant term is the product of a, b, c, and d.
Answer:

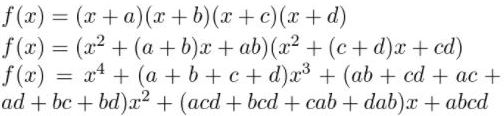
Question 63.
DRAWING CONCLUSIONS Let g(x) = 12x⁴ + 8x + 9 and h(x) = 3x⁵ + 2x³ − 7x + 4.
a. What is the degree of the polynomial g(x) + h(x)?
b. What is the degree of the polynomial g(x) − h(x)?
c. What is the degree of the polynomial g(x) • h(x)?
d. In general, if g(x) and h(x) are polynomials such that g(x) has degree m and h(x) has degree n, and m > n, what are the degrees of g(x) + h(x), g(x) − h(x), and g(x) • h(x)?
Answer:

Question 64.
FINDING A PATTERN In this exercise, you will explore the sequence of square numbers. The first four square numbers are represented below.

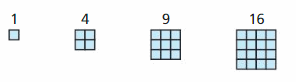
a. Find the differences between consecutive square numbers. Explain what you notice.
b. Show how the polynomial identity (n + 1)² − n² = 2n + 1 models the differences between square numbers.
c. Prove the polynomial identity in part (b).
Answer:

Question 65.
CRITICAL THINKING Recall that a Pythagorean triple is a set of positive integers a, b, and c such that a² + b² = c². The numbers 3, 4, and 5 form a Pythagorean triple because 3² + 4² = 5². You can use the polynomial identity (x² − y²)² + (2xy)² = (x² + y²)² to generate other Pythagorean triples.
a. Prove the polynomial identity is true by showing that the simplified expressions for the left and right sides are the same. b. Use the identity to generate the Pythagorean triple when x = 6 and y = 5.
c. Verify that your answer in part (b) satisfies a² + b² = c².
Answer:

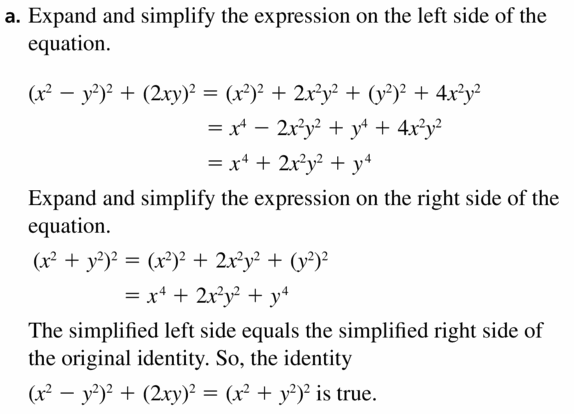
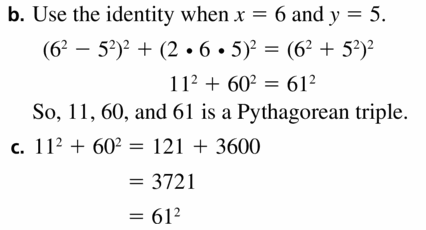
Maintaining Mathematical Proficiency

Perform the operation. Write the answer in standard form. (Section 3.2)

Question 66.
(3 − 2i) + (5 + 9i)
Answer:

Question 67.
(12 + 3i) − (7 − 8i)
Answer:

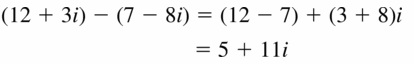
Question 68.
(7i)(−3i)
Answer:

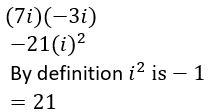
Question 69.
(4 + i)(2 − i)
Answer:

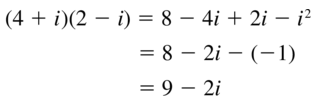
Lesson 4.3 Dividing Polynomials

Essential Question
How can you use the factors of a cubic polynomial to solve a division problem involving the polynomial?

EXPLORATION 1
Dividing Polynomials
Work with a partner. Match each division statement with the graph of the related cubic polynomial f(x). Explain your reasoning. Use a graphing calculator to verify your answers.
a. \(\frac{f(x)}{x}\) = (x − 1)(x + 2)
b. \(\frac{f(x)}{x-1}\) = (x − 1)(x + 2)
c. \(\frac{f(x)}{x+1}\) = (x − 1)(x + 2)
d. \(\frac{f(x)}{x-2}\) = (x− 1)(x+ 2)
e. \(\frac{f(x)}{x+2}\) = (x− 1)(x+ 2)
f. \(\frac{f(x)}{x-3}\) = (x− 1)(x+ 2)

EXPLORATION 2
Dividing Polynomials

Work with a partner. Use the results of Exploration 1 to find each quotient. Write your answers in standard form. Check your answers by multiplying.
a. (x³ + x² − 2x) ÷ x
b. (x³ − 3x + 2) ÷ (x − 1)
c. (x³ + 2x² − x − 2) ÷ (x + 1)
d. (x³ − x² − 4x + 4) ÷ (x − 2)
e. (x³ + 3x² − 4) ÷ (x + 2)
f. (x³ − 2x² − 5x + 6) ÷ (x − 3)

Communicate Your Answer

Question 3.
How can you use the factors of a cubic polynomial to solve a division problem involving the polynomial?

4.3 Lesson

Monitoring Progress

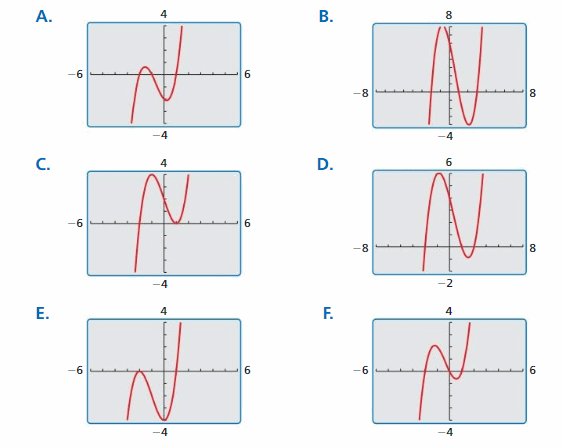
Divide using polynomial long division.

Question 1.
(x³ − x² − 2x + 8) ÷ (x − 1)
Answer:

Question 2.
(x⁴ + 2x² − x + 5) ÷ (x² − x + 1)
Answer:

Divide using synthetic division.

Question 3.
(x³ − 3x² − 7x + 6) ÷ (x − 2)
Answer:

Question 4.
(2x³ − x − 7) ÷ (x + 3)
Answer:

Use synthetic division to evaluate the function for the indicated value of x.

Question 5.
f(x) = 4x² − 10x − 21; x = 5
Answer:

Question 6.
f(x) = 5x⁴ + 2x³ − 20x − 6; x = 2
Answer:

Dividing Polynomials 4.3 Exercises

Monitoring Progress and Modeling with Mathematics

Question 1.
WRITING Explain the Remainder Theorem in your own words. Use an example in your explanation.
Answer:

Question 2.
VOCABULARY What form must the divisor have to make synthetic division an appropriate method for dividing a polynomial? Provide examples to support your claim.
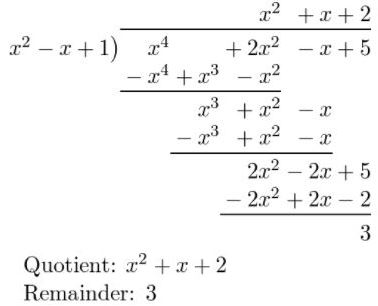
Answer: In order to use the synthetic division, the divisor must be of the first degree and must have the form ax.

Question 3.
VOCABULARY Write the polynomial divisor, dividend, and quotient functions represented by the synthetic division shown at the right.

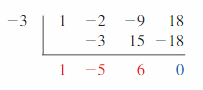
Answer:

Question 4.
WRITING Explain what the colored numbers represent in the synthetic division in Exercise 3.
Answer:
Quotient: Red colors
Remainder: Blue colors

Vocabulary and Core Concept Check

In Exercises 5–10, divide using polynomial long division.

Question 5.
(x² + x − 17 ) ÷ (x − 4)
Answer:

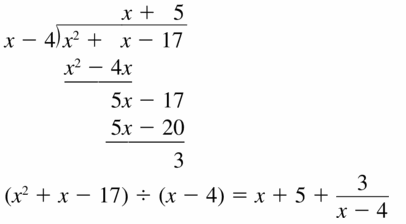
Question 6.
(3x² − 14x − 5) ÷ (x − 5)
Answer:

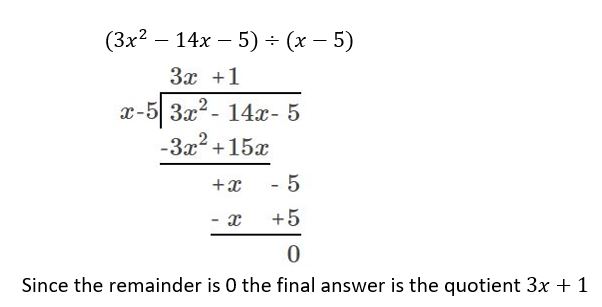
Question 7.
(x³ + x² + x + 2 ) ÷ (x² − 1)
Answer:

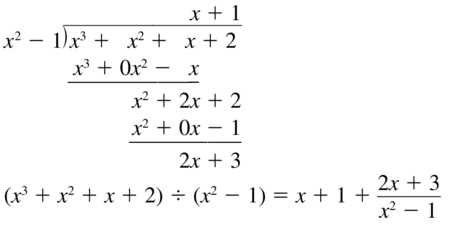
Question 8.
(7x³ + x² + x ) ÷ (x² + 1)
Answer:

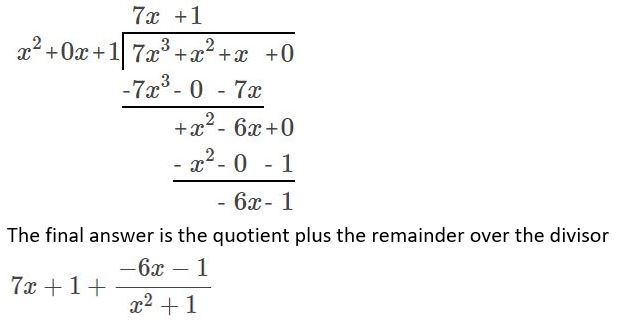
Question 9.
(5x⁴ − 2x³ − 7x² − 39) ÷ (x² + 2x − 4)
Answer:

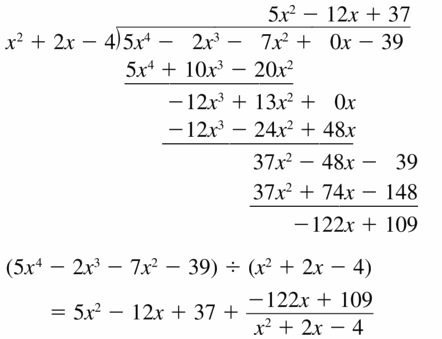
Question 10.
(4x⁴ + 5x − 4) ÷ (x² − 3x − 2)
Answer:

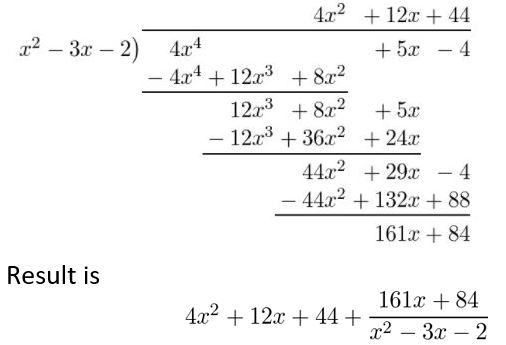
In Exercises 11–18, divide using synthetic division.

Question 11.
(x² + 8x + 1) ÷ (x − 4)
Answer:

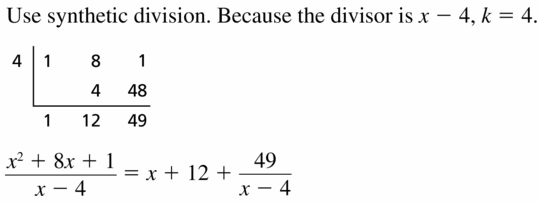
Question 12.
(4x² − 13x − 5) ÷ (x − 2)
Answer:
Given,
(4x² − 13x − 5) ÷ (x − 2)
use synthetic division. Because the divisor is x-2, k=2

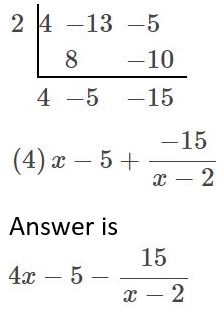
Question 13.
(2x² − x + 7) ÷ (x + 5)
Answer:

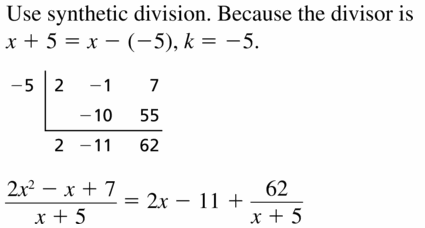
Question 14.
(x³ − 4x + 6) ÷ (x + 3)
Answer:

Question 15.
(x² + 9) ÷ (x − 3)
Answer:
Given,
(x² + 9) ÷ (x − 3)

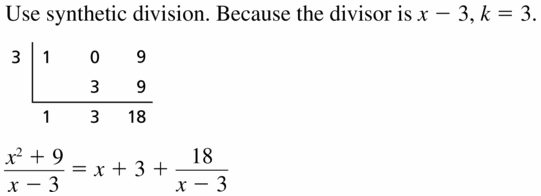
Question 16.
(3x³ − 5x² − 2) ÷ (x − 1)
Answer:
Given,
(3x³ − 5x² − 2) ÷ (x − 1)

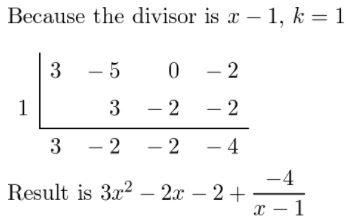
Question 17.
(x⁴ − 5x³ − 8x² + 13x − 12) ÷ (x − 6)
Answer:
Given,
(x⁴ − 5x³ − 8x² + 13x − 12) ÷ (x − 6)

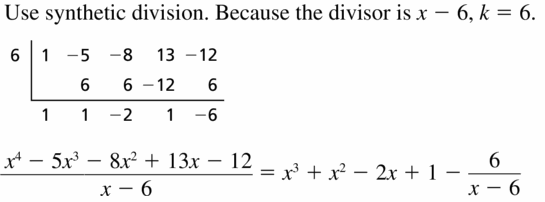
Question 18.
(x⁴ + 4x³ + 16x − 35) ÷ (x + 5 )
Answer:
Given,
(x⁴ + 4x³ + 16x − 35) ÷ (x + 5 )

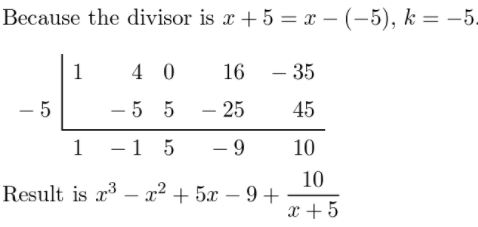
ANALYZING RELATIONSHIPS In Exercises 19–22, match the equivalent expressions. Justify your answers.

Question 19.
(x² + x − 3) ÷ (x − 2)
Answer:
Given,
(x² + x − 3) ÷ (x − 2)

Question 20.
(x² − x − 3) ÷ (x − 2)
Answer:

Question 21.
(x² − x + 3) ÷ (x − 2)
Answer:

Question 22.
(x² + x + 3) ÷ (x − 2)

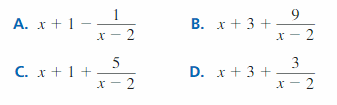
Answer:

ERROR ANALYSIS In Exercises 23 and 24, describe and correct the error in using synthetic division to divide x³ – 5x + 3 by x – 2.

Question 23.

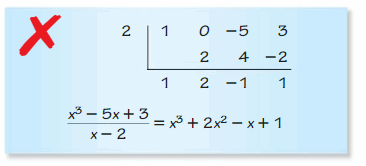
Answer:

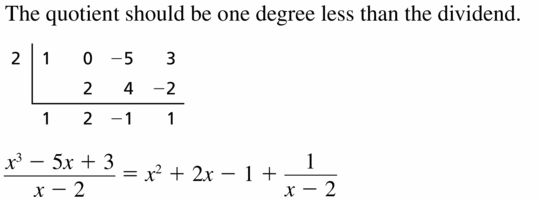
Question 24.

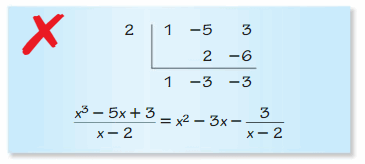
Answer:

In Exercises 25–32, use synthetic division to evaluate the function for the indicated value of x.

Question 25.
f(x) = −x² − 8x + 30; x = −1
Answer:
Given,
f(x) = −x² − 8x + 30

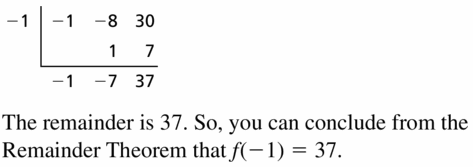
Question 26.
f(x) = 3x² + 2x − 20; x = 3
Answer:
Given,
f(x) = 3x² + 2x − 20

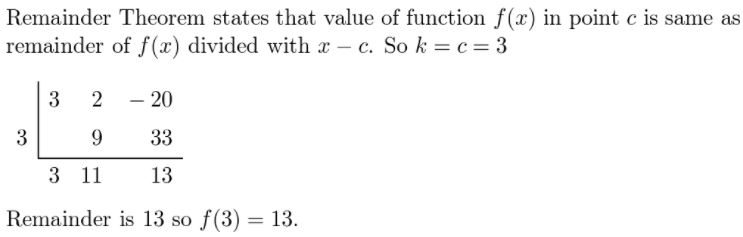
Question 27.
f(x) = x³ − 2x² + 4x + 3; x = 2
Answer:
Given,
f(x) = x³ − 2x² + 4x + 3

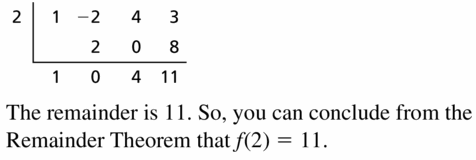
Question 28.
f(x) = x³ + x² − 3x + 9; x = −4
Answer:
Given,
f(x) = x³ + x² − 3x + 9

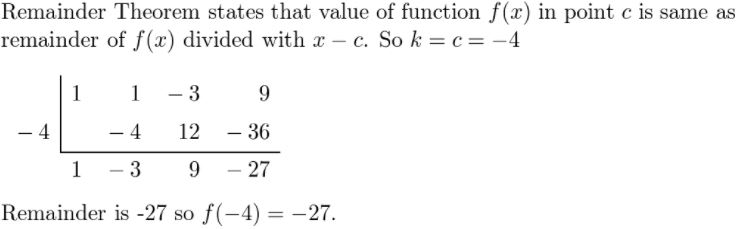
Question 29.
f(x) = x³ − 6x + 1; x = 6
Answer:
Given,
f(x) = x³ − 6x + 1

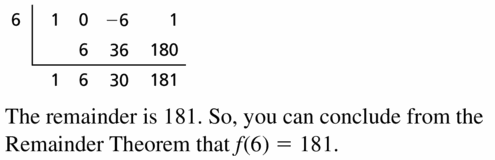
Question 30.
f(x) = x³ − 9x − 7; x = 10
Answer:
Given,
f(x) = x³ − 9x − 7

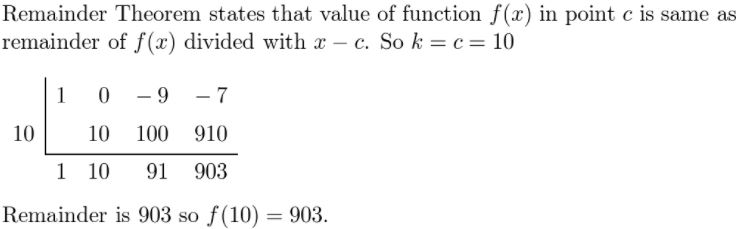
Question 31.
f(x) = x⁴ + 6x² − 7x + 1; x = 3
Answer:
Given,
f(x) = x⁴ + 6x² − 7x + 1

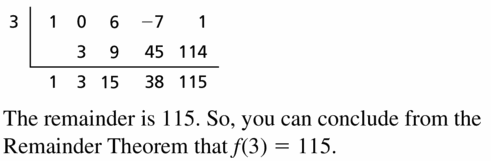
Question 32.
f(x) = −x⁴ − x³ − 2; x = 5
Answer:
Given,
f(x) = −x⁴ − x³ − 2

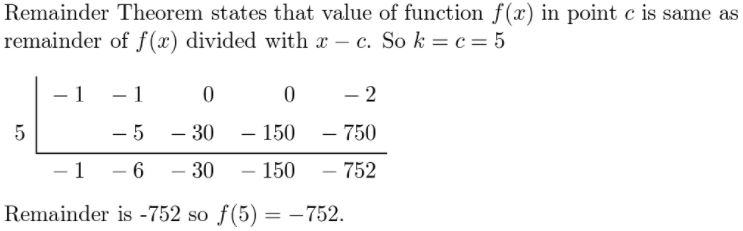
Question 33.
MAKING AN ARGUMENT You use synthetic division to divide f(x) by (x − a) and find that the remainder equals 15. Your friend concludes that f(15) = a. Is your friend correct? Explain your reasoning.
Answer:

Question 34.
THOUGHT PROVOKING A polygon has an area represented by A = 4x² + 8x + 4. The figure has at least one dimension equal to 2x + 2. Draw the figure and label its dimensions.
Answer:
A = 4x² + 8x + 4

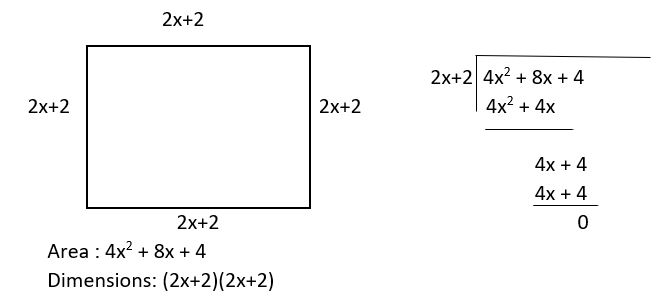
Question 35.
USING TOOLS The total attendance A (in thousands) at NCAA women’s basketball games and the number T of NCAA women’s basketball teams over a period of time can be modeled by
A = −1.95x³ + 70.1x² − 188x + 2150
T = 14.8x + 725
where x is in years and 0 < x < 18. Write a function for the average attendance per team over this period of time.

Answer:

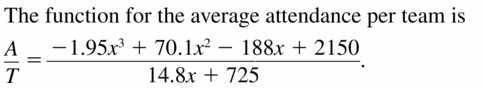
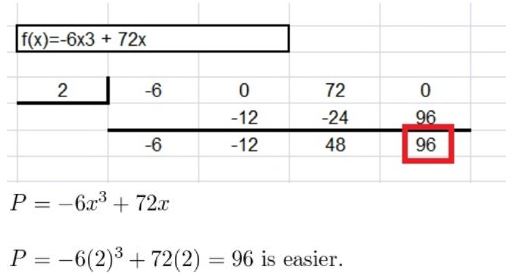
Question 36.
COMPARING METHODS The profit P (in millions of dollars) for a DVD manufacturer can be modeled by P = −6x³ + 72x, where x is the number (in millions) of DVDs produced. Use synthetic division to show that the company yields a profit of $96 million when 2 million DVDs are produced. Is there an easier method? Explain.
Answer:

Question 37.
CRITICAL THINKING What is the value of k such that (x³ − x² + kx − 30) ÷ (x − 5) has a remainder of zero?
A. −14
B. −2
C. 26
D. 32
Answer:
Given,
(x³ − x² + kx − 30) ÷ (x − 5)

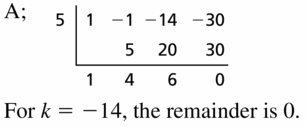
Question 38.
HOW DO YOU SEE IT? The graph represents the polynomial function f(x) = x³ + 3x² − x − 3.

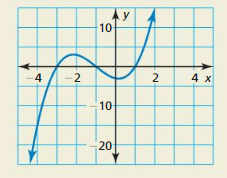
a. The expression f(x) ÷ (x − k) has a remainder of −15. What is the value of k?
b. Use the graph to compare the remainders of (x³ + 3x² − x − 3) ÷ (x + 3) and (x³ + 3x² − x − 3) ÷ (x + 1).
Answer:

Question 39.
MATHEMATICAL CONNECTIONS The volume V of the rectangular prism is given by V = 2x³ + 17x² + 46x + 40. Find an expression for the missing dimension.

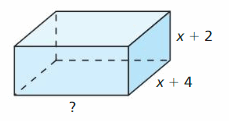
Answer:

Question 40.
USING STRUCTURE You divide two polynomials and obtain the result 5x² − 13x + 47 − \(\frac{102}{x+2}\). What is the dividend? How did you find it?
Answer:

Maintaining Mathematical Proficiency

Find the zero(s) of the function. (Sections 3.1and 3.2)

Question 41.
f(x) = x² − 6x + 9
Answer:
Given,
f(x) = x² − 6x + 9

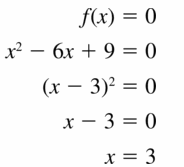
Question 42.
g(x) = 3(x + 6)(x − 2)
Answer:
Given,
g(x) = 3(x + 6)(x − 2)
g(x) = 0
3(x + 6)(x − 2) = 0
(3x + 18)(x – 2) = 0
3x + 18 = 0 or x – 2 = 0
3x = -18 or x = 2
x = -18/3
x = -6
So, the solution x = -6.

Question 43.
g(x) = x² + 14x + 49
Answer:

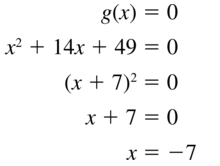
Question 44.
h(x) = 4x² + 36
Answer:
Given,
h(x) = 4x² + 36
4x² + 36 = 0
x² + 9 = 0
x² = -9
x = 3i
The solution is x = 3i

Lesson 4.4 Factoring Polynomials

Essential Question
How can you factor a polynomial?

EXPLORATION 1
Factoring Polynomials
Work with a partner. Match each polynomial equation with the graph of its related polynomial function. Use the x-intercepts of the graph to write each polynomial in factored form. Explain your reasoning.
a. x² + 5x + 4 = 0
b. x³ − 2x² − x + 2 = 0
c. x³ + x² − 2x = 0
d. x³ − x = 0
e. x⁴ − 5x² + 4 = 0
f. x⁴ − 2x³ − x² + 2x = 0

EXPLORATION 2
Factoring Polynomials

Work with a partner. Use the x-intercepts of the graph of the polynomial function to write each polynomial in factored form. Explain your reasoning. Check your answers by multiplying.
a. f(x) = x² − x − 2
b. f(x) = x³ − x² − 2x
c. f(x) = x³ − 2x² − 3x
d. f(x) = x³ − 3x² − x + 3
e. f(x) = x⁴ + 2x³ − x² − 2x
f. f(x) = x⁴ − 10x² + 9

Communicate Your Answer

Question 3.
How can you factor a polynomial?
Answer:
There are four ways to find the factors of a polynomial.

1. Find the greatest common factor.
2. Grouping the method.
3. Adding the difference in two squares.
4. Find the sum or difference in cubes.

Question 4.
What information can you obtain about the graph of a polynomial function written in factored form?

4.4 Lesson

Monitoring Progress

Question 1.
x³ − 7x² + 10x
Answer:

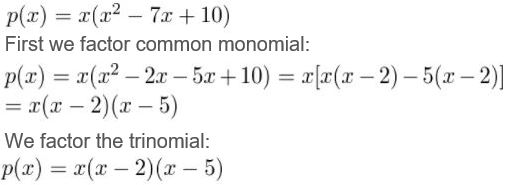
Question 2.
3n⁷ − 75n⁵

Answer:

Question 3.
8m⁵ − 16m⁴ + 8m³

Answer:

Factor the polynomial completely

Question 4.
a³ + 27
Answer:
Given,
a³ + 27

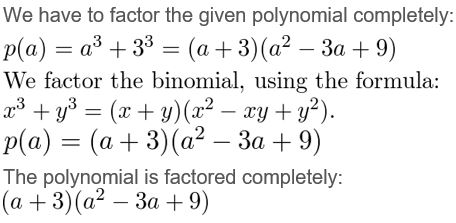
Question 5.
6z⁵ − 750z²

Answer:
Given,
6z⁵ − 750z²

Question 6.
x³ + 4x² − x − 4
Answer:
Given,
x³ + 4x² − x − 4

Question 7.
3y³ + y² + 9y + 3
Answer:
Given,
3y³ + y² + 9y + 3

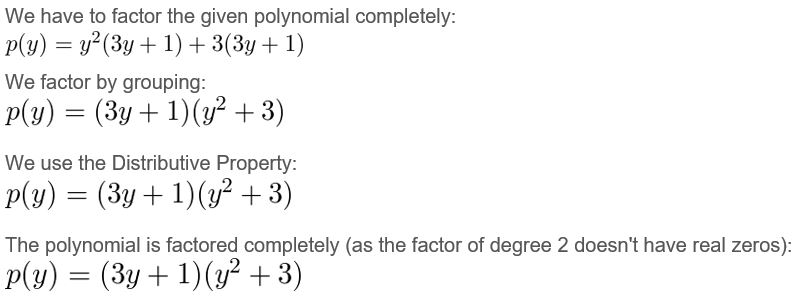
Question 8.
−16n⁴ + 625
Answer:
Given,
−16n⁴ + 625

Question 9.
5w⁶ − 25w⁴ + 30w²

Answer:
Given,
5w⁶ − 25w⁴ + 30w²

Question 10.
Determine whether x− 4 is a factor of f(x) = 2x² + 5x − 12.
Answer:
Given,
f(x) = 2x² + 5x − 12

Question 11.
Show that x − 6 is a factor of f(x) = x³ − 5x² − 6x. Then factor f(x) completely.
Answer:
Given,
f(x) = x³ − 5x² − 6x

Question 12.
In Example 7, does your answer change when you first determine whether 2 is a zero and then whether −1 is a zero? Justify your answer.
Answer:

Factoring Polynomials 4.4 Exercises

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE The expression 9x⁴ − 49 is in _________ form because it can be written as u² − 49 where u = _____.
Answer:
The expression 9x⁴ − 49 is in Quadratic form because it can be written as u² − 49 where u = 3x².

Question 2.
VOCABULARY Explain when you should try factoring a polynomial by grouping.
Answer:

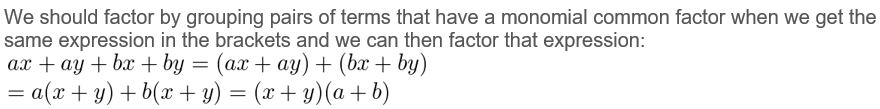
Question 3.
WRITING How do you know when a polynomial is factored completely?
Answer:

Question 4.
WRITING Explain the Factor Theorem and why it is useful.
Answer:

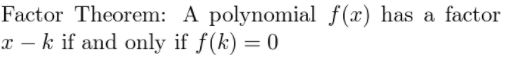
Monitoring Progress and Modeling with Mathematics

In Exercises 5–12, factor the polynomial completely.

Question 5.
x³ − 2x² − 24x
Answer:
Given,

Question 6.
4k⁵ − 100k³
Answer:
Given,

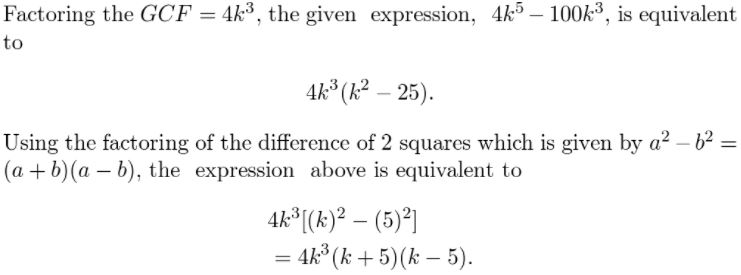
Question 7.
3p⁵ − 192p³
Answer:
Given,

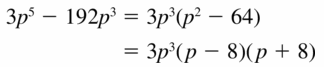
Question 8.
2m⁶ − 24m⁵ + 64m⁴
Answer:
Given,

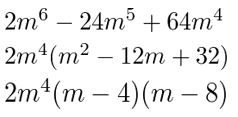
Question 9.
2q⁴ + 9q³ − 18q²
Answer:
Given,
2q⁴ + 9q³ − 18q²

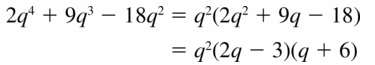
Question 10.
3r⁶ − 11r⁵ − 20r⁴
Answer:
Given,

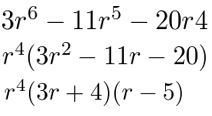
Question 11.
10w¹⁰ − 19w⁹ + 6w⁸
Answer:
Given,

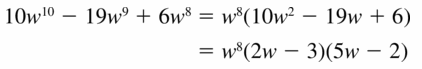
Question 12.
18v⁹ + 33v⁸ + 14v⁷
Answer:
Given,

In Exercises 13–20, factor the polynomial completely.

Question 13.
x³ + 64
Answer:
Given,

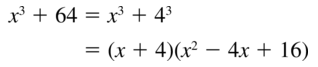
Question 14.
y³ + 512
Answer:
Given,

Question 15.
g³ − 343
Answer:
Given,

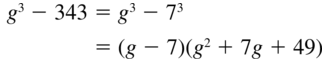
Question 16.
c³ − 27
Answer:
Given,

Question 17.
3h⁹ − 192h⁶
Answer:
Given,

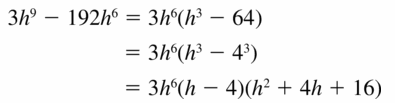
Question 18.
9n⁶ − 6561n³
Answer:
Given,

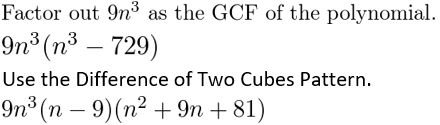
Question 19.
16t⁷ + 250t⁴
Answer:
Given,

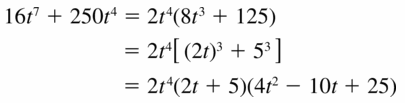
Question 20.
135z¹¹ − 1080z⁸
Answer:
Given,

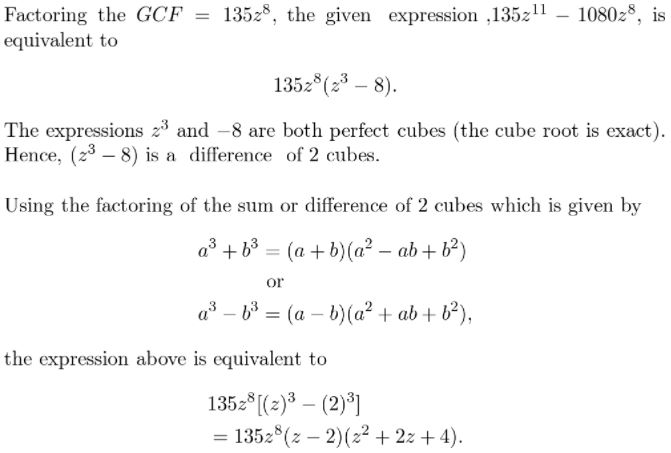
ERROR ANALYSIS In Exercises 21 and 22, describe and correct the error in factoring the polynomial.

Question 21.

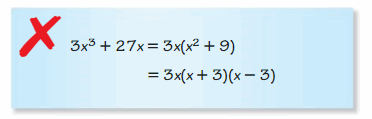
Answer:

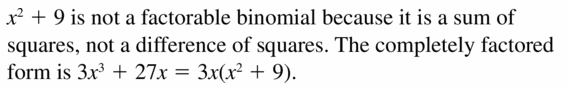
Question 22.

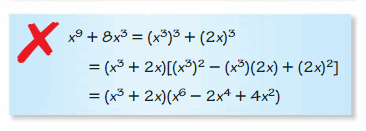
Answer:

In Exercises 23–30, factor the polynomial completely.

Question 23.
y³ − 5y² + 6y − 30
Answer:
Given,

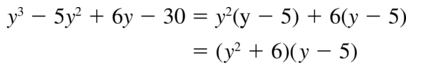
Question 24.
m³ − m² + 7m − 72
Answer:
Given,

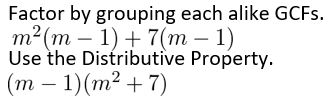
Question 25.
3a³ + 18a² + 8a + 48
Answer:
Given,

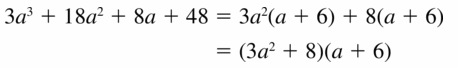
Question 26.
2k³ − 20k² + 5k − 50
Answer:
Given,

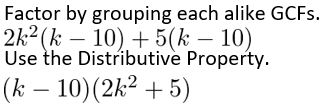
Question 27.
x³ − 8x² − 4x + 32
Answer:
Given,

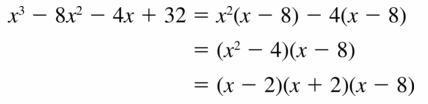
Question 28.
z³ − 5z² − 9z + 45
Answer:
Given,
z³ − 5z² − 9z + 45

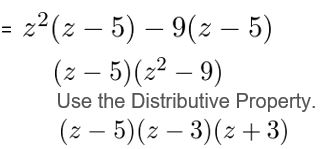
Question 29.
4q³ − 16q⁷ − 9q + 36
Answer:
Given,

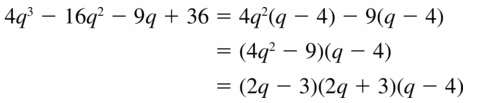
Question 30.
16n³ + 32n⁷ − n − 2
Answer:
Given,

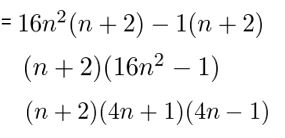
In Exercises 31–38, factor the polynomial completely.

Question 31.
49k⁴ − 9
Answer:
Given,

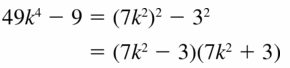
Question 32.
4m⁴ − 25
Answer:
Given,
4m⁴ − 25

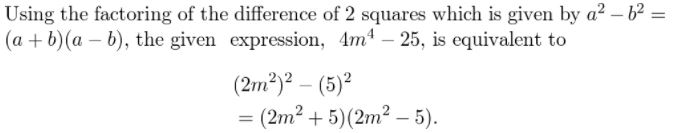
Question 33.
c⁴ + 9c² + 20
Answer:
Given,
c⁴ + 9c² + 20

Question 34.
y⁴ − 3y² − 28
Answer:
Given,

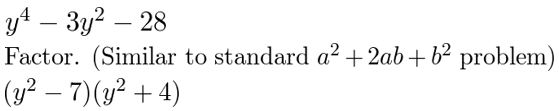
Question 35.
16z⁴ − 81
Answer:
Given,
16z⁴ − 81

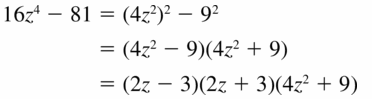
Question 36.
81a⁴ − 256
Answer:
Given,
81a⁴ − 256

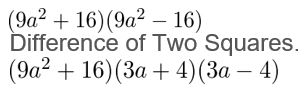
Question 37.
3r⁸ + 3r⁵ − 60r²
Answer:
Given,
3r⁸ + 3r⁵ − 60r²

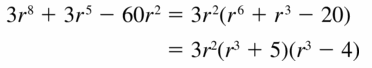
Question 38.
4n¹² − 32n⁷ + 48n²
Answer:
Given,
4n¹² − 32n⁷ + 48n²

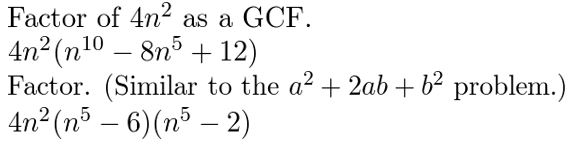
In Exercises 39–44, determine whether the binomial is a factor of the polynomial.

Question 39.
f(x) = 2x³ + 5x² − 37x − 60; x − 4
Answer:
Given,
f(x) = 2x³ + 5x² − 37x − 60
x – 4 = 0
x = 4

Question 40.
g(x) = 3x³ − 28x² + 29x + 140; x + 7
Answer:
Given,
g(x) = 3x³ − 28x² + 29x + 140

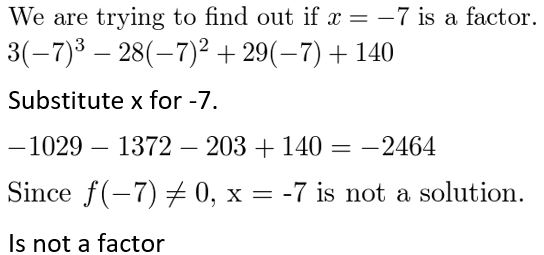
Question 41.
h(x) = 6x⁵ − 15x⁴ − 9x³; x + 3
Answer:
Given,
h(x) = 6x⁵ − 15x⁴ − 9x³

Question 42.
g(x) = 8x⁵ − 58x⁴ + 60x³ + 140; x − 6
Answer:
Given,
g(x) = 8x⁵ − 58x⁴ + 60x³ + 140

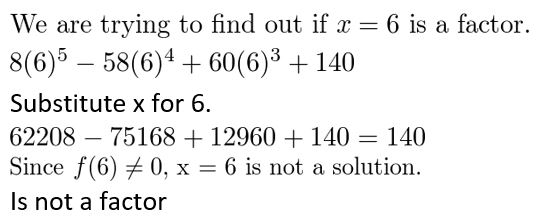
Question 43.
h(x) = 6x⁴ − 6x³ − 84x² + 144x; x + 4
Answer:
Given,
h(x) = 6x⁴ − 6x³ − 84x² + 144x
x + 4 = 0
x = -4

Question 44.
t(x) = 48x⁴ + 36x³ − 138x² − 36x; x + 2
Answer:
Given,
t(x) = 48x⁴ + 36x³ − 138x² − 36x
x + 2 = 0
x = -2

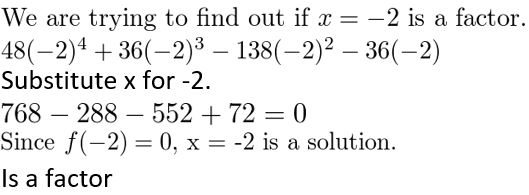
In Exercises 45–50, show that the binomial is a factor of the polynomial. Then factor the polynomial completely.

Question 45.
g(x) = x³ − x² − 20x; x + 4
Answer:
Given,
g(x) = x³ − x² − 20x
x + 4 = 0
x = -4

Question 46.
t(x) = x³ − 5x² − 9x + 45; x − 5
Answer:
Given,
t(x) = x³ − 5x² − 9x + 45
x – 5 = 0
x = 5

Question 47.
f(x) = x⁴ − 6x³ − 8x + 48; x − 6
Answer:
Given,
f(x) = x⁴ − 6x³ − 8x + 48
x – 6 = 0
x = 6

Question 48.
s(x) = x⁴ + 4x³ − 64x − 256; x + 4
Answer:
Given,
s(x) = x⁴ + 4x³ − 64x − 256
x + 4 = 0
x = -4

Question 49.
r(x) = x³ − 37x + 84; x + 7
Answer:
Given,
r(x) = x³ − 37x + 84
x + 7 = 0
x = -7

Question 50.
h(x) = x³ − x² − 24x − 36; x + 2
Answer:
Given,
h(x) = x³ − x² − 24x − 36
x + 2 = 0
x = -2

ANALYZING RELATIONSHIPS In Exercises 51–54, match the function with the correct graph. Explain your reasoning.

Question 51.
f(x) = (x − 2)(x − 3)(x + 1)
Answer:
Given,
f(x) = (x − 2)(x − 3)(x + 1)
x – 2 = 0
x = 1
x – 3 = 0
x = 3
x + 1 = 0
x = -1

Question 52.
g(x) = x(x + 2)(x + 1)(x − 2)
Answer:
Given,
g(x) = x(x + 2)(x + 1)(x − 2)
x = 0
x + 2 = 0
x = -2
x + 1 = 0
x = -1
x – 2 = 0
x = 2
To easily determine the zeroes of the graph, set each factor equal to zero.
Zeroes: 0, -2, -1,2
Based on the zeroes, match them with the graph that has the same number of zeroes at the same location.

Question 53.
h(x) = (x + 2)(x + 3)(x − 1)
Answer:
Given,
h(x) = (x + 2)(x + 3)(x − 1)
x + 2 = 0
x = -2
x + 3 = 0
x = -3
x – 1 = 0
x = 1

Question 54.
k(x) = x(x − 2)(x − 1)(x + 2)

Answer:
Given,
k(x) = x(x − 2)(x − 1)(x + 2)
x = 0
x – 2 = 0
x = 2
x – 1 = 0
x = 1
x + 2 = 0
x = -2
To easily determine the zeroes of the graph, set each factor equal to zero.
Zeroes: 0, 2, 1, -2
Based on the zeroes, match them with the graph that has the same number of zeroes at the same location.

Question 55.
MODELING WITH MATHEMATICS The volume (in cubic inches) of a shipping box is modeled by V = 2x³ − 19x² + 39x, where x is the length (in inches). Determine the values of x for which the model makes sense. Explain your reasoning.

Answer:

Question 56.
MODELING WITH MATHEMATICS The volume (in cubic inches) of a rectangular birdcage can be modeled by V = 3x³ − 17x² + 29x − 15, where x is the length (in inches). Determine the values of x for which the model makes sense. Explain your reasoning.

Answer:

USING STRUCTURE In Exercises 57–64, use the method of your choice to factor the polynomial completely. Explain your reasoning.

Question 57.
a⁶ + a⁵ − 30a⁴
Answer:
Given,
a⁶ + a⁵ − 30a⁴

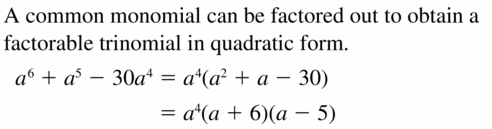
Question 58.
8m³ − 343
Answer:
Given,
8m³ − 343

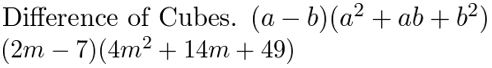
Question 59.
z³ − 7z² − 9z + 63
Answer:
Given,
z³ − 7z² − 9z + 63

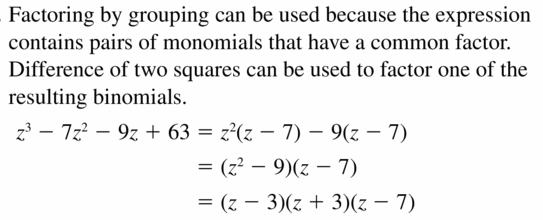
Question 60.
2p⁸ − 12p⁵ + 16p²
Answer:
Given,
2p⁸ − 12p⁵ + 16p²

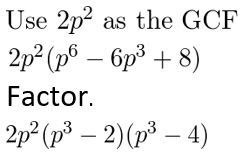
Question 61.
64r³ + 729
Answer:
Given,
64r³ + 729

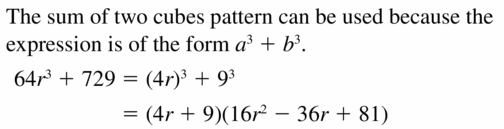
Question 62.
5x⁵ − 10x⁴ − 40x³
Answer:
Given,
5x⁵ − 10x⁴ − 40x³

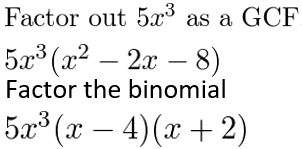
Question 63.
16n⁴ − 1
Answer:
Given,
16n⁴ − 1

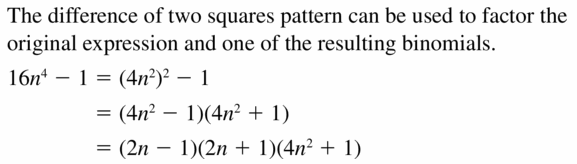
Question 64.
9k³ − 24k² + 3k − 8
Answer:
Given,
9k³ − 24k² + 3k − 8

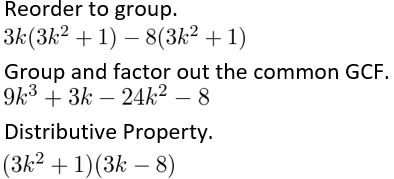
Question 65.
REASONING Determine whether each polynomial is factored completely. If not, factor completely.
a. 7z⁴(2z² − z − 6)
b. (2 − n)(n² + 6n)(3n − 11)
c. 3(4y − 5)(9y² − 6y − 4)
Answer:

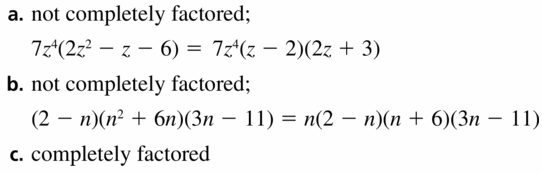
Question 66.
PROBLEM SOLVING The profit P (in millions of dollars) for a T-shirt manufacturer can be modeled by P = −x³ + 4x² + x, where x is the number (in millions) of T-shirts produced. Currently the company produces 4 million T-shirts and makes a profit of $4 million. What lesser number of T-shirts could the company produce and still make the same profit?

Answer:

Question 67.
PROBLEM SOLVING The profit P (in millions of dollars) for a shoe manufacturer can be modeled by P = −21x³ + 46x, where x is the number (in millions) of shoes produced. The company now produces 1 million shoes and makes a profit of $25 million, but it would like to cut back production. What lesser number of shoes could the company produce and still make the same profit?
Answer:

Question 68.
THOUGHT PROVOKING Find a value of k such that \(\frac{f(x)}{x-k}\) has a remainder of 0. Justify your answer.
Answer:

Question 69.
COMPARING METHODS You are taking a test where calculators are not permitted. One question asks you to evaluate g(7) for the function g(x) = x³ − 7x² − 4x + 28. You use the Factor Theorem and synthetic division and your friend uses direct substitution. Whose method do you prefer? Explain your reasoning.
Answer:

Question 70.
MAKING AN ARGUMENT You divide f(x) by (x−a) and find that the remainder does not equal 0. Your friend concludes that f(x) cannot be factored. Is your friend correct? Explain your reasoning.
Answer:

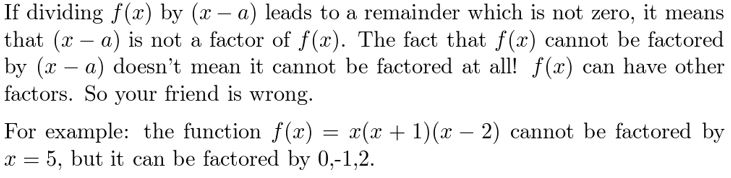
Question 71.
CRITICAL THINKING What is the value of k such that x− 7 is a factor of h(x) = 2x³ − 13x² − kx + 105? Justify your answer.
Answer:

Question 72.
HOW DO YOU SEE IT? Use the graph to write an equation of the cubic function in factored form. Explain your reasoning.

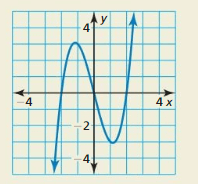
Answer:

Question 73.
ABSTRACT REASONING Factor each polynomial completely.
a. 7ac² + bc² − 7ad² − bd²
b. x²ⁿ − 2xⁿ + 1
c. a⁵b² − a²b⁴ + 2a⁴b − 2ab³ + a³ − b²
Answer:

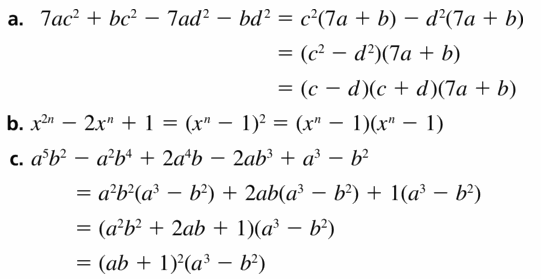
Question 74.
REASONING The graph of the function f(x) = x⁴ + 3x³ + 2x² + x + 3 is shown. Can you use the Factor Theorem to factor f(x)? Explain.
Answer:

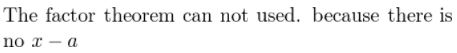
Question 75.
MATHEMATICAL CONNECTIONS The standard equation of a circle with radius r and center (h, k) is (x − h)² + (y − k)² = r². Rewrite each equation of a circle in standard form. Identify the center and radius of the circle. Then graph the circle.

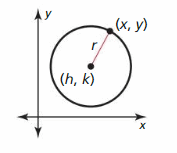
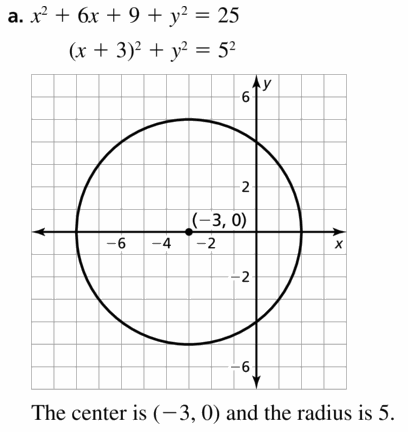
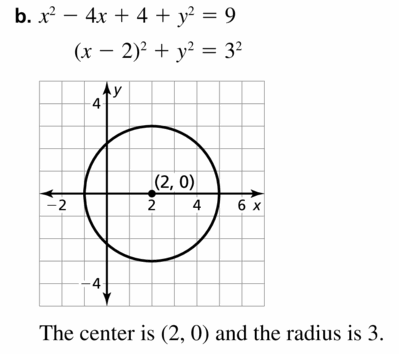
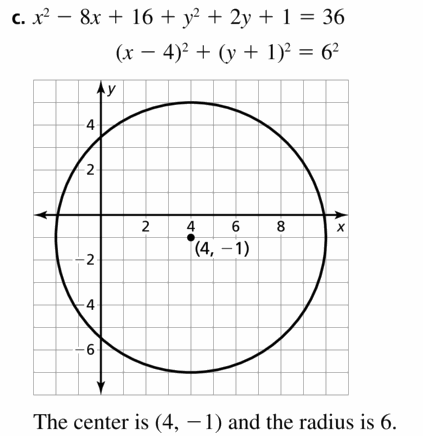
a. x² + 6x + 9 + y² = 25
b. x² − 4x + 4 + y² = 9
c. x² − 8x + 16 + y² + 2y + 1 = 36
Answer:

Question 76.
CRITICAL THINKING Use the diagram to complete parts (a)–(c).
a. Explain why a³ − b³ is equal to the sum of the volumes of the solids I, II, and III.
b. Write an algebraic expression for the volume of each of the three solids. Leave your expressions in factored form.
c. Use the results from part (a) and part (b) to derive the factoring pattern a³ − b³.

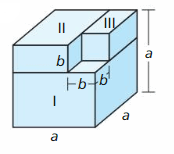
Answer:

Maintaining Mathematical Proficiency

Solve the quadratic equation by factoring.(Section 3.1)

Question 77.
x² − x − 30 = 0
Answer:
Given,

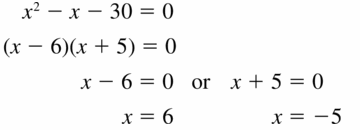
The solution is x = 6 and x = -5

Question 78.
2x² − 10x − 72 = 0
Answer:
Given,
2x² − 10x − 72 = 0

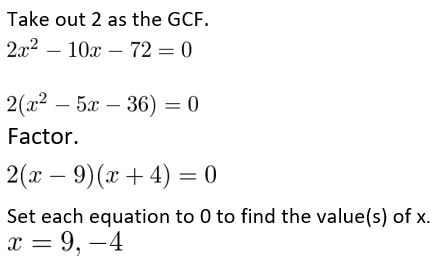
Question 79.
3x² − 11x + 10 = 0
Answer:
Given,

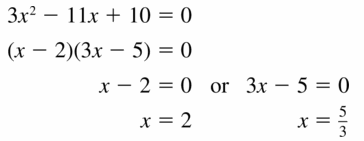
Question 80.
9x² − 28x + 3 = 0
Answer:
Given,

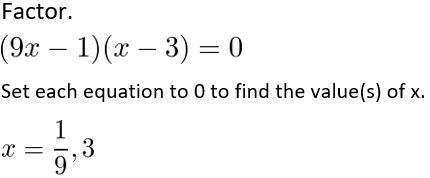
Solve the quadratic equation by completing the square.(Section 3.3)

Question 81.
x² − 12x + 36 = 144
Answer:
Given,

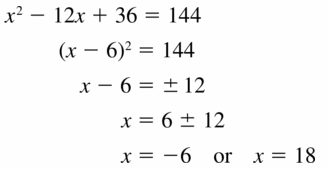
Question 82.
x² − 8x − 11 = 0
Answer:
Given,
x² − 8x − 11 = 0

Question 83.
3x² + 30x + 63 = 0
Answer:
Given,

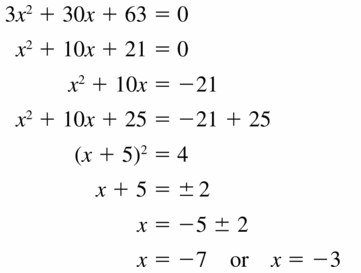
The solution is x = -7 and x = -3.

Question 84.
4x² + 36x − 4 = 0
Answer:
Given,
4x² + 36x − 4 = 0

Polynomial Functions Study Skills : Keeping Your Mind Focused

4.1–4.4 What Did You Learn?

Core Vocabulary

Core Concepts
Section 4.1

Section 4.2

Section 4.3

Section 4.4

Mathematical Practices

Question 1.
Describe the entry points you used to analyze the function in Exercise 43 on page 164.

Question 2.
Describe how you maintained oversight in the process of factoring the polynomial in Exercise 49 on page 185.

Study Skills
Keeping Your Mind Focused

• When you sit down at your desk, review your notes from the last class.
• Repeat in your mind what you are writing in your notes.
• When a mathematical concept is particularly difficult, ask your teacher for another example.

Polynomial Functions 4.1 – 4.4 Quiz

Decide whether the function is a polynomial function. If so, write it in standard form and state its degree, type, and leading coefficient.(Section 4.1)

Question 1.
f(x) = 5 + 2x² − 3x⁴ − 2x − x³

Answer:
Given,
f(x) = 5 + 2x² − 3x⁴ − 2x − x³
The standard form of a polynomial has the exponents of the terms arranged in descending order.
Standard form f (x) = − 3x⁴− x³ + 2x²− 2x+ 5
The degree of a polynomial is the highest exponent of a term.
Degree of the polynomial: 4
Type of function: quadratic
The leading coefficient is the numerical factor of the terms with the highest degree.
Leading coefficient: -3

Question 2.
g(x) = \(\frac{1}{4}\)x³ + 2x − 3x² + 1
Answer:
The type of a polynomial depends on the degree.
Given,
g(x) = \(\frac{1}{4}\)x³ + 2x − 3x² + 1
The standard form of a polynomial has the exponents of the terms arranged in descending order.
Standard form: g(x) = \(\frac{1}{4}\)x³ − 3x² + 2x  + 1
The degree of a polynomial is the highest exponent of a term.
Degree of the polynomial: 3
Type of function: a quadratic function
The leading coefficient is the numerical factor of the terms with the highest degree.
Leading coefficient: \(\frac{1}{4}\)

Question 3.
h(x) = 3 − 6x³ + 4x − 2 + 6x
Answer:
Given,
h(x) = 3 − 6x³ + 4x − 2 + 6x
The standard form of a polynomial has the exponents of the terms arranged in descending order.
Standard form:
h(x) = 3 − 6x³ + 4x − 2 + 6x
h(x) = − 6x³ + 10x + 1
The degree of a polynomial is the highest exponent of a term.
Degree of the polynomial: 3
The type of a polynomial depends on the degree.
Type of polynomial: quadratic
The leading coefficient is the numerical factor of the terms with the highest degree.
Leading coefficient: -6

Question 4.
Describe the x-values for which
(a) f is increasing or decreasing,
(b) f(x) > 0, and
(c) f(x) < 0. (Section 4.1)
Answer:

 

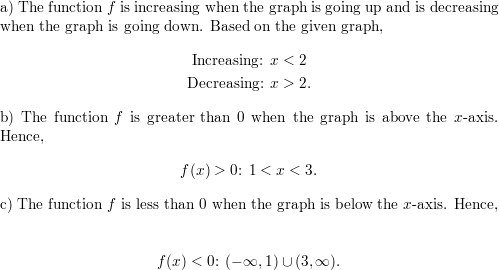
Question 5.
Write an expression for the area and perimeter for the figure shown. (Section 4.2)

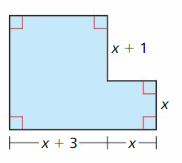
Answer:

Figure 1:
L = (x + 3)
W = (x + 1)
We know that,
Area of the rectangle = l × w
Area of the rectangle = (x + 3)(x + 1)
= x(x + 1) + 3(x + 1)
x² + x + 3x + 3
x² + 4x + 3
A = x² + 4x + 3
Perimeter = 2((x + 3) + (x + 1))
2(x + 3 + x + 1)
= 2(2x + 4)
= 4x + 8
Figure 2:
L = x
W = (2x + 3)
We know that,
Area of the rectangle = l × w
Area of the rectangle = x(2x + 3)
2x² + 3x
A = 2x² + 3x
P = 2(L + W)
Perimeter = 2(x + 2x + 3)
= 2(3x + 3)
= 6x + 6

Question 6.
(7x² − 4) − (3x² − 5x + 1)
Answer:
Given,

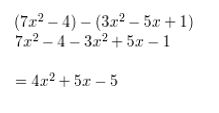
Question 7.
(x² − 3x + 2)(3x − 1)
Answer:
Given,

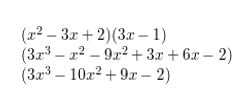
Question 8.
(x − 1)(x + 3)(x − 4)
Answer:
Given,

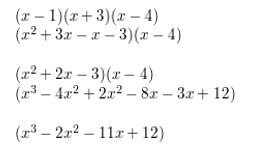
Question 9.
Use Pascal’s Triangle to expand (x + 2)⁵. (Section 4.2)
Answer:
Given,
(x + 2)⁵.
We need to expand the expression.
This is in the form of (a + b)⁵ = a⁵b⁰ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + a⁰b⁵
(x + 2)⁵ = x⁵(2⁰) + 5x⁴(2) + 10x³(2)² + 10x²(2)³ + 5x(2)⁴ + x⁰(2)⁵
= x⁵ + 10x⁴ + 40x³ + 80x² + 80x + 32
So, (x + 2)⁵ = x⁵ + 10x⁴ + 40x³ + 80x² + 80x + 32

Question 10.
Divide 4x⁴ − 2x³ + x² − 5x + 8 by x² − 2x − 1. (Section 4.3)
Answer:

Factor the polynomial completely.(Section 4.4)

Question 11.
a³ − 2a² − 8a
Answer:

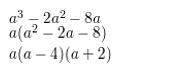
Question 12.
8m³ + 27
Answer:

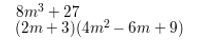
Question 13.
z³ + z² − 4z − 4
Answer:

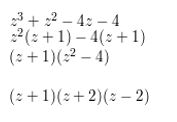
Question 14.
49b⁴ − 64
Answer:

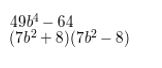
Question 15.
Show that x + 5 is a factor of f(x) = x³ − 2x² − 23x + 60. Then factor f(x) completely. (Section 4.4)
Answer:

Question 16.
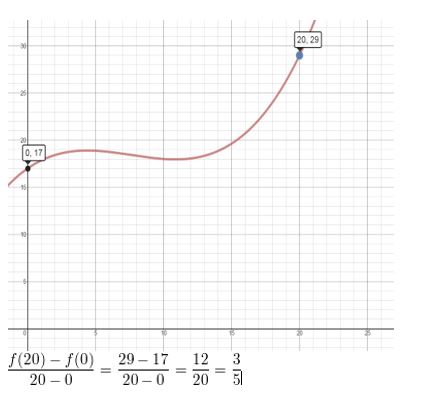
The estimated price P (in cents) of stamps in the United States can be modeled by the polynomial function P(t)= 0.007t³ − 0.16t² + 1t + 17, where t represents the number of years since 1990. (Section 4.1)
a. Use a graphing calculator to graph the function for the interval 0 ≤ t ≤ 20. Describe the behavior of the graph on this interval.
b. What was the average rate of change in the price of stamps from 1990 to 2010?
Answer:

Question 17.
The volume V (in cubic feet) of a rectangular wooden crate is modeled by the function V(x) = 2x³ − 11x² + 12x, where x is the width (in feet) of the crate. Determine the values of x for which the model makes sense. Explain your reasoning. (Section 4.4)

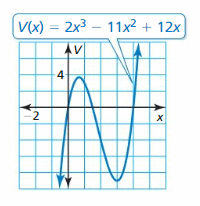
Answer:

Lesson 4.5 Solving Polynomial Equations

Essential Question
How can you determine whether a polynomial equation has a repeated solution?

EXPLORATION 1
Cubic Equations and Repeated Solutions
Work with a partner. Some cubic equations have three distinct solutions. Others have repeated solutions. Match each cubic polynomial equation with the graph of its related polynomial function. Then solve each equation. For those equations that have repeated solutions, describe the behavior of the related function near the repeated zero using the graph or a table of values.

a. x³ − 6x² + 12x − 8 = 0
b. x³ + 3x² + 3x + 1 = 0
c. x³− 3x + 2 = 0
d. x³ + x² − 2x = 0
e. x³ − 3x − 2 = 0
f. x³ − 3x² + 2x = 0

EXPLORATION 2
Quartic Equations and Repeated Solutions
Work with a partner. Determine whether each quartic equation has repeated solutions using the graph of the related quartic function or a table of values. Explain your reasoning. Then solve each equation.
a. x⁴ − 4x³ + 5x² − 2x = 0
b. x⁴ − 2x³ − x² + 2x = 0
c. x⁴ − 4x³ + 4x² = 0
d. x⁴ + 3x³ = 0

Communicate Your Answer

Question 3.
How can you determine whether a polynomial equation has a repeated solution?
Answer:
A solution of a polynomial is a repeated solution if and only if when the polynomial is written in the factored form then it appears more than once.

Question 4.
Write a cubic or quartic polynomial equation that is different from the equations in Explorations 1 and 2 and has a repeated solution.
Answer:

4.5 Lesson

Monitoring Progress

Solve the equation.

Question 1.
4x⁴ − 40x² + 36 = 0
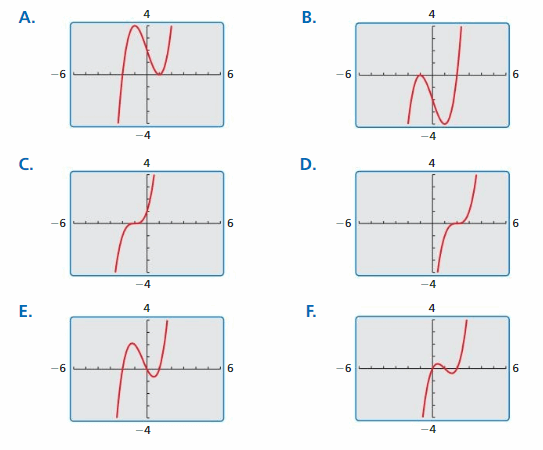
Answer:

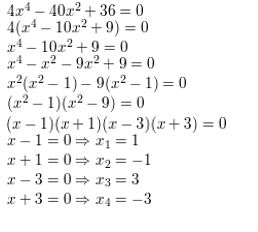
Question 2.
2x⁵ + 24x = 14x³

Answer:

Find the zeros of the function. Then sketch a graph of the function.

Question 3.
f(x) = 3x⁴ − 6x² + 3
Answer:

Question 4.
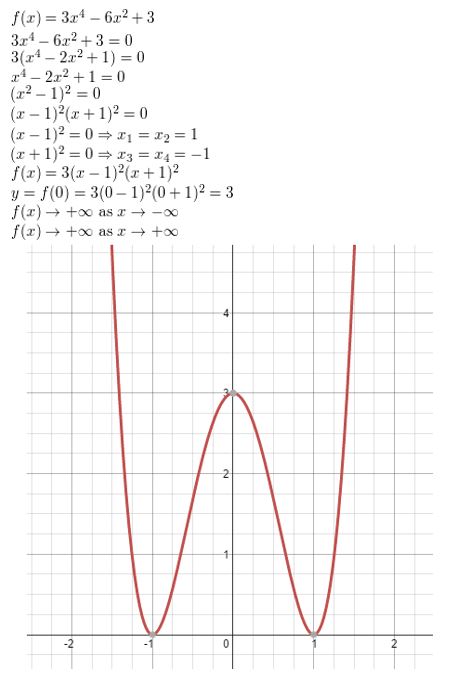
f(x) = x³ + x² − 6x
Answer:

Question 5.
Find all real solutions of x³ − 5x² − 2x + 24 = 0.

Question 6.
Find all real zeros of f(x) = 3x⁴ − 2x³ − 37x² + 24x + 12.
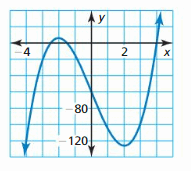
Answer:

Question 7.
Write a polynomial function f of least degree that has rational coefficients, aleading coefficient of 1, and the zeros 4 and 1 − \(\sqrt{5}\).
Answer:

Solving Polynomial Equations 4.5 Exercises

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE If a polynomial function f has integer coefficients, then every rational solution of f(x) = 0 has the form \(\frac{p}{q}\), where p is a factor of the _____________ and q is a factor of the _____________.
Answer:
If a polynomial function f has integer coefficients, then every rational solution of f(x) = 0 has the form \(\frac{p}{q}\), where p is a factor of the constant term and q is a factor of the leading coefficient.

Question 2.
DIFFERENT WORDS, SAME QUESTION Which is different? Find “both” answers.

Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3–12, solve the equation.

Question 3.
z³ − z² − 12z = 0
Answer:

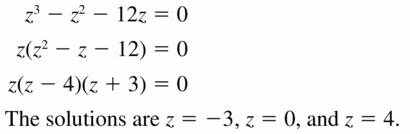
Question 4.
a³ − 4a² + 4a = 0
Answer:

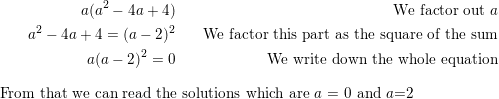
Question 5.
2x⁴ − 4x³ = −2x²
Answer:

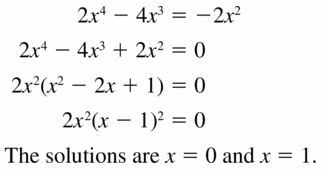
Question 6.
v³ − 2v² − 16v = − 32
Answer:

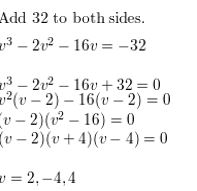
Question 7.
5w³ = 50w
Answer:

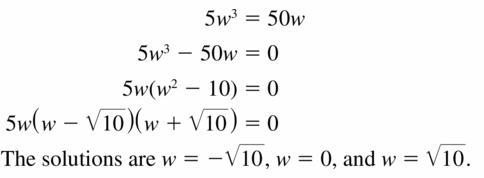
Question 8.
9m⁵ = 27m³
Answer:

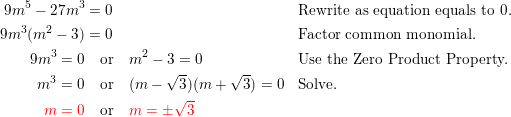
Question 9.
2c⁴ − 6c³ = 12c² − 36c
Answer:

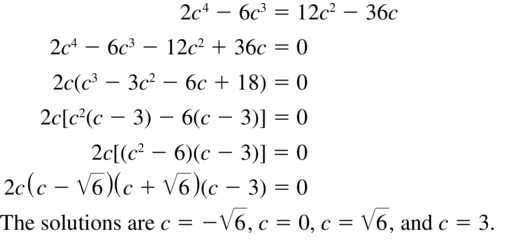
Question 10.
p⁴ + 40 = 14p²
Answer:

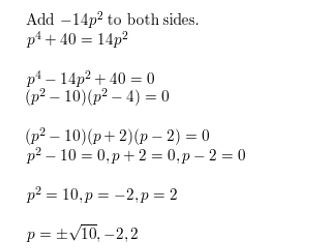
Question 11.
12n² + 48n = −n³ − 64
Answer:

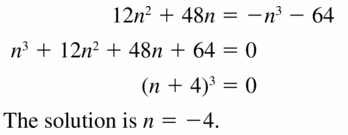
Question 12.
y³ − 27 = 9y² − 27y
Answer:
Given,
y³ − 27 = 9y² − 27y
Take (y – 3) as a common factor
(y – 3)(y^2 + 3y + 9) = 9y(y – 3)
(y – 3)(y^2 + 3y + 9) – 9y(y – 3) = 0
(y – 3)(y^2 + 3y + 9 – 9y) = 0
(y – 3)(y^2 – 6y + 9) = 0
(y – 3)(y – 3)(y – 3) = 0
(y – 3)^3 = 0
y – 3 = 0
y = 3

In Exercises 13–20, find the zeros of the function. Then sketch a graph of the function.

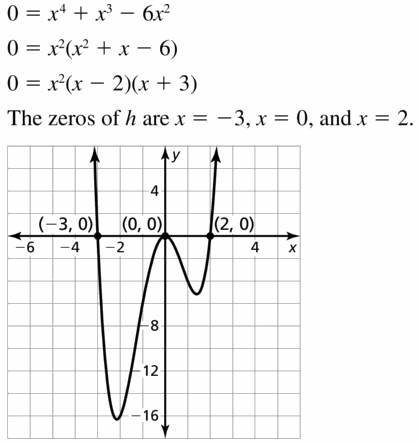
Question 13.
h(x) = x⁴ + x³ − 6x²
Answer:

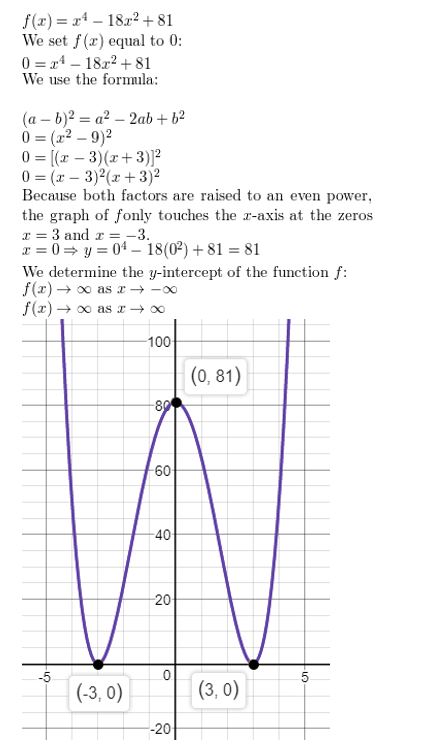
Question 14.
f(x) = x⁴ − 18x² + 81
Answer:

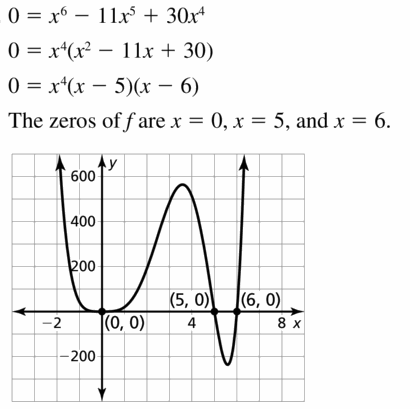
Question 15.
p(x) = x⁶ − 11x⁵ + 30x⁴
Answer:

Question 16.
g(x) = −2x⁵ + 2x⁴ + 40x³
Answer:

Question 17.
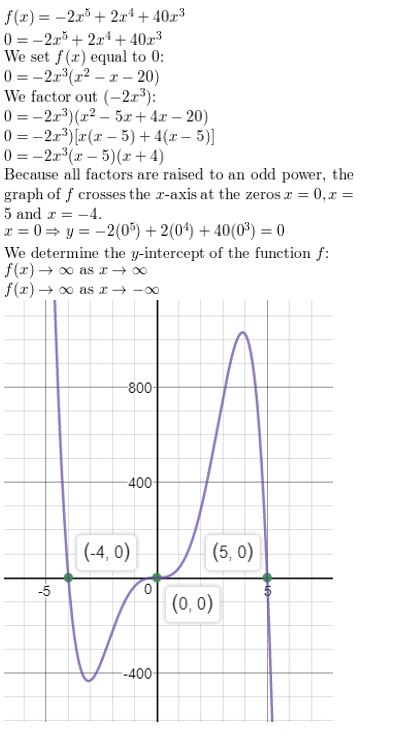
g(x) = −4x⁴ + 8x³ + 60x²
Answer:

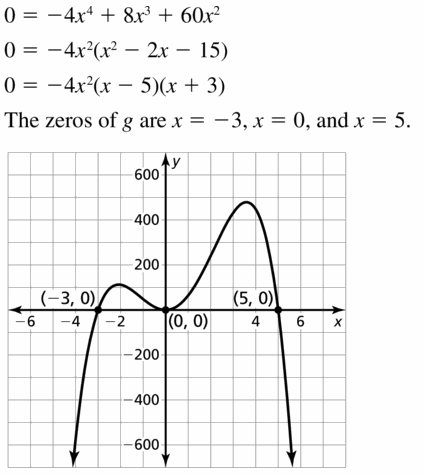
Question 18.
h(x) = −x³ − 2x² + 15x
Answer:

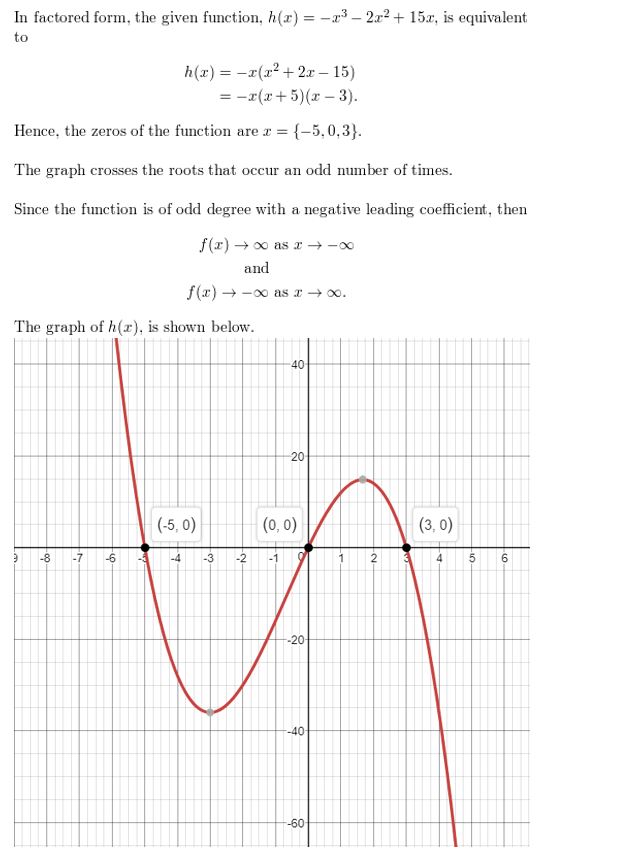
Question 19.
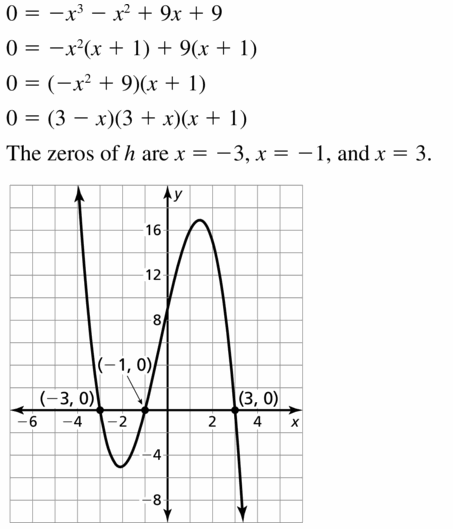
h(x) = −x³ − x² + 9x + 9
Answer:

Question 20.
p(x) = x³ − 5x² − 4x + 20
Answer:

Question 21.
USING EQUATIONS According to the Rational Root Theorem, which is not a possible solution of the equation 2x⁴ − 5x³ + 10x² − 9 = 0?
A. −9
B. −\([\frac{1}{2}/latex]
C. [latex][\frac{5}{2}/latex]
D. 3
Answer:

Question 22.
USING EQUATIONS According to the Rational Root Theorem, which is not a possible zero of the function f(x) = 40x⁵ − 42x⁴ − 107x³ + 107x² + 33x − 36?
A. −[latex][\frac{2}{3}/latex]
B. − [latex][\frac{3}{8}/latex]
C. [latex][\frac{3}{4}/latex]
D. [latex][\frac{4}{5}/latex]
Answer: Option A is the correct answer

ERROR ANALYSIS In Exercises 23 and 24, describe and correct the error in listing the possible rational zeros of the function.

Question 23.

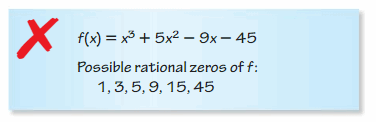
Answer:

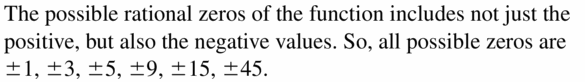
Question 24.

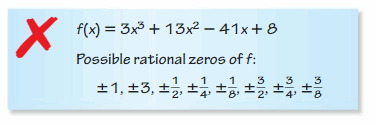
Answer:

In Exercises 25–32, find all the real solutions of the equation.

Question 25.
x³ + x² − 17x + 15 = 0
Answer:

Question 26.
x³ − 2x² − 5x + 6 = 0
Answer:

Question 27.
x³ − 10x² + 19x + 30 = 0
Answer:
Given,
x³ − 10x² + 19x + 30 = 0

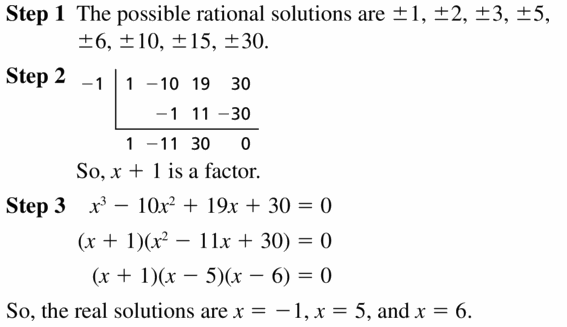
Question 28.
x³ + 4x² − 11x − 30 = 0
Answer:
Given,
x³ + 4x² − 11x − 30 = 0

Question 29.
x³ − 6x² − 7x + 60 = 0
Answer:
Given,
x³ − 6x² − 7x + 60 = 0

Question 30.
x³ − 16x² + 55x + 72 = 0
Answer:

Question 31.
2x³ − 3x² − 50x − 24 = 0
Answer:

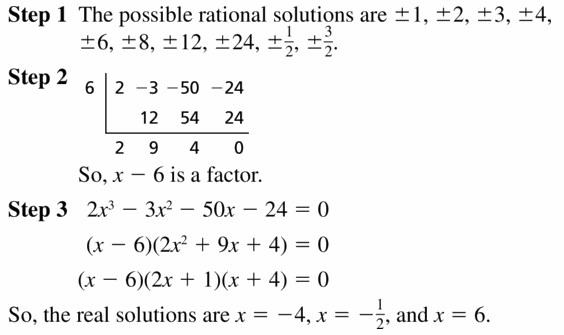
Question 32.
3x³ + x² − 38x + 24 = 0
Answer:

In Exercises 33–38, find all the real zeros of the function.

Question 33.
f(x) = x³ − 2x² − 23x + 60
Answer:
Given,
f(x) = x³ − 2x² − 23x + 60

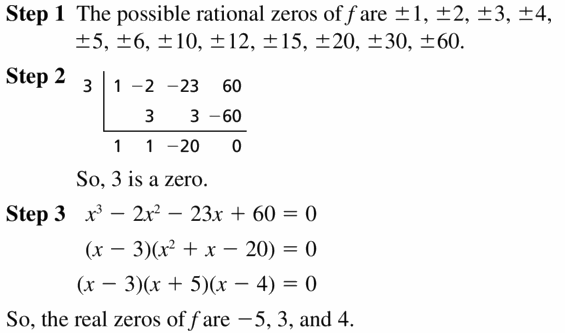
Question 34.
g(x) = x³ − 28x − 48
Answer:
Given,
g(x) = x³ − 28x − 48

Question 35.
h(x) = x³ + 10x² + 31x + 30
Answer:
Given,
h(x) = x³ + 10x² + 31x + 30

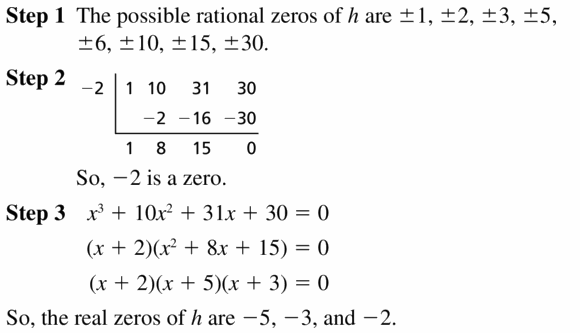
Question 36.
f(x) = x³ − 14x² + 55x − 42
Answer:
Given,
f(x) = x³ − 14x² + 55x − 42

Question 37.
p(x) = 2x³ −x² − 27x + 36
Answer:
Given,
p(x) = 2x³ −x² − 27x + 36

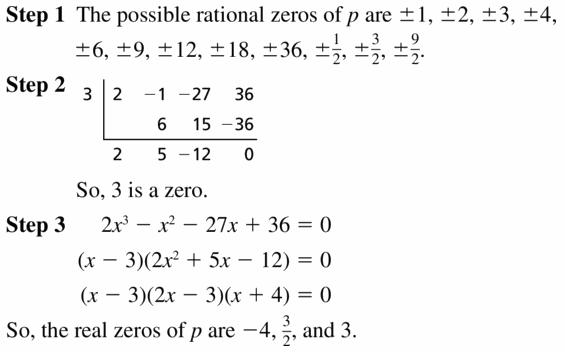
Question 38.
g(x) = 3x³ − 25x² + 58x − 40
Answer:
Given,
g(x) = 3x³ − 25x² + 58x − 40

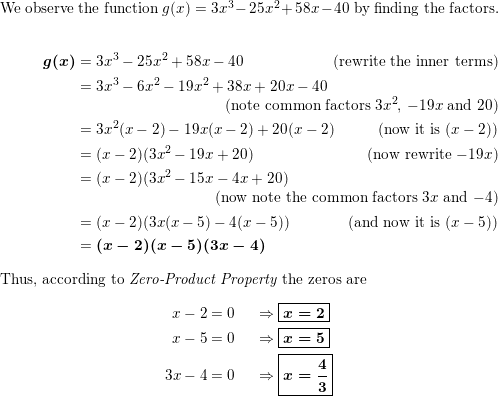
USING TOOLS In Exercises 39 and 40, use the graph to shorten the list of possible rational zeros of the function. Then find all real zeros of the function.

Question 39.
f(x) = 4x³ − 20x + 16

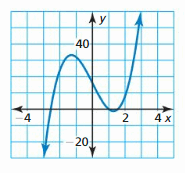
Answer:

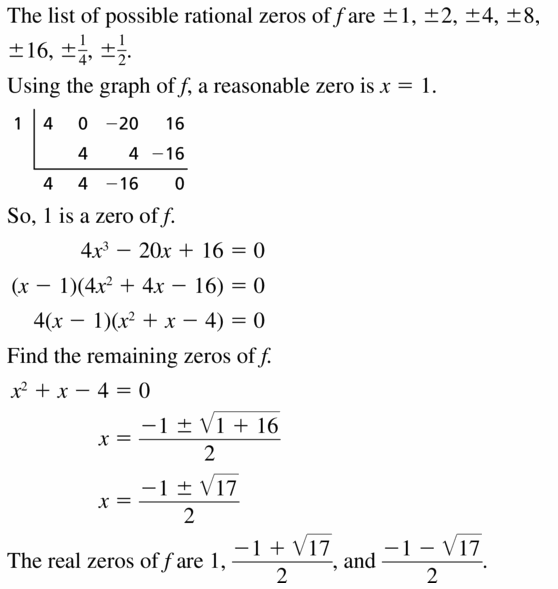
Question 40.
f(x) = 4x³ − 49x − 60

Answer:

In Exercises 41–46, write a polynomial function f of least degree that has a leading coefficient of 1 and the given zeros.

Question 41.
−2, 3, 6
Answer:
Given,
The values of x are −2, 3, 6

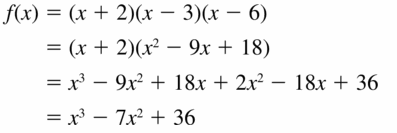
Question 42.
−4, −2, 5
Answer:
Given,
The values of x are −4, −2, 5

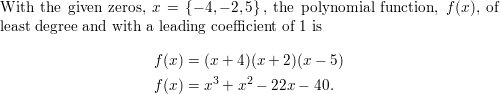
Question 43.
−2, 1 + [latex]\sqrt{7}\)
Answer:
Given,
The values of x are −2, 1 + \(\sqrt{7}\)

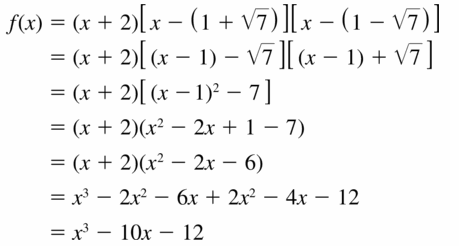
Question 44.
4, 6 − \(\sqrt{7}\)
Answer:
Given,
The values of x are 4, 6 − \(\sqrt{7}\)

Question 45.
−6, 0, 3 −\(\sqrt{5}\)
Answer:
Given,
The values of x are −6, 0, 3 −\(\sqrt{5}\)

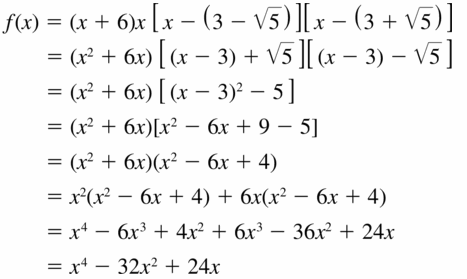
Question 46.
0, 5, −5 + \(\sqrt{8}\)
Answer:
Given,
The values of x are 0, 5, −5 + \(\sqrt{8}\)

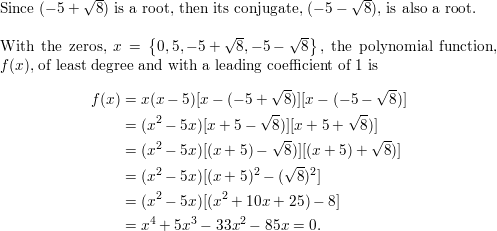
Question 47.
COMPARING METHODS Solve the equation x³ − 4x² − 9x + 36 = 0 using two different methods. Which method do you prefer? Explain your reasoning.
Answer:

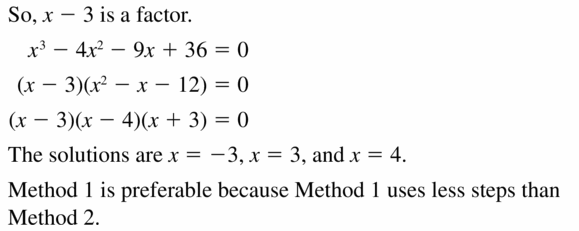
Question 48.
REASONING Is it possible for a cubic function to have more than three real zeros? Explain.
Answer:
No, it is not possible.
A cubic function is to have at most three real zeros.

Question 49.
PROBLEM SOLVING At a factory, molten glass is poured into molds to make paperweights. Each mold is a rectangular prism with a height 3 centimeters greater than the length of each side of its square base. Each mold holds 112 cubic centimeters of glass. What are the dimensions of the mold?
Answer:

Question 50.
MATHEMATICAL CONNECTIONS The volume of the cube shown is 8 cubic centimeters.
a. Write a polynomial equation that you can use to find the value of x.
b. Identify the possible rational solutions of the equation in part (a).
c. Use synthetic division to find a rational solution of the equation. Show that no other real solutions exist.
d. What are the dimensions of the cube?

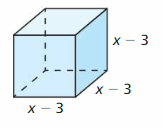
Answer:

Question 51.
PROBLEM SOLVING Archaeologists discovered a huge hydraulic concrete block at the ruins of Caesarea with a volume of 945 cubic meters. The block is x meters high by 12x − 15 meters long by 12x − 21 meters wide. What are the dimensions of the block?

Answer:
Given,
Archaeologists discovered a huge hydraulic concrete block at the ruins of Caesarea with a volume of 945 cubic meters.
The block is x meters high by 12x − 15 meters long by 12x − 21 meters wide.

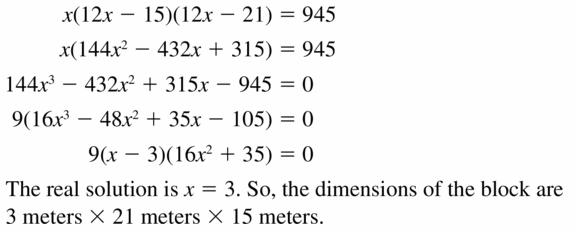
Question 52.
MAKING AN ARGUMENT Your friend claims that when a polynomial function has a leading coefficient of 1 and the coefficients are all integers, every possible rational zero is an integer. Is your friend correct? Explain your reasoning.
Answer:

Question 53.
MODELING WITH MATHEMATICS During a 10-year period, the amount (in millions of dollars) of athletic equipment Esold domestically can be modeled by E(t) = −20t³ + 252t² − 280t + 21,614, where t is in years.
a. Write a polynomial equation to find the year when about $24,014,000,000 of athletic equipment is sold.
b. List the possible whole-number solutions of the equation in part (a). Consider the domain when making your list of possible solutions.
c. Use synthetic division to find when $24,014,000,000 of athletic equipment is sold.
Answer:

Question 54.
THOUGHT PROVOKING Write a third or fourth degree polynomial function that has zeros at ± \(\frac{3}{4}\). Justify your answer.
Answer:

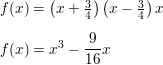
Question 55.
MODELING WITH MATHEMATICS You are designing a marble basin that will hold a fountain for a city park. The sides and bottom of the basin should be 1 foot thick. Its outer length should be twice its outer width and outer height. What should the outer dimensions of the basin be if it is to hold 36 cubic feet of water?

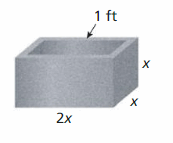
Answer:

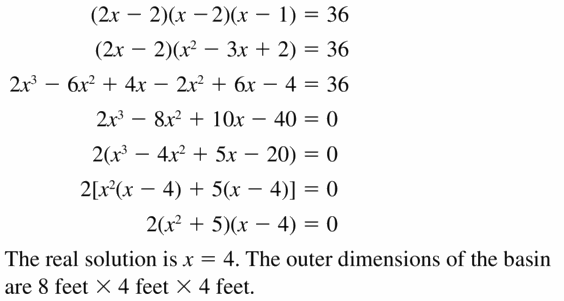
Question 56.
HOW DO YOU SEE IT? Use the information in the graph to answer the questions.

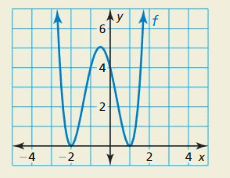
a. What are the real zeros of the function f ?
b. Write an equation of the quartic function in factored form.
Answer:

Question 57.
REASONING Determine the value of k for each equation so that the given x-value is a solution.
a. x³ − 6x² − 7x + k = 0; x = 4
b. 2x³ + 7x² − kx − 18 = 0; x = −6
c. kx³ − 35x² + 19x + 30 = 0; x = 5
Answer:

Question 58.
WRITING EQUATIONS Write a polynomial function gof least degree that has rational coefficients, a leading coefficient of 1, and the zeros −2 + \(\sqrt{7}\) and 3 + \(\sqrt{2}\).
Answer:

In Exercises 59–62, solve f(x) = g(x) by graphing and algebraic methods.

Question 59.
f(x) = x³ + x² − x − 1; g(x) = −x + 1
Answer:

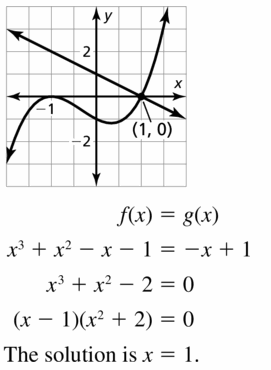
Question 60.
f(x) = x⁴ − 5x³ + 2x² + 8x; g(x) = −x² + 6x − 8
Answer:

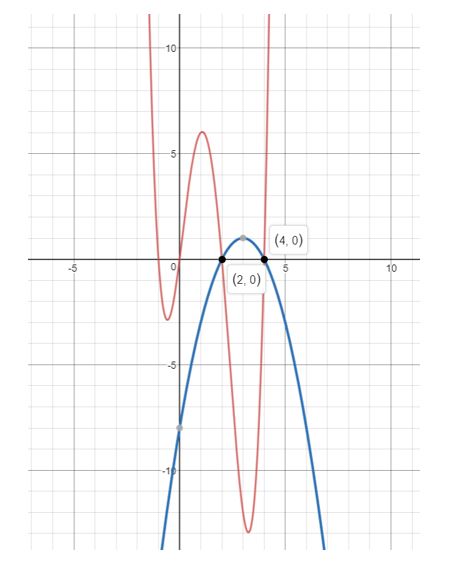
Question 61.
f(x) = x³ − 4x² + 4x; g(x) = −2x + 4
Answer:

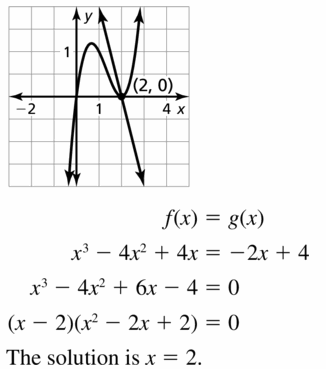
Question 62.
f(x) = x⁴ + 2x³ − 11x² − 12x + 36;
g(x) = −x² − 6x − 9
Answer:

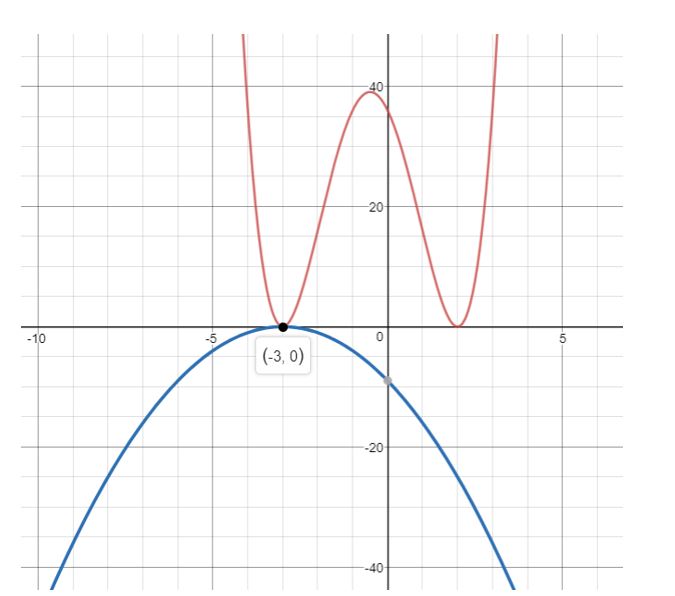
Question 63.
MODELING WITH MATHEMATICS You are building a pair of ramps for a loading platform. The left ramp is twice as long as the right ramp. If 150 cubic feet of concrete are used to build the ramps, what are the dimensions of each ramp?

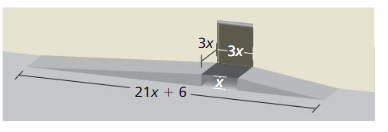
Answer:

Question 64.
MODELING WITH MATHEMATICS Some ice sculptures are made by filling a mold and then freezing it. You are making an ice mold for a school dance. It is to be shaped like a pyramid with a height 1 foot greater than the length of each side of its square base. The volume of the ice sculpture is 4 cubic feet. What are the dimensions of the mold?

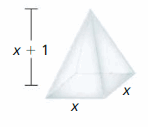
Answer:

Question 65.
ABSTRACT REASONING Let a_n be the leading coefficient of a polynomial function f and a₀ be the constant term. If a_n has r factors and a₀ has s factors, what is the greatest number of possible rational zeros of f that can be generated by the Rational Zero Theorem? Explain your reasoning.
Answer:

Maintaining Mathematical Proficiency

Decide whether the function is a polynomial function. If so, write it in standard form and state its degree, type, and leading coefficient.(Section 4.1)

Question 66.
h(x) = −3x² + 2x − 9 + \(\sqrt{4}\)x³
Answer:
Given,
h(x) = −3x² + 2x − 9 + \(\sqrt{4}\)x³
h(x) =\(\sqrt{4}\)x³ − 3x² + 2x − 9
Degree: 3
Type: Cubic function
Leading Coefficient: \(\sqrt{4}\) or 2

Question 67.
g(x) = 2x³ − 7x² − 3x − 1 + x
Answer:
Given,
g(x) = 2x³ − 7x² − 3x − 1 + x

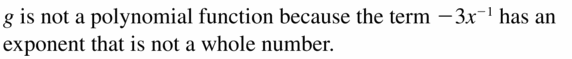
Question 68.
f(x) = \(\frac{1}{3}\)x² + 2x³ − 4x⁴ − \(\sqrt{3}\)
Answer:

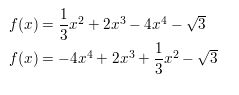
Question 69.
p(x) = 2x − 5x³ + 9x² + \(\sqrt[4]{x}\) + 1
Answer:

Find the zeros of the function.(Section 3.2)

Question 70.
f(x) = 7x² + 42
Answer:

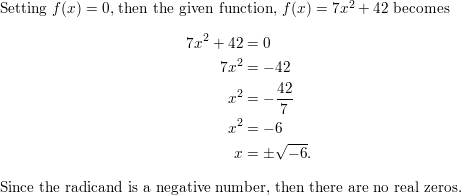
Question 71.
g(x) = 9x² + 81
Answer:
Given,
g(x) = 9x² + 81

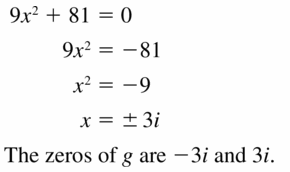
Question 72.
h(x) = 5x² + 40
Answer:
Given,
h(x) = 5x² + 40

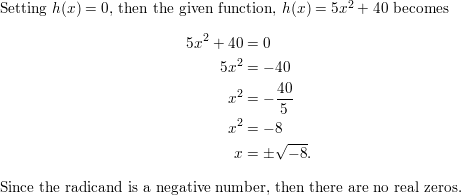
Question 73.
f(x) = 8x² − 1
Answer:
Given,
f(x) = 8x² − 1

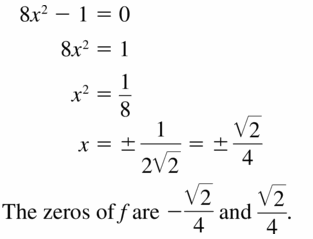
Lesson 4.6 The Fundamental Theorem of Algebra

Essential Question

How can you determine whether a polynomial equation has imaginary solutions?

EXPLORATION 1
Cubic Equations and Imaginary Solutions
Work with a partner. Match each cubic polynomial equation with the graph of its related polynomial function. Then find all solutions. Make a conjecture about how you can use a graph or table of values to determine the number and types of solutions of a cubic polynomial equation.
a. x³ − 3x² + x + 5 = 0
b. x³ − 2x² − x + 2 = 0
c. x³ − x² − 4x + 4 = 0
d. x³ + 5x² + 8x + 6 = 0
e. x³ − 3x² + x − 3 = 0
f. x³ − 3x² + 2x = 0

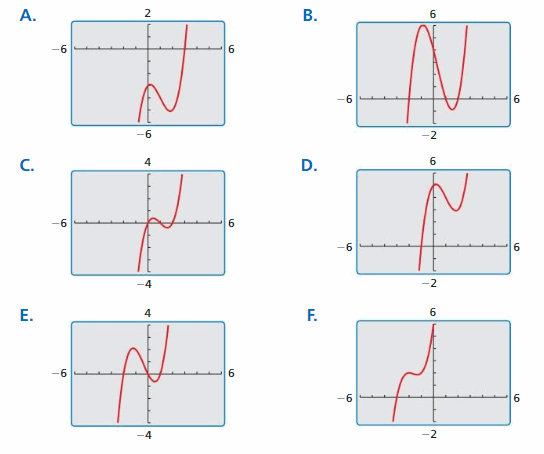
EXPLORATION 2
Quartic Equations and Imaginary Solutions
Work with a partner. Use the graph of the related quartic function, or a table of values, to determine whether each quartic equation has imaginary solutions. Explain your reasoning. Then find all solutions.

a. x⁴ − 2x³ − x² + 2x = 0
b. x⁴ − 1 = 0
c. x⁴ + x³ − x − 1 = 0
d. x⁴ − 3x³ + x² + 3x − 2 = 0

Communicate Your Answer

Question 3.
How can you determine whether a polynomial equation has imaginary solutions?
Answer:
In order to find the Imaginary roots of the function use the quadratic equation when the discriminant of the quadratic equation — the part under the square root sign (b² – 4ac) — is negative.

Question 4.
Is it possible for a cubic equation to have three imaginary solutions? Explain your reasoning.
Answer:
The equation has at most three distinct roots, it follows that it cannot have three distinct complex nonreal or imaginary roots. Your argument is almost correct proof of the fact that a cubic equation cannot have three complexes (non-real) roots.

4.6 Lesson

Monitoring Progress

Question 1.
How many solutions does the equation x⁴ + 7x² − 144 = 0 have?
Answer:

Question 2.
How many zeros does the function f(x) = x³ − 5x² − 8x + 48 have? Find all zeros of the polynomial function.
Answer:

Question 3.
f(x) = x³ + 7x² + 16x + 12
Answer:

Question 4.
f(x) = x⁵ − 3x⁴ + 5x³ − x² − 6x + 4
Answer:

Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros.

Question 5.
−1, 4i
Answer:

Question 6.
3, 1 + i\(\sqrt{5}\)
Answer:

Question 7.
\(\sqrt{2}\), 1 − 3i
Answer:

Question 8.
2, 2i, 4 − \(\sqrt{6}\)
Answer:

Determine the possible numbers of positive real zeros, negative real zeros, and imaginary zeros for the function.

Question 9.
f(x) = x³ + 9x − 25
Answer:

Question 10.
f(x) = 3x⁴ − 7x³ + x² − 13x + 8
Answer:

Question 11.
WHAT IF? In Example 5, what is the tachometer reading when the boat travels 20 miles per hour?
Answer:

The Fundamental Theorem of Algebra 4.6 Exercises

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE The expressions 5 + i and 5 − i are _____________.
Answer:
The expressions 5 + i and 5 − i are complex conjugates.

Question 2.
WRITING How many solutions does the polynomial equation (x + 8)³(x − 1) = 0 have? Explain.
Answer:

Monitoring Progress and Modeling with Mathematics

Question 3.
x⁴ + 2x³ − 4x² + x = 0
Answer:

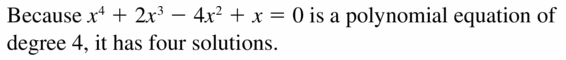
Question 4.
5y³ − 3y² + 8y = 0
Answer:
Given,
5y³ − 3y² + 8y = 0
The degree of the polynomial is 3.
It has 3 solutions.

Question 5.
9t⁶ − 14t³ + 4t − 1 = 0
Answer:
Given,
9t⁶ − 14t³ + 4t − 1 = 0

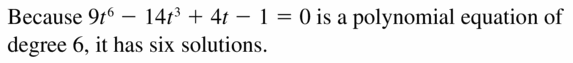
Question 6.
f(z) = −7z⁴ + z² − 25
Answer:
Given,
f(z) = −7z⁴ + z² − 25
Because −7z⁴ + z² − 25 =0 this is a polynomial equation of degree 4.
It has four solutions.

Question 7.
g(s) = 4s⁵ − s³ + 2s⁷ − 2
Answer:
Given,
g(s) = 4s⁵ − s³ + 2s⁷ − 2

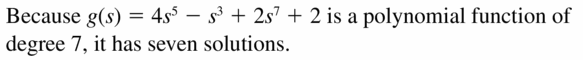
Question 8.
h(x) = 5x⁴ + 7x⁸ − x¹²
Answer:
Given,
h(x) = 5x⁴ + 7x⁸ − x¹²
Because 5x⁴ + 7x⁸ − x¹² is a polynomial equation of degree 12
It has twelve solutions.

In Exercises 9–16, find all zeros of the polynomial function.

Question 9.
f(x) = x⁴ − 6x³ + 7x² + 6x − 8
Answer:

Question 10.
f(x) = x⁴ + 5x³ − 7x² − 29x + 30
Answer:

Question 11.
g(x) = x⁴ − 9x² − 4x + 12
Answer:

Question 12.
h(x) = x³ + 5x² − 4x − 20
Answer:

Question 13.
g(x) = x⁴ + 4x³ + 7x² + 16x + 12
Answer:

Question 14.
h(x) = x⁴ − x³ + 7x² − 9x − 18
Answer:

Question 15.
g(x) = x⁵ + 3x⁴ − 4x³ − 2x² − 12x − 16
Answer:

Question 16.
f(x) = x⁵ − 20x³ + 20x² − 21x + 20
Answer:

ANALYZING RELATIONSHIPS In Exercises 17–20, determine the number of imaginary zeros for the function with the given degree and graph. Explain your reasoning.

Question 17.
Degree: 4

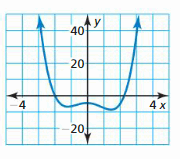
Answer:

Question 18.
Degree: 5

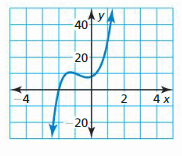
Answer:
The graph has 1 real root, which means there are 4 imaginary roots.

Question 19.
Degree: 2

Answer:

Question 20.
Degree: 3

Answer:
There are three real roots, which means there are no imaginary roots.

In Exercises 21–28, write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros.

Question 21.
−5, −1, 2
Answer:
Given,
−5, −1, 2

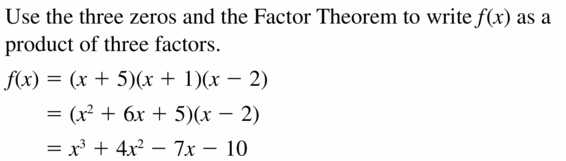
Question 22.
−2, 1, 3
Answer:
Given,
−2, 1, 3

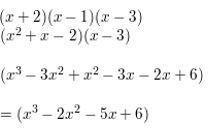
Question 23.
3, 4 + i
Answer:
Given,
3, 4 + i

Question 24.
2, 5 − i
Answer:
Given,
2, 5 − i
f(x) = (x – 2)[x – (5 – i)] [x – (5 + i)]
= (x – 2)[(x – 5) – i] [(x – 5) + i]
= (x – 2)[(x – 5)² – i²]
= (x – 2)[x² + 25 – 10x – 1]
= (x – 2)[x² – 10x + 24]
= x³ – 2x² -10x² + 20x + 24x – 48
= x³ – 12x² + 48x – 48

Question 25.
4, −\(\sqrt{5}\)
Answer:
Given,
4, −\(\sqrt{5}\)

Question 26.
3i, 2 − i
Answer:
Given,
3i, 2 − i

Question 27.
2, 1 + i, 2 −\(\sqrt{3}\)
Answer:

Question 28.
3, 4 + 2i, 1 + \(\sqrt{7}\)
Answer:
Given,
3, 4 + 2i, 1 + \(\sqrt{7}\)

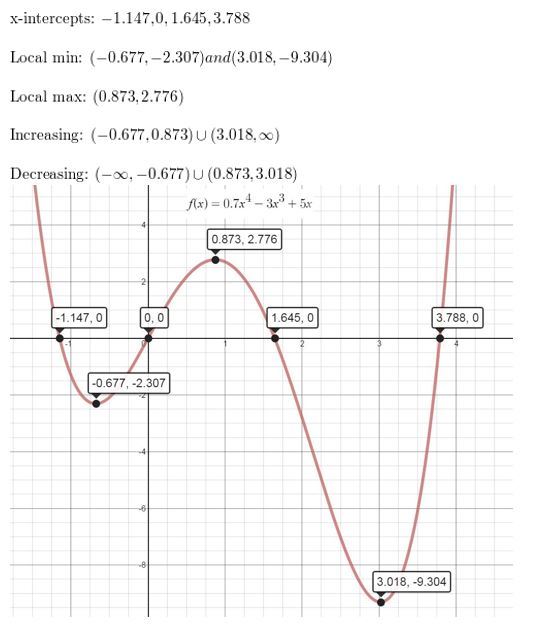
ERROR ANALYSIS In Exercises 29 and 30, describe and correct the error in writing a polynomial function with rational coefficients and the given zero(s).

Question 29.
Zeros: 2, 1 + i

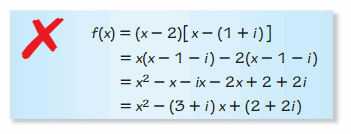
Answer:

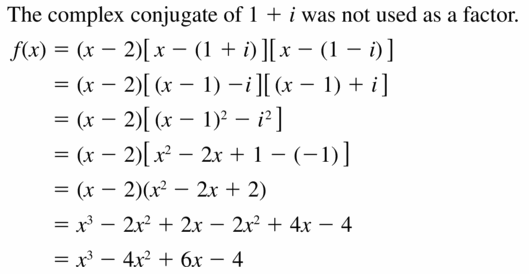
Question 30.
Zero: 2 +i

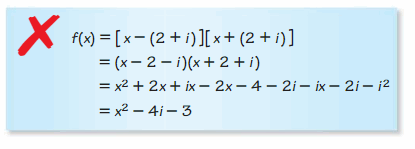
Answer:

Question 31.
OPEN-ENDED Write a polynomial function of degree 6 with zeros 1, 2, and −i. Justify your answer.
Answer:

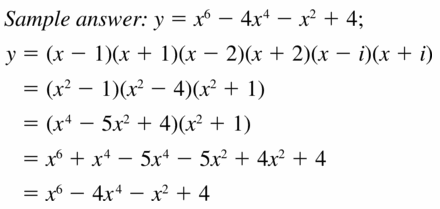
Question 32.
REASONING Two zeros of f(x) = x³ − 6x² − 16x + 96 are 4 and −4. Explain why the third zero must also be a real number.
Answer:

In Exercises 33–40, determine the possible numbers of positive real zeros, negative real zeros, and imaginary zeros for the function.

Question 33.
g(x) = x⁴ − x² − 6
Answer:

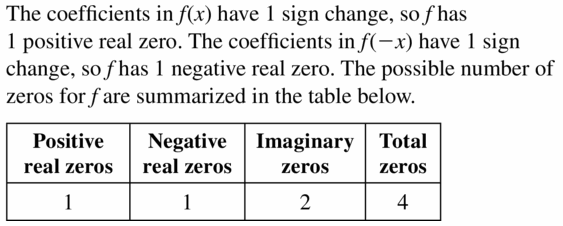
Question 34.
g(x) = −x³ + 5x² + 12
Answer:

Question 35.
g(x) = x³ − 4x² + 8x + 7
Answer:

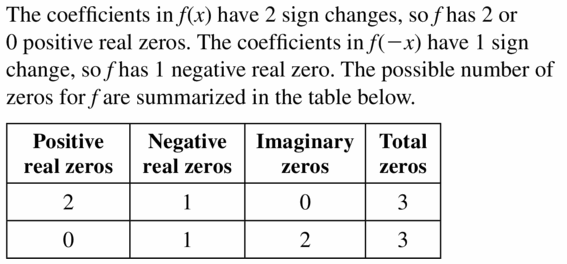
Question 36.
g(x) = x⁵ − 2x³ − x² + 6
Answer:

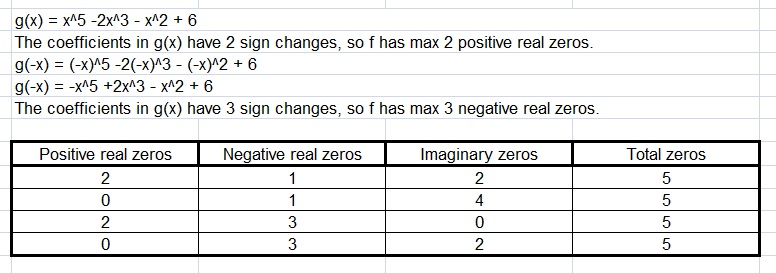
Question 37.
g(x) = x⁵ − 3x³ + 8x − 10
Answer:
Given,
g(x) = x⁵ − 3x³ + 8x − 10

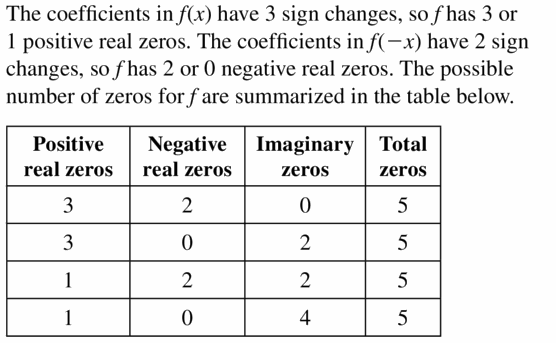
Question 38.
g(x) = x⁵ + 7x⁴ − 4x³ − 3x² + 9x − 15
Answer:
Given,

Question 39.
g(x) = x⁶ + x⁵ − 3x⁴ + x³ + 5x² + 9x − 18
Answer:
Given,
g(x) = x⁶ + x⁵ − 3x⁴ + x³ + 5x² + 9x − 18

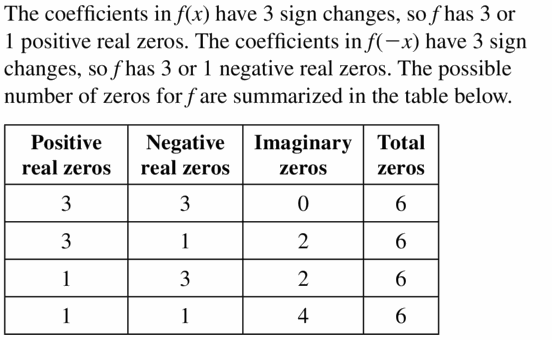
Question 40.
g(x) = x⁷ + 4x⁴ − 10x + 25
Answer:

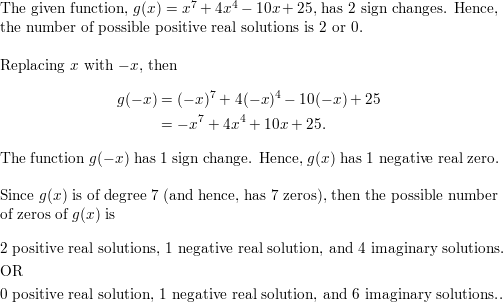
Question 41.
REASONING Which is not a possible classification of zeros for f(x) = x⁵ − 4x³ + 6x² + 2x − 6? Explain.
A. three positive real zeros, two negative real zeros, and zero imaginary zeros
B. three positive real zeros, zero negative real zeros, and two imaginary zeros
C. one positive real zero, four negative real zeros, and zero imaginary zeros
D. one positive real zero, two negative real zeros, and two imaginary zeros
Answer:
Given,
f(x) = x⁵ − 4x³ + 6x² + 2x − 6

Question 42.
USING STRUCTURE Use Descartes’s Rule of Signs to determine which function has at least 1 positive real zero.
A. f(x) = x⁴ + 2x³ − 9x² − 2x – 8
B. f(x) = x⁴ + 4x³ + 8x² + 16x + 16
C. f(x) = −x⁴ − 5x² − 4
D. f(x) = x⁴ + 4x³ + 7x² + 12x + 12
Answer:
A has sign changes, therefore this function has at least 1 positive real zero.

Question 43.
MODELING WITH MATHEMATICS From 1890 to 2000, the American Indian, Eskimo, and Aleut population P (in thousands) can be modeled by the function P = 0.004t³ − 0.24t² + 4.9t + 243, where t is the number of years since 1890. In which year did the population first reach 722,000?
Answer:

Question 44.
MODELING WITH MATHEMATICS Over a period of 14 years, the number N of inland lakes infested with zebra mussels in a certain state can be modeled by
N = −0.0284t⁴ + 0.5937t³ − 2.464t² + 8.33t − 2.5
where t is time (in years). In which year did the number of infested inland lakes first reach 120?

Answer:

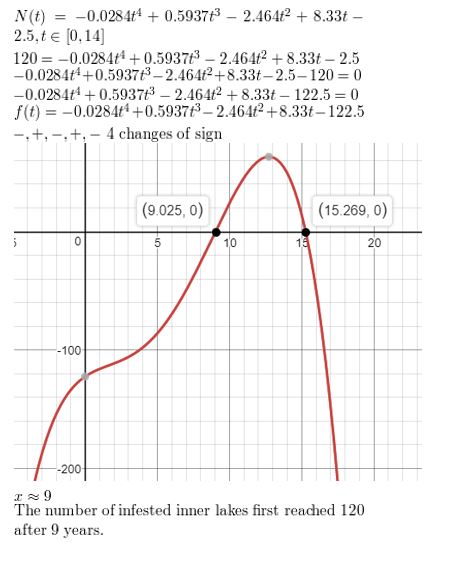
Question 45.
MODELING WITH MATHEMATICS For the 12 years that a grocery store has been open, its annual revenue R (in millions of dollars) can be modeled by the function
R = 0.0001(−t⁴ + 12t³ − 77t² + 600t + 13,650)where t is the number of years since the store opened. In which year(s) was the revenue $1.5 million?

Answer:

Question 46.
MAKING AN ARGUMENT Your friend claims that 2 − i is a complex zero of the polynomial function f(x) = x³ − 2x² + 2x + 5i, but that its conjugate is not a zero. You claim that both 2 − i and its conjugate must be zeros by the Complex Conjugates Theorem. Who is correct? Justify your answer.
Answer:

Question 47.
MATHEMATICAL CONNECTIONS A solid monument with the dimensions shown is to be built using 1000 cubic feet of marble. What is the value of x?

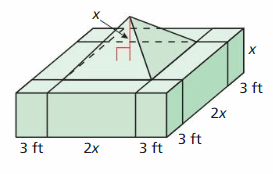
Answer:

Question 48.
THOUGHT PROVOKING Write and graph a polynomial function of degree 5 that has all positive or negative real zeros. Label each x-intercept. Then write the function in standard form.
Answer:

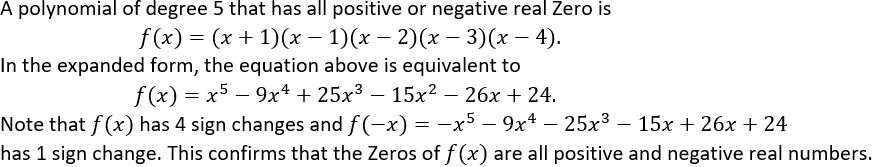
Question 49.
WRITING The graph of the constant polynomial function f(x) = 2 is a line that does not have any x-intercepts. Does the function contradict the Fundamental Theorem of Algebra? Explain.
Answer:

Question 50.
HOW DO YOU SEE IT? The graph represents a polynomial function of degree 6.

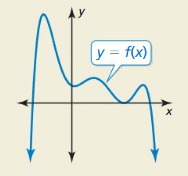
a. How many positive real zeros does the function have? negative real zeros? imaginary zeros?
b. Use Descartes’s Rule of Signs and your answers in part (a) to describe the possible sign changes in the coefficients of f(x).
Answer:

Question 51.
FINDING A PATTERN Use a graphing calculator to graph the function f(x) = (x + 3)ⁿ for n = 2, 3, 4, 5, 6, and 7.
a. Compare the graphs when n is even and n is odd.
b. Describe the behavior of the graph near the zero x = −3 as n increases.
c. Use your results from parts (a) and (b) to describe the behavior of the graph of g(x) = (x − 4)²⁰ near x = 4.
Answer:

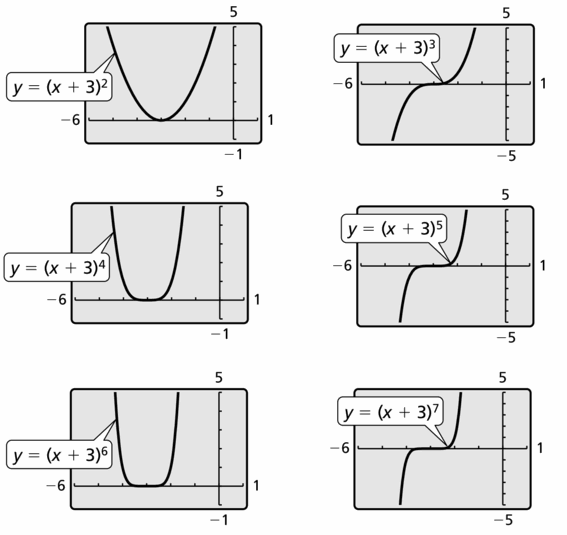
Question 52.
DRAWING CONCLUSIONS Find the zeros of each function.
f(x) = x⁵ − 5x + 6
g(x) = x³ − 7x + 6
h(x) = x⁴ + 2x³ + x² + 8x − 12
k(x) = x⁵ − 3x⁴ − 9x³ + 25x² − 6x
a. Describe the relationship between the sum of the zeros of a polynomial function and the coefficients of the polynomial function.
b. Describe the relationship between the product of the zeros of a polynomial function and the coefficients of the polynomial function.
Answer:

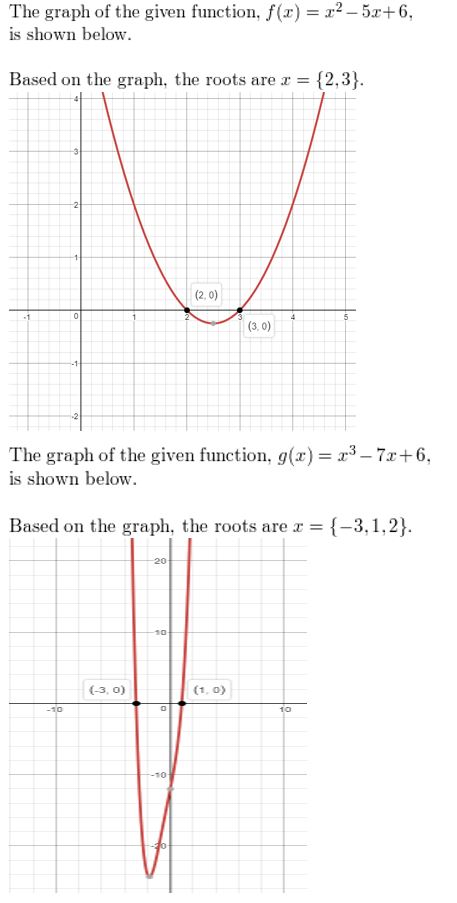
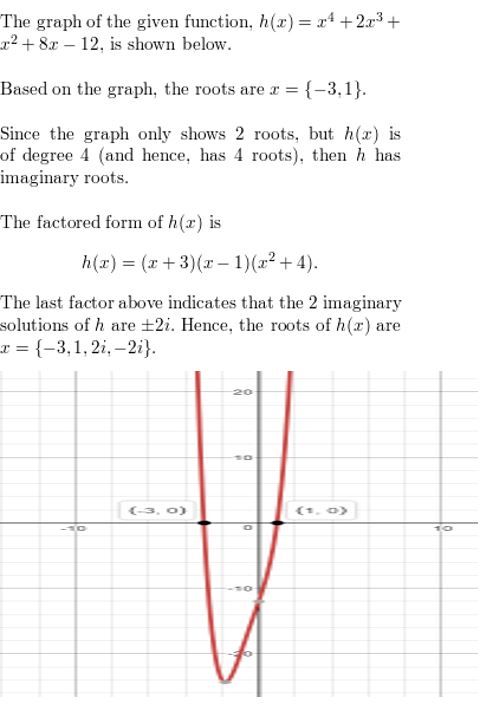
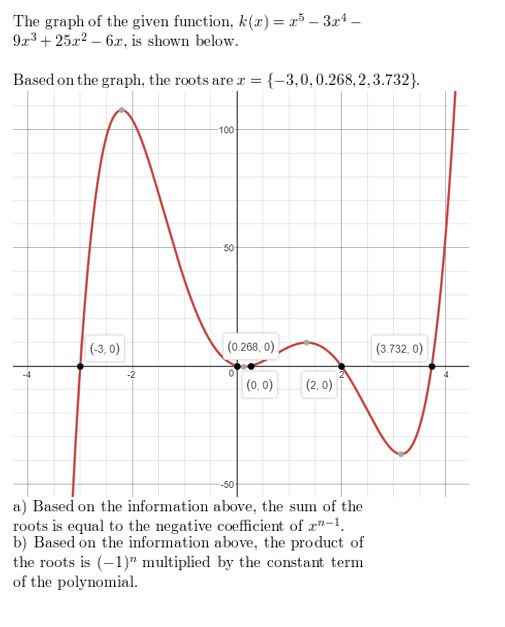
Question 53.
PROBLEM SOLVING You want to save money so you can buy a used car in four years. At the end of each summer, you deposit $1000 earned from summer jobs into your bank account. The table shows the value of your deposits over the four-year period. In the table, g is the growth factor 1 + r, where r is the annual interest rate expressed as a decimal.

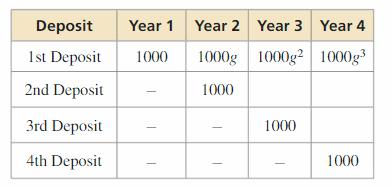
a. Copy and complete the table.
b. Write a polynomial function that gives the value v of your account at the end of the fourth summer in terms of g.
c. You want to buy a car that costs about $4300. What growth factor do you need to obtain this amount? What annual interest rate do you need?
Answer:

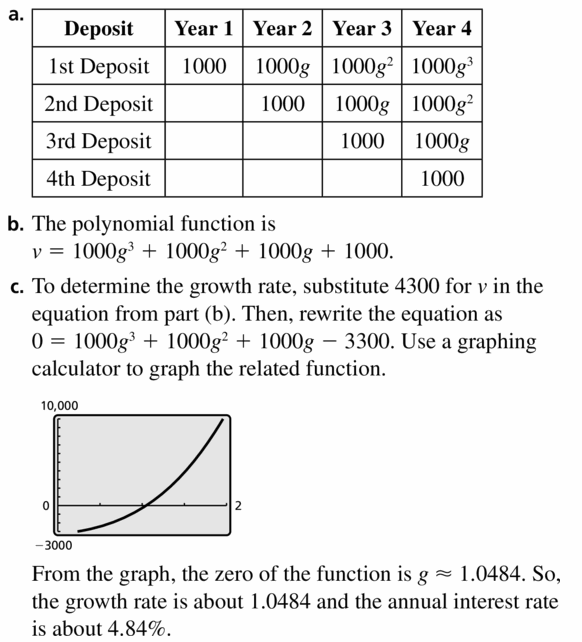
Maintaining Mathematical Proficiency
Describe the transformation of f(x) = x² represented by g. Then graph each function. (Section 2.1)

Question 54.
g(x) = −3x²
Answer:

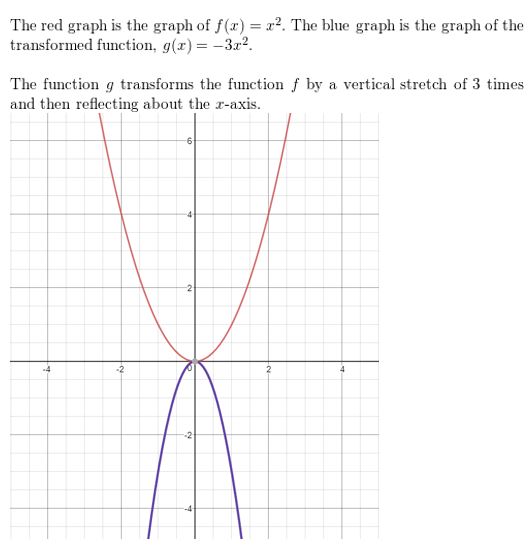
Question 55.
g(x) = (x − 4)² + 6
Answer:

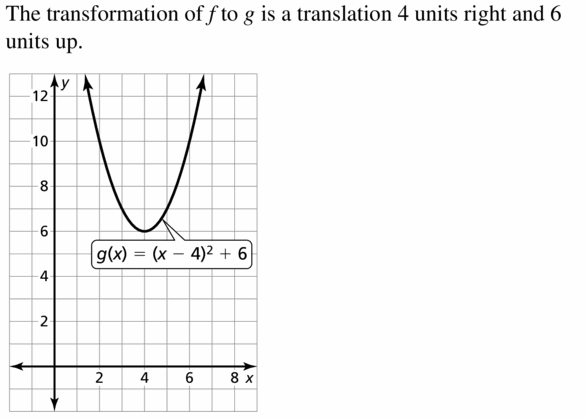
Question 56.
g(x) = −(x − 1)²
Answer:

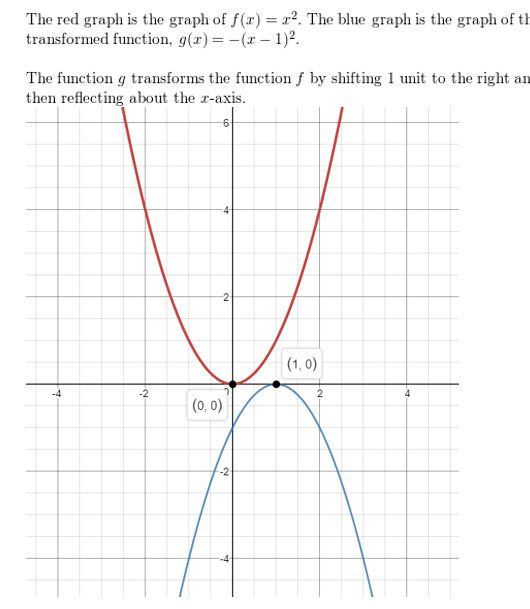
Question 57.
g(x) = 5(x + 4)²
Answer:

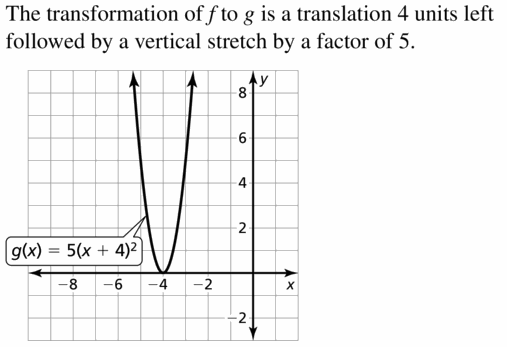
Write a function g whose graph represents the indicated transformation of the graph of f.(Sections 1.2and 2.1)

Question 58.
f(x) = x; vertical shrink by a factor of \(\frac{1}{3}\) and a reflection in the y-axis
Answer:

Question 59.
f(x) = | x + 1 ∣− 3; horizontal stretch by a factor of 9
Answer:

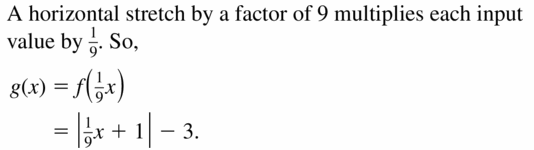
Question 60.
f(x) = x²; reflection in the x-axis, followed by a translation 2 units right and 7 units up
Answer:

Lesson 4.7 Tranformations of Polynomial Functions

Essential Question
How can you transform the graph of a polynomial function?

EXPLORATION 1
Transforming the Graph of a Cubic Function
Work with a partner. The graph of the cubic function f(x) = x³ is shown. The graph of each cubic function g represents a transformation of the graph of f. Write a rule for g. Use a graphing calculator to verify your answers.

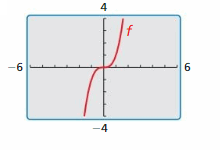
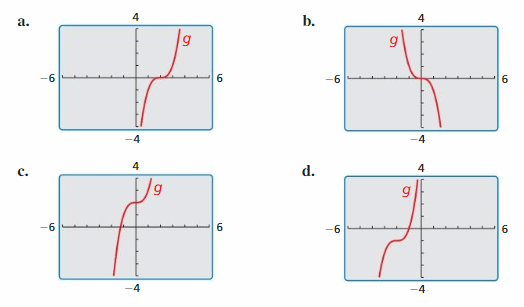
EXPLORATION 2
Transforming the Graph of a Quartic Function
Work with a partner. The graph of the quartic function f(x) = x⁴ is shown. The graph of each quartic function g represents a transformation of the graph of f. Write a rule for g. Use a graphing calculator to verify your answers.

Communicate Your Answer

Question 3.
How can you transform the graph of a polynomial function?
Answer: The polynomial function can be transformed through translation along horizontal and vertical axes, Reflection against horizontal and vertical axes, and Stretching or Shrinking on horizontal and vertical axes.

Question 4.
Describe the transformation of f(x) = x⁴ represented by g(x) = (x + 1)⁴ + 3. Then graph g.
Answer:
First identify what changed from f(x) to g(x), which is the +1 inside of what’s being raised to the 4th and +3 outside of it.
Inside the parentheses means a horizontal shift to the left if positive and right if negative, while outside the parentheses means a vertical shift upwards if positive and downwards if negative.
In this case a+ 1 and a + 3 respectively.
The differences are just matters of teacher preference, the one on the right is more basic while the one on the left is more advanced.

4.7 Lesson

Monitoring Progress

Question 1.
Describe the transformation of f(x) = x⁴ represented by g(x) = (x − 3)⁴ − 1. Then graph each function.
Answer:

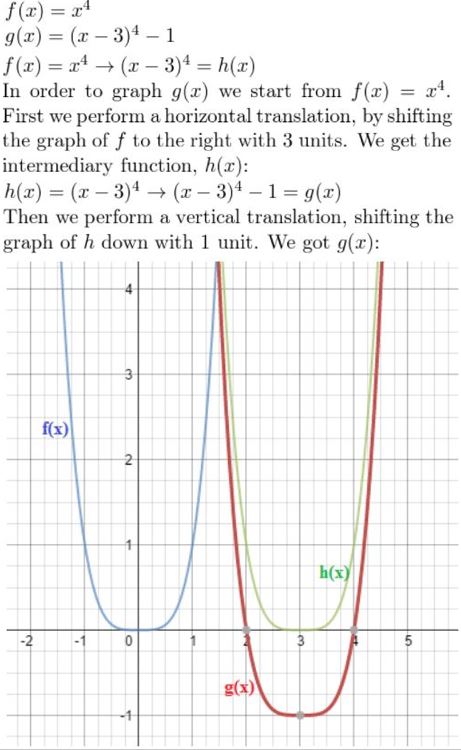
Question 2.
Describe the transformation of f(x) = x³ represented by g(x) = 4(x + 2)³. Then graph each function.
Answer:

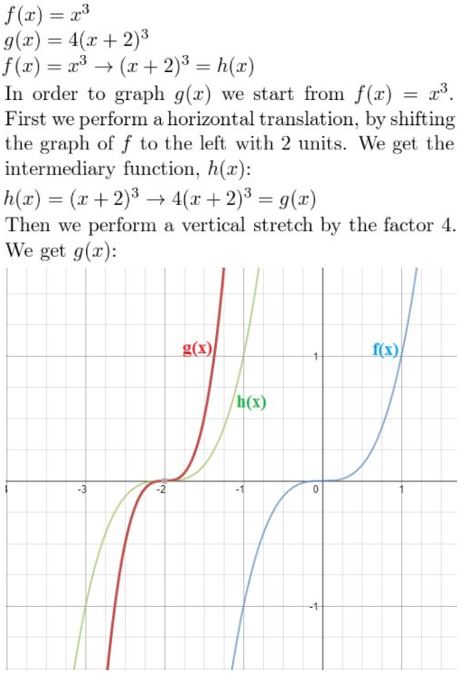
Question 3.
Let f(x) = x⁵ − 4x + 6 and g(x) = −f(x). Write a rule for g and then graph each function. Describe the graph of g as a transformation of the graph of f.
Answer:
Given,

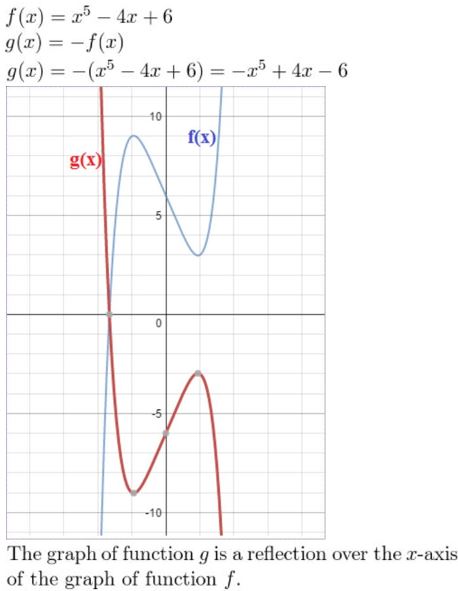
Question 4.
Let the graph of g be a horizontal stretch by a factor of 2, followed by a translation 3 units to the right of the graph of f(x) = 8x³ + 3. Write a rule for g.
Answer:
Given,

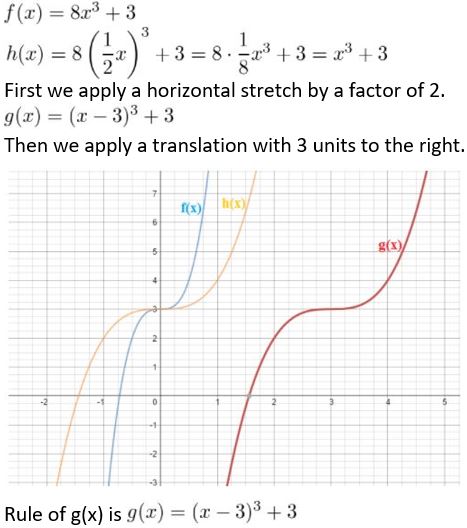
Question 5.
WHAT IF? In Example 5, the height of the pyramid is 6x, and the volume (in cubic feet) is represented by V(x) = 2x³. Write a rule for W. Find and interpret W(7).
Answer:
Given,

Tranformations of Polynomial Functions 4.7 Exercises

Question 1.
COMPLETE THE SENTENCE The graph of f(x) = (x + 2)³ is a ____________ translation of the graph of f(x) = x³.
Answer:
The graph of f(x) = (x + 2)³ is a horizontal translation of the graph of f(x) = x³.

Question 2.
VOCABULARY Describe how the vertex form of quadratic functions is similar to the form f(x) = a(x − h)³ + k for cubic functions.
Answer:

In Exercises 3–6, describe the transformation of f represented by g. Then graph each function.
Question 3.
f(x) = x⁴, g(x) = x⁴ + 3
Answer:

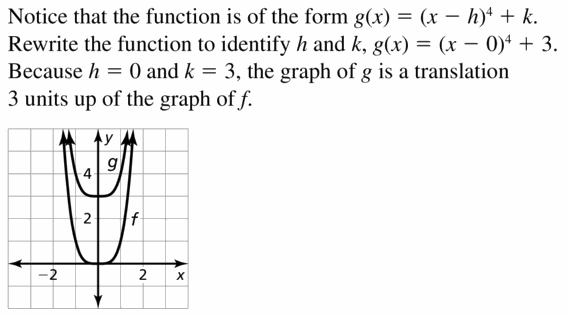
Question 4.
f(x) = x⁴, g(x) = (x − 5)⁴
Answer:
Given,
f(x) = x⁴, g(x) = (x − 5)⁴

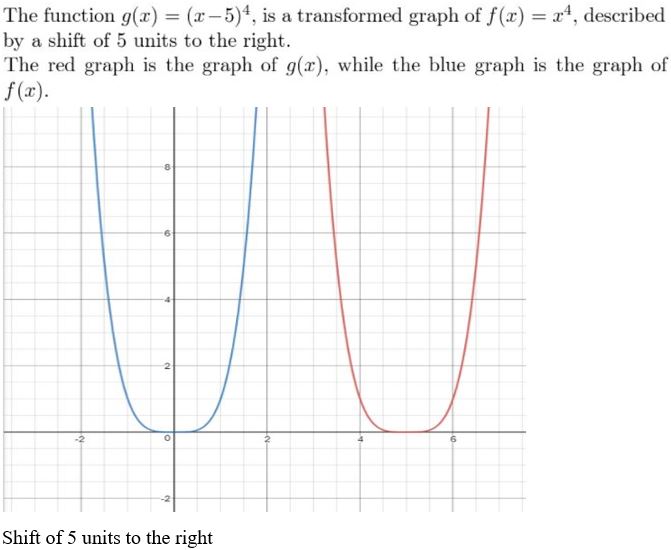
Question 5.
f(x) = x⁵, g(x) = (x − 2)⁵ − 1
Answer:

Question 6.
f(x) = x⁶, g(x) = (x + 1)⁶ − 4
Answer:

ANALYZING RELATIONSHIPS In Exercises 7–10, match the function with the correct transformation of the graph of f. Explain your reasoning.

Question 7.
y = f(x − 2)
Answer:

Question 8.
y = f(x + 2) + 2
Answer:
Graph C is correct.
The graph of f is 2 units left  and 2 units up

Question 9.
y = f(x − 2) + 2
Answer:

Question 10.
y = f(x) − 2
Answer:

In Exercises 11–16, describe the transformation of f represented by g. Then graph each function.

Question 11.
f(x) = x⁴, g(x) = −2x⁴
Answer:

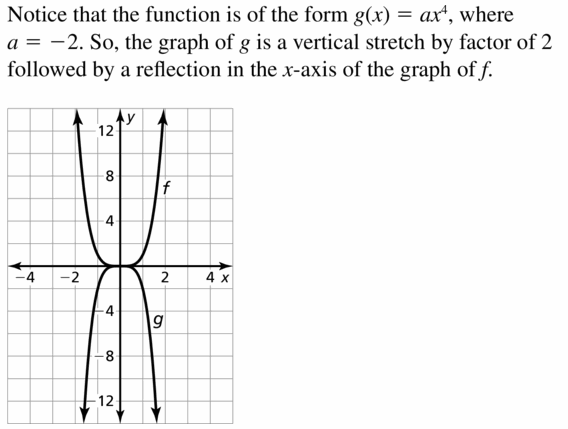
Question 12.
f(x) = x⁶, g(x) = −3x⁶
Answer:

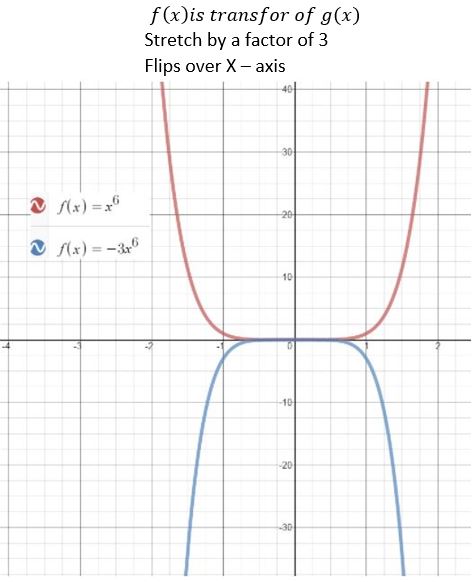
Question 13.
f(x) = x³, g(x) = 5x³ + 1
Answer:

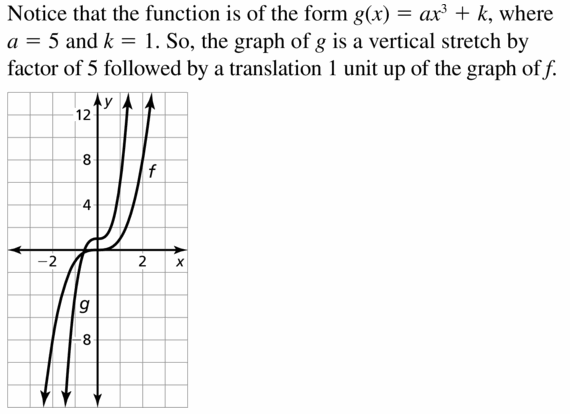
Question 14.
f(x) = x⁴, g(x) = \(\frac{1}{2}\)x⁴ + 1
Answer:

Question 15.
f(x) = x⁵, g(x) = \(\frac{3}{4}\)(x + 4)⁵
Answer:

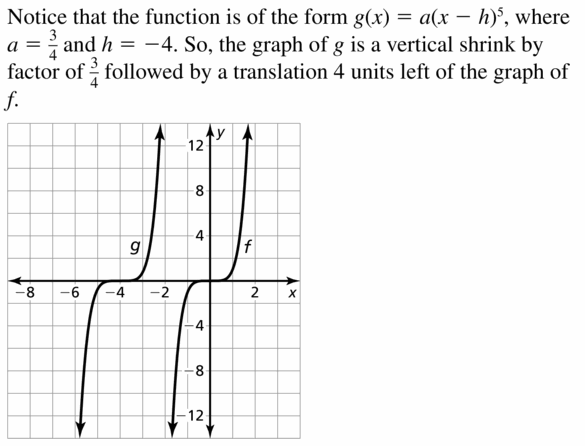
Question 16.
f(x) = x⁴, g(x) = (2x)⁴− 3
Answer:

In Exercises 17–20, write a rule for g and then graph each function. Describe the graph of g as a transformation of the graph of f.

Question 17.
f(x) = x⁴ + 1, g(x) = f(x + 2)
Answer:
Given,
f(x) = x⁴ + 1,
g(x) = f(x + 2)

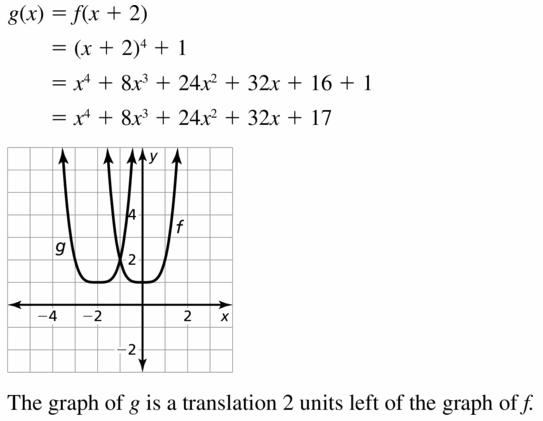
Question 18.
f(x) = x⁵ − 2x + 3, g(x) = 3f(x)
Answer:
Given,

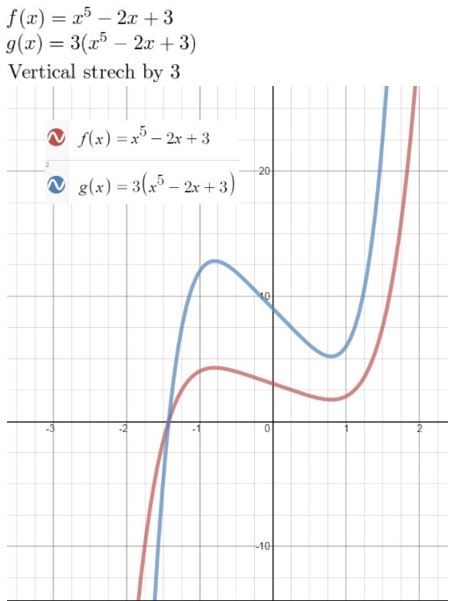
Question 19.
f(x) = 2x³ − 2x² + 6, g(x) = − \(\frac{1}{2}\)f(x)
Answer:

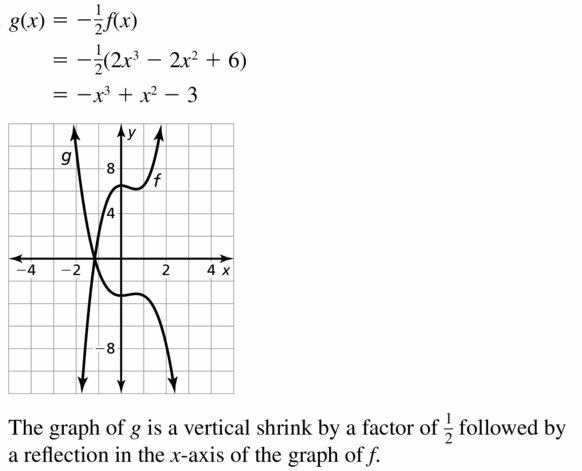
Question 20.
f(x) = x⁴ + x³ − 1, g(x) = f(−x) − 5
Answer:

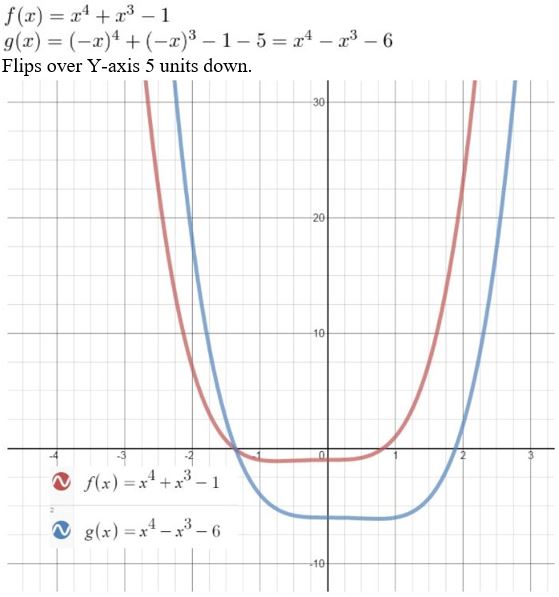
Question 21.
ERROR ANALYSIS Describe and correct the error in graphing the function g(x) = (x + 2)⁴ − 6

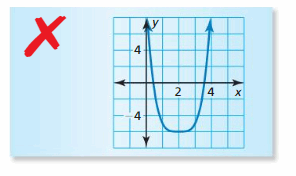
Answer:

Question 22.
ERROR ANALYSIS Describe and correct the error in describing the transformation of the graph of f(x) = x⁵ represented by the graph of g(x) = (3x)⁵− 4.

Answer:
Given,
f(x) = x⁵
g(x) = (3x)⁵− 4.
The graph of g is a horizontal shrink by a factor of 1/3, followed by a translation of 4 units down of the graph of f.

Question 23.
f(x) = x³ − 6; translation 3 units left, followed by a reflection in the y-axis
Answer:

Question 24.
f(x) = x⁴ + 2x + 6; vertical stretch by a factor of 2, followed by a translation 4 units right
Answer:

Question 25.
f(x) = x³ + 2x² − 9; horizontal shrink by a factor of \(\frac{1}{3}\) and a translation 2 units up, followed by a reflection in the x-axis
Answer:

Question 26.
f(x) = 2x⁵ − x³ + x² + 4; reflection in the y-axis and a vertical stretch by a factor of 3, followed by a translation 1 unit down
Answer:

Question 27.
MODELING WITH MATHEMATICS The volume V(in cubic feet) of the pyramid is given by V(x) = x³ − 4x. The function W(x) = V(3x) gives the volume (in cubic feet) of the pyramid when x is measured in yards. Write a rule for W. Find and interpret W(5).

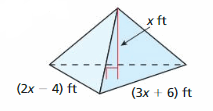
Answer:

Question 28.
MAKING AN ARGUMENT The volume of a cube with side length x is given by V(x) = x³. Your friend claims that when you divide the volume in half, the volume decreases by a greater amount than when you divide each side length in half. Is your friend correct? Justify your answer.
Answer:

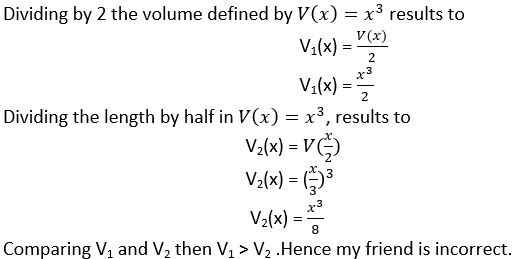
Question 29.
OPEN-ENDED Describe two transformations of the graph of f(x) = x⁵ where the order in which the transformations are performed is important. Then describe two transformations where the order is not important. Explain your reasoning.
Answer:

Question 30.
THOUGHT PROVOKING Write and graph a transformation of the graph of f(x) = x⁵ − 3x⁴ + 2x − 4 that results in a graph with a y-intercept of −2.
Answer:

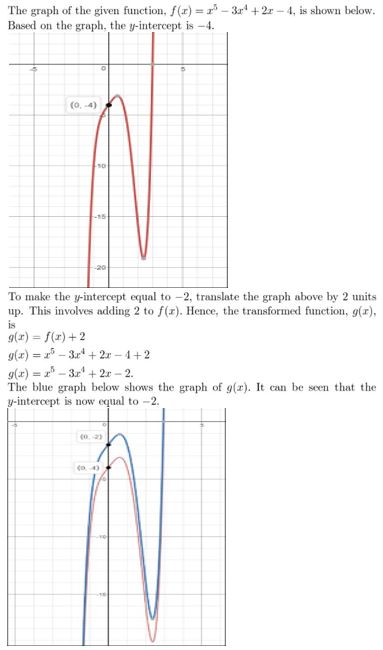
Question 31.
PROBLEM SOLVING A portion of the path that a hummingbird flies while feeding can be modeled by the function
f(x) = −\(\frac{1}{5}\)x(x − 4)2(x − 7), 0 ≤ x ≤ 7 w
here x is the horizontal distance (in meters) and f(x) is the height (in meters). The hummingbird feeds each time it is at ground level.
a. At what distances does the hummingbird feed?
b. A second hummingbird feeds 2 meters farther away than the first hummingbird and flies twice as high. Write a function to model the path of the second hummingbird.

Answer:

Question 32.
HOW DO YOU SEE IT? Determine the real zeros of each function. Then describe the transformation of the graph of f that results in the graph of g.

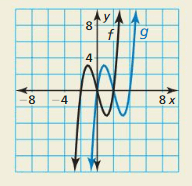
Answer:
Real Zeroes of F is : -2, 0, 2
Real Zeroes of g is : 0, 2, 2
g(x) = f( x- 2).

Question 33.
MATHEMATICAL CONNECTIONS Write a function V for the volume (in cubic yards) of the right circular cone shown. Then write a function W that gives the volume (in cubic yards) of the cone when x is measured in feet. Find and interpret W(3).

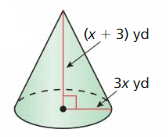
Answer:

Maintaining Mathematical Proficiency

Find the minimum value or maximum value of the function. Describe the domain and range of the function, and where the function is increasing and decreasing.(Section 2.2)

Question 34.
h(x) = (x + 5)² − 7
Answer:

Question 35.
f(x) = 4 − x²
Answer:
Given,
f(x) = 4 − x²

Question 36.
f(x) = 3(x − 10)(x + 4)
Answer:
Given,

Question 37.
g(x) = −(x + 2)(x + 8)
Answer:
Given,
g(x) = −(x + 2)(x + 8)

Question 38.
h(x) = \(\frac{1}{2}\)(x − 1)² − 3
Answer:
Given,

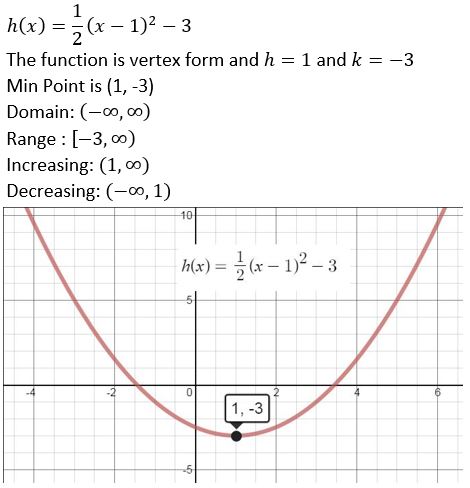
Question 39.
f(x) = −2x² + 4x − 1
Answer:

Lesson 4.8 Analyzing Graphs of Polynomial Functions

Essential Question
How many turning points can the graph of a polynomial function have?

A turning point of the graph of a polynomial function is a point on the graph at which the function changes from

• increasing to decreasing, or
• decreasing to increasing.

EXPLORATION 1
Approximating Turning Points
Work with a partner. Match each polynomial function with its graph. Explain your reasoning. Then use a graphing calculator to approximate the coordinates of the turning points of the graph of the function. Round your answers to the nearest hundredth.
a. f(x) = 2x² + 3x − 4
b. f(x) = x² + 3x + 2
c. f(x) = x³ − 2x² − x + 1
d. f(x) = −x³ + 5x − 2
e. f(x) = x⁴ − 3x² + 2x − 1
f. f(x) = −2x⁵ − x² + 5x + 3

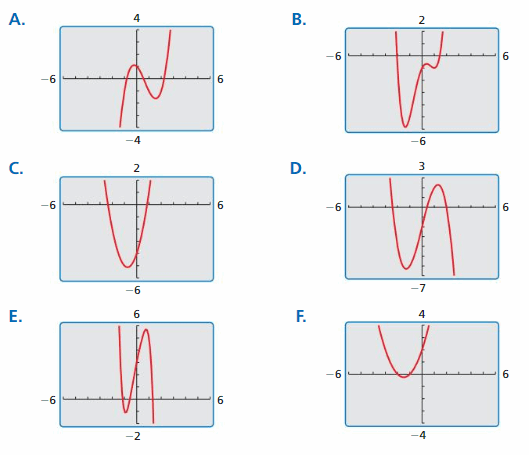
Communicate Your Answer

Question 2.
How many turning points can the graph of a polynomial function have?
Answer:
The turning points are those points where the graph changes direction i.e, where the function changes from growing to decreasing or from decreasing to growing.
x = -2, x = -1, x = 1 and x = 2
It has four turning points.

Question 3.
Is it possible to sketch the graph of a cubic polynomial function that has no turning points? Justify your answer.
Answer:
The maximum number of turning points of a polynomial function is always one less than the degree of the function.

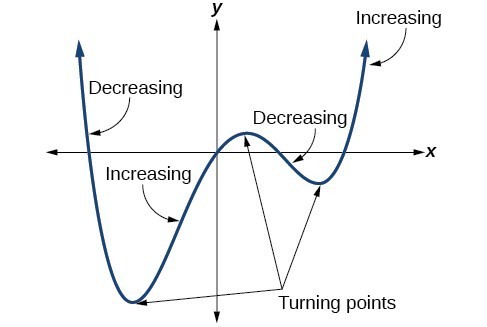
Monitoring Progress

Graph the function.

Question 1.
f(x) = \(\frac{1}{2}\)(x + 1)(x − 4)

Question 2.
f(x) = \(\frac{1}{4}\)(x + 2)(x − 1)(x − 3)

Question 3.
Find all real zeros of f(x) = 18x³ + 21x² − 13x − 6.

Question 4.
Graph f(x) = 0.5x³ + x² − x + 2. Identify the x-intercepts and the points where the local maximums and local minimums occur. Determine the intervals for which the function is increasing or decreasing.

Determine whether the function is even, odd, or neither.

Question 5.
f(x) = −x² + 5

Question 6.
f(x) = x⁴ − 5x³

Question 7.
f(x) = 2x⁵

Answer:
f(x) = 2x⁵
First find f(-x)
Find f(-x) by substituting -x in place of x in f(x).
f(-x) = 2(-x)⁵
Apply the product rule to -x.
f(-x) = 2((-1)⁵ x⁵)
Raise -1 to the power of 5
f(-x) = -2(-x⁵)
Multiply -1 by 2.
f(-x) = -2x⁵
A function is even if f(-x) = f(x).
f(-xx) = f(x)
-2x⁵ ≠ 2x⁵
So, the function is not even.
A function is odd if f(-x) = -f(x)
Multiply 2 by -1.
-f(x) = -2x⁵
Since -2x⁵ = -2x⁵
Thus the function is odd.

Analyzing Graphs of Polynomial Functions 4.8 Exercises

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE A local maximum or local minimum of a polynomial function occurs at a ______________ point of the graph of the function.
Answer:
A local maximum or local minimum of a polynomial function occurs at a turning point in the graph of the function.

Question 2.
WRITING Explain what a local maximum of a function is and how it may be different from the maximum value of the function.
Answer: A local maximum is a maximum point in relation to its nearby points. The maximum value of the function, on the other hand, is the maximum point of the entire graph or equation.

ANALYZING RELATIONSHIPS In Exercises 3–6, match the function with its graph.

Question 3.
f(x) = (x − 1)(x − 2)(x + 2)
Answer:
Graph A matches the equation.

Question 4.
h(x) = (x + 2)²(x + 1)
Answer:
Given,

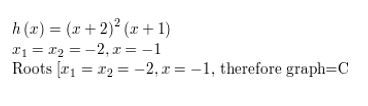
Question 5.
g(x) = (x + 1)(x − 1)(x + 2
Answer:

Question 6.
f(x) = (x − 1)²(x + 2)
Answer:

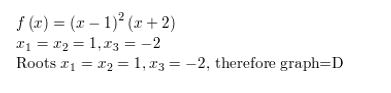
In Exercises 7–14, graph the function.

Question 7.
f(x) = (x − 2)²(x + 1)
Answer:
Given,
f(x) = (x − 2)²(x + 1)

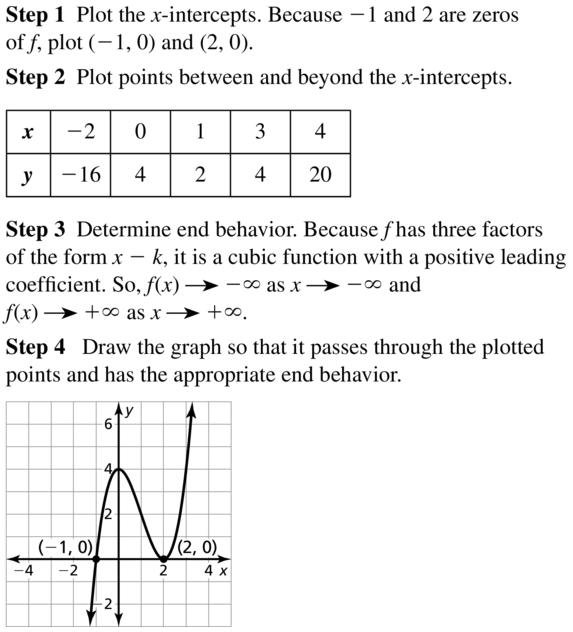
Question 8.
f(x) = (x + 2)²(x + 4)²
Answer:

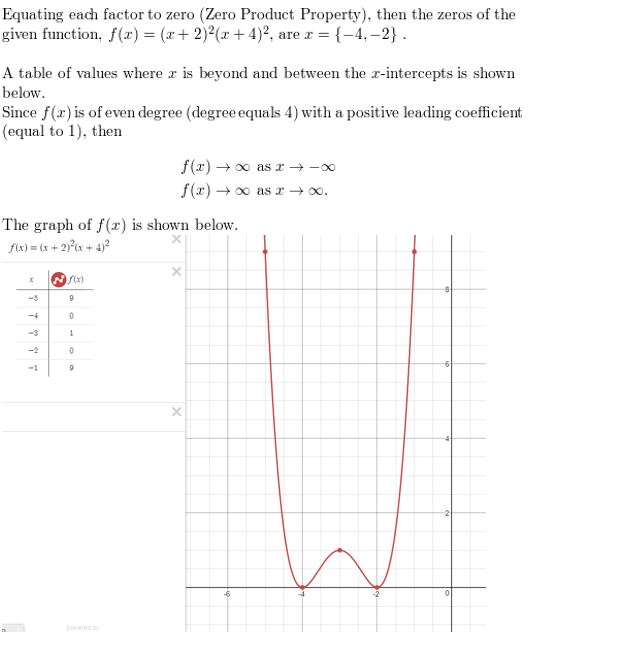
Question 9.
h(x) = (x + 1)²(x − 1)(x − 3)
Answer:
Given,
h(x) = (x + 1)²(x − 1)(x − 3)

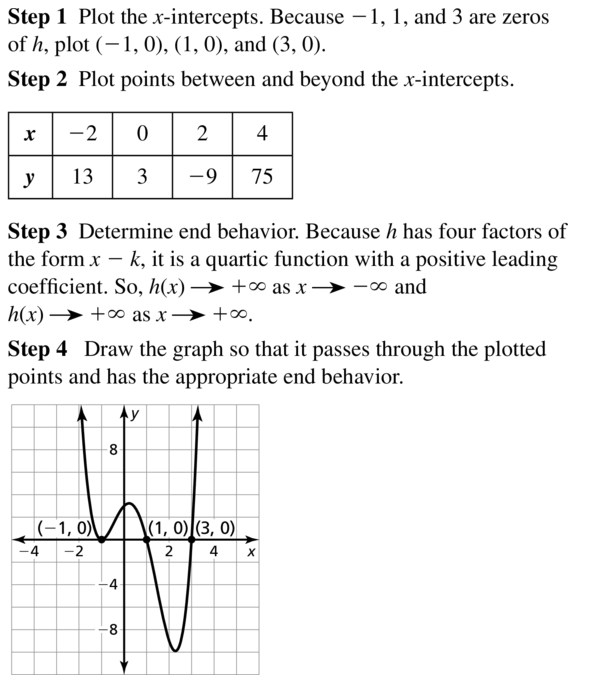
Question 10.
g(x) = 4(x + 1)(x + 2)(x − 1)
Answer:

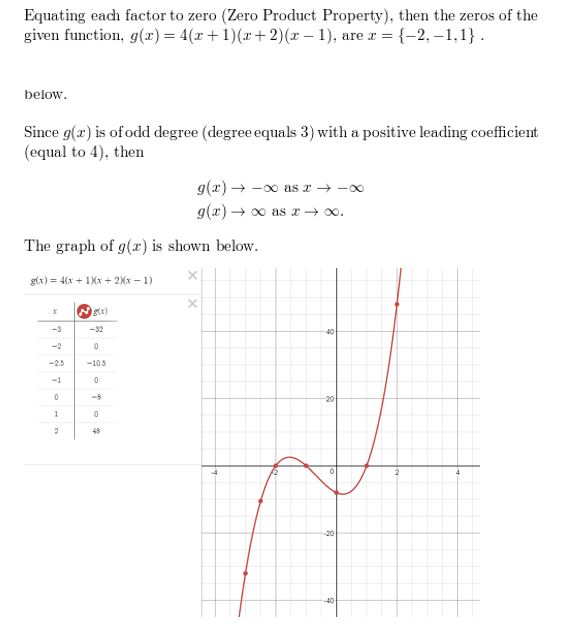
Question 11.
h(x) = \(\frac{1}{3}\)(x − 5)(x + 2)(x − 3)
Answer:

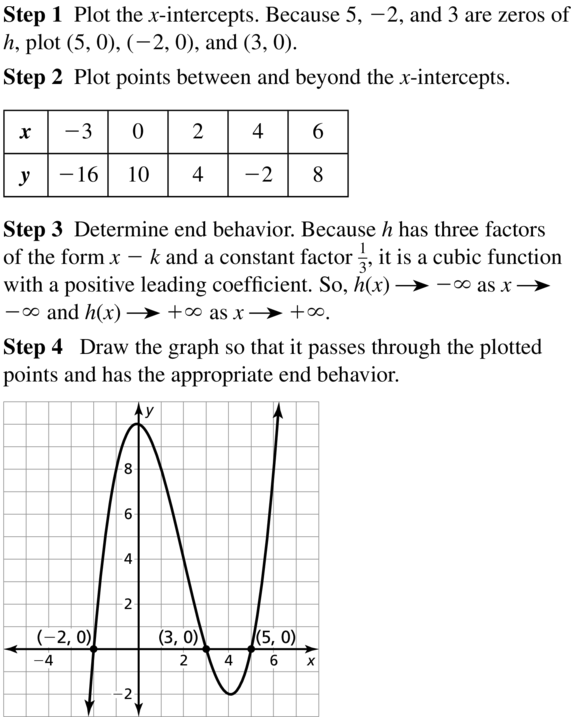
Question 12.
g(x) = \(\frac{1}{12}\)(x + 4)(x + 8)(x − 1)
Answer:

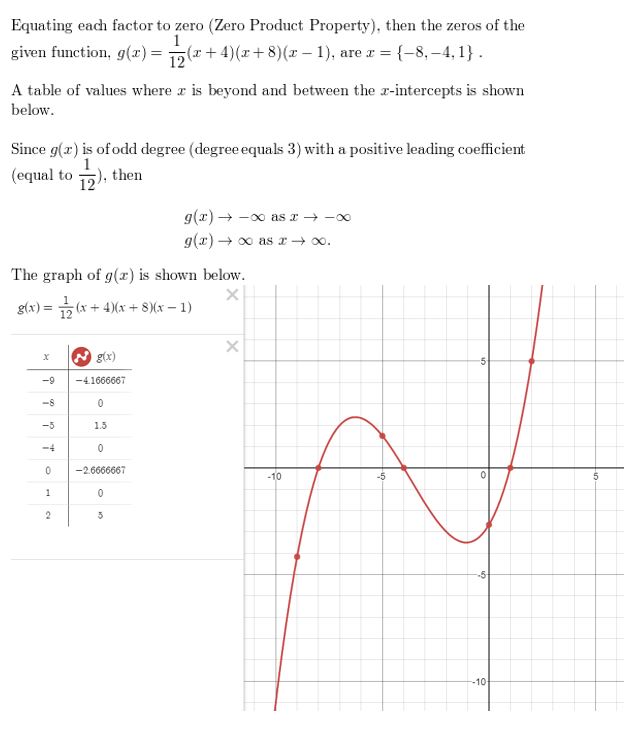
Question 13.
h(x) = (x− 3)(x² + x + 1)
Answer:
Given,
h(x) = (x− 3)(x² + x + 1)

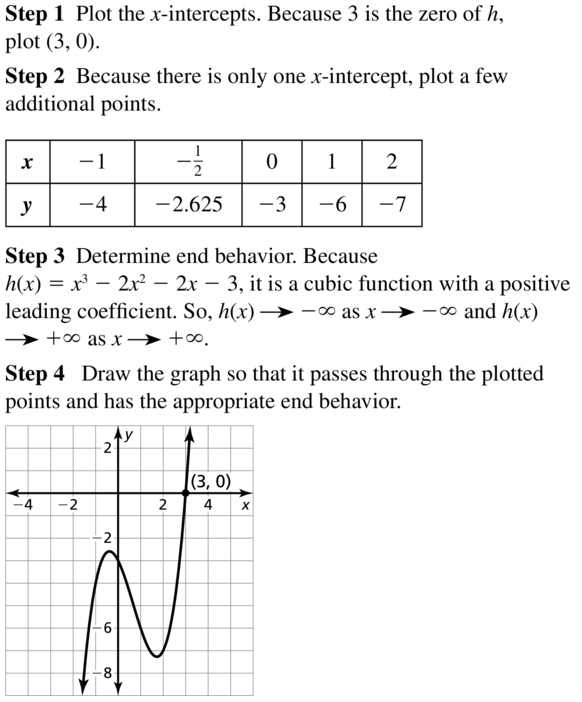
Question 14.
f(x) = (x − 4)(2x² − 2x + 1)
Answer:

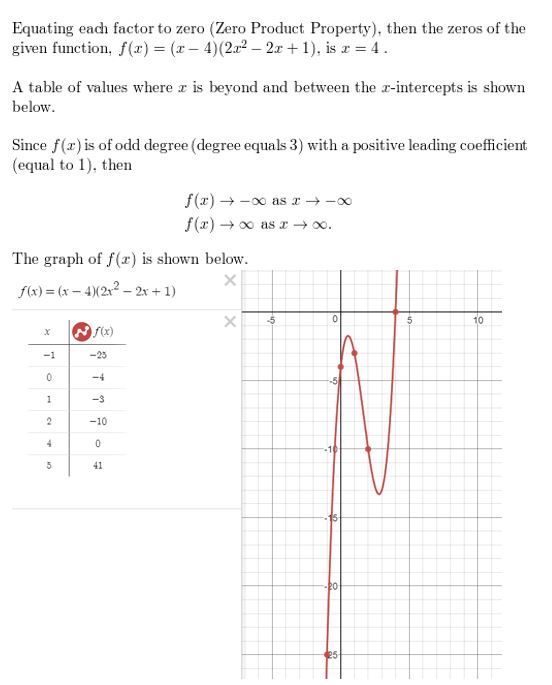
ERROR ANALYSIS In Exercises 15 and 16, describe and correct the error in using factors to graph f.

Question 15.
f(x) = (x + 2)(x − 1)²

Answer:

Question 16.
f(x) = x²(x − 3)

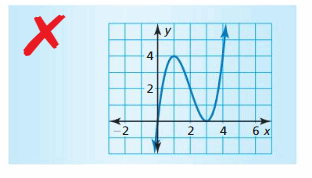
Answer:

In Exercises 17–22, find all real zeros of the function.

Question 17.
f(x) = x³ − 4x² − x + 4
Answer:

Question 18.
f(x) = x³ − 3x² − 4x + 12
Answer:

Question 19.
h(x) = 2x³ + 7x² − 5x − 4
Answer:

Question 20.
h(x) = 4x³ − 2x² − 24x − 18
Answer:

Question 21.
g(x) = 4x³ + x² − 51x + 36
Answer:

Question 22.
f(x) = 2x³ − 3x² − 32x − 15
Answer:

In Exercises 23–30, graph the function. Identify the x-intercepts and the points where the local maximums and local minimums occur. Determine the intervals for which the function is increasing or decreasing.

Question 23.
g(x) = 2x³ + 8x² − 3
Answer:

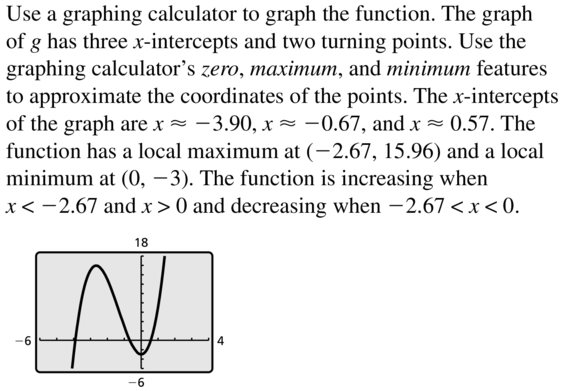
Question 24.
g(x) = −x⁴ + 3x
Answer:

Question 25.
h(x) = x⁴ − 3x² + x
Answer:

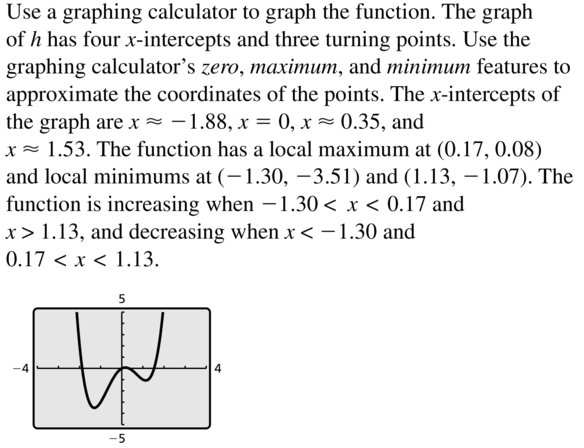
Question 26.
f(x) = x⁵ − 4x³ + x² + 2
Answer:

Question 27.
f(x) = 0.5x³ − 2x + 2.5
Answer:

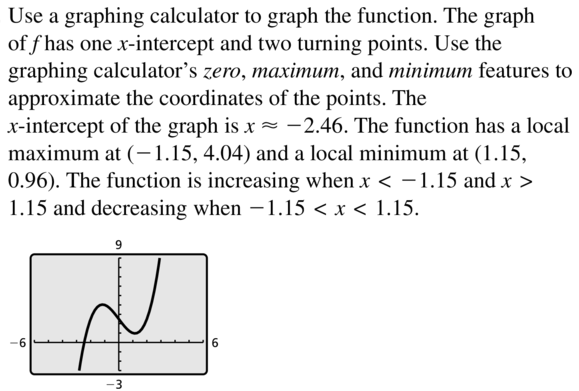
Question 28.
f(x) = 0.7x⁴ − 3x³ + 5x
Answer:

Question 29.
h(x) = x⁵ + 2x² − 17x − 4
Answer:

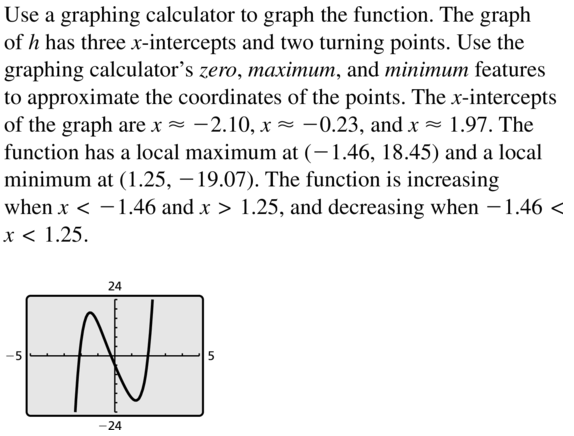
Question 30.
g(x) = x⁴ − 5x³ + 2x² + x − 3
Answer:

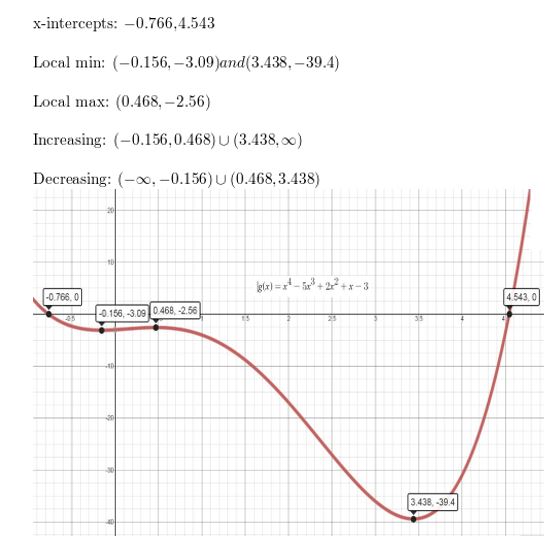
In Exercises 31–36, estimate the coordinates of each turning point. State whether each corresponds to a local maximum or a local minimum. Then estimate the real zeros and find the least possible degree of the function.

Question 31.

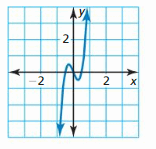
Answer:

Question 32.

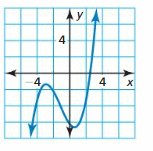
Answer:

Question 33.

Answer:

Question 34.

Answer:

Question 35.

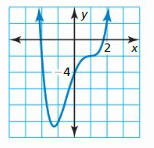
Answer:

Question 36.

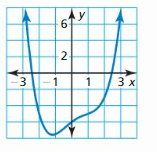
Answer:

OPEN-ENDED In Exercises 37 and 38, sketch a graph of a polynomial function f having the given characteristics.

Question 37.

• The graph of f has x-intercepts at x = −4, x = 0, and x = 2.
• f has a local maximum value when x = 1.
• f has a local minimum value when x = −2.

Answer:

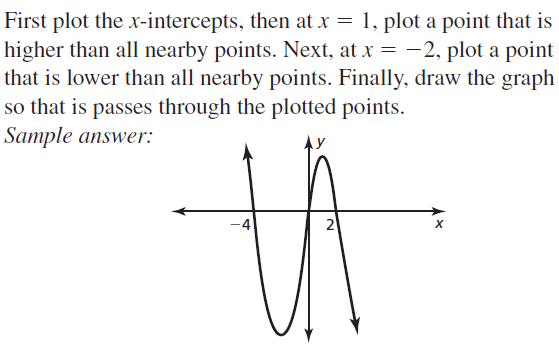
Question 38.

• The graph of f has x-intercepts at x = −3, x = 1, and x = 5.
• f has a local maximum value when x = 1.
• f has a local minimum value when x = −2 and when x = 4.

Answer:

In Exercises 39–46, determine whether the function is even, odd, or neither.

Question 39.
h(x) = 4x⁷
Answer:

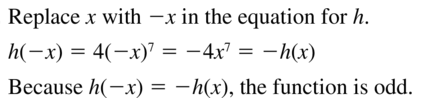
Question 40.
g(x) = −2x⁶ + x²
Answer:

Question 41.
f(x) = x⁴ + 3x² − 2
Answer:

Question 42.
f(x) = x⁵ + 3x³ − x
Answer:

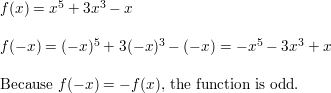
Question 43.
g(x) = x² + 5x + 1
Answer:

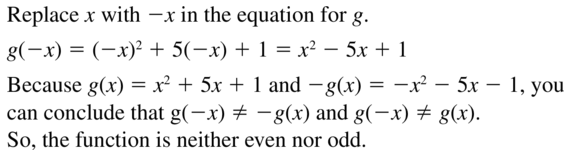
Question 44.
f(x) = −x³ + 2x − 9
Answer:

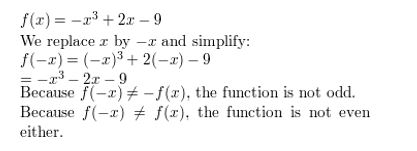
Question 45.
f(x) = x⁴ − 12x²
Answer:

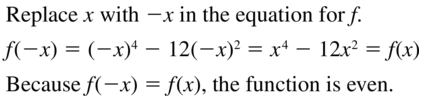
Question 46.
h(x) = x⁵ + 3x⁴
Answer:

Question 47.
USING TOOLS When a swimmer does the breaststroke, the function
S = −241t⁷ + 1060t⁶ − 1870t⁵ + 1650t⁴ − 737t³ + 144t² − 2.43t
models the speed S (in meters per second) of the swimmer during one complete stroke, where t is the number of seconds since the start of the stroke and 0 ≤ t ≤ 1.22. Use a graphing calculator to graph the function. At what time during the stroke is the swimmer traveling the fastest?

Answer:

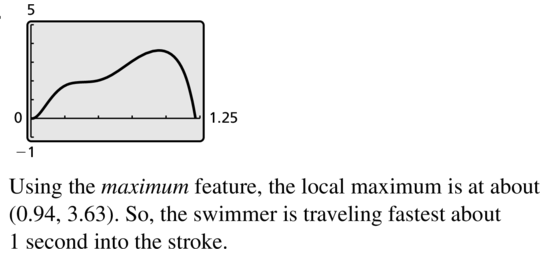
Question 48.
USING TOOLS During a recent period of time, the number S (in thousands) of students enrolled in public schools in a certain country can be modeled by S = 1.64x³ − 102x² + 1710x + 36,300, where x is time (in years). Use a graphing calculator to graph the function for the interval 0 ≤ x ≤ 41. Then describe how the public school enrollment changes over this period of time.
Answer:

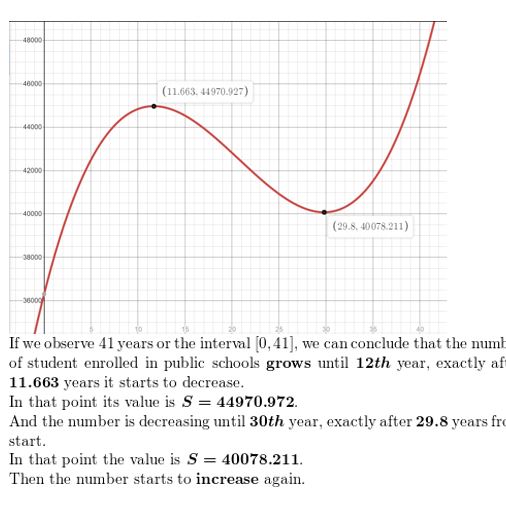
Question 49.
WRITING Why is the adjective local, used to describe the maximums and minimums of cubic functions, sometimes not required for quadratic functions?
Answer:
A quadratic function only has one turning point, and it is always the maximum or minimum value of the function.

Question 50.
HOW DO YOU SEE IT? The graph of a polynomial function is shown.

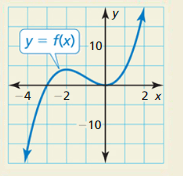
a. Find the zeros, local maximum, and local minimum values of the function.
b. Compare the x-intercepts of the graphs of y = f(x) and y = −f(x).
c. Compare the maximum and minimum values of the functions y = f(x) and y = −f(x).
Answer:

Question 51.
MAKING AN ARGUMENT Your friend claims that the product of two odd functions is an odd function. Is your friend correct? Explain your reasoning.
Answer:

Question 52.
MODELING WITH MATHEMATICS You are making a rectangular box out of a 16-inch-by-20-inch piece of cardboard. The box will be formed by making the cuts shown in the diagram and folding up the sides. You want the box to have the greatest volume possible.

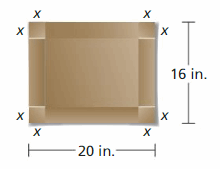
a. How long should you make the cuts?
b. What is the maximum volume?
c. What are the dimensions of the finished box?
Answer:

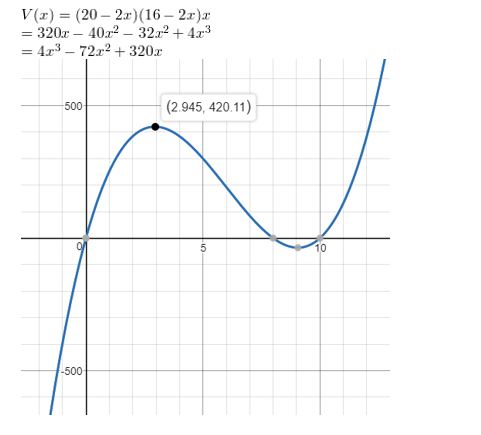
Question 53.
PROBLEM SOLVING Quonset huts are temporary, all-purpose structures shaped like half-cylinders. You have 1100 square feet of material to build a quonset hut.
a. The surface area S of a quonset hut is given by S = πr² + πrℓ. Substitute 1100 for S and then write an expression for ℓ in terms of r.
b. The volume V of a quonset hut is given by V = 1 — 2πr²ℓ. Write an equation that gives V as a function in terms of r only.c. Find the value of r that maximizes the volume of the hut.

Answer:

Question 54.
THOUGHT PROVOKING Write and graph a polynomial function that has one real zero in each of the intervals −2 < x < −1, 0 < x < 1, and 4 < x < 5. Is there a maximum degree that such a polynomial function can have? Justify your answer.
Answer:
As it is seen below example, it is possible.

Question 55.
MATHEMATICAL CONNECTIONS A cylinder is inscribed in a sphere of radius 8 inches. Write an equation for the volume of the cylinder as a function of h. Find the value of h that maximizes the volume of the inscribed cylinder. What is the maximum volume of the cylinder?

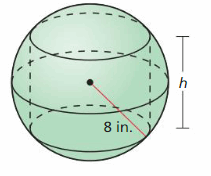
Answer:

Maintaining Mathematical Proficiency

State whether the table displays linear data, quadratic data, or neither. Explain

Question 56.

Answer:

Question 57.

Answer:

Lesson 4.9 Modeling with Polynomial Functions

Essential Question
How can you find a polynomial model for real-life data?

EXPLORATION 1
Modeling Real-Life Data
Work with a partner. The distance a baseball travels after it is hit depends on the angle at which it was hit and the initial speed. The table shows the distances a baseball hit at an angle of 35° travels at various initial speeds.

a. Recall that when data have equally-spaced x-values, you can analyze patterns in the differences of the y-values to determine what type of function can be used to model the data. If the first differences are constant, then the set of data fits a linear model. If the second differences are constant, then the set of data fits a quadratic model. Find the first and second differences of the data. Are the data linear or quadratic? Explain your reasoning.


b. Use a graphing calculator to draw a scatter plot of the data. Do the data appear linear or quadratic? Use the regression feature of the graphing calculator to find a linear or quadratic model that best fits the data.12019075400

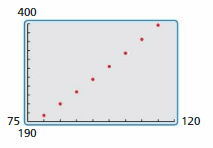
c. Use the model you found in part (b) to find the distance a baseball travels when it is hit at an angle of 35° and travels at an initial speed of 120 miles per hour.
d. According to the Baseball Almanac, “Any drive over400 feet is noteworthy. A blow of 450 feet shows exceptional power, as the majority of major league players are unable to hit a ball that far. Anything in the 500-foot range is genuinely historic.” Estimate the initial speed of a baseball that travels a distance of 500 feet.

Communicate Your Answer

Question 2.
How can you find a polynomial model for real-life data?
Answer:
People use polynomials for modeling various buildings and objects, used in industries, and used in construction. They are even used in marketing, finance, and stocks.

Question 3.
How well does the model you found in Exploration 1(b) fit the data? Do you think the model is valid for any initial speed? Explain your reasoning.

4.9 Lesson

Monitoring Progress

write a cubic function whose graph passes through the given points. 

Question 1.
(−4, 0), (0, 10), (2, 0), (5, 0)
Answer:

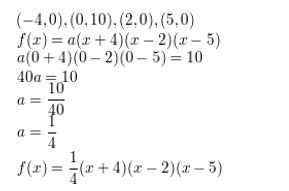
Question 2.
Answer:
(−1, 0), (0, −12), (2, 0), (3, 0)

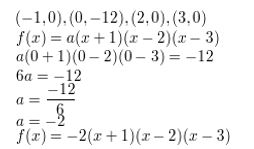
Question 3.
Use finite differences to determine the degree of the polynomial function that fits the data. Then use technology to find the polynomial function.

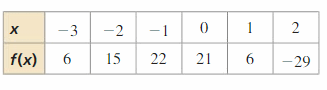
Answer:

Use a graphing calculator to find a polynomial function that fits the data.

Question 4.

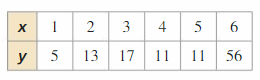
Answer:

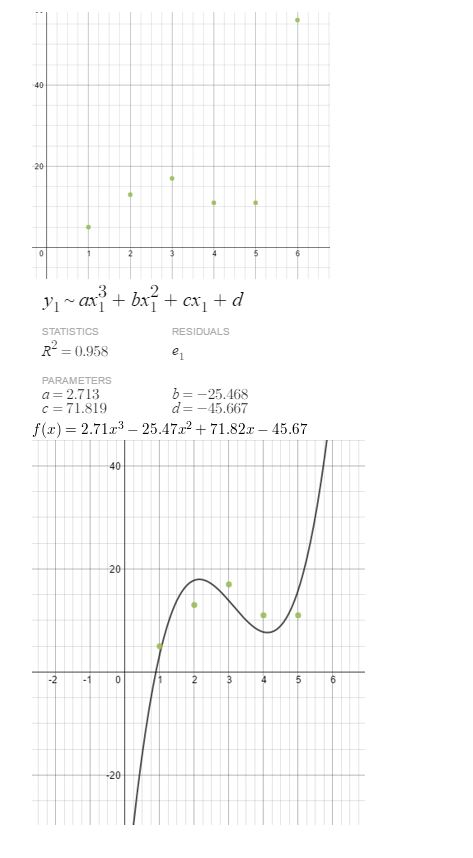
Question 5.

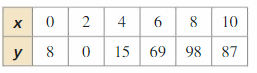
Answer:

Modeling with polynomial Functions 4.9 Exercises

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE When the x-values in a set of data are equally spaced, the differences of consecutive y-values are called ________________.
Answer:
When the x-values in a set of data are equally spaced, the differences of consecutive y-values are called first differences.

Question 2.
WRITING Explain how you know when a set of data could be modeled by a cubic function.
Answer:
Utilizing finite differences to decide the degree of the polynomial function that fits the data, you know when a set of data could be demonstrated by a cubic function on the off chance that you get a third difference that is nonzero and constant.

Monitoring Progress and Modeling with Mathematics

In Exercises 3–6, write a cubic function whose graph is shown.

Question 3.

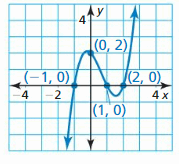
Answer:

Question 4.

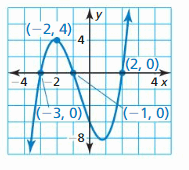
Answer:

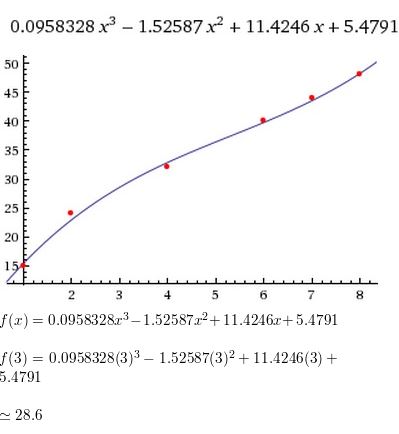
Question 5.

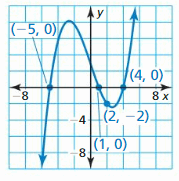
Answer:

Question 6.

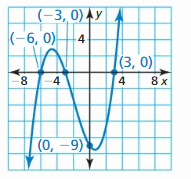
Answer:
Given,
-3, -6, 3 and 0.
y=a(x+6)(x+3)(x-3)
-9=a(0+6)(0+3)(0-3)
-9=-54a
1=6a
a=1/6
y=1/6(x+6)(x+3)(x-3)

In Exercises 7–12, use finite differences to determine the degree of the polynomial function that fits the data. Then use technology to find the polynomial function.

Question 7.

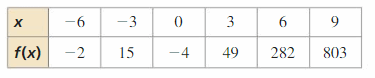
Answer:

Question 8.

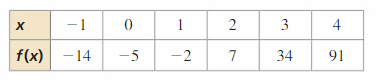
Answer:

Question 9.
(−4, −317), (−3, −37), (−2, 21), (−1, 7), (0, −1), (1, 3), (2, −47), (3, −289), (4, −933)
Answer:

Question 10.
(−6, 744), (−4, 154), (−2, 4), (0, −6), (2, 16), (4, 154), (6, 684), (8, 2074), (10, 4984)
Answer:

Question 11.
(−2, 968), (−1, 422), (0, 142), (1, 26), (2, −4), (3, −2), (4, 2), (5, 2), (6, 16)
Answer:

Question 12.
(1, 0), (2, 6), (3, 2), (4, 6), (5, 12), (6, −10), (7, −114), (8, −378), (9, −904)
Answer:

Question 13.
ERROR ANALYSIS Describe and correct the error in writing a cubic function whose graph passes through the given points.

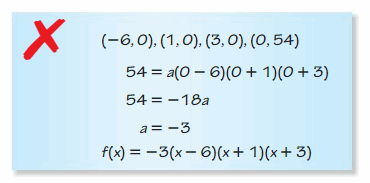
Answer:

Question 14.
MODELING WITH MATHEMATICS The dot patterns show pentagonal numbers. The number of dots in the nth pentagonal number is given by f(n) = \(\frac{1}{2}\)n(3n − 1). Show that this function has constant second-order differences.

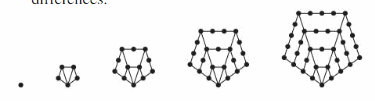
Answer:

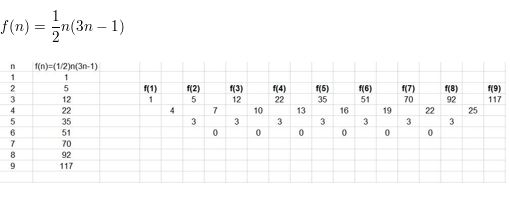
Question 15.
OPEN-ENDED Write three different cubic functions that pass through the points (3, 0), (4, 0), and (2, 6). Justify your answers.
Answer:

Question 16.
MODELING WITH MATHEMATICS The table shows the ages of cats and their corresponding ages in human years. Find a polynomial model for the data for the first 8 years of a cat’s life. Use the model to estimate the age (in human years) of a cat that is 3 years old.

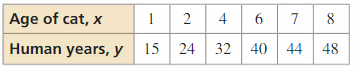
Answer:

Question 17.
MODELING WITH MATHEMATICS The data in the table show the average speeds y (in miles per hour) of a pontoon boat for several different engine speeds x (in hundreds of revolutions per minute, or RPMs). Find a polynomial model for the data. Estimate the average speed of the pontoon boat when the engine speed is 2800 RPMs.

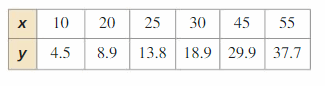
Answer:

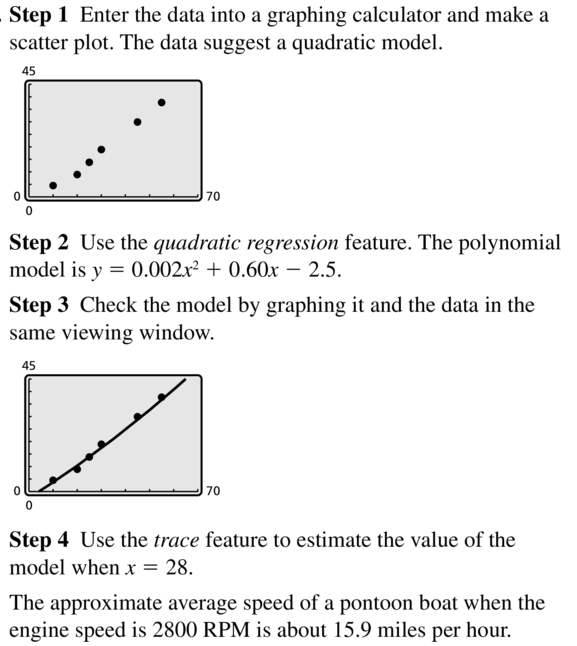
Question 18.
HOW DO YOU SEE IT? The graph shows typical speeds y (in feet per second) of a space shuttle x seconds after it is launched.

a. What type of polynomial function models the data? Explain.
b. Which nth-order finite difference should be constant for the function in part (a)? Explain.
Answer:
a) The given graph suggests a cubic model as it has the shape of a cubic polynomial’s graph.

Question 19.
MATHEMATICAL CONNECTIONS The table shows the number of diagonals for polygons with n sides. Find a polynomial function that fits the data. Determine the total number of diagonals in the decagon shown.


Answer:

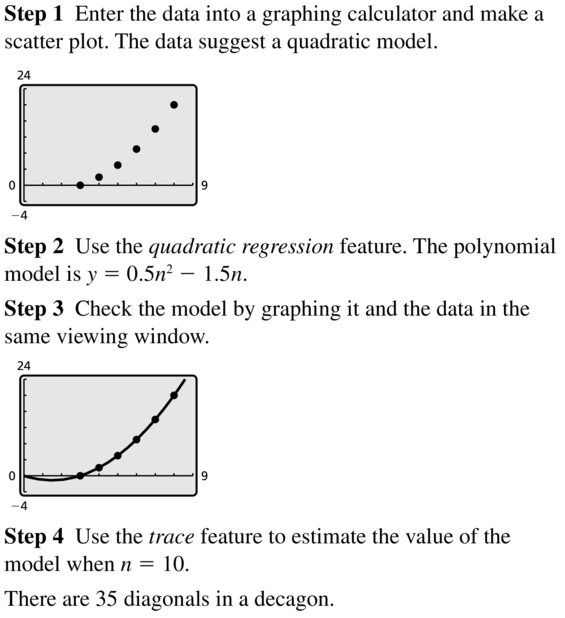
Question 20.
MAKING AN ARGUMENT Your friend states that it is not possible to determine the degree of a function given the first-order differences. Is your friend correct? Explain your reasoning.
Answer:

Question 21.
WRITING Explain why you cannot always use finite differences to find a model for real-life data sets.
Answer:

Question 22.
THOUGHT PROVOKING A, B, and C are zeros of a cubic polynomial function. Choose values for A, B, and C such that the distance from A to B is less than or equal to the distance from A to C. Then write the function using the A, B, and C values you chose.
Answer:

Question 23.
MULTIPLE REPRESENTATIONS Order the polynomial functions according to their degree, from least to greatest.
A.f(x) = −3x + 2x² + 1

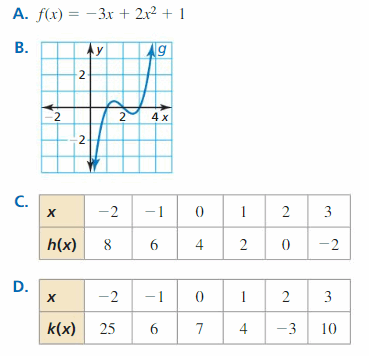
Answer:

Question 24.
ABSTRACT REASONING Substitute the expressions z, z + 1, z + 2, …….. , z + 5 for x in the function f(x) = ax³ + bx² + cx + d to generate six equally-spaced ordered pairs. Then show that the third-order differences are constant.
Answer:

Maintaining Mathematical Proficiency

Solve the equation using square roots.(Section 3.1)

Question 25.
x² − 6 = 30
Answer:

Question 26.
5x² − 38 = 187
Answer:

Question 27.
2(x − 3)² = 24
Answer:

Question 28.
\(\frac{4}{3}\)(x + 5)² = 4
Answer:

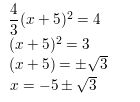
Solve the equation using the Quadratic Formula.(Section 3.4)

Question 29.
2x² + 3x = 5
Answer:

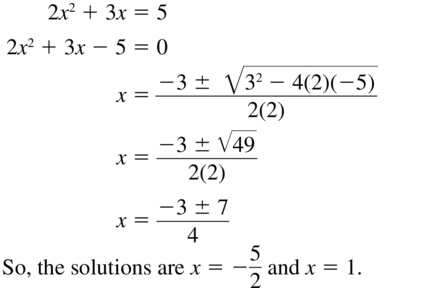
Question 30.
2x² + \(\frac{1}{2}\) = 2x
Answer:

Question 31.
2x² + 3x =−3x² + 1
Answer:

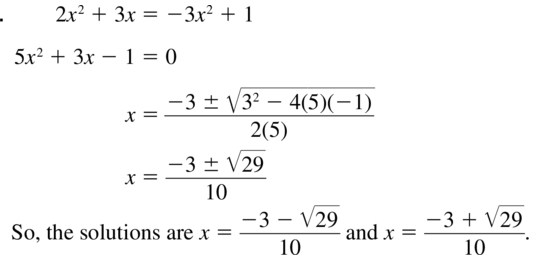
Question 32.
4x − 20 = x²
Answer:

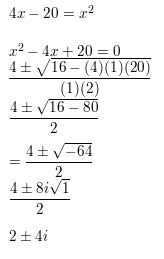
Polynomial Functions Performance Task: For the Birds-Wildlife Management

Core Vocabulary

Core Concepts
Section 4.5

Section 4.6

Section 4.7

Section 4.8

Section 4.9

Mathematical Practices

Question 1.
Explain how understanding the Complex Conjugates Theorem allows you to construct your argument in Exercise 46 on page 203.

Question 2.
Describe how you use structure to accurately match each graph with its transformation in Exercises 7–10 on page 209.

Performance Task
For the Birds -Wildlife Management
How does the presence of humans affect the population of sparrows in a park? Do more humans mean fewer sparrows? Or does the presence of humans increase the number of sparrows up to a point? Are there a minimum number of sparrows that can be found in a park, regardless of how many humans there are? What can a mathematical model tell you?

To explore the answers to these questions and more, go to BigIdeasMath.com.

Polynomial Functions Chapter Review

Decide whether the function is a polynomial function. If so, write it in standard form and state its degree, type, and leading coefficient.

Question 1.
h(x) = −x³ + 2x² − 15x⁷

Answer:

Question 2.
p(x) = x³ − 5x^0.5 + 13x² + 8
Answer:

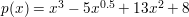
Thus p(x) is not a polynomial function

Graph the polynomial function.

Question 3.
h(x) = x² + 6x⁵ − 5
Answer:

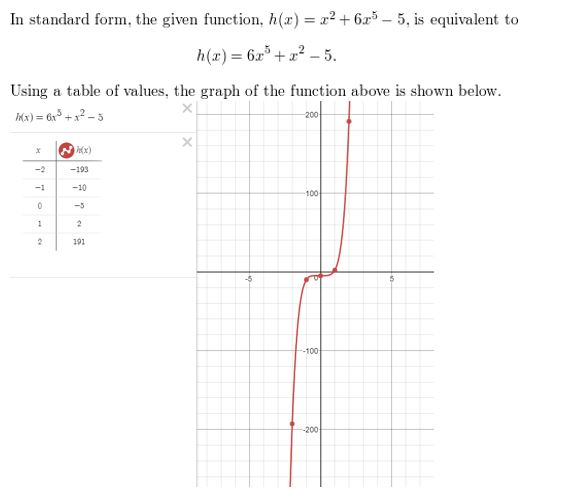
Question 4.
f(x) = 3x⁴ − 5x² + 1
Answer:

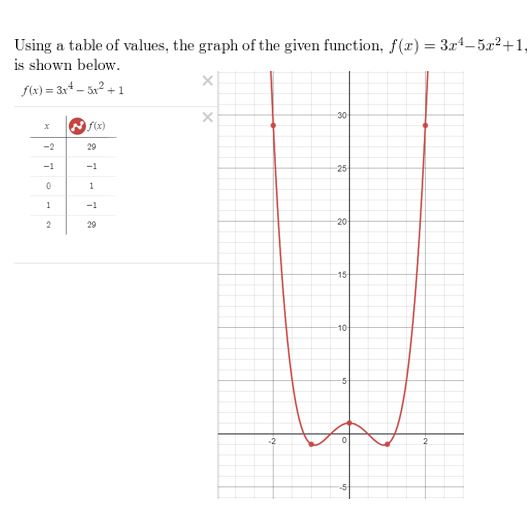
Question 5.
g(x) = −x⁴ + x + 2
Answer:

Find the sum or difference.

Question 6.
(4x³ − 12x² − 5) − (−8x² + 4x + 3)
Answer:
Given,
4x³ − 12x² − 5 + 8x² – 4x – 3
4x³ − 4x² − 8
4(x³ − x² − 2)
So, (4x³ − 12x² − 5) − (−8x² + 4x + 3) = 4(x³ − x² − 2)

Question 7.
(x⁴ + 3x³ − x² + 6) + (2x⁴ − 3x + 9)
Answer:
Given,
(x⁴ + 3x³ − x² + 6) + (2x⁴ − 3x + 9)
x⁴ + 3x³ − x² + 6 + 2x⁴ − 3x + 9
3x⁴ + 3x³ − x² -3x + 15
So, (x⁴ + 3x³ − x² + 6) + (2x⁴ − 3x + 9) = 3x⁴ + 3x³ − x² -3x + 15

Question 8.
(3x² + 9x + 13) − (x² − 2x + 12)
Answer:
Given,
(3x² + 9x + 13) − (x² − 2x + 12)
3x² + 9x + 13 − x² − 2x + 12
2x² + 7x + 25
So, (3x² + 9x + 13) − (x² − 2x + 12) = 2x² + 7x + 25

Find the product.

Question 9.
(2y² + 4y − 7)(y + 3)
Answer:
(2y² + 4y − 7)(y + 3)
y(2y² + 4y − 7) + 3(2y² + 4y − 7)
2y³ + 4y² – 7y + 6y² + 12y – 21
2y³ + 10y² + 5y – 21

Question 10.
(2m + n)³

Answer:
Given,
(2m + n)³
This is in the form of (a + b)³
(2m + n)³ = (2m)³ + (n)³ + 3(2m)²(n) + 3(2m)(n)²
= 8m³ + n³ + 12m²n + 6mn²

Question 11.
(s + 2)(s + 4)(s − 3)
Answer:
Given,
s(s + 4) + 2(s + 4) (s – 3)
(s² + 4s + 2s + 8)(s – 3)
s³ + 4s² + 2s² + 8s – 3s² – 12s – 6s – 24
s³ + 3s² – 10s – 24
So, (s + 2)(s + 4)(s − 3) = s³ + 3s² – 10s – 24

Use Pascal’s Triangle to expand the binomial.

Question 12.
(m + 4)⁴

Answer:
Given,(m + 4)⁴
(m + 4)⁴ = (m)⁴ + (4)⁴ + 6m²(4)² + 4m(4)³
= m⁴ + 256 + 96m² + 256m
So, (m + 4)⁴ = m⁴ + 256 + 96m² + 256m

Question 13.
(3s + 2)⁵

Answer:
Given,
(3s + 2)⁵
This is in the form of (x + y)⁵
1(3s)⁵ + 5(3s)⁴(2) + 10(3s)³ (2) + 10(3s)²(2) + 5(3s)(2)⁴ + 1(2)
= (3s)⁵ – 10(3s)⁴ + 20(3s)³ – 20(3s)² + 80(3s) – 2
= 243s⁵ – 810s⁴ + 540s³ – 180s² + 240s – 2
So, (3s + 2)⁵ = 243s⁵ – 810s⁴ + 540s³ – 180s² + 240s – 2

Question 14.
(z + 1)⁶

Divide using polynomial long division or synthetic division.

Question 15.
(x³ + x² + 3x − 4) ÷ (x² + 2x + 1)
Answer:

Question 16.
(x⁴ + 3x³ − 4x² + 5x + 3) ÷ (x² + x + 4)
Answer:

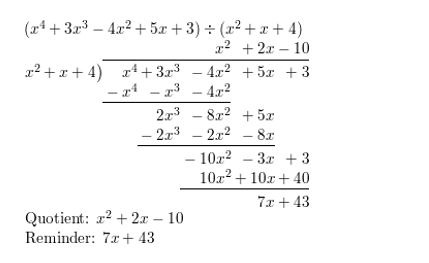
Question 17.
(x⁴ − x² − 7) ÷ (x + 4)
Answer:

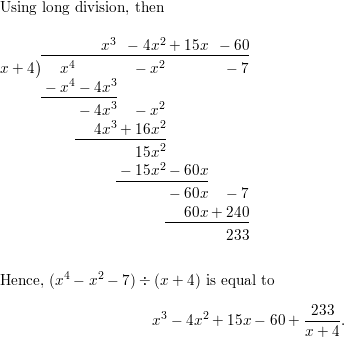
Question 18.
Use synthetic division to evaluate g(x) = 4x³ + 2x² − 4 when x = 5.
Answer:

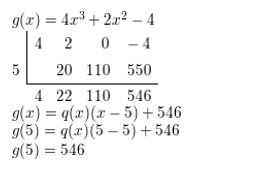
Factor the polynomial completely.

Question 19.
64x³ − 8
Answer:

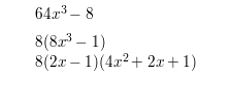
Question 20.
2z⁵ − 12z³ + 10z
Answer:

Question 21.
2a³ − 7a² − 8a + 28
Answer:

Question 22.
Show that x + 2 is a factor of f(x) = x⁴ + 2x³ − 27x − 54. Then factor f(x) completely.
Answer:

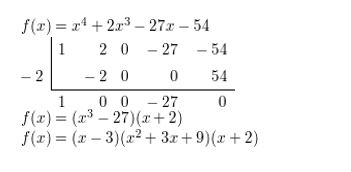
Find all real solutions of the equation.

Question 23.
x³ + 3x² − 10x − 24 = 0
Answer:

Question 24.
x³ + 5x² − 2x − 24 = 0
Answer:

Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros.

Question 25.
1, 2 − \(\sqrt{3}\)
Answer:

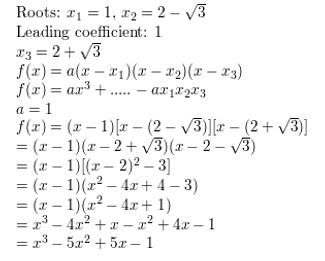
Question 26.
2, 3, \(\sqrt{5}\)
Answer:

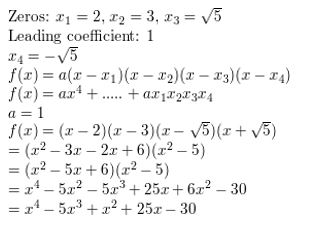
Question 27.
−2, 5, 3 + \(\sqrt{6}\)
Answer:

Question 28.
You use 240 cubic inches of clay to make a sculpture shaped as a rectangular prism. The width is 4 inches less than the length and the height is 2 inches more than three times the length. What are the dimensions of the sculpture? Justify your answer.
Answer:
Given,
L = x
W = x-4
H = 3x + 2
V = 240
We know that,
V = LWH
240 = x × (x – 4) (3x + 2)
240 = 3x³ – 10x² – 8x
3x³ – 10x² – 8x – 240 = 0
3x³ – 18x² – 8x²- 48x – 40x – 240 = 0
3x²(x – 6) + 8x(x – 6) + 40(x – 6) = 0
(x – 6)(3x² + 8x + 40) = 0
x – 6 = 0
x = 6
3x² + 8x + 40 = 0
Δ = 8² – 4 × 3 × 40 = 64 – 480 = -416
x = L = 6
H = 6 – 2 = 4
W = 3 × 6 + 2 = 20

Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros.

Question 29.
3, 1 + 2i
Answer:

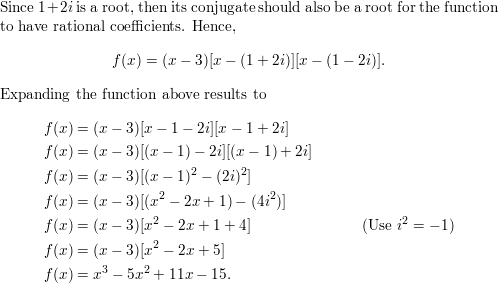
Question 30.
−1, 2, 4i
Answer:

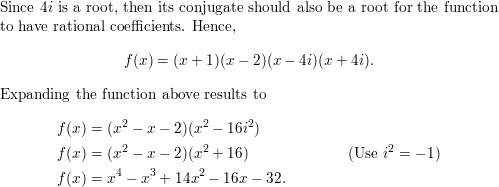
Question 31.
−5, −4, 1 −i\(\sqrt{3}\)
Answer:

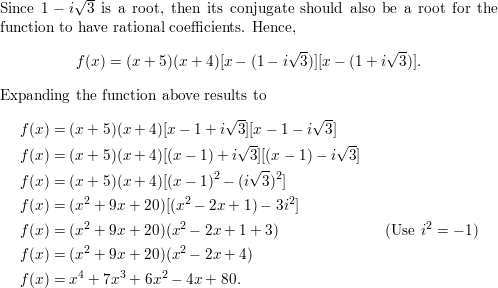
Determine the possible numbers of positive real zeros, negative real zeros, and imaginary zeros for the function.

Question 32.
f(x) = x⁴ − 10x + 8
Answer:

Question 33.
f(x) = −6x⁴ − x³ + 3x² + 2x + 18
Answer:

Describe the transformation of f represented by g. Then graph each function.

Question 34.
f(x) = x³, g(x) = (−x)³ + 2
Answer:

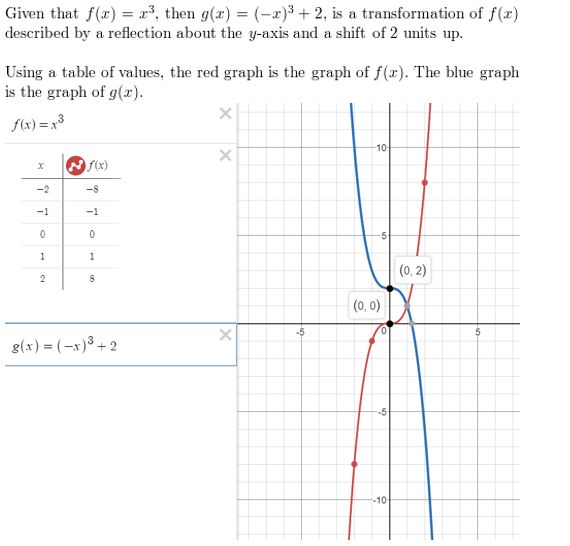
Question 35.
f(x) = x⁴, g(x) = −(x + 9)⁴

Answer:

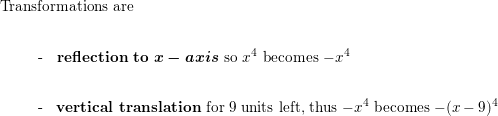
Write a rule for g.

Question 36.
Let the graph of g be a horizontal stretch by a factor of 4, followed by a translation 3 units right and 5 units down of the graph of f(x) = x⁵ + 3x.
Answer:

Question 37.
Let the graph of g be a translation 5 units up, followed by a reflection in the y-axis of the graph of f(x) = x⁴ − 2x³ − 12.
Answer:

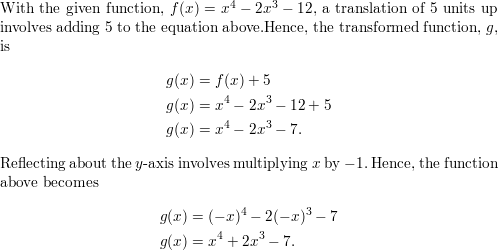
Graph the function. Identify the x-intercepts and the points where the local maximums and local minimums occur. Determine the intervals for which the function is increasing or decreasing.

Question 38.
f(x) = −2x³ − 3x² − 1
Answer:

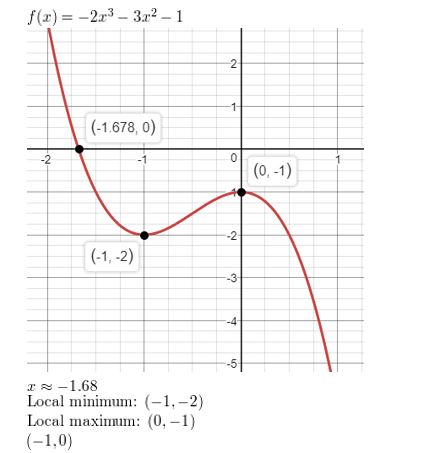
Question 39.
f(x) = x⁴ + 3x³ − x² − 8x + 2
Answer:

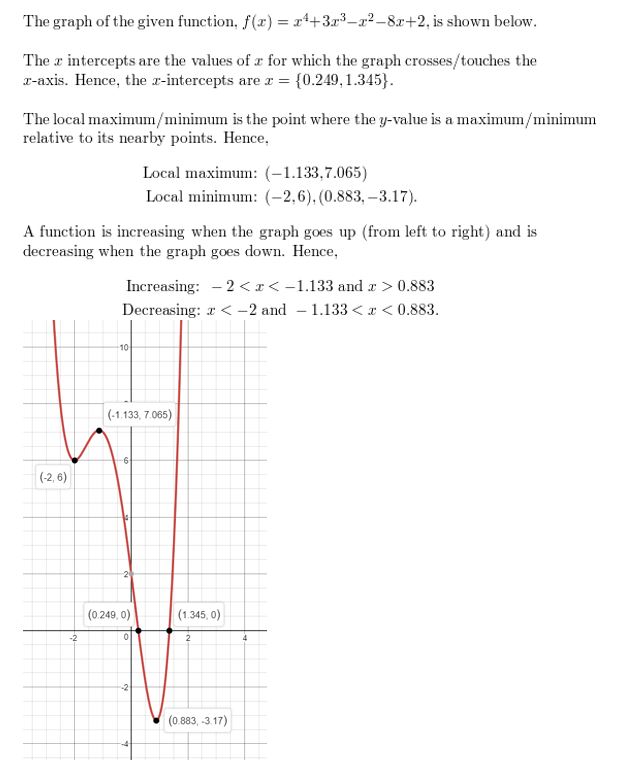
Determine whether the function is even, odd, or neither.

Question 40.
f(x) = 2x³ + 3x
Answer:

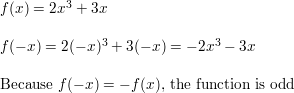
Question 41.
g(x) = 3x² − 7
Answer:

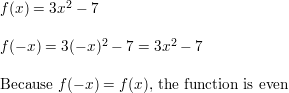
Question 42.
h(x) = x⁶ + 3x⁵

Answer:

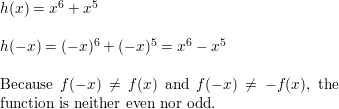
Question 43.
Write a cubic function whose graph passes through the points (−4, 0), (4, 0), (0, 6), and (2, 0).
Answer:
Given,
(-4, 0);
(4, 0);
(0, 6);
(2, 0).
Develop the general equation based on zeros.
f(0) = a(x+4)(0-4)(0-2)
Point (0,6) means x = 0 and y = 6.
6 = a(4)(-4)(-2)
6 = a(32)
6/32 = a
3/16 = a.
f(x) = (3/16)(x+4)(x-4)(x-2).

Question 44.
Use finite differences to determine the degree of the polynomial function that fits the data. Then use technology to find the polynomial function.

Answer:

Polynomial Functions Chapter Test

Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros.

Question 1.
3, 1 − \(\sqrt{2}\)
Answer:

Question 2.
−2, 4, 3i
Answer:

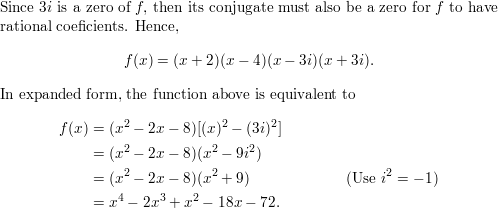
Find the product or quotient.

Question 3.
(x⁶ − 4)(x² − 7x + 5)
Answer:
Given,
(x⁶ − 4)(x² − 7x + 5)
x⁶(x² − 7x + 5) – 4(x² − 7x + 5)
x⁸ – 7x⁷ + 5x⁶ – 4x² + 28x – 20
So, (x⁶ − 4)(x² − 7x + 5) = x⁸ – 7x⁷ + 5x⁶ – 4x² + 28x – 20

Question 4.
(3x⁴ − 2x³ − x − 1) ÷ (x² − 2x + 1)
Answer:

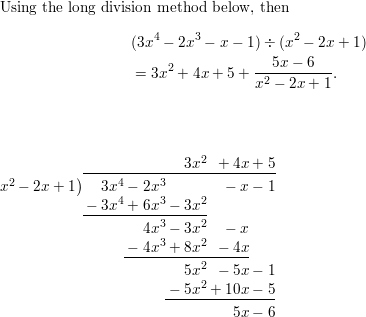
Question 5.
(2x³ − 3x² + 5x − 1) ÷ (x + 2)
Answer:

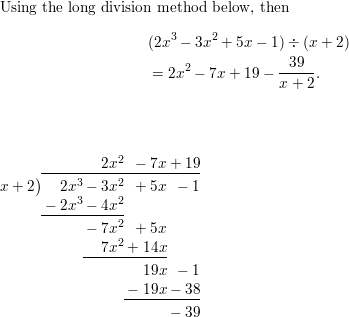
Question 6.
(2x + 3)³

Answer:
Given,
(2x + 3)³
This is in the form of (a + b)³
(2x + 3)³ = (2x)³ + (3)³ + 3(2x)²(3) + 3(2x)(3)²
= 8x³ + 27 + 36x² + 54x

Question 7.
The graphs of f(x) = x⁴ and g(x) = (x − 3)⁴ are shown.
a. How many zeros does each function have? Explain.
b. Describe the transformation of f represented by g.
c. Determine the intervals for which the function g is increasing or decreasing.

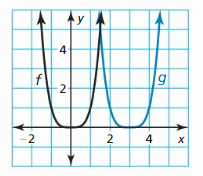
Answer:

Question 8.
The volume V (in cubic feet) of an aquarium is modeled by the polynomial function V(x) = x³ + 2x² − 13x + 10, where x is the length of the tank.
a. Explain how you know x = 4 is not a possible rational zero.
b. Show that x − 1 is a factor of V(x). Then factor V(x) completely.
c. Find the dimensions of the aquarium shown.

Answer:

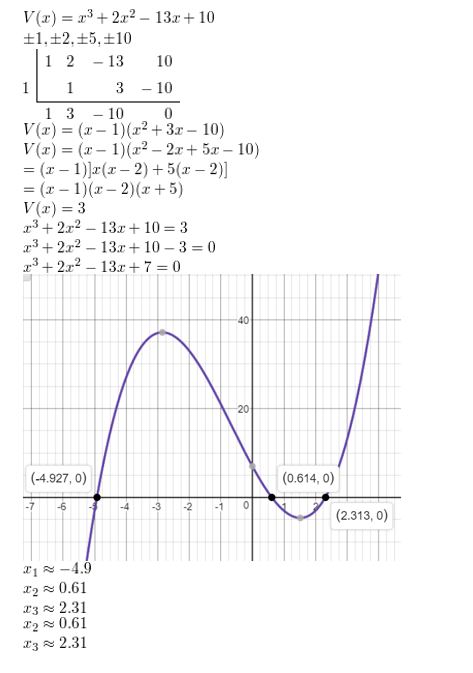
Question 9:
One special product pattern is (a − b)² = a² − 2ab + b². Using Pascal’s Triangle to expand (a − b)² gives 1a² + 2a(−b) + 1(−b)². Are the two expressions equivalent? Explain.
Answer:

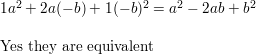
Question 10.
Can you use the synthetic division procedure that you learned in this chapter to divide any two polynomials? Explain.
Answer:

Question 11.
Let T be the number (in thousands) of new truck sales. Let C be the number (in thousands) of new car sales. During a 10-year period, T and C can be modeled by the following equations where t is time (in years).
T = 23t⁴ − 330t³ + 3500t² − 7500t + 9000
C = 14t⁴ − 330t³ + 2400t² − 5900t + 8900
a. Find a new model S for the total number of new vehicle sales.
b. Is the function S even, odd, or neither? Explain your reasoning.
Answer:

Question 12.
Your friend has started a golf caddy business. The table shows the profits p (in dollars) of the business in the first 5 months. Use finite differences to find a polynomial model for the data. Then use the model to predict the profit after 7 months.

Answer:

Polynomial Functions Cumulative Assessment

Question 1.
The synthetic division below represents f(x) ÷ (x− 3). Choose a value for m so that x − 3 is a factor of f(x). Justify your answer.

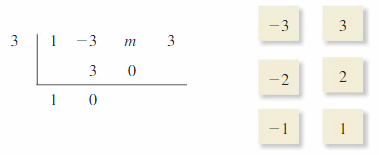
Question 2.
Analyze the graph of the polynomial function to determine the sign of the leading coefficient, the degree of the function, and the number of real zeros. Explain.

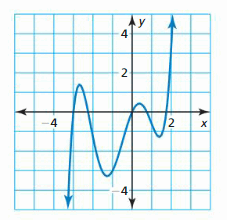
Answer:

Question 3.
Which statement about the graph of the equation 12(x− 6) = −( y + 4)² is not true?
A. The vertex is (6, −4).
B. The axis of symmetry is y = −4.
C. The focus is (3, −4).
D. The graph represents a function.
Answer:

Question 4.
A parabola passes through the point shown in the graph. The equation of the axis of symmetry is x = −a. Which of the given points could lie on the parabola? If the axis of symmetry was x = a, then which points could lie on the parabola? Explain your reasoning.

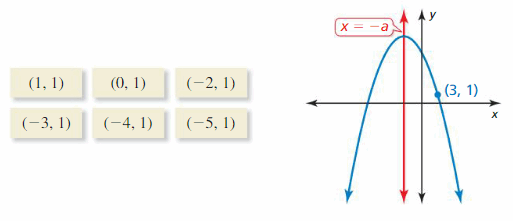
Answer:

Question 5.
Select values for the function to model each transformation of the graph of f(x) = x.

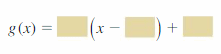
a. The graph is a translation 2 units up and 3 units left.
b. The graph is a translation 2 units right and 3 units down.
c. The graph is a vertical stretch by a factor of 2, followed by a translation 2 units up.
d. The graph is a translation 3 units right and a vertical shrink by a factor of \(\frac{1}{2}\), followed by a translation 4 units down.
Answer:

Question 6.
The diagram shows a circle inscribed in a square. The area of the shaded region is21.5 square meters. To the nearest tenth of a meter, how long is each side of the square?

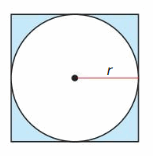
A. 4.6 meters
B. 8.7 meters
C. 9.7 meters
D. 10.0 meters
Answer:

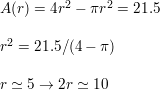
Question 7.
Classify each function as even, odd, or neither. Justify your answer.
a. f(x) = 3x⁵
b. f(x) = 4x³ + 8x
c. f(x) = 3x⁵ + 12x²+ 1
d. f(x) = 2x⁴
e. f(x) = x¹¹ − x⁷
f. f(x) = 2x⁸ + 4x⁴ + x² − 5
Answer:

Question 8.
The volume of the rectangular prism shown is given by V = 2x³ + 7x² − 18x − 63. Which polynomial represents the area of the base of the prism?
A. 2x² + x − 21
B. 2x² + 21 − x
C. 13x + 21 + 2x²
D. 2x² − 21 − 13x

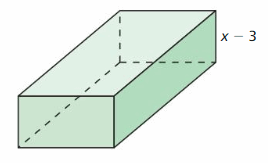
Answer:

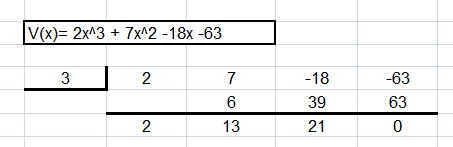
Question 9.
The number R (in tens of thousands) of retirees receiving Social Security benefits is represented by the function R = 0.286t³ − 4.68t² + 8.8t + 403, 0 ≤ t ≤ 10
where t represents the number of years since 2000. Identify any turning points on the given interval. What does a turning point represent in this situation?
Answer: