Download Big Ideas Math Answers Grade 3 Chapter 11 Understand Fraction Equivalence and Comparison from here. The students of grade 3 can get a detailed explanation for all the questions on BIM 3rd std Chapter 11 Understand Fraction Equivalence and Comparison. We have provided the Big Ideas Math Answers for Grade 3 Chapter 11 Understand Fraction Equivalence and Comparison in the pdf format so that you can prepare in offline mode.
Big Ideas Math Book 3rd Grade Answer Key Chapter 11 Understand Fraction Equivalence and Comparison
It is mandatory for the students to check out the topics before you start preparing any chapter. Go through the topics given below and then check the solutions for those questions topic wise. To make your task easy we have attached the links to all the topics. All you have to do is to tap the links and kickstart your preparation.
Lesson 1 Equivalent Fractions
Lesson 2 Equivalent Fractions on a Number Line
- Lesson 11.2 Equivalent Fractions on a Number Line
- Equivalent Fractions on a Number Line Homework & Practice 11.2
Lesson 3 Relate Fractions and Whole Numbers
- Lesson 11.3 Relate Fractions and Whole Numbers
- Equivalent Fractions on a Number Line Homework & Practice 11.3
Lesson 4 Compare Fractions with the Same Denominator
- Lesson 11.4 Compare Fractions with the Same Denominator
- Compare Fractions with the Same Denominator Homework & Practice 11.4
Lesson 5 Compare Fractions with Same Numerator
- Lesson 11.5 Compare Fractions with Same Numerator
- Compare Fractions with Same Numerator Homework & Practice 11.5
Lesson 6 Compare Fractions on a Number Line
- Lesson 11.6 Compare Fractions on a Number Line
- Compare Fractions on a Number Line Homework & Practice 11.6
Lesson 7 Compare Fractions
Lesson 8 Compare and Order Fractions
Understand Fraction Equivalence and Comparison
- Understand Fraction Equivalence and Comparison Performance Task
- Understand Fraction Equivalence and Comparison Activity
- Understand Fraction Equivalence and Comparison Chapter Practice
Lesson 11.1 Equivalent Fractions
Explore and Grow
Use the model to write fractions that are the same size as \(\frac{1}{2}\)
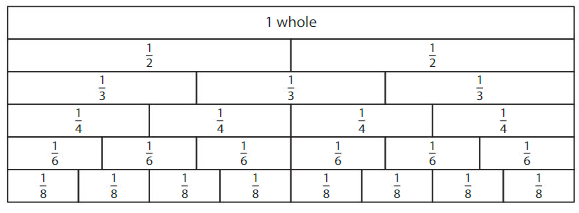
Answer: fraction \(\frac{4}{8}\) , fraction\(\frac{8}{16}\) are the same size as fraction \(\frac{1}{2}\).
Reasoning
Can you write a fraction with a denominator of that is the same size as \(\frac{3}{4}\)? Explain.
Answer: It is nothing but equivalent fraction \(\frac{3}{4}\) and \(\frac{21}{28}\) are equivalent fraction.
Think and Grow: Model Equivalent Fractions
Two or more numbers that have the same value are equivalent. Two or more fractions that name the same part of a whole are equivalent fractions.
Example
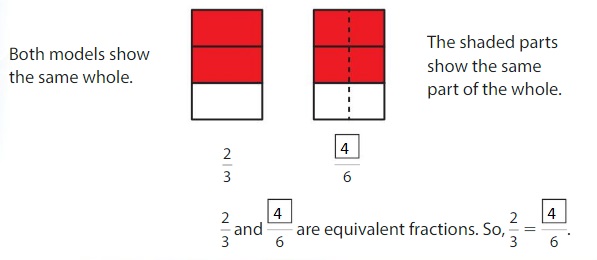
Use the models to find an equivalent fraction for \(\frac{2}{3}\) .
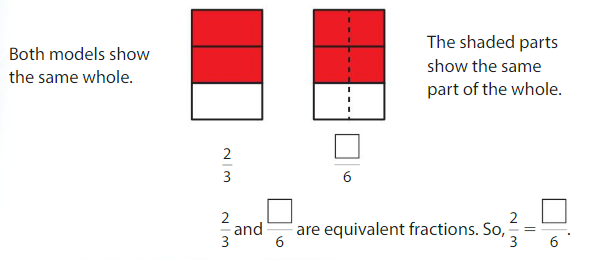
Answer:
Show and Grow
Use the models to find an equivalent fraction. Both models show the same whole.
Question 1.
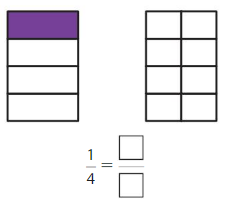
Answer:\(\frac{2}{8}\)
Explanation: \(\frac{1}{4}\) and 2/8 are equivalent fractions both gives the same answer.
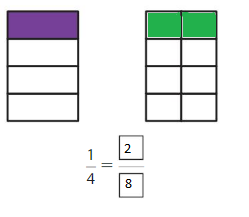
Question 2.
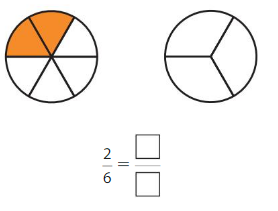
Answer: 1/3
Explanation: \(\frac{2}{6}\) and \(\frac{2}{8}\) are equivalent fractions both gives the same answer.
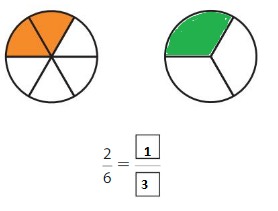
Question 3.
Shade 1 part of the model. Then divide the model into 4 equal parts. Write the equivalent fraction.
Answer: \(\frac{2}{4}\)
Explanation:

\(\frac{1}{4}\) and \(\frac{2}{4}\) are equivalent fractions both gives the same answer.
Apply and Grow: Practice
Use the models to find an equivalent fraction. Both models show the same whole.
Question 4.
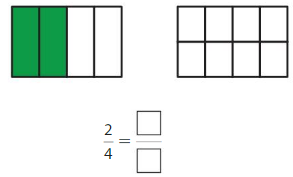
Answer: \(\frac{4}{8}\)
Explanation:
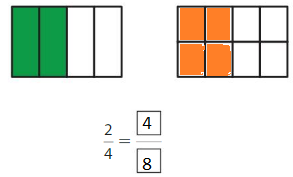
\(\frac{2}{4}\) and \(\frac{4}{8}\) are equivalent fractions both gives the same answer.
Question 5.
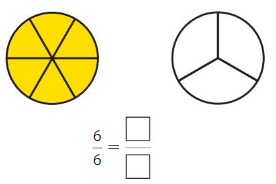
Answer: \(\frac{3}{3}\)
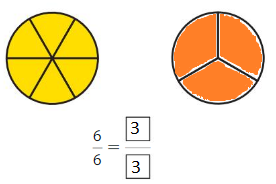
Explanation: \(\frac{6}{6}\) and \(\frac{3}{3}\) are equivalent fractions both gives the same answer.
Question 6.
Shade 1 part of the model. Then divide the model into 6 equal parts. Write the equivalent fraction.
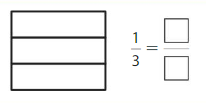
Answer: \(\frac{2}{6}\)
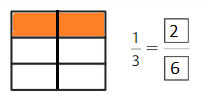
Explanation: \(\frac{1}{3}\) and \(\frac{2}{6}\) are equivalent fractions both gives the same answer.
Find the equivalent fraction
Question 7.
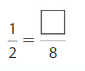
Answer: \(\frac{4}{8}\)
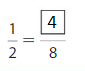
Explanation:
The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Here the numerator of both the fractions is different.
Question 8.
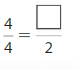
Answer: \(\frac{2}{2}\)
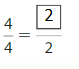
Explanation:
The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Here the numerator of both the fractions is different.
Question 9.
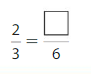
Answer: \(\frac{4}{6}\)
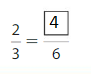
Explanation:
The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Here the numerator of both the fractions is different.
Question 10.
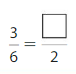
Answer: \(\frac{1}{2}\)
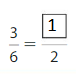
Explanation:
The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Here the numerator of both the fractions is different.
Question 11.
Structure
Descartes shades \(\frac{3}{4}\) of a rectangle. Divide and shade the model to show an equivalent fraction for \(\frac{3}{4}\).
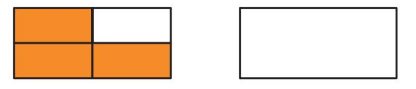
Answer: \(\frac{6}{8}\)
Explanation:
The number equivalent to \(\frac{3}{4}\) is \(\frac{6}{8}\).
So you have to divide the rectangle into 8 equal parts and shade 6 parts among them.
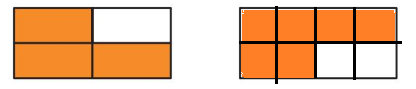
Question 12.
Which One Doesn’t Belong?
Which model does not belong with the other three?
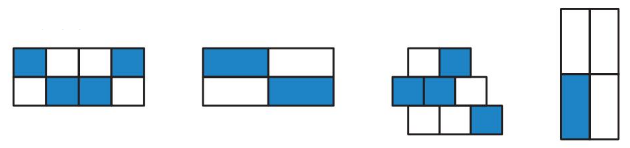
Answer: 4 figure is different
Explanation: From the above pictures 1 and 2 are equivalent fractions the first rectangle represent \(\frac{4}{8}\) and the second represents \(\frac{2}{4}\) both give the answer as \(\frac{1}{2}\)
The fourth figure has 4 parts and 1 part is shaded. So, the name of the fraction is \(\frac{1}{4}\)
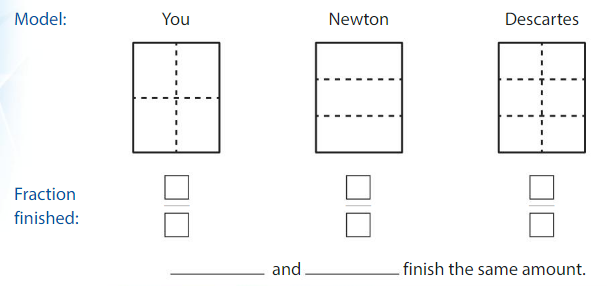
Think and Grow: Modeling Real Life
You, Newton, and Descartes divide your posters for a science fair as shown.You finish 3 parts, Newton finishes 2 parts, and Descartes finishes 4 parts.Who has finished the same amount?
Answer:
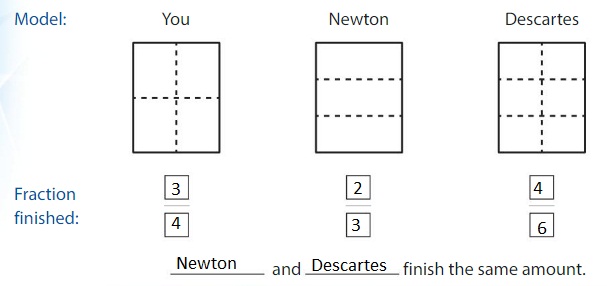
Show and Grow
Question 13.
You, Newton, and Descartes divide your submarine sandwiches as shown. You eat 1 part, Newton eats 2 parts, and Descartes eats 2 parts. Who eats the same amount?

Answer:
Given,
You eat 1 part, Newton eats 2 parts, and Descartes eats 2 parts.
You and Newton eats the same amount
Question 14.
DIG DEEPER!
You and your friend have small pizzas. You cut your pizza sixths. Your friend cuts her pizza into eighths. You eat \(\frac{3}{6}\) of your pizza. Your 6 friend eats the same amount of her pizza. What fraction of her pizza does your friend eat? How many slices does your friend eat? Explain.
Answer:
Given,
You and your friend have small pizzas. You cut your pizza sixths.
Your friend cuts her pizza into eighths. You eat \(\frac{3}{6}\) of your pizza. Your 6 friend eats the same amount of her pizza.
That means \(\frac{6}{8}\) = \(\frac{3}{4}\)
Thus your friend eats \(\frac{3}{4}\) part of the pizza.
Equivalent Fractions Homework & Practice 11.1
Use the models to find an equivalent fraction. Both models show the same whole.
Question 1.
Answer: \(\frac{2}{3}\)
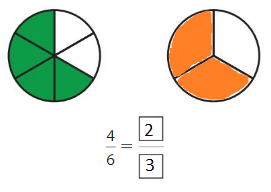
Explanation: \(\frac{4}{6}\) and \(\frac{2}{3}\) are equivalent fractions both gives the same answer.
Question 2.
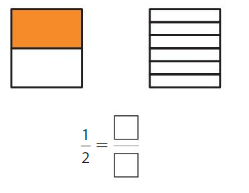
Answer: \(\frac{3}{6}\)
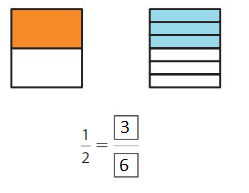
Explanation: \(\frac{1}{2}\) and \(\frac{3}{6}\) are equivalent fractions both gives the same answer.
Question 3.
Shade 1 part of the model. Then divide the model into 8 equal parts. Write the equivalent fraction.
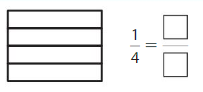
Answer: \(\frac{2}{8}\)
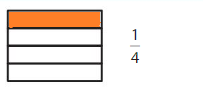
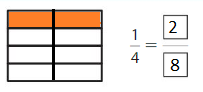
Explanation: \(\frac{1}{4}\) and \(\frac{2}{8}\) are equivalent fractions both gives the same answer.
Find the equivalent fraction
Question 4.
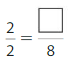
Answer: \(\frac{8}{8}\)
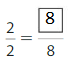
Explanation: \(\frac{2}{2}\) and \(\frac{8}{8}\) are equivalent fractions both gives the same answer.
Question 5.
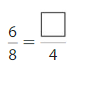
Answer: \(\frac{3}{4}\)
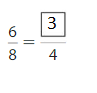
Explanation: \(\frac{6}{8}\) and \(\frac{3}{4}\) are equivalent fractions both gives the same answer.
Question 6.
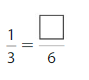
Answer: \(\frac{2}{6}\)
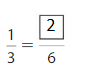
Explanation: \(\frac{1}{3}\) and \(\frac{2}{6}\) are equivalent fractions both gives the same answer.
Question 7.
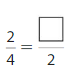
Answer: \(\frac{1}{2}\)
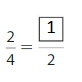
Explanation: \(\frac{2}{4}\) and \(\frac{1}{2}\) are equivalent fractions both gives the same answer.
Question 8.
Open-Ended
Divide one model into an odd number of equal parts and the other model into an even number of equal parts. Then model and write two equivalent fractions.

Answer: \(\frac{1}{2}\) = \(\frac{2}{4}\)
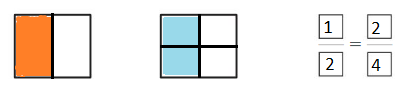
Explanation: \(\frac{1}{2}\) and \(\frac{2}{4}\) are equivalent fractions both gives the same answer.
Question 9.
Modeling Real Life
You, Newton, and Descartes divide your portrait canvases as shown. You paint 2 parts, Newton paints 2 parts, and Descartes paints 8 parts. Who paints the same amount of the portrait canvas?
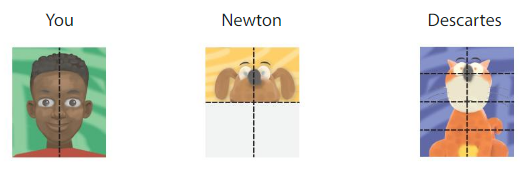
Answer: You and Descartes
Explanation:
You, Newton, and Descartes divide your portrait canvases as shown.
You paint 2 parts, Newton paints 2 parts, and Descartes paints 8 parts.
You completed 2 of 2 parts.
Descartes paints 8 of 8 parts.
\(\frac{2}{2}\) = 1
\(\frac{8}{8}\) = 1
Thus you and Descartes completes the same amount of the portrait canvas.
Question 10.
DIG DEEPER!
You and your friend paint 2 roundabouts for a park. You divide your roundabout into thirds. Your friend divides his roundabout into sixths. You paint \(\frac{1}{3}\) of your roundabout. Your friend paints the same amount of his roundabout. What fraction does your friend paint? Explain.

Answer:
Given,
You and your friend paint 2 roundabouts for a park. You divide your roundabout into thirds.
Your friend divides his roundabout into sixths.
You paint \(\frac{1}{3}\) of your roundabout. Your friend paints the same amount of his roundabout.
\(\frac{6}{6}\)
Review & Refresh
Question 11.
Round to the nearest ten to estimate the sum.
Answer: 540
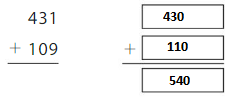
Explanation:
The nearest ten estimation for 431 is 430
and for 109 Nearest ten estimation is 110
hence
430
+ 110
540
Question 12.
Round to the nearest hundred to estimate the sum.
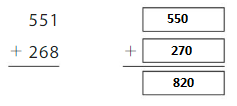
Answer: 820
Explanation:
The nearest ten estimation for 551 is 550
and for 268 Nearest ten estimation is 270
Lesson 11.2 Equivalent Fractions on a Number Line
Explore and Grow
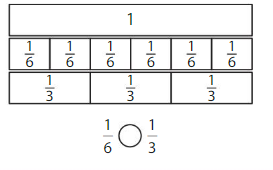
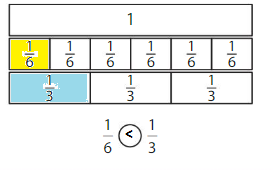
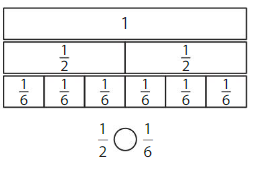
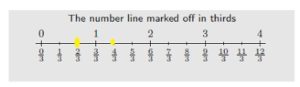
Use Fraction Strips to label thirds on the number line.

Use Fraction Strips to label sixths on the number line.

Use the number lines to complete the equivalent fraction.
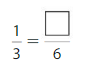
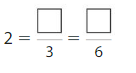
Answer: \(\frac{2}{6}\)
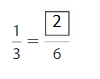
Explanation: \(\frac{1}{3}\) and \(\frac{2}{6}\) are equivalent fractions both gives the same answer.
Structure
How can you tell whether fractions are equivalent using a number line?
Answer:
Step 1: Locate the original fraction on the number line. We’ll first need to locate our fraction on the number line.
Step 2: Divide each your newly created divisions from step 1 into two even spaces.
Step 3: Find the equivalent fraction.
Step 4: Repeat steps 2 and 3 to find more equivalent fractions.
Think and Grow: Equivalent Fractions on a Number Line
You can use a number line to find equivalent fractions. Equivalent fractions represent the same point on a number line.
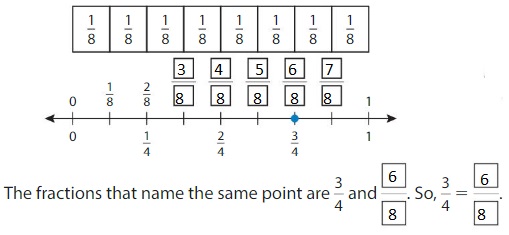
Example
Use a number line to find an equivalent fraction for \(\frac{3}{4}\).

Step 1: Plot \(\frac{3}{4}\) on a number line.
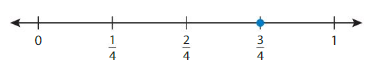
Step 2: Divide the number line into eighths. Label each tick mark to show eighths.
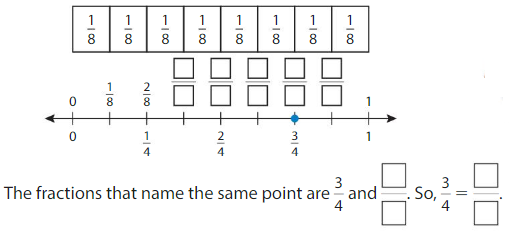
Answer:
Show and Grow
Question 1.
Use the number line to find an equivalent fraction.
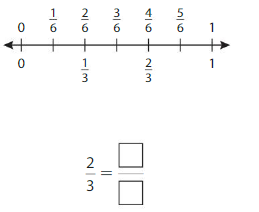
Answer: \(\frac{4}{6}\)
The fractions \(\frac{2}{3}\) and \(\frac{4}{6}\) are on the same point.
So, \(\frac{2}{3}\) = \(\frac{4}{6}\)
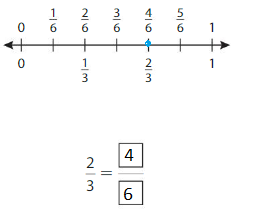
Question 2.
Write two fractions that name the point shown.
Answer: \(\frac{2}{4}\) = \(\frac{1}{2}\)
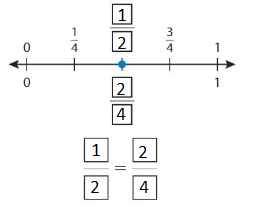
The fractions \(\frac{1}{2}\) and \(\frac{2}{4}\) are on the same point.
So,\(\frac{1}{2}\) = \(\frac{2}{4}\)
Apply and Grow: Practice
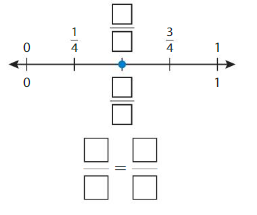
Write two fractions that name the point shown.
Question 3.
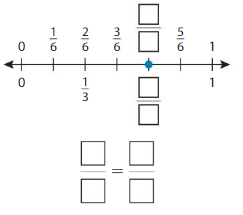
Answer: \(\frac{4}{6}\) = \(\frac{1}{2}\)
The fractions \(\frac{4}{6}\) and \(\frac{1}{2}\) are on the same point.
So,\(\frac{4}{6}\) = \(\frac{1}{2}\)
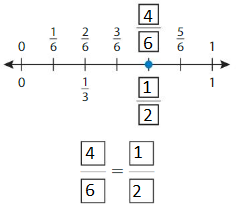
Question 4.
Answer: \(\frac{4}{8}\) = \(\frac{1}{2}\)
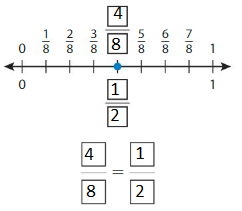
The fractions \(\frac{4}{8}\) and \(\frac{1}{2}\) are on the same point.
So,\(\frac{4}{8}\) = \(\frac{1}{2}\)
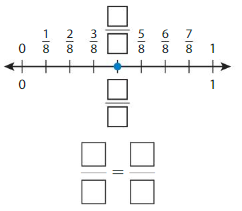
Question 5.
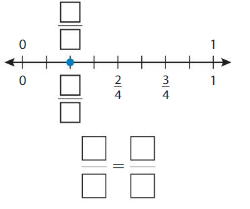
Answer: \(\frac{1}{4}\) = \(\frac{2}{8}\)
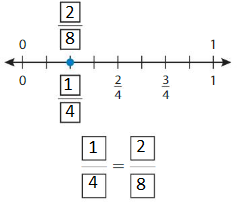
The fractions \(\frac{1}{4}\) and \(\frac{2}{8}\) are on the same point.
So,\(\frac{1}{4}\) = \(\frac{2}{8}\)
Question 6.
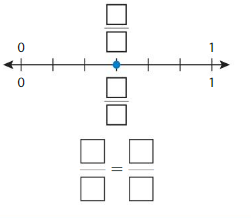
Answer: \(\frac{1}{2}\) = \(\frac{2}{4}\)
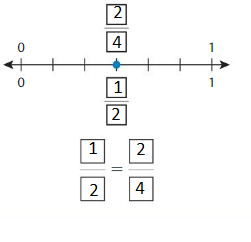
The fractions \(\frac{1}{2}\) and \(\frac{2}{4}\) are on the same point.
So,\(\frac{1}{2}\) = \(\frac{2}{4}\)
Question 7.
YOU BE THE TEACHER
Your friend says \(\frac{3}{4}\) and \(\frac{6}{8}\) are equivalent because they are not the same distance from 0. Is your friend correct? Explain.
Answer: No your friend is not correct. \(\frac{3}{4}\) and \(\frac{6}{8}\) are equivalent fractions irrespective of the distance on the number line.
Question 8.
Reasoning
Explain why \(\frac{1}{3}\) is equal to two \(\frac{1}{6}\)s
Answer:
Divide \(\frac{1}{3}\) by 2. You get \(\frac{1}{6}\)
Think and Grow: Modeling Real Life
Newton rests after biking \(\frac{2}{3}\) of a race. Descartes rests after biking \(\frac{2}{6}\) of the same race. Do they rest at the same point along the race path?

Model:

They ______ rest at the same point.
Explain: No they do not rest at the same point. Because \(\frac{2}{3}\) is not equal to \(\frac{2}{6}\)
Show and Grow
Question 9.
Newton hikes \(\frac{7}{8}\) of a trail. Descartes hikes \(\frac{3}{4}\) of the same trail. Do they hike the same distance along the trail?
Answer:
Newton hikes \(\frac{7}{8}\) of a trail. Descartes hikes \(\frac{3}{4}\) of the same trail.
You have to compare both the fractions.
\(\frac{7}{8}\) is greater than \(\frac{3}{4}\).
By this, we can say that does not hike the same distance along the trail.
Question 10.
Newton chases Descartes for \(\frac{3}{6}\) mile. Descartes turns around and chases Newton an equal distance.Write two equivalent fractions that can describe how far Descartes chases Newton.
Answer:
The equivalent fractions of \(\frac{3}{6}\) are
\(\frac{3}{6}\) × \(\frac{2}{2}\) = \(\frac{6}{12}\)
\(\frac{3}{6}\) = \(\frac{1}{2}\)
Thus the two The equivalent fractions of \(\frac{3}{6}\) are \(\frac{6}{12}\), \(\frac{1}{2}\)
Question 11.
DIG DEEPER!
You cut a quiche into 8 equal slices. Your family eats \(\frac{1}{2}\) of the quiche. How many slices does your family eat? Explain.
Answer:
Given,
You cut a quiche into 8 equal slices. Your family eats \(\frac{1}{2}\) of the quiche.
\(\frac{1}{2}\) × 8 = \(\frac{1}{4}\)
Thus your family eats 4 equal slices.
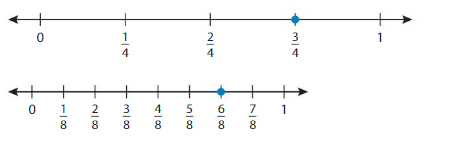
Equivalent Fractions on a Number Line Homework & Practice 11.2
Question 1.
Use the number line to find an equivalent fraction.
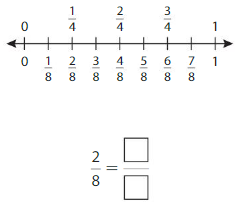
Answer: \(\frac{1}{4}\)
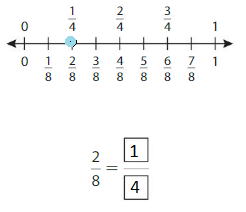
By seeing the above number we can find the equivalent fraction of \(\frac{2}{8}\).
\(\frac{1}{4}\) and \(\frac{2}{8}\) are on the same point.
Question 2.
Write two fractions that name the point shown
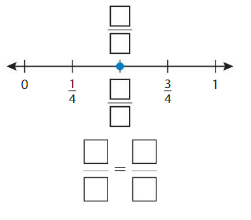
Answer: \(\frac{1}{2}\) = \(\frac{2}{4}\)
By seeing the above number we can find the equivalent fraction of \(\frac{1}{2}\).
\(\frac{1}{2}\) = \(\frac{2}{4}\)
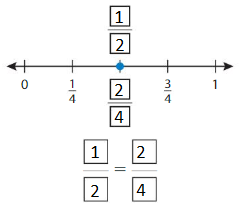
Write two fractions that name the same point shown.
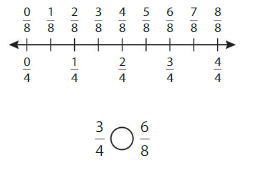
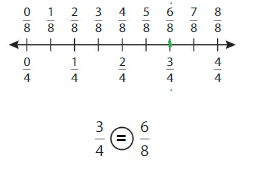
Question 3.
Answer: \(\frac{6}{8}\) = \(\frac{3}{4}\)
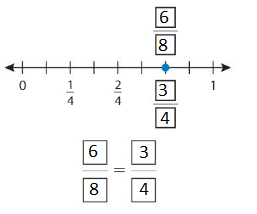
By seeing the above number we can find the equivalent fraction of \(\frac{6}{8}\).
\(\frac{6}{8}\) = \(\frac{3}{4}\)
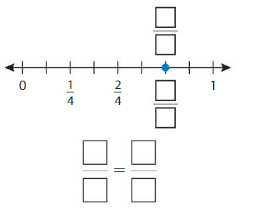
Question 4.
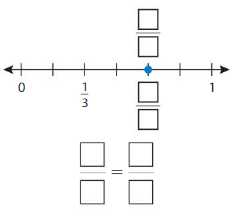
Answer: \(\frac{4}{6}\) = \(\frac{2}{3}\)
By seeing the above number we can find the equivalent fraction of \(\frac{4}{6}\).
\(\frac{4}{6}\) = \(\frac{2}{3}\)
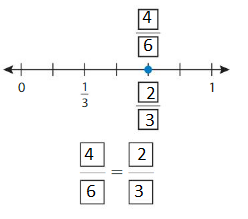
Question 5.
Which One Doesn’tBelong?
Which not fraction does belong with the other three? Explain.
Answer: \(\frac{2}{3}\)

The fraction \(\frac{2}{3}\) does not belong to other three fractions.
Question 6.
Reasoning
How do you know that \(\frac{3}{8}\) and \(\frac{3}{4}\) are equivalent when plotting the fractions on a number line?
Answer:
No, they are not equivalent. The numerators are equals, but the denominators are not, they are not equivalent. If the first one would be 6/8, they would be equivalent, because we can simplify the fractions by 2 and we got 3/4 again.
Question 7.
Modeling Real Life
You run \(\frac{6}{8}\) of a race. Your friend runs \(\frac{3}{4}\) of the same race. Do you and your friend run the same distance?

Answer:
Given,
You run \(\frac{6}{8}\) of a race. Your friend runs \(\frac{3}{4}\) of the same race.
The equivalent fraction of \(\frac{3}{4}\) is \(\frac{6}{8}\)
By this we can say that you and your friend run the same distance.
Question 8.
DIG DEEPER!
You have a frame that holds 8 pictures. You fill \(\frac{1}{4}\) of the frame. How many pictures do you put in the frame? Explain.
Answer:
Given,
You have a frame that holds 8 pictures. You fill \(\frac{1}{4}\) of the frame.
\(\frac{1}{4}\) × 8 = 2
Thus you put 2 pictures in the frame.
Review & Refresh
What fraction of the whole is shaded?
Question 9.
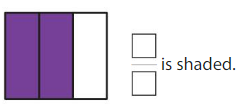
Answer: \(\frac{2}{3}\)
By seeing the figure we can name the fraction of the shaded part. The box is divided into 3 parts among them 2 parts are shaded.
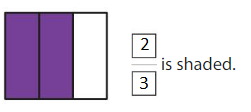
Question 10.
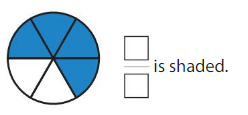
Answer: \(\frac{4}{6}\)
By seeing the figure we can name the fraction of the shaded part. The circle is divided into 6 parts among them 4 parts are shaded.
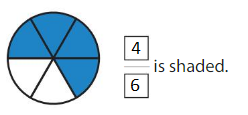
Lesson 11.3 Relate Fractions and Whole Numbers
Explore and Grow
Use Fraction Strips to complete the fractions. Draw to show your models.
Answer:
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Repeated Reasoning
How many more fourths did you use to model 2 than you did to model 1? How many more fourths would you need to model 3? Complete the fraction.
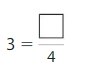
Answer: 12
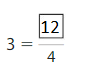
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Think and Grow: Equivalent Fractions and Whole Numbers
Example
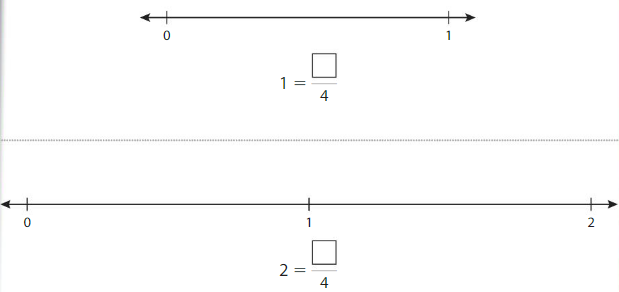
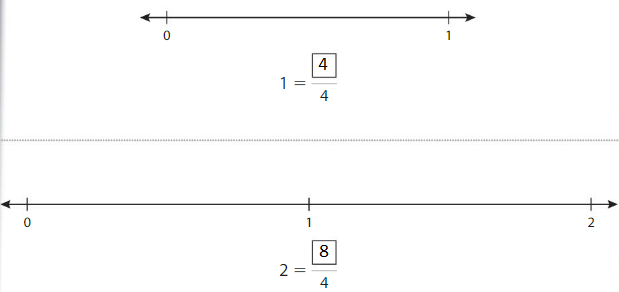
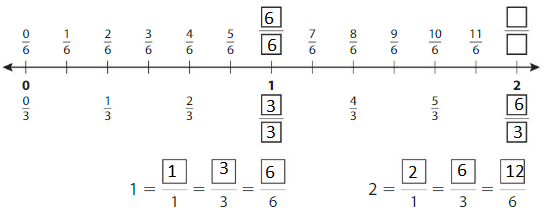
Write the numbers 1 and 2 as fractions. The number line shows 2 wholes. Each whole is divided into1 equal part.
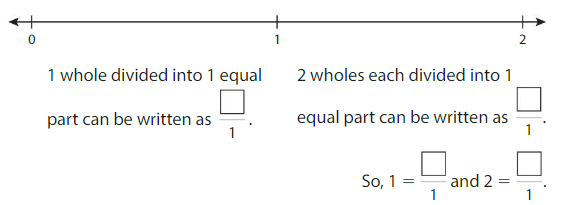
Answer:

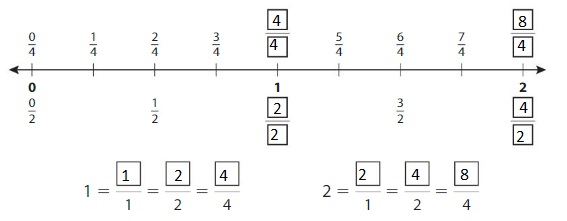
Example
Write equivalent fractions for the numbers 1 and 2.
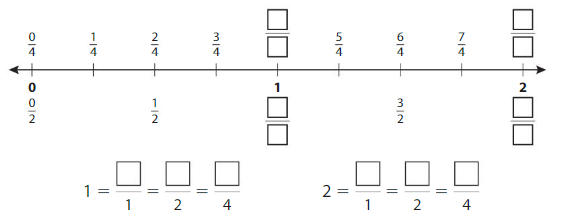
Answer:
Show and Grow
Question 1.
Complete the number line. Then complete the statements.
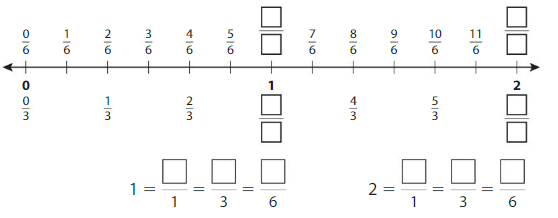
Answer:
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Apply and Grow: Practice
Question 2.
Complete the number line. Then write equivalent fractions for the numbers 3 and 4.
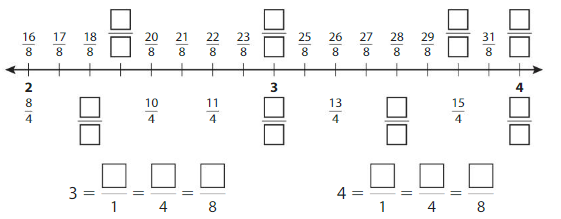
Answer:
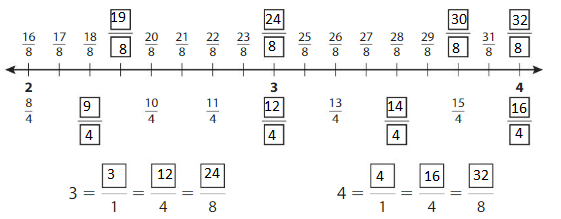
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Write two equivalent fractions for the whole number.
Question 3.
Answer:
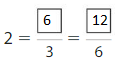
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 4.
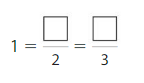
Answer:
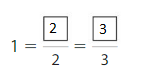
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 5.
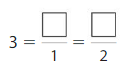
Answer:
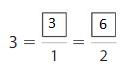
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Write the equivalent whole number.
Question 6.
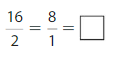
Answer:
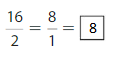
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 7.
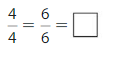
Answer:
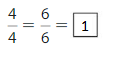
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 8.
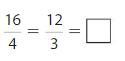
Answer:
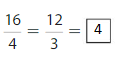
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 9.
You cut a sandwich into 4 pieces. You eat the whole sandwich. What fraction of the sandwich do you eat?

Answer:
Given,
You cut a sandwich into 4 pieces. You eat the whole sandwich.
\(\frac{4}{4}\) = 1
Thus you eat \(\frac{4}{4}\) fraction of the sandwich.
Question 10.
Number Sense
Write three fractions that are equivalent to 6 using the denominators 1, 2, and 6.
Answer:
\(\frac{6}{6}\) = 1
\(\frac{12}{6}\) = 2
\(\frac{36}{6}\) = 6
Question 11.
Use a number line to show \(\frac{5}{5}\) = 1.
Answer:
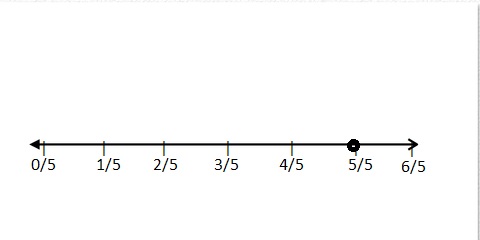
Think and Grow: Modeling Real Life
You run around a track 12 times. Each lap is \(\frac{1}{4}\) mile. How many miles do you run? Write your answer as a whole number and as a fraction.
Model:

You run _____ or ______ miles.
Answer:
Given,
You run around a track 12 times. Each lap is \(\frac{1}{4}\) mile.
12 × \(\frac{1}{4}\) = 3 mile
You run 3 miles.
Show and Grow
Question 12.
You ride your bike around a city block 24 times. Each time around is \(\frac{1}{6}\) mile. How many miles do you ride? Write your answer as a 6 whole number and as a fraction.
Answer:
Given,
You ride your bike around a city block 24 times. Each time around is \(\frac{1}{6}\) mile.
24 × \(\frac{1}{6}\) = 4
Thus you ride 4 miles.
Question 13.
There are 5 Great Lakes: Lake Erie, Lake Huron, Lake Michigan, Lake Ontario, and Lake Superior. You complete a project and use 1 whole poster for each lake. Write a fraction that gives the number of posters you use in all.
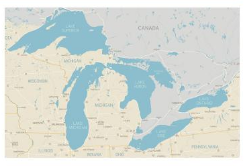
Answer:
Lake Michigan is \(\frac{1}{1}\)
Lake Huron is \(\frac{2}{1}\)
Lake Erie is \(\frac{3}{1}\)
Lake Ontario is \(\frac{4}{1}\)
Lake Superior is \(\frac{5}{1}\)
Question 14.
DIG DEEPER!
You and your friends order 3 pizzas. Each pizza is cut into 8 slices. You and your friends eat \(\frac{16}{8}\) of the pizzas. Write a fraction that shows the number of eighths that are left.
Answer:
Given that,
You and your friends order 3 pizzas. Each pizza is cut into 8 slices.
You and your friends eat \(\frac{16}{8}\) of the pizzas.
3 × 8 = 24 slices
\(\frac{24}{8}\)– \(\frac{16}{8}\) = \(\frac{8}{8}\)
Thus 8 slices are left in the pizza.
Equivalent Fractions on a Number Line Homework & Practice 11.3
Question 1.
Complete the number line. Then write equivalent fractions for the numbers 3 and 4.
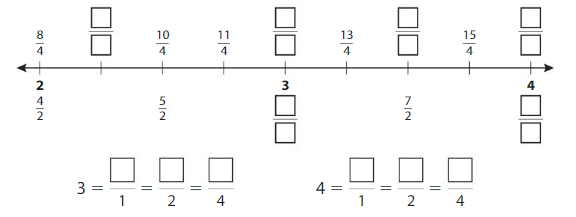
Answer:
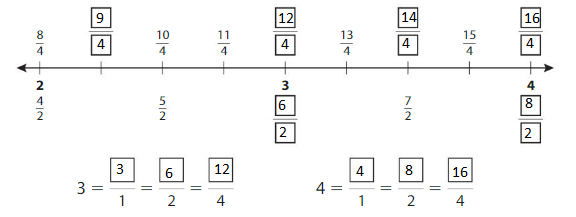
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Write two equivalent fractions for the whole number.
Question 2.
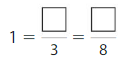
Answer:
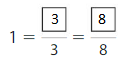
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 3.
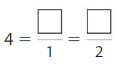
Answer:
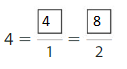
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 4.
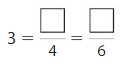
Answer:
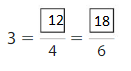
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Write the equivalent whole number.
Question 5.
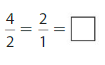
Answer:
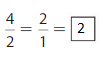
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 6.
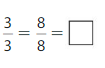
Answer:
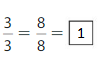
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 7.
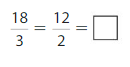
Answer:
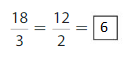
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 8.
Precision
Match each whole number to its equivalent fractions.
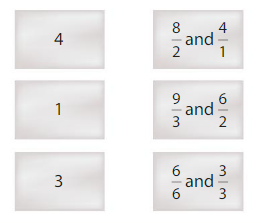
Answer:
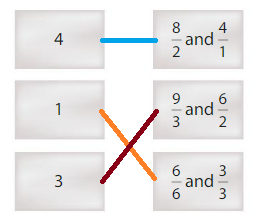
Explanation: The equivalent fractions can be defined as fractions with different numerators and denominators that represent the same value or proportion of the whole.
Question 9.
YOU BE THE TEACHER
Descartes says a fraction equivalent to 3 has a 3 in the denominator and a 1 in the numerator. Is Descartes correct? Explain.
Answer:
Descartes says a fraction equivalent to 3 has a 3 in the denominator and a 1 in the numerator.
Yes 3 is equivalent to \(\frac{3}{1}\)
Thus Descartes is correct.
Question 10.
Patterns
Describe and complete the pattern.
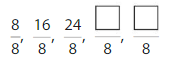
Answer:

The fraction is the multiples of 8. So, the pattern is 8/8, 16/8, 24/8, 32/8, 40/8.
Question 11.
Modeling Real Life
You run around a park 18 times. Each lap is \(\frac{1}{6}\) mile. How many miles do you run? Write your answer as a whole number and as a fraction.
Answer:
Given that,
You run around a park 18 times. Each lap is \(\frac{1}{6}\) mile.
18 × \(\frac{1}{6}\) = 3
Thus you run 3 miles or \(\frac{18}{6}\) miles
Question 12.
Modeling Real Life
Christopher Columbus had 3 ships on his first NiñaPintavoyage: the , the , and the Santa Maria. You complete a project and use 1 whole poster for each ship. Write a fraction that gives the number of posters you use in all.
Answer:
Given,
Christopher Columbus had 3 ships on his first NiñaPintavoyage: the , the , and the Santa Maria.
You complete a project and use 1 whole poster for each ship.
\(\frac{3}{3}\) = 1
Thus you use 1 poster for each ship.
Thus you use 3 posters for all the ships.
Question 13.
DIG DEEPER!
A teacher has 4 tables. Each table is divided into 4 sections. \(\frac{12}{4}\) of the tables have 4 supplies on them. Write a fraction that shows the number of fourths not that do have supplies on them.
Answer:
Given,
A teacher has 4 tables. Each table is divided into 4 sections.
4 × 4 = 16 sections
\(\frac{12}{4}\) of the tables have 4 supplies on them.
\(\frac{12}{4}\) = 3
3 of the tables have 4 supplies.
The fraction that shows the number of fourths not that do have supplies on them is \(\frac{3}{4}\)
Review & Refresh
Estimate. Then find the sum. Check whether your answer is reasonable.
Question 14.
Estimate: _____
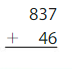
Answer: 890
Explanation:
The nearest ten estimation for 837 is 840
and for 46 Nearest ten estimation is 50
840
+ 50
890
Question 15.
Estimate: _____
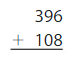
Answer: 510
Explanation:
The nearest ten estimation for 396 is 400
and for 108 Nearest ten estimation is 110
400
+ 110
510
Question 16.
Estimate: _____
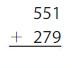
Answer: 830
Explanation:
The nearest ten estimation for 551 is 550
and for 279 Nearest ten estimation is 280
550
+ 280
830
Lesson 11.4 Compare Fractions with the Same Denominator
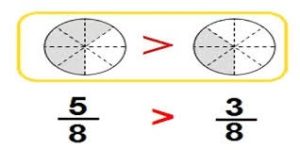
Explore and Grow
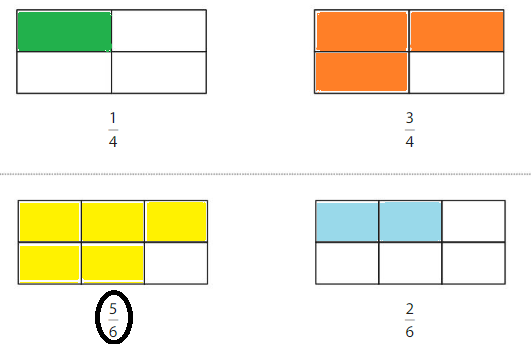
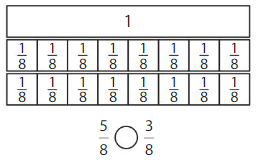
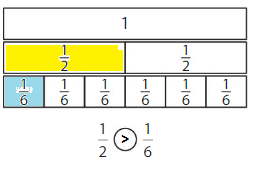
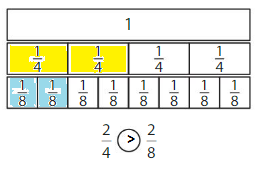
Color to show each fraction. Circle the greater fraction.
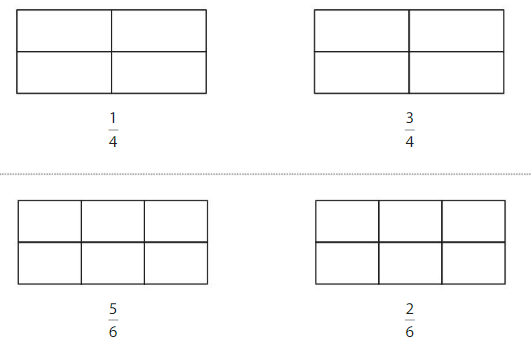
Answer: \(\frac{5}{6}\) is the greater fraction
Construct Arguments
Explain to your partner how you can compare fractions with the same denominator.
Answer:
if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
Think and Grow: Compare Fractions That have the Same Denominator
Example
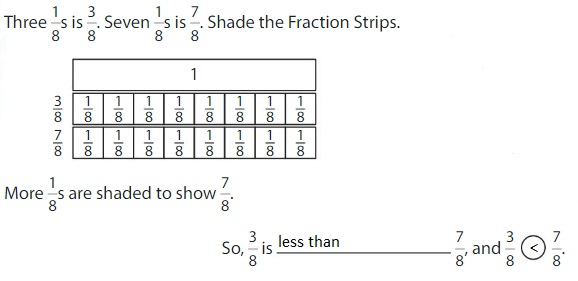
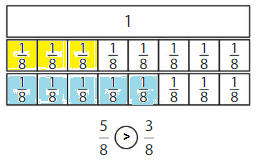
Compare \(\frac{3}{8}\) and \(\frac{7}{8}\).
One Way: Use Fraction Strips.
The fractions have the same denominator, 8.

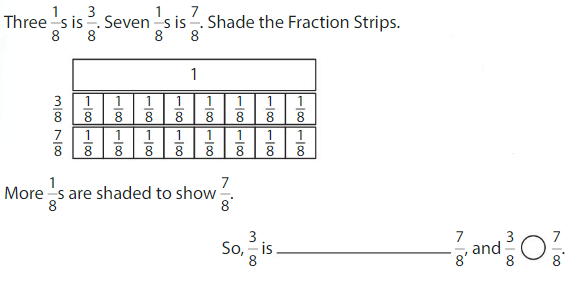
Answer:
Another Way:
When the denominators are the same, the whole is divided into the same number of equal parts. So, look at the numerators 3 and 7 to compare.The fraction with the greater numerator is the greater fraction.
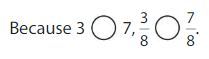
Answer:
Show and Grow
Shade to compare the fractions
Question 1.
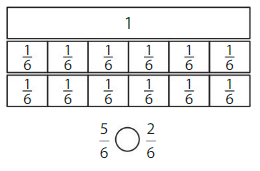
Answer:
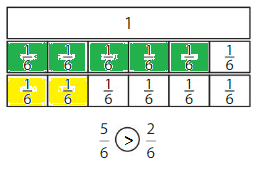
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
Question 2.
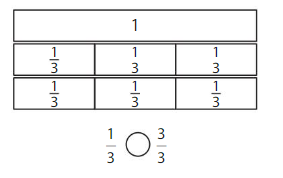
Answer:
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
Apply and Grow: Practice
Shade to compare the fractions.
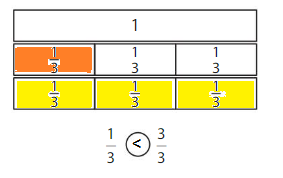
Question 3.
Answer:
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
Question 4.
Answer:
Explanation: Here the numerator and denominator of the fractions are the same so
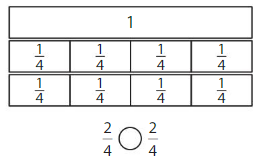
Compare.
Question 5.
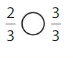
Answer:
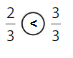
Explanation:
Compare the fractions. The denominators of both the fractions are the same so you have to compare the numerators.
2 is less than 3.
So, \(\frac{2}{3}\) < \(\frac{3}{3}\)
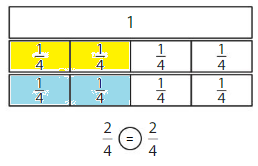
Question 6.
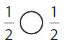
Answer:
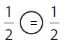
Compare the fractions. The denominators of both the fractions are the same so you have to compare the numerators.
So, \(\frac{1}{2}\) = \(\frac{1}{2}\)
Question 7.
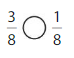
Answer:
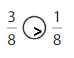
Explanation:
Compare the fractions. The denominators of both the fractions are the same so you have to compare the numerators.
3 is greater than 1.
So, \(\frac{3}{8}\) > \(\frac{1}{8}\)
Question 8.
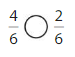
Answer:
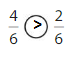
Explanation:
Compare the fractions. The denominators of both the fractions are the same so you have to compare the numerators.
4 is greater than 2.
So, \(\frac{4}{6}\) > \(\frac{2}{6}\)
Question 9.
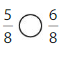
Answer:
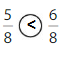
Explanation:
Compare the fractions. The denominators of both the fractions are the same so you have to compare the numerators.
5 is less than 6.
So, \(\frac{5}{8}\) < \(\frac{6}{8}\)
Question 10
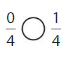
Answer:
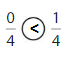
Explanation:
Compare the fractions. The denominators of both the fractions are the same so you have to compare the numerators.
0 is less than 1.
So, \(\frac{0}{4}\) < \(\frac{1}{4}\)
Question 11.
Number Sense
Which statements are true?
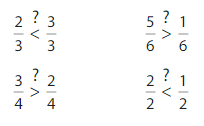
Answer:

Question 12.
Writing
How can you show that \(\frac{3}{8}\) is less than \(\frac{6}{8}\)?
Answer:
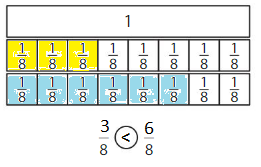
Explanation:
Compare the fractions. The denominators of both the fractions are the same so you have to compare the numerators.
3 is less than 6.
So, \(\frac{3}{8}\) < \(\frac{6}{8}\)
Question 13.
Structure
Which statement correctly compares the fraction of circles shaded in Group A to the fraction of circles shaded in Group B?
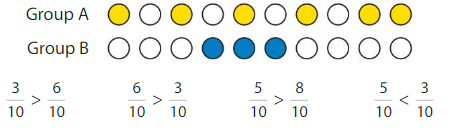
Answer:
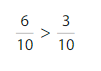
Think and Grow: Modeling Real Life
Newton and Descartes have the same number of chores. Newton finishes \(\frac{2}{3}\) of his chores. Descartes finishes \(\frac{1}{3}\) of his chores. Who finishes more of his chores?
Model:
______ finishes more of his chores.
Explain:
Answer: Newton finishes more of his chores
Explanation:
Given,
Newton and Descartes have the same number of chores.
Newton finishes \(\frac{2}{3}\) of his chores. Descartes finishes \(\frac{1}{3}\) of his chores.
Compare both the fractions \(\frac{2}{3}\) and \(\frac{1}{3}\)
\(\frac{2}{3}\) > \(\frac{1}{3}\)
Therefore Newton finishes more of his chores.
Show and Grow
Question 14.
At the pet store, a green lizard is \(\frac{5}{6}\) foot long. A brown lizard is \(\frac{6}{6}\) foot long. You pick up the longer lizard. Which lizard do you pick up?
Answer:
Given,
At the pet store, a green lizard is \(\frac{5}{6}\) foot long.
A brown lizard is \(\frac{6}{6}\) foot long. You pick up the longer lizard.
Compare both the fractions \(\frac{5}{6}\) and \(\frac{6}{6}\)
\(\frac{5}{6}\) < \(\frac{6}{6}\)
Therefore you pick up brown lizard.
Question 15.
You and a friend each have a burrito. The burritos are the same size. You eat \(\frac{3}{4}\) of your burrito. Your friend eats \(\frac{1}{4}\) of his burrito. Who has less burrito left to eat? Explain.

Answer:
Given,
You and a friend each have a burrito. The burritos are the same size.
You eat \(\frac{3}{4}\) of your burrito. Your friend eats \(\frac{1}{4}\) of his burrito.
\(\frac{3}{4}\) > \(\frac{1}{4}\)
You have less burrito left to eat.
Question 16.
DIG DEEPER!
You walk \(\frac{5}{8}\) of the distance to the library from your home. Your friend walks \(\frac{5}{8}\) of the distance to school from his home. You walk a greater distance than your friend. Explain how this is possible.
Answer:
Given,
You walk \(\frac{5}{8}\) of the distance to the library from your home. Your friend walks \(\frac{5}{8}\) of the distance to school from his home.
\(\frac{5}{8}\) = \(\frac{5}{8}\)
Compare Fractions with the Same Denominator Homework & Practice 11.4
Shade to compare the fractions
Question 1.
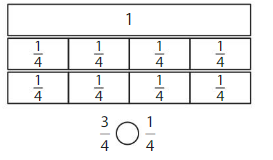
Answer:
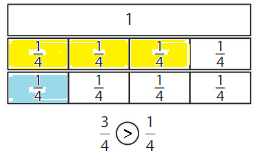
if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
3 is greater than 1
So, \(\frac{3}{4}\) > \(\frac{1}{4}\)
Question 2.
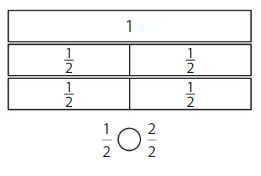
Answer:
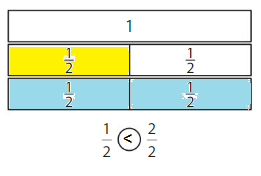
if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
\(\frac{1}{2}\) < \(\frac{2}{2}\)
Compare
Question 3.
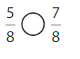
Answer:
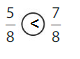
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
5 is less than 7.
So, \(\frac{5}{8}\) < \(\frac{7}{8}\)
Question 4.
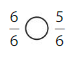
Answer:
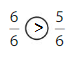
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
6 is greater than 5.
So, \(\frac{6}{6}\) > \(\frac{5}{6}\)
Question 5.
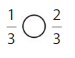
Answer:
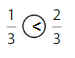
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
1 is less than 2.
So, \(\frac{1}{3}\) < \(\frac{2}{3}\)
Question 6.
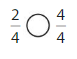
Answer:
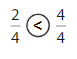
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
2 is less than 4.
So, \(\frac{2}{4}\) < \(\frac{4}{4}\)
Question 7.
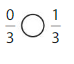
Answer:
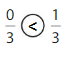
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
0 is less than 1.
So, \(\frac{0}{3}\) < \(\frac{1}{3}\)
Question 8.
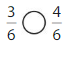
Answer:
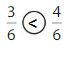
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
3 is less than 4.
So, \(\frac{3}{6}\) < \(\frac{4}{6}\)
Question 9.
YOU BE THE TEACHER
Your friend says \(\frac{3}{4}>\frac{2}{4}\). Is your friend correct? Explain.
Answer: Your friend is correct.
\(\frac{3}{4}\) = 0.75
\(\frac{1}{2}\) = 0.50
\(\frac{3}{4}>\frac{2}{4}\)
Question 10.
Logic
Two fractions are equivalent and have the same denominator. What must be true about the numerators of the fractions?
Answer:
Two fractions are equivalent fractions when they represent the same part of a whole. Since equivalent fractions do not always have the same numerator and denominator, one way to determine if two fractions are equivalent is to find a common denominator and rewrite each fraction with that denominator.
Open-Ended
Write a number to make the statement true.
Question 11.

Answer: 5
Explanation:
Here the denominators of both the fractions are the same. You have to write the numerator of less than 6.
So, to make the statement true we are writing 5.
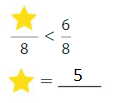
Question 12.
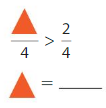
Answer: 4
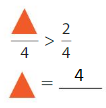
Explanation:
Here the denominators of both the fractions are the same. You have to write the numerator of greater than 2.
So, to make the statement true we are writing 4.
Question 13.
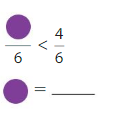
Answer: 1
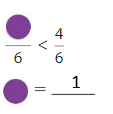
Explanation:
Here the denominators of both the fractions are the same. You have to write the numerator of less than 4.
So, to make the statement true we are writing 1.
Question 14.
Modeling Real Life
You and your friend had the same number of baby teeth. You have lost \(\frac{3}{4}\) of your baby teeth. Your friend has lost \(\frac{2}{4}\) of her baby teeth. Who has lost more teeth?
Answer: you have lost more teeth
Explanation:
Given,
You and your friend had the same number of baby teeth. You have lost \(\frac{3}{4}\) of your baby teeth. Your friend has lost \(\frac{2}{4}\) of her baby teeth.
\(\frac{3}{4}\) = 0.75
\(\frac{1}{2}\) = 0.50
\(\frac{3}{4}>\frac{2}{4}\)
Thus you lost more teeth.
Question 15.
Modeling Real Life
Two classes each paint a mural. The murals are the same size. The third-grade class paints \(\frac{5}{8}\) of one mural. The fourth-grade class paints \(\frac{7}{8}\) of the other mural. Which class has less left to paint? Explain.
Answer: The fourth-grade class has one part left to paint
Review & Refresh
Find the product.
Question 16.
9 × 80 = _____
Answer: 720
Explanation:
Multiply 9 with 80 we get 720
9 × 80 = 720
Question 17.
5 × 30 = _____
Answer: 150
Explanation:
Multiply 5 with 30 we get 150
5 × 30 = 150
Question 18.
6 × 40 = _____
Answer: 240
Explanation:
Multiply 6 with 40 we get 240
6 × 40 = 240
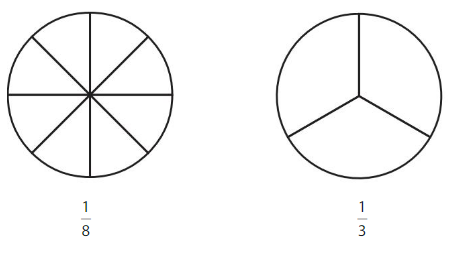
Lesson 11.5 Compare Fractions with Same Numerator
Explore and Grow
Color to show each fraction. Circle the greater fraction.
Answer:
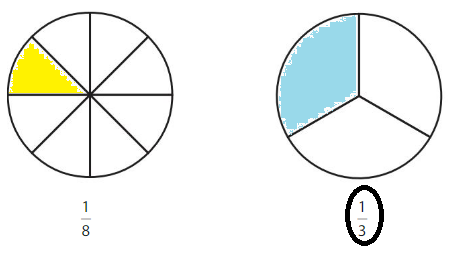
Precision
How can you use Fraction Strips to check your answer? Draw to show.
Answer:
Think and Grow: Compare Fractions That Have the Same Numerator
Example
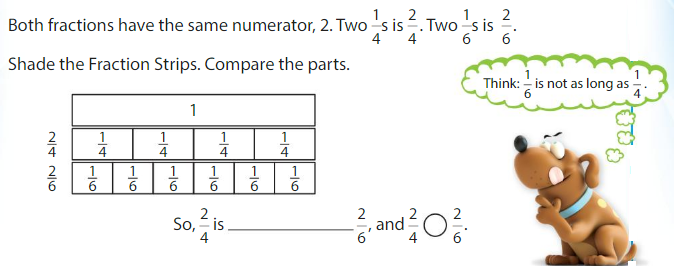
Compare \(\frac{2}{4}\) and \(\frac{2}{6}\).
One Way: Use Fraction Strips
Answer:
Another Way:
When the numerators are the same, look at the denominators 4 and 6 to compare the sizes of the parts.
• The more parts the whole is divided into, the smaller the parts are.
• The fewer parts the whole is divided into, the larger the parts are.
The fraction with the greater denominator is the lesser fraction.

Answer:
![]()
Show and Grow
Shade to compare the fractions.
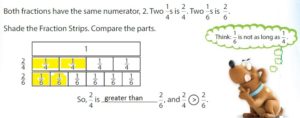
Question 1.
Answer:
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 2.
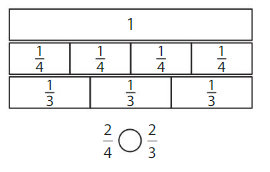
Answer:
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Apply and Grow: Practice
Shade to compare the fractions
Question 3.
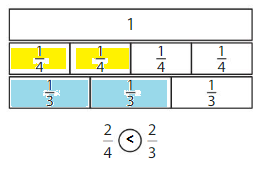
Answer:
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 4.
Answer:
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Compare
Question 5.
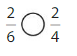
Answer:
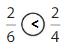
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 6.
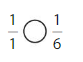
Answer:
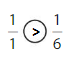
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 7.
Answer:
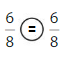
Explanation: Here the numerator and denominator of the fractions are the same so \(\frac{6}{8}\) = \(\frac{6}{8}\)
Question 8.
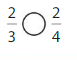
Answer:
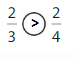
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 9.
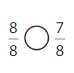
Answer:
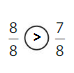
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
Question 10.
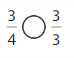
Answer:
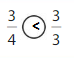
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 11.
Use the models to compare two fractions that have the same numerators.
Answer:
Here the numerators are the same and the denominators are different. The denominator with the highest number will be the lesser fraction.
8 > 4.
Thus 2/8 > 2/4
Question 12.
You spend \(\frac{2}{3}\) of an hour playing soccer on Wednesday. You spend \(\frac{2}{6}\) of an hour playing soccer on Friday. On which day do you spend more time playing soccer? Explain.
Answer:
Given,
You spend \(\frac{2}{3}\) of an hour playing soccer on Wednesday.
You spend \(\frac{2}{6}\) of an hour playing soccer on Friday.
\(\frac{2}{3}\) > \(\frac{2}{6}\)
Thus you spend more time playing soccer on wednesday.
Question 13.
YOU BE THE TEACHER
Your friend says \(\frac{1}{4}>\frac{1}{2}\) because \(\frac{1}{4}\) of one circle is bigger than \(\frac{1}{2}\) of the other circle. Is your friend correct? Explain.
Answer: Your friend is incorrect.
The size of the circles is different.
\(\frac{1}{4}>\frac{1}{2}\)
Think and Grow: Modeling Real Life
Newton and Descartes have piggy banks that are the same size. Newton fills \(\frac{3}{4}\) of his bank with pennies. Descartes fills \(\frac{3}{6}\) of his bank with pennies. Whose bank is filled more?
Model:

Explain:
______ bank is filled more.
Answer: Newton bank is filled more
Explanation:
Given,
Newton and Descartes have piggy banks that are the same size.
Newton fills \(\frac{3}{4}\) of his bank with pennies. Descartes fills \(\frac{3}{6}\) of his bank with pennies.
\(\frac{3}{4}\) > \(\frac{3}{6}\)
Thus Newton bank is filled more
Show and Grow
Question 14.
You use \(\frac{1}{3}\) of a bottle of glitter for an art project. Your friend uses \(\frac{1}{4}\) of a bottle for his art project. The bottles are the same size. Who uses more glitter?
Answer:
Given,
You use \(\frac{1}{3}\) of a bottle of glitter for an art project.
Your friend uses \(\frac{1}{4}\) of a bottle for his art project. The bottles are the same size.
\(\frac{1}{3}\) > \(\frac{1}{4}\)
Thus you used more glitter.
Question 15.
A train and a plane are traveling the same distance from New York to Pittsburgh. The train completes \(\frac{5}{8}\) of its journey. The plane completes \(\frac{5}{6}\) of its journey. Which is farther away from Pittsburgh? Explain.
Answer:
A train and a plane are traveling the same distance from New York to Pittsburgh.
The train completes \(\frac{5}{8}\) of its journey. The plane completes \(\frac{5}{6}\) of its journey.
\(\frac{5}{8}\) < \(\frac{5}{6}\)
Question 16.
DIG DEEPER!
You cut a piece of lasagna that is \(\frac{1}{8}\) of a tray. Your friend cuts a piece of lasagna that is \(\frac{1}{6}\) of a tray. Your piece is larger than your friend’s piece. Explain how this is possible.
Answer:
You cut a piece of lasagna that is \(\frac{1}{8}\) of a tray.
Your friend cuts a piece of lasagna that is \(\frac{1}{6}\) of a tray.
Your piece is larger than your friend’s piece.
\(\frac{1}{8}\) < \(\frac{1}{6}\)
Your piece is smaller than your friend’s piece.
Compare Fractions with Same Numerator Homework & Practice 11.5
Shade to compare the fractions
Question 1.
Answer:
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 2.
Answer:
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Compare
Question 3.
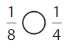
Answer:
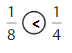
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 4.
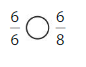
Answer:
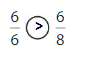
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 5.
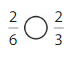
Answer:
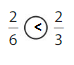
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 6.
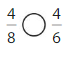
Answer:
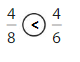
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 7.
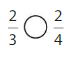
Answer:
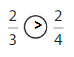
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 8.
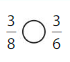
Answer:
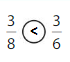
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Question 9.
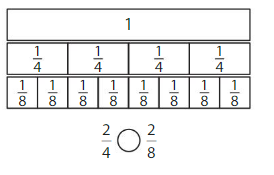
Use the models to compare two fractions that have the same numerators.
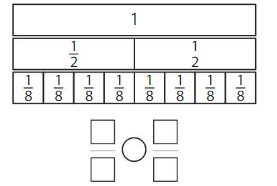
Answer:
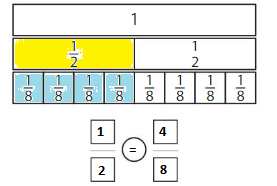
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{1}{2}\) Equal to \(\frac{4}{8}\).
Question 10.
Newton says that if two fractions have the same numerator, then the fraction with the greater denominator is the greater fraction. Is Newton correct? Explain.
Answer: wrong
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction.
Example: \(\frac{4}{4}\) Greater than \(\frac{4}{5}\).
Question 11.
Writing
How is comparing fractions with the same numerator similar to comparing fractions with the same denominator? How is it different?
Answer:
if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction.
Example: \(\frac{4}{4}\) Greater than \(\frac{4}{5}\).
if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
Example: \(\frac{5}{8}\) Greater than \(\frac{4}{8}\).
Question 12.
Modeling Real Life
You play a video game for \(\frac{1}{2}\) of an hour. Your friend plays the video game for \(\frac{1}{6}\) of an hour. Who plays the video 6 game longer? Explain.

Answer:
Given,
You play a video game for \(\frac{1}{2}\) of an hour.
Your friend plays the video game for \(\frac{1}{6}\) of an hour.
\(\frac{1}{2}\) > \(\frac{1}{6}\)
Thus you play a video game for a long time.
Question 13.
Modeling Real Life
Two cars have the same-sized gasoline tank. Tank A is \(\frac{4}{6}\) full. Tank B is \(\frac{4}{8}\) full. Which tank is less full? Explain.
Answer:
Given,
Two cars have the same-sized gasoline tank.
Tank A is \(\frac{4}{6}\) full.
Tank B is \(\frac{4}{8}\) full.
\(\frac{4}{6}\) > \(\frac{4}{8}\)
Tank B is less filled.
Review & Refresh
Plot the fraction on the number line.
Question 14.
\(\frac{1}{4}\)

Answer:
Plot the given fraction on the below number line..

Question 15.
\(\frac{2}{3}\)
![]()
Answer:
Plot the given fraction on the below number line..
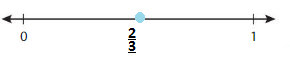
Lesson 11.6 Compare Fractions on a Number Line
Explore and Grow
Use Fraction Strips to plot each fraction on the number line. Circle the greater fraction.
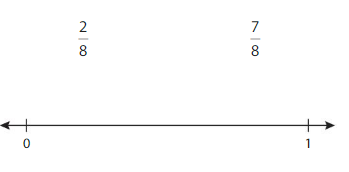
Answer:
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
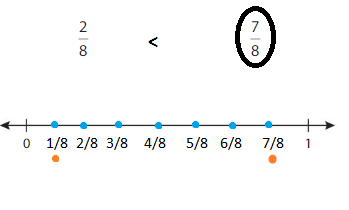
Construct Arguments
Tell your partner how to use a number line to compare the fractions.
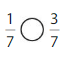
Answer:
Step-1 Draw a number line from 0 to 1
Step-2 plot the fractions from \(\frac{0}{7}\) to \(\frac{7}{7}\)
Step-3 Now put a mark on \(\frac{1}{7}\) \(\frac{3}{7}\)
Step-4 Now compare the distance of both the fractions on the number line
Step-5 Here the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
Step-6 \(\frac{1}{7}\) less than \(\frac{3}{7}\)
Think and Grow: Compare Fractions on a Number Line
On a number line, fractions to the left are less than fractions to the right. Fractions to the right are greater than fractions to the left.
Example
Use a number line to compare \(\frac{3}{4}\) and \(\frac{1}{4}\).
Plot the fractions on a number line. Both have the same denominator.
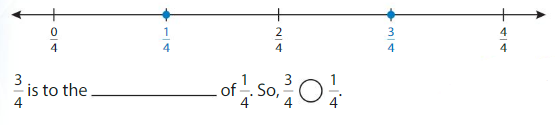

Answer:

Example
Use number lines to compare \(\frac{2}{8}\) and \(\frac{2}{3}\).
Plot each fraction on a number line. Both fractions have the same numerator.
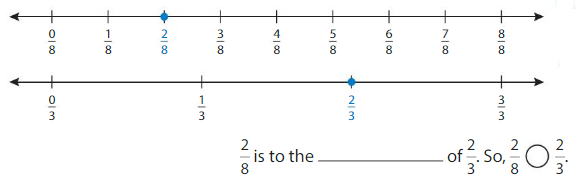
Answer:
Show and Grow
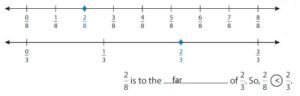
Use the number line to compare the fractions.
Question 1.
Answer:
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{5}{8}\) Greater than \(\frac{4}{6}\).
Question 2.
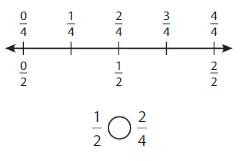
Answer:
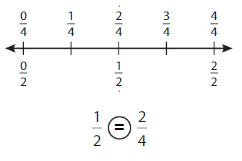
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{1}{2}\) equal to \(\frac{2}{4}\).
Apply and Grow: Practice
Compare.
Question 3.
Answer:
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{3}{4}\) equal to \(\frac{6}{8}\).
Question 4.
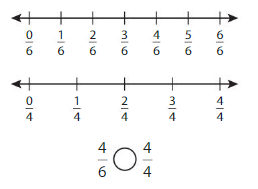
Answer:
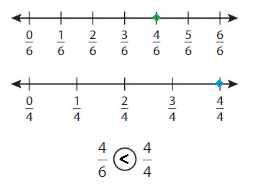
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{4}{6}\) lesser than \(\frac{4}{4}\).
Question 5.
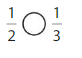
Answer:
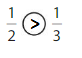
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{1}{2}\) Greater than \(\frac{4}{4}\).
Question 6.
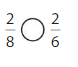
Answer:
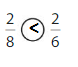
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{2}{8}\) lesser than \(\frac{2}{6}\).
Question 7.
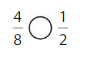
Answer:
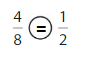
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{4}{8}\) equal to \(\frac{1}{2}\).
Question 8.
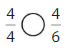
Answer:
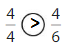
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{4}{4}\) Greater than \(\frac{4}{6}\).
Question 9.
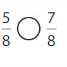
Answer:
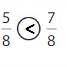
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{5}{8}\) lesser than \(\frac{7}{8}\).
Question 10.
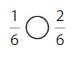
Answer:
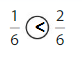
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{6}\) Lesser than \(\frac{2}{6}\).
Question 11.
Write a fraction that is greater than \(\frac{5}{6}\).
Answer: \(\frac{6}{6}\).
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{6}{6}\) Greater than \(\frac{5}{6}\).
Question 12.
Write a fraction that is less than \(\frac{3}{4}\).
Answer: \(\frac{1}{4}\).
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{4}\) lesser than \(\frac{3}{4}\).
Question 13.
Newton buys \(\frac{1}{4}\) pound of cheese. Descartes buys \(\frac{3}{4}\) pound of cheese. Who buys more cheese?

Answer: Descartes buys More \(\frac{3}{4}\) pound of cheese.
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{4}\) lesser than \(\frac{3}{4}\).
Question 14.
Number Sense
Which fractions are greater than \(\frac{2}{4}\)?

Answer: \(\frac{4}{4}\) is greater than \(\frac{2}{4}\)
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{4}{4}\) is greater than \(\frac{2}{4}\)
Think and Grow: Modeling Real Life
Does the recipe call for more salt or more pepper?
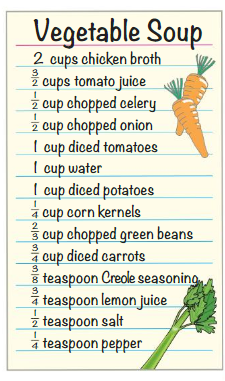
Models:

The recipe calls for more _______.
Explain:
Answer:
By seeing the above table we can find the recipe call for more salt or more pepper.
The recipe calls for more salt.
\(\frac{1}{4}\) > \(\frac{1}{2}\)
Show and Grow
Question 15.
Does the recipe above call for more Creole seasoning or more lemon juice?
Answer:
By seeing the above table we can find the recipe call for more Creole seasoning or more lemon juice.
The recipe calls for more lemon juice.
\(\frac{3}{4}\) > \(\frac{3}{8}\)
Question 16.
You and your friend each catch a fish. Your fish is \(\frac{5}{3}\) feet long, and your friend’s fish is \(\frac{2}{3}\) foot long. Whose fish is shorter? Explain.
Answer:
Given,
You and your friend each catch a fish.
Your fish is \(\frac{5}{3}\) feet long, and your friend’s fish is \(\frac{2}{3}\) foot long.
\(\frac{5}{3}\) > \(\frac{2}{3}\)
5 is greater than 2.
Thus your friend’s fish is shorter.
Question 17.
DIG DEEPER!
You eat \(\frac{4}{8}\) of a quesadilla. Your friend eats \(\frac{2}{8}\) of a different quesadilla. Can you tell who ate more quesadilla? Explain

Answer:
Given,
You eat \(\frac{4}{8}\) of a quesadilla. Your friend eats \(\frac{2}{8}\) of a different quesadilla.
\(\frac{4}{8}\) > \(\frac{2}{8}\)
Thus you ate more quesadilla.
Compare Fractions on a Number Line Homework & Practice 11.6
Use the number line to compare the fractions
Question 1.
Answer:
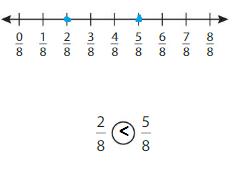
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{2}{8}\) Lesser than \(\frac{5}{8}\).
Question 2.
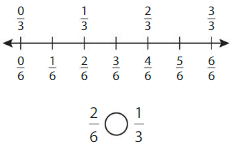
Answer:
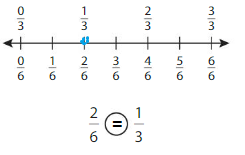
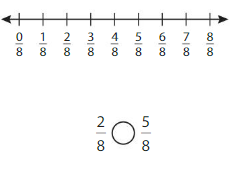
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{2}{6}\) Equal to \(\frac{1}{3}\).
Compare
Question 3.
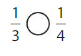
Answer:
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{1}{3}\) Greater than \(\frac{1}{4}\).
Question 4.
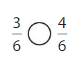
Answer:
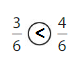
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{3}{6}\) lesser than \(\frac{4}{6}\).
Question 5.
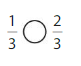
Answer:
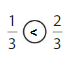
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{3}\) lesser than \(\frac{2}{3}\).
Question 6.
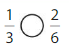
Answer:
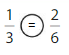
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{1}{3}\) Equal to \(\frac{2}{6}\).
Question 7.
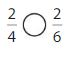
Answer:
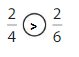
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{2}{4}\) Greater than \(\frac{2}{6}\).
Question 8.
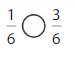
Answer:
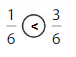
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{6}\) lesser than \(\frac{3}{6}\).
Question 9.
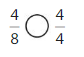
Answer:
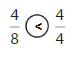
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{4}{8}\) lesser than \(\frac{4}{4}\).
Question 10.
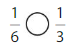
Answer:
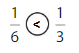
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{1}{6}\) lesser than \(\frac{1}{3}\).
Question 11.
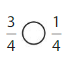
Answer:
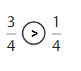
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{3}{4}\) Greater than \(\frac{1}{4}\).
Question 12.
Write a fraction that is greater than \(\frac{1}{3}\).
Answer: \(\frac{2}{3}\)
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{2}{3}\) Greater than \(\frac{1}{3}\).
Question 13.
Write a fraction that is less than \(\frac{1}{2}\).
Answer: \(\frac{1}{6}\)
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{1}{6}\) lesser than \(\frac{1}{2}\).
Question 14.
Writing
Explain how to compare \(\frac{2}{3}\) and \(\frac{4}{3}\) on a number line.
Answer:
By seeing the number line we can say that \(\frac{2}{3}\) < \(\frac{4}{3}\)
Question 15.
Number Sense
Which fractions are less than \(\frac{4}{6}\)?

Answer:
\(\frac{2}{6}\) and \(\frac{1}{6}\) are less than \(\frac{4}{6}\).
Modeling Real Life
Use the recipe shown.

Question 16.
Does the recipe call for more butter or more sugar? Explain.
Answer:
Recipe call for butter is \(\frac{1}{3}\)
Recipe call for sugar is \(\frac{2}{3}\)
\(\frac{1}{3}\) < \(\frac{2}{3}\)
Thus the recipe call for more sugar.
Question 17.
Does the recipe call for less flour or less nuts? Explain.
Answer:
Recipe call for flour is \(\frac{3}{2}\)
Recipe call for nuts is \(\frac{3}{4}\)
\(\frac{3}{2}\) > \(\frac{3}{4}\)
Thus the recipe call for less nuts.
Review & Refresh
Find the missing number.
Question 18.
98 + ____ = 98
Answer: 0
Explanation:
Add 98 with 0 we get 98
Question 19.
52 + (____ + 16) = (52 + 28) + 16
Answer: 28
Explanation:
The associative property allows us to change groupings of addition and keep the same value. (a+b)+c = a+(b+c)
hence the missing number is 28
Question 20.
33 + _____ + 46 = 33 + 46
Answer: 0
Explanation:
Fill the blank with 0 we get 33 + 46
Question 21.
14 + 67 = 67 + ______
Answer: 148
Explanation:
Add 14,67 & 67 we get 148
Lesson 11.7 Compare Fractions
Explore and Grow
Use a strategy to find the greater fraction.
\(\frac{2}{3}\)
\(\frac{2}{8}\)
Use a different strategy to check your answer.
Answer:
if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
Construct Arguments
Tell your partner which strategy you prefer. Explain.
Answer:
I will compare the denominators to find which fraction is greater or lesser.
In the given fraction \(\frac{2}{3}\), \(\frac{2}{8}\)
In this case, the numerators are the same and denominators are different.
The denominator with the greatest number will be the smallest one.
\(\frac{2}{3}\) > \(\frac{2}{8}\)
Think and Grow: Compare Fractions
Example
Compare \(\frac{5}{6}\) and \(\frac{2}{3}\).
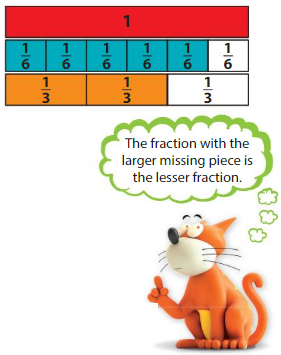
Use Fraction Strips.
In some cases, it is easier to compare the This is an image333parts that are missing. Notice that each fraction is 1 part away from being equivalent to 1. Compare the missing pieces.
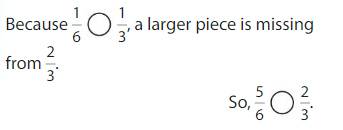
Answer:
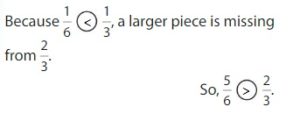
Example
Compare \(\frac{3}{8}\) and \(\frac{5}{8}\).
The denominators are the same. Compare the numerators, 3 and 5.
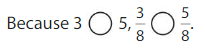
Answer:
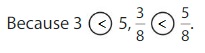
Example
Compare \(\frac{4}{6}\) and \(\frac{4}{8}\).
The numerators are the same. Look at the denominators 6 and 8 to compare the sizes of the parts. The fraction with the greater denominator is the lesser fraction.
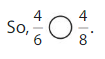
Answer:
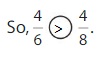
Show and Grow
Compare.
Question 1.
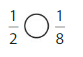
Answer:
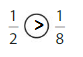
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{1}{2}\) Greater than \(\frac{1}{8}\).
Question 2.
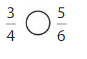
Answer:
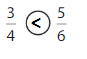
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{3}{4}\) lesser than \(\frac{5}{6}\).
Question 3.
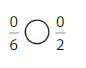
Answer:
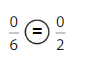
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{0}{6}\) Equal to \(\frac{0}{2}\).
Question 4.
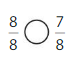
Answer:
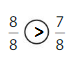
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{8}{8}\) Greater than \(\frac{7}{8}\).
Apply and Grow: Practice
Compare
Question 5.
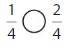
Answer:
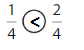
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{4}\) lesser than \(\frac{2}{4}\).
Question 6.
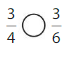
Answer:
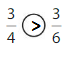
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{3}{4}\) Greater than \(\frac{3}{6}\).
Question 7.
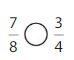
Answer:
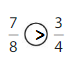
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{7}{8}\) Greater than \(\frac{3}{4}\).
Question 8.
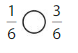
Answer:
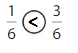
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{6}\) lesser than \(\frac{3}{6}\).
Question 9.
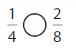
Answer:
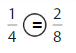
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{1}{4}\) equal to \(\frac{2}{8}\).
Question 10.
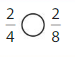
Answer:
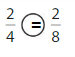
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{2}{4}\) equal to \(\frac{2}{8}\).
Question 11.
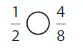
Answer:
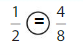
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{1}{2}\) equal to \(\frac{4}{8}\).
Question 12.
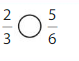
Answer:

Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{2}{3}\) lesser than \(\frac{5}{6}\).
Question 13.
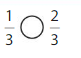
Answer:
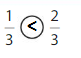
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{3}\) lesser than \(\frac{2}{3}\).
Complete the statement.
Question 14.

Answer:
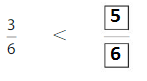
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{3}{6}\) lesser than \(\frac{5}{6}\).
Question 15.
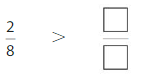
Answer:

Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{2}{8}\) Greater than \(\frac{1}{8}\).
Question 16.
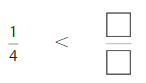
Answer:

Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{4}\) lesser than \(\frac{3}{4}\).
Question 17.
Newton and Descartes have the same-sized lunch. Newton eats \(\frac{2}{3}\) of his lunch. Descartes eats \(\frac{1}{2}\) of his lunch. Who eats more of his lunch?

Answer:
Given,
Newton and Descartes have the same-sized lunch. Newton eats \(\frac{2}{3}\) of his lunch. Descartes eats \(\frac{1}{2}\) of his lunch.
\(\frac{2}{3}\) > \(\frac{1}{2}\)
Thus Newton eats more of his lunch.
Question 18.
DIG DEEPER!
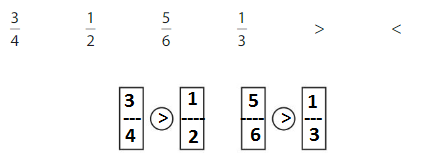
Use the fractions and symbols to make two true statements.
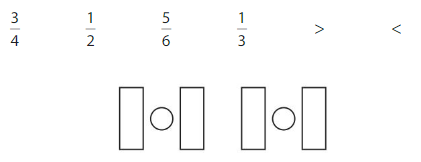
Answer:
Think and Grow: Modeling Real Life
Newton walks \(\frac{3}{8}\) mile to school. Descartes walks \(\frac{5}{6}\) mile to school. Who walks farther to school?

Understand the problem:
Make a plan:
Solve:
_______ walks farther to school.
Answer:
Given,
Newton walks \(\frac{3}{8}\) mile to school.
Descartes walks \(\frac{5}{6}\) mile to school.
\(\frac{5}{6}\) > \(\frac{3}{8}\)
Thus Descartes walks farther to the school.
Show and Grow
Question 19.
Two apartment buildings have the same number of floors. New carpeting is installed on \(\frac{2}{3}\) of the floors in Building A and \(\frac{3}{6}\) of the floors in Building B. Which building has more floors with new carpeting?
Answer:
Given,
Two apartment buildings have the same number of floors.
New carpeting is installed on \(\frac{2}{3}\) of the floors in Building A and \(\frac{3}{6}\) of the floors in Building B.
\(\frac{2}{3}\) > \(\frac{3}{6}\)
Building A has more floors with new carpeting.
Question 20.
Newton buys \(\frac{5}{8}\) pound of peanuts and \(\frac{1}{2}\) pound of cashews.Which weighs less? Explain.

Answer:
Given,
Newton buys \(\frac{5}{8}\) pound of peanuts and \(\frac{1}{2}\) pound of cashews.
Compare both the fractions
\(\frac{5}{8}\) > \(\frac{1}{2}\)
Thus Cashews weights less than peanuts.
Question 21.
DIG DEEPER!
You are painting a backdrop for a school play. You paint \(\frac{1}{3}\) of the backdrop blue. You paint more of the backdrop yellow than blue. What fraction can represent the part of the backdrop that is yellow? Explain.
Answer:
Given,
You are painting a backdrop for a school play.
You paint \(\frac{1}{3}\) of the backdrop blue. You paint more of the backdrop yellow than blue.
\(\frac{3}{3}\) – \(\frac{1}{3}\) = \(\frac{2}{3}\)
Thus the fraction can represent the part of the backdrop that is yellow is \(\frac{2}{3}\)
Compare Fractions Homework & Practice 11.7
Compare
Question 1.
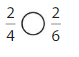
Answer:
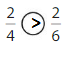
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{2}{4}\) Greater than \(\frac{2}{6}\).
Question 2.
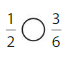
Answer:
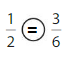
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{1}{2}\) equal \(\frac{3}{6}\).
Question 3.
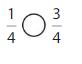
Answer:
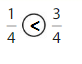
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{4}\) lesser than \(\frac{3}{4}\).
Question 4.
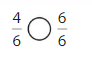
Answer:
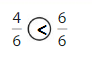
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{4}{6}\) lesser than \(\frac{6}{6}\).
Question 5.
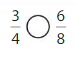
Answer:
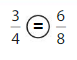
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{3}{4}\) equal \(\frac{6}{8}\).
Question 6.
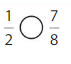
Answer:
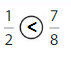
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{1}{2}\) lesser than\(\frac{7}{8}\).
Question 7.
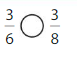
Answer:

Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{3}{6}\) Greater than \(\frac{3}{8}\).
Question 8.
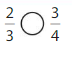
Answer:
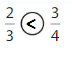
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{2}{3}\) lesser than\(\frac{3}{4}\).
Complete the statement
Question 9.

Answer:

Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{5}{6}\) lesser than \(\frac{6}{6}\).
Question 10.
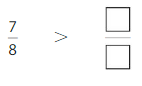
Answer:
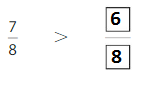
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{7}{8}\) Greater than \(\frac{6}{8}\).
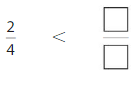
Question 11.
Answer:

Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{2}{4}\) lesser than \(\frac{3}{4}\).
Question 12.
Number Sense
Which statements are true?

Answer:
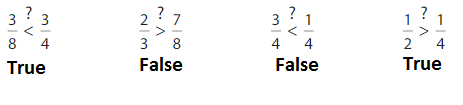
Question 13.
Writing
Explain how to compare \(\frac{2}{3}\) and \(\frac{7}{8}\) using missing pieces.
Answer:
The least common denominator (LCD) is: 24.
Rewriting as equivalent fractions with the LCD:
2/3 = 16/24
7/8 = 21/24
Comparing the numerators of the equivalent fractions we have:
16/24 < 21/24
\(\frac{2}{3}\) < \(\frac{7}{8}\)
Question 14.
Modeling Real Life
Newton and Descartes each have a phone with the same amount of storage. Newton’s storage is \(\frac{3}{4}\) full. Descartes’s storage is \(\frac{2}{8}\) full. Whose phone has more storage left?

Answer:
Given,
Newton and Descartes each have a phone with the same amount of storage.
Newton’s storage is \(\frac{3}{4}\) full. Descartes’s storage is \(\frac{2}{8}\) full
\(\frac{3}{4}\) > \(\frac{2}{8}\)
Descartes phone has more storage left
Question 15.
DIG DEEPER!
A restaurant wants to serve two different-sized hamburgers. The larger hamburger will be \(\frac{1}{2}\) pound. Name a fraction that could represent the other hamburger’s size.

Answer:
Given,
A restaurant wants to serve two different-sized hamburgers. The larger hamburger will be \(\frac{1}{2}\) pound.
The other size could represent \(\frac{2}{4}\)
Review & Refresh
Question 16.
There are 37 students on a bus. The bus stops 5 times. Seven students get off at each stop. How many students are left on the bus?
Answer:
Given,
There are 37 students on a bus. The bus stops 5 times. Seven students get off at each stop.
5 × 7 = 35
37 – 35 = 2
Therefore 2 students left on the bus
Lesson 11.8 Compare and Order Fractions
Explore and Grow
Plot the fractions on the number line. Order the fractions from least to greatest.
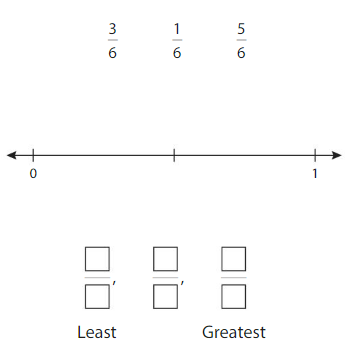
Answer:
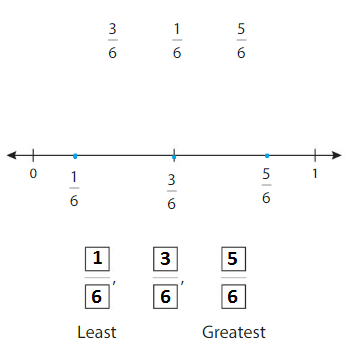
Explanation: Ordering fraction simply means arranging fraction either from the smallest to the largest (ascending order) or largest to smallest (descending order). There are two common methods of ordering fractions.
Reasoning
How can you use the fraction \(\frac{1}{2}\) to compare and order fractions?
Answer: \(\frac{1}{2}\), \(\frac{2}{2}\), \(\frac{3}{2}\), \(\frac{4}{2}\)
Think and Grow: Compare and Order Fractions
Example
Order the fractions \(\frac{7}{8}, \frac{1}{8}\) and \(\frac{5}{8}\) from least to greatest.
Plot the fractions on the number line. All 3 fractions have the same denominator,8.
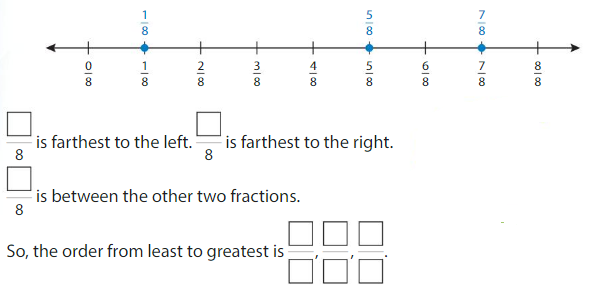

Answer:
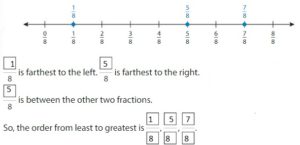
Example
Order the fractions \(\frac{2}{4}, \frac{2}{3}\) and \(\frac{2}{6}\) and from least to greatest.
Use Fraction Strips. All three fractions have the same numerator, 2.
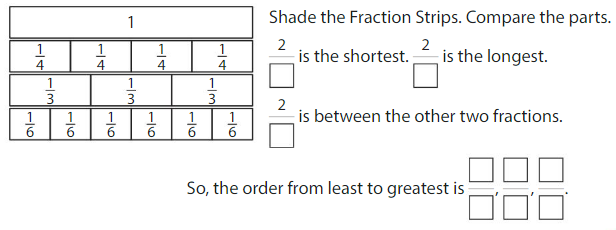
Show and Grow
Question 1.
Order the fractions \(\frac{3}{3}, \frac{3}{4}\) and \(\frac{3}{8}\) from least to greatest.
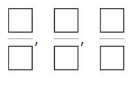
Answer:
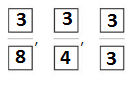
Apply and Grow: Practice
Order the fractions from least to greatest
Question 2.
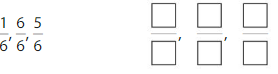
Answer:
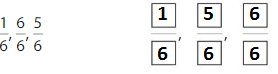
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
by using this statement we can write the order of fractions from least to greatest
Question 3.
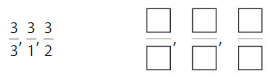
Answer:
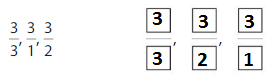
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
by using this statement we can write the order of fractions from least to greatest
Question 4.

Answer:

Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
by using this statement we can write the order of fractions from least to greatest
Question 5.
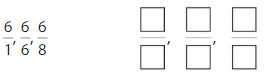
Answer:
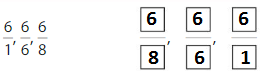
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
by using this statement we can write the order of fractions from least to greatest
Order the fractions from greatest to least.
Question 6.
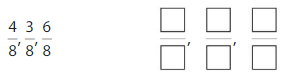
Answer:
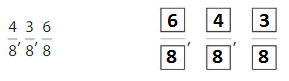
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
by using this statement we can write the order of fractions from Greatest to least
Question 7.
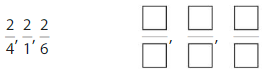
Answer:
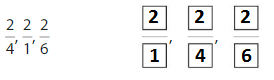
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
by using this statement we can write the order of fractions from Greatest to least
Question 8.
Reasoning
Three fractions have the same denominator. How do you know which fraction is the greatest?
Answer:
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
Example:

Question 9.
Open-Ended
Write a fraction that is between \(\frac{2}{8}\) and \(\frac{2}{3}\).
Answer:
Question 10.
Patterns
The fractions below are in order from least to greatest. Describe and complete the pattern.

Answer:
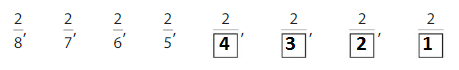
Think and Grow: Modeling Real Life
A construction crew replaces \(\frac{1}{8}\) mile of a road on Monday, \(\frac{1}{4}\)mile of the road on Tuesday, and \(\frac{1}{6}\) mile of the road on Wednesday. On which day does the crew replace the longest piece of the road? On which day does the crew replace the shortest piece? Explain.

Model:
The crew replaces the longest piece of the road on ______ and the shortest piece on ______.
Explain:
The crew replaces the longest piece of the road on Tuesday and the shortest piece on Monday.
Explanation:
A construction crew replaces \(\frac{1}{8}\) mile of a road on Monday, \(\frac{1}{4}\)mile of the road on Tuesday, and \(\frac{1}{6}\) mile of the road on Wednesday
Order of fraction from longest piece to shortest piece is \(\frac{1}{4}\) , \(\frac{1}{6}\) \(\frac{1}{8}\)
Show and Grow
Question 11.
You place three plants in order from shortest to tallest. A cactus is \(\frac{4}{6}\) foot tall, a fern is \(\frac{4}{4}\) foot tall, and an aloe vera plant is \(\frac{4}{8}\) foot tall. Which plant is first? Which plant is last? Explain.
Answer:
Given,
place three plants in order from shortest to tallest. A cactus is \(\frac{4}{6}\) foot tall, a fern is \(\frac{4}{4}\) foot tall, and an aloe vera plant is \(\frac{4}{8}\) foot tall
\(\frac{4}{8}\) , \(\frac{4}{6}\) , \(\frac{4}{4}\)
Question 12.
You measure the lengths of three spiders. The longest one is \(\frac{3}{4}\) inch long. The shortest one is \(\frac{1}{4}\) inch long. What is a possible length for the third spider? Explain.

Answer: \(\frac{2}{4}\)
Explanation:
Given,
You measure the lengths of three spiders. The longest one is \(\frac{3}{4}\) inch long. The shortest one is \(\frac{1}{4}\) inch long.
so possibility length for the third spider is \(\frac{2}{4}\)
Question 13.
DIG DEEPER!
You are ordering three fractions. You know which fraction is the greatest and which fraction is the least. What do you know about the third fraction?
Answer:
Example:
if You measure the lengths of three spiders. The longest one is \(\frac{3}{4}\) inch long. The shortest one is \(\frac{1}{4}\) inch long.
so possibility length for the third spider is \(\frac{2}{4}\)
Compare and Order Fractions Homework & Practice 11.8
Order the fractions from least to greatest
Question 1.

Answer:
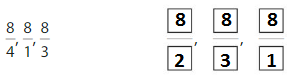
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
by using this statement we can write the order of fractions from Least to Greatest
Question 2.

Answer:

Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
by using this statement we can write the order of fractions from Least to Greatest
Question 3.

Answer:
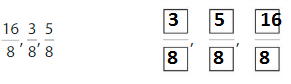
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
by using this statement we can write the order of fractions from Least to Greatest
Question 4.
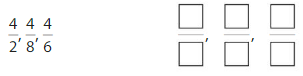
Answer:

Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
by using this statement we can write the order of fractions from Least to Greatest
Order the fractions from greatest to least.
Question 5.
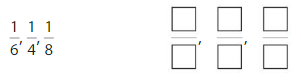
Answer:

Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
by using this statement we can write the order of fractions from Greatest to least
Question 6.
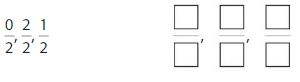
Answer:
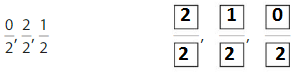
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
by using this statement we can write the order of fractions from Greatest to least
Question 7.

Answer:
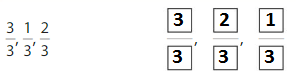
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction
by using this statement we can write the order of fractions from Greatest to least
Question 8.
Answer:
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
by using this statement we can write the order of fractions from Greatest to least
Question 9.
Reasoning
Three fractions have the same numerator. How do you know which fraction is the greatest?
Answer:if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction.
Example:
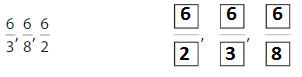
Question 10.
Precision
Which set of fractions is ordered from least to greatest?

Answer:
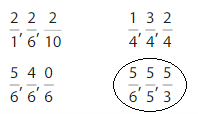
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction
by using this statement we can write the order of fractions from least to greatest
Question 11.
Modeling Real Life
You survey your classmates about their favorite subject. \(\frac{5}{8}\) of the students choose math, \(\frac{1}{8}\) choose reading, \(\frac{2}{8}\) and choose science.Which subject receives the most votes? Which8subject receives the least votes? Explain.
Answer:
Given, You survey your classmates about their favorite subject. \(\frac{5}{8}\) of the students choose math, \(\frac{1}{8}\) choose reading, \(\frac{2}{8}\) and choose science
Math subject receives the most votes
\(\frac{5}{8}\) , \(\frac{2}{8}\) , \(\frac{1}{8}\)
Which subject receives the least vote is
reading of \(\frac{1}{8}\) having least vote
Question 12.
Modeling Real Life
A carpenter has three drill bits. The thickest one is \(\frac{3}{4}\) inch. The thinnest one is \(\frac{3}{8}\) inch. What is a possible width for the third drill bit? Explain.

Answer: \(\frac{3}{6}\)
Explanation:
Given
A carpenter has three drill bits. The thickest one is \(\frac{3}{4}\) inch.
The thinnest one is \(\frac{3}{8}\) inch
The possibility of Width for the third drill bit is \(\frac{3}{6}\)
Review & Refresh
Question 13.
You clean the lunch tables. There are 6 rows of tables with 7 tables in each row. How many tables do you clean?
Answer: 42
Explanation:
Given clean lunch tables There are 6 rows of tables with 7 tables in each row
we apply the row multiply columns concept
so 6 × 7 we get 42
Therefore the number of tables cleaned is 42
Understand Fraction Equivalence and Comparison Performance Task
Question 1.
You invite five friends to dinner. You start making chili using the recipe shown at 4:00.

a.What time should you tell your friends the chili will be ready?
Answer: by seeing the above image you can tell to your friends that the chili will be ready in 60 minutes
b.Which ingredient do you use the same amount of as crushed garlic?
Answer: chili powder is the ingredient that use the same amount as crushed garlic
c. Do you use more chopped green pepper or onion?
Answer: we use more chopped green pepper than onion
d. How many ounces of beans do you use in all?
Answer: 2 8 ounce cans of pinto beans and 2 8- an ounce cans of black beans
so we get 32 ounces of beans in all
e. You know there is \(\frac{1}{4}\) cup of diced tomatoes in each serving. How many cups of diced tomatoes do you need?
Answer:
No.of servings are 16
You know there is \(\frac{1}{4}\) cup of diced tomatoes in each serving
\(\frac{1}{4}\) × 16 we get 4
Thus we need 4 cups of diced tomatoes
f. You and your friends each eat 2 servings of chili. How many servings are left? Write an equation to solve. Use letters to represent unknown numbers.
Answer: 12
No.of servings are 16
You and your friends each eat 2 servings of chili we get 2+2= 4
thus 16-4 we get 12 servings are left

Understand Fraction Equivalence and Comparison Activity
Fraction Spin and Compare
Directions:
1.Players take turns.
2.On your turn, spin both spinners. Cover a box that makes the statement true.
3.If there are no fractions left that make the statement true, then you lose your turn.
4.Play until all boxes are covered.
5.The player with the most boxes covered wins!
Understand Fraction Equivalence and Comparison Chapter Practice
11.1 Equivalent Fractions
Use the models to find an equivalent fraction. Both models show the same whole.
Question 1.
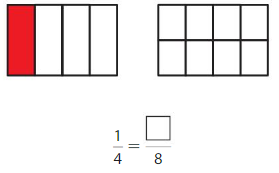
Answer: \(\frac{2}{8}\)
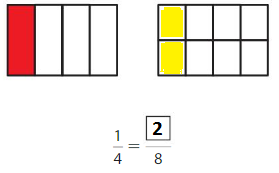
Explanation: \(\frac{1}{4}\) and \(\frac{2}{8}\) are equivalent fractions both gives the same answer.
Question 2.
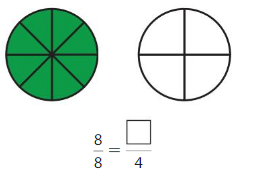
Answer: \(\frac{4}{4}\)
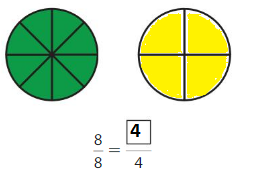
Explanation: \(\frac{8}{8}\) and \(\frac{4}{4}\) are equivalent fractions both gives the same answer.
Question 3.
Which One Doesn’t Belong?
Which one does belong with the other three?

Answer:

Explanation: above all the figures has the fraction \(\frac{4}{6}\) except circled figure
so second doest belong to the other three
11.2 Equivalent Fractions on a Number Line
Write two fractions that name the point shown.
Question 4.
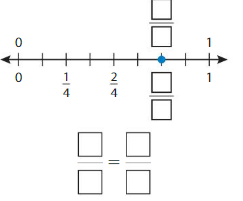
Answer:
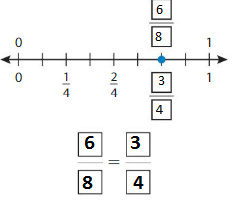
Explanation: \(\frac{6}{8}\) and \(\frac{3}{4}\) are equivalent fractions both gives the same answer.
Question 5.
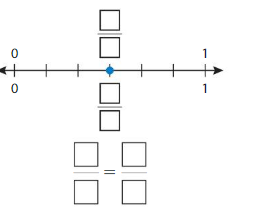
Answer:
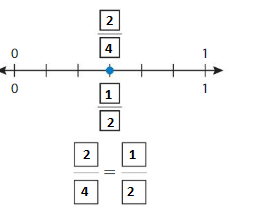
Explanation: \(\frac{2}{4}\) and \(\frac{1}{2}\) are equivalent fractions both gives the same answer.
11.3 Relate Fractions and Whole Numbers
Question 6.
Complete the number line. Then write equivalent fractions for the numbers 1 and 2.
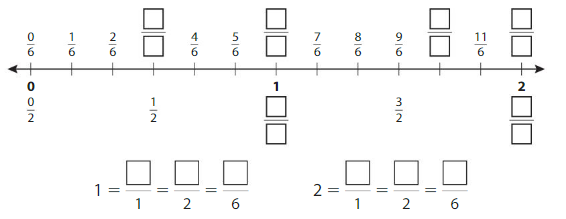
Answer:
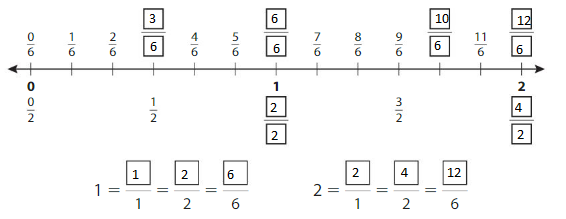
Write two equivalent fractions for the whole number.
Question 7.
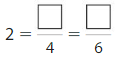
Answer:
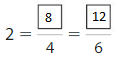
Explanation:
2 is equivalent to the fractions \(\frac{8}{4}\) and \(\frac{12}{6}\).
Question 8.
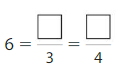
Answer:
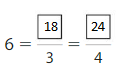
Explanation:
6 is equivalent to the fractions \(\frac{18}{3}\) and \(\frac{24}{4}\).
Question 9.
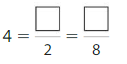
Answer:

Explanation:
4 is equivalent to the fractions \(\frac{8}{2}\) and \(\frac{32}{8}\).
Write the equivalent whole number.
Question 10.
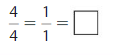
Answer:
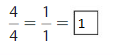
The number equivalent to \(\frac{1}{1}\) and \(\frac{4}{4}\) is 1.
Question 11.
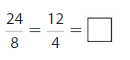
Answer:
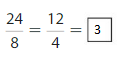
The number equivalent to \(\frac{24}{8}\) and \(\frac{12}{4}\) is 3.
Question 12.
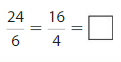
Answer:
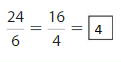
The number equivalent to \(\frac{24}{6}\) and \(\frac{16}{4}\) is 4.
11.4 Compare Fractions with the Same Denominator
Shade to compare the fractions.
Question 13.
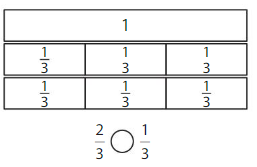
Answer:
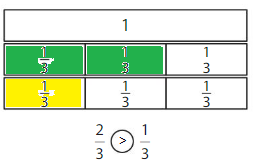
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{2}{3}\) Greater than \(\frac{1}{3}\).
Question 14.
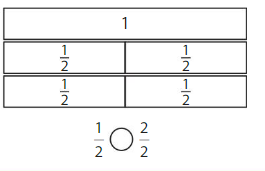
Answer:
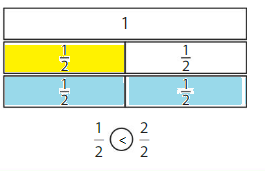
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{2}\) lesser than \(\frac{2}{2}\).
Compare
Question 15.
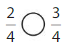
Answer:
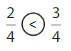
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{2}{4}\) lesser than \(\frac{3}{4}\).
Question 16.
![]()
Answer:
![]()
By seeing the above number we can find the equivalent fraction of
\(\frac{1}{3}\) = \(\frac{1}{3}\)
Question 17.
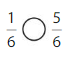
Answer:
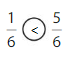
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{6}\) lesser than \(\frac{5}{6}\).
11.5 Compare Fractions with the Same Numerator
Compare.
Question 18.
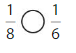
Answer:
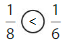
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{1}{8}\) lesser than \(\frac{1}{6}\).
Question 19.
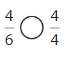
Answer:
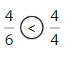
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{4}{6}\) lesser than \(\frac{4}{4}\).
Question 20.
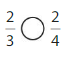
Answer:
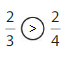
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{2}{3}\) Greater than \(\frac{2}{4}\).
Question 21.
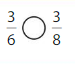
Answer:
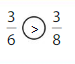
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{3}{6}\) Greater than \(\frac{3}{8}\).
Question 22.
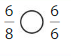
Answer:
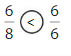
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{6}{8}\) lesser than \(\frac{6}{6}
Question 23.
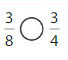
Answer:

Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So [latex]\frac{3}{8}\) lesser than \(\frac{3}{4}
Question 24.
Modeling Real Life
Your glass of orange juice is [latex]\frac{1}{2}\) full. Your friend’s glass of orange juice is \(\frac{1}{3}\) full. Your friend has more orange juice. Explain how this is possible.

Answer:
Given,
Your glass of orange juice is \(\frac{1}{2}\) full.
Your friend’s glass of orange juice is \(\frac{1}{3}\) full. Your friend has more orange juice.
\(\frac{1}{2}\) > \(\frac{1}{3}\)
Thus your friend has more orange juice.
11.6 Compare Fractions on a Number Line
Compare
Question 25.
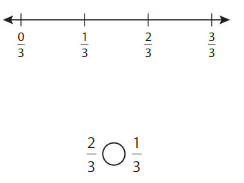
Answer:
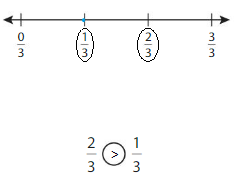
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{2}{3}\) Greater than \(\frac{1}{3}\).
Question 26.
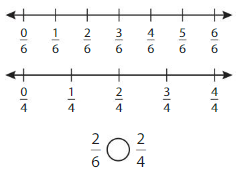
Answer:
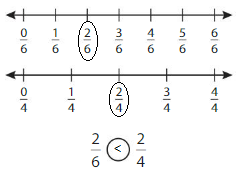
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{2}{6}\) lesser than \(\frac{2}{4}
Question 27.
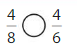
Answer:
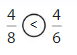
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So [latex]\frac{4}{8}\) lesser than \(\frac{4}{6}
Question 28.
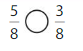
Answer:
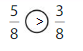
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So [latex]\frac{5}{8}\) Greater than \(\frac{3}{8}\).
Question 29.
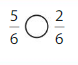
Answer:
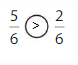
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{5}{6}\) Greater than \(\frac{2}{6}\).
Question 30.
Write a fraction that is greater than \(\frac{1}{8}\).
Answer: \(\frac{3}{8}\).
Explanation:
The fraction greater than \(\frac{1}{8}\) is \(\frac{3}{8}\).
Question 31.
Write a fraction that is less than \(\frac{2}{3}\).
Answer: \(\frac{1}{3}\).
Explanation:
The fraction less than \(\frac{2}{3}\) is \(\frac{1}{3}\).
11.7 Compare Fractions
Compare.
Question 32.
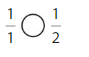
Answer:
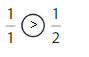
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{1}{1}\) Greater than \(\frac{1}{2}\).
Question 33.
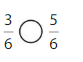
Answer:
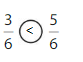
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{3}{6}\) Greater than \(\frac{5}{6}\).
Question 34.
![]()
Answer:
![]()
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{4}{6}\) Greater than \(\frac{4}{8}\).
Question 35.
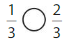
Answer:
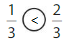
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. So \(\frac{1}{3}\) lesser than \(\frac{2}{3}\).
Question 36.
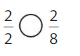
Answer:
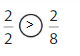
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction. So \(\frac{2}{2}\) Greater than \(\frac{2}{8}\).
Question 37.
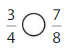
Answer:
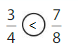
Explanation: if the Numerator and denominators are different then we have to make the denominator as common and then compare the fractions. So \(\frac{3}{4}\) lesser than \(\frac{7}{8}\).
Question 38.
Number Sense
Which statements are true?

Answer:

all the statements are true
11.8 Compare and Order Fractions
Order the fractions from least to greatest.
Question 39.
Answer:

Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction.
Question 40.
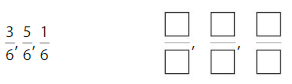
Answer:
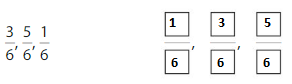
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
Question 41.
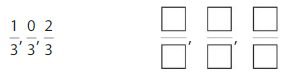
Answer:
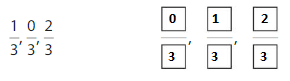
Explanation: if the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction.
Question 42.
Answer:
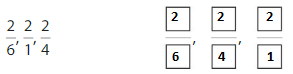
Explanation: if the numerators are the same, denominators are different then we have to compare the Denominator of both the fractions. The fraction with the Greater denominators is the lesser fraction.
Question 43.
Modeling Real Life
You, your friend, and your cousin have the same-sized aquarium. You fill your aquarium \(\frac{2}{3}\) full, your friend fills hers \(\frac{2}{6}\) full, and your cousin fills his \(\frac{2}{4}\) full. Which aquarium is the least full? Which aquarium is the most full? Explain.

Answer:
Given,
You, your friend, and your cousin have the same-sized aquarium.
You fill your aquarium \(\frac{2}{3}\) full, your friend fills hers \(\frac{2}{6}\) full, and your cousin fills his \(\frac{2}{4}\) full.
\(\frac{2}{6}\), \(\frac{2}{4}\), \(\frac{2}{3}\)
Conclusion:
I Hope the details mentioned in this Big Ideas Math Grade 3 Understand Fraction Equivalence and Comparison Solution Key is beneficial for you. Follow this Big Ideas Math Grade 3 Chapter 11 Answer Key and score the highest marks in the exams. Feel free to clarify your doubts by posting the comments in the below comment section. And also stay tuned to get the latest pdfs of all the Big Ideas Math Grade 3 Chapters