Are you looking for a solution key for BIM 4th Grade Chapter 6? If yes, then get the detailed explanation for all the questions on Big Ideas Math Book 4th Grade Answer Key Chapter 6 Factors, Multiples, and Patterns. There are a lot of benefits by referring to the Big Ideas Math Answer Key Grade 4 Chapter 6 Factors, Multiples, and Patterns. The solutions are prepared as per the latest edition. So, check the topics and Download Big Ideas Math Answers Grade 4 Chapter 6 Factors, Multiples, and Patterns pdf for free of cost.
Big Ideas Math Book 4th Grade Answer Key Chapter 6 Factors, Multiples, and Patterns
It is very difficult for the parents to make their children complete homework in time. Refer to our Big Ideas Math Answers Grade 4 Chapter 6 Factors, Multiples, and Patterns and explain the methods to your children clearly. Improve your math skills by practicing the problems from Big Ideas Math Book 4th Grade Answer Key Chapter 6 Factors, Multiples, and Patterns. Make use of the links and kickstart your preparation.
Lesson: 1 Understand Factors
Lesson: 2 Factors and Divisibility
Lesson: 3 Relate Factors and Multiples
Lesson: 4 Identify Prime and Composite Numbers
- Lesson 6.4 Identify Prime and Composite Numbers
- Identify Prime and Composite Numbers Homework & Practice 6.4
Lesson: 5 Number Patterns
Lesson: 6 Shape Patterns
Performance Task
- Factors, Multiples, and Patterns Performance Task
- Factors, Multiples, and Patterns Activity
- Factors, Multiples, and Patterns Chapter Practice
Lesson 6.1 Understand Factors
Explore and Grow
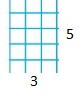
Draw two different rectangles that each have an area of 24 square units. Label their side lengths.

Compare your rectangles to your partner’s rectangles. How are they the same? How are they different?
Answer:
Explanation:
My rectangle is 6 × 4 and my partner’s rectangle is 3 × 8
We know that,
Area of rectangle = l × b
Hence,
According to the above formula, the areas of rectangles are the same irrespective of different lengths and different breadths.
Structure
How is each side length related to 24?
Answer: 

We know that,
The factors of 24 = 4 × 6, 3 × 8, 1 × 24, 2 × 12
Remember that,
a × b = b × a
So,
4 × 6 = 6 × 4
This pattern will be applicable to all factor pairs
Hence, from the above,
We can conclude that each side length is related to 24 because of the factor pair.
Think and Grow: Find Factor Pairs
You can write whole numbers as products of two factors. The two factors are called a factor pair for the number
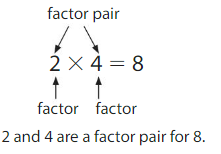
Example
Find the factor pairs for 20.
Find the side lengths of as many different rectangles with an area of 20 square units as possible.
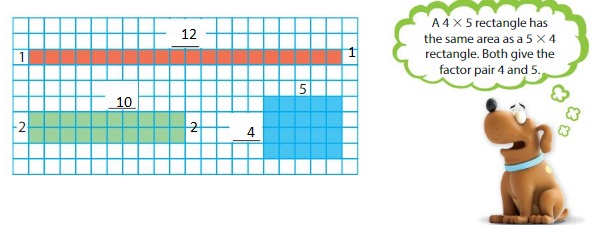
The side lengths of each rectangle are a factor pair.
So, the factor pairs for 20 are 12 and 1, 10 and 2, and 5 and 4.
Show and Grow
Question 1.
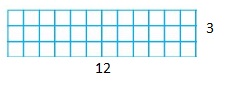
Use the rectangles to find the factor pairs for 12.
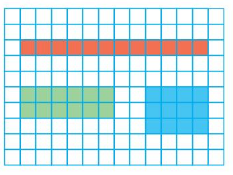
Answer: Factor pairs of 12 are: 12 and 1, 6 and 2, and 4 and 3
Explanation:
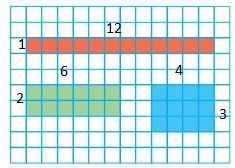
The factor pairs are nothing but the side lengths of a rectangle and the area of a rectangle gives the factor
Hence,
The factor pairs of 12 are: 12 and 1, 6 and 2, and 4 and 3
Question 2.
Draw rectangles to find the factor pairs for 16.
Answer: The factor pairs of 16 are: 1 and 16, 2 and 8, 4 and 4
Explanation:
![]()
The factor pairs are nothing but the side lengths of a rectangle and the area of a rectangle gives the factor
Hence,
The factor pairs of 16 are: 1 and 16, 2 and 8, 4 and 4
Apply and Grow: Practice
Draw rectangles to find the factor pairs for the number.
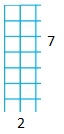
Question 3.
14
Answer: The factor pairs of 14 are: 1 and 14, 2 and 7
Explanation:
![]()
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 14 are: 1 and 14, 2 and 7
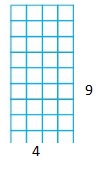
Question 4.
15
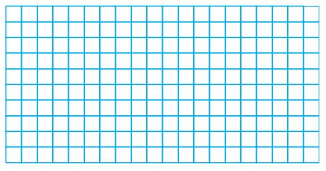
Answer: The factor pairs of 15 are: 1 and 15, 3 and 5
Explanation:
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 15 are: 1 and 15, 3 and 5
Question 5.
20
Answer: The factor pairs of 20 are: 1 and 20, 2 and 10, 4 and 5
Explanation:
![]()
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 15 are: 1 and 15, 3 and 5
Question 6.
36
Answer: The factor pairs of 36 are: 1 and 36, 2 and 18, 3 and 12, 4 and 9, 6 and 6
Explanation:
Factors are the numbers that divide the number completely.
Hence,
The factor pairs of 36 are: 1 and 36, 2 and 18, 3 and 12, 4 and 9, 6 and 6
Find the factor pairs for the number.
Question 7.
11
Answer: The factor pairs of 11 are: 1 and 11
Explanation:
![]()
Factors are the numbers that divide the original number completely.Hence,
The factor pairs of 15 are: 1 and 15, 3 and 5
Question 8.
9
Answer: The factor pairs of 9 are: 1 and 9, and 3 and 3
Explanation:
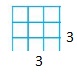
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 15 are: 1 and 15, 3 and 5
Question 9.
4
Answer: The factor pairs of 4 are: 1 and 4, 2 and 2
Explanation:
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 4 are:
1 × 4, 2 × 2 ( Since 4 ×1 and 1 × 4 are equal, we will take any 1 factor )
Question 10.
25
Answer: The factor pairs of 25 are: 1 and 25, 5 and 5
Explanation:
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 25 are:
1 × 25, 5 × 5
Question 11.
10
Answer: The factor pairs of 10 are: 1 and 10, 2 and 5
Explanation:
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 10 are:
1 × 10, 5 × 5
Question 12.
40
Answer: The factor pairs of 40 are: 1 and 40, 2 and 20, 4 and 10, 5 and 8
Explanation:
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 40 are:
1 × 40, 2 × 20, 4 × 10 and 5 × 8
Question 13.
Writing
Use the word to explain one way that 2 and 6 are related.
Answer: The factor pair of 6 are: 1 and 6, 2 and 3
Explanation:
The one way 2 and are related is the “Factor-pair method”
According to the factor-pair method,
The factors of 6 are:
1 × 6 and 2 × 3
Hence, from the above,
We can conclude that 2 and 6 are related due to the factor-pair method.
Think and Grow: Modeling Real Life
Example
You want to organize 30 pictures into a rectangular array on a wall. How many different arrays can you make?

To find the number of arrays you can make, find the number of factor pairs for 30.
There are 3-factor pairs for 30.
You can use each factor pair to make 30 arrays.
So, there are 30 ×3 = 90 ways to organize the pictures in different arrays.
Show and Grow
Question 14.
A city mayor buys 27 solar panels. She wants to organize the panels into a rectangular array. How many different arrays can she make?
Answer: The different arrays she can make are: 1 × 27, 3 × 9, 9 × 3, and 27 × 1
Explanation:
Given that a city mayor buys 27 solar panels and she wants to organize the panels into a rectangular array.
The “Array” is nothing but the number of patterns ( Factor pairs) that we can arrange the given things.
Hence,
The factors of 27 are: 1 and 27, 3 and 9, 9 and 3, and 27 and 1
Hence,
The different arrays she can make in arranging the solar panels are:
1 × 27, 3 × 9, 9 × 3, and 27 × 1
Question 15.
DIG DEEPER!
A store owner has 42 masks to hang in a rectangular array on a wall. The owner does not have room for more than 10 masks in each row or column. What are the possible numbers of masks the owner should hang in each row?

Answer: The number of possible masks the owner should hang in each row is: 7 masks
Explanation:
Given that a store owner has 42 masks to hang in a rectangular array on a wall.
So now,
The number of arrays ( Factor pairs ) of 42 are:
1 × 42, 2 × 21, 3 × 14, 6 × 7, 7 × 6, 14 × 3, 21 × 2, and 41 × 1
It is also given that the owner does not have enough room for more than 10 masks in each row or column.
So, from the above factor pairs, we can say that the possible array of masks is: 6 × 7 and 7 × 6
Hence, from the above,
we can conclude that the maximum number of masks the owner can put either in rows or columns is: 7 masks
Question 16.
A teacher wants to set up a chair for each of the 48 students in chorus. He wants to set up the chairs in a rectangular array. He can fit no more than 20 rows and no more than 30 chairs in each row in the room. What are the possible numbers of rows that he could set up?
Answer: The possible number of rows that he could set up are: 16 rows
Explanation:
Given that a teacher wants to set up a chai for each of the 48 students in the chorus and he wants to set up the chairs in a rectangular array.
Hence, the number of arrays ( factor pairs) of 48 are:
1 × 48, 2 × 24, 3 × 16, 4 × 12, 6 × 8, 8 × 6, 12 × 4, 16 × 3, 24 × 2, and 48 × 1
It is also given that he can fit no more than 20 rows and no more than 30 chairs in each row in the room.
Hence, from the above,
We can conclude that the possible number of rows that he could set up are: 16 rows
Understand Factors Homework & Practice 6.1
Question 1.
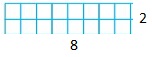
Use the rectangles to find the factor pairs for 8.
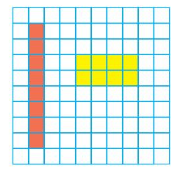
Answer: The factors of 8 are: 1 and 8, 2 and 4
Explanation:
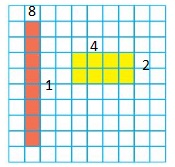
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 8 are: 1 × 8 and 2 × 4
Question 2.
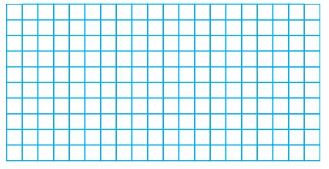
Draw rectangles to find the factor pairs for 21.
Answer: The factor pairs of 21 are: 1 × 21, 3 × 7
Explanation:
![]()
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 21 are: 1 × 21, 3 × 7
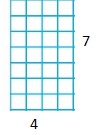
Question 3.
Draw rectangles to find the factor pairs for 28.

Answer: The factor pairs of 28 are: 1 × 28, 2 × 14, 4 × 7
Explanation:

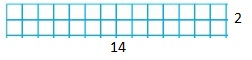
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 28 are: 1 × 28, 2 × 14, 4 × 7
Find the factor pairs for the number.
Question 4.
13
Answer: The factor pairs of 13 are: 1 × 13 and 13 × 1
Explanation:
Factors are the numbers that divide the original number completely. Hence,
The factor pairs of 13 are:
1 × 13 and 13 × 1
Question 5.
5
Answer: The factor pairs of 5 are: 1 × 5 and 5 × 1
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 5 are:
1 × 5 and 5 × 1
Question 6.
35
Answer: The factor pairs of 35 are: 1 × 35, 5 × 7
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 35 are:
1 × 35, 5 × 7
Question 7.
45
Answer: The factor pairs of 45 are: 1 × 45, 3 × 15, 5× 9
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 45 are:
1 × 45, 3 × 15, 5× 9
Question 8.
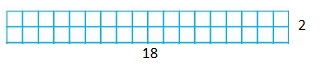
18
Answer: The factor pairs of 18 are: 1 × 18, 2 × 9, 3 × 6
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 18 are:
1 × 18, 2 × 9, 3 × 6
Question 9.
36
Answer: The factor pairs of 36 are: 1 × 36, 2 × 18, 3 × 12, 4 × 9, 6 × 6
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 36 are:
1 × 36, 2 × 18, 3 × 12, 4 × 9, 6 × 6
Question 10.
YOU BE THE TEACHER
Descartes says there are 5-factor pairs for 16. Newton says there are 3-factor pairs for 16. Who is correct? Explain.

Answer: Newton is correct
Explanation:
We know that,
a × b = b × a
Hence,
The factor pairs of 16 are:
1 × 16, 2 × 8, 4 × 4, 8 × 2, 16 × 1
But according to the above,
We don’t have to consider the factor pairs 8 × 2 and 16 × 1
Hence,
There are only 3-factor pairs.
But, Descartes says that there are 5-factor pairs for 16 while Newton says it three.
Hence, from the above,
We can conclude that Newton is correct.
Question 11.
Modeling Real Life
A race volunteer has 50 cases of bottled water. He wants to arrange the cases into a rectangular array. How many different arrays can he make?

Answer: The number of different arrays he can make is: 6 arrays
Explanation:
Given that a race volunteer has 50 cases of bottled water and he wants to arrange the cases into a rectangular array.
The array is nothing but the factor pairs.
Hence, the number of arrays of 50 he can make = 1 × 50, 2 × 25, 5 × 10, 10 × 5, 25 × 2, 50 × 1
Hence, from the above,
we can conclude that the number of different arrays to arrange the 50 cases of bottled water are:
a) 1 × 50 b) 2 × 25 c) 5 × 10 d) 10 × 5 e) 25 × 2 f) 50 × 1
Review & Refresh
Find the product.
Question 12.
2 × 14 = _____
Answer: 2 × 14 = 28
Explanation:
According to the Distributive Property of Multiplication,
2 × 14 = ( 10 + 4 ) × 2
= ( 2 × 10 ) + ( 2 × 4 )
= 20 + 8
= 28
Hence, 2 × 14 = 28
Question 13.
22 × 7 = ______
Answer: 22 × 7 = 154
Explanation:
According to the Distributive Property of Multiplication,
22 × 7 = ( 20 + 2 ) × 7
= ( 20 × 7 ) + ( 2 × 7 )
= 140 + 14
= 154
Hence, 22 × 7 = 154
Question 14.
9 × 27 = ______
Answer: 27 × 9 = 243
Explanation:
According to the Distributive Property of Multiplication,
27 × 9 = ( 20 + 7 ) × 9
= ( 20 × 9 ) + ( 7 × 9 )
= 180 + 63
= 243
Hence, 27 × 9 = 243
Lesson 6.2 Factors and Divisibility
Explore and Grow
List any 10 multiples of 3. What do you notice about the sum of the digits in each multiple?
Answer:
The 10 multiples of 3 are:
3, 6, 9, 12, 15, 18 ,21, 24, 27, and 30
From the sum of the digits in the above multiples,
0 + 3 =3
0 + 6 = 6
0 + 9 = 9
1 + 2 = 3
1 + 5 = 6
2 + 1 = 3
2 + 4= 6
2 + 7 = 9
3 + 0 = 3
Hence, from the above sums,
We can conclude that the sum of the digits in the 10 multiples are also the multiples of 3.
List any 10 multiples of 9. What do you notice about the sum of the digits in each multiple?
Answer:
The 10 multiples of 9 are:
9, 18, 27, 36, 45, 54, 63, 72, 81, and 90
From the sum of the digits in the above multiples,
0 + 9 = 9
1 + 8 = 9
2 + 7 = 9
3 + 6 = 9
4 + 5 = 9
5 + 4 = 9
6 + 3 = 9
7 + 2 = 9
8 + 1 = 9
9 + 0 = 9
Hence, from the above,
We can conclude that the sum of the digits in all the multiples of 9 is equal to 9 only.
Structure
How can you use your observations above to determine whether 3 and 9 are factors of a given number? Explain.
Answer: The factors of 9 are: 1,3, and 9
Explanation:
The factor pairs of 9 are:
1 × 9, 3 × 3 and 9 × 1
Hence, from the above,
We can conclude that 3 and 9 are the factors of 9.
Think and Grow: Find Factors and Factor Pairs
A number is divisible by another number when a quotient is a whole number and the remainder is 0.
Some numbers have divisibility rules that you can use to determine whether they are factors of other numbers.
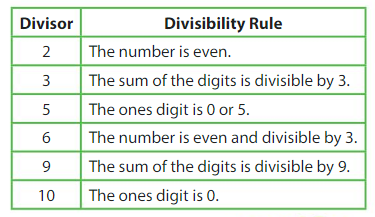
Example
Find the factor pairs for 48.
Use divisibility rules and division to find the factors of 48.

The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
The factor pairs for 48 are 6.
Show and Grow
Find the factor pairs for the number.
Question 1.
30
Answer:
The factor pairs of 30 are:
1 × 30, 2 × 15, 3 × 10, 5 × 6, 6 × 5, 10 × 3, 15 × 2, 30 × 1
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 30 are:
1 × 30, 2 × 15, 3 × 10, 5 × 6, 6 × 5, 10 × 3, 15 × 2, 30 × 1
Question 2.
54
Answer:
The factor pairs of 54 are:
1 × 54, 2 × 27, 3 × 18, 6 × 9, 9 × 6, 18 × 3, 27 × 2, 54 × 1
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 54 are:
1 × 54, 2 × 27, 3 × 18, 6 × 9, 9 × 6, 18 × 3, 27 × 2, 54 × 1
Apply and Grow: Practice
Find the factor pairs for the number.
Question 3.
29
Answer:
The factor pairs of 29 are:
1 × 29 and 29 × 1
Explanation:
Factors are the numbers that divide the original numbers completely.
Hence,
The factor pairs of 29 are:
1 × 29 and 29 × 1
Question 4.
50
Answer:
The factor pairs of 50 are:
1 × 50, 2 × 25, 5 × 10, 10 × 5, 25 × 2, and 50 × 1
Explanation:
Factors are the numbers that divide the original numbers completely.
Hence,
The factor pairs of 50 are:
1 × 50, 2 × 25, 5 × 10, 10 × 5, 25 × 2, and 50 × 1
Question 5.
63
Answer:
The factor pairs of 63 are:
1 × 63, 3 × 21, 7 × 9, 9 × 7, 21 × 3 and 63 × 1
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factor pairs of 63 are:
1 × 63, 3 × 21, 7 × 9, 9 × 7, 21 × 3 and 63 × 1
Question 6.
33
Answer:
The factor pairs of 33 are:
1 × 33, 3 × 11, 11 × 3 and 33 × 1
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factor pairs of 33 are:
1 × 33, 3 × 11, 11 × 3 and 33 × 1
Question 7.
60
Answer:
The factor pairs of 60 are:
1 × 60, 2 × 30, 3 × 20, 4 × 15, 5 × 12, and 6 × 10
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factor pairs of 60 are:
1 × 60, 2 × 30, 3 × 20, 4 × 15, 5 × 12, and 6 × 10
Question 8.
64
Answer:
The factor pairs of 64 are:
1 × 64, 2 × 32, 4 × 16, and 8 ×8
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factor pairs of 64 are:
1 × 64, 2 × 32, 4 × 16, and 8 ×8
List the factors of the number.
Question 9.
39
Answer:
The factors of 39 are: 1, 3, 13, and 39
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factors of 39 are: 1, 3, 13, and 39
Question 10.
44
Answer:
The factors of 44 are: 1, 2, 4, 11, 22, and 44
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factors of 44 are: 1, 2, 4, 11, 22, and 44
Question 11.
72
Answer:
The factors of 72 are: 1, 2, 3,4, 6, 8, 9, 12, 18, 24, 36, and 72
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factors of 72 are: 1, 2, 3,4, 6, 8, 9, 12, 18, 24, 36, and 72
Question 12.
67
Answer:
The factors of 7 are: 1 and 67
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factors of 7 are: 1 and 67
Question 13.
42
Answer:
The factors of 42 are: 1, 2, 3, 6, 7, 14, 21, and 42
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factors of 42 are: 1, 2, 3, 6, 7, 14, 21, and 42
Question 14.
28
Answer:
The factors of 28 are:
1, 2, 4, 7, 14, and 28
Explanation:
Factors are the numbers that divide the number originally
Hence,
The factors of 28 are:
1, 2, 4, 7, 14, and 28
Question 15.
Reasoning
Can an odd number have an even factor? Explain.
Answer: No, an odd number doesn’t have an even factor
Explanation:
Let the number which we want to find the factors is: 15
The factors of 15 are:
1, 3, 5, and 15
Hence, from the above factors,
We can conclude that an odd number doesn’t have an even factor.
Note: The “Odd number” is the number that can’t be divisible by 2.
Question 16.
Writing
Use the diagram to explain why you do not have to check whether any numbers greater than 4 are factors of 12.
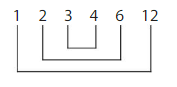
Answer: We don’t have to check the numbers greater than 4 are the factors of 12 because the factors of 12 greater than 4 are repeating.
Explanation:
The given number is 12
The factors of 12 are:
1, 2, 3, 4, 6, and 12
Hence, from the above
We can conclude that we don’t have to check the numbers greater than 4 are the factors of 12.
Think and Grow: Modeling Real Life
Example
There are 4 classes going on a field trip. The classes will use 3 buses. Can the teachers have an equal number of students on each bus?
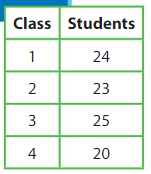
Think: What do you know? What do you need to find? How will you solve it?
Step 1: Add to find how many students are going on the field trip.
24 + 23 + 25 + 20 = 92
92 students are going on the field trip.
Step 2: Is the total number of students divisible by the number of buses?
Find the sum of the digits of 92. 9 + 2 =11
The sum of the digits not divisible by 3.
The teachers don’t have an equal number of students on each bus.
Show and Grow
Question 17.
A teacher is making a 5-page test with 28 vocabulary problems and 7 reading problems. Can the teacher put an equal number of problems on each page?
Answer: Yes, the teacher can put an equal number of problems on each page
Explanation:
Given that a teacher is making a 5- page test.
It is also given that there are 28 vocabulary problems and 7 reading problems.
So,
Total number of problems = 28 + 7 = 35 problems
So,
The number of problems that each page contains = 35 ÷ 5
Now,
By using the Distributive Property of Multiplication,
35 ÷ 5 = ( 30 + 5 ) ÷ 5
= ( 30 ÷ 5 ) + ( 5 ÷ 5 )
= 6 + 1
= 7
Hence, from the above,
We can conclude that the teacher can put an equal number of problems on each page.
Question 18.
A relay race is 39 laps long. Each team member must bike the same number of laps. Could a team have 8, 6, or 3 members? Explain.
Answer: A team has 3 members.
Explanation:
Given that a relay race is 39 laps long and each member must bike the same number of laps.
Now,
The factors of 39 are: 1, 3, 13, and 39
The factors are the numbers that divide the number originally.
So, 39 can be divided by 3 only.
Hence, from the above,
We can conclude that each team has only 3 members.
Question 19.
DIG DEEPER!
You have 63 clay figures to display on 7 shelves. Not all of the shelves need to be used and each shelf can hold no more than 25 figures. Each shelf must have the same number of figures. What are all the ways you could arrange the figures?

Answer: The number of ways you could arrange the figures is to find the number of factors of 63.
So,
The number of factors of 63 is: 1, 3, 7,9 21, and 63
Explanation:
Given that you have 63 clay figures to display on 7 shelves.
It is also given that each shelf holds no more than 25 figures.
Now,
The factors of 63 are: 1, 3, 7,9 21, and 63
The “Factors” are the ways to arrange the given clay figures.
So,
The number of ways to arrange the clay figures that do not hold more than 25 is: 3, 7, 9, and 21
Hence, from the above,
We can conclude that the number of ways to arrange the clay figures in each shelf that do not hold more than 25 figures is: 3, 7, 9, and 21 ways
Factors and Divisibility Homework & Practice 6.2
Find the factor pairs for the number.
Question 1.
24
Answer:
The factor pairs of 24 are:
1 × 24, 2 × 12, 3 × 8, 4 × 6, 6 × 4, 8 × 3, 12 × 2, and 24 × 1
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factor pairs of 24 are:
1 × 24, 2 × 12, 3 × 8, 4 × 6, 6 × 4, 8 × 3, 12 × 2, and 24 × 1
Question 2.
48
Answer:
The factor pairs of 48 are:
1 × 48, 2 × 24, 3 × 16, 4 × 12, 6 × 8
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factor pairs of 48 are:
1 × 48, 2 × 24, 3 × 16, 4 × 12, 6 × 8
Question 3.
31
Answer:
The factor pairs of 31 are:
1 × 31 and 31 × 1
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factor pairs of 31 are:
1 × 31 and 31 × 1
Question 4.
99
Answer:
The factor pairs of 99 are:
1 × 99, 3 × 33, 9 × 11
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factor pairs of 99 are:
1 × 99, 3 × 33, 9 × 11
Question 5.
45
Answer:
The factor pairs of 45 are:
1 × 45, 3 × 15, and 5 × 9
Explanation:
factors are the numbers that divide the number originally.
Hence,
The factor pairs of 45 are:
1 × 45, 3 × 15, and 5 × 9
Question 6.
26
Answer:
The factor pairs of 26 are:
1 × 26, 2 × 13
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factor pairs of 26 are:
1 × 26, 2 × 13
List the factors of the number.
Question 7.
25
Answer:
The factors of 25 are: 1, 5, and 25
Explanation:
Factors are the numbers that divide the numbers originally.
Hence,
The factors of 25 are: 1, 5, and 25
Question 8.
56
Answer:
The factors of 56 are: 1, 2, 4, 7, 8, 14, 28 and 56
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factors of 56 are: 1, 2, 4, 7, 8, 14, 28 and 56
Question 9.
75
Answer:
The factors of 75 are: 1, 3, 5, 15, 25, and 75
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factors of 75 are: 1, 3, 5, 15, 25, and 75
Question 10.
80
Answer:
The factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20,40 and 80
Explanation:
Factors are the numbers that divide the numbers originally.
Hence,
The factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20,40 and 80
Question 11.
93
Answer:
The factors of 93 are: 1, 3, 31 and 93
Explanation;
Factors are the numbers that divide the number originally.
Hence,
The factors of 93 are: 1, 3, 31 and 93
Question 12.
61
Answer:
The factors of 61 are: 1 and 61
Explanation:
Factors are the numbers that divide the number originally.
Hence,
The factors of 61 are: 1 and 61
Question 13.
Reasoning
Why does a number that has 9 as a factor also have 3 as a factor?
Answer: The number that has 9 as a factor also have 3 as a factor because 9 is a multiple of 3
Explanation:
Let the number that has 9 as a factor and that has also 3 as a factor be: 18
Now,
The factors of 18 are: 1, 2, 3, 6, 9, and 18
Hene, from the above,
We can conclude that the number that has 9 as a factor also have 3 as a factor.
Question 14.
DIG DEEPER!
The number below has 3 as a factor. What could the unknown digit be?
3 _____ 5.
Answer: The unknown digit could be: 1 or 4 or 7
Explanation:
Given that the number has 3 as a factor.
To have 3 as a factor, the sum of the digits in the given number should be a multiple of 3
Hence,
The unknown digit in 3____5 could be: 1 or 4 or 7
Question 15.
Number Sense
Which numbers have 5 as a factor?
![]()
Answer: The numbers which have 5 as a factor are: 50, 25, 1,485 and 100
Explanation:
Given numbers are: 50, 34, 25, 1,485, 100 and 48
The numbers that have the factor of 5 must have the last digits 0 or 5
Hence,
The numbers that have 5 as a factor are: 50, 25, 1,485, and 100
Question 16.
Modeling Real Life
You and a partner are conducting a bottle flipping experiment. You have 3 bottles with different amounts of water in each. You need to flip each bottle 15 times. If you take turns, will you and your partner each get the same number of flips?
Answer: Yes, you and your partner will each get the same number of flips.
Explanation:
Given that you and your partner are conducting a bottle flipping experiment and you have 3 bottles with different amounts of water in each and you need to flip each bottle 15 times.
So,
The number of flips each will get = 15 ÷ 3
Now,
By using the Distributive Property of Multiplication,
15 ÷ 3 = ( 12 + 3 ) ÷ 3
= ( 12 ÷ 3 ) + ( 3 ÷ 3 )
= 4 + 1
= 5
Hence, from the above,
We can conclude that each bottle will flip 5 times.
Question 17.
Modeling Real Life
A florist has 55 flowers. She wants to put the same number of flowers in each vase without any leftover Should she put 2, 3, or 5 flowers in each vase? Explain.

Answer: The florist put 5 flowers in each vase.
Explanation:
Given that a florist has 55 flowers and she wants to put the same number of flowers in each vase without any leftover.
The number 55 will be divided by to not have any leftover because the last digit is 5.
Hence,
The florist puts 5 flowers in each vase.
Review & Refresh
Compare.
Question 18.
![]()
Answer: 7,914 is greater than 7,912
Explanation:
Given numbers are 7,914 and 7,912
Hence, from the above,
We can conclude that 7,914 is greater than 7,912
Question 19.
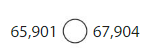
Answer: 65,901 is less than 67,904
Explanation:
Given numbers are 65,901 and 67,904
Hence, from the above,
We can conclude that 65,901 is less than 67,904
Question 20.
![]()
Answer: 839,275 is equal to 839,275
Explanation:
Given numbers are 839,275 and 839,275
Hence, from the above,
We can conclude that 839,275 is equal to 839,275
Lesson 6.3 Relate Factors and Multiples
Explore and Grow
List all factors of 24.
Answer:
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24
Explanation:
Factors are the numbers that divide the numbers originally.
Hence,
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24
List several multiples of each factor. What number appears in each list?
Answer:
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24
Explanation:
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24
Now,
There are no other multiples of 1
The multiples of 2 are: 1, 2
The multiples of 3 are: 1,3
The multiples of 4 are: 1, 2, 4
The multiples of 6 are: 1, 2, 3 and 6
The multiples of 8 are: 1, 2, 4 and 8
The multiples of 12 are: 1, 2, 3, 4, 6, and 12
The multiples of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24
Hence, from the above,
We can conclude that 1 appears in each list
Number Sense
How are factors and multiples related?
Answer:
Factors are the numbers that can divide the numbers originally.
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
Think and Grow: Identify Multiples
A whole number is a multiple of each of its factors.
12 is a multiple of 1, 2, 3, 4, 6, and 12.
1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
12 × 1 = 12
Example
Is 56 a multiple of 7?
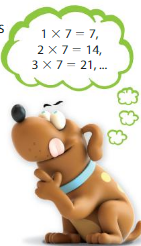
One Way:
List multiples of 7.
7, 14, 21, 28, 35, 42, 49, 56
So, 56 is a multiple of 7.
Another Way:
Use division to determine whether 7 is a factor of 56.
56 ÷ 7 = 8
7 is a factor of 56.
So, 56 is a multiple of 7.
Example
Is 9 a factor of 64?
One Way:
Use divisibility rules to determine whether 9 is a factor of 64.
9 is not a factor of 64 because 6 + 4 = 10 is not divisible by 9.
Another Way:
List the multiples of 9.
9, 18, 27, 36, 45, 54, 63, 72
64 is not a multiple of 9.
So, 9 is not a factor of 64.
Show and Grow
Question 1.
Is 23 a multiple of 3? Explain.
Answer: 23 is not a multiple of 3
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
The multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, 24, 27 and 30
Hence, from the above,
We can conclude that 23 is not a multiple of 3.
Question 2.
Is 8 a factor of 56? Explain.
Answer: 8 is a factor of 56.
Explanation:
Factors are the numbers that divide the numbers originally.
Now,
The factors of 56 are: 1, 2, 4, 7, 8, 14, 28, and 56
Hence, from the above,
We can conclude that 8 is a factor of 56.
Apply and Grow: Practice
Question 3.
Is 65 a multiple of 5? Explain.
Answer: 65 is a multiple of 5
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
The multiples of 5 are: 5, 10, 15, 20, 25, 30, 35,40, 45, 50, 55, 60 and 65
Hence, fro the above,
We can conclude that 65 is a multiple of 5.
Question 4.
Is 14 a multiple of 4? Explain.
Answer: 14 is not a multiple of 4.
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
The multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, and 40
Hence, from the above,
We can conclude that 14 is not a multiple of 4.
Question 5.
Is 23 a multiple of 2? Explain.
Answer: 23 is not a multiple of 2
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
The multiples of 2 are: 2, 4, 6, 8, 10, 1, 14, 16, 18, 20, 22, 24 and 26
Hence, from the above,
We can conclude that 23 is not a multiple of 2.
Question 6.
Is 6 a factor of 96? Explain.
Answer: 6 is a factor of 96
Explanation:
Factors are the numbers that divide the number originally.
The factors of 96 are: 1, 2, 3, 4, 6, 8, 12, 16, 28, 32, 48 and 96
Hence, from the above,
We can conclude that 6 is a factor of 96.
Question 7.
Is 3 a factor of 82? Explain.
Answer: 82 is not a factor of 3
Explanation:
Factors are the numbers that divide the number originally.
The given number is 82
The sum of digits of 82 = 8 + 2 = 11
The number is a multiple of 3 only then the sum of the digits of that number is a multiple of 3.
But the sum of digits of 82 is not a multiple of 3
Hence, from the above,
we can conclude that 3 is not a factor of 82
Question 8.
Is 9 a factor of 72? Explain.
Answer: 9 is a factor of 72
Explanation:
Factors are the numbers that divide the number originally.
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72
Hence, from the above,
We can conclude that 9 is a factor of 72.
Tell whether 8 is a multiple or a factor of the number. Write multiple, factor or both.
Question 9.
4
Answer: 8 is a multiple of 4.
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
So,
The multiples of 4 are: 4, 8, 12, 16, and 20
Hence, from the above,
We can conclude that 8 is a multiple of 4
Question 10.
8
Answer: 8 is a multiple of 8
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
So,
The multiples of 8 are: 8, 16, 24, 32, 0, etc.
Hence, from the above,
We can conclude that 8 is a multiple of 8
Question 11.
32
Answer: 32 is a multiple of 8
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
So,
The multiples of 8 are: 8, 16, 24, 32, 40, 48 etc
Hence, from the above,
We can conclude that 32 is a multiple of 8
Question 12.
Writing
Use numbers 6 and 12 to explain how factors and multiples are related.
Answer:
The multiplication Expression using numbers 6 and 12 is:
6 × 2 = 12
From the multiplication Expression,
6 is a factor of 12
12 is a multiple of 6
Explanation:
The given numbers re 6 and 12
From the given numbers, the multiplication Expression is:
6 × 2 = 12
Hence, from the above multiplication Expression,
6 is a factor of 12
12 is a multiple of 6.
Question 13.
Complete the Venn diagram.
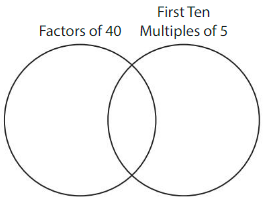
Answer:
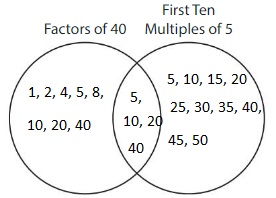
Explanation:
From the given Venn diagram,
The factors of 40 are: 1, 2, 4, 5, 8, 10, 20, and 40
The first 10 multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50
Hence, from the above,
The common numbers from both the factors of 4 and the multiples of 5 are:
5, 10, 20 and 40
Think and Grow: Modeling Real Life
Example
You need 96 balloons for a school dance. Balloons come in packs of 4, packs of 6, and packs of 9. Which packs could you buy so you have no leftover balloons?

Use division to determine whether 96 is a multiple of 4.
4 √96 So, 4 is a factor of 96, and 96 is a multiple of 4.
Use the divisibility rules to check whether 96 is a multiple of 6.
96 is even and 9 + 6 = 15 divisible by 3. So, 6 is a factor of 96 and 96 is a multiple of 6.
Use the divisibility rules to check whether 96 is a multiple of 9.
9 + 6 = 15 is not divisible by 9. So, 9 is not a factor of 96 and
96 is not a multiple of 9.
You could buy packs of 4 balloons or packs of 6 balloons.
Show and Grow
Question 14.
A teacher needs 88 batteries for science experiments. Batteries are sold in packs of 2, packs of 6, and packs of 8. Which packs could the teacher buy so she has no leftover batteries?

Answer: The teacher should buy the packs of 2 and packs of 8 so that there will be no leftover batteries.
Explanation:
Given that a teacher needs 88 batteries for science experiments and that batteries are sold in packs of 2, 6, and 8.
So,
The factors of 88 are: 1, 2, 4, 8, 11, 22, 44, and 88
So, from the factors of 88, we see that there is no 6 as a factor of 88
So, from this, we can say that we can’t pack 88 batteries in packs of 6 but in the packs of 2 and 8 ( Since 2 and 8 both are the factors of 88 )
We know that,
Factors are the numbers that divide the number originally.
Hence, from the above,
We can conclude that the 88 batteries can be packed in packs of 2 or packs of 8.
Question 15.
DIG DEEPER!
Descartes buys 2 books for a total of $15. Each book costs a multiple of $3. How much could each book cost?

Answer: The cost of each book that Descartes bought is: $15
Explanation:
Given that Descartes bought 3 books for a total of $15 and each book costs a multiple of $3
So,
The cost of each book = The total cost of 2 books ÷ Total number of books
= 15 ÷ 2
Now,
By using the Distributive Property of Multiplication,
15 ÷ 2 = ( 12 + 3 ) ÷ 2
( 12 ÷ 2 ) + ( 3 ÷ 2 )
= 6 + 1.5
= 7.5
Hence, from the above,
We can conclude that the cost of each book is: $7.5 and the cost of each book is also a multiple of $3
Question 16.
Newton buys some boxes of dog treats for $9 each. Descartes buys some bags of cat treats for $6 each. Newton and Descartes spend the same amount of money on treats. What is the least amount of money they could have spent?
Answer: The least amount of money that Newton and Descartes spent on dog treats = $18
Explanation:
Given that Newton buys some boxes of dog treats for $9 each and Descartes buys some bags of cat treats for $6 each.
It is also given that Newton and Descartes spend the same amount of money on treats
So, we have to find the least number that can be a multiple of both 6 and 9.
Now,
the multiples of 6 are: 6, 12, 18, 24, 30, 36, 42, 48, 54, and 60
The multiples of 9 are: 9, 18, 27, 36, 45, 54, 63, 72, 81, and 90
From the multiples of 6 and 9,
We can see that the least number that can be the multiple of both 6 and 9 is: 18
Hence, from the above,
We can conclude that the least amount of money that Newton and Descartes spent on dog treats is: $18
Relate Factors and Multiples Homework & Practice 6.3
Question 1.
Is 16 a multiple of 3? Explain.
Answer: 16 is not a multiple of 3
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
So,
The multiples of 16 are 3, 6,9, 12, 15, 18, etc.
Hence, from the above,
We can conclude that 16 is not a multiple of 3.
Question 2.
Is 21 a multiple of 7? Explain.
Answer: 21 is a multiple of 7
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
So,
The multiples of 7 are: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70
Hence, from the above,
We can conclude that 21 is a multiple of 7
Question 3.
Is 46 a multiple of 2? Explain.
Answer: 46 is a multiple of 2
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
So,
For the multiple of 2, the last digit should be 2, 4, 6, 8, 0
So,
46 can be said as a multiple of 2
Hence, from the above,
We can conclude that 46 is a multiple of 2.
Question 4.
Is 5 a factor of 71? Explain.
Answer: 5 is not a factor of 71
Explanation:
Factors are the numbers that divide the number completely.
So,
The factors of 71 are: 1, 71
Hence, from the above,
We can conclude that 5 is not a factor of 71.
Question 5.
Is 8 a factor of 88? Explain.
Answer: 8 is a factor of 88
Explanation:
Factors are the numbers that divide the numbers completely
So,
The factors of 88 are: 1, 2, 4, 8, 11, 22, 44, 88
Hence, from the above factors,
We can conclude that 8 is a factor of 88
Question 6.
Is 4 a factor of 80? Explain.
Answer: 4 is a factor of 80
Explanation:
Factors are the numbers that divide the number completely.
So,
The factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Hence, from the above factors,
We can conclude that 4 is a factor of 80.
Tell whether 30 is a multiple or a factor of the number. Write multiple, factor, or both.
Question 7.
30
Answer: 30 is a multiple and factor of 30
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
Factors are the numbers that divide the number completely
So,
The multiples of 30 are: 30, 60, 90, 120, 150, 180, 210, 240, 270 and 300
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
Hence,
From the above,
We can conclude that 30 is a multiple and factor of 30
Question 8.
90
Answer: 90 is a multiple of 30
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
So,
The multiples of 30 are: 30, 60, 90, 120, 150, 180, 210, 240, 270, 300
Hence, from the above multiples,
We can conclude that 90 is a multiple of 30
Question 9.
10
Answer: 10 is a factor of 30
Explanation:
Factors are the numbers that divide the number originally.
So,
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
Hence, from the above factors,
We can conclude that 10 is a factor of 30
Tell whether 10 is a multiple or a factor of the number. Write multiple, factor, or both.
Question 10.
5
Answer: 5 is a factor of 10
Explanation:
Factors are the numbers that divide the number completely.
So,
The factors of 10 are: 1, 2, 5, 10
Hence, from the above factors,
We can conclude that 5 is a factor of 10
Question 11.
60
Answer: 60 is a multiple of 10
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
So,
The multiples of 10 are: 10, 20, 30, 40, 50, 60, 70, 80 , 90, 100
Hence, from the above multiples,
We can conclude that 60 is a multiple of 10
Question 12.
10
Answer: 10 is a multiple and factor of 10
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
Factors are the numbers that divide the number completely
So,
The number of factors of 10 is: 1, 2, 5, 10
The multiples of 10 are: 10, 20, 30, 40, 50, 60, 70, 80 , 90, 100
Hence, from the above,
We can conclude that 10 is a factor and a multiple of 10
Question 13.
DIG DEEPER!
Name two numbers that are each a multiple of both 3 and 4. What do you notice about the two multiples?
Answer: 12 is a multiple of both 3 and 4
Explanation:
We know that,
If the number is divisible by 3, then the sum of the digits of that given number must be divisible by 3
If the number is divisible by 4, then the last 2 digits of that given number must also be divisible by 4
Hence,
The number which is a multiple of both 3 and 4 is: 12
12 will satisfy both the conditions of the number divisible by 3 and 4
Hence, from the above,
We can conclude that 12 is a multiple of both 3 and 4
Question 14.
YOU BE THE TEACHER
Is Newton correct? Explain.

Answer: Yes, Newton is correct
Explanation:
Given that,
According to Newton, all numbers that are multiples of 10 have 2 as a factor.
Now,
The multiples of 10 are: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100
So,
Let a multiple of 10 be 20
So,
The factors of 20 are: 1, 2, 4, 5, 10, 20
Hence, from the above,
We can conclude that Newton’s statement is correct
Question 15.
Logic
A quotient is a multiple of 4. The dividend is a multiple of 8. The divisor is a factor of 6. Write one possible equation for the problem.
Answer:
The possible equation for the problem is:
24 ÷ 6 = 4
Explanation:
Given that a quotient is a multiple of 4.
It is also given that the dividend is a multiple of 8 and the divisor is a factor of 6.
So,
The possible Equation for the given problem is:
24 ÷ 6 = 4
Where,
24 is a dividend
6 is a divisor
4 is a quotient
Hence, from the above,
We can conclude that the possible equation according to the given conditions is:
24 ÷ 6 = 4
Question 16.
Modeling Real Life
Your friend needs our friend needs t0 50 US state capitals. She wants to memorize the same number of capitals each day. Which numbers of capitals can she memorize each day: 2, 3, 4, or 5?
Answer: The number of capitals she can memorize each day in packs of 2 and 5
Explanation:
Given that your friend needs 50 US state capitals and she wants to memorize the same number of capitals each day.
It is also given that the number of capitals she had to memorize in the packs of 2, 3, 4, or 5
So,
If the number has to be divided by 5, the last digit of that given number should be 5 (or) 0
So,
The factors of 50 are: 1, 2, 5, 10, 25, 50
Hence, from the above,
We can conclude that 50 US capitals she had to memorize is in the packs of 2 or packs of 5
Question 17.
Modeling Real Life
Zookeepers plan an enrichment day for the animals every 7 days and bathe the elephants every 2 days. You want to go to the zoo when both events are happening. What other dates in May will this happen?
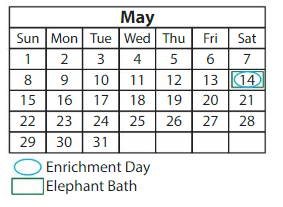
Answer: The events of both Enrichment day and Elephant Day come in the month of May other than 14 May is:
21 May and 28 May
Explanation:
Given that Zookeepers plan an enrichment day for the animals every 7 days
It is also given that the Elephant bathing takes place every 2 days.
So, other than 14 May,
The other days that these two events will take place on May are: 21 May and 28 May with 7 days gap from 14 May
Hence, from the above,
We can conclude that both the events are happening on 21 and 28 May
Review & Refresh
Estimate the sum or difference.
Question 18.
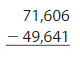
Answer: 71,606 – 49,641 = 21,965
Question 19.
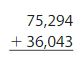
Answer: 75,294 + 36,043 = 111,337
Question 20.
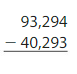
Answer: 93,294 – 40,293 = 53,001
Lesson 6.4 Identify Prime and Composite Numbers
Explore and Grow
Draw as many different rectangles as possible that each has the given area. Label their side lengths.

Compare the numbers of factors of 32 and 13.
Answer: 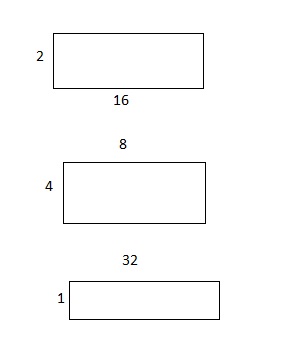
The factors of 32 are: 1, 2, 4, 8, 16, 32
The factors of 13 are: 1, 13
On comparison of the factors of 32 and 13, we can say that 13 has less number of factors than 32
Reasoning
Can a whole number have fewer than two factors? exactly two factors? more than two factors?
Answer: Yes, a whole number has exactly 2 factors and more than 2 factors but not less than 2 factors.
Explanation:
A whole number will be divided into 2 types based on the number of factors. They are:
A) Composite numbers:
The numbers that have more than 2 factors are called “Composite numbers”
B) Prime numbers:
The numbers that have exactly 2 factors are called “Prime numbers”
There will no less than 2 factors for any number.
Think and Grow: Identify Prime and Composite Numbers
A prime number is a whole number greater than 1 with exactly two factors, 1 and itself. A composite number is a whole number greater than 1 with more than two factors.
Example
Tell whether 27 is a prime composite
Use divisibility rules.

• 27 is odd, so it is not divisible by 2 or any other even number.
• 2 + 7 = 9 is divisible by 3,
so 27 is divisible by 3.
27 has factors in addition to 1 and itself.
So, 27 is a Composite number.
Example
Tell whether 11 is a prime composite
Use divisibility rules.
• 11 is odd, so it is not divisible by 2 or any other even number.
• 1 + 1 = 2 is not divisible by 3 or 9,
so 11 is not divisible by 3 or 9.
• The ones digit is not 0 or 5,
so 11 is not divisible by 5.
11 has exactly two factors, 1 and itself.
So, 11 is a prime number.
Show and Grow
Tell whether the number is prime or composite. Explain.
Question 1.
7
Answer: 7 is a prime number
Explanation:
Prime number:
The numbers which have exactly 2 factors 1 and itself is called “Prime numbers”
Now,
The factors of 7 are: 1, 7
Hence, from the above,
We can conclude that 7 is a prime number
Question 2.
12
Answer: 12 is a Composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are called “Composite numbers”
Now,
The factors of 12 are: 1, 2, 3, 4, 6, 12
Hence, from the above,
We can conclude that 12 is a Composite number
Question 3.
2
Answer: 2 is a prime number.
Explanation:
Prime number:
The numbers which have exactly 2 factors 1 and itself are called “Prime numbers”
Now,
The factors of 2 are: 1, 2
Hence, from the above,
We can conclude that 2 is a prime number
Question 4.
19
Answer: 19 is a prime number
Explanation:
Prime number:
The numbers which have exactly 2 factors 1 and itself are called “Prime numbers”
Now,
The factors of 19 are: 1, 19
Hence, from the above,
we can conclude that 19 is a prime number
Question5.
45
Answer: 45 is a Composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are called “Composite numbers”
Now,
The factors of 45 are: 1, 3, 5, 9, 15, 45
Hence, from the above,
we can conclude that 45 is a Composite number
Question 6.
54
Answer 54 is a Composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are called “Composite numbers”
Now,
The factors of 54 are: 1, 2. 3. 6, 9, 18, 27, 54
Hence, from the above,
We can conclude that 54 is a Composite number
Apply and Grow: Practice
Tell whether the number is prime or composite. Explain.
Question 7.
35
Answer:35 is a Composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are called “Composite numbers”
Now,
The factors of 35 are: 1, 5, 7, 35
Hence, from the above,
We can conclude that 35 is a Composite number
Question 8.
5
Answer: 5 is a prime number
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are called “prime numbers”
Now,
The factors of 5 are: 1, 5
Hence, from the above,
we can conclude that 5 is a prime number
Question 9.
23
Answer: 23 is a prime number
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are called ” Prime numbers”
Now,
The factors of 23 are: 1, 23
Hence, from the above,
We can conclude that 23 is a prime number
Question 10.
40
Answer: 40 is a Composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are called “Composite numbers”
Now,
The factors of 40 are: 1, 2, 4, 5, 8, 10, 20, 40
Hence, from the above,
We can conclude that 40 is a Composite number
Question 11.
41
Answer: 41 is a prime number
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are called “Prime numbers”
Now,
The factors of 41 are: 1, 41
Hence, from the above,
we can conclude that 41 is a prime number
Question 12.
81
Answer: 81 is a Composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are called “Composite numbers”
Now,
The factors of 81 are: 1, 3, 9, 27, 81
hence, from the above,
we can conclude that 81 is a Composite number
Question 13.
Structure
To create a list of the prime numbers that are less than 100, do the following.
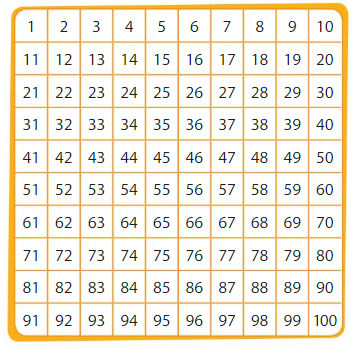
- Place a square around 1. It is neither prime nor composite.
- Circle 2 and cross out all other multiples of 2.
- Circle 3 and cross out all other multiples of 3.
- Circle 5 and cross out all other multiples of 5.
- Circle the next number that is not crossed out. This number is prime. Cross out all other multiples of this number.
- Continue until every number is either circled or crossed out.
What are the prime numbers that are less than 100? Explain why these numbers not were crossed out on the chart.
Answer:
The prime numbers below 100 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 73, 79, 83, 87, 89, 93, and 97
Think and Grow: Modeling Real Life
Example
A museum volunteer has 76 shark teeth to display. Can the volunteer arrange the teeth into a rectangular array with more than 1 row and more than 1 tooth in each row? Explain.

Use divisibility rules to determine whether 76 is prime or composite.
76 is even, so it is divisible by 2.
76 has factors in addition to 1 and itself.
So, 76 is the Composite number.
So,
The volunteer will arrange the teeth into a rectangular array with more than 1 row and more than 1 tooth in each row.
Show and Grow
Question 14.
A teacher has 29 students in class. Can the teacher separate the students into equal groups? Explain.
Answer: No, the teacher can’t separate the students into equal groups.
Explanation:
Given that a teacher has 29 students in the class
Now,
Let find whether 29 is Prime or Composite
Now,
Factors of 29 are: 1, 29
Hence, from the above factors,
We can conclude that 29 is a prime number
Hence,
The teacher can’t divide 29 students into equal groups.
Question 15.
A band instructor wants to have several ways to organize band members into rectangular arrays on the field for a performance.Should the instructor have 89 members or 99 members on the field? Explain.
Answer: The Instructor should have 99 members on the field so that he can arrange the band members into rectangular arrays.
Explanation:
Given that a band instructor wants to organize band members into rectangular arrays on the field for a performance.
It is also given that the instructor wants to arrange into an array of whether 89 members or 99 members
Now,
Factors of 89 are: 1, 89
Factors of 99 are: 1, 3, 9, 11, 33, 99
Hence, from the above,
Since the 99 members can be arranged into different arrays,
We can conclude that the instructor can arrange the participants into an array of 99 members.
Question 16.
DIG DEEPER!
A paramedic is arranging bandages into 4 bins. An equal number of bandages are in each bin. Did the paramedic arrange a prime number or a composite number of bandages? Explain.
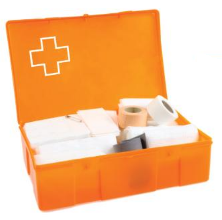
Answer: The paramedic has to arrange a composite number of bandages.
Explanation:
Gien that a paramedic is arranging bandages into 4 bins.
It is also given that there is an equal number of bandages in each bin.
Now,
Given there are 4 bins and 4 is a Composite number
So, 4 can divide only a Composite number but not a prime number.
Prime numbers:
The numbers which have exactly only 2 factors 1 and itself are “Prime numbers”
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Hence, from the above,
We can conclude that the paramedic has to arrange a Composite number of bandages.
Identify Prime and Composite Numbers Homework & Practice 6.4
Tell whether the number is prime or composite. Explain.
Question 1.
3
Answer: 3 is a prime number
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
Now,
The factors of 3 are: 1, 3
Hence, from the above,
We can conclude that 3 is a prime number
Question 2.
27
Answer: 27 is a composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Now,
The factors of 27 are: 1, 3, 9, 27
Hence, from the above,
We can conclude that 27 is a composite number
Question 3.
46
Answer: 46 is a composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Now,
The factors of 46 are: 1, 2, 23, 46
Hence, from the above,
We can conclude that 46 is a composite number
Question 4.
17
Answer: 17 is a prime number
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
Now,
The factors of 17 are: 1, 17
Hence, from the above,
We can conclude that 17 is a prime number
Question 5.
53
Answer: 53 is a prime number
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Composite numbers”
Now,
The factors of 53 are: 1, 53
Hence, from the above,
we can conclude that 53 is a prime number
Question 6.
63
Answer: 63 is a composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Now,
The factors of 63 are: 1, 3, 7, 9, 21, 63
Hence, from the above,
We can conclude that 63 is a composite number
Question 7.
29
Answer: 29 is a prime number
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
Now,
The factors of 29 are: 1, 29
Hence, from the above,
We can conclude that 29 is a prime number
Question 8.
31
Answer: 31 is a prime number
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
Now,
The factors of 31 are: 1, 31
Hence, from the above,
We can conclude that 31 is a prime number
Question 9.
75
Answer: 75 is a composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Now,
The factors of 75 are: 1, 3, 5, 15, 25, 75
Hence, from the above,
We can conclude that 75 is a composite number
Question 10.
DIG DEEPER!
Can a number be both prime and composite? Explain.
Answer: No, a number can’t be both prime and composite
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Hence, from the number of factors,
We can say a number can’t be both prime and composite at the same time
Question 11.
Logic
Your friend is thinking of a prime number between 60 and 80. The tens digit is one less than the ones digit. What is the number?
Answer: The number is 67
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
So,
The prime numbers between 60 and 80 are: 61, 67, 73, 79
It is also given that the tens digit is one less than the ones digit
So,
Tens position value – 1 = ones position value
Hence, from the above,
We can conclude that 67 is the number.
Number Sense
Write true or false for the statement. If false, provide an example to support your answer.
Question 12.
All odd numbers are prime. _______
Answer: False
Explanation:
Given that all odd numbers are prime.
Prime numbers:
The number of factors which have exactly 2 factors 1 and itself is “Prime numbers”
So, let take the off numbers from 1 to 10
The odd numbers from 1 to 10 are: 1, 3, 5, 7, 9
So, from 1 to 10,
The prime numbers are: 3, 5, 7
So, from the above
9 is an odd number but it is not prime.
Hence, from the above,
We can conclude that all odd numbers are not prime
Question 13.
All even numbers, except 2, are composite. _______
Answer: True
Explanation:
Given that all even numbers except 2 are composite numbers
Now,
The even numbers from 1 to 0 are: 2, 4, 6, 8
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
So,
The composite numbers from 1 to 10 are: 4, 6, 8
Note: 2 is an even prime number
Hence, from the above,
WE can conclude that all even numbers except are composite numbers
Question 14.
A composite number cannot have exactly three factors. _______
Answer: True
Explanation:
Given that a composite number has exactly 3 factors
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Let the number be 63
Now,
The factors of 63 are: 1, 3, 7, 9, 21, 63
Hence, from the above,
We can conclude that a composite number don’t have exactly 3 factors
Question 15.
Modeling Real Life
There are 43 students trying out for a basketball team. Can the coach separate the students into equal groups? Explain.

Answer: No, the coach can’t separate the students into equal groups
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
Now,
The factors of 43 are: 1, 43
Hence, from the above,
We can conclude that the coach can’t separate the students into equal groups since 43 is a prime number
Question 16.
Modeling Real Life
Which planet not does have a prime number of rings?

Answer: Saturn does not have a prime number of rings.
Explanation:
Given that,
1 full circle = 2 rings
So,
1 half circle = 1 ring

So, from the above table,
The number of rings of Jupiter is: 3
The number of rings of Saturn is: 9
The number of rings of Uranus is: 13
The number of rings of Neptune is: 5
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
Hence, from the above,
We can conclude that Saturn does not have a prime number of rings ( Because 9 is a composite number )
Review & Refresh
Use properties to find the product. Explain your reasoning
Question 17.
4 × 9 × 25
Answer: 4 × 9 × 25 = 900
Explanation:
Using the Distributive Property of multiplication,
4 × 9 × 25 = 4 × 9 × ( 20 + 5 )
= 36 × ( 20 + 5 )
= ( 36 × 20 ) + ( 36 × 5 )
= 720 + 180
= 900
Hence, 4 × 9 × 25 = 900
Question 18.
405 × 3
Answer: 403 × 3 = 1,215
Explanation:
Using the Distributive Property of Multiplication,
405 × 3 = ( 400 + 5 ) × 3
= ( 400 × 3 ) + ( 5 × 3 )
= 1,200 + 15
= 1,215
Hence, 405 × 3 = 1,215
Question 19.
698 × 7
Answer: 698 × 7 = 4,886
Explanation:
Using the Distributive Property of Multiplication,
698 × 7 = ( 600 + 90 + 8 ) × 7
= ( 600 × 7 ) + ( 90 × 7 ) + ( 8 × 7 )
= 4,200 + 630 + 56
= 4,886
Hence, 698 × 7 = 4,886
Lesson 6.5 Number Patterns
Explore and Grow
Shade every third square in the table.
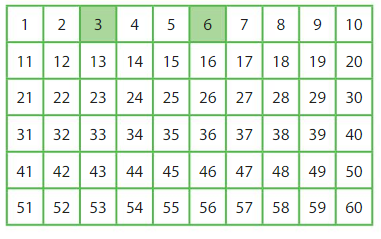
Write the shaded numbers. What patterns do you see?
What other patterns do you see in the table?
Answer:
The shaded numbers are:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60
From the shaded numbers, we can see that each third square is a multiple of 3
The other patterns we can observe in the given table is:
a) If we first shaded the second square and then shaded each second square, then we get the multiples of 2
b) The same pattern will have to be applied for the fourth square
There will also be other patterns by shading 5th square, 6th square, etc.
Structure
Circle every fourth square in the table. Write the circled numbers. What patterns do you see?
Answer:
The circled numbers are:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60
From the circled numbers of every fourth square, we can see that every fourth square is a multiple of 4.
Think and Grow: Create Number Patterns
A rule tells how numbers or shapes in a pattern are related.
Example
Use the rule “Add 3.” to create a number pattern. The first number in the pattern is 3. Then describe another feature of the pattern.
Create a pattern.
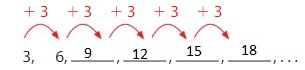
So,
The numbers in the pattern are multiples of 3.

Example
Use the rule “Multiply by 2.” to create a number pattern. The first number in the pattern is 10. Then describe another feature of the pattern.
Create a pattern.
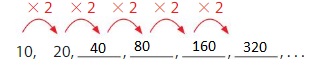
So,
The one’s digit of each number in the pattern is 0.
Show and Grow
Write the first six numbers in the pattern. Then describe another feature of the pattern.
Question 1.
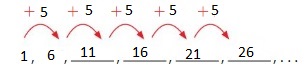
Rule: Add 5.
First number: 1
1, ____, _____, _____, _____, _____
Answer: The first 6 numbers are: 1, 6, 11, 16, 21 and 26
Explanation:
For the formation of the pattern,
The given rules are:
Rule 1 : Add 5
Rule 2: Add 5
Hence,
The given pattern is
Question 2.
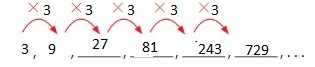
Rule: Multiply by 3.
First number: 3
3, _____, _____, ____, _____, _____
Answer: The first 6 numbers are: 3, 9, 27, 81, 243, 729
Explanation:
For the formation of the pattern,
the given rules are:
Rule 1: Multiply by 3
Rule 2: First number: 3
Hence,
The given pattern is
Question 3.
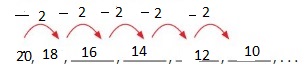
Rule: Subtract 2.
First number: 20
Answer: The first 6 numbers are: 20, 18, 16, 14, 12, 10
Explanation:
For the formation of the pattern,
the given rules are:
Rule 1: Subtract 20
Rule 2: First number: 20
Hence,
The given pattern is:
Question 4.
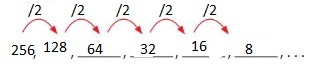
Rule: Divide by 2.
First number: 256
Answer: The first 6 numbers are: 256, 128, 64, 32, 16, 8
Explanation:
For the formation of the pattern,
the given rules are:
Rule 1: Divide by 2
Rule 2: First number: 256
Hence,
The given pattern is:
Apply and Grow: Practice
Write the first six numbers in the pattern. Then describe another feature of the pattern.
Question 5.
Rule: Add 11.
First number: 11
Answer: The first 6 numbers are: 11, 22, 33, 44, 55, 66
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Add 11
First number: 11
Hence,
The given pattern is:

Question 6.
Rule: Multiply by 4.
First number: 4
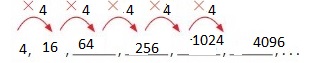
Answer: The first 6 numbers are: 4, 16, 64, 256, 1024, 4096
Explanation:
For the formation of the pattern,
the given rules are:
Rule 1: Multiply by 4
First number: 4
Hence,
The given pattern is
Question 7.
Rule: Subtract 3.
First number: 21
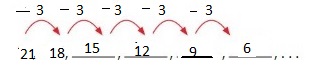
Answer: The first 6 numbers are: 21, 18, 15, 12, 9, 6
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Subtract 3
First number: 21
Hence,
The given pattern is:
Question 8.
Rule: Divide by 3.
First number: 729
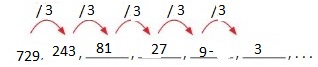
Answer: The first 6 numbers are: 729, 243, 81, 27, 9, 3
Explanation:
For the formation of the pattern,
the given rules are:
Rule 1: Divide by 3
First number: 729
Hence,
The given pattern is
Question 9.
Rule: Add 9.
First number: 8
Answer: The first numbers are: 8, 17, 26, 35, 44, 53
Explanation:
For the formation of the pattern,
the given rules are:
Rule 1: Add 9
First number: 8
Hence,
The given pattern is:

Question 10.
Rule: Multiply by 5.
First number: 5
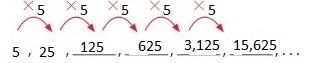
Answer: The first 6 numbers are: 5, 25, 125, 625, 3125, 15,625
Explanation:
For the formation of the pattern,
the given rules are:
Rule 1: Multiply by 5
First number: 5
Hence,
The given pattern is:
Open-Ended
Use the rule to generate a pattern of four numbers.
Question 11.
Rule: Multiply by 2.
Answer:
Let the first number be 2.
Hence,
The pattern of four numbers is: 2, 4, 8, 16
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Multiply by 2
Let the first number be: 2
Hence,
The obtained pattern will be:
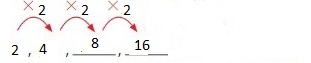
Question 12.
Rule: Subtract 9.
Answer:
Let the first number be 36
Hence,
The pattern of four numbers is: 36, 27, 18, 9
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Subtract 9
Let the first number be 36
Hence,
The obtained pattern will be:
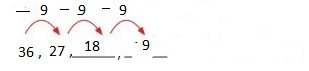
Question 13.
Rule: Divide by 4.
Answer:
Let the first number be 16
Hence,
The pattern of 4 numbers are: 16, 12, 8, 4
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Divide by 4
Let the first number be 16
Hence,
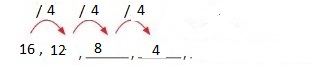
The obtained pattern will be:
Question 14.
Rule: Add 7.
Answer:
Let the first number be 7
Hence,
The pattern of the four numbers are: 7, 14, 21, 28
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Add 7
Let the first number be 7
Hence,
The obtained pattern will be:

Question 15.
Patterns
Write a rule for the pattern below. Then write a different pattern that follows the same rule.
3, 6, 12, 24, 48
Answer: The rule for the given pattern is: Multiply by 2
Explanation:
Given numbers are: 3, 6, 12, 24, 48
So, from the given numbers,
We can say that the given pattern follows the “Multiply by 2” rule
Question 16.
Reasoning
What is the missing number in the pattern? Explain.
39, 37, 35, _____, 31, 29
Answer: The missing number in the pattern is: 33
Explanation:
The given numbers are: 39, 37, 35, 31, 29
From the given pattern,
the numbers that are following the rule is “Subtract by 2”
Hence, from the above,
The missing number will be: 35 – 2 = 33
Think and Grow: Modeling Real Life
Example
A presidential election is held every 4 years. There was a presidential election in 2016. How many presidential elections will occur between 2017 and 2030?

The rule is to add 4 years to each presidential election year. Start with 2016. Then count the years in the pattern that is between 2017 and 2030.
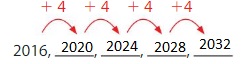
So,
3 presidential elections will occur between 2017 and 2030.
Show and Grow
Question 17.
The pattern of animals on a Chinese calendar repeats every 12 years. The year 2000 was the year of the dragon. How many times will the year of the dragon occur between 2001 and 2100?

Answer: The number of times the dragon will appear between 2001 and 2100 is: 8
Explanation:
Given that the pattern of animals on a Chinese calendar repeats every 12 years
It is also given that the year 2000 was the year of the dragon
Now, between the year 2001 and 2100, there are 99 years
So,
The number of times the dragon will appear = The difference between the years 2001 and 2100 ÷ The number of years the pattern will change
= 99 ÷ 12
Now,
99 ÷ 12 = 8 R 3
Hence, from the above,
We can conclude that the dragon will appear 8 times between the years 2001 and 2021
Question 18.
A robotics team raised $25 the first month of school. Each month of school, the team wants to raise 2 times as much money as the month before. How much money should they raise in the fifth month of school?
Answer: The money should they raise in the fifth month of school is: $400
Explanation:
Given that a robotics team raised $25 for the first month of the school and each month of the school, the team wants to raise 2 times as much money as the month before.
Hence,
The rule followed here is: Multiply by 2
The given first number is: $25
Hence,
The pattern we will obtain is:

Hence, from the above,
We can conclude that the money they should raise in the fifth month is: $400
Question 19.
DIG DEEPER!
You start with 128 pictures on your tablet. You take 6 pictures and delete 3 pictures each day. How many pictures do you have on your tablet after 6 days?
Answer: The pictures you have on your tablet after 6 days is: 110 pictures
Explanation:
Given that you have 128 pictures on your tablet and you take 6 pictures and delete 3 pictures each day.
So,
The number of pictures you have each day = 6 – 3 = 3 pictures
So,
The total number of pictures in 6 days = 6 × 3 = 18 pictures
So,
The total number of pictures you have in 6 days = Total number of pictures – Total number f pictures in 6 days
= 128 – 18
= 110 pictures
Hence, from the above,
We can conclude that there are 110 pictures you have in 6 days.
Number Patterns Numbers Homework & Practice 6.5
Write the first six numbers in the pattern. Then describe another feature of the pattern.
Question 1.
Rule: Subtract 8.
First number: 88
88, ____, ____, ____, _____, _____
Answer:
The first 6 numbers in the given pattern are: 88, 80, 72, 64, 56, 48
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Subtract 8
First number: 88
Hence,
The pattern we will obtain is:
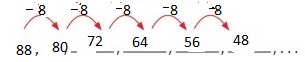
Question 2.
Rule: Multiply by 10.
First number: 2
2, _____, _____, _____, ____, ____
Answer:
The first 6 numbers of the given pattern are: 2, 20, 200, 2,000, 20,000, 200,000
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Multiply by 10
First number: 2
Hence,
The pattern we will obtain is:
Question 3.
Rule: Add 9.
First number: 17
Answer:
The first 6 numbers for the given pattern is: 17, 26, 35, 44, 53, 62
Explanation:
For the formation,
the given rules are:
Rule: Add 9
First number: 17
Hence,
The pattern we will obtain is:
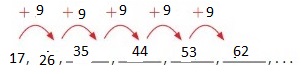
Question 4.
Rule: Divide by 2.
First number: 1,600
Answer:
The first 6 numbers of the given pattern are: 1,600, 800, 400, 200, 100, 50
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Divide by 2
First number: 1,600
Hence,
The pattern we will obtain is:
Open-Ended Use the rule to generate a pattern of four numbers.
Question 5.
Rule: Divide by 5.
Answer:
Let the first number be: 625
Hence,
The four numbers of the given pattern will be: 625, 125, 25, 5
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Divide by 5
Let the first number be: 625
Hence,
The pattern we will obtain is:
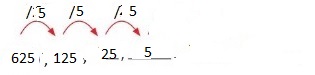
Question 6.
Rule: Add 8.
Answer:
Let the first number be 8
Hence,
The four numbers of the given pattern are: 8, 16, 24, 32
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Add 8
Let the first number be 8
Hence,
The pattern we will obtain will be:
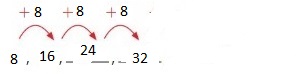
Question 7.
Rule: Multiply by 9.
Answer:
Let the first number be 9
Hence,
The four numbers of the pattern will be: 9, 81, 729, 6551
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Multiply 9
Let the first number be 9
Hence,
The pattern we obtain will be:

Question 8.
Rule: Subtract 3.
Answer:
Let the first number be 27
Hence,
The four numbers of the given pattern will be: 27, 24, 21, 18
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Subtract 3
Let the first number be 27
Hence,
The pattern we obtain will be:
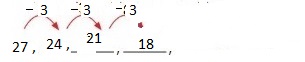
Question 9.
Structure
List the first ten multiples of 9. What patterns do you notice with the digits in the one’s place? in the tens place?
Does this pattern continue beyond the tenth number in the pattern?
Answer: The first 10 multiples of 9 are: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
Explanation:
The first 10 multiples of 9 are: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
So,
from the above 10 multiples of 9,
The pattern we can observe in the one’s place is: Decreasing of numbers from 9 to 0 i.e., 9, 8, 7, ………..0
The pattern we can observe in the ten’s place is: Increasing of numbers from 0 to 9 i.e., 0, 1, 2 …………..9
The above 2 patterns will continue beyond the first 10 multiples of 9
Hence, from the above,
We can conclude that the patterns we observed are:
The pattern we can observe in the one’s place is: Decreasing of numbers from 9 to 0 i.e., 9, 8, 7, ………..0
The pattern we can observe in the ten’s place is: Increasing of numbers from 0 to 9 i.e., 0, 1, 2 …………..9
Question 10.
Modeling Real Life
It takes the moon about 28 days to orbit Earth. How many times will the moon orbit Earth in 1 year?

Answer: The moon will orbit the earth 10,220 times in 1 year
Explanation:
Given that it takes the moon about 28 days to orbit the earth.
We know that,
1 year = 365 days
So,
The number of times the moon will orbit around the earth in 1 year = 365 × 28
Now,
By using the partial products method,
365 × 28 = ( 300 + 65 ) × ( 20 + 8 )
= ( 300 × 20 ) + ( 300 × 8 ) + ( 65 × 20 ) + ( 65 × 8 )
= 6,000 + 2,400 + 1,300 + 520
= 10,220 times
Hence, from the above,
We can conclude that the moon will orbit around the Earth 10,220 times
Question 11.
DIG DEEPER!
In each level of a video game, you can earn up to 10 points and lose up to 3 points. Your friend earns 9 points in the first level. If he earns and loses the maximum number of points at each level, how many total points will he have after level 6?
Answer: The total points your friend will have is: 44 points
Explanation:
Given that in each level of a video game, you can earn up to 10 points and lose up to 3 points
So,
The maximum number of points you can get = 10 – 3 = 7 points
It is also given that your friend earns 9 points in the first level
So,
The number of points he will have at level 6 = The number of points he has at the first level + 5 × ( The maximum number of points he can get )
= 9 + ( 5 × 7 )
= 9 + 35
= 44 points
Hence, from the above,
We can conclude that he will have 44 points at the sixth level.
Review & Refresh
Find the product.
Question 12.
14 × 23 = _____
Answer: 14 × 23 = 322
Explanation:
By using the partial products method,
14 × 23 = ( 10 + 4 ) × ( 20 + 3 )
= ( 10 × 20 ) + ( 10 × 3 ) + ( 4 × 20 ) + ( 4 × 3 )
= 200 + 30 + 80 + 12
= 322
Hnece, 14 × 23 = 322
Question 13.
48 × 60 = _____
Answer: 48 × 60 = 2,880
Explanation:
By using the Distributive Property of Multiplication,
48 × 60 = ( 40 + 8 ) × 60
= ( 40 × 60 ) + ( 8 × 60 )
= 2,400 + 480
= 2,880
Hence, 48 × 60 = 2,880
Question 14.
55 × 31 = _____
Answer: 55 × 31 = 1,705
Explanation:
By using the partial products method,
55 × 31 = ( 50 + 5 ) × ( 30 + 1 )
= ( 50 × 30 ) + ( 50 × 1 ) + ( 5 × 30 ) + ( 5 × 1 )
= 1,500 + 50 + 150 + 5
= 1,705
Hence, 55 × 31 = 1,705
Lesson 6.6 Shape Patterns
Explore and Grow
Create a rule using 3 different shapes. Draw the first six shapes in the pattern.
What is the next shape in the pattern?
What is the 9th shape in the pattern? Explain.
What is the 99th shape? 1,000th shape? Explain?
Answer: 
From the above 3 shapes,
The rule we can create is: Add 1
So,
We can say the above pattern will repeat after every 3 shapes.
So,
The 9th shape will be: Pentagon
The 99th shape will be: 99 / 3 = 33 R 0
So, The 99th shape will be: Pentagon
The 100th shape will be: Triangle (Because the remainder will be 1 i.e., the shapes will completely repeat 99 times and for the 100th time, it will start from 1st shape)
Structure
You want to show the first 40 shapes in the pattern above. Without modeling, how many of each shape do you think you will need?
Answer:
The number of times each shape will appear in the first 40 shapes is:
Triangle: 14 times
Square: 13 times
Pentagon: 13 times
Explanation:
In the above pattern, the shapes are: Triangle, Square, Pentagon
The rule we obtained by using these 3 shapes is: Add 1
So,
The pattern for the first 40 shapes will be: 40 ÷ 3
Now,
By using the Distributive Property of Division,
40 ÷ 3 = ( 36 + 3 ) ÷ 3
= ( 36 ÷ 3 ) + ( 3 ÷ 3 )
= 12 + 1
= 13 R 1
Hence, the 3 shapes will appear 39 times
So,
The number of times each shape will appear = 13 times
Hence, from the above,
We can conclude that the number of times the shape will appear is:
Triangle: 14 times ( 13 + 1. This 1 is because 40th time, the triangle will repeat again )
Square: 13 times
Pentagon: 13 times
Think and Grow: Create Shape Patterns
Example
Create a shape pattern by repeating the rule “triangle, hexagon, square, rhombus.”What is the 42nd shape in the pattern?
Create a pattern.

42 ÷ 4 is 10 R2, so when the pattern repeats 10 times, the 40th shape is a rhombus So, the 41st shape is a Triangle and the 42nd shape is a hexagon.


Figure 1 has 1 column of 4 dots, so it has 1 × 4 = 4 dots.
Figure 2 has 2 columns of 4 dots, so it has 2 × 4 = 8 dots.
Figure 3 has 3 columns of 4 dots, so it has 3 × 4 = 12 dots.
So,
The 25th figure has 1 column of 4 dots, ( Because the 3 figures will be repeated 24 times and the first figure will appear again 25th time)
So, it has 1 × 4 =4 dots.
Show and Grow
Question 1.
Extend the pattern of shapes by repeating the rule “square, trapezoid, triangle, hexagon, triangle.”What is the 108th shape in the pattern?

Answer: The 108th shape in the pattern will be: Triangle
Explanation:
The given pattern is: Square, trapezoid, triangle, hexagon, triangle
So, there is a total of 5 shapes.
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
108 ÷ 5 = ( 100 + 5 ) ÷ 5
= ( 100 ÷ 5 ) + ( 5 ÷ 5 )
= 20 + 1
= 21 R 3
Hence, from the above,
We can conclude that the 108th shape will be the triangle.
Question 2.
Describe the dot pattern. How many dots are in the 76th figure?
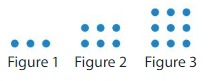
Answer: The number of dots in the 76th figure is: 3 dots
Explanation:

From the above pattern,
In figure 1, the number of dots = 1 × 3 = 3 dots
In figure 2, the number of dots = 2 × 3 = dots
In figure 3, the number of dots = 3 × 3 = 9 dots
So,
The total number of patterns is: 3
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
76 ÷ 3 = ( 66 +9 ) ÷ 3
= ( 66 ÷ 3 ) + ( 9 ÷ 3 )
= 22 + 3
= 25 R 1
Hence, from the above,
We can conclude that there are 3 dots in the 76th figure.
Apply and Grow: Practice
Question 3.
Extend the pattern of shapes by repeating the rule “oval, triangle.”What is the 55th shape?

Answer: The 55th shape is: Oval
Explanation:
The given pattern of shapes is: Oval, Triangle
So,
The total number of patterns is: 2
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
55 ÷ 2 = ( 50 + 4 ) ÷ 2
= ( 50 ÷ 2 ) + ( 4 ÷ 2 )
= 25 + 2
= 27 R 1
Hence, from the above,
We can conclude that the 55th shape is: Oval
Question 4.
Extend the pattern of symbols by repeating the rule “add, subtract, multiply, divide.”What is the 103rd symbol?

Answer: The 103rd symbol is: Multiply
Explanation:
The given patterns are: Add, Subtract, Multiply, Divide
So,
The total number of patterns is: 4
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
103 ÷ 4 = ( 80 + 20 ) ÷ 4
= ( 80 ÷ 4 ) + ( 20 ÷ 4 )
= 20 + 5
= 25 R 3
Hence, from the above,
We can conclude that the 103rd shape is: Multiply
Question 5.
Describe the pattern. How many squares are in the 24th figure?
Answer: The number of squares in the 24th figure is: 4 squares
Explanation:

In figure 1, the number of squares is: 2
In figure 2, the number of squares is: 3
In figure 3, the number of squares is: 4
So,
Total number of figures = 3
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
24 ÷ 3 = ( 21 + 3 ) ÷ 3
= ( 21 ÷ 3 ) + ( 3 ÷ 3 )
= 7 + 1
= 8 R 0
Hence, from the above,
We can conclude that in the 24th figure, the number of squares is: 4
Question 6.
Describe the pattern of the small triangles. How many small triangles are in the 10th figure?
Answer: The small triangles in the 10th figure is: 1
Explanation:

From the given figure,
In fig 1, the number of triangles is: 1
In fig 2, the number of triangles is: 2
In fig 3, the number of triangles is: 4
So,
Total number of figures = 3
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
10 ÷ 3 = ( 3 + 6 ) ÷ 9
= ( 3 ÷ 3 ) + ( 6 ÷ 3 )
= 1 + 2
= 3 R 1
Hence, from the above,
We can conclude that the 10th figure has 1 triangle
Question 7.
Structure
Make a shape pattern that uses twice as many squares as triangles.
Answer:
Question 8.
Number Sense
Which shape patterns have a heart as the 12th shape?

Answer:
Let the patterns be named as A), B), C) and D)
So,
The shape patterns that have a heart as the 12th shape is: A), B) and D)
Explanation:

Let the patterns be named as A), B), C) and D)
A) In pattern A,
The total number of figures = 2
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
12 ÷ 2 = 6
Hence, A) will have a heart as the 12th shape
B) In pattern B,
The total number of figures = 4
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
12 ÷ 4 = 3
Hence, B) will have a heart as the 12th shape
C) In pattern C,
The total number of figures = 2
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
12 ÷ 2 = 6
But, the 12th shape in C) will be a circle
D) In pattern D,
The total number of figures = 3
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
12 ÷ 3 = 4
Hence, C) will have a heart as the 12th shape
Think and Grow: Modeling Real Life
Example
You make a necklace with a cube, hexagon, and star beads. You string the beads in a pattern. You use the rule “cube, star, cube, hexagon.”It takes 64 beads to complete the necklace. How many times do you repeat the pattern?

Divide the number of beads it takes to complete the necklace by the number of beads in the rule. There are 4 beads in the rule.
So,
4√64 = 64 ÷ 4
By using the Distributive Property of division,
64 ÷ 4 = ( 60 + 4 ) ÷ 4
= ( 60 ÷ 4 ) + ( 4 ÷ 4 )
= 15 + 1
= 16
Hence,
You repeat the pattern 16 times
Show and Grow
Question 9.
The path on a board game uses the rule “red, green, pink, yellow, blue.”There are 55 spaces on the game board. How many times does the pattern repeat?

Answer: The number of times the pattern will repeat is: 11 times
Explanation:
Given that the path on a board game uses the rule ” red, green, pink, yellow, blue ”
It is also given that there are 55 spaces on the game board
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the Distributive Property of division,
55 ÷ 5 = ( 50 + 5 ) ÷ 5
= ( 50 ÷ 5 ) + ( 5 ÷ 5 )
= 10 + 1
= 11
Hence, from the above,
We can conclude that the number of times the patterns repeat is: 11 times
Question 10.
You make a walkway in a garden using different-shaped stepping stones. You use the rule “square, circle, square, hexagon.”You use 24 square stepping stones. How many circle and hexagon stepping stones do you use altogether? How many stones do you use in all?
Answer:
The Total number of stones used are: 24
The number of circle and hexagon stepping stones use are: 12
Explanation:
Given that there is a walkway in a garden using different-shaped stepping stones.
The rule used here is: Square, circle, square, hexagon
It is also given that there are 24 stepping stones you used
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the Distributive Property of division,
24 ÷ 4 = ( 20 + 4 ) ÷ 4
= ( 20 ÷ 4 ) + ( 4 ÷ 4 )
= 5 + 1
= 6
So,
The number of stones used each time is: 6 times
So,
The number of circle and hexagon stepping stones used altogether is: 6 + 6 = 12
Hence, from the above,
We can conclude that circle and hexagon stepping stones you used altogether is: 12
Question 11.
DIG DEEPER!
You make a rectangular picture frame using square tiles. The picture frame is 12 tiles long and 8 tiles wide. You arrange the tiles in a pattern. You use the rule “red, orange, yellow.” How many of each color tile do you use?
Answer: The number of each color tiles do you use is: 32
Explanation:
Given that you make a rectangular picture frame using square tiles and it is also given that the picture frame is 12 tiles long and 8 tiles wide.
So,
The area of a rectangular picture frame = 12 × 8 = 96 square- meters
The rule used is: red, orange, yellow
So,
The total number of colors is: 3
So,
The number of each color tile you used = Area of rectangular picture frame ÷ Total number of colors
= 96 ÷ 3
Now,
By using the Distributive Property of division,
96 ÷ 3 = ( 90 + 6 ) ÷ 3
= ( 90 ÷ 3 ) + ( 6 ÷ 3 )
= 30 + 2
= 32
Hence, from the above,
we can conclude that each number of color tile used is: 32
Shape Patterns Numbers Homework & Practice 6.6
Question 1.
Extend the pattern of shapes by repeating the rule “up, right, down, left.”What is the 48th shape in the pattern?

Answer: The 48th shape in the pattern is: Left
Explanation:
Given pattern is:

The rule for the given pattern is: up, right, down, left
So,
The total number of patterns is: 4
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
48 ÷ 4 = ( 40 + 8 ) ÷ 4
= ( 40 ÷ 4 ) + ( 8 ÷ 4 )
= 10 + 2
= 12 R 0
Hence, from the above
We can conclude that the 48th figure in the given pattern is: Left
Question 2.
Extend the pattern of shapes by repeating the rule “small circle, medium circle, large circle.”What is the 86th shape in the pattern?

Answer: The 86th shape in the pattern is: Medium circle
Explanation:
Given pattern is:

The rule for the pattern is: Small circle, Medium circle, large circle
So,
The total number of patterns = 3
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
86 ÷ 3 = ( 75 + 9 ) ÷ 3
= ( 75 ÷ 3 ) + ( 9 ÷ 3 )
= 25 + 3
= 28 R 2
Hence, from the above,
We can conclude that the 86th shape in the pattern is: Medium circle
Question 3.
Describe the dot pattern. How many dots are in the 113th figure?
Answer: The number of dots in the 113th figure is: 4 dots
Explanation:
Given pattern is:

So,
In fig 1, the number of dots = 2
In fig 2, the number of dots = 4
In fig 3, the number of dots = 6
So,
The total number of figures = 3
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
113 ÷ 3 = ( 99 + 12 ) ÷ 3
= ( 99 ÷ 3 ) + ( 12 ÷ 3 )
= 33 + 4
= 37 R 2
Hence, from the above,
we can conclude that the number of dots in the 113th figure is: 4 dots
Question 4.
YOU BE THE TEACHER
You and your friend each create a shape pattern with 100 shapes. Your friend says both patterns will have the same number of circles. Is your friend correct? Explain.

Answer: Yes, both patterns will have the same number of circles.
Explanation:
Given patterns are:

The pattern of the friend is: Star, circle
The pattern of you si: Heart, circle, pentagon, circle
It is also given that,
The total number of figures = 100
So,
The total number of figures for your friend = 2
The total number of figures for you = 4
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So
For your friend,
By using the partial quotients method,
100 ÷ 2 = ( 50 + 50 ) ÷ 2
= ( 50 ÷ 2 ) + ( 50 ÷ 2 )
= 25 + 25
= 50
Hence,
The number of circles = 50
The number of stars = 50
For you,
By using the partial quotients method,
100 ÷ 4 = ( 80 + 20 ) ÷ 4
= ( 80 ÷ 4 ) + ( 20 ÷ 4 )
= 20 + 5
= 25
Hence,
The number of circles altogether = 25 + 25 = 50
Hence, from the above,
We can conclude that there are equal number of circles in both the patterns
Question 5.
Structure
Draw the missing figure in the pattern. Explain the pattern.
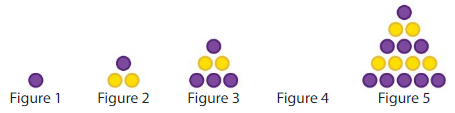
Answer:
Question 6.
Reasoning
Newton uses the rule “bone, bone, paw print” to make a shape pattern. He wants the pattern to repeat 8 times. How many bones will be in Newton’s pattern?

Answer: The number of bones in Newton’s pattern is: 16
Explanation:
Given pattern is:

The rule followed in the pattern is: Bone, Bone, pawprint
So,
The total number of figures in the given pattern = 3
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
It is also given that the pattern repeated 8 times.
So,
The total number of figures when the pattern repeated 8 times = 8 × 3 = 24 figures
So,
By using the partial quotients method,
24 ÷ 3 = ( 21 + 3 ) ÷ 3
= ( 21 ÷ 3 ) + ( 3 ÷ 3 )
= 7 + 1
= 8
So,
The number of each figure in a pattern = 8
From the pattern, we can say there are 2 bones
So,
The total number of bones when the pattern repeated 8 times = 2 × 8 = 16
Hence, from the above,
We can conclude that there are 16 bones in the pattern when the pattern repeated 8 times
Question 7.
Modeling Real Life
The black keys on a piano follow the pattern “two black keys, three black keys.” There are 36 black keys on a standard piano. How many times does this entire pattern repeat?
Answer: The entire pattern repeat 12 times
Explanation:
Given that the black keys on a pattern follow the pattern
The given pattern is: two black keys, three black keys
So,
The total number of patterns = 2
It is also given that there are 36 black keys on a standard piano.
So,
The total number of black keys on a piano = 36
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
36 ÷ 2 = ( 30 + 6 ) ÷ 2
= ( 30 ÷ 2 ) + ( 6 ÷ 2 )
= 15 + 3
= 18
Hence, from the above,
We can conclude that the entire pattern will repeat 18 times.
Review & Refresh
Find the quotient.
Question 8.
30 ÷ 5 = _____
Answer: 30 ÷ 5 = 6
Explanation:
By using the partial products method,
30 ÷ 5 = ( 25 + 5 ) ÷ 5
= ( 25 ÷ 5 ) + ( 5 ÷ 5 )
= 5 + 1
= 6
Hence, 30 ÷ 5 = 6
Question 9.
360 ÷ 9 = ______
Answer: 360 ÷ 9 = 40
Explanation:
By using the partial quotients method,
360 ÷ 9 = ( 270 + 90 ) ÷ 9
= ( 270 ÷ 9 ) + ( 90 ÷ 9 )
= 30 + 10
= 40
Hence, 360 ÷ 9 = 40
Question 10.
6,400 ÷ 8 = _____
Answer: 6,400 ÷ 8 = 800
Explanation:
By using the place -value method,
6,400 ÷ 8 = 64 hundreds ÷ 8
= 8 hundred
= 8 × 100
= 800
Hence, 6,400 ÷ 8 = 800
Question 11.
140 ÷ 2 = _____
Answer: 140 ÷ 2 = 70
Explanation:
By using the place-value method,
140 ÷ 2 = 14 tens ÷ 2
= 7 tens
= 7 × 10
= 70
Hence, 140 ÷ 2 = 70
Question 12.
4,200 ÷ 7 = _____
Answer: 4,200 ÷ 7 = 600
Explanation:
By using the place-value method,
4,200 ÷ 7 = 42 hundreds ÷ 7
= 6 hundred
= 6 × 100
= 600
Hence, 4,200 ÷ 7 = 600
Question 13.
40 ÷ 2 = _____
Answer: 40 ÷ 2 = 20
Explanation:
By using the place-value method,
40 ÷ 2 = 4 tens ÷ 2
= 2 tens
= 2 × 10
= 20
Hence, 40 ÷ 2 = 20
Factors, Multiples, and Patterns Performance Task
You play basketball in a youth basketball program.

Question 1.
There are 72 players in the program. Each team needs an equal number of players and must have at least 5 players. What are two different ways the teams can be made?
Answer: The different ways the teams can be made and to have at least 5 members are: 8 × 9 and 9 × 8
Explanation:
Given that there are 72 players in the program and each team needs an equal number of players.
It is also given that each team must have at least 5 players.
Now,
To find the different ways the teams can be made, we have to find the factors of 72
Now,
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Now, to make an equal number of players and to have at least 5 players,
The different ways the teams can be made is: 8 × 9, 9 × 8
Hence, from the above,
We can conclude that the 2 different ways the teams can be made are: 8 × 9 and 9 × 8
Question 2.
The width of a basketball court is 42 feet and the length is 74 feet. You run around the perimeter of the court 4 times to warm up. How many feet do you run?
Answer: The number of feet you run is: 464 feet
Explanation:
Given that the width of a basketball court is 42 feet high and the length is 74 feet
So,
The perimeter of the basketball court = 42 + 74 = 116 feet
It is also given that you run around the perimeter of the basketball court 4 times to warm up.
So,
The number of feet you run to warm up = The perimeter of the basketball court × 4
= 116 × 4
Now,
By using the partial products method,
116 × 4 = ( 100 + 16 ) × 4
= ( 100 × 4 ) + ( 16 × 4 )
= 400 + 64
= 464 feet
Hence, from the above,
We can conclude that you will run up 464 feet to warm up your body.
Question 3.
You and your friend are on the same team. You played your first game last week.
a. Your team scored 4 more points than the other team. The total number of points scored by both teams was 58. How many points did your team score?
b. You and your friend scored the same number of points. You made 2-point shots and your friend made 3-point shots. What could be the greatest number of points you and your friend each scored?
Answer:
Question 4.
Your team uses the pattern below to decide which jersey color to wear to each game. Which color jersey will your team wear on the 20th game?

Answer: The color of jersey your team will wear on the 20th game is: Game 4
Explanation:
Given that your team uses the following pattern:

From the above pattern,
The total number of shirts is: 4
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
20 ÷ 4 = 5 R 0
Hence, from the above,
We can conclude that the color of the shirt your team will wear on the 20th game is: Game 4
Factors, Multiples, and Patterns Activity
Multiple Lineup
Directions:
1. Players take turns rolling a die.
2. On your turn, place a counter on a multiple of the number of your roll. If there is not a multiple of the number of your roll, you lose your turn.
3. The first player to create a line of 5 in a row, horizontally, vertically, or diagonally, wins!
Answer:
Factors, Multiples, and Patterns Chapter Practice
6.1 Understand Factors
Question 1.
Use the rectangles to find the factor pairs for 6.

Answer: The factor pairs of 6 are: 1 and 6, 2 and 3
Explanation:
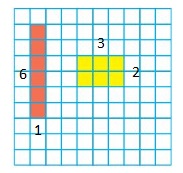
The factor pairs are nothing but the side lengths of a rectangle and the area of a rectangle gives the factor
Hence,
The factor pairs of 6 are: 1 and 6, 2 and 3
Question 2.
Draw rectangles to find the factor pairs for 12.
Answer: The factor pairs of 12 are: 1 and 12, 2 and 6, 3 and 4
Explanation:
![]()
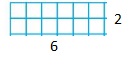

The factor pairs are nothing but the side lengths of a rectangle and the area of a rectangle gives the factor
Hence,
The factor pairs of 12 are: 1 and 12, 2 and 6, 3 and 4
Find the factor pairs for the number.
Question 3.
17
Answer: The factor pairs of 17 are: 1 and 17
Explanation:
Factors are the numbers that divide the original completely.
Hence,
The factor pairs of 17 are: 1 × 17
Question 4.
10
Answer: The factor pairs of 10 are: 1 and 10, 2 and 5
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 10 are: 1 × 10, 2 × 5
Question 5.
21
Answer: The factor pairs of 21 are: 1 and 21, 3 and 7
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 21 are: 1 × 21, 3 × 7
Question 6.
20
Answer: The factor pairs of 20 are: 1 and 20, 2 and 10, 4 and 5
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 20 are: 1 × 20, 2 × 10, 5 × 4
Question 7.
36
Answer: The factor pairs of 36 are: 1 and 36, 2 and 18, 3 and 12, 4 and 9, 6 and 6
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 36 are: 1 × 36, 2 × 18, 3 × 12, 4 × 9, 6 × 6
Question 8.
50
Answer: The factor pairs of 50 are: 1 and 50, 2 and 25, 5 and 10
Explanation:
factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 50 are: 1 × 50, 2 × 25, 5 × 10
6.2 Factors and Divisibility
Find the factor pairs for the number.
Question 9.
16
Answer: The factor pairs of 16 are: 1 and 16, 2 and 8, 4 and 4
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 16 are: 1 × 16, 2 × 8, 4 × 4
Question 10.
24
Answer: The factor pairs of 24 are: 1 and 24, 2 and 12, 3 and 8, 4 and 6
Explanation:
factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 24 are: 1 × 24, 2 × 12, 3 × 8, 4 × 6
Question 11.
56
Answer: The factor pairs of 56 are: 1 and 56, 2 and 28, 4 and 14, 7 and 8
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factor pairs of 56 are: 1 × 56, 2 × 28, 4 × 14, 7 × 8
List the factors of the number.
Question 12.
25
Answer: The factors of 25 are: 1, 5, 25
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factors of 25 are: 1, 5, 25
Question 13.
60
Answer: The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Question 14.
72
Answer: The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Explanation:
Factors are the numbers that divide the original number completely.
Hence,
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Question 15.
Number Sense
Which numbers have 3 as a factor?
![]()
Answer: The numbers which have 3 as a factor are: 21, 36, 48, 93
Explanation:
Given numbers are: 56, 21, 3, 48, 93, 71
For the given number to have 3 as a factor, the sum of the digits of the given number must be a multiple of 3
So,
The sum of digits of:
56: 5 + 6 = 11: 1 + 1 = 2
21: 2 + 1 = 3
36: 3 + 6 = 9
48: 4 + 8 = 12: 1 + 2 = 3
93: 9 + 3 = 12: 1 + 2 = 3
71: 7 + 1 = 8
Hence, from the above,
we can conclude that the numbers which have 3 as a factor are: 21, 36, 48, 93
6.3 Relate Factors and Multiples
Question 16.
Is 54 a multiple of 3? Explain.
Answer: 54 is a multiple of 3
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
The multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33
To be a multiple of 3, the sum of the digits of the given number should also be a multiple of 3.
So,
54: 5 + 4 = 9 ( Divisible by 3 )
Hence, from the above,
we can conclude that 54 is a multiple of 3
Question 17.
Is 45 a multiple of 7? Explain.
Answer: 45 is not a multiple of 7
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
The multiples of 7 are: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70
Hence, from the above,
we can conclude that 45 is not a multiple of 7
Question 18.
Is 2 a factor of 97? Explain.
Answer: 2 is not a factor of 97
Explanation:
Factors are the numbers that divide the original number completely.
The factors of 97 are: 1, 97
Hence, from the above,
We can conclude that 2 is not a factor of 97
Question 19.
Is 5 a factor of 60? Explain.
Answer: 5 is a factor of 60
Explanation:
Factors are the numbers that divide the original number completely.
The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Hence, from the above,
We can conclude that 5 is a factor of 60
Tell whether 20 is a multiple or a factor of the number. Write multiple, factor, or both.
Question 20.
60
Answer: 20 is a factor of 60
Explanation:
Factors are the numbers that divide the original number completely.
The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Hence, from the above,
We can conclude that 20 is a factor of 60
Question 21.
4
Answer: 20 is a multiple of 4
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
The multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
Hence, from the above,
We can conclude that 20 is a multiple of 4
Question 22.
20
Answer: 20 is a multiple and factor of 20
Explanation:
Multiples are the numbers that can be divided by another number a certain number of times without any remainder.
Factors are the numbers that divide the original number completely
Now,
Factors of 20 are: 1, 2, 4, 5, 10, 20
Multiples of 20 are: 20, 40, 60, 80, 100
Hence, from the above,
we can conclude that 20 is a multiple and factor of 20
Question 23.
Number Sense
Name two numbers that are each a multiple of both 5 and 2. What do you notice about the two multiples?
Answer: The 2 numbers that are each a multiple of both 5 and 2 are: 10 and 20
Explanation;
Multiples of 2 are: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
Multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
So,
From the multiples of both 2 and 5,
The numbers which have common multiples of both 5 and 2 are: 10, 20
The multiples of 2 have the one’s digit as 2 or 4 or 6 or 8 or 0
The multiples of 5 have the one’s digit as 5 or 0
Question 24.
Logic
A quotient is a multiple of 5. The dividend is a multiple of 4. The divisor is a factor of 8. Write one possible equation for the problem.
Answer: The possible equation is:
80 ÷ 8 = 10
Explanation:
Given that,
Quotient: Multiple of 5
Dividend: Multiple of 4
Divisor: Factor of 8
Hence, from the above,
we can conclude that the possible equation for the problem is:
80 ÷ 8 = 10
6.4 Identify Prime and Composite Numbers
Tell whether the number is prime or composite. Explain.
Question 25.
5
Answer: 5 is a prime number
Explanation;
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
Now,
The factors of 5 are: 1, 5
Hence, from the above,
We can conclude that 5 is a prime number
Question 26.
25
Answer: 25 is a composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Now,
The factors of 25 are: 1, 5, 25
Hence, from the above,
We can conclude that 25 is a composite number
Question 27.
51
Answer: 51 is a composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Now,
The factors of 51 are: 1, 3, 17, 51
Hence, from the above,
We can conclude that 51 is a composite number
Question 28.
21
Answer: 21 is a composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Now,
The factors of 21 are: 1, 3, 7, 21
Hence, from the above,
We can conclude that 21 is a composite number
Question 29.
50
Answer: 50 is a composite number
Explanation:
Composite numbers:
The numbers which have more than 2 factors are “Composite numbers”
Now,
The factors of 50 are: 1, 2, 5, 10, 25, 50
Hence, from the above,
We can conclude that 50 is a composite number
Question 30.
83
Answer: 83 is a prime number
Explanation:
Prime numbers:
The numbers which have exactly 2 factors 1 and itself are “Prime numbers”
Now,
The factors of 83 are: 1, 83
Hence, from the above,
We can conclude that 83 is a prime number
Question 31.
Modeling Real Life
A prime number of students have which type of fingerprint?
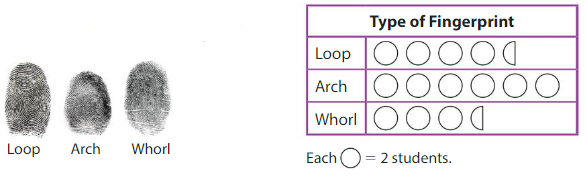
Answer: A prime number of students have Whorl fingerprint
Explanation:

From the given figure,
Each half-circle = 1 student
The number of fingerprints of loop-type fingerprint: 9
The number of fingerprints of Arch-type fingerprint: 12
The number of fingerprints on Whorl-type fingerprint: 7
Hence, from the above,
We can conclude that the prime number of students has Whorl-type fingerprint
6.5 Number Patterns
Write the first six numbers in the pattern. Then describe another feature of the pattern.
Question 32.
Rule: Subtract 11.
First number: 99
99, ___, _____, _____, _____, _____
Answer:
The first 6 numbers in the given pattern are: 99, 88, 77, 66, 55, 44
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Subtract 11
First number: 99
Hence,
The pattern we will obtain is:
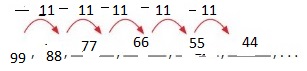
Question 33.
Rule: Multiply by 5.
First number: 10
10, _____, _____, ____, _____, _____
Answer:
The first 6 numbers of the given pattern is: 10, 50, 250, 1,250, 6,250, 31,250
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Multiply by 5
First number: 10
Hence,
The pattern we will obtain is:
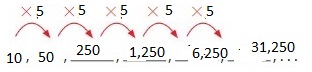
Question 34.
Rule: Add 8.
First number: 15
Answer:
The first 6 numbers of the given pattern are: 15, 23, 31, 39, 47, 55
Explanation:
For the formation of the pattern,
the rules are:
Rule: Add 8
First number: 15
Hence,
The pattern we will obtain is:
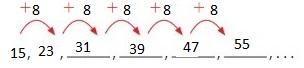
Question 35.
Rule: Divide by 4.
First number: 4,096
Answer:
The first 6 numbers in the given pattern is: 4,096, 1,024, 256, 64, 16, 4
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Divide by 4
First number: 4,096
Hence,
The pattern we will obtain is:
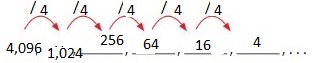
Open-Ended
Use the rule to generate a pattern of four numbers.
Question 36.
Rule: Divide by 2.
Answer:
Let the first number be 16
Hence,
The first 4 numbers of the given pattern are: 16, 8, 4, 2
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Divide by 2
Let the first number be 16
Hence,
The pattern we will obtain is:
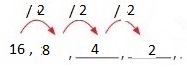
Question 37.
Rule: Add 3.
Answer:
Let the first number be 3
Hence,
The first four numbers of the given pattern are: 3, 6, 9, 12
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Add 3
Let the first number be 3
Hence,
The pattern we will obtain is:
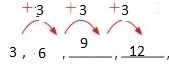
Question 38.
Rule: Multiply by10.
Answer:
Let the first number be 10
Hence,
The first 4 numbers of the given pattern are: 10, 100, 1,000, 10,000
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Multiply by 10
Let the first number be 10
Hence,
The pattern we will obtain is:
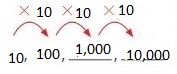
Question 39.
Rule: Subtract 6.
Answer:
Let the first number be 36
Hence,
The first 4 numbers of the given pattern are: 36, 30, 24, 18
Explanation:
For the formation of the pattern,
the given rules are:
Rule: Subtract 6
Let the first number be 36
Hence,
The pattern we will obtain is:

6.6 Shape Patterns
Question 40.
Extend the pattern of shapes by repeating the rule “trapezoid, circle.” What is the 57th shape in the pattern?
Answer: The 57th shape in the pattern is: Trapezoid
Explanation:
Given pattern is:
The rule given for the pattern is: trapezoid, circle
So,
The total number of figures in the given pattern is: 2
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotient method,
57 ÷ 2 = ( 40 + 16 ) ÷ 2
= ( 40 ÷ 2 ) + ( 16 ÷ 2 )
= 20 + 8
= 28 R 1
Hence, from the above,
we can conclude that the 57th shape in the pattern is: Trapezoid
Question 41.
Extend the pattern of shapes by repeating the rule “top left, top right, bottom right, bottom left.” What is the 102nd shape in the pattern?

Answer: The 102nd shape in the pattern is: Bottom left
Explanation:
The given pattern is:

The rule given for the pattern is: top left, top right, bottom right, bottom left
So,
The total number of figures in the given pattern is: 4
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
102 ÷ 3 = ( 99 + 3 ) ÷ 3
= ( 99 ÷ 3 ) + ( 3 ÷ 3 )
= 33 + 1
= 34 R 0
Hence, from the above,
We can conclude that the 102nd shape in the pattern is: Bottom left
Question 42.
Describe the pattern. How many squares are in the 61st figure?
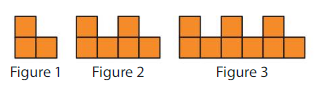
Answer: The number of squares in the 61st figure is: 3
Explanation:
The given pattern is:

In figure 1, the total number of squares = 3
In figure 2, the total number of squares = 6
In figure 3, the total number of squares = 9
So,
The total number of figures = 3
So,
for this, when we divide any number by the total number of patterns, the value of the quotient will be a total repetition of the patterns and the remainder will be the counting of the pattern from the 1st figure.
So,
By using the partial quotients method,
61 ÷ 3 = ( 57 + 3 ) ÷ 3
= ( 57 ÷ 3 ) + ( 3 ÷ 3 )
= 19 + 1
= 20 R 1
Hence, from the above,
We can conclude that the number of squares in the 61st figure in the pattern is: 4
Question 43.
Structure
Draw the missing figure in the pattern. Explain the pattern.
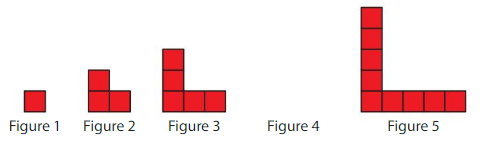
Answer: The missing figure has: 7 squares
Explanation:
The given pattern is:

The rule-following in the given pattern is: Add 2
The first number: 1
According to the rule,
The number of squares in the pattern will be like 1, 3, 5, 7, 9
Conclusion:
We hope the details mentioned in the Big Ideas Math Answers Grade 4 Chapter 6 Factors, Multiples, and Patterns are helpful for you to finish your homework in time. Learn the concepts in depth so that you can solve any kind of problem easily. If you have any queries you can post your comments in the below section.