In Order to attempt the 5th Grade Exam, you need to have strong fundamentals. Download Big Ideas Math Answers Grade 5 Chapter 12 Patterns in the Coordinate Plane free of cost and get the homework help you need. Attempt the chapter practice to know your preparation level within the Chapter. Practice as much as you can using the Big Ideas Math Answers Grade 5 Chapter 12 Patterns in the Coordinate Plane and clear the exam with better grades.
Big Ideas Math Book 5th Grade Answer Key Chapter 12 Patterns in the Coordinate Plane
You will not feel the Concept of Patterns in the Coordinate Plane difficult anymore with our Big Ideas Math Book 5th Grade Answer Key Chapter 12 Patterns in the Coordinate Plane. Make the most out of the Big Ideas Math Answers Grade 5 Chapter 12 Patterns in the Coordinate Plane and solve various questions in it and master the subject. Hit the below links and start practicing from now itself.
Lesson: 1 Plot Points in a Coordinate Plane
- Lesson 12.1 Plot Points in a Coordinate Plane
- Plot Points in a Coordinate Plane Homework & practice 12.1
Lesson: 2 Relate Points in a Coordinate Plane
- Lesson 12.2 Relate Points in a Coordinate Plane
- Relate Points in a Coordinate Plane Homework & Practice 12.2
Lesson: 3 Draw polygons in a Coordinate Plane
- Lesson 12.3 Draw polygons in a Coordinate Plane
- Draw polygons in a Coordinate Plane Homework & Practice 12.3
Lesson: 4 Graph Data
Lesson: 5 Make and Interpret Line Graphs
Lesson: 6 Numerical Patterns
Lesson: 7 Graph and Analyze Relationships
- Lesson 12.7 Graph and Analyze Relationships
- Graph and Analyze Relationships Homework & Practice 12.7
Chapter: 12 – Patterns in the Coordinate Plane
- Patterns in the Coordinate Plane Performance Task 12
- Patterns in the Coordinate Plane Treasure Hunt
- Patterns in the Coordinate Plane Chapter Practice 12
Lesson 12.1 Plot Points in a Coordinate Plane
Explore and Grow
Choose a location for your buried treasure on the grid. Choose a point where two grid lines My Treasure intersect. An example is shown.

Take turns with a partner guessing the location of each other’s buried treasure. Keep track of your guesses on the grid. After each guess, give a clue to help yourMy Guessespartner, such as “my treasure is northwest of your guess.”This is an image Continue to guess until a treasure is located.
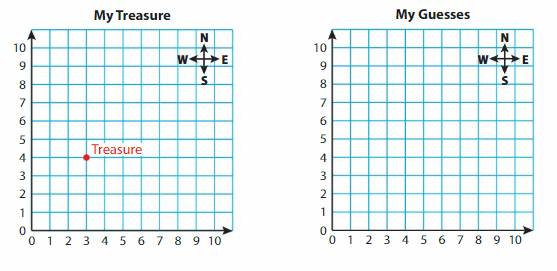
Reasoning
The point where the horizontal number line and the vertical number line intersect is called the origin. Why do you think it is called that?
Think and Grow: The Coordinate Plane
Key Idea
A coordinate plane is formed by the intersection of a horizontal number line and a vertical number line. An ordered pair is a pair of numbers that is used to locate a point in a coordinate plane.

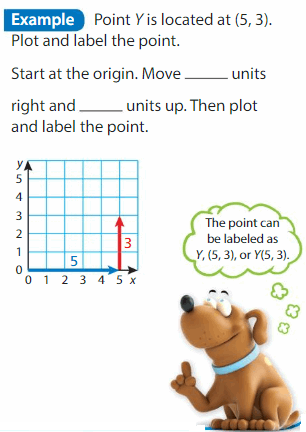
Example
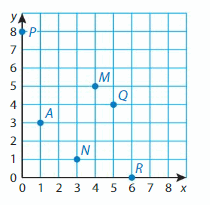
Write the ordered pair that corresponds to point M.
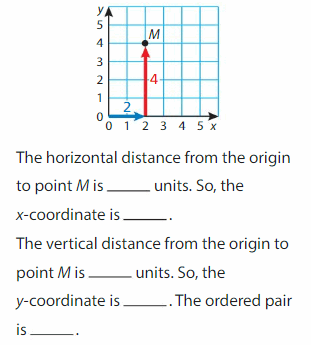
The horizontal distance from the origin to point M is __ units. So, the x-coordinate is __.
The vertical distance from the origin to point M is ___ units. So, the y-coordinate is ___. The ordered pair is __.
Answer:
The horizontal distance from the origin to point M is 5 units. So, the x-coordinate is 5.
The vertical distance from the origin to point M is 5units. So, the y-coordinate is 3. The ordered pair is (5, 3).
Show and Grow
Write the ordered pair corresponding to the point.
Question 1.
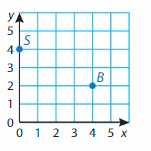
Point B
Answer:(4,2)
Explanation:
The horizontal distance from the origin to point B is _4_ units.
So, the x-coordinate is _4_.
The vertical distance from the origin to point B is __2_ units.
So, the y-coordinate is _2__. The ordered pair is _(4,2)_.
Question 2.
Point S
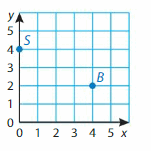
Answer:(0,4)
Explanation:
The horizontal distance from the origin to point S is 0 units.
So, the x-coordinate is _0_.
The vertical distance from the origin to point S is __4_ units.
So, the y-coordinate is _4__.
The ordered pair is _(0,4)_.
Plot and label the point in the coordinate plane.
Question 3.
F(5, 4)
Answer:(5,4)
Explanation:
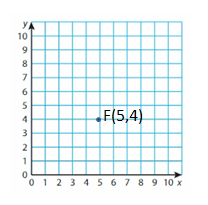
Start the Origin. Move 5 Units right and 4 units up. Then plot and label the point.
The point can be labeled as Y,(5,4)
Question 4.
P(3, 0)
Answer:(3,0)
Explanation:
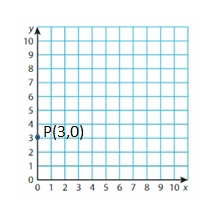
Start the Origin. Move 3 Units right and 0 units up. Then plot and label the point.
The point can be labeled as Y,(3,0)
Apply and Grow: Practice
Use the coordinate plane to write the ordered pair corresponding to the point.
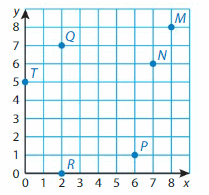
Question 5.
Point M
Answer:(8,8)
Explanation:

The horizontal distance from the origin to point M is 8 units.
So, the x-coordinate is _8_.
The vertical distance from the origin to point M is __8 units.
So, the y-coordinate is 8_.
The ordered pair is _(8,8)_.
Question 6.
Point Q
Answer:(2,7)
Explanation:

The horizontal distance from the origin to point Q is 2 units.
So, the x-coordinate is _2_.
The vertical distance from the origin to point Q is __7_ units.
So, the y-coordinate is _7__.
The ordered pair is _(2,7)_.
Question 7.
Point N
Answer: (7,6)
Explanation:

The horizontal distance from the origin to point N is 7 units.
So, the x-coordinate is _7_.
The vertical distance from the origin to point N is _6_ units.
So, the y-coordinate is _6__.
The ordered pair is _(7,6)_.
Question 8.
Point R
Answer:(2,0)
Explanation:

The horizontal distance from the origin to point R is 2 units.
So, the x-coordinate is _2_.
The vertical distance from the origin to point R is __0_ units.
So, the y-coordinate is _0_.
The ordered pair is _(2,0)_.
Question 9.
Point P
Answer:(6,1)
Explanation:

The horizontal distance from the origin to point P is 6 units.
So, the x-coordinate is _6_.
The vertical distance from the origin to point P is __1_ units.
So, the y-coordinate is _4__.
The ordered pair is _(6,1)_.
Question 10.
Point T
Answer: (0,5)
Explanation:

The horizontal distance from the origin to point T is 0 units.
So, the x-coordinate is _0_.
The vertical distance from the origin to point P is __5_ units.
So, the y-coordinate is _5__.
The ordered pair is _(0,5)_.
Plot and label the point in the coordinate plane above.
Question 11.
S(0, 3)
Answer: The Point can be labeled as (0,3)
Explanation:
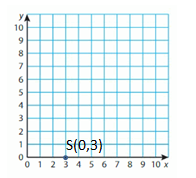
Start the Origin. Move 0 Units right and 3 units up then plot and label the point.
The point can be labeled as Y,(0,3)
Question 12.
F(2, 5)
Answer: (2,5)
Explanation:
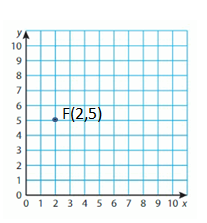
Start the Origin. Move 2 Units right and 5 units up then plot and label the point.
The point can be labeled as Y,(2,5)
Question 13.
W(0, 0)
Answer:(0,0)
Explanation:
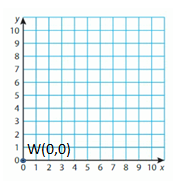
Start the Origin. Move 0 Units right and 0 units up then plot and label the point.
The point can be labeled as Y,(0,0)
Name the point for the ordered pair.
Question 14.
(5, 2)
Answer: D(5,2)
Explanation:
Start the Origin. Move 5 Units right and 2 units up then label the point.
The point can be Named as D(5,2)
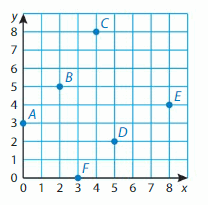
Question 15.
(8, 4)
Answer: E(8,4)
Explanation:

Start the Origin. Move 8 Units right and 4 units up then label the point.
The point can be Named as E(8,4)
Question 16.
(0, 3)
Answer: F(0,3)
Explanation:

Start the Origin. Move 0 Units right and 3 units up then label the point.
The point can be Named as D(5,2)
Question 17.
Reasoning
How are the locations of the points A(0, 4) and B(4, 0) different in a coordinate plane?
Answer: A(0,4) is in Y axis as x is 0 and y is 4. B(4,0) is in X axis as x is 4 and y is 0.
Question 18.
DIG DEEPER!
Newton buries a bone in a park at the location shown. How can he use a coordinate plane to describe its location?
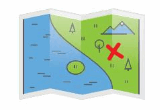
Answer:
He can use the x-coordinate and y-coordinate to describe the location.
Think and Grow: Modeling Real Life
Example
In a video game, you move an aircraft carrier and a tugboat away from your base. Use the directions to plot and label the locations of the aircraft carrier and the tugboat.
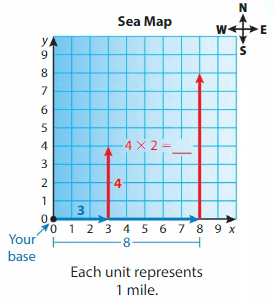
• Aircraft carrier: Located 3 miles east and 4 miles north of your base.
• Tugboat: Located 8 miles east and twice as many miles north of your base as the aircraft carrier.
To find the location of the aircraft carrier, start at your base, which is at the origin.
Move __ units east, or right, and ___ units north, or up.
Plot and label the point as A(___, ___ ).
To find the location of the tugboat, start at your base, which is at the origin.
Move ___ units east, or right, and ___ × __ = ___ units north, or up.
Plot the label the point as T(__, ___).
Answer: Mov
Show and Grow
Question 19.
A guidebook describes how to get to various statues in Chicago, Illinois, from Willis Tower. Plot and label the location of each statue on the map.
Dubuffet’s Monument with Standing Beast: Walk 2 blocks east and 5 blocks north.
• Miró’s Sun, Moon, and One Star: Walk twice as many blocks east as you do to get to the Standing Beast, and 3 blocks north.
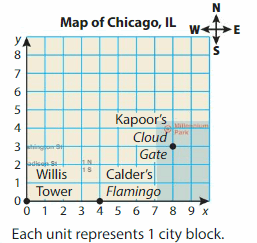
Answer:
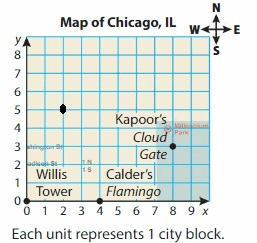
Question 20.
DIG DEEPER!
Which statue is closer to Moon, and One Star, Cloud Gate or Flamingo? Explain.
Plot Points in a Coordinate Plane Homework & practice 12.1
Use the coordinate plane to write the ordered pair corresponding to the point.
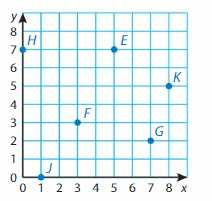
Question 1.
Point E
Answer: (5,7)
Explanation:

The horizontal distance from the origin to point E is 5 units.
So, the x-coordinate is _5_.
The vertical distance from the origin to point E is __7_ units.
So, the y-coordinate is _7__.
The ordered pair is _(5,7)_.
Question 2.
Point H
Answer: (0,7)
Explanation:

The horizontal distance from the origin to point H is 0 units.
So, the x-coordinate is _0_.
The vertical distance from the origin to point H is __7_ units.
So, the y-coordinate is _7__.
The ordered pair is _(0,7)_.
Question 3.
Point F
Answer: (3,3)
Explanation:

The horizontal distance from the origin to point F is 3 units.
So, the x-coordinate is _3_.
The vertical distance from the origin to point F is __3 units.
So, the y-coordinate is _3__.
The ordered pair is _(3,3)_
Question 4.
Point J
Answer: (1,0)
Explanation:

The horizontal distance from the origin to point J is 1 units.
So, the x-coordinate is _1_.
The vertical distance from the origin to point J is __0_ units.
So, the y-coordinate is _0__.
The ordered pair is _(1,0)_.
Question 5.
Point G
Answer: (7,2)
Explanation:

The horizontal distance from the origin to point G is 7 units.
So, the x-coordinate is _7_.
The vertical distance from the origin to point G is __2_ units.
So, the y-coordinate is _2__.
The ordered pair is _(7,2)_.
Question 6.
Point K
Answer: (8,5)
Explanation:

The horizontal distance from the origin to point K is 8 units.
So, the x-coordinate is _8_.
The vertical distance from the origin to point K is __5_ units.
So, the y-coordinate is _5_.
The ordered pair is _(8,5)_.
Plot and label the point in the coordinate plane above.
Question 7.
Z(8, 0)
Answer: The Point can be labeled as (8,0)
Explanation:
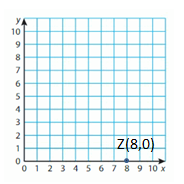
Start the Origin. Move 8 Units right and 0 units up then plot and label the point.
The point can be labeled as Y,(8,0)
Question 8.
B(5, 5)
Answer: The Point can be labeled as (5,5)
Explanation:
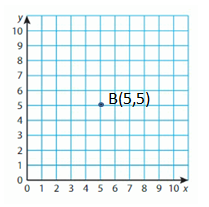
Start the Origin. Move 5 Units right and 5 units up then plot and label the point.
The point can be labeled as Y,(5,5)
Question 9.
M(1, 2)
Answer: The Point can be labeled as (1,2)
Explanation:
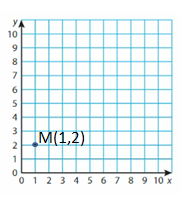
Start the Origin. Move 1 Units right and 2 units up then plot and label the point.
The point can be labeled as Y,(1,2)
Name the point for the ordered pair.
Question 10.
(5, 4)
Answer: Q(5,2)
Explanation:

Start the Origin. Move 5 Units right and 4 units up then label the point.
The point can be Named as Q(5,4)
Question 11.
(0, 8)
Answer: P(0,8)
Explanation:

Start the Origin. Move 0 Units right and 8units up then label the point.
The point can be Named as P(0,8)
Question 12.
(3, 1)
Answer: N(5,2)
Explanation:

Start the Origin. Move 3 Units right and 1 units up then label the point.
The point can be Named as N(3,1)
Question 13.
Open-Ended
Use the coordinate plane above. Point T is 3 units from point M. Name two possible ordered pairs for point T.
Answer: T(7,8), (7,0)&(0,8)
Explanation:
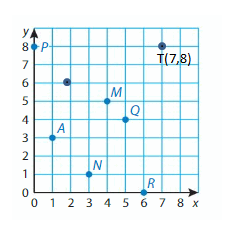
The horizontal distance from the origin to point M is 4 units.
So, the x-coordinate is _4_.
The vertical distance from the origin to point M is _5_ units.
So, the y-coordinate is _5_.
The ordered pair is _(4,5)_.
Point T is 3 units from point M
The horizontal distance from point M is 4 units to add 3
So, the x-coordinate is _4+3=7_.
The vertical distance from the point M is 5 units to add 3 units.
So, the y-coordinate is _5+3=8_.
The ordered pair is _(7,8)_.
The two possible ordered pairs for point T is (0,7)& (8,0).
Question 14.
Writing
Explain why the order of the x- and y-coordinates is important when identifying or plotting points in a coordinate plane.
Answer: Locations on the coordinate plane are described as ordered pairs. An ordered pair tells you the location of a point by relating the point’s location along the x-axis (the first value of the ordered pair) and along the y-axis (the second value of the ordered pair).
Question 15.
To get from the school to the arcade, you walk 4 blocks east and 3 blocks north. To get from the school to the skate park, your friend walks 2 blocks east and twice as many blocks north as you. Plot and label the locations of the arcade and the skate park.
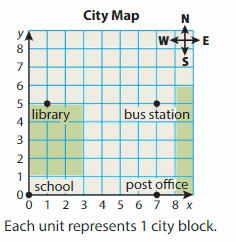
Question 16.
DIG DEEPER!
Which building is closer to the bus station, the library or the post office? Explain.
Review & Refresh
Multiply.
Question 17.
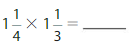
Answer: 5/3=1 2/3
Explanation: First Multiply with the whole number(1) with the denominator(4) then add numerator (4+1=5)
and denominator is same as original. i.e, 5/4
then same as next mixed fraction Multiply with the whole number(1) with the denominator(3) then add numerator (3+1=4)
and denominator is same as original. i.e, 4/3
Multiply 5/4*4/3=20/12
This fraction can be reduced by dividing both the numerator and denominator by the Greatest Common Factor of 20 and 12 using 4 i.e, 5/3=1 2/3
Question 18.
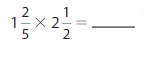
Answer: 7/2= 3 1/2
Explanation: First Multiply with the whole number(1) with the denominator(5) then add numerator (5+2=7)
and denominator is same as original. i.e, 7/5
then same as next mixed fraction Multiply with the whole number(2) with the denominator(2) then add numerator (4+1=5)
and denominator is same as original. i.e, 5/2
Multiply 7/5*5/2=35/10
This fraction can be reduced by dividing both the numerator and denominator by the Greatest Common Factor of 35 and 10 using 5 i.e, 7/2=3 1/2
Question 19.
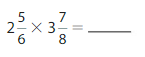
Answer: 527/48=10 47/48
Explanation: First Multiply with the whole number(2) with the denominator(6) then add numerator (12+5=17)
and denominator is same as original. i.e, 17/6
then same as next mixed fraction Multiply with the whole number(3) with the denominator(8) then add numerator (24+7=31)
and denominator is same as original. i.e, 31/8
Multiply 17/6*31/8= 527/48.
therefore we can write it as 10 47/48.
Lesson 12.2 Relate Points in a Coordinate Plane
Plot and label the points in the coordinate plane.

Draw a line segment to connect each pair of points.
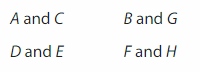
Plot and label more points that lie on the line segments you drew. What do you notice about the coordinates?
A and C
Explanation:
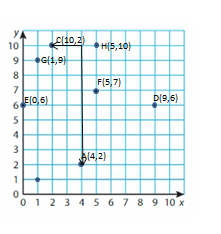
In A and C line segment we observed that the y- Coordinate of A and C is same.
B and G
Explanation:
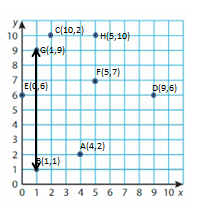
In B and G line segment we observed that the X- Coordinate of B and G is same.
D and E
Explanation:
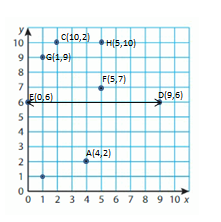
In D and E line segment we observed that the Y- Coordinate of D and E is same.
F and H
Explanation:
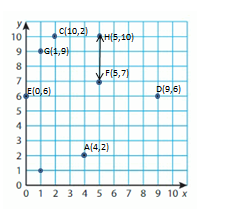
In F and H line segment we observed that the X- Coordinate of F and H is same.
Construct Arguments
How can you find the distance between each pair of points? Explain your reasoning.
Think and Grow: Relate Points in a Coordinate Plane
Key Idea
Points on a horizontal line have the same-coordinates. Points on a vertical line have the same x-coordinates.
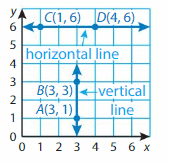
You can count units or use subtraction to find the distance between two points when they lie on the same horizontal line or vertical line.
Example
Find the distance between points G and H.
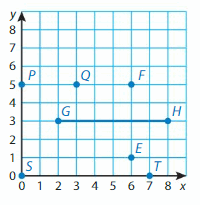
One Way: Count units.
Step 1: Identify the locations of the points: Point G is located at (2, 3). Point H is located at (8, 3).
Step 2: Draw a line segment to connect the points.
Step 3: Count horizontal units: There are __ units between points G and H.
So, the distance between points G and H is ___.
Another Way: Use subtraction
Points G and H have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
8 – 2 = _6__
So, the distance between points G and H is 6___.
Show and Grow
Find the distance between the points in the coordinate plane above.
Question 1.
E and F
Answer: 4 Units
Explanation
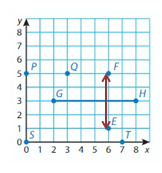
Points E and F have the same X-coordinates. They lie on a Vertical line. Subtract the Y-coordinates to find the distance.
5 – 1 = __4_
So, the distance between points E and F is _4__ units
Question 2.
P and Q
Answer: 3 Units
Explanation:
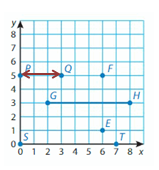
Points P and Q have the same Y-coordinates. They lie on a Vertical line. Subtract the X-coordinates to find the distance.
3 – 0 = __3_
So, the distance between points P and Q is _3__ units.
Question 3.
S and T
Answer: 7 Units
Explanation:
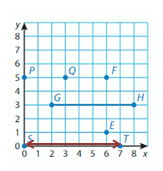
Points S and T have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
7 – 0 = __7_
So, the distance between points S and T is _7_ Units.
Apply and Grow: Practice
Find the distance between the points in the coordinate plane.
Question 4.
E and F
Answer: 7 Units
Explanation:
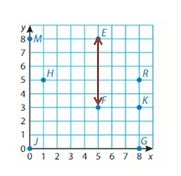
Points E and F have the same X-coordinates. They lie on a Vertical line. Subtract the Y-coordinates to find the distance.
8 – 3 = __5
So, the distance between points E and F is _5_ units
Question 5.
J and G
Answer: 7 Units
Explanation:
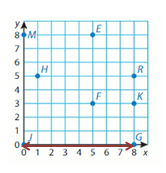
Points J and G have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
8 – 0 = __8_
So, the distance between points J and G is _8_ Units.
Question 6.
F and K
Answer: 7 Units
Explanation:
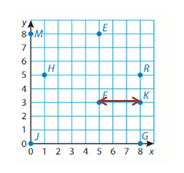
Points F and K have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
8 – 5 = __3_
So, the distance between points F and K is _3_ Units.
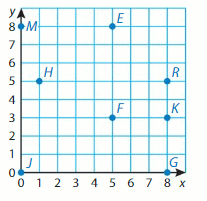
Question 7.
Which is longer, \(\overline{J M}\) or \(\overline{H R}\)?
Find the distance between the points.
Question 8.
(1, 7) and (7, 7)
Answer: 6 Units
Explanation:
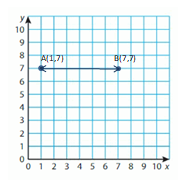
Lets take point A is (1,7) and Point B is (7,7)
Points A and B have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
7 – 1 = __6_
So, the distance between points A and B is _6_ Units.
Question 9.
(0, 1) and (3, 1)
Answer: 3 Units
Explanation:
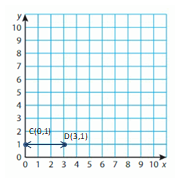
Lets take point C is (0,1) and Point D is (3,1)
Points C and D have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
3 – 0 = __3_
So, the distance between points C and D is _3_ Units.
Question 10.
(0, 0) and (6, 0)
Answer: 7 Units
Explanation:
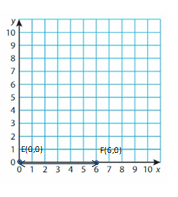
Lets take point E is (0,0) and Point F is (6,0)
Points E and F have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
6 – 0 = __6_
So, the distance between points E and F is _6_ Units.
A line passes through the given points. Name two other points that lie on the line.
Question 11.
(0, 6) and (5, 6)
Answer: (1,6),(2,6),(3,6),(4,6)
Explanation:
Lets take point A is (0,6) and Point B is (5,6)
Points A and B have the same y-coordinates. They lie on a horizontal line.
So the other points lie on the line are (1,6),(2,6),(3,6),(4,6)
Question 12.
(4, 2) and (4, 8)
Answer: (4,3),(4,4),(4,5),(4,6)
Explanation:
Lets take point C is (4,2) and Point D is (4,8)
Points C and D have the same X-coordinates. They lie on a Vertical line.
So the other points lie on the line are (4,3),(4,4),(4,5),(4,6) etc
Question 13.
(3, 3) and (3, 6)
Answer: (3,4),(3,5)
Explanation:
Lets take point E is (3,3) and Point F is (3,6)
Points E and F have the same X-coordinates. They lie on a Vertical line.
So the other points lie on the line are (3,4),(3,5)
Question 14.
YOU BE THE TEACHER
Newton plots the points (2, 7) and (6, 7) and connects them with a line segment. Descartes says that (10, 7) also lies on the line segment. Is he correct? Explain.
Answer: Yes
Explanation:
Points on a Vertical line have the same-coordinates. They lie on a horizontal line.
Question 15.
DIG DEEPER!
Which pair of points does not lie on a line that is parallel to x-axis? Explain.
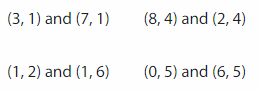
Answer: (1,2) and (1,6)
Explanation:
Points on a Vertical line have the same-coordinates. They lie on a horizontal line. Except (1,2) and (1,6) , these two
Points on a horizontal line have the same-coordinates. They lie on a Vertical line.
Think and Grow: Modeling Real Life
Example
An archaeologist uses rope to section off a rectangular dig site. How many meters of rope does the archaeologist use?
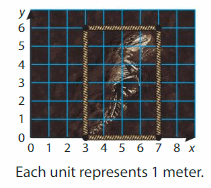
To find how many meters of rope the archaeologist uses, find the perimeter of the rectangular dig site.


Use a formula to find the perimeter of the site.
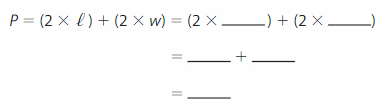
So, the archaeologist uses __ meters of rope.
Show and Grow
Question 16.
The owner of an animal shelter uses fencing to create a rectangular dog pen. How many yards of fencing does the owner use?

Answer:
yards of fencing the owner use
To find how many yards of fencing the owner use, to find the perimeter of the rectangular dog pen.
Question 17.
DIG DEEPER!
You run 5 laps around the edges of the volleyball court. How far do you run in feet? in yards?
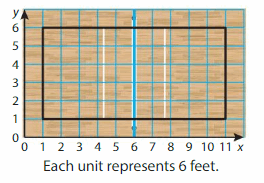
Answer:
10 × 6 = 60 feet
Convert from foot to yards
1 feet = 0.33 yards
60 feet = 20 yards
Relate Points in a Coordinate Plane Homework & Practice 12.2
Find the distance between the points in the coordinate plane.
Question 1.
P and M
Answer: 6 Units
Explanation:
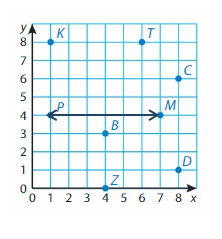
Points P and M have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
7 – 1 = __6_
So, the distance between points P and M is _6_ Units.
Question 2.
B and Z
Answer: 3 Units
Explanation:
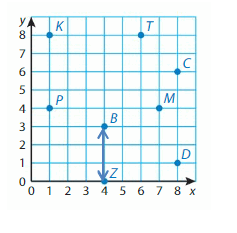
Points B and Z have the same X-coordinates. They lie on a Vertical line. Subtract the Y-coordinates to find the distance.
3 – 0 = _0
So, the distance between points B and Z is _0_ units
Question 3.
K and T
Answer: 5 Units
Explanation:
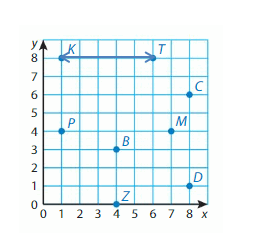
Points K and T have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
6 – 1 = __5_
So, the distance between points K and T is _5_ Units.
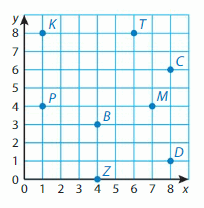
Question 4.
Which is longer, \(\overline{C D}\) or \(\overline{K P}\)?
Answer: \(\overline{C D}\) longer than \(\overline{K P}\)
Find the distance between the points.
Question 5.
(1, 5) and (6, 5)
Answer: 5 Units
Explanation:
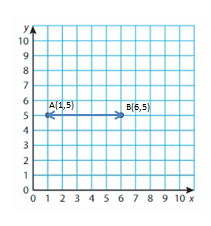
Lets take point A is (1,5) and Point B is (6,5)
Points A and B have the same y-coordinates. They lie on a horizontal line. Subtract the x-coordinates to find the distance.
6 – 1 = _5_
So, the distance between points A and B is _5_ Units.
Question 6.
(3, 4) and (3, 6)
Answer: 2 Units
Explanation:
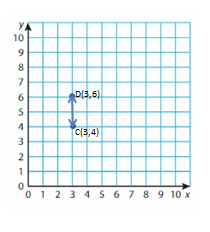
Lets take point C is (3,4) and Point D is (3,6)
Points C and D have the same X-coordinates. They lie on a Vertical line. Subtract the Y-coordinates to find the distance.
6 – 4 = _2
So, the distance between points C and D is _2_ Units.
Question 7.
(0, 2) and (0, 9)
Answer: 7 Units
Explanation:
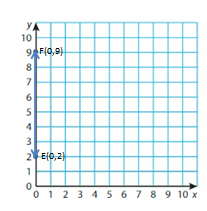
Lets take point E is (0,2) and Point F is (0,9)
Points E and F have the same X-coordinates. They lie on a Vertical line. Subtract the Y-coordinates to find the distance.
9 – 2 = _7
So, the distance between points E and F is _7_ Units.
A line passes through the given points. Name two other points that lie on the line.
Question 8.
(6, 0) and (6, 7)
Answer: (6,1),(6,2),6,3)
Explanation:
Lets take point A is (6,0) and Point B is (6,7)
Points A and B have the same X-coordinates. They lie on a Vertical line.
So the other points lie on the line are (6,1),(6,2),(6,3)
Question 9.
(5, 3) and (1, 3)
Answer: (2,3),(3,3)(4,3)
Explanation:
Lets take point C is (5,3) and Point D is (1,3)
Points C and D have the same y-coordinates. They lie on a horizontal line.
So the other points lie on the line are (2,3),(3,3)(4,3)
Question 10.
(2, 2) and (2, 9)
Answer: (2,3),(2,4),(2,5)
Explanation:
Lets take point E is (2,2) and Point F is (2,9)
Points E and F have the same X-coordinates. They lie on a Vertical line.
So the other points lie on the line are (2,3),(2,4),(2,5)
Question 11.
Structure
Name four different points that are 3 units away from (5, 4).
Answer:
A distance of 5 units from the origin represents the hypotenuse of a right triangle with sides 3- 4 – 5
If the x-coordinate is 4 then the y-coordinate is | 3 | = ± 3
the coordinates are (4, 3 ) and (4, – 3 )
Question 12.
Number Sense
Which point is farther from (3, 4)? Explain.
![]()
Answer: K(9, 4)
Question 13.
Modeling Real Life
A farmer builds a coop for his chickens. He uses poultry netting to enclose the coop. How many feet of netting does he use?
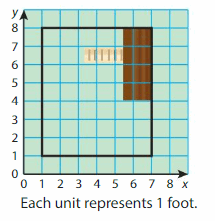
Answer: 6 feet
Question 14.
Modeling Real Life
A giant chessboard is painted on the ground in a park. How many square yards of space does the chessboard occupy?
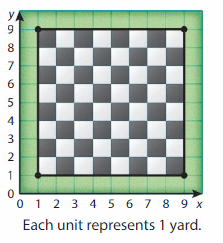
Answer: 81 yards
Review & Refresh
Find the quotient. Then check your answer.
Question 15.
23.6 ÷ 4 = ___
Answer:
Divide 23.6 by 4
We get
23.6/4 = 5.9
Thus the quotient is 5.9
Question 16.
36.9 ÷ 3 = ___
Answer:
Divide the two numbers 36.9 and 3.
36.9 ÷ 3 = 12.3
Question 17.
114.87 ÷ 7 = ___
Answer:
Divide the two numbers 114.87 and 7
114.87 ÷ 7 = 16.41
Lesson 12.3 Draw polygons in a Coordinate Plane
Explore and Grow
Plot and label three points in which two of the ordered pairs have the same x-coordinates and two of the ordered pairs have the same y-coordinates.
The points represent the vertices of a polygon. Describe the polygon.
Structure
Explain how you can plot another point above to form a rectangle.
Think and Grow: Draw Polygons in a Coordinate Plane
Key Idea
You can use ordered pairs to represent vertices of polygons. To draw a polygon in a coordinate plane, plot and connect the vertices.
Example
The vertices of a polygon are A (2, 2), B(3, 5), C(6, 6), and D(6, 2). Draw the polygon in a coordinate plane. Then identify it.
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.

Show and Grow
Draw the polygon with the given vertices in a coordinate plane. Then identify it.
Question 1.
J(0, 8), K(4, 7), L(5, 0)
Answer: Triangle
Explanation:
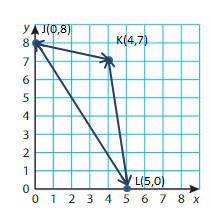
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon J,K,L is a Triangle.
Question 2.
P(1, 4), Q(2, 7), R(6, 7), S(7, 4), T(4, 1)
Answer: Pentagon.
Explanation:
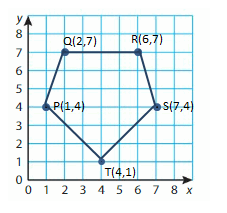
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon P,Q,R,S,T is a Pentagon.
Apply and Grow: Practice
Draw the polygon with the given vertices in a coordinate plane. Then identify it.
Question 3.
C(1, 6), D(4, 6), E(4, 1), F(1, 1)
Answer: Rectangle.
Explanation:
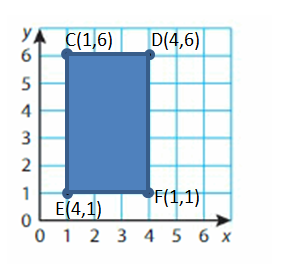
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon C,D,E,F is a Rectangle.
Question 4.
J(2, 2), K(2, 4), L(4, 6), M(6, 4), N(6, 2), P(4, 1)
Answer: Hexagon.
Explanation:
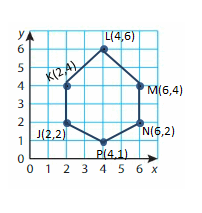
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon J,K,L,M,N,P is a Hexagon.
Identify the polygon with the given vertices.
Question 5.
A(2, 6), B(6, 2), C(3, 2)
Answer: Triangle.
Explanation:
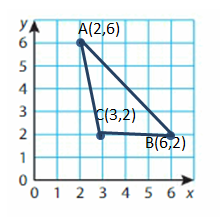
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon A ,B , C is a Tringle.
Question 6.
G(0, 3), H(6, 3), I(4, 1), J(2, 1)
Answer: Isosceles Trapezoid
Explanation:
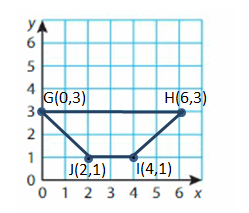
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon G,H,I,J is a Isosceles Trapezoid .
Question 7.
P(1, 1), Q(1, 6), R(6, 6), S(6, 1)
Answer: Square
Explanation:
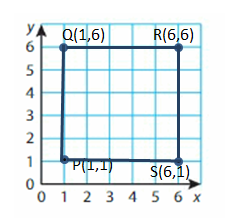
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon P, Q ,R, S is a Rectangle.
Question 8.
X(0, 0), Y(0, 7), Z(2, 0)
Answer: Triangle.
Explanation:
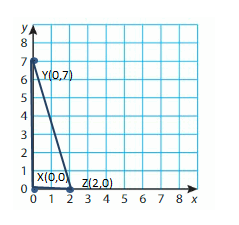
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon X ,Y, Z is a Triangle.
Plot (6, 3), (6, 8), and (9, 3) in a coordinate plane. Plot another point to form the given quadrilateral. Name the point.
Question 9.
rectangle
Answer:
Explanation:
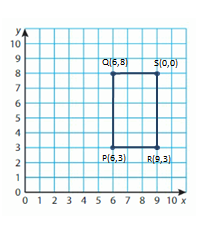
Question 10.
trapezoid
Answer:
Explanation:
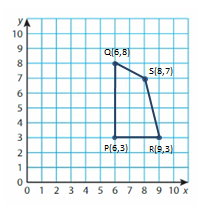
Question 11.
Open-Ended
Write four ordered pairs that represent the vertices of a square
Answer:
(2, 2), (4, 2), (2, 4), (4, 4)
Question 12.
YOU BE THE TEACHER
Your friend draws the polygon shown. She names the polygon. Is your friend correct? Explain.
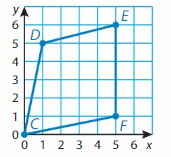
Answer:
No your friend is incorrect because the given figure has 4 sides so it is a quadrilateral not a polygon.
Think and Grow: Modeling Real Life
Example
You and a friend use computer software to create a symmetric company logo using a coordinate plane. Your friend completes one half of the logo as shown. Draw the other half. Then list the vertices of the logo.
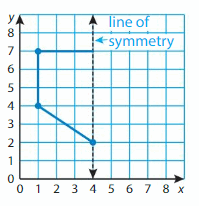
Step 1: Plot the vertices for the other half of the logo on the opposite side of the line of symmetry.
Step 2: Draw line segments to connect the points.
![]()
Answer:
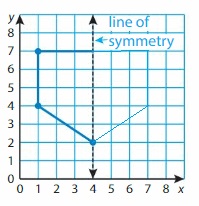
Show and Grow
Draw the other half of the symmetric logo. Then list its vertices.
Question 13.
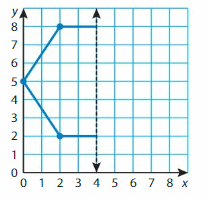
Answer:
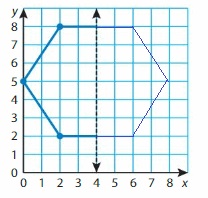
Question 14.
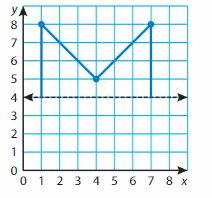
Answer:
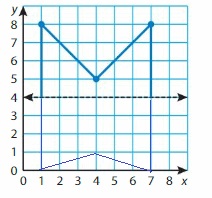
Question 15.
DIG DEEPER!
One half of the design for a symmetric flower garden is shown in the coordinate plane. The line of symmetry is represented by the walkway. Draw the other half of the design for the flower garden. Then list its vertices.
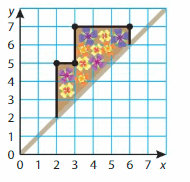
Answer:
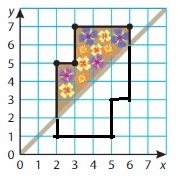
Draw polygons in a Coordinate Plane Homework & Practice 12.3
Draw the polygon with the given vertices in a coordinate plane. Then identify it.
Question 1.
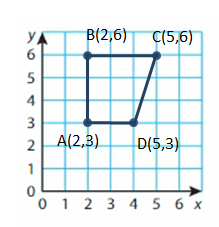
A(2, 3), B(2, 6), C(5, 6), D(5, 3)
Answer:
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon A, B, C, D is a Trapezoid..
Question 2.
J(3, 2), K(3, 5), L(6, 5)
Answer: Triangle
Explanation:
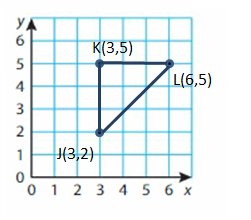
Step 1: Plot and label the vertices.
Step 2: Draw line segments to connect the points. Be sure to connect the points in order to draw the polygon.
Polygon J, K, L is a Triangle.
Identify the polygon with the given vertices.
Question 3.
M(2, 6), N(4, 4), P(4, 0), Q(2, 2)
Answer:
Explanation:
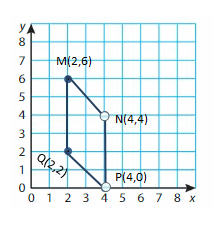
Question 4.
A(1, 2), B(1, 6), C(4, 6), D(6, 4), E(4, 2)
Answer:
Explanation:
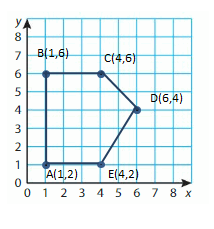
Question 5.
P(4, 1), Q(0, 1), R(1, 4), S(5, 5)
Answer:
Explanation:
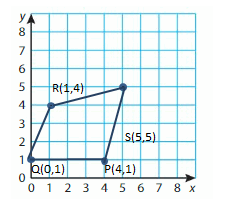
Question 6.
E(1, 2), F(1, 3), G(6, 3), H(6, 2)
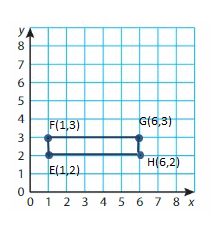
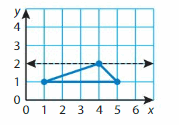
Plot (1, 2), (4, 2), and (3, 4) in a coordinate plane. Plot another point to form the given quadrilateral. Name the point.
Question 7.
trapezoid
Question 8.
parallelogram
Question 9.
Open-Ended
Write the coordinates of the vertices of a rectangle that has a perimeter of 12 units and an area of 5 square units.
Question 10.
Reasoning
Five ordered pairs represent the vertices of a polygon. Will the polygon always be a pentagon?
Question 11.
Modeling Real Life
Draw the other half of the symmetric logo. Then list its vertices.
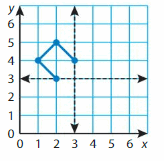
Question 12.
DIG DEEPER!
You complete one fourth of an image with graphic design software. The computer generates the rest of the image with the two lines of symmetry. Draw the rest of the image.
Review & Refresh
Estimate the sum or difference.
Question 13.
![]()
Answer: 1/4
Question 14.
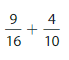
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
77/80
Question 15.
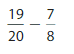
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
= 3/40
Lesson 12.4 Graph Data
Explore and Grow
The table shows the amount of snow that falls each day for 7 days. Show how you can use ordered pairs in the coordinate plane to represent this information. Explain.
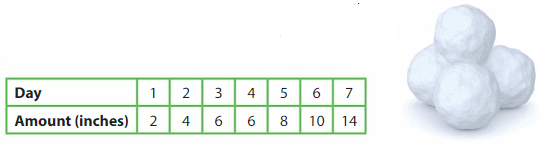
What conclusions can you make from your data display?
Answer:(1,2), (2,4), (3,6),(4,6),(,5,8),(6,10),(7,14)
Explanation:
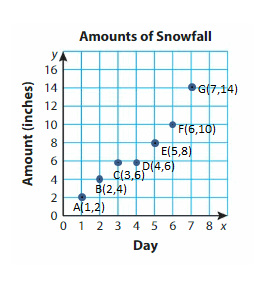
Lets take A(1,2), B(2,4), C(3,6), D(4,6), E(,5,8), F(6,10), G(7,14)
The horizontal distance from the origin to points A.B.C.D.E.F.G.H are 1,2,3,4,5,6,7_ units respectively. So, the x-coordinates are 1,2,3,4,5,6,7 .
The vertical distance from the origin to points A.B.C.D.E.F.G.H are 2,4,6,6,8,10,14 _ units. So, the y-coordinate are __2,4,6,6,8,10,14_. The ordered pair is _A(1,2), B(2,4), C(3,6), D(4,6), E(,5,8), F(6,10), G(7,14)_.
Reasoning
On Day 8, 1 inch of snow falls. How can you represent this information in the coordinate plane?
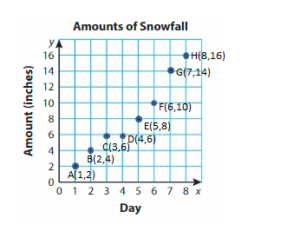
Answer: (8,16)
Explanation:
Start the Origin. Move 8 Units right and 16 units up. label the point.
The point can be labeled as H,(8,16).
Think and Grow: Graph Data
Key Idea
Data are values collected from observations or measurements. You can use a coordinate plane to graph and interpret two categories of related data.
Example
The table shows how many gold bars you collect at each level of a video game. Graph the data in a coordinate plane. In how many levels do you collect more than 30 gold bars?
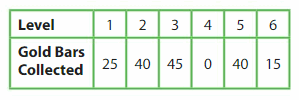
Step 1: Write the ordered pairs from the table.
Step 2: For each axis, choose appropriate numbers to represent the data in the table.
Step 3: Write a title for the graph and label each axis.
Step 4: Plot a point for each ordered pair.
Three points are above the grid line that represents 30 bars. So, you collect more than 30 gold bars in __ levels.
Show and Grow
Question 1.
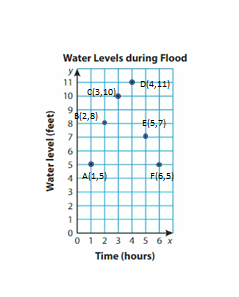
The table shows the water levels of a portion of a river during a flood. Graph the data.
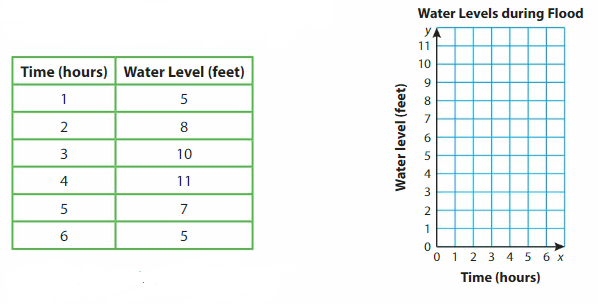
What does the point (5, 7) represent?
Answer: In 5 hours time span 7 feet water level during flood.
Explanation:
Apply and Grow: Practice
Question 2.
The table shows how many cars a salesman sells in each of 6 months. Graph the data.
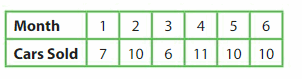
What does the point (1, 7) represent?
What is the difference of the greatest number of cars sold and the least number of cars sold? Explain.
Use the graph.
Answer: in month of span salesman sells 7 cars.
Explanation:
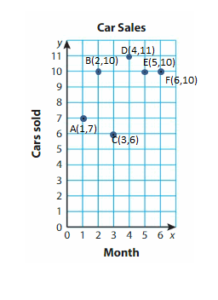
Question 3.
The graph shows how many receiving yards a football player has in each of seven games. How many receiving yards does he have in Game 3?
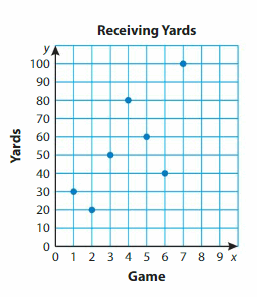
How many times as many receiving yards does he have in Game 4 as in Game 2?
In how many games does he have more than 40 receiving yards?
Answer:
Explanation:
In each game receiving yards are lets label it as A,B,C,D,E,F,G.
A(1,30), B(2,20), C(3,50), D(4,80), E(5,60), F(6,40), G(7,100).
receiving yards a football player has in each of game 30,20,50,80,60,40,100.
In Game 3Receiving yards are 50
So, the distance between points Game 4 and game 2 is 80-60=60
60 times as many receiving yards does he have in Game 4 as in Game 2.
There are 4 games more than 40 receiving yards.
Question 4.
DIG DEEPER!
The player has 75 receiving yards in Game 8. The player has \(\frac{1}{5}\) of this number of receiving yards in Game 9. Graph the data in the coordinate plane above.
Think and Grow: Modeling Real Life
Example
The table shows the ages of eight students and the time they spend on the Internet for 1 week. Graph the data. Of the students who spend more than 15 hours on the Internet, how many are older than 10?

Step 1: Write the ordered pairs from the table.
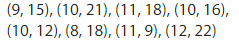
Step 2: For each axis, choose appropriate numbers to represent the data in the table.
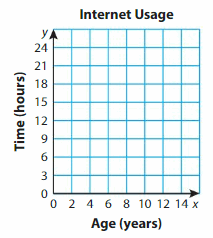
Step 3: Write a title for the graph and label each axis.
Step 4: Plot a point for each ordered pair.
Five points are above the grid line that represents points represents 15 hours. Of those, ___ points represents students older than 10.
So, __ students older than 10 spend more than 15 hours on the Internet.
Show and Grow
Question 5.
The table show much five students sleep the night before a quiz and their quiz scores. Graph the data. Of the students who sleep more than 7 hours, how many score higher than 8 points?
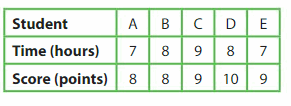
Answer:
Explanation:
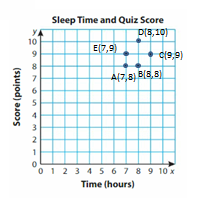
The students who sleep more than 7 hours are 3(B,C,D)
3 members score higher than 8 points
Graph Data Homework & Practice 12.4
Question 1.
The table shows how many students are in a choir club in each of 6 years. Graph the data.
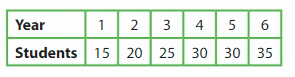
What does the point (2, 20) represent?
What is the difference of the greatest number of students and least number of students? Explain.
Answer: In 2 years 20 students are joined in a choir club
Explanation:
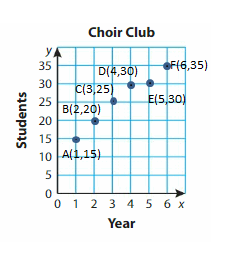
What is the difference of the greatest number of students and least number of students
Grates number of students joined in the year of 6th that is 35 members
least number of students joined in the year of 1st that is 15 members
The difference of the greatest number(6,65) of students and least number of students(1,15) is 35-15=20
Use the graph.
Question 2.
The graph shows how many students earn an A on each of seven tests. How many students earn an A on Test 4?
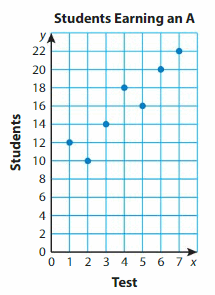
How many times as many students earn an A on Test 6 as on Test 2?
On how many tests do fewer than 20 students earn an A? more than 20 students?
Answer: students earn an A on Test 4 is 18 students
students earn an A on Test 6 as on Test 2 is 10
5 students are fewer than 20students earn an A
1 test only More than 20 students earn A.
Question 3.
DIG DEEPER!
Twenty-five students take Test 1. How many students do not earn an A on the test?
Answer:
25 – 12 = 13
Question 4.
Modeling Real Life
The table shows the ages of five students and how many baby teeth each of them has lost. Graph the data. Of the students who are older than 10 years, how many lost more than 18 baby teeth?
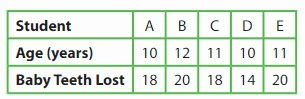
Answer:
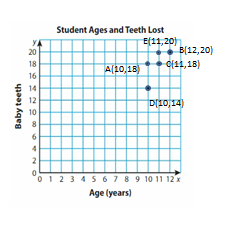
Baby teeth lost from each team A,B ,C,D.E respectively 18,20,18,14,20
B,C,E are older than 10 years
2 (B&E) students are lost more than 18 baby teeth.
Review & Refresh
Find the quotient. Then check your answer.
Question 5.
5 ÷ 0.8 = ___
Answer:
Divide two numbers 5 and 0.8
5 ÷ 0.8 = 6.25
Question 6.
91.2 ÷ 15 = __
Answer:
Divide two numbers 91.2 and 15
91.2 ÷ 15 = 6.08
Question 7.
14.4 ÷ 3.2 = ___
Answer:
Divide two numbers 14.4 and 3.2
14.4 ÷ 3.2 = 4.5
Lesson 12.5 Make and Interpret Line Graphs
Explore and Grow
The table shows the heights of a bamboo plant over several days. Show how you can use a coordinate plane to represent this information. Explain.

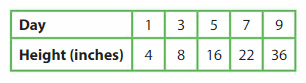
How can you use your graph to estimate the height of the plant on Day 4? Explain.
Reasoning
What could the height of the bamboo plant be on Day 10? Explain your reasoning.
Answer 42 on day 10
Think and Grow: Make and Interpret Line Graphs
Key Idea
A line graph is a graph that uses line segments to show how data values change over time.
Example
The table shows the weights of a dog over 6 months. Make a line graph of the data. Between which two months of age does the dog gain the most weight?

Step 1: Write the ordered pairs from the table.
(1, 10), (2, 20), (3, 30), (4, 50), (5, 55), (6, 58)
Step 2: For each axis, choose appropriate numbers to represent the data in the table.
Step 3: Write a title for the graph and label each axis.
Step 4: Plot a point for each ordered pair. Then connect the points with line segments.
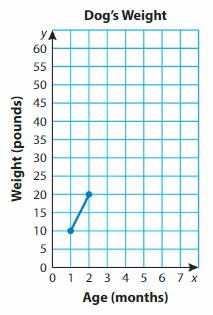
The greatest difference in weights occurs between the points (___, ___ ) and (___, ___ ).
So, the dog gains the most weight between ___ and ___ months of age.
Answer: 3&4 months age
Explanation:
The greatest difference in weights occurs between the points (_3__, __30_ ) and (__4_, __50_ ).
So, the dog gains the most weight between __3_ and _4__ months of age.
Show and Grow
Use the graph above.
Question 1.
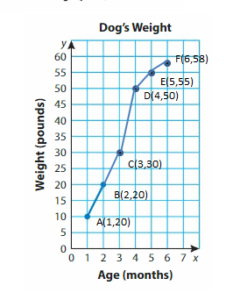
Between which two months of age does the dog gain the least amount of weight? Explain.
Answer: 55 & 58
Explanation:
The Least difference in weights occurs between the points (5__, __55_ ) and (__6_, _58_ ).
So, the dog gains the least amount of weight __5 and _6_ months of age.
Question 2.
How much do you think the dog weighs when it is 7 months of age? Explain your reasoning.
Answer: 60
Apply and Grow: Practice
Use the graph.
Question 3.
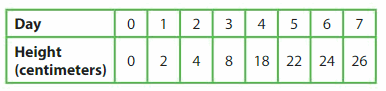
The table shows the height of a seedling over 7 days. Make a line graph of the data.
Between which two days did the seedling grow the most? Explain.
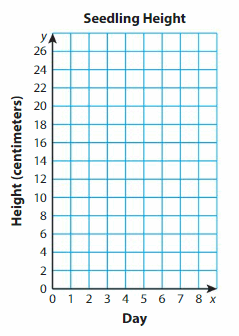
How tall do you think the seedling will be after 8 days? Explain.
Answer: 3& 4 days,
Explanation
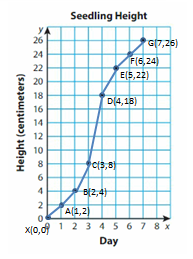
The greatest difference in seedling grow occurs between the points (_3__, __8_ ) and (__4_, _18_ ).
So, the Seeding grow between __3_ and _4__ days.
After 8 days Seeding may decrease.
Question 4.
Reasoning
Interpret the point (0, 0) in the context of the situation.
Use the graph.
Question 5.
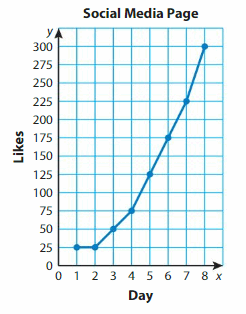
The graph shows the total numbers of likes a social media page has over 8 days. How many likes does the page have after 4 days?
What is the difference of likes on Day 7 and Day 3?
Answer: After 4 days Social media likes are 225.
Difference between 7th day Social media likes and 3rd day Social media likes are=175.
Explanation:
Given that 8th day Social media likes are 300
4th day Social media likes are 75
Difference between 8th day Social media likes and 4th day Social media likes =300-75=225
After 4 days Social media likes are 225.
Given that 7th day Social media likes are 225
3rd day Social media likes are 50
Difference between 7th day Social media likes and 3rd day Social media likes are =225-50=175.
Question 6.
DIG DEEPER!
You track the likes between Days 7 and 8 by each hour. Does the total number of likes at every hour fall between 225 and 300? Explain.
Answer: Yes:
Explanation:
The graph shows between 7th and 8th day the social media likes are increased 225 to 300.
So, the total number of likes at every hour fall between 225 and 300.
Think and Grow: Modeling Real Life
Example
The table shows your heart rate during an exercise routine. Make a line graph of the data. Use the graph to estimate your heart rate after exercising for 15 minutes.


Step 1: Write the ordered pairs from the table.
(0, 80), (10, 110), (20, 140), (30, 148), (35, 135)
Step 2: For each axis, choose appropriate numbers to represent the data in the table. You can show a break in the vertical axis between 0 and 80 because there are no data values between 0 and 80.
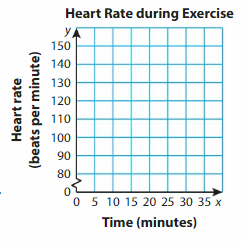
Step 3: Write a title for the graph and label each axis.
Step 4: Plot a point for each ordered pair. Then connect the points with line segments. Use the line segment that connects (10, 110) and (20, 140) to estimate your heart rate after exercising for 15 minutes.
After exercising for 15 minutes, your heart rate is about __ beats per minute.
Show and Grow
Question 7.
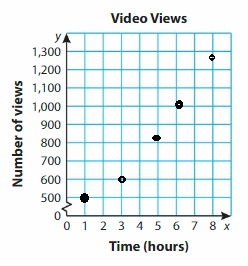
The table shows how many views a video has over several hours. Make a line graph of the data. Use the graph to estimate the total number of views the video has after 2 hours.
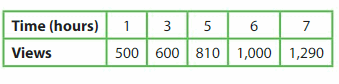
Answer:
Make and Interpret Line Graphs Homework & Practice 12.5
Example
The table shows the temperatures of a city over several hours during a snowstorm. Make a line graph of the data.
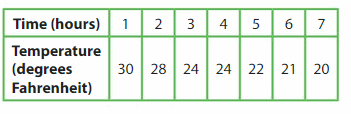
Between which two hours does the temperature decrease the most? Explain.
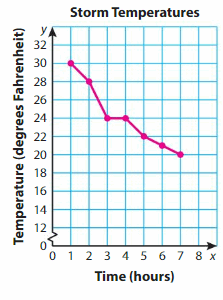
The greatest difference in temperatures occurs between the points (2, 28) and (3, 24). So, the temperature decreases the most between Hours 2 and 3.
Estimate the temperature at 4 hours and 30 minutes.
23 degrees Fahrenheit
Question 1.
The table shows the total number of pieces of beach glass you find during an hour at the beach. Make a line graph of the data.
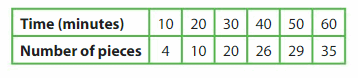
Between which two times did you find the most pieces of beach glass? Explain.
Estimate how many pieces you had after 25 minutes.
Use the graph.
Question 2.
The graph shows the total amounts of money your class raises over 8 days. How much money does your class raise after 6 days?
How much money does your class raise between Days 2 and 7?
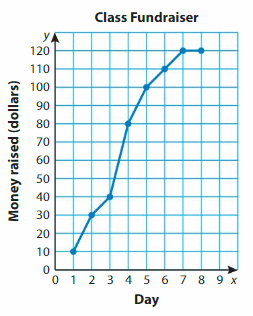
Answer:
120 – 30 = 90
Question 3.
Logic
Your friend says that your class raises $115 after 9 days. Explain why your friend’s statement does not make sense.
Answer Your friend’s statement makes sense.
Use the graph.
Question 4.
Modeling Real Life
The table shows a bald eagle’s heights above the ground after several seconds. Make a line graph of the data. Use the graph to estimate the eagle’s height above the ground after 6 seconds.
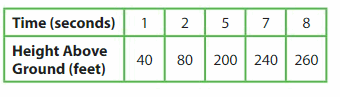
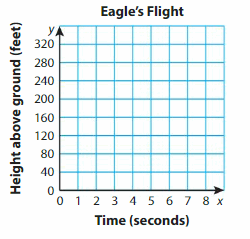
Question 5.
DIG DEEPER!
The eagle flies past her nest, which is 120 feet above the ground. After how many seconds do you think the eagle flies past her nest? Explain.
Review & Refresh
Question 6.
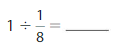
Answer: 8
Question 7.
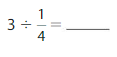
Answer: 12
Question 8.
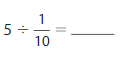
Answer: 50
Lesson 12.6 Numerical Paterns
Explore and Grow
Newton saves $10 each month. Descartes saves $30 each month. Complete each table. What patterns do you notice?
Newton:

Answer:

Descartes:

Answer:

Repeated Reasoning
How much will Newton have saved when Descartes has saved $300? Explain your reasoning.
Answer: 10 months
Think and Grow: Numerical Paterns
Example
You use 2 pounds of beef to make a batch of empanadas. Each batch makes eight servings. Complete the rule that relates the number of servings to the number of pounds of beef.

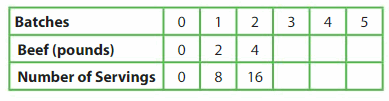
Step 1: Create each pattern and complete the table.
Use the rule “Add __” to find the number of pounds of beef.
0, 2, 4, ___, ___, ___
Use the rule “Add __” to find the number of servings.
0, 8, 16, ___, ___, ___
Step 2: Write ordered pairs that relate the number of servings to the number of pounds of beef.
(0, 0), (8, 2), (16, 4), ___, ___, ___
Step 3: Write a rule. As you make each batch, the number of pounds of beef is always __ as much as the number of servings.

So, divide the number of servings by __ to find the number of pounds of beef.
Answer:
Step 1: Create each pattern and complete the table.
Use the rule “Add __” to find the number of pounds of beef.
0, 2, 4, 6, 8, 10
Use the rule “Add __” to find the number of servings.
0, 8, 16, 24, 32, 40
Step 2: Write ordered pairs that relate the number of servings to the number of pounds of beef.
(0, 0), (8, 2), (16, 4), (24, 6), (32, 8), (40, 10)
Step 3: Write a rule. As you make each batch, the number of pounds of beef is always __ as much as the number of servings.
Show and Grow
Question 1.
Use the given rules to complete the table. Then complete the rule that relates the number of hours worked to the amount earned.
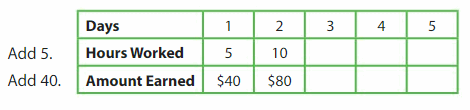
Multiply the number of hours worked by __ to find the amount earned.
Answer:
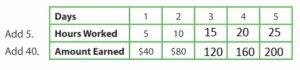
Multiply the number of hours worked by 8 to find the amount earned.
Apply and Grow: Practice
Use the given rules to complete the table. Then complete the rule.
Question 2.
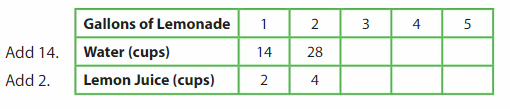
Divide the number of cups of water __ by to find the number of cups of lemon juice.
Answer:
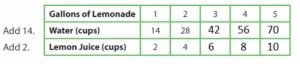
Divide the number of cups of water 7 by to find the number of cups of lemon juice.
Question 3.
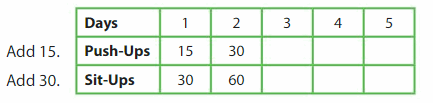
Multiply the number of push-ups by __ to find the number of sit-ups.
Answer:
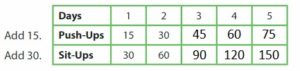
Multiply the number of push-ups by 2 to find the number of sit-ups.
Question 4.
Complete the rule. Then use the rule to complete the table.
Multiply the amount of money that Newton saves by __ to find the amount of money that Descartes saves.
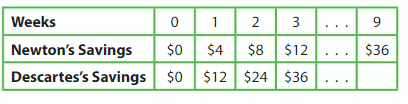
Answer:
Multiply the amount of money that Newton saves by 3 to find the amount of money that Descartes saves.
Question 5.
Structure
The ordered pairs (3, 2), (6, 4), and (9, 6) relate the number of avocados to the number of plum tomatoes in a guacamole recipe. Use the relationship to complete the table.
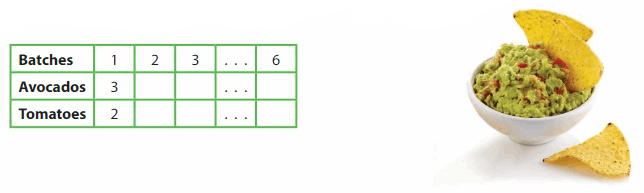
Answer:
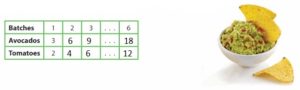
Think and Grow: Modeling Real Life
Example
For each $1 bill you pay, you get 4 tokens and can play 2 games. You have 60 tokens. How many games can you play?

Think: What do you know? What do you need to find? How will you solve?
Use a rule to create each pattern. Use a table to organize the information.

Write ordered pairs that relate the number of tokens to the number of games you can play.
(4, 2), ___, ___, ___
Write a rule. The number of games you can play is always ___ as much as the number of tokens.
So, divide the number of tokens by __ to find the number of games you can play.
60 ÷ __ = ___
So, you can play games.
Answer:
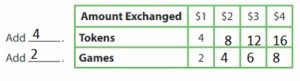
(4, 2), (8,2), (12,6), (16,8)
Write a rule. The number of games you can play is always half as much as the number of tokens.
So, divide the number of tokens by 2 to find the number of games you can play.
60 ÷ 2= 30
So, you can play 30 games.
Show and Grow
Question 6.
Each day, you read 33 pages and your friend reads 11 pages. How many pages does your friend read when you read 396 pages?
Answer: 132 pages
Explanation:
Given that,
Each day, you read 33 pages and your friend reads 11 pages.
33/11 = 3
396/3 = 132
Thus your friend read 132 pages when you read 396 pages.
Question 7.
DIG DEEPER!
Each pack of trading cards has 1 hero card, 5 combination cards, and 30 action cards. You buy packs of trading cards and get 35 combination cards. How many hero cards and action cards do you get?
Answer: 7 hero cards
Numerical Paterns Homework & Practice 12.6
Question 1.
Use the given rules to complete the table. Then complete the rule.
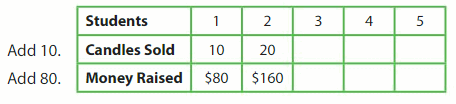
Multiply the number of candles sold by __ to find the amount of money raised.
Answer:
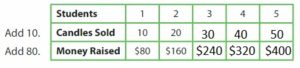
Multiply the number of candles sold by 8 to find the amount of money raised.
Question 2.
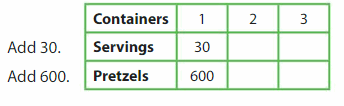
Multiply the number of servings by __ to find the number of pretzels.
Answer:
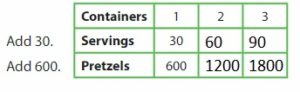
Multiply the number of servings by 20 to find the number of pretzels.
Question 3.
Complete the rule. Then use the rule to complete the table.
Divide the number of contestants by __ to find the number of winners.
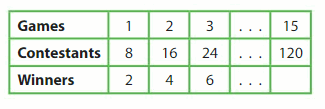
Answer:
Divide the number of contestants by 4 to find the number of winners.
Question 4.
DIG DEEPER!
Draw Figure 4. How many red squares are in Figure 8? How many yellow squares are in Figure 8? Explain your reasoning.
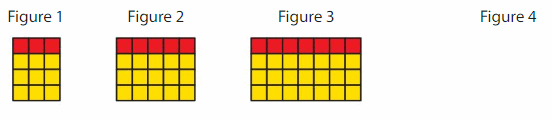
Answer:
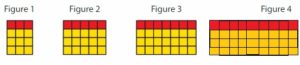
Question 5.
Modeling Real Life
Each person at a baseball game receives 3 raffle tickets and a $2 certificate for the team store. A group of people receives 39 raffle tickets. How much money in certificates does the group receive?
Answer:
Given,
Each person at a baseball game receives 3 raffle tickets and a $2 certificate for the team store. A group of people receives 39 raffle tickets.
39 × 2 = $78
Question 6.
DIG DEEPER!
Write a rule that relates the number of months to the cost of a gym membership. What is the cost of a 1-year membership?

Answer:
Given,
1 month $15
12 months = 15 × 12
= $180
Review & Refresh
Convert the mass.
Question 7.
7 g = __ mg
Answer:
Question 8.
92 g = ___ kg
Answer:
convert from grams to kgs.
92 grams = 0.92 kg
Convert the capacity
Question 9.
800 mL = __ L
Answer:
Convert from ml to l
1 ml = 0.001
800 ml = 0.8 liters
Question 10.
3 L = __ mL
Answer:
Convert from liters to ml
1 liter = 1000 ml
3 liter = 3 × 1000 ml = 3000 ml
Lesson 12.7 Graph and Analyze Relationships
Explore and Grow
Complete each table and graph the data in the coordinate plane. What do you notice about the points?
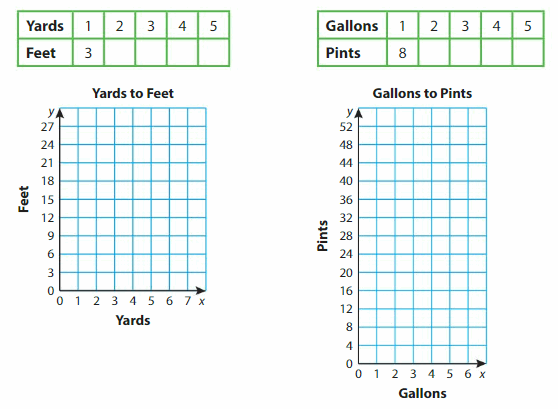
Structure
How can you use the graphs to find the number of feet in 7 yards and the number of pints in 6 gallons? Explain your reasoning.
Think and Grow: Graph and Analyze Relationships
Example
For each glass of iced tea Newton makes, he uses 2 spoonfuls of iced-tea mix and 10 fluid ounces of water. Newton uses 16 spoonfuls of iced-tea mix. How many fluid ounces of water does he use?
Step 1: Find the first several numbers in the numerical patterns for the amounts of iced-tea mix and water.
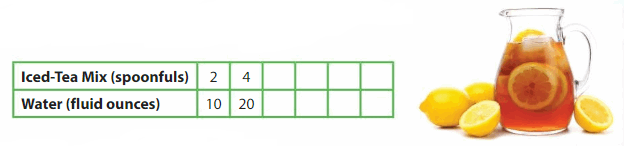
Step 2: Write the ordered pairs from the table.
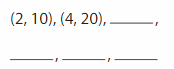

Step 3: Plot the ordered pairs. Connect the points with line segments.
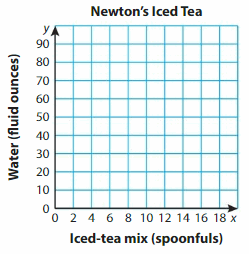
Because the ordered pairs follow a pattern, you can extend the line to the point where the x-coordinateis 16.
When the x-coordinate is 16, the y-coordinate is ___
So, Newton uses __ fluid ounces of water.
Answer:
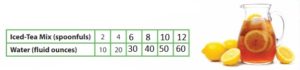
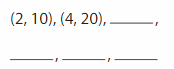
(2, 10), (4, 20), (6, 30), (8, 40), (10, 50), (12, 60), (14, 70), (16, 80)
Because the ordered pairs follow a pattern, you can extend the line to the point where the x-coordinate is 16.
When the x-coordinate is 16, the y-coordinate is 80
So, Newton uses 80 fluid ounces of water.
Show and Use
Question 1.
Use the graph above. Newton uses 18 spoonfuls of iced-tea mix. How many fluid ounces of water does he use? Explain your reasoning
Answer: 100
When the x-coordinate is 18, the y-coordinate is 100
So, Newton uses 100 fluid ounces of water.
Apply and Grow: Practice
Use the given information to complete the table. Describe the relationship between the two numerical patterns and plot the points.
Question 2.
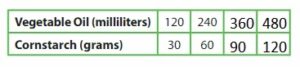
A slime recipes calls for 120 milliliters of vegetable oil and 30 grams of cornstarch. You measure 600 milliliters of vegetable oil. How many grams of cornstarch do you need?

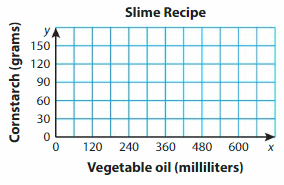
Answer:
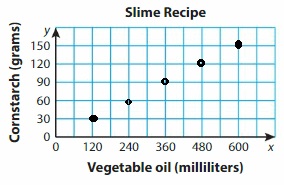
Question 3.
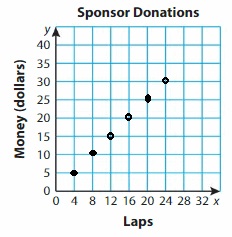
A sponsor donates $5 for every 4 laps walked around a track. How much money does the sponsor donate for 28 laps walked?
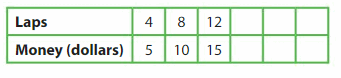
Answer:

Question 4.
Writing
How can you use the graph to determine the number of cups in 4 gallons?
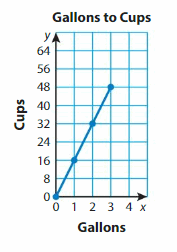
Answer: (4, 64)
Question 5.
Number Sense
What does the ordered pair (0, 0) represent in the graph?
Answer: Origin
Question 6.
DIG DEEPER!
Use the graph to determine the number of cups in 2\(\frac{1}{2}\) gallons.
Answer: 40 cups
Think and Grow: Modeling Real Life
Example
Some friends plan to go to a trampoline park for 2 hours. They want to go to the park that costs less money. Which park should they choose? What is the cost for each person?

Graph the relationship between time and cost at both parks. Park A has been done for you.
Step 1: Make a table for time and cost at Park B.
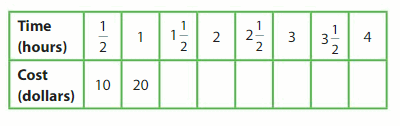
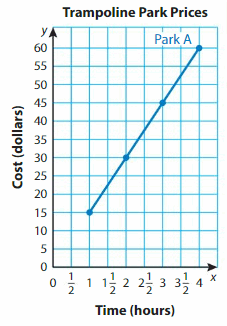
Step 2: Write the ordered pairs from the table.
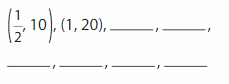
Step 3: Plot the ordered pairs. Connect the points with line segments.
Use the graph to compare the costs for 2 hours at the parks.
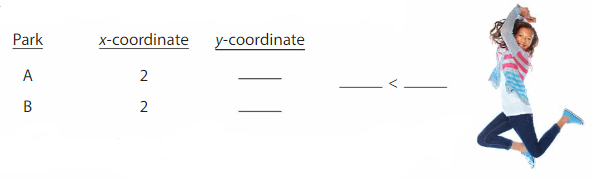
So, the group of friends should choose Trampoline Park __
The cost for each person is $ ___.
Answer:
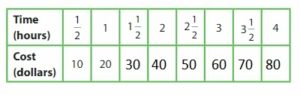
So, the group of friends should choose Trampoline Park A.
The cost for each person is $ 15.
Show and Grow
Question 7.
On your map, every centimeter represents 20 kilometers. On your friend’s map, every 2 centimeters represents 50 kilometers. On whose map does 6 centimeters represent a greater distance? How much greater? Explain.
Answer:
Given that,
On your map, every centimeter represents 20 kilometers.
On your friend’s map, every 2 centimeters represents 50 kilometers.
4 cm = 100 kilometers
6 cm = 150 kilometers
Graph and Analyze Relationships Homework & Practice 12.7
Question 1.
Use the graph above. You plan to park your car for 140 minutes. How much money do you put into the meter?
Answer: $35 for 140 minutes
Question 2.
A boxer exercises by jumping rope. He completes 150 repetitions every minute. He completes 750 repetitions. For how many minutes does he jump rope?
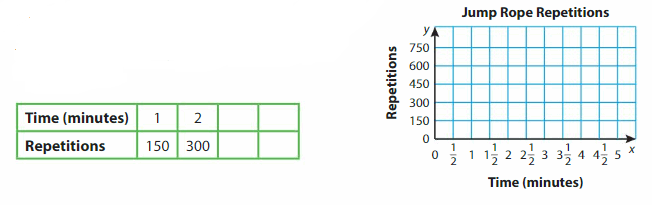
Answer:

Question 3.
YOU BE THE TEACHER
Your friend says a baker makes 60 plain bagels in 5 hours. Is your friend correct? Explain.
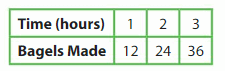
Answer: Yes, your friend is correct
Question 4.
Modeling Real Life
Some friends plan to rent bicycles for 6 hours. They want to choose the option that costs less money. Which option should they choose? What is the cost for each person?

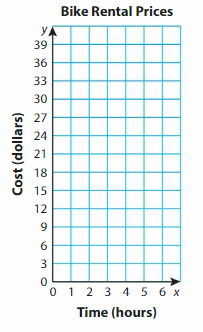
Answer: They should choose option B.
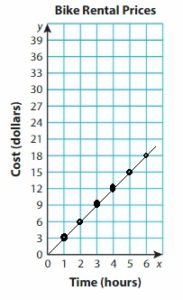
Review & Refresh
Convert the length.
Question 5.

Answer:
Convert from feet to inches
3.3 feet = 39.6 inches
Question 6.
6 mi = __ yd
Answer:
Convert from miles to yards
1 mile = 1760 yards
6 miles = 10560 yards
Patterns in the Coordinate Plane Performance Task 12
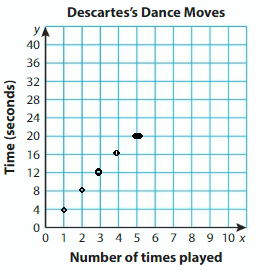
You use a series of commands on an app to create an animation of Descartes dancing and jumping.
Question 1.
a. Complete the animation commands to moveDescartes. Plot the points to show his movement.
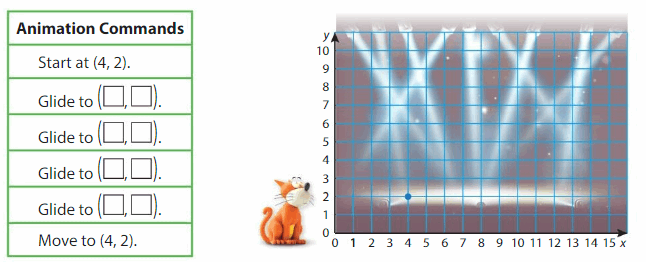
b. Connect the points. Describe the animation in your own words.
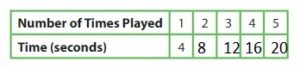
Question 2.
You play the animation commands to make Descartes dance.
a. It takes 4 seconds for Descartes to move through the animation commands 1 time. Complete the table and graph the data in the coordinate plane.

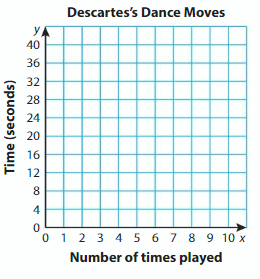
b. You want Descartes to dance for an exact number of seconds. How can you find the number of times to play the animation commands? Use an example to justify your reasoning.
Answer:
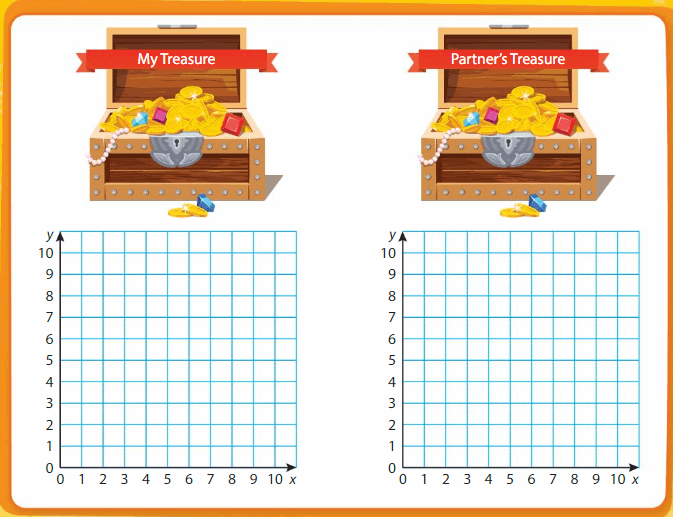
Patterns in the Coordinate Plane Treasure Hunt
Directions:
- Each player arranges four Treasure Hunt Gold Bars on the My Treasure coordinate plane, horizontally or vertically.
- On your turn, name an ordered pair in the coordinate plane. If your partner says you found part of a gold bar, then plot the ordered pair in red. Otherwise, plot the ordered pair in black. Your turn is over.
- On your partner’s turn, if your partner finds part of a gold bar, then plot a red on the ordered X pair in the coordinate plane. Tell your partner when all parts of a gold bar have been found.
- The first player to find all parts of the partner’s gold bars wins!
Patterns in the Coordinate Plane Chapter Practice 12
12.1 Plot Points in a Coordinate Plane
Use the coordinate plane to write the ordered pair corresponding to the point.
Question 1.
Point A
Answer: The ordered pair of Point A is (4, 6)
Question 2.
Point D
Answer: The ordered pair of Point B is (0, 0)
Question 3.
Point B
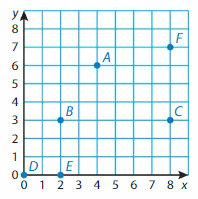
Answer: The ordered pair of Point B is (2, 3)
Question 4.
Point E
Answer: The ordered pair of Point E is (2, 0)
Question 5.
Point C
Answer: The ordered pair of Point C is (8, 3)
Question 6.
Point F
Answer: The ordered pair of Point F is (8, 7)
Plot and label the point in the coordinate plane above.
Question 7.
N(3, 0)
Answer:
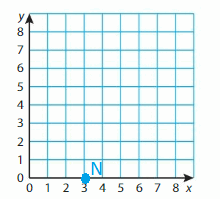
Question 8.
P(1, 5)
Answer:
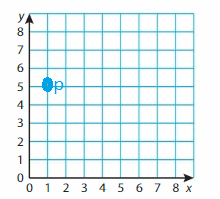
Question 9.
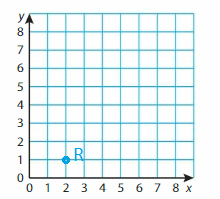
R(2, 1)
Answer:
Name the point for the ordered pair.
Question 10.
(0, 8)
Answer: G is the point for the ordered pair (0, 8)
Question 11.
(5, 6)
Answer: J is the point for the ordered pair (5, 6)
Question 12.
(4, 2)
Answer: H is the point for the ordered pair (4, 2)
Question 13.
Open-Ended
Use the coordinate plane above. Point S is 2 units from point J. Name two possible ordered pairs for point S.
Answer: The two possible ordered pairs for point S are (6, 2) or (4, 4)
12.2 Relate Points in a Cooordinate Plane
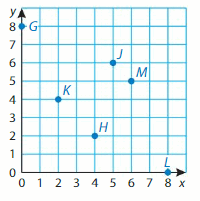
Find the distance between the points in the coordinate grid.
Question 14.
A and B
Answer:
The distance between the two points A and B is 2 units.
Question 15.
E and F
Answer: The distance between the two points E and F is 3 units.
Question 16.
C and D
Answer: The distance between the two points C and D is 7 units.
Question 17.
Which is longer, \(\overline{A C}\) or \(\overline{G E}\) ?
Answer: \(\overline{A C}\) is longer than \(\overline{G E}\).
Find the distance between the points.
Question 18.
(0, 0) and (0, 4)
Answer:
The formula for distance between the points is √(x2 – x1)² + (y2 – y1)²
= √(0 – 0)² + (4 – 0)²
= √16
= 4
Thus the distance between the points is 4.
Question 19.
(3, 2) and (3, 9)
Answer:
The formula for distance between the points is √(x2 – x1)² + (y2 – y1)²
= √(3 – 3)² + (9 – 2)²
= √49
= 7
Thus the distance between the points is 7.
Question 20.
(0, 5) and (7, 5)
Answer:
The formula for distance between the points is √(x2 – x1)² + (y2 – y1)²
= √(7 – 0)² + (5 – 5)²
= √49
= 7
Thus the distance between the points is 7.
A line passes through the given points. Name two other points that lie on the line.
Question 21.
(0, 1) and (0, 7)
Answer: (0, 5) and (0, 6) these two points lie on the same line.
Question 22.
(5, 2) and (5, 8)
Answer: (5, 3) and (5, 7) these two points lie on the same line.
Question 23.
(6, 3) and (0, 3)
Answer: (4, 3) and (3, 3) these two points lie on the same line.
12.3 Draw Polygons in a Coordinate Plane
Draw the polygon with the given vertices in a coordinate plane. Then identify it.
Question 24.
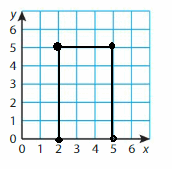
A(2, 5), B(5, 5), C(5, 0), D(2, 0)
Answer:
Question 25.
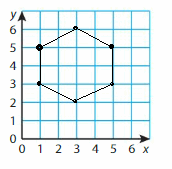
D(1, 3), E(1, 5), F(3, 6), G(5, 5), H(5, 3), J(3, 2)
Answer:
12.4 Graph Data
Question 26.
The table shows how many home runs your team scores in each of six kickball games. Graph the data.
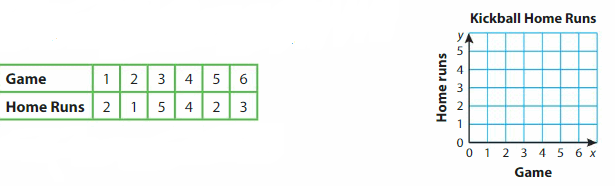
What does the point (6, 3) represent? What is the difference of the greatest number of home runs and the least number of home runs? Explain.
Answer:

(2, 1) is the least number of home runs.
12.5 Make an Interpret Line Graphs
Question 27.
The table shows the total numbers of coupon books you sell over 7 days. Make a line graph of the data.
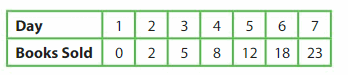
On which day do you sell the most books? Explain.
Answer: 7th day
How many books do you think you sell after 9 days? Explain.
Answer: 29 books
12.7 Numerical Patterns
Question 28.
Use the given rules to complete the table. Then complete the rule.

Multiply the number of ounces of pudding mix by __ to find the number of ounces of pumpkin.
Answer:

12.7 Graph and Analyze Relationships
Question 29.
An employee earns $80 every 8 hours. How much money does she earn after 40 hours?

Answer:
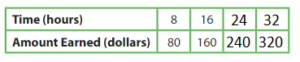
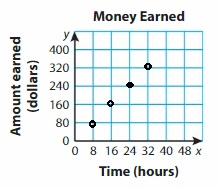
Question 30.
Modeling Real Life
A group of friends wants to play laser tag for 60 minutes. They want to go to the facility that costs less money. Which facility should they choose? What is the cost for each person?

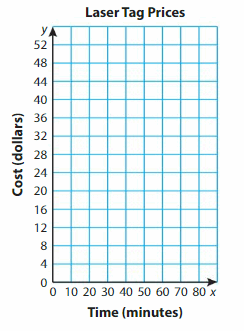
Answer: They need to choose Facility B.
Final Words:
Learn the Big Ideas Math Book 5th Grade Solution Key Chapter 12 Patterns in the Coordinate Plane provided and improve your math as well as problem-solving skills. You can achieve greater heights and fall in love with Math with our Big Ideas Math Answers Grade 5 Chapter 12 Patterns in the Coordinate Plane. Bookmark our ccssanswers.com to get the solutions of Big Ideas Math Grade 5 Chapters from 1 to 13.