Big Ideas Math Answers Grade 5 Chapter 14 Classify Two-Dimensional Shapes pdf is available here. So, the students who are in search of Big Ideas Math Book 5th Grade Answer Key Chapter 14 Classify Two-Dimensional Shapes can get them on this page. Go through the Big Ideas Math Answers Grade 5 Chapter 14 Classify Two-Dimensional Shapes and improve your performance skills. Test your skills by solving the Performance Task, Activity, Chapter Practice which is provided at the end of the chapter.
Big Ideas Math Book 5th Grade Answer Key Chapter 14 Classify Two-Dimensional Shapes
Big Ideas Math Answers 5th Grade Chapter 14 Classify Two-Dimensional Shapes are very easy to understand. You can quickly grasp the mathematical practices with the help of Big Ideas Math Answer Key Grade 5 Chapter 14 Classify Two-Dimensional Shapes. The topics covered in this chapter are Classify Triangles, Quadrilaterals, Relate Quadrilaterals. Just hit the below-provided links and Download Big Ideas Math Book 5th Grade Answer Key Chapter 14 Classify Two-Dimensional Shapes.
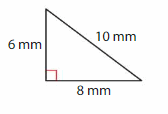
Lesson: 1 Classify Triangles
Lesson: 2 Classify Quadrilaterals
Lesson: 3 Relate Quadrilaterals
Classify Two-Dimensional Shapes
- Classify Two-Dimensional Shapes Performance Task 14
- Classify Two-Dimensional Shapes Activity
- Classify Two-Dimensional Shapes Chapter Practice 14
- Classify Two-Dimensional Shapes Cumulative Practice 1-14
- Classify Two-Dimensional Shapes Steam Performance Task 1-14
Lesson 14.1 Classify Triangles
Explore and Grow
Draw and label a triangle for each description. If a triangle cannot be drawn, explain why.

Precision
Draw a triangle that meets two of the descriptions above.
Answer:
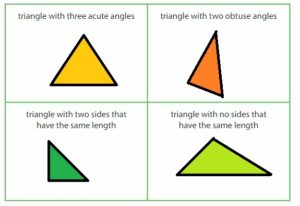
Think and Grow: Classify Triangles
Key Idea
Triangles can be classified by their sides.
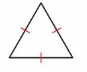
An equilateral triangle has three sides with the same length.

An isosceles triangle has two sides with the same length.
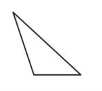
A scalene triangle has no sides with the same length.

Key Idea
Triangles can be classified by their angles.
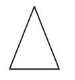
An acute triangle has three acute angles.
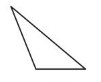
An obtuse triangle has one obtuse angle.
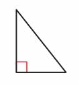
A right triangle has one right angle.

An equiangular triangle has three angles with the same measure.
Example
Classify the triangle by its angles and its sides.
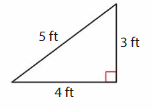
The triangle has one ___ angle
and ___ sides with the same length.
So, it is a ___ triangle.
Answer:
The triangle has one right angle
and no sides with the same length.
So, it is a right triangle.
Show and Grow
Classify the triangle by its angles and its sides
Question 1.
Answer: Equilateral triangle.
Explanation: An equilateral triangle has three sides of the same length.
Question 2.
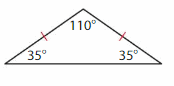
Answer: Isosceles triangle
Explanation: An Isosceles triangle has two sides of the same size. Two of its angle also measure equal.
Question 3.
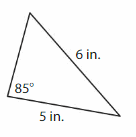
Answer: Scalene triangle.
Explanation: A Scalene triangle has no sides are congruent (same size)
Apply and Grow: Practice
Classify the triangle by its angles and its sides.
Answer: Right triangle.
Explanation: In a triangle one of the angle is a right angle (90 Deg ) called as Right triangle.
Question 5.
Answer: Isosceles triangle.
Explanation: An Isosceles triangle has two sides of the same size. Two of its angle also measure equal.
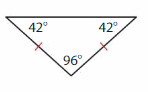
Question 6.
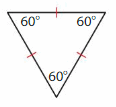
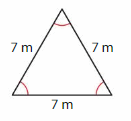
Answer: Equiangular triangle
Explanation: In an equilateral triangle, all the lengths of the sides are equal. In such a case, each of the interior angles will have a measure of 60 degrees. Since the angles of an equilateral triangle are the same, it is also known as an equiangular triangle. The figure given below illustrates an equilateral triangle.
Question 7.
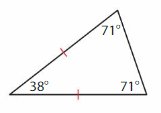
Answer: Isosceles triangle.
Explanation: An Isosceles triangle has two sides of the same length. Two of its angle also measure equal.
Question 8.
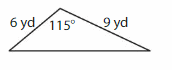
Answer: Scalene triangle.
Explanation: A Scalene triangle has no sides are congruent (Same size) and angles also all different.
Question 9.

Answer: Right triangle.
Explanation: In a triangle one of the angle is a right angle (90 deg ) called a Right triangle.
Question 10.
A triangular sign has a 40° angle, a 55° angle, and an 85° angle. None of its sides have the same length. Classify the triangle by its angles and its sides.
Answer: Scalene triangle.
Explanation: A Scalene triangle has no sides that are congruent (Same size) and angles also all different.
Question 11.
YOU BE THE TEACHER
Your friend says the triangle is an acute triangle because it has two acute angles. Is your friend correct? Explain.
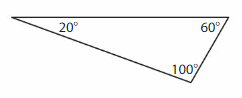
Answer: Above is no acute triangle and it is called a scalene triangle.
Explanation: A Scalene triangle has only no sides that are congruent (Same size) and angles also all different. So it is called a scalene triangle.
Question 12.
DIG DEEPER!
Draw one triangle for each category. Which is the appropriate category for an equiangular triangle? Explain your reasoning.
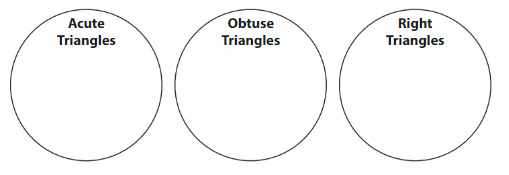
Answer:
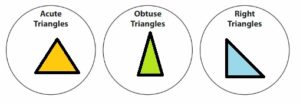
From the figure, we can say that acute triangles have the same length. So, the first triangle is the equiangular triangle.
Think and Grow: Modeling Real Life
Example
A bridge contains several identical triangles. Classify each triangle by its angles and its sides. What is the length of the bridge?
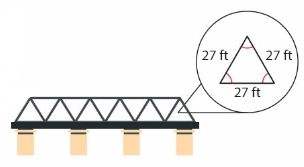
Each triangle has ___ angles with the same measure and ___ sides with the same length.
So, each triangle is ___ and ___.
The side lengths of 6 identical triangles meet to form the length of the bridge. So, multiply the side length by 6 to find the length of the bridge.
27 × 6 = ___
So, the bridge is ___ long.
Answer:
Each triangle has 3 angles with the same measure and 3 sides with the same length.
The side lengths of 6 identical triangles meet to form the length of the bridge. So, multiply the side length by 6 to find the length of the bridge.
27 × 6 = 162
So, the bridge is 162 ft long.
Show and Grow
Question 13.
The window is made using identical triangular panes of glass. Classify each triangle by its angles and its sides. What is the height of the window?
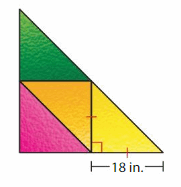
Answer:
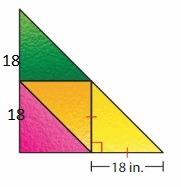
The length of the two sides of the triangle is the same.
18 in + 18 in = 36 inches
Thus the height of the window is 36 inches
Question 14.
DIG DEEPER!
You connect four triangular pieces of fabric to make the kite. Classify the triangles by their angles and their sides. Use a ruler and a protractor to verify your answer.
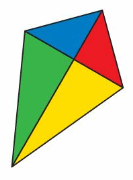
Answer:
The name of the blue triangle is isosceles right angle triangle.
The two sides of the triangle are the same.
The name of the red triangle is isosceles right-angle triangle.
The two sides of the triangle are the same.
The name of the green triangle is isosceles right angle triangle.
The two sides of the triangle are the same.
The name of the yellow triangle is isosceles right angle triangle.
The two sides of the triangle are the same.
Classify Triangles Homework & Practice 14.1
Classify the triangle by its angles and its sides.
Question 1.
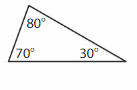
Answer: Scalene triangle.
Explanation: A Scalene triangle has only no sides that are congruent (Same size) and angles also all different. So it is called a scalene triangle
Question 2.
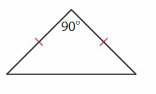
Answer: Isosceles triangle.
Explanation: An Isosceles triangle has two sides of the same size. Two of its angle also measure equal.
Question 3.
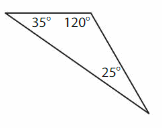
Answer: Scalene triangle.
Explanation: A Scalene triangle has no sides that are congruent (Same size) and angles also all different.
Question 4.
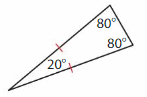
Answer: Isosceles triangle.
Explanation: An Isosceles triangle has two sides of the same length. Two of its angle also measure equal.
Question 5.
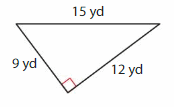
Answer: Scalene triangle.
Explanation: A Scalene triangle has no sides that are congruent (Same size) and angles also all different.
Question 6.
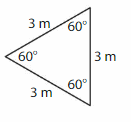
Answer: Equiangular triangle.
Explanation:
In an equilateral triangle, all the lengths of the sides are equal. In such a case, each of the interior angles will have a measure of 60 degrees. Since the angles of an equilateral triangle are the same, it is also known as an equiangular triangle. The figure given below illustrates an equilateral triangle.
Question 7.
A triangular race flag has two 65° angles and a 50° angle. Two of its sides have the same length. Classify the triangle by its angles and its sides.
Answer: Isosceles triangle.
Explanation: An Isosceles triangle has two sides of the same size. Two of its angle also measure equal.
Question 8.
A triangular measuring tool has a 90° angle and no sides of the same length. Classify the triangle by its angles and its sides.
Answer: Right triangle.
Explanation: In a triangle one of the angle is a right angle (90 Deg ) called a Right triangle.
Question 9.
Structure
Draw a triangle with vertices A(2, 2), B(2, 6), and C(6, 2) in the coordinate plane. Classify the triangle by its angles and its sides. Explain your reasoning.
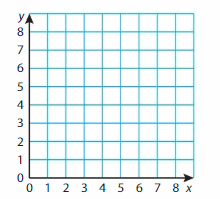
Answer:
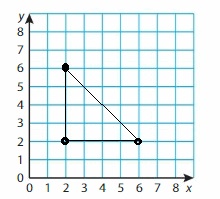
Question 10.
YOU BE THE TEACHER
Your friend says that both Newton and Descartes are correct. Is your friend correct? Explain.
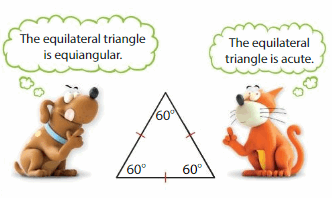
Answer: Yes
Explanation: An acute triangle is a triangle in which each angle is an acute angle. Any triangle which is not acute is either a right triangle or an obtuse triangle. All acute triangle angles are less than 90 degrees. For example, an equilateral triangle is always acute, since all angles (which are 60) are all less than 90.
Question 11.
DIG DEEPER!
The sum of all the angle measures in a triangle is 180°. A triangle has a 34° angle and a 26° angle. Is the triangle acute, right, or obtuse? Explain.
Answer: Scalene triangle.
Explanation: A Scalene triangle has no sides that are congruent (Same size) and angles also all different.
Question 12.
Modeling Real Life
A designer creates the logo using identical triangles. Classify each triangle by its angles and its sides. What is the perimeter of the logo?
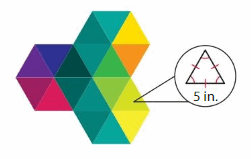
Answer: Equiangular triangle
Explanation: In an equilateral triangle, all the lengths of the sides are equal. In such a case, each of the interior angles will have a measure of 60 degrees. Since the angles of an equilateral triangle are the same, it is also known as an equiangular triangle. The figure given below illustrates an equilateral triangle.
Question 13.
DIG DEEPER!
The window is made using identical triangular panes of glass. Classify each triangle by its angles and its sides. What are the perimeter and the area of the window? Explain your reasoning.
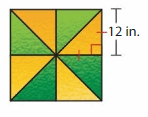
Answer: Right triangle.
Explanation: A right triangle is a triangle in which one of the angles is 90 degrees. In a right triangle, the side opposite to the right angle (90-degree angle) will be the longest side and is called the hypotenuse. You may come across triangle types with combined names like right isosceles triangle and such, but this only implies that the triangle has two equal sides with one of the interior angles being 90 degrees. The figure given below illustrates a right triangle
Review & Refresh
Question 14.
![]()
Answer : \(\frac{1}{4}\) =0.25
Explanation: 2 divides by 8 with 1/4 times, So the answer is 1/4.
Question 15.
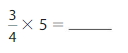
Answer : \(\frac{15}{4}\) = 3.75
Explanation: 15 divides by 4 with \(\frac{15}{4}\) times, So the answer is \(\frac{15}{4}\) or 3.75.
Question 16.
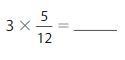
Answer : \(\frac{15}{12}\) = \(\frac{1}{4}\) = 1.25
Explanation: 15 divides by 12 with \(\frac{1}{4}\) times, So the answer is \(\frac{1}{4}\).
Lesson 14.2 Classify Quadrilaterals
Explore and Grow
Draw and label a quadrilateral for each description. If a quadrilateral cannot be drawn, explain why
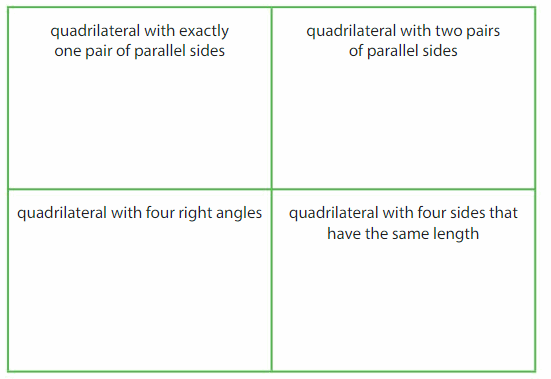
Precision
Draw a quadrilateral that meets three of the descriptions above.
Answer:
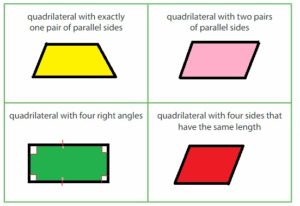
Think and Grow: Classify Quadrilaterals
Key Idea
Quadrilaterals can be classified by their angles and their sides.
A trapezoid is a quadrilateral that has exactly one pair of parallel sides.
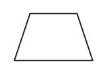
A parallelogram is a quadrilateral that has two pairs of parallel sides. Opposite sides have the same length.
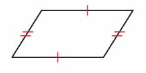
A rectangle is a parallelogram that has four right angles.
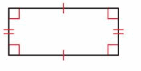
A rhombus is a parallelogram that has four sides with the same length.
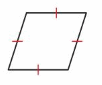
A square is a parallelogram that has four right angles and four sides with the same length.
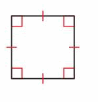
Example
Classify the quadrilateral in as many ways as possible.
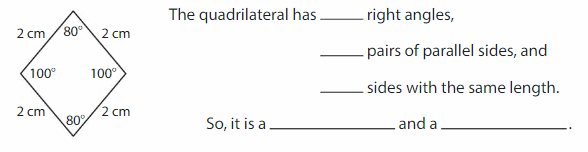
Answer:

Show and Grow
Classify the quadrilateral in as many ways as possible.
Question 1.
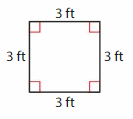
Answer: Square
Explanation: A square is a parallelogram that has four right angles and four sides with the same length.
Question 2.
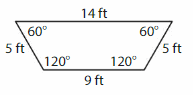
Answer: Trapezoid
Explanation: A trapezoid is a quadrilateral that has exactly one pair of parallel sides
Apply and Grow: Practice
Classify the quadrilateral in as many ways as possible.
Question 3.
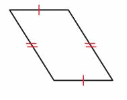
Answer: Parallelogram
Explanation: A parallelogram is a quadrilateral that has two pairs of parallel sides. The opposite sides have the same length.
Question 4.
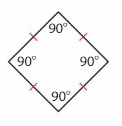
Answer: Square
Explanation: A square is a parallelogram that has four right angles and four sides with the same length.
Question 5.
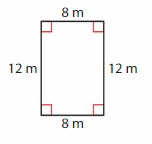
Answer: Rectangle
Explanation: A rectangle is a parallelogram that has four right angles and diagonals are congruent.
Question 6.
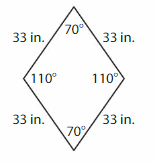
Answer: Rhombus
Explanation: A rhombus is a parallelogram with four congruent sides and A rhombus has all the properties of a parallelogram. The diagonals intersect at right angles.
Question 7.
A sign has the shape of a quadrilateral that has two pairs of parallel sides, four sides with the same length, and no right angles
Answer: Parallelogram
Explanation:
Assume that a quadrilateral has parallel sides or equal sides unless that is stated. A parallelogram has two parallel pairs of opposite sides. A rectangle has two pairs of opposite sides parallel, and four right angles.
Question 8.
A tabletop has the shape of a quadrilateral with exactly one pair of parallel sides.
Answer: A trapezoid is a quadrilateral that has exactly one pair of parallel sides. A parallelogram is a quadrilateral that has two pairs of parallel sides.
Question 9.
YOU BE THE TEACHER
Your friend says that a quadrilateral with at least two right angles must be a parallelogram. Is your friend correct? Explain.
Explanation: A trapezoid is only required to have two parallel sides. However, a trapezoid could have one of the sides connecting the two parallel sides perpendicular to the parallel sides which would yield two right angles.
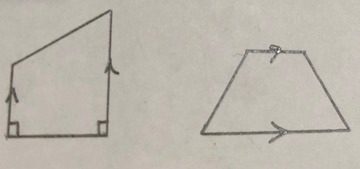
Question 10.
Which One Doesn’t Belong? Which cannot set of lengths be the side lengths of a parallelogram?
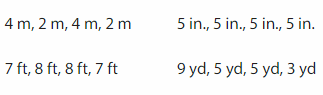
Answer: 9 yd, 5 yd, 5 yd, 3 yd
Explanation: A parallelogram is a quadrilateral that has two pairs of parallel sides. Opposite sides have the same length, So the above one is not a parallelogram.
Think and Grow: Modeling Real Life
Example
The dashed line shows how you cut the bottom of a rectangular door so it opens more easily. Classify the new shape of the door.

Draw the new shape of the door.
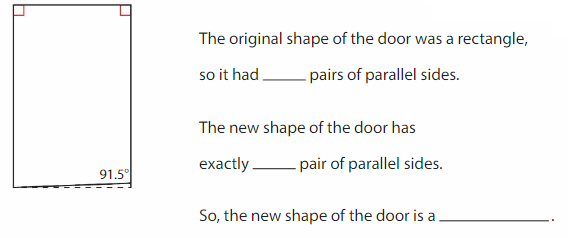
Answer:
The original shape of the door was a rectangle, so it had one pairs of parallel sides. The new shape of the door has exactly one pair of parallel sides. So, the new shape of the door is a trapezoid.
Show and Grow
Question 11.
DIG DEEPER!
The dashed line shows how you cut the corner of the trapezoidal piece of fabric. The line you cut is parallel to the opposite side. Classify the new shape of the four-sided piece of fabric.

Answer: Parallelogram
Explanation: A parallelogram is a quadrilateral that has two pairs of parallel sides. The opposite sides have the same length.
Question 12.
A farmer encloses a section of land using the four pieces of fencing. Name all of the four-sided shapes that the farmer can enclose with the fencing.
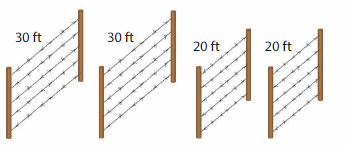
Answer: Parallelogram
Explanation: A parallelogram is a quadrilateral that has two pairs of parallel sides. Opposite sides have the same length, So four-sided shapes of fencing look like Parallelogram.
Classify Quadrilaterals Homework & Practice 14.2
Classify the quadrilateral in as many ways as possible.
Question 1.
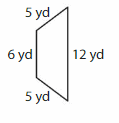
Answer: Trapezoid
Explanation: A trapezoid is a quadrilateral that has exactly one pair of parallel sides
Question 2.
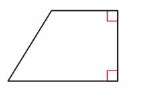
Answer: Trapezoid
Explanation: A Trapezoid is a quadrilateral with exactly one pair of parallel sides. (There may be some confusion about this word depending on which country you’re in. In India and Britain, they say trapezium; in America, trapezium usually means a quadrilateral with no parallel sides.)
Question 3.
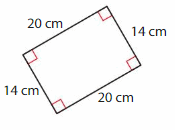
Answer: Rectangle
Explanation: A rectangle is a parallelogram that has four right angles and diagonals are congruent.
Question 4.
Answer: Square
Explanation: The diagonals of a square bisect each other and meet at 90°. The diagonals of a square bisect its angles. The opposite sides of a square are both parallel and equal in length. All four angles of a square are equal (each being 360°/4 = 90°, a right angle).
Question 5.
A name tag has the shape of a quadrilateral that has two pairs of parallel sides and four right angles. Opposite sides are the same length, but not all four sides are the same length.
Answer: Rectangle
Explanation: A rectangle is a parallelogram that has four right angles and diagonals are congruent.
Question 6.
A napkin has the shape of a quadrilateral that has two pairs of parallel sides, four sides with the same length, and four right angles.
Answer: Square
Explanation: A square is a parallelogram that has four right angles and four sides of the same length.
Question 7.
Reasoning
Can you draw a quadrilateral that is not a square, but has four right angles? Explain.
Answer: A rectangle is a parallelogram that has four right angles

Question 8.
Structure
Plot two more points in the coordinate plane to form a square. What two points can you plot to form a parallelogram? What two points can you plot to form a trapezoid? Do not use the same pair of points twice.
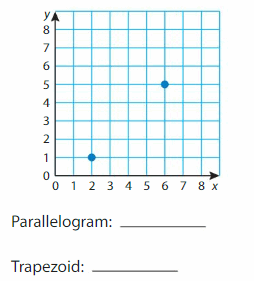
Answer:
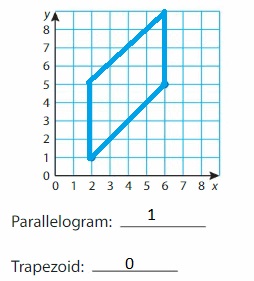
Question 9.
DIG DEEPER!
Which quadrilateral can be classified as a parallelogram, and rectangle, square, rhombus? Explain.
Answer: Square
Explanation: A square can be defined as a rhombus which is also a rectangle – in other words, a parallelogram with four congruent sides and four right angles. A trapezoid is a quadrilateral with exactly one pair of parallel sides.
Question 10.
Modeling Real Life
The dashed line shows how you fold the flap of the envelope so it closes. Classify the new shape of the envelope.
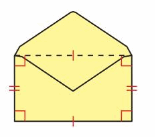
Answer: Rectangle
Explanation: A rectangle is a parallelogram that has four right angles and diagonals are congruent.
Question 11.
DIG DEEPER!
A construction worker tapes off a section of land using the four pieces of caution tape. Name all of the possible shapes that the worker can enclose with the tape.
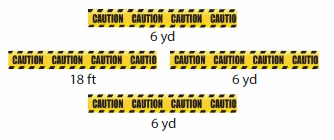
Answer: Trapezoid
Explanation: A trapezoid is a quadrilateral that has exactly one pair of parallel sides.
Question 12.
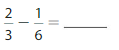
Answer: \(\frac{1}{2}\)
Explanation: \(\frac{2}{3}\) –\(\frac{1}{6}\) equal to \(\frac{1}{2}\).
Question 13.
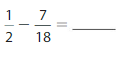
Answer: 0.112
Explanation: \(\frac{1}{2}\) is equal to 0.5 and 7/18 is equal to 0.3888.So subtraction from 0.5 to 0.3888 is 0.112.
Question 14.
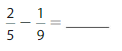
Answer: 0.289
Explanation: \(\frac{2}{5}\) is equal to 0.4 and 1/9 is equal to 0.111,So subtraction from 0.4 to 0.111is 0.289.
Lesson 14.3 Relate Quadrilaterals
Explore and Grow
Label the Venn diagram to show the relationships among quadrilaterals. The first one has been done for you.
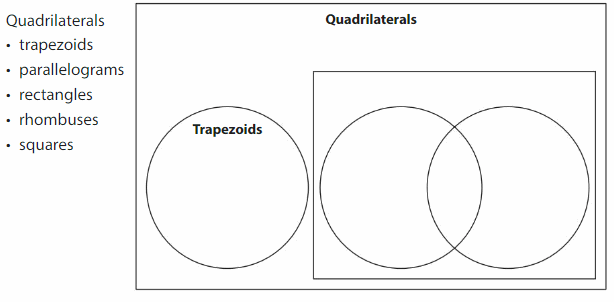
Reasoning
Explain how you decided where to place each quadrilateral.
Think and Grow: Relate Quadrilaterals
Key Idea
The Venn diagram shows the relationships among quadrilaterals.
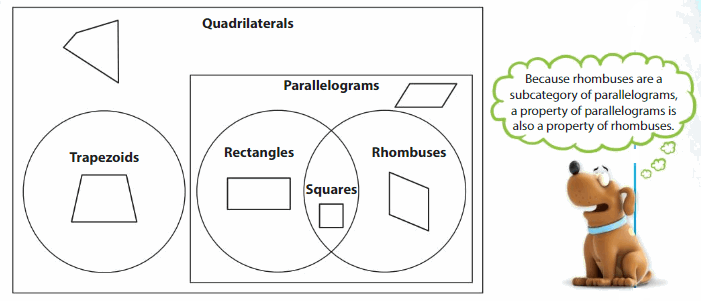
Example
Tell whether the statement is true or false.
All rhombuses are rectangles.
Rhombuses do not always have four right angles.
So, the statement is ___.
Answer: So, the statement is true.
Example
Tell whether the statement is true or false.
All rectangles are parallelograms.
All rectangles have two pairs of parallel sides.
So, the statement is ___.
Show and Grow
Tell whether the statement is true or false. Explain.
Question 1.
Some rhombuses are squares.
Answer: true
Explanation: A rhombus is a quadrilateral (plane figure, closed shape, four sides) with four equal-length sides and opposite sides parallel to each other. All squares are rhombuses, but not all rhombuses are squares. The opposite interior angles of rhombuses are congruent.
Question 2.
All parallelograms are rectangles.
Answer: False
Explanation: A rectangle is a parallelogram with four right angles, so all rectangles are also parallelograms and quadrilaterals. On the other hand, not all quadrilaterals and parallelograms are rectangles. A rectangle has all the properties of a parallelogram
Apply and Grow: Practice
Tell whether the statement is true or false. Explain.
Question 3.
All rectangles are squares.
Answer: False
Explanation: All squares are rectangles, but not all rectangles are squares.
Question 4.
Some parallelograms are trapezoids.
Answer: True
Explanation: A trapezoid has one pair of parallel sides and a parallelogram has two pairs of parallel sides. So a parallelogram is also a trapezoid.
Question 5.
Some rhombuses are rectangles.
Answer: False
Explanation: A rhombus is defined as a parallelogram with four equal sides. Is a rhombus always a rectangle? No, because a rhombus does not have to have 4 right angles. Kites have two pairs of adjacent sides that are equal.
Question 6.
All trapezoids are quadrilaterals.
Answer: True
Explanation: Trapezoids have only one pair of parallel sides; parallelograms have two pairs of parallel sides. The correct answer is that all trapezoids are quadrilaterals. Trapezoids are four-sided polygons, so they are all quadrilaterals
Question 7.
All squares are rhombuses.
Answer: True
Explanation: All squares are rhombuses, but not all rhombuses are squares. The opposite interior angles of rhombuses are congruent
Question 8.
Some trapezoids are squares.
Answer: True
Explanation: A trapezoid is a quadrilateral with at least one pair of parallel sides. In a square, there are always two pairs of parallel sides, so every square is also a trapezoid. Conversely, only some trapezoids are squares
Question 9.
Reasoning
Use the word cards to complete the graphic organizer.
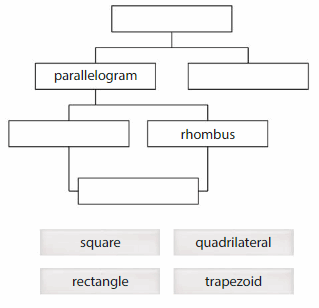
Answer: The first box to be filled with Square, 3d box to be filled with Rectangle,4th box to be filled with trapezoid and final box to be filled with Quadrilateral.
Explanation: A Square can be defined as a rhombus which is also a rectangle, in other words, a parallelogram with four congruent sides and four right angles. A trapezoid is a quadrilateral with exactly one pair of parallel sides.
Question 10.
Reasoning
All rectangles are parallelograms. Are all parallelograms rectangles? Explain.
Answer: True
Explanation: A rectangle is considered a special case of a parallelogram because, A parallelogram is a quadrilateral with 2 pairs of opposite, equal and parallel sides. A rectangle is a quadrilateral with 2 pairs of opposite, equal and parallel sides but also forms right angles between adjacent sides.
Question 11.
Precision
Newton says the figure is a square. Descartes says the figure is a parallelogram. Your friend says the figure is a rhombus. Are all three correct? Explain.

Answer: No
Explanation: A square has two pairs of parallel sides, four right angles, and all four sides are equal. It is also a rectangle and a parallelogram. A rhombus is defined as a parallelogram with four equal sides. No, because a rhombus does not have to have 4 right angles.
Think and Grow: Modeling Real Life
Example
You use toothpicks to create several parallelograms. You notice that opposite angles of parallelograms have the same measure. For what other quadrilaterals is this also true?
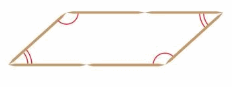
Parallelograms have the property that opposite angles have the same measure. Subcategories of parallelograms must also have this property.
___, ___, and ___ are subcategories of parallelograms.
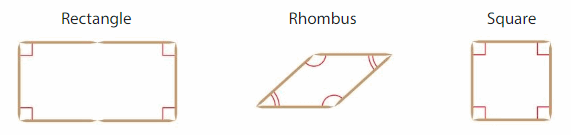
So, ___, ____, and ____ also have opposite angles with the same measure.
Answer: Rectangle, Rhombus and Square are subcategories of parallelograms.
Show and Grow
Question 12.
You use pencils to create several rhombuses. You notice that diagonals of rhombuses are perpendicular and divide each other into two equal parts. For what other quadrilateral is this also true? Explain your reasoning.
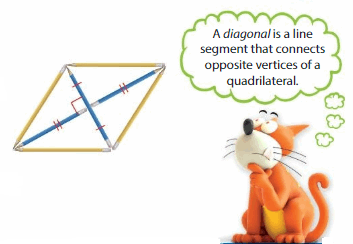
Answer: Square, Parallelogram, Rhombus are perpendicular and divided into the equal parts.
Question 13.
DIG DEEPER!
You place two identical parallelograms side by side. What can you conclude about the measures of adjacent angles in a parallelogram? For what other quadrilaterals is this also true? Explain your reasoning.

Answer:
The adjacent angles of the parallelogram is supplementary.
Opposite angles of the parallelogram are equal.
Relate Quadrilaterals Homework & Practice 14.3
Tell whether the statement is true or false. Explain.
Question 1.
All trapezoids are parallelograms.
Answer: False
All rectangles are parallelograms.
Answer: True
Question 3.
All squares are quadrilaterals.
Answer: True
Some quadrilaterals are trapezoids.
Answer: True
Question 5.
Some parallelograms are rectangles.
Answer: True
Question 6.
All squares are rectangles and rhombuses.
Answer: False
Question 7.
YOU BE THE TEACHER
Newton says he can draw a quadrilateral that is not a trapezoid and not a parallelogram. Is Newton correct? Explain.
Answer: False
Question 8.
Writing
Explain why a parallelogram is not a trapezoid.
Explanation: a square is a quadrilateral, a parallelogram, a rectangle, and a rhombus Is a trapezoid a parallelogram? No, because a trapezoid has only one pair of parallel sides.
Reasoning
Write always, sometimes, or never to make the statement true? Explain.
Question 9.
A rhombus is ___ a square.
Answer: A rhombus is some times a square
Explanation: A rhombus is a square. This is sometimes true. Â It is true when a rhombus has 4 right angles. It is not true when a rhombus does not have any right angles.
Question 10.
A trapezoid is __ a rectangle.
Answer: A trapezoid is sometimes a rectangle.
Explanation: A rectangle has one pair of parallel sides.
Question 11.
A parallelogram is ___ a quadrilateral.
Answer: A parallelogram is always a quadrilateral.
Explanation: A parallelogram must have 4 sides, so they must always be quadrilaterals.
Question 12.
DIG DEEPER!
A quadrilateral has exactly three sides that have the same length. Why can the figure not be a rectangle?
Explanation: A rectangle is a parallelogram that has four right angles. opposite sides are in the same length, so the above one is not a rectangle.
Question 13.
Modeling Real Life
You fold the rectangular piece of paper. You notice that the line segments connecting the halfway points of opposite sides are perpendicular. For what other quadrilateral is this also true?

Explanation: A rectangle is a parallelogram that has four right angles. opposite sides are in the same length, so the above one is not a rectangle.
Question 14.
DIG DEEPER!
You tear off the four corners of the square and arrange them to form a circle. You notice that the sum of the angle measures of a square is equal to 360°. For what other quadrilaterals is this also true?
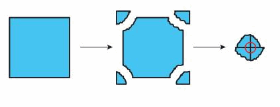
Answer: The sum of the angles in a parallelogram are 360°
Review & Refresh
Question 15.
5 pt = ___ c
Answer : 5 pt = 10 c
Explanation:
Convert from pints to cups.
1 pint = 2 cups
5 pints = 5 × 2 cups
5 pints = 10 cups
32 fl oz = ___ c
Convert from fl oz to cups.
1 fl oz = 0.125 cups
32 fl oz are equal to 4 c.
Question 17.
20 qt = ___ c
Answer : 20 qt = 80 c
Explanation:
Convert from quarts to cups.
1 quart = 4 cups
20 qt = 20 × 4 cups = 80 cups
Classify Two-Dimensional Shapes Performance Task 14
A homeowner wants to install solar panels on her roof to generate electricity for her house. A solar panel is 65 inches long and 39 inches wide.
Question 1.
a. The shape of the panel has 4 right angles. Sketch and classify the shape of the solar panel.
Answer : 
Explanation: A rectangle is a parallelogram that has four right angles. So the shape of the solar panel is a rectangle.
b. There are 60 identical solar cells in a solar panel, arranged in an array. Ten cells meet to form the length of the panel, and six cells meet to form the width. Classify the shape of each solar cell. Explain your reasoning.

Answer: A rectangle is a parallelogram that has four right angles. So the shape of the solar panel is a rectangle.
Question 2.
The home owner measures three sections of her roof.
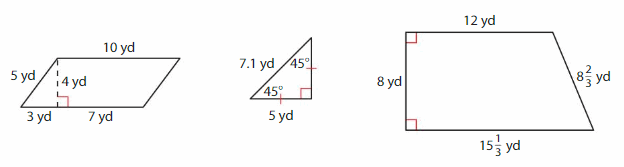
a. Classify the shape of each section in as many ways as possible.
Answer: Right triangle.
Explanation: In a triangle one of the angle is a right angle (90 Deg ) called as Right triangle
Answer: Rectangle
Explanation: Rectangle is a parallelogram with four right angles, so all rectangles are also parallelograms and quadrilaterals. On the other hand, not all quadrilaterals and parallelograms are rectangles.
Answer: Isosceles trapezoid
Explanation: An isosceles trapezoid is a trapezoid whose non-parallel sides are congruent.
b. About how many solar panels can fit on the measured sections of the roof? Explain your reasoning.
Question 3.
One solar panel can produce about 30 kilowatt-hours of electricity each month. The homeowner uses her electric bills to determine that she uses about 1,200 kilowatt-hours of electricity each month.
a. How many solar panels should the homeowner install on her roof?
Answer: 40 Solar panels
Explanation: 40 Solar panels X 30 kilowatt-hours of electricity each month per one solar panel equal to 1,200 kilowatt-hours of electricity per month, So the answer is 40 solar panels.
b. Will all of the solar panels fit on the measured sections of the roof? Explain.
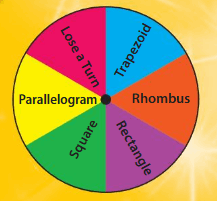
Classify Two-Dimensional Shapes Activity
Quadrilateral Lineup
Directions:
- Players take turns spinning the spinner.
- On your turn, cover a quadrilateral that matches your spin.
- If you land on, Lose a turn, then do not cover a quadrilateral.
- The first player to get four in a row twice, horizontally, vertically, Recor diagonally, wins!

Classify Two-Dimensional Shapes Chapter Practice 14
14.1 Classify Triangles
Classify the triangle by its angles and its sides.
Question 1.
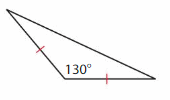
Answer: Scalene triangle.
Explanation: A Scalene triangle has no sides that are congruent (Same size) and angles also all different.
Question 2.
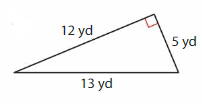
Answer: Right triangle.
Explanation: In a triangle one of the angle is a right angle (90 deg ) called as Right triangle.
Question 3.
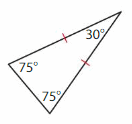
Answer: Isosceles triangle.
Explanation: An Isosceles triangle has two sides of the same length. Two of its angle also measure equal.
Question 4.
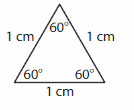
Answer: Equiangular triangle
Explanation: In an equilateral triangle, all the lengths of the sides are equal. In such a case, each of the interior angles
Question 5.
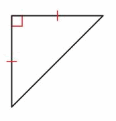
Answer: Right triangle.
Explanation: In a triangle one of the angle is a right angle (90° ) called as Right triangle.
Question 6.
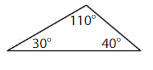
Answer: Scalene triangle.
Explanation: A Scalene triangle has no sides that are congruent (Same size) and angles also all different.
14.2 Classify Quadrilaterals
Classify the quadrilateral in as many ways as possible.
Question 7.
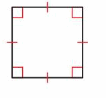
Answer: Square
Explanation: A square is a parallelogram that has four right angles and four sides of the same length.
Question 8.
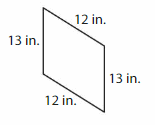
Answer: Rectangle
Explanation: A rectangle is a parallelogram that has four right angle, Opposite sides are the same length
Question 9.
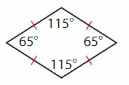
Answer: Square
Explanation: The diagonals of a square bisect each other and meet at 90°. The diagonals of a square bisect its angles. The opposite sides of a square are both parallel and equal in length. All four angles of a square are equal (each being 360°/4 = 90°, a right angle).
Question 10.
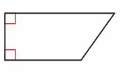
Answer: Isosceles trapezoid
Explanation: An isosceles trapezoid is a trapezoid whose non-parallel sides are congruent.
Question 11.
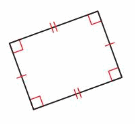
Answer: Rectangle
Explanation: A rectangle is a parallelogram that has four right angle, Opposite sides are the same length
Question 12.
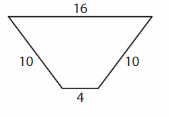
Answer: Trapezoid
Explanation: A trapezoid is a quadrilateral that has exactly one pair of parallel sides.
Question 13.
Structure
Plot two more points in the coordinate plane to form a quadrilateral that has exactly two a rectangle. What two points can you plot to form a trapezoid? What two points can you plot to form a rhombus? Do not use the same pair of points twice.
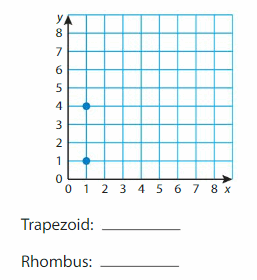
Answer:

Question 14.
Reasoning
Can you draw a quadrilateral that has exactly two right angles? Explain.
Explanation: A quadrilateral with only 2 right angles and it is called a trapezoid .

Question 15.
Modeling Real Life
The dashed line shows how you break apart the graham cracker. Classify the new shape of each piece of the graham cracker.

Answer: Square
Explanation: The diagonals of a square bisect each other and meet at 90°.
14.3 Relate Quadrilaterals
Tell whether the statement is true or false.
Question 16.
All rectangles are quadrilaterals.
Answer: True
Explanation: A closed figure with four sides. For example, kites, parallelograms, rectangles, rhombuses, squares, and trapezoids are all quadrilaterals
Question 17.
Some parallelograms are squares.
Answer: True
Explanation: Squares fulfill all criteria of being a rectangle because all angles are right angle and opposite sides are equal. Similarly, they fulfill all criteria of a rhombus, as all sides are equal and their diagonals bisect each other.
Question 18.
All trapezoids are rectangles.
Answer: False
Explanation: Rectangles are defined as a four-sided polygon with two pairs of parallel sides. On the other hand, a trapezoid is defined as a quadrilateral with only one pair of parallel sides.
Question 19.
Some rectangles are rhombuses.
Answer: True
Explanation: A rectangle is a parallelogram with all its interior angles being 90 degrees. A rhombus is a parallelogram with all its sides equal. This means that for a rectangle to be a rhombus, its sides must be equal. A rectangle can be a rhombus only if has extra properties which would make it a square
Question 20.
Some squares are trapezoids.
Answer: True
Explanation: The definition of a trapezoid is that it is a quadrilateral that has at least one pair of parallel sides. A square, therefore, would be considered a trapezoid.
Question 21.
All quadrilaterals are squares.
Answer: False
Explanation : Quadrilateral: A closed figure with four sides. For example, kites, parallelograms, rectangles, Square: A rectangle with four sides of equal length. Trapezoid: A quadrilateral with at least one pair of parallel sides So, All quadrilaterals are not squares.
Classify Two-Dimensional Shapes Cumulative Practice 1-14
Question 1.
Which model shows 0.4 × 0.2?
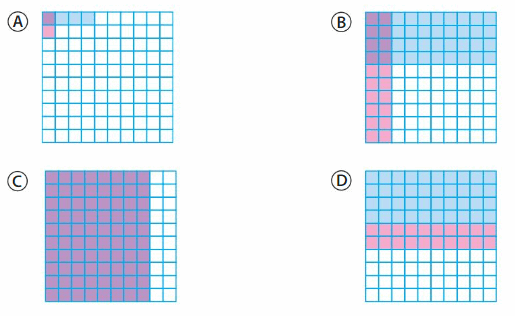
Answer:
Question 2.
A triangle has angle measures of 82°, 53°, and 45°. Classify the triangle by its angles.

Answer: C
Explanation: An obtuse triangle has one angle measuring more than 90º but less than 180º (an obtuse angle). It is not possible to draw a triangle with more than one obtuse angle
Question 3.
Which expressions have an estimated difference of \(\frac{1}{2}\) ?
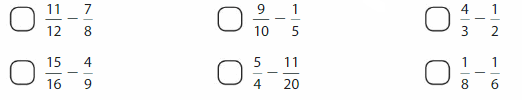
Answer:
Question 4.
A rectangular prism has a volume of 288 cubic centimeters. The height of the prism is 8 centimeters. The base is a square. What is a side length of the base?
![]()
Answer: A
Explanation: volume of a rectangular prism, multiply its 3 dimensions: length x width x height. The volume is expressed in cubic units. So,6 X 6 X 8 is equal to 288 cubic centimeters, Therefore the side length of the base is 6 cm.
Question 5.
A sandwich at a food stand costs $3.00. Each additional topping costs the same extra amount. The coordinate plan shows the costs, in dollars, of sandwiches with different numbers of additional toppings. What is the cost of a sandwich with 3 additional toppings?

Answer:
Question 6.
Which statements are true?

Answer: The following statements are true
Option 2,option 3 and option 4 .
Explanation :
Option 2 :
All squares are rectangles are parallelograms is true, why because squares fulfill all criteria of being a rectangle because all angles are right angle and opposite sides are equal. Similarly, they fulfill all criteria of a rhombus, as all sides are equal and their diagonals bisect each other.
Option 3: All squares are rhombuses is true, why because All squares are rhombuses, but not all rhombuses are squares. The opposite interior angles of rhombuses are congruent.
Option 4: Every trapezoid is a quadrilateral is true, why because Trapezoids have only one pair of parallel sides; parallelograms have two pairs of parallel sides.
Question 7.
Your friend makes a volcano for a science project. She uses 10 cups of vinegar. How many pints of vinegar does he use?

Answer: Option B
Explanation: 1 cup is equal to 0.5 pints, therefore 10 cups are equal to 5 pints.
Question 8.
The volume of the rectangular prism is 432 cubic centimeters. What is the length of the prism?
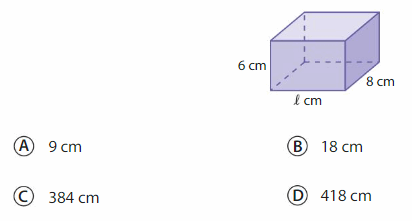
Answer: Option A
Explanation: volume of a rectangular prism, multiply its 3 dimensions: length x width x height. The volume is expressed in cubic units.
So, 6 cm X 9 cm X 8 cm is equal to 432 cubic centimeters.
Therefore the length of prim is 9 cm.
Question 9.
Descartes draws a pentagon by plotting another point in the coordinate plane and connecting the points. Which coordinates could he use?

Answer:
Question 10.
Newton rides to the dog park in a taxi. He owes the driver $12. He calculates the driver’s tip by multiplying $12 by 0.15. How much does he pay the driver, including the tip?
Answer: Option C
Explanation: Driver cost $12 + ($12 X 0.15 )= 12+1.8 =13.8
Therefore answer is $13.8.
Question 11.
A quadrilateral has four sides with the same length, two pairs of parallel sides, and four 90° angles. Classify the quadrilateral in as many ways as possible.

Answer: Square, Parallelogram
Explanation: A quadrilateral has four sides with the same length, two pairs of parallel sides and four 90° angles is called as square. All squares are parallelograms.
Question 12.
Which ordered pair represents the location of a point shown in the coordinate plane?

Answer:
Question 13.
What is the product of 5,602 and 17?

Answer: 95234
Explanation: 5602 X 17 is equal to 95234.
Question 14.
Which pair of points do not lie on a line that is perpendicular to the x-axis?

Answer:
Question 15.
Newton has a gift in the shape of a rectangular prism that has a volume of 10,500 cubic inches. The box he uses to ship the gift is shown.

Part A What is the volume of the box?
Part B What is the volume, in cubic inches, of the space inside the box that is not taken up by gift? Explain.?
Answer:
Question 16.
Which expressions have a product greater than \(\frac{5}{6}=\)?
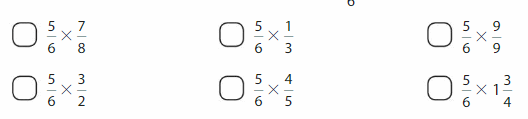
Answer:
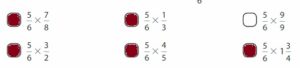
Question 17.
Newton is thinking of a shape that has 4 sides, only one pair of parallel sides, and angle measures of 90°, 40°, 140°, and 90°. Which is Newton’s shape?

Answer: D
Explanation: Trapezoid Only one pair of opposite sides is parallel.
Question 18.
Which rectangular prisms have a volume of 150 cubic feet?
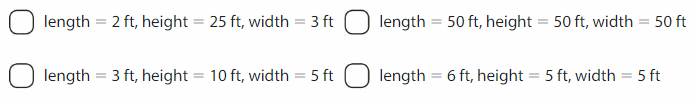
Answer: Option 1
Explanation: volume of a rectangular prism, multiply its 3 dimensions: length x width x height. The volume is expressed in cubic feet.
So,2 ft X 25 ft X 3 ft is equal to 150 cubic ft, Therefore the right answer is option 1.
Classify Two-Dimensional Shapes Steam Performance Task 1-14
Each student in your grade makes a constellation display by making holes for the stars of a constellation on each side of the display. Each display is a rectangular prism with a square base.

Question 1.
Your science teacher orders a display for each student. The diagram shows the number of packages that can fit in a shipping box.
a. How many displays come in one box?

b. There are 108 students in your grade. How many boxes of displays does your teacher order? Explain.
c. The volume of the shipping box is 48,000 cubic inches. What is the volume of each display?
d. The height of each display is 15 inches. What are the dimensions of the square base?
e. Estimate the dimensions of the shipping box.
f. You paint every side of the display except the bottom. What is the total area you will paint?
g. You need a lantern to light up your display. Does the lantern fit inside of your display? Explain.
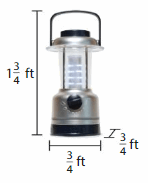
Question 2.
On one side of your display, you create an image of the constellation Libra. Each square on the grid is 1 square inch.
a. Classify the triangle formed by the points of the constellation.
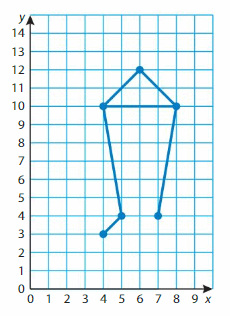
Answer: Equiangular triangle
Explanation: In an equilateral triangle, all the lengths of the sides are equal. In such a case, each of the interior angles
b. What are the coordinates of the points of the constellation?
c. What is the height of the constellation on your display?
Question 3.
You use the coordinate plane to create the image of the Big Dipper.
a. Plot the points A(6, 2), B(8, 2), C(7, 6), D(5, 5), E(7, 9), F(6, 12), and G(4, 14).
b. Draw lines connecting the points of quadrilateral ABCD. Draw \(\overline{C E}\), \(\overline{E F}\) and \(\overline{F G}\).

Answer:
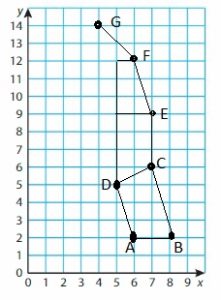
c. Is quadrilateral ABCD a trapezoid? How do you know?
Answer: Yes ABCD is a trapezoid because all sides are not equal and only one pair has parallel sides.
Question 4.
Use the Internet or some other resource to learn more about constellations. Write one interesting thing you learn.
Answer: A constellation is a group of stars that appears to form a pattern or picture like Orion the Great Hunter, Leo the Lion, or Taurus the Bull. Constellations are easily recognizable patterns that help people orient themselves using the night sky. There are 88 “official” constellations.
Conclusion:
Sharpen your math skills by practicing the problems from Big Ideas Math Book 5th Grade Answer Key Chapter 14 Classify Two-Dimensional Shapes. All the solutions of Grade 5 Chapter 14 Classify Two-Dimensional Shapes are prepared by the math professionals. Thus you can prepare effectively and score good marks in the exams.