In order to solve real-life mathematical problems, students must understand the concept behind the question. You have to know what is probability. This is the most interesting chapter among all the grade 7 chapters. Download Free Pdf of Big Ideas Math Answers Grade 7 Chapter 7 Probability to practice the exercise and homework problems.
Big Ideas Math Book 7th Grade Answer Key Chapter 7 Probability
Improve your math skills with the help of Big Ideas Math Answers Grade 7 Chapter 7 Probability. Unlimited practice with all the question and answers along with the practice test. It is mandatory to practice with the Big Ideas Math Answer Key for Grade 7 Chapter 7 Probability to secure maximum marks in the exams. Check out the links given the below sections before you start your preparation.
Performance Task
Lesson: 1 Probability
Lesson: 2 Experimental and Theoretical Probability
- Lesson 7.2 Experimental and Theoretical Probability
- Experimental and Theoretical Probability Homework & Practice 7.2
Lesson: 3 Compound Events
Lesson: 4 Simulations
Chapter: 7 – Probability
- Probability Connecting Concepts
- Probability Chapter Review
- Probability Practice Test
- Probability Cumulative Practice
Probability STEAM Video/Performance Task
STEAM Video
Massively Multiplayer Rock Paper Scissors.
You can use experimental probability to describe the percent of times that you win, lose, or tie in Rock Paper Scissors. Describe a real-life situation where it is helpful to describe the percent of times that a particular outcome occurs.
Watch the STEAM Video “Massively Multiplayer Rock Paper Scissors.”Then answer the following questions.
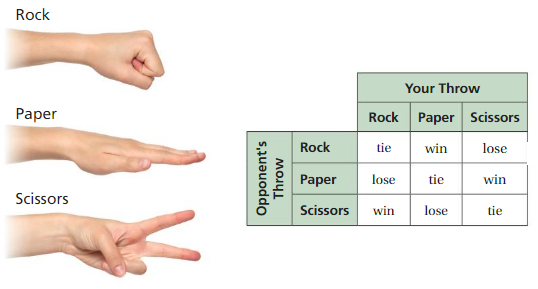
1. The table shows the ways that you can win, lose, or tie in Rock Paper Scissors. You and your opponent throw the signs for rock, paper, or scissors at random. What percent of the time do you expect to win? lose? tie?
2. You play Rock Paper Scissors 15 times. About how many times do you expect to win? Explain your reasoning.
Performance Task
Fair and Unfair Carnival Games
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task.

You will be given information about a version of Rock Paper Scissors used at a carnival. Then you will be asked to design your own “unfair” carnival game using a spinner or a number cube, and test your game with a classmate.
In what ways can a game of chance be considered fair? unfair? Explain your reasoning.
Probability Getting Ready for Chapter 7
Chapter Exploration
Work with a partner.
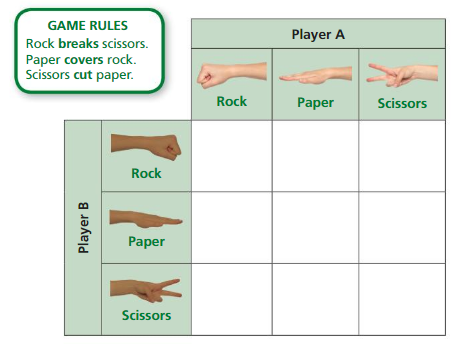
1. Play Rock Paper Scissors 30 times. Tally your results in the table.
2. How many possible results are there?
3. Of the possible results, in how many ways can Player A win? In how many ways can Player B win? In how many ways can there be a tie?
4. Is one of the players more likely to win than the other player? Explain your reasoning.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
probability
theoretical probability
simulation
relative frequency
sample space
experimental probability
compound event
Lesson 7.1 Probability
EXPLORATION 1
Determining Likelihood
Work with a partner. Use the spinners shown.
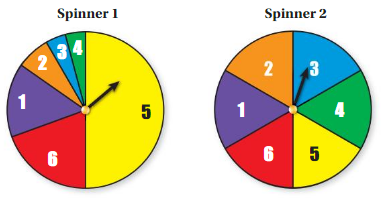
a. For each spinner, determine which numbers you are more likely to spin and which numbers you are less likely to spin. Explain your reasoning.
b. Spin each spinner 20 times and record your results in two tables. Do the data support your answers in part(a)? Explain why or why not.
c. How can you use percents to describe the likelihood of spinning each number? Explain.
Answer:

Try It
Question 1.
You randomly choose one of the tiles shown from a hat.

a. How many possible outcomes are there?
Answer:
There are 5 number of unique possible outcomes
They are { A,B,C,D,E}
Therefore, there are 5 possible outcomes for the event.
b. What are the favorable outcomes of choosing a vowel ?
Answer:
There are 2 favorable outcomes of choosing an vowel
They are {A,E}
Therefore, there are 2 favorable outcomes of choosing an vowel.
C. In how many ways can choosing a consonant occur?
Answer: 3 ways
Explanation:
There are 3 unique consonant tiles. They are {B,C,D}
Describe the likelihood of the event given its probability.
Question 2.
The probability that you land a jump on a snowboard is \(\frac{1}{10}\).
Answer:
Given, Probability of landing a jump on snowboard = 1/10 = 0.1
So, the likelihood of the event of jumping on to the snowboard after every jump is 1 out of 10 times.
Question 3.
There is a 100% chance that the temperature will be less than 120°F tomorrow.
Answer:
Certain event .
Given that , there is 100% chance that the temperature will be less than 1200 F tomorrow.
The probability for a certain event is P(E)= 1.
So, the probability that the temperature being 1200 F tomorrow is 1.
Question 4.
You attempt three-point shots on a basketball court and record the number of made and missed shots. Describe the likelihood of each event.̇̇̇̇̇̇̇̇̇
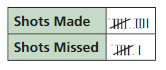
̇̇a. You make your next shot.
b. You miss your next shot.
Answer:
a.
Explanation:
Total number of shots = 15
Frequency of shots made = 9
The likelihood of making next shot is
Shots made/ Total = 9/15=0.6
So, the next shot is likely to occur
b.
Explanation:
Total number of shots = 15
Frequency of missed shots = 6
The likelihood of the next shot will miss is shots missed/ Total =6/15 0.4
So, the next shot is not likely to occur.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
IDENTIFYING OUTCOMES
You roll a number cube. What are the possible outcomes?

Answer: 6
A cube has 6 faces .
They are {1,2,3,4,5,6} .
There are 6 possible outcomes.
Therefore , there are 6 possible outcomes for a cube.
Question 6.
USING RELATIVE FREQUENCIES
A bag contains only red marbles and blue marbles. You randomly draw a marble from the bag and replace it. The table shows the results of repeating this experiment. Find the likelihood of each event.̇̇̇̇̇̇̇̇̇̇
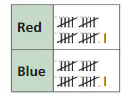
a. The next marble you choose is red. ̇̇
b. The next marble you choose is neither red nor blue.
Answer:
a.
Explanation:
Total number of balls = 42
Number of red balls = 21
The likelihood of drawing the red marble in the next turn=
Number of red balls/ Total number of balls
= 21/42 =0.5
There is only 50% chance of chance of drawing a red ball in the next turn
So, the likelihood of the event is may or ,ay not occur evenly.
b.The likelihood of drawing neither red nor blue ball is 0
0%= Impossible
Because, there are only red and blue marbles
So, it is impossible to draw another ball other than red and blue.
Therefore, the likelihood of the event is cannot occur
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
The table shows the number of days you have a pop quiz and the number of days you do not have a pop quiz in three weeks of school. How many days can you expect to have a pop quiz during a 180-day school year? Explain.
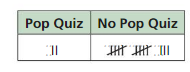
Answer:
Total number of days for pop quiz for 3 weeks = 2
Total frequency = 15
Now, the number of times to have a pop quiz in 180 days be x
Total number of days =180
2/15 = x/180
15x = 360
x = 360/ 15
x = 24
Therefore, we can expect 24 days to have a pop quiz during a 180-day school year.
Question 8.
In a football game, the teams pass the ball on 40% of the plays. Of the passes thrown, greater than 75% are completed. You watch the film of a randomly chosen play. Describe the likelihood that the play results in a complete pass. Explain your reasoning.
Answer:
Given ,
The team pass the ball on 40% of the plays
And also, 75% are completed
75% = 0.75
Therefore 75% = 3/4
Therefore , the likelihood is likely to happen of the plays results in a complete pass = 0.34
Probability Homework & Practice 7.1
Review & Refresh
An account earns simple interest. Find the interest earned.
Question 1
$700 at 3% for 4 years
Answer: $84
The formula for simple interest= Principal x rate x time
I = P x r x t
= $700 x0.03 x 4 =$84
Therefore , the interest earned = $84
Question 2.
$650 at 2% for 6 years
Answer: $78
The formula for simple interest= Principal x rate x time
I = P x r x t
= $650 x0.02 x 6 =$78
Therefore , the interest earned = $78
Question 3.
$480 at 1.5% for 5 years
Answer: $36
The formula for simple interest= Principal x rate x time
I = P x r x t
= $480 x0.015 x 5 =$36
Therefore , the interest earned = $36
Question 4.
$1200 at 2.8% for 30 months
Answer: $84
The formula for simple interest= Principal x rate x time
I = P x r x t
= $1200 x0.028 x 2.5 =$84
Therefore , the interest earned = $84
Write the indicated ratio. Then find and interpret the value of the ratio.

Question 5.
rolled oats : chopped peanuts
Answer:
2 : 1/2
2/1 : 1/2
Multiplying with 2
2/1 x 2 : 1/2 x 2
4/2 : 2/4
2/1 : 1/2
2/1 x 2 : 1/2:2
4 : 1
Therefore, the value of ratio = 4: 1
Question 6.
sunflower seeds : pumpkin seeds
Answer:
1/3 :1/4
Multiplying with 12
1/3 x 12 : 1/4 x 12
12/36 : 12/ 48
1/3: 1 /4
1/3 x 12 : 1/4 x12
12/3 : 12/4
4 : 3
Therefore, the ratio = 4 : 3
Question 7.
pumpkin seeds : rolled oats
Answer:
1/4 :2
On multiplying with 4
1/4 x 4 : 2/1 x 4
4/16 : 8/4
1/4: 2
1/4 x 4 : 2 x 4
1 : 8
Therefore , ratio = 1:8
Solve the inequality. Graph the solution.
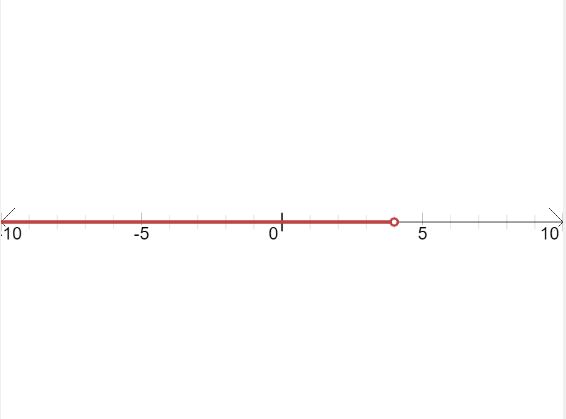
Question 8.
x + 5 < 9
Answer: x<4
Explanation:
x + 5 < 9
=x < 9-5
x<4
So, the inequality form = x<4
Graph:
Question 9.
b – 2 ≥ – 7
Answer: b≥-5
Explanation:
b – 2 ≥ – 7
= b ≥ -7+2
= b≥-5
Graph:
Question 10.
1 > – \(\frac{w}{3}\)
Answer:
Question 11.
6 ≤ – 2g
Answer: g≤ -3
Explanation:
= g≤ 6/-3
= g≤ -3
The inequality = g≤ -3
Graph:
Concepts, Skills, & Problem Solving
DETERMINING LIKELIHOOD Determine which numbers you are more likely to spin and which numbers you are less likely to spin. Explain your reasoning. (See Exploration 1, p. 283.)
Question 12.
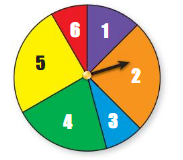
Answer:
The spinner is divided into 6 parts (unequal)
They are numbered as {1,2,3,4,5,6}
The numbers {2,4,5} are more likely to happen
Because, they occupy more space than remaining.
And , the numbers {1,3,6] are less likely to happen
Because , they occupy less space .
Question 13.
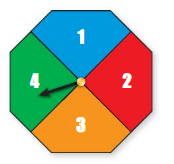
Answer:
The spinner is divided into 4 equal parts
The 4 parts are numbered as {1,2,3,4}
So, each number have equal chance of spinning
Such events are also called as equally likely happen events.
IDENTIFYING OUTCOMES You spin the spinner shown.

Question 14.
How many possible outcomes are there?
Answer: 8
Explanation:
The spinner is divided into 8 equal parts
The number of possible outcomes for the spinner are 8
{ 1,2,3,4,5,6,7,8}
Question 15.
What are the favorable outcomes of spinning a number not greater than 3?
Answer: 3
Explanation:
There are 3 numbers those are not greater than 3, they are {1,2,3}.
There are 3 favorable outcomes.
Question 16.
In how many ways can spinning an even number occur?
Answer: 4
Explanation:
There are 4 even numbers , they are {2,4,6,8}
So, there are 4 ways of getting an even number.
Question 17.
In how many ways can spinning a prime number occur?
Answer:4
Explanation:
There are 4 prime numbers , they are {2,3,5,7}
So, there are 4 ways of getting a prime number.
IDENTIFYING OUTCOMES You randomly choose one marble from the bag.(a) Find the number of ways the event can occur. (b) Find the favorable outcomes of the event.

There are 9 colored balls in the bag in which ,
The number of red balls = 3 .
The number of blue balls = 2
The number of yellow balls = 1
The number of purple balls = 2.
The number of green balls =1
The number of favorable outcomes = 9.
Question 18.
Choosing blue
Answer: 2/9
Explanation :
The total number of out comes = 9.
The number of blue balls in the bag = 2
Consider B is the event of getting Blue ball
So, the probability of getting blue ball, P(B)= (Number of Favorable outcomes) / (Total number of outcomes)
P(B) = 2 / 9.
Therefore, the probability of getting blue ball is 2/9 = 0.22.
Question 19.
Choosing green
Answer: 1/9
Explanation :
The total number of out comes = 9.
The number of green balls in the bag = 1
Consider G is the event of getting Blue ball
So, the probability of getting green ball, P(G)= (Number of Favorable outcomes) / (Total number of outcomes)
P(G) = 2 / 9.
Therefore, the probability of getting green ball is 1/9 = 0.11.
Question 20.
Choosing purple
Answer: 2/9
Explanation :
The total number of out comes = 9.
The number of purple balls in the bag = 2
Consider P is the event of getting purple ball
So, the probability of getting purple ball, P(P)= (Number of Favorable outcomes) / (Total number of outcomes)
P(P) = 2 / 9.
Therefore, the probability of getting purple ball is 2/9 = 0.22.
Question 21.
Choosing yellow
Answer: 1/9
Explanation :
The total number of out comes = 9.
The number of yellow balls in the bag = 1
Consider Y is the event of getting yellow ball
So, the probability of getting yellow ball, P(Y)= (Number of Favorable outcomes) / (Total number of outcomes)
P(Y) = 2 / 9.
Therefore, the probability of getting yellow ball is 1/9 = 0.11.
Question 22.
Choosing not red
Answer: 0.67
There are 3 red balls in the bag
The total number of colored balls in the bag are 9
The balls other than red balls are 9 – 3 = 6
Therefore, the probability of getting a ball other than red is
P(E) = Favorable outcomes / Total number of outcomes .
Where, E is the event of getting a ball other than red
P(E) = 6/9 = 2/3
Therefore , the probability of choosing not red ball is 2/3 = 0.67.
Question 23.
Choosing not blue
Answer: 7/9 = 0.78
Explanation:
There are 2 blue balls in the bag
The total number of colored balls in the bag are 9
The balls other than blue balls are 9 – 2 = 7
Therefore, the probability of getting a ball other than blue is
P(E) = Favorable outcomes / Total number of outcomes .
Where, E is the event of getting a ball other than blue
P(E) = 7/9 = 0.78
Therefore , the probability of choosing not blue ball is 7/9.
Question 24.
YOU BE THE TEACHER
Your friend finds the number of ways that choosing not purple can occur. Is your friend correct? Explain your reasoning.

Answer: Yes, he is correct
Given, the number of not purple colors=4
They are red, blue, green, yellow
Therefore the number of ways that choosing not purple can occur = 4 .
CRITICAL THINKING Tell whether the statement is true or false. If it is false, change the italicized word to make the statement true.
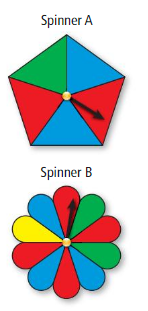
Question 25.
Spinning blue and spinning green have the same number of favorable outcomes on Spinner A.
Answer: False
Spinning blue and spinning Red have the same number of favorable outcomes on spinner A.
Question 26.
There are three possible outcomes of spinning Spinner A.
Answer: True
Question 27.
Spinning red can occur in four ways on Spinner B.
Answer: True
Question 28.
Spinning not green can occur in three ways on Spinner B.
Answer: False
Spinning not green can occur in four ways on Spinner B.
DESCRIBING LIKELIHOOD Describe the likelihood of the event given its probability.
Question 29.
Your soccer team wins \(\frac{3}{4}\) of the time.
Answer:50
The likelihood of the event is may or may not happen .
Question 30.
There is a 0% chance that you will grow12 feet.
Answer:
The probability =0
Thus, the likelihood of the event is Impossible
Therefore , It is impossible to to grow 12 feet.
Question 31.
The probability that the sun rises tomorrow is 1.
Answer:
The probability 1=100%
The likelihood of the event is certain
So, it is sure that the sun rises tomorrow
Question 32.
It rains on \(\frac{1}{5}\) of the days in June.
Answer:
The likelihood of the event is not likely to happen .
Question 33.
MODELING REAL LIFE
You have a 50% chance of being chosen to explain a math problem in front of the class. Describe the likelihood that you are chosen.
Answer:
Given, there is 50% chance of being chosen to explain a math problem in front of the class
50% = 0.5
So, the likelihood of the event is may or may not occur .
there is 50% chance
Question 34.
MODELING REAL LIFE
You roll a number cube and record the number of times you roll an even number and the number of times you roll an odd number. Describe the likelihood of each event.̇̇̇̇̇̇̇̇̇̇̇̇̇̇̇̇̇̇̇̇

a. You roll an even number on your next roll.
b. You roll an odd number on your next roll.
Answer:
a.Explanation:
Total number times cube rolled = 50
The frequency for even number =26
Consider E be the event of rolling an even number
P(E)=(Number of times an event occurs)/ (Total number of trails)
P(E)= 26/50 = 0.72
Therefore , the chances of rolling an even number = 0.72
b.Explanation:
Total number times cube rolled = 50
The frequency for odd number =24
Consider O be the event of rolling a odd number
P(O)=(Number of times an event occurs)/ (Total number of trails)
P(O)= 24/50 = 0.48
Therefore , the chances of rolling a odd number = 0.48
Question 35.
REASONING
You want to determine whether a coin is fair. You flip the coin and record the number of times you flip heads and the number of times you flip tails.

a Describe the likelihood that you flip heads on your next flip.
b. Describe the likelihood that you flip tails on your next flip.
c. Do you think the coin is a fair coin? Explain. ̇̇̇̇̇
Answer:
a.Total number of flips = 25
The total frequency for heads = 22
Now, the likelihood that you flip heads on your next flip
= Number of heads/ total
= 22 / 25 = 0.88
=88%
The likelihood of the event is more likely to occur
b.Total number of flips =25
The total frequency for tails = 3
Now, the likelihood that you flip tails on your next flip
= Number of tails/ Total
= 3/25 =0.12
Therefore, the likelihood of the event is not likely to occur
c.Every coin has both sides, { heads, tails}
But, the probability of tossing coin is not fair
They do not have 50/50 outcomes for both heads and tails .
So the coin is not fair in tossing.
Question 36.
LOGIC
At a carnival, each guest randomly chooses 1 of 50 rubber ducks and then replaces it. The table shows the numbers of each type of duck that have been drawn so far. Out of 150 draws, how many can you expect to not be a losing duck? Justify your answer.̇̇̇̇̇̇̇̇̇̇̇̇̇̇̇̇

Answer:
Total number of ducks = 25
Total number of win ducks = 6
Now,
The probability to expect to not be a losing duck after 105 draws =
won ducks/ total =x/150
6/25 =x/150
25x= 900
x= 900/25
x= 36 =0.36
The chance to expect to not be a losing duck after 105 draws is ‘not likely to occur
Question 37.
CRITICAL THINKING
A dodecahedron has twelve sides numbered 1 through 12. Describe the likelihood that each event will occur when you roll the dodecahedron. Explain your reasoning.

a. rolling a 1
b. rolling a multiple of 3
c. rolling a number greater than 6
a. rolling a 1
Answer: The probability of rolling a 1 is 1/12
Explanation :
There are 12 number of outcomes for a dodecahedron,
{1,2,3,4,5,6,7,8,9,10,11,12}
P{O}= favorable outcomes / Total number of outcomes.
Where O is the event of getting number 1
p{O}= 1 /12
Therefore , the probability of rolling 1 is 1/12.
b. Rolling a multiple of 3
Answer: 1/3
Explanation:
There are 4 multiples of 3 in a dodecahedron.
They are, {3,6,9,12}
There are 12 number of outcomes for a dodecahedron,
{1,2,3,4,5,6,7,8,9,10,11,12}
P{M}= Favorable outcomes/ Total number of outcomes
Where, M is the event of rolling a multiple of 3
P{M}= 4/12 = 1/3
Therefore, the probability of getting a multiple of 3 is 1/3
C. Rolling a number greater than 6.
Answer: 1/2
Explanation:
There are 6 numbers of which are greater than 6 . they are, {7,8,9,10,11,12}
There are 12 number of outcomes for a dodecahedron,
{1,2,3,4,5,6,7,8,9,10,11,12}
P{G}= Favorable outcome / Total number of outcomes
Where, G is the event of getting a number greater than 6
P{G} = 6/12=1/2
Therefore, the probability of getting a number greater than 6 is 1/2.
Question 38.
DIG DEEPER!
A bargain bin contains classical CDs and rock CDs. There are 60 CDs in the bin. Choosing a rock CD and not choosing a rock CD have the same number of favorable outcomes. How many rock CDs are in the bin?
Answer: 30 Rock CDs
Explanation:
Given that,
There are 60 CDs in the bin
So, There are 60 total number of outcomes
Also given that, choosing a rock CD and not choosing a rock CD have the same number of favorable outcomes
So, there is equal probability .
We can conclude that there are same number of classical CDs and rock CDs
Which means , 30 +30 = 60
Therefore, there are 30 rock CDs in the bin.
Question 39.
REASONING
You randomly choose one of the cards and set it aside. Then you randomly choose a second card. Describe how the number of possible outcomes changes after the first card is chosen.

Answer:
Initially,
Total number cards =5
So, the number of possible outcome =5
If you choose one card and set it aside , the number of possible outcomes decreases by 1
Then when you randomly choose second card , there are only four cards left
Therefore, the number of possible outcomes decreases by 1 after the first card is chosen.
STRUCTURE A Punnett square is a grid used to show possible gene combinations for the offspring of two parents. In the Punnett square shown, a boy is represented by XY. A girl is represented by XX.
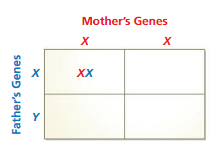
Question 40.
Complete the Punnett square. Explain why the events “having a boy” and “having a girl” are equally likely.
Answer:
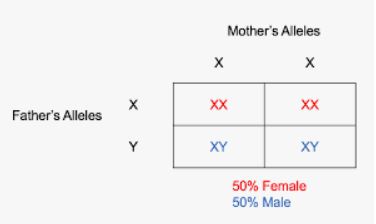
There is a chance of 50% female and 50% male
The probability = 50%
Therefore , the likelihood of the event is equally likely.
Question 41.
Two parents each have the gene combination Cs. The gene C is for curly hair. The gene s is for straight hair. Any gene combination that includes a C results in curly hair. When all outcomes are equally likely, what is the probability of a child having curly hair?
Answer: 4
C is considered as X which results for curly hair
since, there are 4 outcomes includes X
Thus, the probability of child having curly hair = 4/4 =1
Therefore , the probability = 1
So, the likelihood or the chances of a child having curly hair is certain.
Lesson 7.2 Experimental and Theoretical Probability
EXPLORATION 1
Conducting Experiments
Work with a partner. Conduct the following experiments and find the relative frequencies.
Experiment 1
• Flip a quarter 25 times and record whether each flip lands heads up or tails up.

Experiment 2
• Toss a thumbtack onto a table 25 times and record whether each toss lands point up or on its side.

a. Combine your results with those of your classmates. Do the relative frequencies change? What do you notice?
b. Everyone in your school conducts each experiment and you combine the results. How do you expect the relative frequencies to change?
c. How many times in 1000 flips do you expect a quarter to land heads up? How many times in 1000 tosses do you expect a thumbtack to land point up? Explain your reasoning.
d. In a uniform probability model, each outcome is equally likely to occur. Can you use a uniform probability model to describe either experiment? Explain.
Answer:

Try It
The table shows the results of rolling a number cube 50 times. Find the experimental probability of the event.

Question 1.
rolling a 3
Answer: 8/50 = 0.16
Explanation:
Total number of trails = 50
Frequency for 3 = 8
Consider T be the event of rolling a 3
Experimental probability = P(T)(Number of times an event occurs)/ (Total number of trails)
P(T)= 8/50= 0.16
Therefore , the probability of rolling a 3 is 0.16.
Question 2.
rolling an odd number.
Answer:
The probability of rolling an odd number = 0.58
Explanation:
Total number of odd numbers = 3
They are {1,3,5,}
The frequency for 1 = 10
The frequency for 3 =8
The frequency for 5= 11
Total frequency = 10 +8+11 = 29
Total number of trails = 50
Consider O be the event of rolling a Odd number
Experimental probability = P(O)=(Number of times an event occurs)/ (Total number of trails)
P(O)= 29/50= 0.58
Therefore , the probability of rolling an odd number = 0.58
Question 3.
What is the theoretical probability of randomly choosing an X?

Answer: 1/7 =0.142
Explanation:
Number of favorable outcomes = 7
Consider X be the event of choosing an X
Theoretical probability P(X)=(Number of favorable outcomes)/(Total number of outcomes)
P(X)= 1/7 = 0.142
Therefore, the probability of randomly choosing X =0.142
Question 4.
How does the experimental probability of rolling a number greater than 1 compare with the theoretical probability?
Answer:
Theoretical probability is what we expect to happen, where experimental probability is what actually happens when we try it out.
The experimental probability of an event cannot be greater than 1 since the number of trials in which the event can happen cannot be greater than the total number of trials.
Question 5.
An inspector randomly selects 200 pairs of jeans and finds 5 defective pairs. About how many pairs of jeans do you expect to be defective in a shipment of 5000?

Answer: 125 defective jeans
Explanation:
Total number of pairs = 200
Number of defective pairs = 5
Let ,x be the number of defective pairs of jeans in a shipment of 5000
Now, the number of defective pair of jeans in a shipment of 5000 =
Defective / Total= x/5000
5/200 = X/5000
200 x x = 5000 x 5
200x = 25000
x = 25000/200
x = 125
Therefore there are 125 pairs of jeans are expected to be defective in a shipment of 5000
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
Explain what it means for an event to have a theoretical probability of 0.25 and an experimental probability of 0.3.
Answer:
If you have a fair coin, and flip it twice,
The theoretical probability of getting 2 heads = 0.25
There’s 4 outcomes: HH, TT, TH, and HT.
1 out of 4 is 0.25 chance of 2 heads.
But if you run the experiment and do actual flips, maybe 100 times,
The average times you get 2 heads might be 0.3 if you got 2 heads 30 times out of a 100.
It could be just random chance or maybe the coin is slightly heavier on the head side, causing slightly more heads than the theoretical probability.
Question 7.
DIFFERENT WORDS, SAME QUESTION
You flip a coin and record the results in the table. Which is different? Find “both” answers.

Answer:
- Experimental probability of flipping heads = frequency of heads / Total number of trails = 32/60 =0.53
2. The fraction of the flips you can expect a result of heads = 32/60 =0.53
3. The percent of flips result in heads = 0.53 =53%
4. The relative frequency of flipping heads = 32/60 = 0.53
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
Contestants randomly draw a ticket from a hat and replace it. The table shows the results after 40 draws. There are 7 winning tickets in the hat. Predict the total number of tickets in the hat. Explain.
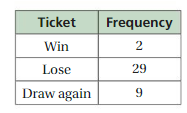
Answer:
Let, the total numbers of tickets in the hat = x
Given that , Number of winning tickets = 7
Number of winning won after 40 draws = 2
Total number of tickets =
2/40 = 7/x
2x = 280
x = 280/2
x= 140
Therefore, The total number of tickets in the hat = 140
Question 9.
DIG DEEPER!
You choose two different songs on a music play list at random. Out of 80 songs on the playlist, 36 are hip hop songs. The first song you choose is a hip hop song. What is the probability that the second song is also a hip hop song? Explain your reasoning.

Answer:
Total number of songs = 80
Number of hip pop songs = 36
Given that the first song is hip pop
The probability of playing second song also hip pop =
Total number of hip pop songs / total number of songs
Consider H be the event of playing hip pop
P(H)= 36/ 80 =0.45
If there is no repeat :
Total number of hip pop songs after playing one song = 35
P(H)= 0.43
Therefore ,the likelihood of the event is unlikely to happen.
Experimental and Theoretical Probability Homework & Practice 7.2
Review & Refresh
Describe the likelihood of the event given its probability.
Question 1.
You randomly guess the correct answer of a multiple choice question \(\frac{1}{4}\) of the time.
Answer:
The likelihood of the event is not likely to happen .
Question 2.
There is a 95% chance that school will not be cancelled tomorrow.
Answer:
Given , 95% chance that school will be cancelled tomorrow
95%= 0.95
Probability = 0.95
So the likelihood of the event is more likely to happen
Find the annual interest rate.
Question 3.
I = $16, P = $200, t = 2 years
Answer: 4%
The formula for simple interest= Principal x rate x time
I = P x r x t
$16 = $200 x r x 2
$16= 400r
r = 16/400
r= 0.04
0.04 x 100= 4
Therefore, the annual interest rate = 4%
Question 4.
I = $26.25, P = $500, t = 18 months
Answer:3.5
The formula for simple interest= Principal x rate x time
I = P x r x t
$26.25 = $500 x r x 1.5
$26.25= 750r
r = 26.25/750
r= 0.035
0.035 x 100= 3.5
Therefore, the annual interest rate = 3.5%
Tell whether x and y are proportional.
Question 5.
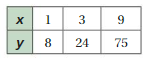
Answer:
The ratio of x and y for the given values is
1/8 = 0.12
3/24= 0.12
9/75 = 0.12
We get equal values for all the ratios
Therefore, the relationship given in the table is proportional.
Question 6.
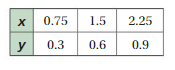
Answer:
The ratio of x and y for the given values is
0.75/0.3 =2.5
1.5/0.6 = 2.5
2.25/0.9 = 2.5
We get equal values for all the ratios
Therefore, the relationship given in the table is proportional.
Concepts, Skills, & Problem Solving
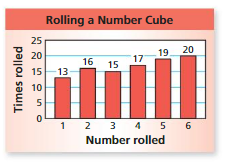
CONDUCTING AN EXPERIMENT Use the bar graph below to find the relative frequency of the event. (See Exploration 1, p. 291.)
Question 7.
spinning a 6
Answer: 0.14
Explanation:
Total number of spins =50
The number of times 6 spun =7
Consider X be the event of spinning a 6
Experimental probability = P(T)=(Number of times an event occurs)/ (Total number of trails)
P(X)= 7/50= 0.14
Therefore, the probability spinning a 6= 0.14
Question 8.
spinning an even number
Answer:0.48
Explanation:
Total number of spins =50
Numbers of even numbers = 3
They are {2,4,6}
Number of times 2 spun = 6
Number of times 4 spun = 11
Number of times 6 spun =7
Total : 24
Consider E be the event of spinning a number less than 3
Experimental probability P(E)=(Number of times an event occurs)/ (Total number of trails)
P(T)= 24/50=0.48
Therefore the probability of spinning a even number = 0.48
FINDING AN EXPERIMENTAL PROBABILITY Spinning a Spinner .Use the bar graph to find the experimental probability of the event.
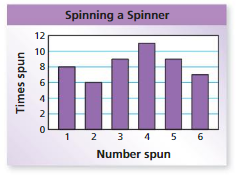
Question 9.
spinning a number less than 3
Answer: 14/50=0.28
Explanation:
Total number of spins =50
Numbers less than 3 are {1,2}
Number of times 1 spun =8
Number of times 2 spun =6
Total : 8 +6 = 14
Consider T be the event of spinning a number less than 3
Experimental probability = P(T)=(Number of times an event occurs)/ (Total number of trails)
P(T)= 14/50=0.28
Therefore, the probability spinning a number less than 3 =0.28
Question 10.
not spinning a 1
Answer: 42/50= 0.84
Explanation:
Total number of spins =50
The numbers other than 1 are{2,3,4,5,6}
The number of times 2 spun = 6
The number of times 3 spun= 9
The number of times 4 spun= 11
The number of times 5 spun= 9
The number of times 6 spun= 7
Total : 6+9+11+9+7=42
Consider O be the event of spinning a number less than 3
Experimental probability = P(O)=(Number of times an event occurs)/ (Total number of trails)
P(O)= 42/ 50= 0.84
Therefore, the probability of spinning a number other than 1 is 0.84.
Question 11.
spinning a 1 or a 3
Answer:
Total number of spins =50
Number of times 1 spun = 8
The number of times 3 spun= 9
Total : 8+9 = 17
Consider S be the event spinning a 1 or 3
Experimental probability = P(S)=(Number of times an event occurs)/ (Total number of trails)
P(S)= 17/ 50= 0.34
Therefore, the probability of spinning a 1 OR 3 is 0.34.
Question 12.
spinning a 7
Answer: 0
Explanation:
The bar graph consists 6 numbers
They are, {1,2,3,4,5,6}
So, it is impossible to spin 7
Therefore the probability of spinning is 0.
Question 13.
YOU BE THE TEACHER
Your friend uses the bar graph above to find the experimental probability of spinning. Is your friend correct? Explain your reasoning.

Answer:
No, he is wrong
Explanation:
The formula for finding experimental probability is
Experimental probability P(O)=(Number of times an event occurs)/ (Total number of trails)
Consider O be the event of spinning 4
P(O)=11/50
Therefore, the experimental probability of spinning a 4 is 0.22
So, he is wrong
Question 14.
MODELING REAL LIFE
You check 20 laser pointers at random. Three of the laser pointers are defective. What is the experimental probability that a laser pointer is defective?

Answer: 0.3
Experimental probability = P(T)=(Number of times an event occurs)/ (Total number of trails)
Total number of lasers = 20
Number of defective lasers =3
P(T) = 3/20
= 0.3
Therefore, the experimental probability that a laser pointer is defective is 0.3
FINDING A THEORETICAL PROBABILITY Use the spinner to find the theoretical probability of the event.

Question 15.
spinning red
Answer: 0.33
Explanation:
The spinner is divided into 6 equal parts.
So, the total number of outcomes of a spinner = 6
In which 2 parts are red and remaining parts are blue, green , orange and purple
Consider R is the event of getting a red color.
So, the probability of spinning red color P(R) = ( number of favorable outcomes)/(Total number of outcomes)
P(R)= 2/6= 0.33
Question 16.
spinning a 1
Answer: 1/6 = 0.16
Explanation:
The spinner is divided into 6 equal parts.
So, the total number of outcomes of a spinner = 6
{1,2,3,4,5,6}
Consider ,O is the event of getting 1
So, the probability of getting 1 is P(O)=( number of favorable outcomes)/(Total number of outcomes)
P(O)= 1/6 = 0.16
Therefore the probability of spinning a 1= 0.16
Question 17.
spinning an odd number
Answer: 3/6= 0.5
Explanation:
The number of total outcomes of a spinner = 6
They are , {1,2,3,4,5,6}
There are 3 odd numbers, They are {1,3,5}
Consider N is the event of getting an odd number
So, the probability of spinning an odd number P(N) =( number of favorable outcomes)/(Total number of outcomes)
P(N)= 3/6= 0.5.
Therefore, the probability of spinning an odd number = 3/6 =0.5
Question 18.
spinning a multiple of 2
Answer: 3/6= 0.5
Explanation:
The total number of outcomes of a spinner = 6
They are , {1,2,3,4,5,6}
There are 3 multiples of 2 , They are {2,4,6}
Consider M is the event of getting an odd number
So, the probability of spinning a multiple of 2is P(M) =( number of favorable outcomes)/(Total number of outcomes)
P(M)= 3/6= 0.5.
Therefore, the probability of spinning a multiple of 2 = 3/6 =0.5
Question 19.
spinning a number less than 7
Answer: 1
Explanation:
The spinner is divided into 6 equal parts.
So, the total number of outcomes of a spinner = 6
{1,2,3,4,5,6}
Consider, S is the event of spinning a number less than 7
So, the probability of spinning a number less than 7 P(S) =( number of favorable outcomes)/(Total number of outcomes)
P(S)= 6/6 =1
So, the probability of spinning a number less than 7 = 1
Question 20.
spinning a 9
Answer: 0
The spinner is divided into 6 equal parts numbering from 1 to 6
={1,2,3,4,5,6}
There is no 9 in the spinner
So, the probability of spinning 9 is 0
It is also called as impossible event .
Question 21.
REASONING
Each letter of the alphabet is printed on an index card. What is the theoretical probability of randomly choosing any letter except Z?
Answer: 25/26 =0.96
Explanation:
We know that, there are 26 alphabets.
Also, the number of alphabets other than Z are: 25
Let us consider Z is the event of choosing any letter except Z .
P(Z)= (number of favorable outcomes) / (Total number of outcomes )
p(Z)= 25/ 26 =0.96
Therefore, the theoretical probability of choosing a letter except Z is 25/26 = 0.96
COMPARING PROBABILITIES The bar graph shows the results of spinning the spinner below 200 times. Compare the theoretical and experimental probabilities of the event.
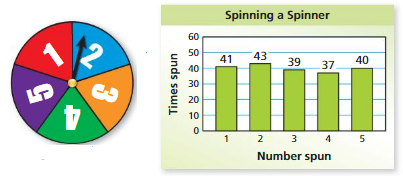
Question 22.
spinning a 4
Answer:
Theoretical probability:
Total number of outcomes = 5
Consider F be the event of spinning 4
Theoretical probability P(F)= (Number of favorable outcome )/(Total number of outcomes)
P(F)= 1/5= 0.2
Experimental probability :
Total number of spins = 200
Number of times 4 spun =37
Consider F be the event of spinning 4
Experimental probability = P(F)=(Number of times an event occurs)/ (Total number of trails)
P(F)= 37/200= 0.185
Therefore, the theoretical probability = 0.2
The experimental probability = 0.18
Question 23.
spinning a 3
Answer:
Theoretical probability:
Total number of outcomes = 5
Consider T be the event of spinning 3
Theoretical probability P(T)= (Number of favorable outcome )/(Total number of outcomes)
P(T)= 1/5= 0.2
Experimental probability :
Total number of spins = 200
Number of times 3 spun = 39
Consider T be the event of spinning 3
Experimental probability = P(T)=(Number of times an event occurs)/ (Total number of trails)
P(T)= 39/200= 0.195
Therefore, the theoretical probability = 0.16
The experimental probability = 0.195
Question 24.
spinning a number greater than 4
Answer:
Theoretical probability:
Total number of outcomes = 5
Consider N be the event of spinning a number greater than 4
Numbers greater than 4 = {5}
Theoretical probability P(T)= (Number of favorable outcome )/(Total number of outcomes)
P(T)= 1/5= 0.2
Experimental probability :
Total number of spins = 200
Consider N be the event of spinning a number greater than 4
Number of times 5 spun =40
Experimental probability = P(T)=(Number of times an event occurs)/ (Total number of trails)
P(T)= 40/200= 0.2
Therefore, the theoretical probability = 0.2
The experimental probability = 0.2
Question 25.
spinning an odd number
Answer:
Theoretical probability:
Total number of outcomes = 5
Consider S be the event of spinning an odd number
Total odd numbers = 3
They are {1,3,5}
Theoretical probability P(T)= (Number of favorable outcome )/(Total number of outcomes)
P(T)= 3/5= 0.6
Experimental probability :
Total number of spins = 200
Consider S be the event of spinning an odd number
The number of time 1 spun=41
The number of time 3 spun=39
The number of time 5 spun=40
Total : 41+39+40= 120
Experimental probability = P(T)=(Number of times an event occurs)/ (Total number of trails)
P(T)= 120/200= 0.6
Therefore, the theoretical probability = 0.6
The experimental probability = 0.6
Question 26.
REASONING
Should you use theoretical or experimental probability to predict the number of times you will spin a 3 in 10,000 spins? Explain.
Answer: theoretical probability
Explanation:
Theoretical probability of event =
Theoretical probability = P(T)=(Number of favorable outcomes)/ (Total number of outcomes)
Now,
Consider T be the event of spinning 3
P(T)= 1/6.
Question 27.
MODELING REAL LIFE
A board game uses a bag of 105 lettered tiles. You randomly choose a tile and then return it to the bag. The table shows the number of vowels and the number of consonants after 50 draws. Predict the number of vowels in the bag.
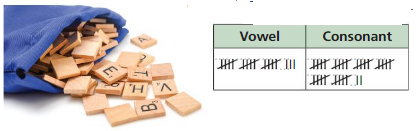
Answer:
let , X be the number of vowels in the bag.
Total number of tiles = 105
Number of vowels after 50 draws = 18
Now, the number of vowels in the bag =
X/150 = 18/50
50X=2700
X = 2700/50
X = 54
Therefore, 54 vowels are expected to be in the bag.
Question 28.
MODELING REAL LIFE
On a game show, a contestant randomly draws a chip from a bag and replaces it. Each chip says either win or lose. The theoretical probability of drawing a winning chip is \(\frac{3}{10}\). The bag 10contains 9 winning chips.
a. How many chips are in the bag?
b. Out of 20 contestants, how many do you expect to draw a winning chip?
Answer:
Given , the probability of drawing a winning chip = 3/10
Consider , x be the number of chips in the bag
The number of chips = 9
The ration of strikes in the bag = 9/x
3/10 = 9/x
3x = 90
x= 30
Therefore , there are 30 chips in the bag
Question 29.
PROBLEM SOLVING
There are 8 females and 10 males in a class.
a. What is the theoretical probability that a randomly chosen student is female?
b. One week later, there are 27 students in the class. The theoretical probability that a randomly chosen student is a female is the same as last week. How many males joined the class?
Answer:
a.Number of females=8
Total number of students = 8+10= 18
The theoretical probability that a randomly chosen student is female
Consider F be the event of chosen a female =
P(F)= Number of favorable outcomes / Total number of outcomes
P(F)= 8/18 =0.44
b.Initially,
Total number of students = 18
In which , number of females =8
Number of males =10
one week later , the total number of students = 27
Given, the theoretical probability for choosing girl is same
So, Number of males joined = 27 -18 = 9
Therefore, 9 males joined
Question 30.
NUMBER SENSE
The table at the right shows the results of flipping two coins 12 times each.
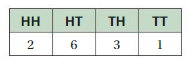
a. What is the experimental probability of flipping two tails? Using this probability, how many times can you expect to flip two tails in 600 trials?
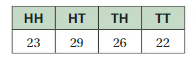
b. The table at the left shows the results of flipping the same two coins 100 times each. What is the experimental probability of flipping two tails? Using this probability, how many times can you expect to flip two tails in 600 trials?
c. Why is it important to use a large number of trials when using experimental probability to predict results?
Answer:
a.Explanation:
According to table,
Number of turns = 12
Frequency of flipping 2 tails = 1
The probability of flipping two tails in 600 trails =
1/12 = x/600
12x =600
x = 600/ 12
x = 50
In 600 trails , flipping 2 tails is expected to be 50 times.
b.Explanation:
According to table,
Number of turns = 100
Frequency of flipping 2 tails = 22
The probability of flipping two tails in 600 trails =
22/100= x/600
100x =13,200
x = 13200/100
x = 132
In 600 trails , flipping 2 tails is expected to be 132 times.
c.In experimental probability, as the number of trials increases, the experimental probability gets closer to the theoretical probability.
So, it is important to use a large number of trails.
Question 31.
COMPARING PROBABILITIES
The table shows the possible outcomes of rolling a pair of number cubes. You roll a pair of number cubes 60 times and record your results in the bar graph shown.
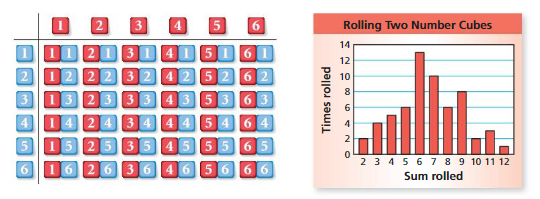
a. Compare the theoretical and experimental probabilities of rolling each sum.
b. Which sum do you expect to be most likely after 500 trials? 1000 trials? Explain your reasoning.
c. Predict the experimental probability of rolling each sum after 10,000 trials. Explain your reasoning.
Answer:
a.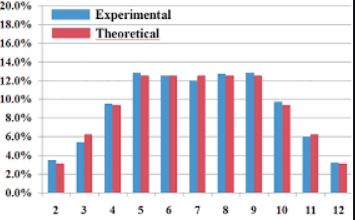
b. 6 sum is more likely to happen after after 500 trials, 1000 trials, and even after 10,000 trails because the the number of times 6 rolled is greater than other numbers sum.
Question 32.
PROJECT
When you toss a paper cup into the air, there are three ways for the cup to land: open-end up, open-end down, or on its side.
a. Toss a paper cup 100 times and record your results. Do the outcomes for tossing the cup appear to be equally likely? Explain.
b. Predict the number of times each outcome will occur in 1000 tosses. Explain your reasoning.
c. Suppose you tape a quarter to the bottom of the cup. Do you think the cup will be more likely less likely or to land open-end up? Justify your answer.

Answer:
The answer will vary
a. The results of tossing a cup 100 times are :
Open end up = 18
Open end down = 31
On its side = 51
The events of tossing the cup are not equally likely.
b.The probability of the events in 1000 tosses
open end up =18/ 100 x 1000 =180
Open end down = 31/100 x 1000 =310
On its side = 51 / 100 x1000 =510
c.If you tape quarter to the bottom, it will probably be more likely to land open end up since the weight of the bottom
will pull the bottom of the cup down and the top of the cap up.
Lesson 7.3 Compound Events
EXPLORATION 1
Comparing Combination Locks
Work with a partner. You are buying a combination lock. You have three choices.
a. One lock has 3 wheels. Each wheel is numbered from 0 to 9. How many possible outcomes are there for each wheel? How many possible combinations are there?

b. How can you use the number of possible outcomes on each wheel to determine the number of possible combinations?
c. Another lock has one wheel numbered from 0 to 39. Each combination uses a sequence of three numbers.How many possible combinations are there?

d. Another lock has 4 wheels as described. How many possible combinations are there?

e. For which lock are you least likely to guess the combination? Why?
Answer:
The set of all possible outcomes of one or more events is called the sample space. You can use tables and tree diagrams to find the sample space of two or more events.

Try It
Question 1.
WHAT IF?
The sandwich shop adds a multi-grain bread. Find the sample space. How many sandwiches are possible?
Answer: sample space = {Sandwich , multi grain bread }
Question 2.
Find the total number of possible outcomes of spinning the spinner and randomly choosing a number from 1 to 5.

Answer:
Number of colors in the spinner(a) =4
They are {red, blue, green, yellow}
Total numbers (b)= 5
{1,2,3,4,5}
Total number of possible outcomes =
According to fundamental principle ,(a x b)=
4 x 5 = 20
Therefore , total number of outcomes = 20
Question 3.
How many different outfits can you make from 4 T-shirts, 5 pairs of jeans, and 5 pairs of shoes?

Answer: 100
Explanation:
Number of T-shirts(a) = 4
Number of jeans pairs(b) = 5
Number of pair of shoes (C)= 5
According to fundamental principle,
Total number of outcomes = a x b x c
=4 x 5 x5
=100
Therefore , about 100 outfits can be made .
Question 4.
In Example 2, what is the probability of rolling at most 4 and flipping heads?
Answer:
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
FINDING THE SAMPLE SPACE
You randomly choose a flower and ornament for a display case. Find the sample space. How many different displays are possible?

Answer:
Total number of flowers =3
They are {daffodil, hyacinth, tulip}
Total number of ornament =2
They are {figurine, trophy}
Total number of outcomes = 3 x 2 = 6
sample space =
{daffodil, figurine} {daffodil, trophy}
{hyacinth, figurine } {hyacinth, trophy }
{tulip, figurine}{tulip, trophy }.
Question 6.
FINDING THE TOTAL NUMBER OF POSSIBLE OUTCOMES
You randomly choose a number from 1 to 5 and a letter from A to D. Find the total number of possible outcomes.
Answer: 20
Total numbers (a) = 5
They are {1,2,3,4,5}
Total number of letters (b)=4
They are {A,B,C,D}
According to fundamental theory ,
Total number of possible outcomes = a x b
= 4 x 5
=20
Therefore , the total number of possible outcomes = 20
Question 7.
WHICH ONE DOESN’T BELONG?
You roll a number cube and flip a not coin. Which probability does belong with the other three? Explain your reasoning.

Answer: P(greater than 2 and tails ) probability does not belong with the other three.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
A tour guide organizes vacation packages at a beach side town. There are 7 hotels, 5 cabins, 4 meal plans, 3 escape rooms, and 2 amusement parks. The tour guide chooses either a hotel or a cabin and then selects one of each of the remaining options. Find the total number of possible vacation packages.
Answer:
Given, the tour guide chooses either a hotel or a cabin and then selects one of each of the remaining options.
Event 1 :
If the tour guide choose hotel , the total number of possible vacation packages.
According to fundamental counting principle ,
7 hotels x 4 meal plans x 3 escape rooms x 2 amusement parks =168
Therefore, The total number of possible vacation packages = 168
Event 2 :
If the tour guide choose cabin , the total number of possible vacation packages.
According to fundamental counting principle ,
5 cabins x4 meal plans x 3 escape rooms x 2 amusement parks =120
Therefore, The total number of possible vacation packages = 120
Question 9.
DIG DEEPER!
A fitness club with 100 members offers one free training session per member in either running, swimming, or weightlifting. Thirty of the fitness center members sign up for the free session. The running and swimming sessions are each twice as popular as the weightlifting session. What is the probability that a randomly chosen fitness club member signs up for a free running session?

Answer:
Total number of fitness club = 100
The number of members signed for free up session = 30
Given , the running and swimming sessions are each twice as popular as the weightlifting session
let , x be the event of weight lifting and 2x be the event of running and swimming
2x + 2x + x = 30
5x = 30
x = 6
Now,
the probability that a randomly chosen fitness club member signs up for a free running session=
P(R) =2x /30
= 2×6/ 30
= 12/30
P(R) = 0.4
Therefore , the probability of that a randomly chosen fitness club member signs up for a free running session= 0.4
Compound Events Homework & Practice 7.3
Review & Refresh
Use the bar graph to find the experimental probability of the event.
Question 1.
rolling a 5
Answer:
Explanation:
Total number of spins =100
Total number of times 5 rolled= 19
Consider T be the event of rolling a 5
Experimental probability = P(T)=(Number of times an event occurs)/ (Total number of trails)
P(T)= 19/100=0.19
Therefore, the probability of rolling 5 =19/100=0.19
Question 2.
rolling a 2 or 6
Answer:
Total number of spins =100
The number of times 2 rolled =16
The probability of rolling 2 = 16 /100 =0.16
The number of times 6 rolled = 20
The probability of rolling 6 = 20/100 =0.20
Question 3.
rolling at least a 3
Answer:
Explanation:
The number of spins = 100
The number of times 3 =15
Consider S be the event of spinning at least 3 =
P(S) = 15/100
P(S) = 0.15
Question 4.
rolling a number less than or equal to 4
Answer: 0.6
Explanation:
Total number of spins =100
Total number of times 1 rolled = 12
Total number of times 2 rolled= 16
Total number of times 3 rolled = 15
Total number of times 4 rolled= 17
Total : 12 + 16 + 15 +17 = 60
Consider L be the event of rolling a number less than or equal to 4
Experimental probability = P(T)=(Number of times an event occurs)/ (Total number of trails)
P(T)= 60 /100=0.6
Therefore, the probability of rolling a number less than or equal to 4 = 0.6
Find the product.
Question 5.
3 . 2
Answer: 6
Question 6.
5(- 3)
Answer:
= -12
Question 7.
– 6(- 2)
Answer:
= 12
Concepts, Skills, & Problem Solving
COMPARING PASSWORDS Determine which password is less likely to be guessed. (See Exploration 1, p. 299.)
Question 8.
a password with 3 numbers or a password with 3 capital letters
Answer: the likelihood of the event is certain to happen with the passwords
Question 9.
a password with 6 numbers or a password with 4 capital letters
Answer: The password with 4 capital letters is more likely to guess than the password with 6 numbers .
USING A TREE DIAGRAM Use a tree diagram to find the sample space and the total number of possible outcomes.
Question 10.
Answer:
Total number of possible outcomes = 3x 2 =6
Question 11.

Answer:
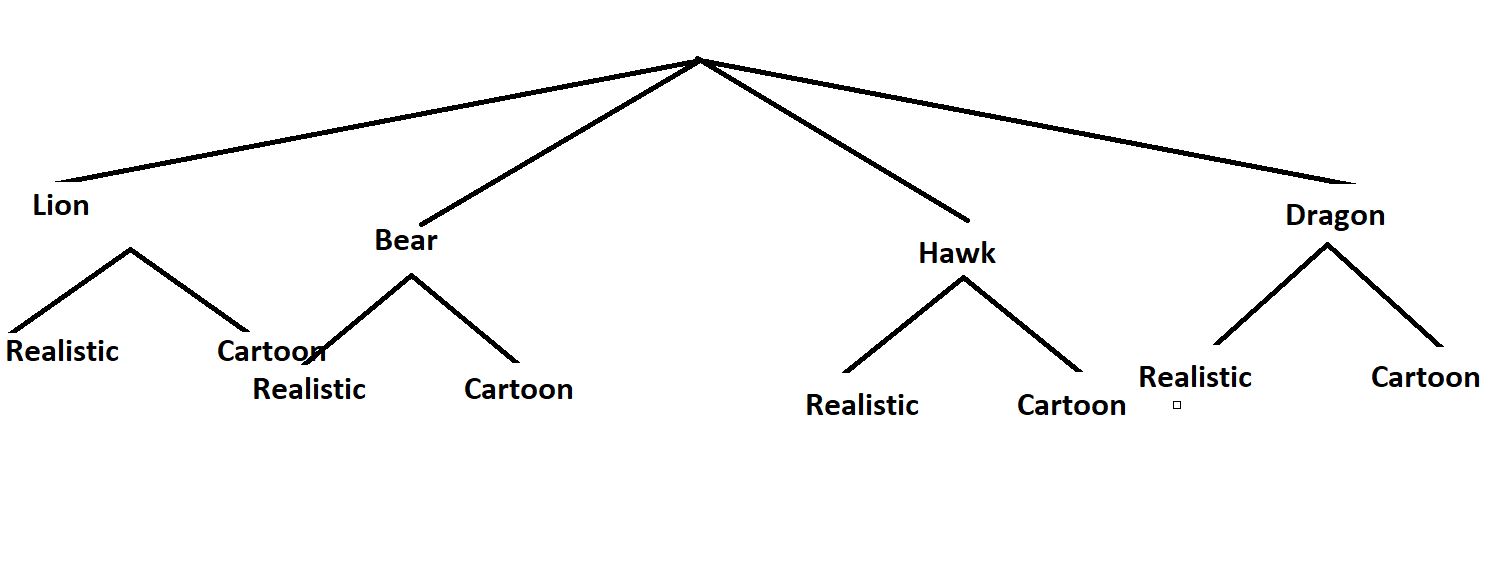
Question 12.
Answer:
Question 13.

Answer:
Question 14.
YOU BE THE TEACHER
Your friend finds the total number of ways that you can answer a quiz with five true-false questions. Is your friend correct? Explain your reasoning.

Answer: No,
Explanation ,
The number of outcomes for each question =
Possible answers for question number 1 = 2
Possible answers for question number 2 = 2
Possible answers for question number 3= 2
Possible answers for question number 4= 2
Possible answers for question number 5 = 2
According to fundamental counting principle ,
Total number of outcomes = 2 x 2 x 2 x 2 x 2 = 32
Therefore , You can answer the quiz in 32 different ways
USING THE FUNDAMENTAL COUNTING PRINCIPLE Use the Fundamental Counting Principle to find the total number of possible outcomes.
Question 15.

Answer: 12
Explanation:
Total number of sizes (a) = 3
Number of flavors (b) = 4
By using fundamental counting principle ,(a x b)
The total number of possible outcomes = 3 x 4 = 12
Therefore, total number of outcomes = 12
Question 16.
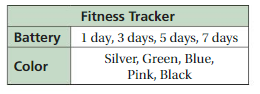
Answer:20
Explanation:
Number of batteries (a)= 4
Number of colors (b)= 5
By using fundamental counting principle ,( a x b)
The total number of possible outcomes = 4 x 5 = 20
Therefore, total number of outcomes = 20
Question 17.
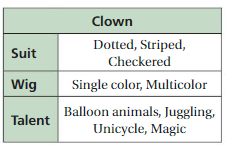
Answer:24
Explanation:
Number of suits (a)= 3
Number of wigs (b)= 2
Number of talents (c)= 4
By using fundamental counting principle ,( a x b x c)
The total number of possible outcomes = 3 x 2 x 4=24
Therefore, total number of outcomes = 24
Question 18.
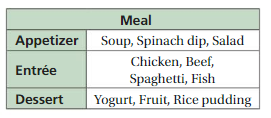
Answer:36
Explanation:
Number of appetizer (a)= 3
Number of Entre (b)= 4
Number of dessert (c)= 3
By using fundamental counting principle ,( a x b x c)
The total number of possible outcomes = 3 x 4 x 3 = 36
Therefore, total number of outcomes = 36
Question 19.
CHOOSE TOOLS
You randomly choose one of the marbles. Without replacing the first marble, you choose a second marble.

a. Name two ways you can find the total number of possible outcomes.
b. Find the total number of possible outcomes.
Answer:
a. Explanation:
The tree diagram and fundamental counting principle
b.There are 12 number of possible outcomes
Total number of balls = 4
Therefore, there are 4 possible outcomes
without replacing the first ball, the number of possible outcomes =3
According to fundamental principle ,( a x b )
= 4 x 3 = 12
Therefore there are 12 number of outcomes
Tree diagram:
Question 20.
FINDING A PROBABILITY
You roll two number cubes. What is the probability of rolling double threes?
Answer:
Number of cubes =2
{1,2,3,4,5,6} , {1,2,3,4,5,6}
Total number of possible outcomes = 6 x 6 = 36
The probability of rolling double threes =
P(T) = 2/36 = 0.05
Therefore, the probability of rolling double threes = 0.05
FINDING THE PROBABILITY OF A COMPOUND EVENT You spin the spinner and flip a coin. Find the probability of the compound event.
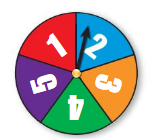
Question 21.
spinning a 1 and flipping heads
Answer: 0.1
Explanation:
The spinner is divided into 5 equal parts
They are {12,3,4,5}
Total number of outcomes =5
Consider O be the event of spinning a 1
P(O)= (Number of favorable outcomes )/ (Total number of outcomes)
P(O)= 1/ 5
Total number of outcomes for a coin =2
They are {Heads, Tails}
The probability of flipping a heads
P(H)= 1/2
The probability of compound event =
1/5 x 1/2 = 1/10 =0.1
Therefore ,the probability of compound event = 1/10
Question 22.
spinning an even number and flipping heads
Answer: 0.2
Explanation:
Number of even numbers = 2
They are {2,4}
Total number of outcomes = 5
Consider E be the event of spinning an even number
P(E) = 2/5
Total number of outcomes for a coin =2
They are {Heads, Tails}
The probability of flipping a heads
P(H)= 1/2
The probability of compound event (a x b)=
2/5 x 1/2 = 2/10 =0.2
Therefore, the probability of compound event = 0.2
Question 23.
spinning a number less than 3 and flipping tails
Answer: 0.2
Explanation:
Total number of outcomes = 5
Number of numbers less than 3 =2
They are {1,2}
Consider, S be the event of spinning a number less than 3
P(S) = 2/5
Total number of outcomes for a coin =2
They are {Heads, Tails}
The probability of flipping a heads
P(H)= 1/2
The probability of compound event (a x b)=
2/5 x 1/2 =2/10 =0.2
Therefore the probability of compound event = 0.2
Question 24.
spinning a 6 and flipping tails
Answer: 0
Explanation:
The spinner is divided into 5 equal parts
They are {12,3,4,5}
Total number of outcomes =5
Consider O be the event of spinning a 6
P(O)= (Number of favorable outcomes )/ (Total number of outcomes)
P(O)= 0
Therefore it is impossible to spin 6
Total number of outcomes for a coin =2
They are {Heads, Tails}
The probability of flipping a tails
P(H)= 1/2
The probability of compound event =
0 x 1/2 =0
Therefore ,the probability of compound event =0
Question 25.
not spinning a 5 and flipping heads
Answer:0.4
Explanation:
The spinner is divided into 5 equal parts
They are {12,3,4,5}
Total number of outcomes =5
Consider N be the event of not spinning a 5
Favorable outcomes = 4 .They are {1,2,3,4}
P(N)= (Number of favorable outcomes )/ (Total number of outcomes)
P(N)= 4/ 5
Total number of outcomes for a coin =2
They are {Heads, Tails}
The probability of flipping a heads
P(H)= 1/2
The probability of compound event =
4/5 x 1/2 = 4/10 =0.4
Therefore ,the probability of compound event = 0.4
Question 26.
spinning a prime number and not flipping heads
Answer:0.3
Explanation:
Total number of outcomes = 5
Number of prime numbers = 3
They are {2,3,5}
Consider P be the event of spinning a prime number
P(P) = (Number of favorable outcomes )/ (Total number of outcomes)
P(P) = 3/5
Total number of outcomes for a coin =2
They are {Heads, Tails}
The probability of not flipping a heads
P(H)= 1/2
The probability of compound event =
3/5 x 1/2 = 3/10 =0.3
Therefore ,the probability of compound event = 0.3
FINDING THE PROBABILITY OF A COMPOUND EVENT You spin the spinner, flip a coin, and then spin the spinner again. Find the probability of the compound event.
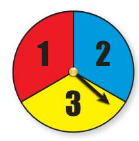
Question 27.
spinning blue, flipping heads, then spinning a 1
Answer:
The spinner is divided into 3 equal parts
Indicated numerally as {1,2,3} also colored in {red, blue , yellow}
Consider B be the event of spinning blue
P(B) = 1/3
Number of outcomes for a coin =2
They are {Heads , Tails }
Consider H be the event of flipping heads
P(H) = 1/2
Consider O be the event of spinning 1
P(O)= 1/3
The compound probability of compound event =
= 1/3 x 1/2 x1/3
= 1/18
Therefore , the compound probability of the event is 1/18.
Question 28.
spinning an odd number, flipping heads, then spinning yellow
Answer:
The spinner is divided into 3 equal parts
Indicated numerally as {1,2,3} also colored in {red, blue , yellow}
Consider Y be the event of spinning yellow
P(Y) = 1/3
Number of outcomes for a coin =2
They are {Heads , Tails }
Consider H be the event of flipping heads
P(H) = 1/2
Consider O be the event of spinning Odd number
Number of odd numbers = 2
They are {1,3}
P(O)= 2/3
The compound probability of compound event =
= 1/3 x 1/2 x2/3
= 2/18 =0.11
Therefore , the compound probability of the event is 2/18.
Question 29.
spinning an even number, flipping tails, then spinning an odd number
Answer:
The spinner is divided into 3 equal parts
Indicated numerally as {1,2,3} also colored in {red, blue , yellow}
Consider E be the event of spinning an even number
Number of even numbers =1
They are {2}
P(B) = 1/3
Number of outcomes for a coin =2
They are {Heads , Tails }
Consider T be the event of flipping Tails
P(T) = 1/2
Consider O be the event of spinning an odd number
Number of odd numbers =2
They are {1,3}
P(O)= 2/3
The compound probability of compound event =
= 1/3 x 1/2 x2/3
= 2/18 =0.11
Therefore , the compound probability of the event is 2/18.
Question 30.
not spinning red, flipping tails, then not spinning an even number
Answer:
The spinner is divided into 3 equal parts
Indicated numerally as {1,2,3} also colored in {red, blue , yellow}
Consider R be the event of not spinning red
The colors other than red are {blue , yellow}
P(R) = 2/3
Number of outcomes for a coin =2
They are {Heads , Tails }
Consider T be the event of flipping tails
P(T) = 1/2
Consider E be the event of not spinning an even number
number of not even numbers =2
They are {1,3}
P(E)= 2/3
The compound probability of compound event =
= 2/3 x 1/2 x2/3
= 4/18 =0.22
Therefore , the compound probability of the event is 0.22
Question 31.
REASONING
You randomly guess the answers to two questions on a multiple-choice test. Each question has three choices: A,B, and C.

a. What is the probability that you guess the correct answers to both questions?
b. Suppose you can eliminate one of the choices for each question. How does this change the probability that both of your guesses are correct?
Answer:
Probability of an event = Number of favorable outcomes / Total number of outcomes
There is one correct answer for each question.
So, the number of favorable outcomes = 2
Given that, there are 3 choices {a, b, c} for each question
So, total number of outcomes = 6
Consider, C be event that you guess the correct answers to both questions=
P(C)= 2/6 = 1/3
Therefore, the probability that you guess the correct answers to both questions =1/3
b.
Answer:
There is a correct answer for each question
So, the favorable outcomes =2
If you eliminate one of the choices for each question ,
Now, the choices for the questions are {a, b}
So, the total number of outcomes =4
Consider, S be the event of choosing correct answer
P(S) = 2/4
= 0.5
Therefore, the probability of choosing a correct answer is 0.5
Question 32.
REASONING
You forget the last two digits of your cell phone password.
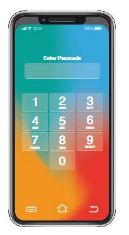
a. What is the probability that you randomly choose the correct digits?
b. Suppose you remember that both digits are even. How does this change the probability that you choose the correct digits?
Answer:
a.Number of digits to be guessed = 2
There are 10 possible numbers from 0 to 9
By using fundamental counting principle,
Number of possible outcomes = 10 x 10 =100
Each digit has one correct answer
So, the number of favorable outcomes = 2
Probability = Number of favorable outcomes/ Total number of outcomes
Consider C be the event of choosing correct digits
P(C) = 2/100 =1/50
Therefore the probability of choosing correct digits is 1/50
b.Given that, the two digits to be guessed are even numbers
The number of even numbers from 0 to 9 = 5
They are {0,2,4,6,8}
According to fundamental counting principle ,
So, total number of possible outcomes = 5 x 5= 25
Each digit has only one correct answer,
So number of favorable outcomes = 2
Consider S be the event of choosing correct digits
P(S) = 2/25 =0.08
Therefore, the probability of choosing correct answer = 0.08
Question 33.
MODELING REAL LIFE
A combination lock has 3 wheels, each numbered from 0 to 9. You try to guess the combination by writing five different numbers from 0 to 999 on a piece of paper. Find the probability that the correct combination is written on the paper.
Answer:
The number of digits numbered from 0 to 9 = 10
You get to try 5 of the 1000 possible combinations
So, the probability of getting them all right is 5/1000 or 1/200
Therefore ,5 tries, with a 1/1000 chance each time = 5/1000 = 1/200
Question 34.
MODELING REAL LIFE
A train has one engine and six train cars. Find the total number of ways an engineer can arrange the train. (The engine must be first.)

Answer:
Total number of train cars = 6
The engine must be first So, the total outcomes for train cars
So , there are 6 possible places for the train cars
Number of possible outcomes for the first train car = 6
Number of possible outcomes for the second train car =5
Number of possible outcomes for the third train car = 4
Number of possible outcomes for the fourth train car = 3
Number of possible outcomes for the fifth train car = 2
Number of possible outcomes for the sixth train car = 1
According to fundamental principle ,
6 x 5 x 4 x 3 x 2 x 1 = 720
Therefore, the number of ways you can arrange the train = 720
Question 35.
REPEATED REASONING
You have been assigned a nine-digit identification number.
a. Should you use the Fundamental Counting Principle or a tree diagram to find the total number of possible identification numbers? Explain.
b. How many identification numbers are possible?
c. RESEARCH Use the Internet to find out why the possible number of Social Security numbers is not the same as your answer to part(b).
Answer:
a.It is difficult to use tree diagram to find the total number of possible identification numbers because, the total number of identification is very large . So, it is impossible to use tree diagram
Therefore , it is easy to easy to use the fundamental counting principle .
b.Total number of identification digits are from 0 to 9
They are {0,1,2,3,4,5,6,7,8,9}
The number of possible numbers from 0 to 9 for first digit = 10
The number of possible numbers from 0 to 9 for second digit = 10
The number of possible numbers from 0 to 9 for third digit = 10
The number of possible numbers from 0 to 9 for fourth digit = 10
The number of possible numbers from 0 to 9 for fifth digit = 10
The number of possible numbers from 0 to 9 for sixth digit = 10
The number of possible numbers from 0 to 9 for seventh digit = 10
The number of possible numbers from 0 to 9 for eighth digit = 10
The number of possible numbers from 0 to 9 for ninth digit = 10
According to fundamental principle
10x10x10x10x10x10x10x10x10 = 1,000,000,000
Therefore there are 1,000,000,000 possible identification numbers
c.The possible number of Social Security numbers is not the same as your answer to part(b)
Because , some special numbers are never allocated.
Question 36
DIG DEEPER!
A social media account password includes a number from 0 to 9, an uppercase letter, a lowercase letter, and a special character, in that order.
a. There are 223,080 password combinations. How many special characters are there?
b. What is the probability of guessing the account password if you know the number and uppercase letter, but forget the rest?
Answer:
a.From 0 to 9, there are a total of 10 values.
For uppercase letters, there are a total of 26 values from A, B, C, D …Z
For lower case letters, there are also a total of 26 values from a, b, c, d …z.
So out of these three characters, we have a total of 10 × 26 × 26 = 6,760 different combinations.
If there are 223,080 password combinations
We need to divide this by 6,760 to calculate the possible values of the special characters.
6,760 × Number of possible special characters = 223,080,
Number of special characters = 223,080 / 6760= 33.
So there are 33 special characters.
If the number and uppercase values are known then the various lowercase letters and special characters are the unknown values.
The number of possible combinations = number of lowercase letters × number of special characters = 26 × 33 = 858.
So the probability of guessing the password is 1 out of 858 combinations.
Question 37.
PROBLEM SOLVING
From a group of 5 scientists, an environmental committee of 3 people is selected. How many different committees are possible?
Answer:
Let,
The 5 scientists be indicated as A,B,C,D,E
The environmental committee of three people =
ABC, ABD, ABE ,ACD,ACE , ADE
BCD,BCE, BDE,CDE .
Therefore, there are 10 different ways to form a committee.
Lesson 7.4 Simulations
EXPLORATION 1
Using a Simulation
Work with a partner. A basketball player makes 80% of her free throw attempts.
a. Is she likely to make at least two of her next three free throws? Explain your reasoning.
b. The table shows 30 randomly generated numbers from 0 to 999. Let each number represent three shots. How can you use the digits of these numbers to represent made shots and missed shots?

c. Use the table to estimate the probability that of her next three free throws, she makes
- exactly two free throws.
- at most one free throw.
- at least two free throws.
- at least two free throws in a row.
d. The experiment used in parts (b) and (c) is called a simulation. Another player makes \(\frac{3}{5}\) of her free throws. Describe a simulation that can be 5used to estimate the probability that she makes three of her next four free throws.
Answer:
A simulation is an experiment that is designed to reproduce the conditions of a situation or process.Simulations allow you to study situations that are impractical to create in real life.

Try It
Question 1.
You randomly guess the answers to four true-false questions.
a. Design a simulation that you can use to model the answers.
b. Use your simulation to find the experimental probability that you answer all four questions correctly.
Answer:a. There are two answers in a true-false question.
There is an equal chance of being correct or incorrect.
Therefore, we can use a coin to simulate answers where heads is correct and tails is incorrect.
Flip 4 coins in each trial to simulate the four answers. Run the simulation 50 times.
b.The table below shows the results of simulation 50 times
Out of 50 trails , there are only 4 times all the answers are correct
So, the probability that you answer all four questions correct =
Consider C be the event of answer all four questions correct
P(C) =4 /50 = 0.08
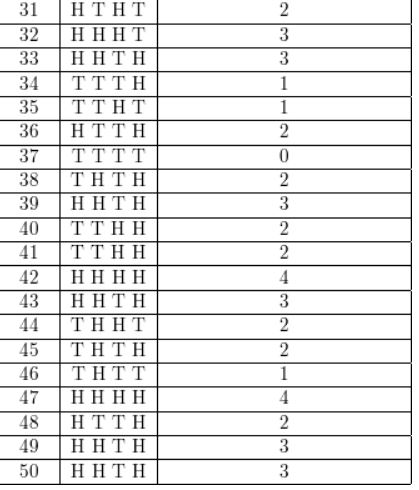
Question 2.
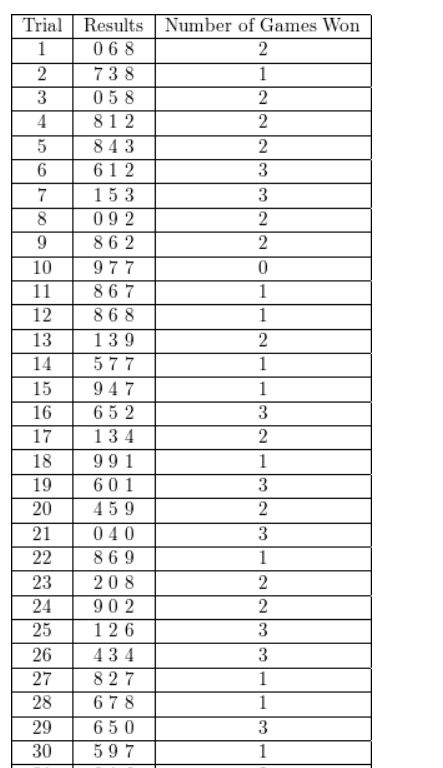
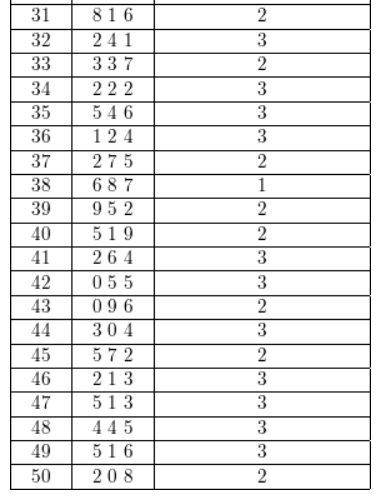
A baseball team wins 70% of the time. Design and use a simulation to estimate the probability that the team wins the next three games.
Answer:
Given that there is 70% chance of winning
let us use numbers to determine the win or lose of game
Assume 0-6 numbers to represent win and 7-9 numbers represent lose since, there is 70% chance of winning.
The table below shows the possible results after simulation 3 numbers 50 times on a random number on a graphing calculator.
Out of 50 trails , 19 of them had three wins
Therefore, the probability = 19/50 =0.38
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
SIMULATING OUTCOMES
Four multiple-choice questions on a quiz each have five answer choices. You randomly guess the answer to each question. Design and use a simulation to find the experimental probability that you answer all of the questions correctly.
Answer:
Given , the number of questions = 4
The number of answer choices for each question = 5
The experimental probability that you answer all of the questions correctly = 0.5%
Question 4.
SIMULATING OUTCOMES
You select a marble from a bag and a chip from a box. You have a 20% chance of choosing a green marble and a 90% chance of choosing a red chip. Estimate the probability that you choose a green marble and a red chip.

Answer:
Given ,
The chance of choosing green marble = 20%
The chance of choosing a red chip =90%
The simulation about the probability that you choose green marble and red marble
88 5 86 13 31 49 33 21 99 97
30 62 18 4 63 3 32 94 8 77
24 87 74 56 19 42 61 75 81
45 84 51 17 15 46 66 69 34 28
36 9 64 53 59 10 58 57 39 43 93
The digits from 1 through 2 in tens place indicate green marble
The digits from 1 through 9 in tens place indicates red chip
The experimental probability of choosing green marble and red marble
P(B) = 8/50 = 0.16
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
Each day there is a 50% chance that your tablet overheats. Estimate the probability that your tablet overheats on exactly 2 of the next 3 days.
Answer:
Given that ,
The percent of tablet overheats each day = 50%
The digits from 1 through 5 in the numbers
460 677 330 467 654 942 875 217 734 692
646 421 222 804 399 380 103 977 991 996
367 337 760 495 280 359 726 349 605 649
573 836 413 196 475 470 315 911 122 970
369 666 908 431 396 230 885 863 333 762
The digits 1 through 5 at least two in a three digit number indicate that your tablet overheats on exactly 2 of the next 3 days.
The experimental probability that your tablet overheats on exactly 2 of the next 3 days
P(S) = 15/ 50 = 0.3
Question 6.
DIG DEEPER
The probability that a homeowner needs a plumber this year is 22%. The probability that the homeowner needs a septic tank specialist is 14%. Estimate the probability that the homeowner needs a plumber, but not a septic tank specialist.

Answer:
Given that,
The probability home owner needs a plumber this year = 22%
The probability that home owner needs septic tank specialist = 14%
The probability that the home owner needs plumber but not septic tank specialist
80 52 96 94 77 49 74 16 79 68
45 98 34 47 48 57 12 62 21 71
60 82 78 11 64 28 43 22 75 19
76 65 17 81 87 14 38 27 6 42
37 40 51 15 2 13 92 90 73 7
The numbers 1 through 2 in tens place indicates owner needs plumber
The number 2 through 9 in once place indicate owner does not needs tank specialist
P(S) = 11 / 50 = 0.22
Simulations Homework & Practice 7.4
Review & Refresh
You flip a coin and roll the 20-sided figure. Find the probability of the compound event.

Question 1.
Flipping tails and rolling at least a 14
Answer:
The total numbers of outcomes for a coin = 2
They are {Tails, heads }
Consider T be the event of flipping tails
P(T) = 1/2
The number of outcomes for a 20 sided figure = 20
The probability of rolling at least a 14
Consider F be the event of rolling at least a 14
P(F) = 1/ 20
Compound event ( a x b )
= 1/2 x 1/20 = 1/40
Question 2.
Flipping heads and rolling less than 3
Answer:
The total numbers of outcomes for a coin = 2
They are {Tails, heads }
Consider H be the event of flipping heads
P(H ) = 1/2
The number of outcomes for a 20 sided figure = 20
Consider L be the event of rolling less than 3
Number of numbers less than 3 = 2
They are {1,2}
P(L) = 2/ 20 = 1/10
Compound event ( a x b )
= 1/2 x 1/10 = 1/20
Simplify the expression.
Question 3.
5(a – 2)
Answer:
5(a – 2) =0
5a -10 =0
5a =10
a=10/5
a =2
Question 4.
– 7(1 + 3x)
Answer:
– 7(1 + 3x) =0
-7 – 21x=0
-21x= 7
x= 7/-21
x = -0.33
Question 5.
– 1(3p – 8)
Answer:
– 1(3p – 8) =0
-3p +8 =0
p =-8/-3 =-2.6
Concepts, Skills, & Problem Solving
USING A SIMULATION A medicine is effective for 80% of patients. The table shows 30 randomly generated numbers from 0 to 999. Use the table to estimate the probability of the event. (See Exploration 1, p. 307.)
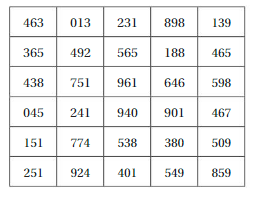
Question 6.
The medicine is effective on each of three patients.
Answer:
Let the, digits 1 through 8 in the tens place represent the medicine is effective
P(E) = 24/30
Question 7.
The medicine is effective on fewer than two of the next three patients.
Answer:
P(N) = 6/30 = 0.2
SIMULATING OUTCOMES Design and use a simulation to find the experimental probability.
Question 8.
In your indoor garden, 50% of seeds sprout. What is the experimental probability that at least one of your next three seeds sprouts?

Answer:
Use the random number generator on a graphing calculator.
Randomly generate 50 numbers from 0 to 99. The table below shows the results.
Let the digits 1 through 5 in the tens place represent the seeds are sprout
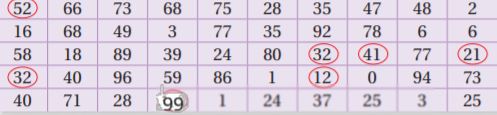
P(rain both days) =6/50
The experimental probability is 6/50 = 0.12, or 12%.
Question 9.
An archer hits a target 50% of the time. What is the experimental probability that the archer hits the target exactly four of the next five times?
Answer:
Given , the archer hits the target = 50%
25 82 53 49 24 95 31 66 40 90
42 30 9 78 4 80 16 99 23 85 39
44 6 61 46 5 87 64 36 21 57 58
98 81 13 97 29 18 92 22 77 35
55 14 60 28 38 89 56 69
Because, the makes 50 % of shots 1 to 50 represents successful shots .
the experimental probability that the archer hits the target exactly four of the next five times
P(X) = 25/50 =0.5 = 50%.
Question 10.
A bank randomly selects one of four free gifts to send to each new customer. Gifts include a calculator, a key chain, a notepad, and a pen. What is the experimental probability that the next two new customers both receive calculators? that neither receives a calculator?

Answer:
Given that ,
Gifts include a calculator, a key chain, a notepad, and a pen.
The experimental probability that the next two new customers both receive calculators=
P(C) =1/4 x1/4 = 1/16
The experimental probability that the next two new customers both neither receive calculators=
P(N) = 3/4 x 3/4 = 9/16
Question 11.
Employees spin a reward wheel. The wheel is equally likely to stop on each of six rewards labeled A–F. What is the experimental probability that fewer than two of the next three spins land on reward A?
Answer:
Given , The six rewards are labelled as {A,B,C,D,E,F}
What is the experimental probability that fewer than two of the next three spins land on reward A
92 72 41 33 83 4 60 32 6 81
1 12 61 57 93 27 46 29 42 47
21 79 23 45 16 63 26 87 14 68
75 38 94 24 20 86 82 70 8 97
39 59 19 64 55 25 77 9 88 37
the experimental probability that fewer than two of the next three spins land on reward A = 4/50
USING NUMBER CUBES Design and use a simulation with number cubes to estimate the probability.
Question 12.
Your lawnmower does not start on the first try \(\frac{1}{6}\) of the time. Estimate the probability that your lawnmower will not start on the first try exactly one of the next two times you move the lawn.

Answer:
Given the probability of the event is 1/6 = 16
The simulation of random generate calculator about 50 numbers
The digits from 1 through 16 indicates the event
50 99 88 6 98 76 63 21 65 42
96 84 92 37 27 33 11 57 69 68
48 40 10 30 24 26 67 47 60 34
59 87 18 78 7 79 12 95 9 8 1
86 38 45 93 44 4 15 73 39
The experimental probability of the event is 10/50
P(S) = 0.2
Question 13.
An application on your phone correctly identifies four out of every six songs. Estimate the probability that at least three of the next four songs are correctly identified.
Answer:
SIMULATING OUTCOMES Design and use a simulation to find the experimental probability.
Question 14.
Two beakers are used in a lab test. What is the experimental probability that there are reactions in both beakers during the lab test?
Answer:
The simulation of beaker 1 and beaker 2 have reactions
The digits 1 through 8 in tens place indicate probability of beaker 1
The digits 1 through 5 in once place indicate probability of beaker 2
52 66 73 68 75 28 35 47 48 2
16 68 49 3 77 35 92 78 6 6
58 18 89 39 24 80 32 41 77 21
32 40 96 59 86 1 12 0 94 73
40 71 28 61 1 24 37 25 3 25
The experimental probability that there are reactions in both beakers during the lab test
P(R) =32/50 = 0.64
Question 15.
You use a stain remover on two separate stains on a shirt. What is the experimental probability that the stain remover removes both the mud stain and the food stain?
Answer:
The simulation of random generator calculator is as follows:
The digits 1 through 9 in tens place indicate the event in mud
The digits 1 through 8 in once place indicate the event of stain removal in food
62 35 50 43 96 37 70 31 59 40
55 92 89 14 10 41 87 95 11 99
12 53 71 26 38 24 80 36 16 42
85 32 3 33 47 1 49 51 8 23 88
69 15 64 84 81 60 66 72 74
The experimental probability that the stain remover removes both the mud stain and the food stain
P(S) = 41/50 = 0.82
Question 16.
DIG DEEPER!
The probability that a computer crashes one or more times in a month is 10%. Estimate the probability that the computer crashes at least one or more times per month for two months in a row during the first half of the year.
Answer:
Question 17.
MODELING REAL LIFE
You visit an orchard. The probability that you randomly select a ripe apple is 92%. The probability that you randomly select a ripe cherry is 86%. Estimate the probability that you pick an apple that is ripe and a cherry that is not ripe.

Answer:
Given , the probability that you randomly select a ripe apple = 92%
The probability that you pick a ripe cherry = 86%
The digits from 1 through 8 in tens place indicates event of choosing a ripe apple
The digits 9 in once place indicates event of not choosing a ripe cherry
75 99 69 33 67 1 22 17 18 37
29 27 9 12 54 7 31 39 26 87
10 72 82 42 36 85 74 3 5 92
29 11 21 81 76 77 52 13 90
15 73 69 70 8 23 53 59 51 44 48
The probability that you pick an apple that is ripe and a cherry that is not ripe = 9/50
Question 18
CRITICAL THINKING
You use a simulation to find an experimental probability. How does the experimental probability compare to the theoretical probability as the number of trials increases?
Answer:
Experimental probability is the result of an experiment. Theoretical probability is what is expected to happen.
In experimental probability, as the number of trials increases, the experimental probability gets closer to the theoretical probability.
Question 19.
LOGIC
At a restaurant,30% of customers donate to charity in exchange for a coupon. Estimate the probability that it will take at least four customers to find one who donates.
Answer:
Probability Connecting Concepts
Using the Problem-Solving Plan
Question 1.
In an Internet contest, gift cards and bicycles are given as prizes in the ratio 9 : 1. Estimate the probability that at least two of three randomly selected winners receive bicycles.

Understand the problem.
You know the ratio of gift cards to bicycles awarded in the contest. You want to find the probability that atleast two of three randomly selected winners receive bicycles.
Make a plan.
Use the ratio to find the theoretical probability that a randomly selected winner receives a bicycle. Then use a simulation involving 50 randomly generated three-digit numbers to estimate the probability that at least two of three randomly selected winners receive bicycles.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
Question 2.
A board game uses the spinner shown.
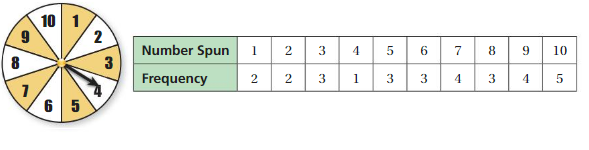
a. Use theoretical probability to predict the number of times you will spin a number greater than or equal to 8 in 30 spins.
b. You play the game and record the results of 30 spins. Find the percent error of your prediction in part(a).
Answer:
a. Theoretical probability = number of favorable/ outcomes by total number of outcomes
Total number of outcomes = 10
The probability of spinning a number greater than or equal to 8 P(S) = 3/8 = 0.375
b. The experimental probability =
P(S) = 12/30= 0.4
Question 3.
The tiles shown are placed in a bag. You randomly select one of the tiles, return it to the bag, and then randomly select another tile. What is the probability that the product of the numbers on the tiles selected is greater than zero? Justify your answer.

Answer:
Total number of tiles = 5
= 5×5 = 25 total number of outcomes
The probability that the product of the numbers on the tiles selected is greater than zero
P(Z) = 2/ 25
They are {1 x 2= 2 } and {2x 1 = 2 }
Therefore the probability of the product of the numbers on the tiles selected is greater than zero = 2/25 = 0.08
Performance Task
Fair and Unfair Carnival Games
At the beginning of this chapter, you watched a STEAM Video called “Massively Multi player Rock Paper Scissors.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Probability Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Graphic Organizers
You can use a Four Square to organize information about a concept. Each of the four squares can be a category, such as definition, vocabulary, example, non-example, words, algebra, table, numbers, visual, graph,or equation. Here is an example of a Four Square for probability.
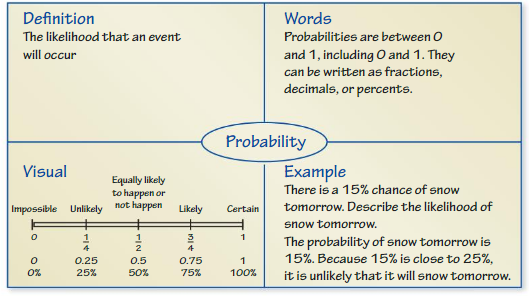
Choose and complete a graphic organizer to help you study the concept.

1. favorable outcomes
2. relative frequency
3. experimental probability
4. theoretical probability
5. Fundamental Counting Principle
6. compound event
7. simulation
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

7.1 Probability (pp. 283–290)
Learning Target: Understand how the probability of an event indicates its likelihood.
You randomly choose one toy race car.

Question 1.
How many possible outcomes are there?
Answer:
There are 5 green cars , one blue car and one red car
So the possible outcomes are 7
They are {green , red, blue}
Question 2.
What are the favorable outcomes of choosing a car that is not green?
Answer: 2
Number of green cars = 5
Number of cars that is not green = 2
They are {blue , red}
Therefore the possible outcomes of choosing a car that is not green = 2
Question 3.
In how many ways can choosing a green car occur?
Answer: 5
Number of green cars = 5
So, choosing a green car can occur in 5 ways
You spin the spinner. (a) Find the number of ways the event can occur. (b) Find the favorable outcomes of the event.

Question 4.
spinning a 1
Answer:
The spinner is divided into 8 equal parts
numbered with two 1s , three 2s and three 3s
{1,1,2,2,2,3,3,3}
The number of favorable outcomes of spinning a 1 = 2
Total number of outcomes = 8
Consider O be the event of spinning a 1
Probability P(O) = Number of favorable outcomes/ Total number of outcomes
P(O) = 2/8 =1/4
So, the probability of spinning a 1 is 0.25
Question 5.
spinning a 3
Answer:
The spinner is divided into 8 equal parts
numbered with two 1s , three 2s and three 3s
{1,1,2,2,2,3,3,3}
The number of favorable outcomes of spinning a 3 = 3
Total number of outcomes = 8
Consider T be the event of spinning a 3
Probability P(T) = Number of favorable outcomes/ Total number of outcomes
P(T) = 3/8 = 0.37
Therefore, the probability of spinning a 3 = 0.37
Question 6.
spinning an odd number
Answer:
The spinner is divided into 8 equal parts
numbered with two 1s , three 2s and three 3s
{1,1,2,2,2,3,3,3}
The number of favorable outcomes of spinning an odd number = 5
They are {1,1,3,3,3}
Total number of outcomes = 8
Consider O be the event of spinning an odd number
Probability P(O) = Number of favorable outcomes/ Total number of outcomes
P(O) = 5/8 =0.62
Therefore , the probability of spinning an odd number = 0.62
Question 7.
spinning an even number
Answer:
The spinner is divided into 8 equal parts
numbered with two 1s , three 2s and three 3s
{1,1,2,2,2,3,3,3}
The number of favorable outcomes of spinning an even number = 3
They are {2,2,2}
Total number of outcomes = 8
Consider E be the event of spinning an even number
Probability P(E) = Number of favorable outcomes/ Total number of outcomes
P(E) = 3/8 = 0.37
Question 8.
spinning a number greater than 0
Answer:
The spinner is divided into 8 equal parts
numbered with two 1s , three 2s and three 3s
{1,1,2,2,2,3,3,3}
The number of favorable outcomes of spinning a number greater than 0 =8
They are {1,1,2,2,2,3,3,3}
Total number of outcomes = 8
Consider S be the event of spinning a 1
Probability P(S) = Number of favorable outcomes/ Total number of outcomes
P(S) = 8/8 =1
Question 9.
spinning a number less than 3
Answer:
The spinner is divided into 8 equal parts
numbered with two 1s , three 2s and three 3s
{1,1,2,2,2,3,3,3}
The number of favorable outcomes of spinning a number less than a 3 = 5
They are {1,1,2,2,2}
Total number of outcomes = 8
Consider T be the event of spinning a number less than a 3
Probability P(T) = Number of favorable outcomes/ Total number of outcomes
P(T) = 5/8 = 0.62
Describe the likelihood of the event given its probability.
Question 10.
There is a 0% chance of snow in July for Florida.
Answer:
Given , the probability = 0
So the likelihood of the event is impossible
Question 11.
The probability that you are called on to answer a question in class is \(\frac{1}{25}\).
Answer:
Question 12.
There is an 85% chance the bus is on time.
Answer:
Given, 85% chance = 0.85
So, the probability is more likely to happen
Question 13.
The probability of flipping heads on a coin is 0.5.
Answer:
Given 0.5 = 50%
So, the probability of flipping heads is may or may not occur
Question 14.
During a basketball game, you record the number of rebounds from missed shots for each team. (a)Describe the likelihood that your team rebounds the next missed shot. (b) How many rebounds should your team expect to have in 15 missed shots?
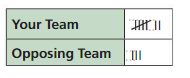
Answer:
a.Total number of shots = 10
Consider M be the event of rebounds the next missed shot
The probability = Number of missed shots / total number of trails
P(M) = 7/10 = 0.7
Therefore , the likelihood that your team rebounds the next missed shot is likely to happen
b.Total number of shots = 15
Consider S be the event of rebounds the your team misses the shot
probability P(S) = Number of rebounds / total number of trails
P(S) = 7/15 = 0.46
Therefore, the likelihood that the rebounds are expected to happen in 15 shots is not likely to occur
7.2 Experimental and Theoretical Probability (pp. 291–298)
Learning Target :Develop probability models using experimental and theoretical probability.
The bar graph shows the results of spinning a spinner 100 times. Use the bar graph to find the experimental probability of the event.
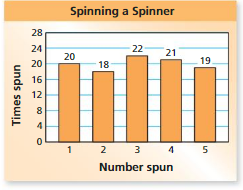
Question 15.
spinning a 2
Answer: 0.18
Explanation :
Total number of spins = 100
The number of times 2 spun = 18
Experimental probability = Number of times an event occur / Total number of spins
Consider T be the event of spinning a 2
P(T) = 18/100 =0.18
Therefore , experimental probability of spinning a 2 = 0.18
Question 16.
spinning an even number
Answer: 0.39
Explanation:
Total number of spins = 100
Number of even numbers = 2
They are {2,4}
The number of times 2 spun = 18
The number of times 4 spun = 21
Total : 18+21 = 39
Experimental probability = Number of times an event occur / Total number of spins
Consider T be the event of spinning an even number
P(T) = 38/100 =0.39
Therefore , experimental probability of spinning an even number = 0.39
Question 17.
not spinning a 5
Answer: 0.81
Total number of spins = 100
Number of numbers other than 5 = 4
They are {1,2,3,4}
The number of times 1 spun = 20
The number of times 2 spun = 18
The number of times 3 spun = 22
The number of times 4 spun = 21
Total : 81
Experimental probability = Number of times an event occur / Total number of spins
Consider F be the event of not spinning a 5
P(F) = 81/100 =0.81
Therefore , experimental probability of not spinning a 5 = 0.81
Question 18.
spinning a number less than 3
Answer:
Total number of spins = 100
The numbers less than 3 = 2
They are {1,2}
The number of times 1 spun = 20
The number of times 2 spun = 18
Total : 18 + 20 = 38
Experimental probability = Number of times an event occur / Total number of spins
Consider T be the event of spinning a number less than 3
P(T) = 38/100 =0.38
Therefore , experimental probability of spinning a number less than 3 = 0.38
Question 19.
In Exercise 16, how does the experimental probability of spinning an even number compare with the theoretical probability?
Answer:
Use the spinner to find the theoretical probability of the event.
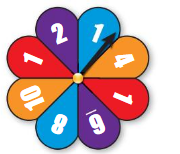
Question 20.
spinning blue
Answer:
The spinner is divided into 8 equal parts
They are numbered with three 1 s ,one 2 ,one 4 ,one 6 , one 8 , and one 10
And colored in 2 red , 2 blue , 2 purple and 2 orange in color
Consider , B be the event of spinning a blue
P(B) = 2/8
P(B) = 0.25
Question 21.
spinning a 1
Answer:
The spinner is divided into 8 equal parts
They are numbered with three 1 s ,one 2 ,one 4 ,one 6 , one 8 , and one 10
Consider , O be the event of spinning a 1
P(O) = 3/8
P(O) = 0.37
Question 22.
spinning an even number
Answer:
The spinner is divided into 8 equal parts
They are numbered with three 1 s ,one 2 ,one 4 ,one 6 , one 8 , and one 10
Total number of even numbers = 5
They are {2,4,6,8,10}
Consider , E be the event of spinning an even number
P(E) = 5/8
P(E) = 0.62
Question 23.
spinning a 4
Answer:
The spinner is divided into 8 equal parts
They are numbered with three 1 s ,one 2 ,one 4 ,one 6 , one 8 , and one 10
Consider , F be the event of spinning a blue
P(F) = 1/8
P(F) = 0.125
Question 24.
The theoretical probability of choosing a red grape from a bag of grapes is \(\frac{2}{9}\). There are 8 red grapes in the bag. How many grapes are in the bag?
Answer:
Given theoretical probability = 2/9
Number of red grapes = 8
Total number of grapes = x
8/x = 2/9
72 = 2x
x = 72/2
x = 35
Question 25.
The theoretical probability of choosing Event A is \(\frac{2}{7}\). What is the theoretical probability of not choosing Event A? Explain your reasoning.
Answer:
7.3 Compound Events (pp. 299–306)
Learning Target: Find sample spaces and probabilities of compound events.
Question 26.
You have 6 bracelets and 15 necklaces. Find the number of ways you can wear one bracelet and one necklace.
Answer:
Number of bracelets = 6
Number of necklaces = 15
According to fundamental counting principle,
a x b = 6 x 15 = 90
Therefore, In 90 ways you can wear one bracelet and one necklace
Question 27.
Use a tree diagram to find how many different home theater systems you can make from 6 DVD players,8 TVs, and 3 brands of speakers.
Answer:
Number of DVDs = 6
Number of TVs = 8
Number of brands of speaker = 3
Total number of outcomes = 6 x 8 x 3 = 144
Question 28.
A red, green, and blue book are on a shelf. You randomly pick one of the books. Without replacing the first book, you choose another book. What is the probability that you picked the red and blue book?
Answer:
Number of books in shelf = 3
Question 29.
You flip two coins and roll a number cube. What is the probability of flipping two tails and rolling an even number?
Answer:
number of total outcomes for coin = 2
The probability of flipping tails P(T ) = 1/2
For two coins , probability of flipping tails = 1/2 x 2 = 1/4
The number of total outcomes for 6
even numbers = {2,4,6}
The probability for flipping an even number = 3/6 = 1/2
So, the probability of flipping two tails and rolling an even number
= 1/4 x 1/2 = 1/8
Question 30.
Describe a compound event that has a probability between 50% and 80%.
Answer:
Question 31.
Your science teacher sets up six flasks. Two of the flasks contain water and four of the flasks contain hydrogen peroxide. A reaction occurs when you add yeast to hydrogen peroxide. You add yeast to two of the flasks. What is the probability that at least one reaction will occur?

Answer:
7.4 Simulations (pp. 307–312)
Learning Target: Design and use simulations to find probabilities of compound events.
Question 32.
You select a marble from two different bags. You have a 30% chance of choosing a blue marble from the first bag and a 70% chance of choosing a blue marble from the second bag. Design and use a simulation to estimate the probability that you choose a blue marble from both bags.
Answer:
Given , the chance of choosing blue marble from first bag =30%
The chance of choosing blue marble from second bag = 70%
82 4 90 96 18 65 11 71 97 53
48 63 32 54 52 17 14 5 83 50
61 36 10 81 58 84 9 80 94 95
15 42 2 45 68 64 33 38 12 60
35 16 21 99 59 55 22 20 37 87
Let the digits 1 through 3 in the tens place represents choosing blue marble from first bag
the digits 1 and 7 in the ones place represent choosing blue marble from second bag
let P(S) be the event choosing both blue marbles from both bags = 18/50
Therefore, the experimental probability = 0.36 = 36%
Question 33.
A cereal company is including a prize in each box. There are 5 different prizes, all of which are equally likely.
a. Describe a simulation involving 50 trials that you can use to model the prizes in the next 3 boxes of cereal you buy.
b. Use your simulation to find the experimental probability that all three boxes contain a different prize.
Answer:
Given ,
There are 5 different prizes, all of which are equally likely.
Question 34.
In the past month, your cell phone has lost its entire charge on 40% of days. Design and use a simulation to estimate the experimental probability that your cell phone loses its entire charge on exactly 2 of the next 5 days.
Answer:
Given,
Cell phone has lost its entire charge on 40%
Let the numbers 1 through 40 represents possible
6 79 3 23 82
84 67 14 59 88
11 47 26 68 18
69 91 51 56 42
15 99 58 92 62
13 41 55 17 35
28 54 85 97 65
98 57 71 73 38
89 90 87 39 72
19 8 21 45 31
There are 2 or more successes in trails {1,3,6,10 }
The experimental probability that your cell phone loses its entire charge on exactly 2 of the next 5 days = 4/50
P(S) = 0.08 = 8%
Question 35.
You and your friends form a team in gym class. You have an 80% chance of winning a game of basketball and a 10% chance of winning a game of soccer. Design and use a simulation involving 50 randomly generated numbers to estimate the probability of winning both games.

Answer:
Given , The chance of winning a game of basket ball = 80%
The probability of winning a soccer game = 10%
33 91 74 87 53 67 63 9 47 52 17 8
40 58 100 11 44 20 49 72 60 66 79 51
69 73 76 43 77 97 2 93 12 36 6 86 92 59
84 29 15 85 88 96 32 38 64 71 98 34
Let the digits 1 through 8 in the tens place represents winning a basketball
Let digits 1 and 2 in the ones place represent winning a soccer game.
let P(S) be the event of winning both the games = 7/50
Therefore, the experimental probability = 0.14 = 14%
Probability Practice Test
You randomly choose one game piece. (a) Find the number of ways the event can occur. (b) Find the favorable outcomes of the event.

Question 1.
choosing green
Answer:
Number of game pieces = 10
In which , 3 are yellow , 2 blue , 2 red and 1 are green in color
Probability P(G)= Number of favorable outcomes / Total number of outcomes
Consider G be the event of choosing green
P(G) = 1 / 10= 0..1
Therefore, the probability of choosing green = 0.1
Question 2.
choosing not yellow
Answer:
Number of game pieces = 10
In which , 3 are yellow , 2 blue , 2 red and 1 are green in color
Number of not yellow colors = 5
They are { blue , green , red }
P(N) = Number of favorable outcomes / Total umber of outcomes
P(N) = 5/10 = 0.5
Therefore, the probability of not choosing yellow= 0.5
Find the sample space and the total number of possible outcomes.
Question 3.
Answer:
Number of SPF = 5
Number of types = 3
The total number of outcomes = 5 x 3 =15
Therefore number of possible outcomes = 15
{10,lotion} {15,lotion} {30, lotion} {45, lotion} {50, lotion}
{10, spray } {15, spray} {30, spray } {45, spray} {50, spray}
{10,gel} {15, gel} {30 , gel} {45 ,gel} {50 , gel}
Question 4.
Answer:
Number of types = 4
Number of colors = 3
Total number of possible outcomes = 4 x3 = 12
{Basic display, Black } {Basic display, white } {Basic display , silver}
{Scientific, Black} {Scientific, white} {Scientific , silver}
{Graphing ,black } {Graphing , white} {Graphing , silver}
Use the bar graph to find the experimental probability of the event.
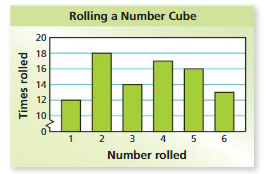
Question 5.
rolling a 1 or a 2
Answer:
Total Number of rolls = 90
The number of times 1 rolled = 12
The number of times 2 rolled = 18
Total = 30
The probability of rolling a 1 or a 2 =
P(R) = 30/90
P(R) = 0.33
Question 6.
rolling an odd number
Answer:
The number of odd numbers = 3
They are {1,3,5}
Number of times 1 rolled = 12
Number of times 3 rolled = 14
Number of times 5 rolled = 16
Total : 12 + 14 + 16 =42
Consider O be the event of spinning an odd number
P(O) = 42/90 = 0.46
Question 7.
not rolling a 5
Answer:
The total number of rolls = 90
The number of numbers other than 5 are =5
They are 1,2,3,4,6
The number of times 1 rolled = 12
The number of times 2 rolled = 18
The number of times 3 rolled = 14
The number of times 4 rolled = 17
The number of times 6 rolled = 13
Total = 74
The probability of rolling not 5 = 74/ 90
P(G) = 0.82
Question 8.
rolling a number less than 7
Answer:
The total number of rolls = 90
The number of numbers less than 7 are = 6
They are 1,2,3,4,5,6
The number of times 1 rolled = 12
The number of times 2 rolled = 18
The number of times 3 rolled = 14
The number of times 4 rolled = 17
The number of times 5 rolled = 16
The number of times 6 rolled = 13
Total = 90
The probability of rolling a number less than 7 = 90/ 90
P(L) =1
Use the spinner to find the theoretical probability 93of the event(s).

Question 9.
spinning an even number
Answer:
The spinner is divided into 9 equal parts
Numbered as {1,2,3,4,5,6,7,8,9}
So, total number of outcomes = 9
Number of even numbers = 4
They are {2,4,6,8}
Theoretical probability = Number of favorable outcomes / Total number of outcomes
Consider , E be the event of choosing an even number
P(E) = 4/ 9 = 0.44
Therefore , the probability for spinning an even number =0.44
Question 10.
spinning a 1 and then a 2
Answer:
The spinner is divided into 9 equal parts
Numbered as {1,2,3,4,5,6,7,8,9}
So, total number of outcomes = 9
The probability of spinning 1 = 1/9
Then the probability of spinning 2 = 1/9
Total probability of the event spinning a 1 and then 2 = 1/9 x 1/9
Total P(B) = 1/ 81
Therefore , the probability of spinning a 1 and then 2 = 0.012

Question 11.
You randomly choose one of the pens shown. What is the theoretical probability of choosing a black pen?
Answer:
Theoretical probability = Number of favorable outcomes / Total number of outcomes
Total number of pens = 5
Number of black pens = 2
Consider B be the event of choosing a black pen
P(B) = 2/5 = 0.4
Therefore, the theoretical probability of choosing a black pen = 0.4
Question 12.
You randomly choose one of the pens shown. Your friend randomly chooses one of the remaining pens. What is the probability that you and your friend both choose a blue pen?
Answer:
Total number of pens = 5
Number of blue pens = 2
The probability that you and your friend both choose a blue pen
P(B) = 2/5
P(B) = 0.4
Question 13.
There is an 80% chance of a thunderstorm on Saturday. Describe the likelihood that there is not a thunderstorm on Saturday.
Answer:
Given probability 80% = 0.8
Not thunder storm probability = 20 % = 0.2
The likelihood of the event is not likely to happen
Probability Cumulative Practice

Question 1.
A school athletic director asked each athletic team member to name his or her favorite professional sports team. The results are below:
- D.C.United: 3
- Florida Panthers: 8
- Jacksonville Jaguars: 26
- Jacksonville Sharks: 7
- Miami Dolphins: 22
- Miami Heat: 15
- Miami Marlins: 20
- Minnesota Lynx: 4
- New YorkKnicks: 5
- Orlando Magic: 18
- Tampa Bay Buccaneers: 17
- Tampa Bay Lightning: 12
- Tampa Bay Rays: 28
- Other: 6
One athletic team member is picked at random. What is the likelihood that this team member’s favorite professional sports team is not located in Florida?
A. certain
B. likely, but not certain
C. unlikely, but not impossible
D. impossible
Answer: B
13/14 = 0.92
The likelihood of the event is likely, but not certain
Question 2.
Each student in your class voted for his or her favorite day of the week. Their votes are shown in the circle graph:
A student from your class is picked at random. What is the probability that this student’s favorite day of the week is Sunday?
Answer:
Total number of students =30
Total number of Sunday = 6
The probability of that this student’s favorite day of the week is Sunday
P(S) = 6/30
= 0.2
Question 3.
What value makes the equation 11 – 3x = – 7 true?
F. – 6
G. \(-\frac{4}{3}\)
H. 6
I. 54
Answer: F
Explanation:
11 – 3x = -7
Consider the value of x = -6
L.H.S = 11-3X
11 – 3 (-6)
11 – 18
= -4
L.H.S = R.H.S
Therefore, the value of x =-6
Question 4.
Your friend solved the proportion in the box below.
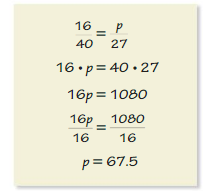
What should your friend do to correct the error that he made?
A. Add 40 to 16 and 27 to p.
B. Subtract 16 from 40 and 27 from p.
C. Multiply 16 by 27 and p by 40.
D. Divide 16 by 27 and p by 40.
Answer: C
Multiply 16 by 27 and p by 40
Question 5.
Which value is a solution of the inequality?
3 – 2y < 7
F. – 6
G. – 3
H. – 2
I. – 1
Answer: H
3- 2y < 7 =0
3-2y >7
-2y > 7-3
-2y >4
y > -4/2
y > -2
Question 6.
A spinner is divided into eight equal sections, as shown. You spin the spinner twice. What is the probability that the arrow will stop in a yellow section both times?

Answer:
The spinner is divided 8 equal parts
In which , 3 are red , 2 are blue, 2 are yellow and 1 part is in pink color
so the probability of landing on yellow would be
P(Y) = 3/8 on first spun.
Therefore, for spinning the spinner twice then the probability of landing it on yellow would be
P(Y) = (3/8)/2
P(Y) =3/16
Question 7.
A pair of running shoes is on sale for 25% off the original price. Which price is closest to the sale price of the running shoes?

A. $93
B. $99
C. $124
D. $149
Answer: A
Explanation :
Original price = $122.76
Percent of discount = 25% = 0.25
The amount of discount :
Amount of discount = Discount x original price
= 0.25 x $125
= $30.39
Sale price :
Sale price = Original price – discount
= $122.76 – $30.39
= $92.07
It is very close to the sale price of the running shoes = $ 93
Question 8.
The value of a baseball card was $6 when it was sold. The value of this card is now $15. What is the percent increase in the value of the card?
F. 40%
G. 90%
H. 150%
I. 250%
Answer: H
Given,
Original price of the basket ball = $6
New price = $15
The original price increases so, the percent of change is called percent of increase
Percent of increase = New price – original price/ Original price
On substituting ,
= 15 – 6/ 6
= 9 / 6
=3/2
On multiplying with 100
= 3/2 x 100
= 150%
Therefore , the percent increase in the value of the card = 150%
Question 9.
You roll a number cube twice. You want to roll two even numbers.

Part A Find the number of favorable outcomes and the number of possible outcomes of each roll.
Part B Find the probability of rolling two even numbers. Explain your reasoning.
Answer:
Part A :
The even numbers on a number cube are 2, 4, and 6
The favorable outcomes for 2 are =3
They are : 2 and 2 , 2 and 4 , 2 and 6
The favorable outcomes for 4 are =3
They are : 4 and 2 , 4 and 4 , 4 and 6
The favorable outcomes for 6 are =3
They are : 6 and 2 , 6 and 4 , 6 and 6
So, total number favorable outcomes = 9
There are 6 outcomes for each cube so there are 6(6) = 36 total outcomes.
Part B :
There are 9 favorable outcomes of a total of 36 outcomes
So, the probability is 9/36 = 1/4
Question 10.
You put $600 into an account. The account earns 5% simple interest per year. What is the balance after 4 years?
A. $120
B. $720
C. $1800
D. $12,600
Answer: B
Simple interest = principle x annual rate of interest x Time
I = P x r x t
5% = 0.5
I = 600 x 0.05 x 4
I = $120
The interest earned = $120
The balance after 4 years = principle + Interest
= 600 + 120
=$720
Question 11.
You are comparing the prices of four boxes of cereal. Two of the boxes contain free extra cereal.
- Box F costs $3.59 and contains 16 ounces.
- Box G costs $3.79 and contains 16 ounces, plus an additional 10% for free.
- Box H costs $4.00 and contains 500 grams.
- Box I costs $4.69 and contains 500 grams, plus an additional 20% for free.
Which box has the least unit cost?
F. Box F
G. Box G
H. Box H
I. Box I
Answer: Box G
Explanation :
Box F
The unit cost of box F = 3.59/16
The unit cost = $0.224 per ounces
Box G
Given 10% free
Which means, 10% = 16.01 = 0.6 ounces
The unit cost box G = $3.79 / 16 +0.6
=$0.215 ounces
Box H
Given, 500 grams
Which means , 500/28.35 = 17. 64 ounces