Big Ideas Math Geometry Answers Chapter 10 Circles

Big Ideas Math Book Geometry Chapter 10 Circles Answers are provided here. Students who have been looking for the BIM Geometry Chapter 10 Circles Answers can read the following sections. The high school students can find a direct link to download Big Ideas Math Geometry Answers Chapter 10 Circles pdf for free of cost. With the help of this answer key, you can prepare well for the exam.

Big Ideas Math Book Geometry Answer Key Chapter 10 Circles

The different chapters included in Big Ideas Math Geometry Solutions are Lines and Segments That Intersect Circles, Finding Arc Measures, Inscribed Angles and Polygons, Angle Relationships in Circles, Segment Relationships in Circles, Circles in the Coordinate Plane, and Using Chords. Students have to practise all the questions from Big Ideas Math Textbook Geometry Chapter 10 Circles.

This Big Ideas Math Book Geometry Answer Key Chapter 10 Circles helps the students while doing the assignments. Get the solutions for all the questions through the quick links provided in the following sections. Test your skills through performance task, chapter review, and maintaining mathematical proficiency.

Circles Maintaining Mathematical Proficiency

Find the Product.

Question 1.
(x + 7) (x + 4)

Solution:
x² + 4x + 28

Explanation:
Given,
(x + 7) (x + 4)
= x(x + 4) + 7(x + 4)
= x² + 4x + 7x + 28
= x² + 4x + 28

Question 2.
(a + 1) (a – 5)

Solution:
a² – 4a – 5

Explanation:
Given,
(a + 1) (a – 5)
= a(a – 5) + 1(a – 5)
= a² – 5a + a – 5
= a² – 4a – 5

Question 3.
(q – 9) (3q – 4)

Solution:
3q² – 31q + 32

Explanation:
Given,
(q – 9) (3q – 4)
= q(3q – 4) – 9(3q – 4)
= 3q² – 4q – 27q + 32
= 3q² – 31q + 32

Question 4.
(2v – 7) (5v + 1)

Solution:
10v² – 33v – 7

Explanation:
Given,
(2v – 7) (5v + 1)
= 2v(5v + 1) – 7(5v + 1)
= 10v² + 2v – 35v – 7
= 10v² – 33v – 7

Question 5.
(4h + 3) (2 + h)

Solution:
4h² + 11h + 6

Explanation:
Given,
(4h + 3) (2 + h)
= 4h(2 + h) + 3(2 + h)
= 8h + 4h² + 6 + 3h
= 4h² + 11h + 6

Question 6.
(8 – 6b) (5 – 3b)

Solution:
18b² – 54b + 40

Explanation:
Given,
(8 – 6b) (5 – 3b)
= 8(5 – 3b) – 6b(5 – 3b)
= 40 – 24b – 30b + 18b²
= 18b² – 54b + 40

Solve the equation by completing the square. Round your answer to the nearest hundredth, if necessary.

Question 7.
x² – 2x = 5

Solution:
x = √6 + 1, x = 1 – √6

Explanation:
Given,
x² – 2x = 5
x² – 2x + 1² = 5 + 1²
(x – 1)² = 6
x – 1 = ±√6
x = ±√6 + 1
So, x = √6 + 1, x = -√6 + 1

Question 8.
r² + 10r = -7

Solution:
r = √18 – 5, r = 5 – √18

Explanation:
Given,
r² + 10r = -7
r² + 10r + 5² = -7 + 5²
(r + 5)² = -7 + 25 = 18
r + 5 = ±√18
r = ±√18 – 5
So, r = √18 – 5, r = 5 – √18

Question 9.
w² – 8w = 9

Solution:
w = 9, w = -1

Explanation:
Given,
w² – 8w = 9
w² – 8w + 4² = 9 + 4²
(w – 4)² = 9 + 16 = 25
w – 4 = ±5
w = 5 + 4, w = -5 + 4
So, w = 9, w = -1

Question 10.
p² + 10p – 4 = 0

Solution:
p = √29 – 5, p = 5 – √29

Explanation:
Given,
p² + 10p – 4 = 0
Transformation of -4 from L.H.S to R.H.S
p² + 10p = 4
p² + 10p + 5² = 4 + 5²
(p + 5)² = 4 + 25
(p + 5)² = 29
p + 5 = ±√29
p = ±√29 – 5
So, p = √29 – 5, p = 5 – √29

Question 11.
k² – 4k – 7 = 0

Solution:
k = √11 + 2, k = 2 – √11

Explanation:
Given,
k² – 4k – 7 = 0
Transformation of -7 from L.H.S to R.H.S
k² – 4k = 7
k² – 4k + 2² = 7 + 4
(k – 2)² = 11
k – 2 = ±√11
k = √11 + 2, k = 2 – √11
So, k = √11 + 2, k = 2 – √11

Question 12.
– z² + 2z = 1

Solution:
z = 1

Explanation:
Given,
-z² + 2z = 1
z² – 2z = -1
z² – 2z + 1 = -1 + 1
(z – 1)² = 0
z = 1

Question 13.
ABSTRACT REASONING
write an expression that represents the product of two consecutive positive odd integers. Explain your reasoning.

Solution:
x(x + 2) = x² + 2x

Explanation:
Given to write an expression that represents the product of two consecutive positive odd integers.
Let us take two consecutive odd integers are x and (x + 2)
The product of two consecutive odd integers is x • (x + 2)
So, the product of consecutive integers is x(x + 2) = x² + 2x

Circles Mathematical Practices

Monitoring progress

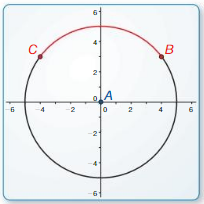
Let ⊙A, ⊙B, and ⊙C consist of points that are 3 units from the centers.

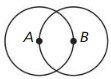
Question 1.
Draw ⊙C so that it passes through points A and B in the figure at the right. Explain your reasoning.

Solution:

Explanation:
As we know,
A circle is the set of all points in a plane that are equidistant from a given point is known as the center of the circle.
Circle with center A is called “circle A” and can be written as ⊙A.
Circles ⊙A, ⊙B, and ⊙C consist of points that are 3 units from the centers.
⊙C is passes through points A and B as shown in the above figure.

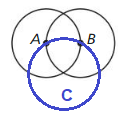
Question 2.
Draw ⊙A, ⊙B, and ⊙C so that each is tangent to the other two. Draw a larger circle, ⊙D, that is tangent to each of the other three circles. Is the distance from point D to a point on ⊙D less than, greater than, or equal to 6? Explain.

Solution:
The distance from point D to a point on ⊙D  greater then 6 units.

Explanation:
As we know,
A circle is the set of all points in a plane that are equidistant from a given point is called the center of the circle.
A circle with center D is called “circle D” and can be written as ⊙D.
Coplanar circles that intersect in one point are called tangent circles.

10.1 Lines and Segments that Intersect Circles

Exploration 1

Lines and Line Segments That Intersect Circles

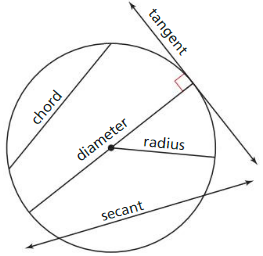
Work with a partner: The drawing at the right shows five lines or segments that intersect a circle. Use the relationships shown to write a definition for each type of line or segment. Then use the Internet or some other resource to verify your definitions.
Chord: _________________
Secant: _________________
Tangent: _________________
Radius: _________________
Diameter: _________________

Solution:
Chord:
A chord of a circle is a straight line segment whose endpoints both lie on a circular arc.
Secant:
A straight line that intersects a circle in two points is called a secant line.
Tangent:
Tangent line is a line that intersects a curved line at exactly one point.
Radius:
It is the distance from the center of the circle to any point on the circle.
Diameter:
It the straight that joins two points on the circle and passes through the center of the circle.

Exploration 2

Using String to Draw a Circle

Work with a partner: Use two pencils, a piece of string, and a piece of paper.

a. Tie the two ends of the piece of string loosely around the two pencils.
Answer:

b. Anchor one pencil of the paper at the center of the circle. Use the other pencil to draw a circle around the anchor point while using slight pressure to keep the string taut. Do not let the string wind around either pencil.

Answer:

c. Explain how the distance between the two pencil points as you draw the circle is related to two of the lines or line segments you defined in Exploration 1.
REASONING ABSTRACTLY
To be proficient in math, you need to know and flexibly use different properties of operations and objects.
Answer:

Communicate Your Answer

Question 3.
What are the definitions of the lines and segments that intersect a circle?
Answer:

Question 4.
Of the five types of lines and segments in Exploration 1, which one is a subset of another? Explain.
Answer:

Question 5.
Explain how to draw a circle with a diameter of 8 inches.
Answer:

Lesson 10.1 Lines and Segments that Intersect Circles

Monitoring progress

Question 1.
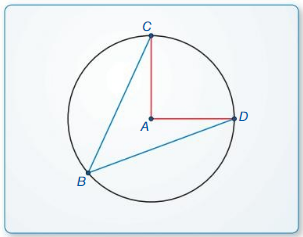
In Example 1, What word best describes \(\overline{AG}\)? \(\overline{CB}\)?

Solution:
\(\overline{A G}\) is secant because it is a line that intersects the circle at two points.
\(\overline{C B}\) is the radius as it is the distance from the center to the point of a circle.

Explanation:

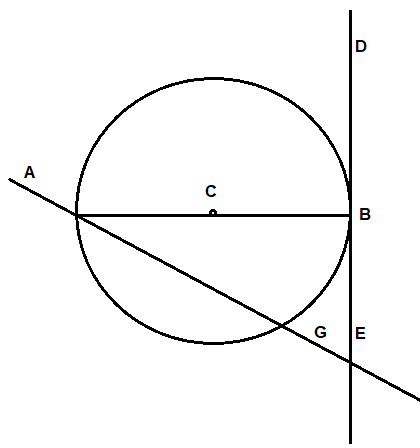
secant is a line that intersects a circle in two points.
\(\overline{AG}\) is a line that intersects the circle at two points.

A segment whose endpoints are the center and any point on a circle is a radius.
\(\overline{CB}\) is the radius as it is the distance from the center to the point of a circle.

Question 2.
In Example 1, name a tangent and a tangent segment.

Solution:
\(\overline{D E}\) is the tangent of the circle
\(\overline{D E}\) is the tangent segment of the circle.

Explanation:
A tangent is a line in the plane of a circle that intersects the circle in exactly one point, the
point of tangency.
The tangent ray \(\overline{AB}\) and the tangent segment \(\overline{AB}\) are also called tangents.

Tell how many common tangents the circles have and draw them. State whether the tangents are external tangents or internal tangents.

Question 3.

Solution:
4 tangents.

Explanation:

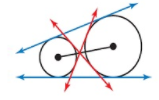
A tangent is a line segment that intersects the circle at exactly one point.
Internal tangents are the lines that intersect the segments joining the centers of two circles.
External tangents are the lines that do not cross the segment joining the centers of the circles.
Blue lines represent the external tangents and red lines represent the internal tangents.

Question 4.

Solution:
One tangent.

Explanation:
External tangents are the lines that do not cross the segment joining the centers of the circles.

One external tangent.

Question 5.

Solution:
No tangent.

Explanation:
As circles are of different size with common center, there is no overlapping circles.
It is not possible to draw a common tangent for this type of circles.

Question 6.
Is \(\overline{DE}\) tangent to ⊙C?

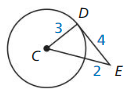
Solution:
Yes,

Explanation:
By using the converse of Pythagorean theorem,
CE² = CD² + DE²
(r + 2)² = 3² + 4²
(3 + 2)² = 3² + 4²
25 = 9 + 16
So, the Tangent Line to Circle Theorem that CD⊥ DE, so △CDE is a right triangle.
By the tangent line to the circle theorem, \(\overline{DE}\) is a tangent to ⊙C

Question 7.
\(\overline{S T}\) is tangent to ⊙Q.
Find the radius of ⊙Q.

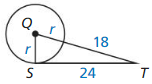
Solution:
The radius of ⊙Q is 7 units.

Explanation:
Given,
The Tangent Line to Circle Theorem that QS⊥ ST, so △QST is a right triangle.
By using the tangent line to the circle theorem,
\(\overline{ST}\) is a tangent to ⊙Q.
By using the Pythagorean theorem,
(18 + r)² = r² + 24²
324 + 36r + r² = r² + 576
36r = 576 – 324
36r = 252
r = 7 units.

Question 8.
Points M and N are points of tangency. Find the value(s) of x.

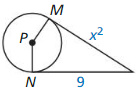
Solution:
The values of x are 3 or -3.

Explanation:
Given that, Points M and N are points of tangency.
x² = 9
x = ±3

Exercise 10.1 Lines and Segments that Intersect Circles

Vocabulary and Core Concept Check

Question 1.
WRITING
How are chords and secants alike? How are they different?

Solution:

Question 2.
WRITING
Explain how you can determine from the context whether the words radius and diameter are referring to segments or lengths.

Solution:
Radius and diameter are the lengths of the line segments that pass through the center of a circle.
So, radius is half of the diameter.

Question 3.
COMPLETE THE SENTENCE
Coplanar circles that have a common center are called ____________ .

Solution:

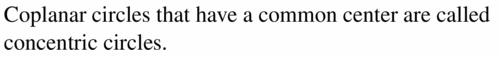
Question 4.
WHICH ONE DOESNT BELONG?
Which segment does not belong with the other three? Explain your reasoning.
chord radius tangent diameter

Solution:
A chord, a radius and a diameter are segments and they intersect a circle in two points.
Where as tangent is a line that intersects a circle at one point.

Monitoring Progress and Modeling with Mathematics

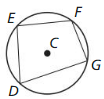
In Exercises 5 – 10, use the diagram.

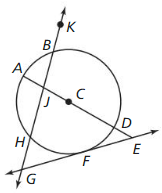
Question 5.
Name the circle.

Solution:

Question 6.
Name two radii.

Solution:
The name of the two radii is CD and AC.

Explanation:
Radius:
It is the distance from the center of the circle to any point on the circle.
In the above given figure the two radii are CD and AC.

Question 7.
Name two chords.

Solution:

Explanation:
A chord is a segment whose endpoints are on a circle.
There are two chords in the given diagram,
\(\overline{BH}\) and \(\overline{AD}\)

Question 8.
Name a diameter.

Solution:
The name of diameter is AD.

Explanation:
Diameter:
It the straight that joins two points on the circle and passes through the center of the circle.
In the given figure the name of diameter is AD.
\(\overline{AD}\)

Question 9.
Name a secant.

Solution:

Explanation:
Secant:
A straight line that intersects a circle in two points is called a secant line.
In the above given figure \(\overline{KG}\) is a secant.

Question 10.
Name a tangent and a point of tangency

Solution:
GE is the tangent and F is the point of tangency.

Explanation:
Tangent:
Tangent line is a line that intersects a curved line at exactly one point.
In the given figure, \(\overline{GE}\) is the tangent and F is the point of tangency.

In Exercises 11 – 14, copy the diagram. Tell how many common tangents the circles have and draw them.

Question 11.

Solution:

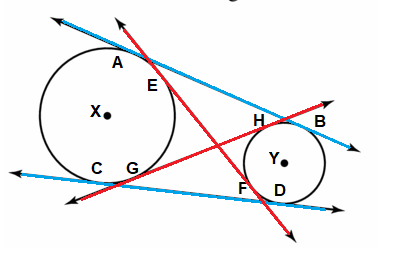
Explanation:
Based on the above figure,
Tangent: Tangent line is a line that intersects a curved line at exactly one point.
\(\overline{AB}\) is the tangent and A and B are the points of tangency of circles X and Y.
\(\overline{CD}\) is the tangent and C and D are the points of tangency of circles X and Y.
\(\overline{GH}\) is the tangent and A and B are the points of tangency of circles X and Y.
\(\overline{EF}\) is the tangent and A and B are the points of tangency of circles X and Y.

Question 12.

Solution:
No common tangent because two circles do not intersect at one point.

Explanation:
With reference to the above figure, circles do not overlap each other.
Circle to be overlap at common point for common tangent of circles.

Question 13.

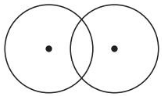
Solution:

Explanation:
With reference to the above figure,
There are two common tangents, as circles are of same size and shape due to same radius.

Question 14.

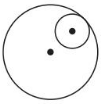
Solution:
One common tangent.

Explanation:
The above two circles given in the figure are of two different size and intersected at one point.
So, there is one tangent drawn as shown in the above diagram.

In Exercises 15 – 18, tell whether the common tangent is internal or external.

Question 15.

Solution:
External tangent.

Explanation:

Question 16.

Solution:
Internal tangent.

Explanation:
The common tangent is the internal tangent because it intersects the segment that joins the centers of two circles as shown in the given figure.

Question 17.

Solution:
Internal tangent.

Explanation:

Question 18.

Solution:
Internal tangent.

Explanation:
The common tangent is the internal tangent because it intersects the segment that joins the centers of two circles as shown in the above figure.

In Exercises 19 – 22, tell whether \(\overline{A B}\) is tangent to ⊙C. Explain your reasoning.

Question 19.

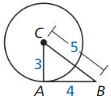
Solution:
\(\overline{AB}\) is the tangent to ⊙C at point A.

Explanation:

Question 20.

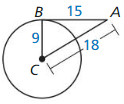
Solution:
△ ACB is not a right angled triangle.
So, \(\overline{A B}\) is not tangent to ⊙C at B.

Explanation:
Use the converse of the Pythagorean theorem,
18² _____________ 15² + 9²
324 _____________ 225 + 81
324 ≠ 304
△ ACB is not a right angled triangle.
So, \(\overline{A B}\) is not tangent to ⊙C at B.

Question 21.

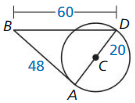
Solution:
△ ABD is not a right angled triangle.
So, \(\overline{AB}\) is not tangent to ⊙C at A.

Explanation:

Question 22.

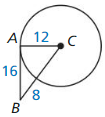
Solution:
\(\overline{AB}\) is tangent to ⊙C at A.

Explanation:
Use the converse of the Pythagorean theorem,
(8+12)² _____________ 12² + 16²
20 x 20 _____________ 144 + 256
400 = 400
△ ACB is a right angled triangle.
So, \(\overline{AB}\) is tangent to ⊙C at A.

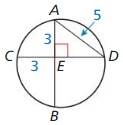
In Exercises 23 – 26, point B is a point of tangency. Find the radius r of ⊙C.

Question 23.

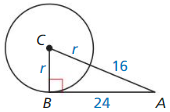
Solution:
r = 10 units.

Explanation:

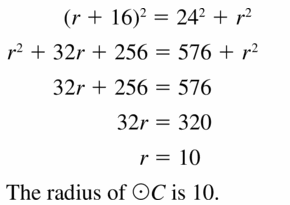
Question 24.

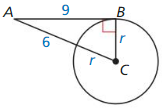
Solution:
r = \(\frac {15}{4} \) units.

Explanation:
(r + 6)² = r² + 9²
r² + 12r + 36 = r² + 81
12r = 81 – 36
12r = 45
r = \(\frac { 15 }{ 4 } \)
Therefore, the radius of ⊙C is \(\frac { 15 }{ 4 } \)

Question 25.

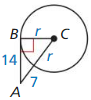
Solution:
r = 10.5 units.

Explanation:

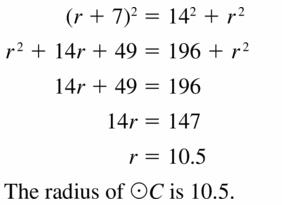
Question 26.

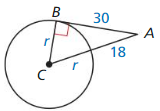
Solution:
r = 16 units.

Explanation:
(r + 18)² = r² + 30²
r² + 36r + 324 = r² + 900
36r = 900 – 324
36r = 576
r = 16
Therefore, the radius of ⊙C is 16

CONSTRUCTION
In Exercises 27 and 28. construct ⊙C with the given radius and point A outside of ⊙C. Then construct a line tangent to ⊙C that passes through A.

Question 27.
r = 2 in.

Solution:

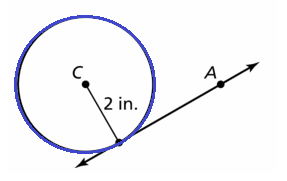
Explanation:
⊙C circle, the given radius 2 in and point A outside of ⊙C.
The construct  line tangent to ⊙C that passes through A.

Question 28.
r = 4.5 cm

Solution:

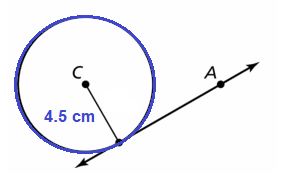
Explanation:
⊙C circle, the given radius 4.5 cm and point A outside of ⊙C.
The construct  line tangent to ⊙C that passes through A.

In Exercises 29 – 32, points B and D are points of tangency. Find the value(s) of x.

Question 29.

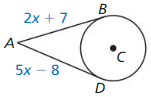
Solution:

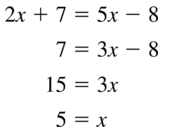
Question 30.

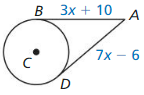
Solution:
x = 4

Explanation:
With reference to above figure,
3x + 10 = 7x – 6
7x – 3x = 10 + 6
4x = 16
x = 4

Question 31.

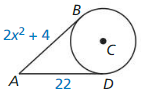
Solution:

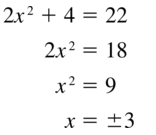
Question 32.

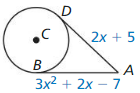
Solution:
x = ±2

Explanation:
2x + 5 = 3x² + 2x – 7
3x² = 5 + 7
3x² = 12
x² = 4
x = ±2

Question 33.
ERROR ANALYSIS
Describe and correct the error in determining whether \(\overline{X Y}\) is tangent to ⊙Z.

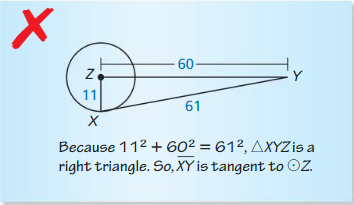
Solution:

Question 34.
ERROR ANALYSIS
Describe and correct the error in finding the radius of ⊙T.

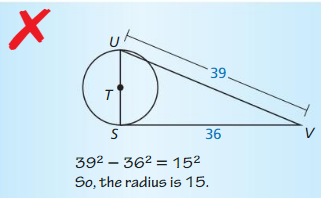
Solution:
The radius is \(\frac { 15 }{ 2 } \).

Explanation:
39² = 36² + 15²
So, 15 is the diameter.
The radius is \(\frac { 15 }{ 2 } \).

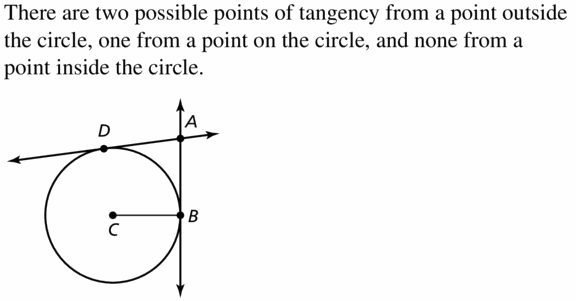
Question 35.
ABSTRACT REASONING
For a point outside of a circle, how many lines exist tangent to the circle that pass through the point? How many such lines exist for a point on the circle? inside the circle? Explain your reasoning.

Solution:

Question 36.
CRITICAL THINKING
When will two lines tangent to the same circle not intersect? Justify your answer.

Solution:

Explanation:
When two tangents are drawn at the two ends of the same diameter of the same circle they will not intersect.
Since at this point of contact both the angles will be right angles.
So, these tangents will be parallel lines as shown in the above figure.

Using tangent line to circle theorem, it follow that the angle between tangent and radius is a right angle. Let’s draw these tangents at the two ends of the same diameter. We can observe a diameter AD like a transversal of these tangents.

Question 37.
USING STRUCTURE
Each side of quadrilateral TVWX is tangent to ⊙Y. Find the perimeter of the quadrilateral.

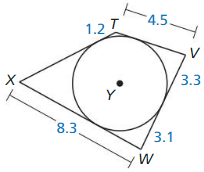
Solution:

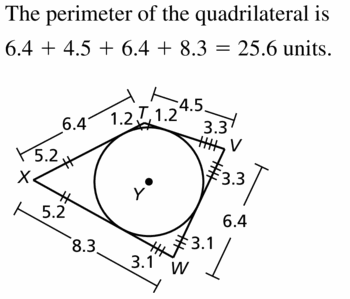
Question 38.
LOGIC
In ⊙C, radii \(\overline{C A}\) and \(\overline{C B}\) are perpendicular. are tangent to ⊙C.

a. Sketch ⊙C, \(\overline{C A}\), \(\overline{C B}\), .
Answer:

b. What type of quadrilateral is CADB? Explain your reasoning.
Answer:

Question 39.
MAKING AN ARGUMENT
Two hike paths are tangent to an approximately circular pond. Your class is building a nature trail that begins at the intersection B of the bike paths and runs between the bike paths and over a bridge through the center P of the pond. Your classmate uses the Converse of the Angle Bisector Theorem (Theorem 6.4) to conclude that the trail must bisect the angle formed by the bike paths. Is your classmate correct? Explain your reasoning.

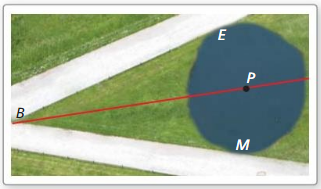
Solution:

Question 40.
MODELING WITH MATHEMATICS
A bicycle chain is pulled tightly so that \(\overline{M N}\) is a common tangent of the gears. Find the distance between the centers of the gears.

Solution:
The distance between the center of the gear is 17.8 in.

Explanation:
Given,
height h = 4.3 – 1.8
h = 2.5 in
x² = MN² + h²
x² = 17.6² + 2.5²
x² = 316.01
x = 17.8
Therefore, the distance between the center of the gear is 17.8 in.

Question 41.
WRITING
Explain why the diameter of a circle is the longest chord of the circle.

Solution:

Question 42.
HOW DO YOU SEE IT?
In the figure, \(\vec{P}\)A is tangent to the dime. \(\vec{P}\)C is tangent to the quarter, and \(\vec{P}\)B is a common internal tangent. How do you know that \(\overline{P A} \cong \overline{P B} \cong \overline{P C}\)

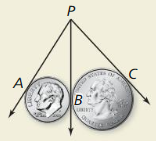
Answer:

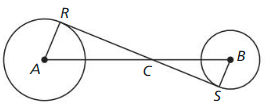
Question 43.
PROOF
In the diagram, \(\overline{R S}\) is a common internal tangent to ⊙A and ⊙B. Prove that \(\frac{\Lambda C}{B C}=\frac{R C}{S C}\)

Solution:

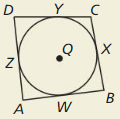
Question 44.
THOUGHT PROVOKING
A polygon is circumscribed about a circle when every side of the polygon is tangent to the circle. In the diagram. quadrilateral ABCD is circumscribed about ⊙Q. Is it always true that AB + CD = AD + BC? Justify your answer.

Answer:

Question 45.
MATHEMATICAL CONNECTIONS
Find the values of x and y. Justify your answer.

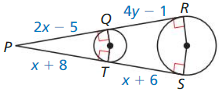
Solution:

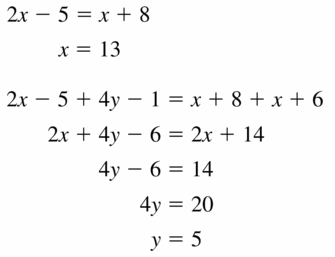
Question 46.
PROVING A THEOREM
Prove the External Tangent Congruence Theorem (Theorem 10.2).

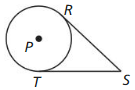
Given \(\overline{S R}\) and \(\overline{S T}\) are tangent to ⊙P.
Prove \(\overline{S R} \cong \overline{S T}\)

Solution:

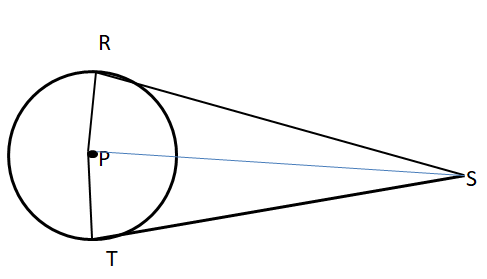
Explanation:
Given that,
\(\overline{S R}\) and \(\overline{S T}\) are tangent to ⊙P.
According to the external tangent theorem,
if from one external point, two tangents are drawn to a circle then they have equal tangent segments. Tangent segment means line joining to the external point and the point of tangency.
We observe that,
∠PRS and ∠PTS are the right angles.
So, the legs of circles are congruent.
Therefore, \(\overline{S R} \cong \overline{S T}\)

Question 47.
PROVING A THEOREM
Use the diagram to prove each part of the biconditional in the Tangent Line to Circle Theorem (Theorem 10.1 ).

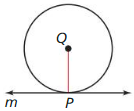
a. Prove indirectly that if a line is tangent to a circle, then it is perpendicular to a radius. (Hint: If you assume line m is not perpendicular to \(\overline{Q P}\), then the perpendicular segment from point Q to line m must intersect line m at some other point R.)
Ghen Line m is tangent to ⊙Q at point P.
Prove m ⊥ \(\overline{Q P}\)
b. Prove indirectly that if a line is perpendicular to a radius at its endpoint, then the line is tangent to the circle.
Gien m ⊥ \(\overline{Q P}\)
Prove Line m is tangent to ⊙Q.

Solution:

Question 48.
REASONING
In the diagram, AB = AC = 12, BC = 8, and all three segments are Langent to ⊙P. What is the radius of ⊙P? Justify your answer.

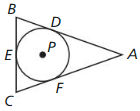
Answer:

Maintaining Mathematical Proficiency

Find the indicated measure.

Question 49.
m∠JKM

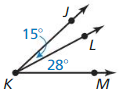
Solution:

Question 50.
AB

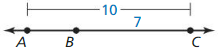
Solution:
AB = 3

Explanation:
Given,
AC = 10
We know that,
AC = AB + BC
10 = AB + 7
AB = 10 – 7
AB = 3

10.2 Finding Arc Measures

Exploration 1

Measuring Circular Arcs

Work with a partner: Use dynamic geometry software to find the measure of \(\widehat{B C}\). Verify your answers using trigonometry.

a.

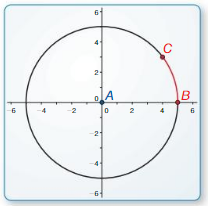
Points
A(0, 0)
B(5, 0)
C(4, 3)

Solution:
30 degrees.

Explanation:
We know that the length of an arc in a circle is to plot two lines from the arc’s endpoints to the center of the circle as shown in the given figure.
Then measure the angle where the two lines meet the center.
measure of angle in degrees/360° = L/circumference.

b.

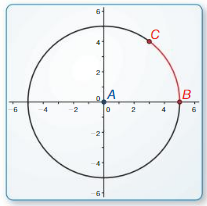
Points
A(0, 0)
B(5, 0)
C(3, 4)

Solution:
60 degrees.

Explanation:
We know that the length of an arc in a circle is to plot two lines from the arc’s endpoints to the center of the circle as shown in the given figure.
Then measure the angle where the two lines meet the center.
measure of angle in degrees/360° = L/circumference.

c.

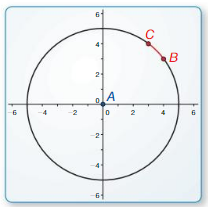
Points
A(0, 0)
B(4, 3)
C(3, 4)

Solution:
15 degrees.

Explanation:
We know that the length of an arc in a circle is to plot two lines from the arc’s endpoints to the center of the circle as shown in the given figure.
Then measure the angle where the two lines meet the center.
measure of angle in degrees/360° = L/circumference.

d.

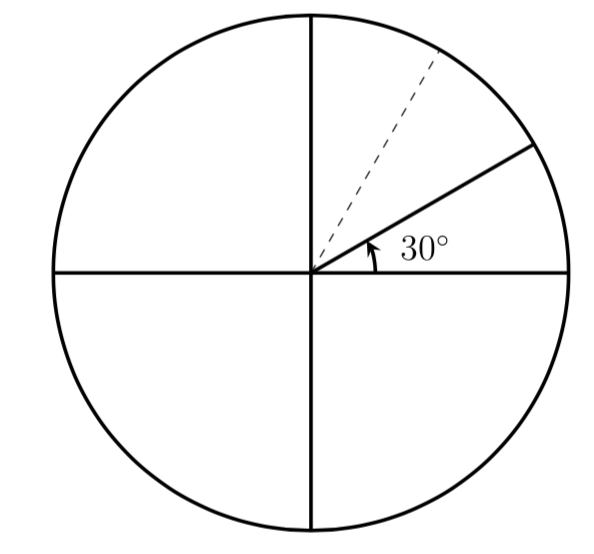
Points
A(0, 0)
B(4, 3)
C(- 4, 3)

Solution:
90 degrees.
Explanation:
We know that the length of an arc in a circle is to plot two lines from the arc’s endpoints to the center of the circle as shown in the given figure.
Then measure the angle where the two lines meet the center.
measure of angle in degrees/360° = L/circumference.

Communicate Your Answer

Question 2.
How are circular arcs measured?

Solution:
If an arc in a circle is to plot two lines from the arc’s endpoints to the center of the circle,
Then measure the angle where the two lines meet the center.
measure of angle in degrees/360° = L/circumference.

Question 3.
Use dynamic geometry software to draw a circular arc with the given measure.
USING TOOLS STRATEGICALLY
To be proficient in math, you need to use technological tools to explore and deepen your understanding of concepts.
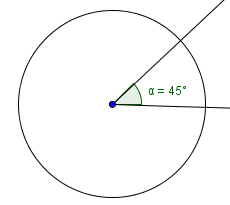
a. 30°

Solution:

b. 45°

Solution:

c. 60°
Solution:

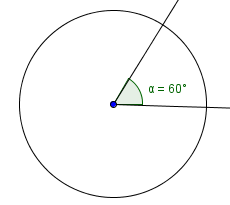
d. 90°

Solution:

Lesson 10.2 Finding Arc Measures

Monitoring Progress

Identify the given arc as a major arc, minor arc, or semicircle. Then find the measure of the arc.

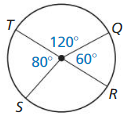
Question 1.
\(\widehat{T Q}\)

Solution:
\(\widehat{T Q}\) = 120°

Explanation:
With reference to the above figure,
\(\widehat{T Q}\) is a minor arc.
\(\widehat{T Q}\) = 120°

Question 2.
\(\widehat{Q R T}\)

Solution:
\(\widehat{Q R T}\) = 240°

Explanation:
With reference to the above figure,
Given,
\(\widehat{Q R T}\)
RS = QR + RS + ST
RS = 360° – (60 + 120 + 80)
So, 360 – 260 = 100°
So, \(\widehat{Q R T}\) = 60° + 100° + 80°
\(\widehat{Q R T}\) = 240°

Question 3.
\(\widehat{T Q R}\) is a major arc.

Solution:
\(\widehat{Q R T}\) = 240°

Explanation:
With reference to the above figure,
Given,
\(\widehat{Q R T}\) is a major arc.
RS = QR + RS + ST
RS = 360° – (60 + 120 + 80)
So, 360 – 260 = 100°
So, \(\widehat{Q R T}\) = 60° + 100° + 80°
\(\widehat{Q R T}\) = 240°

Question 4.
\(\widehat{Q S}\)

Solution:
\(\widehat{Q S}\) = 160°

Explanation:
With reference to the above figure,
Given,
\(\widehat{Q S}\)
QS = QR + RS
So, 60 + 100 = 160°
Therefore, \(\widehat{Q S}\) = 160° and it is a minor arc.

Question 5.
\(\widehat{T S}\)

Solution:
\(\widehat{T S}\) = 80° and it is a minor arc.

Explanation:
With reference to the above figure,
\(\widehat{T S}\) is a minor arc.
\(\widehat{T S}\) = 80°

Question 6.
\(\widehat{R S T}\)

Solution:
\(\widehat{R S T}\) = 180°

Explanation:
With reference to the above figure,
Given,
\(\widehat{R S T}\)
RS + TS = 100 + 80 = 180
Therefore, \(\widehat{R S T}\) = 180° and it is a minor arc.

Tell whether the red arcs are congruent. Explain why or why not.

Question 7.

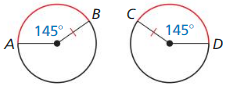
Solution:
\(\widehat{A B}\), \(\widehat{C D}\) are congruent as they measure same radius and same arc length.

Explanation:
We know that,
Congruent angles are two or more angles that are identical to each other.
Therefore, the measure of these angles is equal to each other as in the above figure.

Question 8.

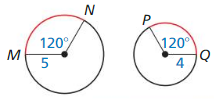
Solution:
\(\widehat{M N}\), \(\widehat{P Q}\) are not congruent as they measure different radius.

Explanation:
We know that,
Congruent radius are two or more radius that are identical to each other.
Therefore, the measure of these radii also equal to each other,
as in the above figure the measure of radii is different.
Hence the given circles are not congruent.

Exercise 10.2 Finding Arc Measures

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
Copy and complele:
If ∠ACB and ∠DCE are congruent central angles of ⊙C, then \(\widehat{A B}\) and \(\widehat{D E}\) arc.

Solution:

Question 2.
WHICH ONE DOESNT BELONG?
Which circle does not belong with the other three? Explain your reasoning.

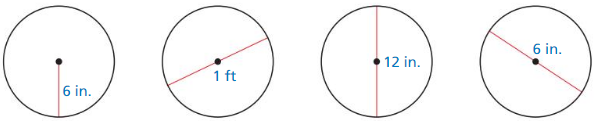
Solution:
We know that 1 ft = 12 in
So, the fourth circle does not belong to the other three as its diameter is different.

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6, name the red minor arc and find its measure. Then name the blue major arc and find its measure.

Question 3.

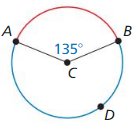
Solution:

Question 4.

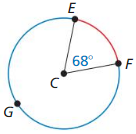
Solution:
The minor arc \(\widehat{E F}\) = 68°
The major arc \(\widehat{F G E}\) = 360° – 68° = 292°.

Explanation:
An arc whose measure is less than 180 degrees is called a minor arc. An arc whose measure is greater than 180 degrees is called a major arc.

Question 5.

Solution:

Question 6.

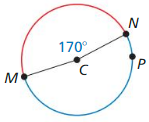
Solution:
The minor arc is \(\widehat{M N}\) = 170°,
major arc \(\widehat{N P M}\) = 360° – 170° = 190°.

Explanation:
An arc whose measure is less than 180 degrees is called a minor arc. An arc whose measure is greater than 180 degrees is called a major arc.

In Exercises 7 – 14. identify the given arc as a major arc, minor arc, or semicircle. Then find the measure of the arc.

Question 7.
\(\widehat{B C}\)

Solution:

Question 8.
\(\widehat{D C}\)

Solution:
\(\widehat{D C}\) is a minor arc and it has a measure of 65°.

Explanation:
With reference to the above figure,
An arc whose measure is less than 180 degrees is called a minor arc.

Question 9.
\(\widehat{E D}\)

Solution:

Question 10.
\(\widehat{A E}\)

Solution:
\(\widehat{A E}\) is a minor arc and it has a measure of 70°.

Explanation:
With reference to the above figure,
An arc whose measure is less than 180 degrees is called a minor arc.

Question 11.
\(\widehat{E A B}\)

Solution:

Question 12.
\(\widehat{A B C}\)

Solution:
\(\widehat{A B C}\) is a semicircle and it has a measure of 180°.

Explanation:
With reference to the above figure,
An arc whose measure is less than 180 degrees is called a minor arc.

Question 13.
\(\widehat{B A C}\)

Solution:

Question 14.
\(\widehat{E B D}\)

Solution:
\(\widehat{E B D}\) is a major arc and it has a measure of 315°.

Explanation:
With reference to the above figure,
An arc whose measure is less than 180 degrees is called a minor arc.

In Exercises 15 and 16, find the measure of each arc.

Question 15.

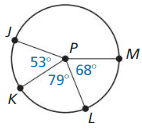
a. \(\widehat{J L}\)

b. \(\widehat{K M}\)

c. \(\widehat{J L M}\)

d. \(\widehat{J M}\)

Solution:

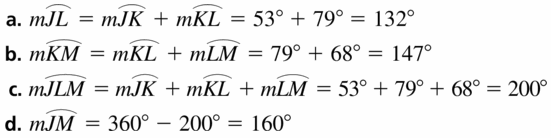
Question 16.

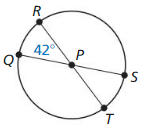
a. \(\widehat{R S}\)

Solution:
\(\widehat{R S}\) = 138°

Explanation:
Given,
\(\widehat{R S}\)
\(\widehat{R S}\) = \(\widehat{Q R S}\) – \(\widehat{Q R}\)
= 180 – 42
= 138°
So, \(\widehat{R S}\) = 138°

b. \(\widehat{Q R S}\)

Solution:
\(\widehat{Q R S}\) = 180°

Explanation:
With reference to the above figure,

c. \(\widehat{Q S T}\)

Solution:
\(\widehat{Q S T}\) = 222°

Explanation:
\(\widehat{Q S T}\) = \(\widehat{Q R S}\) + \(\widehat{S T}\)
= 180 + 42 = 222
So, \(\widehat{Q S T}\) = 222°

d. \(\widehat{Q T}\)

Solution:
\(\widehat{Q T}\) = 138°

Explanation:
\(\widehat{Q T}\) = 360 – (42 + 138 + 42)
= 360 – (222)
= 138°
\(\widehat{Q T}\) = 138°

Question 17.
MODELING WITH MATHEMATICS
A recent survey asked high school students their favorite type of music. The results are shown in the circle graph. Find each indicated arc measure.

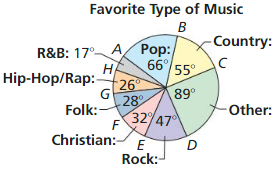
a. m\(\widehat{A E}\)
b. m\(\widehat{A C E}\)
c. m\(\widehat{G D C}\)
d. m\(\widehat{B H C}\)
e. m\(\widehat{F D}\)
f. m\(\widehat{F B D}\)

Solution:

Question 18.
ABSTRACT REASONING
The circle graph shows the percentages of students enrolled in fall Sports at a high school. Is it possible to find the measure of each minor arc? If so, find the measure of the arc for each category shown. If not, explain why it is not possible.

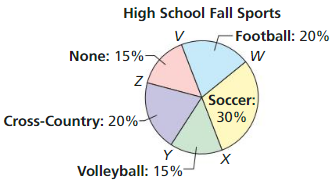
Solution:
Soccer angle = 30% of 360
(30/100) x 360
3 x 36= 108°
Volleyball angle = 15% of 360
(15/100) x 360= 54°
Cross-country angle = 20% of 360
(20/100) x 360 = 72°
None angle = 15% of 360
(15/100) x 360 = 54°
Football angle = 20% of 360
(20/100) x 360= 72°

In Exercises 19 – 22, tell whether the red arcs are congruent. Explain why or why not.

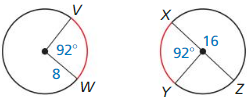
Question 19.

Solution:

Question 20.

Solution:
\(\widehat{L P}\) and \(\widehat{M N}\) are not congruet because they are not in the same circle.

Explanation:
We know that,
Congruent angles are two or more angles that are identical to each other.
Therefore, the measure of these angles also equal to each other,
as in the above figure the measure of angles are different.
Hence the given circles are not congruent.

Question 21.

Solution:

Question 22.

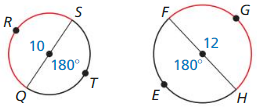
Solution:
\(\widehat{R S Q}\), \(\widehat{F G H}\) are not congruent because those two circles have different radii.

Explanation:
We know that,
Congruent radius are two or more radius that are identical to each other.
Therefore, the measure of these radii also equal to each other,
as in the above figure the measure of radii is different.
Hence the given circles are not congruent.

MATHEMATICAL CONNECTIONS
In Exercises 23 and 24. find the value of x. Then find the measure of the red arc.

Question 23.

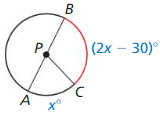
Solution:

Question 24.

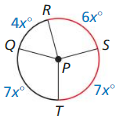
Solution:
m\(\widehat{R S T}\) = 195°

Explanation:
Given,
4x + 6x + 7x + 7x = 360
24x = 360°
x = 15°
m\(\widehat{R S T}\) = 6(15) + 7(15)
= 90 + 105 = 195°
So, m\(\widehat{R S T}\) = 195°

Question 25.
MAKING AN ARGUMENT
Your friend claims that any two arcs with the same measure are similar. Your cousin claims that an two arcs with the same measure are congruent. Who is correct? Explain.

Solution:

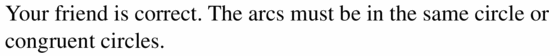
Question 26.
MAKING AN ARGUMENT
Your friend claims that there is not enough information given to find the value of x. Is your friend correct? Explain your reasoning.

Solution:
x = 36°

Explanation:
Given,
4x + x + x + 4x = 360°
10x = 360°
x = 36°

Question 27.
ERROR ANALYSIS
Describe and correct the error in naming the red arc.

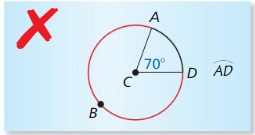
Solution:

Question 28.
ERROR ANALYSIS
Describe and correct the error in naming congruent arc.

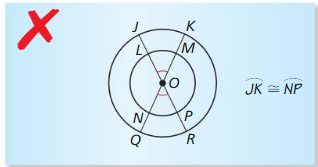
Solution:
\(\widehat{J K}\), \(\widehat{N P}\) are not congruent because those two arcs are form different circles.

Explanation:
We know that,
Congruent arcs are two or more arcs that are identical to each other.
Therefore, the measure of these arcs also equal to each other,
as in the above figure the measure of arc is different.
Hence the given circles are not congruent.

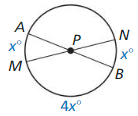
Question 29.
ATTENDING TO PRECISION
Two diameters of ⊙P are \(\widehat{A B}\) and \(\widehat{C D}\). Find m\(\widehat{A C D}\) and m\(\widehat{A C}\) when m\(\widehat{A D}\) = 20°.

Solution:

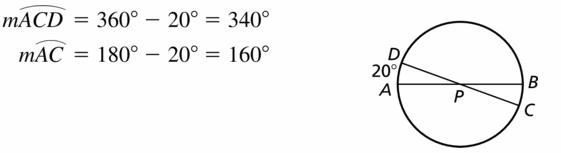
Question 30.
REASONING
In ⊙R, m\(\widehat{A B}\) = 60°, m\(\widehat{B C}\) = 25°. m\(\widehat{C D}\) = 70°, and m\(\widehat{D E}\) = 20°. Find two possible measures of \(\widehat{A E}\).

Solution:
The two possibilities of \(\widehat{A E}\) are 185°, 175°

Explanation:
Given,
\(\widehat{A E}\) = 360 – (\(\widehat{A B}\) + \(\widehat{B C}\) + \(\widehat{C D}\) + \(\widehat{D E}\))
= 360 – (60 + 25 + 70 + 20)
= 360 – (175)
= 185°
\(\widehat{A E}\) = \(\widehat{A B}\) + \(\widehat{B C}\) + \(\widehat{C D}\) + \(\widehat{D E}\)
= 60 + 25 + 70 + 20 = 175°
So, the two possibilities of \(\widehat{A E}\) are 185°, 175°

Question 31.
MODELING WITH MATHEMATICS
On a regulation dartboard, the outermost circle is divided into twenty congruent sections. What is the measure of each arc in this circle?

Solution:

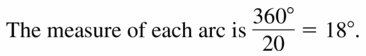
Question 32.
MODELING WITH MATHEMATICS
You can use the time zone wheel to find the time in different locations across the world. For example, to find the time in Tokyo when it is 4 P.M. in San Francisco, rotate the small wheel until 4 P.M. and San Francisco line up, as shown. Then look at Tokyo to see that it is 9 A.M. there.

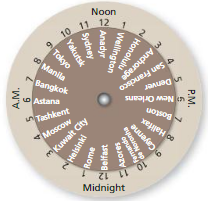
a. What is the arc measure between each time zone 0n the wheel?

Solution:
As the circle is divided into 24 sectors,
each time zone angle = \(\frac { 360 }{ 24 } \) = 15°

b. What is the measure of the minor arc from the Tokyo zone to the Anchorage zone?

Solution:
The measure of the minor arc from the Tokyo zone to the Anchorage zone,
15 + 15 + 15 + 15 + 15 + 15 = 90°

c. If two locations differ by 180° on the wheel, then it is 3 P.M. at one location when it is _________ at the other location.

Solution:
Kuwaiti city.

Question 33.
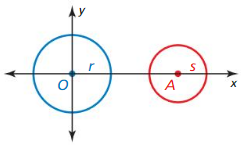
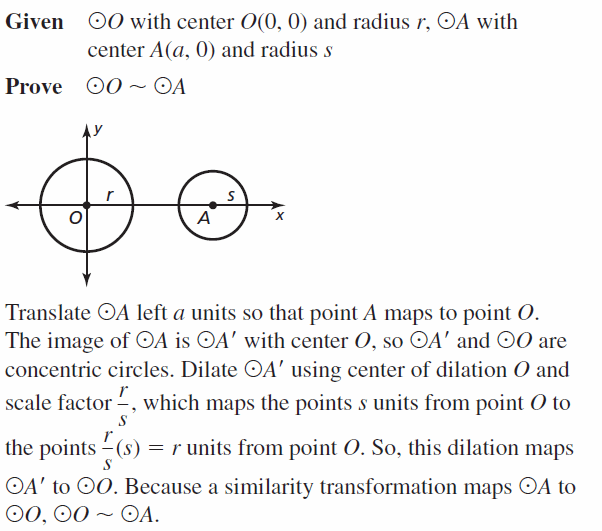
PROVING A THEOREM
Write a coordinate proof of the Similar Circles Theorem (Theorem 10.5).
Given ⊙O with center O(0, 0) and radius r.
⊙A with center A(a, 0) and radius s
Prove ⊙O ~ ⊙A

Solution:

Question 34.
ABSTRACT REASONING
Is there enough information to tell whether ⊙C ≅ ⊙D? Explain your reasoning.

Solution:
Both circles ⊙C and ⊙D have the same radius so those circles are congruent.

Explanation:
We know that the term congruent means exactly equal shape and size.

Question 35.
PROVING A THEOREM
Use the diagram to prove each part of the biconditional in the Congruent Circles Theorem (Theorem 10.3).

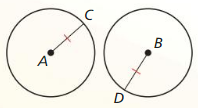
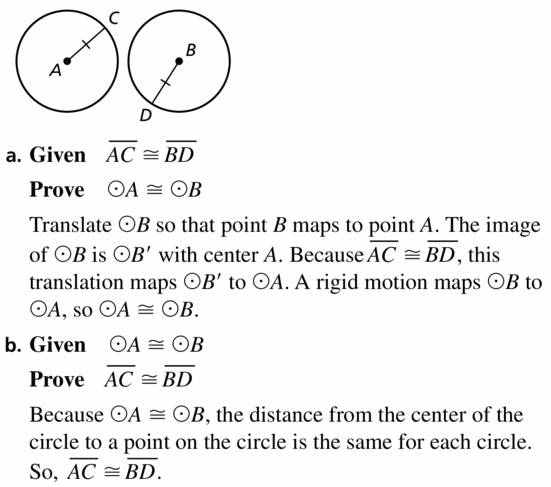
a. Given \(\overline{A C} \cong \overline{B D}\)
Prove ⊙A ≅ ⊙B
b. Given ⊙A ≅ ⊙B
prove \(\overline{A C} \cong \overline{B D}\)

Solution:

Question 36.
HOW DO YOU SEE IT?
Are the circles on the target similar or congruent? Explain your reasoning.

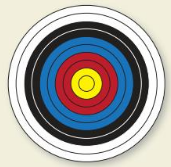
Answer:

Question 37.
PROVING A THEOREM
Use the diagram to prove each part of the biconditional in the Congruent Central Angles Theorem (Theorem 10.4).

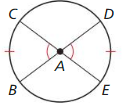
a. Given ∠ABC ≅ ∠DAE
Prove \(\widehat{B C}\) ≅ \(\widehat{D E}\)
b. Given \(\widehat{B C}\) ≅ \(\widehat{D E}\)
Prove ∠ABC ≅ ∠DAE

Solution:

Question 38.
THOUGHT PROVOKING
Write a formula for the length of a circular arc. Justify your answer.

Solution:
The formula to find the length of a circular arc is radius x angle.

Explanation:
Arc length formula is used to calculate the measure of the distance along the curved line making up the arc.

Maintaining Mathematical Proficiency

Find the value of x. Tell whether the side lengths form a Pythagorean triple.

Question 39.

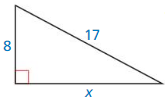
Solution:

Question 40.

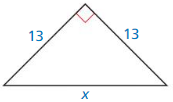
Solution:
x = 13√2

Explanation:
According to Pythagoras theorem,
AC² = AB² + BC²
x² = 13² + 13²
x² = 169 + 169
x² = 338
x = 13√2

Question 41

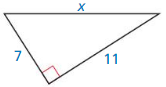
Solution:

Question 42.

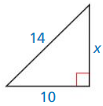
Solution:
x = 4√6

Explanation:
According to Pythagoras theorem,
AC² = AB² + BC²
14² = x² + 10²
196 = x² + 100
x² = 196 – 100
x² = 96
x = 4√6

10.3 Using Chords

Exploration 1

Drawing Diameters

Work with a partner: Use dynamic geometry software to construct a circle of radius 5 with center at the origin. Draw a diameter that has the given point as an endpoint. Explain how you know that the chord you drew is a diameter.
a. (4, 3)
b. (0, 5)
c. (-3, 4)
d. (-5, 0)

Answer:
Exploration 2

Writing a Conjecture about Chords

Work with a partner. Use dynamic geometry software to construct a chord \(\overline{B C}\) of a circle A. Construct a chord on the perpendicular bisector of \(\overline{B C}\). What do you notice? Change the original chord and the circle several times. Are your results always the same? Use your results to write a conjecture.
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.

Answer:

Exploration 3

A Chord Perpendicular to a Diameter

Work with a partner. Use dynamic geometry software to construct a diameter \(\overline{B C}\) of a circle A. Then construct a chord \(\overline{D E}\) perpendicular to \(\overline{B C}\) at point F. Find the lengths DF and EF. What do you notice? Change the chord perpendicular to \(\overline{B C}\) and the circle several times. Do you always get the same results? Write a conjecture about a chord that is perpendicular to a diameter of a circle.

Answer:

Communicate Your Answer

Question 4.
What are two ways to determine when a chord is a diameter of a circle?

Solution:
If a chord passes through the center of the circle, then it is known as the diameter of a circle.
The longest chord of the circle is the diameter of a circle.

Lesson 10.3 Using Chords

Monitoring Progress

In Exercises 1 and 2, use the diagram of ⊙D.

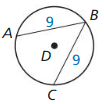
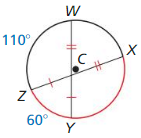
Question 1.
If m\(\widehat{A B}\) = 110°. find m\(\widehat{B C}\).

Solution:
m\(\widehat{B C}\) = 110°

Explanation:
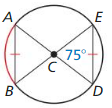
With reference to the above figure,
AB and BC are congruent chords in congruent circles.
So, the corresponding minor arcs \(\widehat{A B}\), \(\widehat{B C}\) are congruent according to the congruent corresponding chords theorem.
So, \(\widehat{A B}\) = \(\widehat{B C}\)
\(\widehat{B C}\) = 110°

Question 2.
If m\(\widehat{A C}\) = 150° find m\(\widehat{A B}\).

Solution:
m\(\widehat{A B}\) = 105°

Explanation:
With reference to the above figure,
\(\widehat{A C}\) = 360 – (\(\widehat{A B}\) + \(\widehat{B C}\))
Given,
m\(\widehat{A C}\) = 150°
150 = 360 – 2(\(\widehat{A B}\))
2(\(\widehat{A B}\)) = 360 – 150 = 210
\(\widehat{A B}\) = 210/2
\(\widehat{A B}\) = 105°

In Exercises 3 and 4. find the indicated length or arc measure.

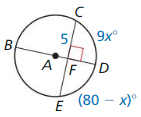
Question 3.
CE

Solution:
10 units.

Explanation:
With reference to the above given figure,
CD and DE = 5
CE = CD + DE
CE = 5 + 5
CE = 10 units

Question 4.
m\(\widehat{C E}\)

Solution:
m\(\widehat{C E}\) = 180 – 8x

Explanation:
With reference to the above given figure,
m\(\widehat{C E}\) = 9x + 180 – x
m\(\widehat{C E}\) = 180 – 8x

Question 5.
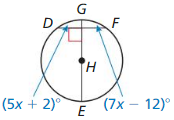
In the diagram, JK = LM = 24, NP = 3x, and NQ = 7x – 12. Find the radius of ⊙N

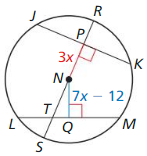
Answer:

Exercise 10.3 Using Chords

Vocabulary and Core Concept Check

Question 1.
WRITING
Describe what it means to bisect a chord.

Solution:

Question 2.
WRITING
Two chords of a circle are perpendicular and congruent. Does one of them have to be a diameter? Explain your reasoning.

Solution:

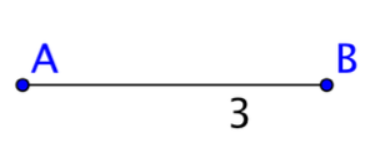
Imagine a line segment of length 3 units, AB.

A second congruent segment of length 3 that is perpendicular to AB called CD.

Explanation:
Circumscribe both these line segments and note that AB and CD are new chords.
While both chords are perpendicular and congruent, none of the chord is a diameter.
So, it is possible to have two chords of this type with one diameter of the circle.

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6, find the measure of the red arc or chord in ⊙C.

Question 3.

Solution:

Question 4.

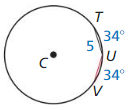
Solution:
170°

Explanation:
Given,
radius = 5 units, angle = 34°
Arc length = radius x angle
= 5 x 34 = 170°

Question 5.

Solution:

Question 6.

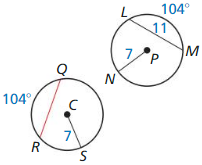
Solution:
Chord length is 11 units.

Explanation:
With reference to the above data given in the figure,
we observe that the  two circles radius is the same and the angle is also the same.
So, the chord length is 11 units.

In Exercise 7-10, find the value of x.

Question 7.

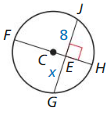
Solution:

Question 8.

Solution:
x = 40°

Explanation:
According to the perpendicular bisector theorem,
if a point is on the perpendicular bisector of a segment,
then it is equidistant from the segment’s endpoints.
RS = ST
x = 40°

Question 9.

Solution:

Question 10.

Solution:
x = 7

Explanation:
According to the perpendicular bisector theorem,
if a point is on the perpendicular bisector of a segment,
then it is equidistant from the segment’s endpoints.
5x + 2 = 7x – 12
7x – 5x = 2 + 12
2x = 14
x = 7

Question 11.
ERROR ANALYSIS
Describe and correct the error in reasoning.

Solution:

Question 12.
PROBLEM SOLVING
In the cross section of the submarine shown, the control panels are parallel and the same length. Describe a method you can use to find the center of the cross section. Justify your method.

Answer:

In Exercises 13 and 14, determine whether \(\overline{A B}\) is a diameter of the circle. Explain your reasoning.

Question 13.

Solution:

Question 14.

Solution:
AB is not diameter of the circle.

Explanation:
With reference to the above given figure,
AD² = AC² + ED²
Let ED be x
5² = 3² + x²
25 = 9 + x²
x² = 25 – 9
x = 4
So, AB is not diameter of the circle.

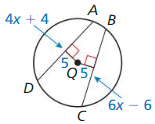
In Exercises 15 and 16, find the radius of ⊙Q.

Question 15.

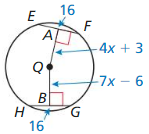
Solution:

Question 16.

Solution:
radius = 13

Explanation:
With reference to the above given figure,
we know that:
AD = BC
Given,
4x + 4 = 6x – 6
6x – 4x = 4 + 6
2x = 10
x = 10/2
x = 5
BC = 6(5) – 6
BC = 30 – 6
BC = 24
QC² = 5² + 12²
QC² = 25 + 144
QC² = 169
QC = 13
Therefore, the radius is 13.

Question 17.
PROBLEM SOLVING
An archaeologist finds part of a circular plate. What was the diameter of the plate to the nearest tenth of an inch? Justify your answer.

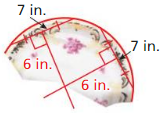
Solution:

Question 18.
HOW DO YOU SEE IT?
What can you conclude from each diagram? Name a theorem that justifies your answer.
a.

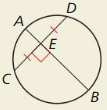
Solution:
Perpendicular chord bisector converse theorem.

Explanation:
With reference to the above figure:
If a point is on the perpendicular bisector of a segment,
then it is equidistant from the segment’s endpoints.
So, the given figure shows perpendicular chord bisector converse theorem.ws

b.

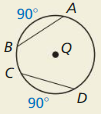
Solution:
Congruent Corresponding Chords theorem.

Explanation:
With reference to the given figure,
if two minor arcs are congruent then their corresponding chords are also congruent.
So, it the given figure proves Congruent Corresponding Chords theorem.

c.

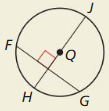
Solution:
Perpendicular chord bisector theorem.

Explanation:
With reference to the given figure,
if the line passes through the center of the circle and is perpendicular to the chord also bisects that chord is known as Perpendicular chord bisector theorem.

d.

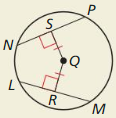
Solution:
Equidistant chords theorem.

Explanation:
With reference to the given figure,
If a point is on the perpendicular bisector of a segment,
then it is equidistant from the endpoints of that segment as shown in the above given figure.
So, the above given figure proves Equidistant chords theorem.

Question 19.
PROVING A THEOREM
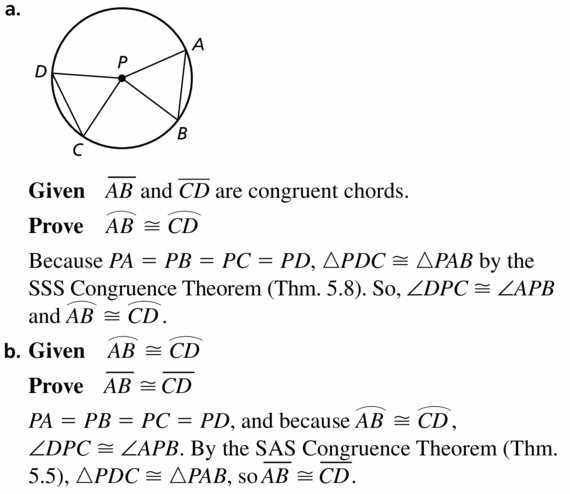
Use the diagram to prove each part of the biconditional in the Congruent Corresponding Chords Theorem (Theorem 10.6).

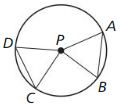
a. Given \(\overline{A B}\) and \(\overline{C D}\) are congruent chords.
Prove \(\widehat{A B} \cong \widehat{C D}\)
b. Given \(\widehat{A B} \cong \widehat{C D}\)
Prove \(\overline{A B}\) ≅ \(\overline{C D}\)

Solution:

Question 20.
MATHEMATICAL CONNECTIONS
In ⊙P, all the arcs shown have integer measures. Show that x must be even.

Answer:

Question 21.
REASONING
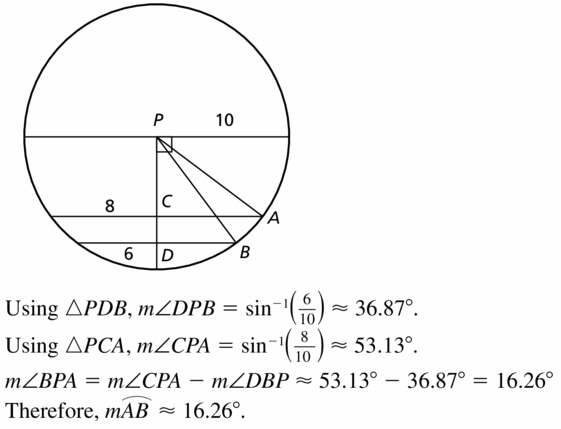
In ⊙P. the lengths of the parallel chords are 20, 16, and 12. Find m\(\widehat{A B}\). Explain your reasoning.

Solution:

Question 22.
PROVING A THEOREM
Use congruent triangles to prove the Perpendicular Chord Bisector Theorem (Theorem 10.7).

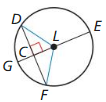
Given \(\overline{E G}\) is a diameter of ⊙L.
\(\overline{E G}\) ⊥ \(\overline{D F}\)
Prove \(\overline{D C}\) ≅ \(\overline{F C}\), \(\widehat{D G} \cong \widehat{F G}\)

Solution:
According to the Perpendicular Chord Bisector Theorem,
if any point on the perpendicular bisector is equidistant from both the endpoints of the line segment.
Let L be the center of the circle.
Draw a chord from any point as DF on the circle.
As DF passes through LG.
The length of DC is the same as FC as shown in the given figure.
Therefore it prove the Perpendicular Chord Bisector Theorem.

Question 23.
PROVING A THEOREM
Write a proof of the Perpendicular Chord Bisector Converse (Theorem 10.8).

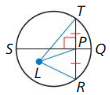
Given \(\overline{Q S}\) is a perpendicular bisector of \(\overline{R T}\).
Prove \(\overline{Q S}\) is a diameter of the circle L.
(Hint: Plot the center L and draw △LPT and △LPR.)

Solution:

Question 24.
THOUGHT PROVOKING
Consider two chords that intersect at point P. Do you think that \(\frac{A P}{B P}=\frac{C P}{D P}\)? Justify your answer.

Answer:

Question 25.
PROVING A THEOREM
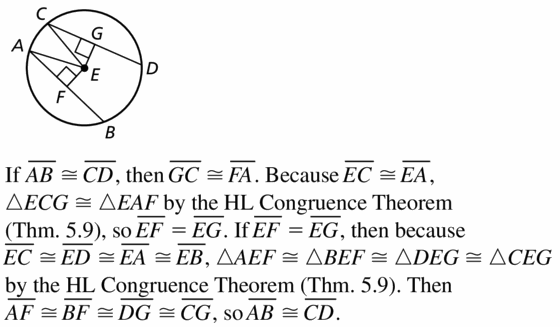
Use the diagram with the Equidistant Chords Theorem (Theorem 10.9) to prove both parts of the biconditional of this theorem.

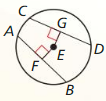
\(\overline{A B}\) ≅ \(\overline{C D}\) if and only if EF = EG

Solution:

Question 26.
MAKING AN ARGUMENT
A car is designed so that the rear wheel is only partially visible below the body of the car. The bottom edge of the panel is parallel [o the ground. Your friend claims that the point where the tire touches the ground bisects \(\widehat{A B}\). Is your friend correct? Explain your reasoning.

Answer:

Maintaining Mathematical Proficiency

Find the missing interior angle measure.

Question 27.
Quadrilateral JKLW has angle measures m∠J = 32°, m∠K = 25°, and m∠L = 44°. Find m∠M.

Solution:

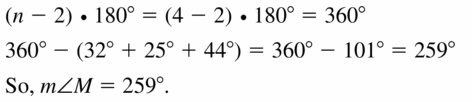
Question 28.
Pentagon PQRST has angle measures m∠P = 85°, m∠Q = 134°, m∠R = 97°, and m∠S =102°.
Find m∠T.

Solution:
m∠T = 122°.

Explanation:
Given, Pentagon PQRST
angle measures m∠P = 85°, m∠Q = 134°, m∠R = 97°, and m∠S =102°.
We know that the sum of interior angles of a pentagon = 540°
m∠T = 540 – (85 + 134 + 97 + 102)
= 540 – 418 = 122
So, m∠T = 122°.

10.1 – 10.3 Quiz

In Exercises 1 – 6, use the diagram. (Section 10.1)

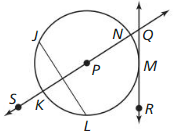
Question 1.
Name the circle.

Solution:
The circle has a chord, diameter, radius, secant and tangent.

Explanation:
With reference to the above given figure,
P is the center, NP is the radius, KN is the diameter, JL is the chord, SN is the secant and QR is the tangent.

Question 2.
Name a radius.

Solution:
NP is the radius of the circle.

Explanation:
The common distance between the points from the center is called a radius.

Question 3.
Name a diameter.

Solution:
KN is the diameter of the circle.

Explanation:
A line that crosses from the center of the circle starting from one point to the other is called a diameter.

Question 4.
Name a chord.

Solution:
JL is the chord.

Explanation:
A chord is the line segment that joins two distinct points of the circle.

Question 5.
Name a secant.

Solution:
SN is the secant.

Explanation:
A straight line that intersects a circle in two points is called a secant line.

Question 6.
Name a tangent.

Solution:
QR is the tangent.

Explanation:
A straight line that touches the curve of the circle at only one point and does not enter the circle’s interior.

Find the value of x.

Question 7.

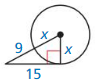
Solution:
x = 8

Explanation:
With reference to the given figure,
(9 + x)² = x² + 15²
(9 + x)² is in the form of (a + b)²
81 + 18x + x² = x² + 225
18x = 225 – 81
18x = 144
x = 144/18
x = 8

Question 8.

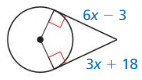
Solution:
x = 7

Explanation:
With reference to the given figure,
6x – 3 = 3x + 18
6x – 3x = 18 + 3
3x = 21
x = 21/3
x = 7

Identify the given arc as a major arc, minor arc, or semicircle. Then find the measure of the arc.

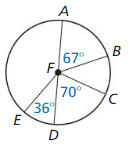
Question 9.
\(\widehat{A E}\)

Solution:
Minor Arc.

Explanation:
With reference to the above given figure,
\(\widehat{A E}\) = 180 – 36
\(\widehat{A E}\) = 144°
So, an arc whose measure is less than 180 degrees is called a minor arc.

Question 10.
\(\widehat{B C}\)

Solution:
Minor arc.

Explanation:
With reference to the above given figure,
\(\widehat{B C}\) = 180 – (67 + 70)
\(\widehat{B C}\) = 180 – 137
\(\widehat{B C}\) = 43°
So, an arc whose measure is less than 180 degrees is called a minor arc.

Question 11.
\(\widehat{A C}\)

Solution:
Minor Arc.

Explanation:
With reference to the above given figure,
\(\widehat{A C}\) = 43 + 67
\(\widehat{A C}\) = 110°
So, an arc whose measure is less than 180 degrees is called a minor arc.

Question 12.
\(\widehat{A C D}\)

Solution:
Semin circle.

Explanation:
With reference to the above given figure,
\(\widehat{A C D}\) = 180°
So, an arc whose measure is equal to 180 degrees is called a semi circle.

Question 13.
\(\widehat{A C E}\)

Solution:
Major Arc.

Explanation:
With reference to the above given figure,
\(\widehat{A C E}\) = 180 + 36 = 216°
So, an arc whose measure is greater than 180 degrees is called a Major Arc.

Question 14.
\(\widehat{B E C}\)

Solution:
Explanation:
With reference to the above given figure,
\(\widehat{B E C}\) = 70 + 36 + 43 = 149°
So, an arc whose measure is less than 180 degrees is called a minor arc.

Tell whether the red arcs are congruent. Explain why or why not.

Question 15.

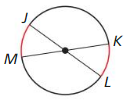
Solution:
Those two red arcs are congruent.

Explanation:
A chord is the line segment that joins two distinct points of the circle.

Question 16.

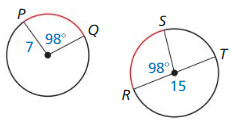
Solution:
Red arcs are not congruent.

Explanation:
When we observe both  radii of the circle the radius of the two circles is different.
So, the given red arcs ae not congruent.

Question 17.
Find the measure of the red arc in ⊙Q.

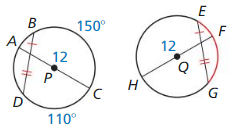
Answer:

Question 18.
In the diagram. AC = FD = 30, PG = x + 5, and PJ = 3x – 1. Find the radius of ⊙P.

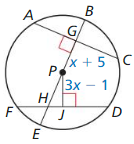
Answer:

Question 19.
A circular clock can be divided into 12 congruent sections.

a. Find the measure of each arc in this circle.

Solution:
The measure of each arc = \(\frac { 360 }{ 12 } \) = 30°

Explanation:
An arc whose measure equals 180 degrees is called a semicircle, since it divides the circle in two. Every pair of endpoints on a circle either defines one minor arc and one major arc, or two semicircles.

b. Find the measure of the minor arc formed by the hour and minute hands when the times is 7:00.

Solution:
150°

Explanation:
Given the time is 7:00 the minute hand is at 12 and hour hand is at 7,
so the minor arc is subtended by 12 – 7 = 5 of these sections and so the angle subtended is 30 x 5 = 150°

c. Find a time at which the hour and minute hands form an arc that is congruent to the arc in part (b).

Solution:
5:00

Explanation:
We know from the above that,
A minor arc is equal to 150° which can be formed by multiplication placements of the hour and the minute hand.
One of them can be the time 5:00 when the minute hand is at 12 and the hour hand is at 5.

10.4 Inscribed Angles and Polygons

Exploration 1

Inscribed Angles and Central Angles

work with a partner: Use dynamic geometry software.

Sample

a. Construct an inscribed angle in a circle. Then construct the corresponding central angle.
Answer:

b. Measure both angles. How is the inscribed angle related to its intercepted arc?
Answer:

c. Repeat parts (a) and (b) several times. Record your results in a table. Write a conjecture about how an inscribed angle is related to its intercepted arc.

ATTENDING TO PRECISION
To be proficient in math, you need to communicate precisely with others.
Answer:

Exploration 2

A Quadrilateral with Inscribed Angles

work with a partner: Use dynamic geometry software.

Sample

a. Construct a quadrilateral with each vertex on a circle.
Answer:

b. Measure all four angles. What relationships do you notice?
Answer:

c. Repeat parts (a) and (b) several times. Record your results in a table. Then write a conjecture that summarizes the data.
Answer:

Communicate Your Answer

Question 3.
How are inscribed angles related to their intercepted arcs? How are the angles of an inscribed quadrilateral related to each other?
Answer:

Question 4.
Quadrilateral EFGH is inscribed in ⊙C. and m ∠ E = 80°. What is m ∠ G? Explain.

Solution:
m ∠ G = 100°

Explanation:
Given,
m ∠ E = 80°
Quadrilateral EFGH is inscribed in ⊙C.
We know that the sum of the angles in quadrilateral is 360°
m ∠ E + m ∠ H = 80 + 80 = 160°
m ∠ E + m ∠ H + m ∠ G + m ∠ F = 360°
160° + m ∠ G + m ∠ F = 360°
m ∠ G + m ∠ F = 360 – 160 = 200
m ∠ G = 200/2
m ∠ G = 100°

Lesson 10.4 Inscribed Angles and Polygons

Monitoring Progress

Find the measure of the red arc or angle.

Question 1.

Solution:
45°

Explanation:
With reference to the above figure,
The measure of an arc angle is found by dividing the arc length by the circle’s circumference.
m∠G = \(\frac { 90 }{ 2 } \) = 45°

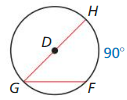
Question 2.

Solution:
76°

Explanation:
With reference to the above figure,
The measure of an arc angle is found by dividing the arc length by the circle’s circumference,
\(\widehat{T V}\) = 2 • 38 = 76°

Question 3.

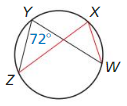
Solution:
m∠W = 72°

Explanation:
With reference to the above given figure,
YZ and XW are two arcs of the same circle and form ∠YOZ and ∠XOW at the center.
So, the measure of these two angles are also the same,
then ∠YZ and ∠XW are said to be congruent arcs.
Therefore, m∠W = 72°

Find the value of each variable.

Question 4.

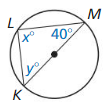
Solution:
y° = 50°

Explanation:
With reference to the above given figure,
x° = 90°
We know that the sum of the angles = 180°
y° = 180 – (40 + 90)
y° = 180 – 130
y° = 50°

Question 5.

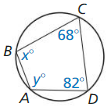
Solution:
x° = 98°
y° = 112°

Explanation:
With reference to the above given figure,
∠B + ∠D = 180
Given,
∠D = 98°, ∠B = x°, ∠C  = 68°
∠B + 82 = 180
∠B = 180 – 82
x° = 98°
∠C + ∠A = 180
68 + y° = 180
y° = 112°

Question 6.

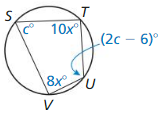
Solution:
x° = 10°
c = 62°

Explanation:
With reference to the above given figure
∠S + ∠U = 180°
Given,
∠S = c°, ∠U = 2c – 6
c + 2c – 6 = 180
3c = 186
c = 186/3
c = 62°
∠T + ∠V = 180°
Given,
∠T = 10x, ∠V = 8x
10x + 8x = 180
18x = 180
x = 180/18
x = 10°

Question 7.
In Example 5, explain how to find locations where the left side of the statue is all that appears in your camera’s field of vision.
Answer:

Exercise 10.4 Inscribed Angles and Polygons

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
If a circle is circumscribed about a polygon, then the polygon is an ___________ .

Solution:

Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different?
Find “both” answers.

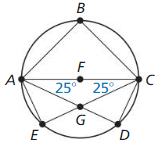
Find m∠ABC.

Solution:
m∠ABC = 60°

Explanation:
With reference to the above given figure it is equilateral triangle.
We know that an equilateral triangle is a triangle in which all three sides have the same length and same angles i.e., 60°.

Find m∠AGC.

Solution:
m∠AGC = 130°

Explanation:
With reference to the above given figure,
m∠AGC = 180 – (∠AF + ∠FC)
m∠AGC = 180 – (25 + 25)
m∠AGC = 180 – 50
m∠AGC  = 130°

Find m∠AEC.

Solution:
m∠AEC = 80°

Explanation:
With reference to the above given figure,
m∠AEC = 180 – (∠AE + ∠CE)
m∠AEC = 180 – (50 + 50)
m∠AEC = 180 – 100
m∠AEC = 80°

Find m∠ADC.

Solution:
m∠AEC = 105°

Explanation:
With reference to the above given figure,
m∠ADC = 180 – (∠AD + ∠CD)
m∠ADC = 180 – (25 + 50)
m∠ADC = 180 – 75
m∠ADC = 105°

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 8, find the indicated measure.

Question 3.
m∠A

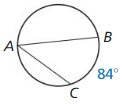
Solution:

Question 4.
m∠G

Solution:
m∠G = 170°

Explanation:
We know that the sum of the angles in circle is 360°
Given,
m∠F = 70°, m∠D = 120°
m∠G = 360 – (70 + 120)
m∠G = 360 – 190
m∠G = 170°

Question 5.
m ∠ N

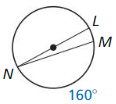
Solution:

Question 6.
m\(\widehat{R S}\)

Solution:
m\(\widehat{R S}\) = 134°

Explanation:
With reference to the above given figure,
m\(\widehat{R S}\) = 2 x m\(\widehat{R QS}\)
Giveen,
m\(\widehat{R QS}\) = 67°
m\(\widehat{R S}\) = 2 • 67
m\(\widehat{R S}\) = 134°

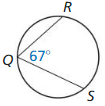
Question 7.
m\(\widehat{V U}\)

Solution:

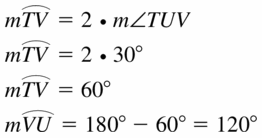
Question 8.
m\(\widehat{W X}\)

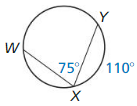
Solution:
m\(\widehat{W X}\) = 37.5°

Explanation:
With reference to the data given in the above figure,
m\(\widehat{W X}\) = \(\frac { 75 }{ 2 } \)
m\(\widehat{W X}\) = 37.5

In Exercises 9 and 10, name two pairs of congruent angles.

Question 9.

Solution:

Question 10.

Solution:
m∠W = m∠Z, m∠X = m∠Y

Explanation:
With reference to the above given figure,
YZ and XW are two arcs of the same circle and form ∠YOZ and ∠XOW at the center.
So, the measure of these two angles are also the same,
then ∠YZ and ∠XW are said to be congruent arcs.
Therefore, m∠W = m∠Z, m∠X = m∠Y

In Exercises 11 and 12, find the measure of the red arc or angle.

Question 11.

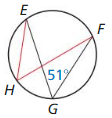
Solution:
m∠EHF = 51°

Explanation:
We know that,
if an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the circle.

Question 12.

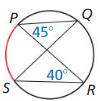
Solution:
\(\widehat{P S}\) = 80°

Explanation:
With reference to the given figure,
\(\widehat{P S}\) = 2 • 40
\(\widehat{P S}\) = 80°

In Exercises 13 – 16, find the value of each variable.

Question 13.

Solution:

Question 14.

Solution:
k = 60°

Explanation:
With reference to the given figure,
m∠E + m∠G = 180°
m + 60 = 180°
m = 120°
m∠D + m∠F = 180°
60 + 2k = 180°
k = 60°

Question 15.

Solution:

Question 16.

Solution:
y° = 28°

Explanation:
With reference to the given figure,
3x° = 90°
x° = 30°
2y° + 90° + 34° = 180°
2y° + 124° = 180°
2y° = 56°
y° = 28°

Question 17.
ERROR ANALYSIS
Describe and correct the error in finding m\(\widehat{B C}\).

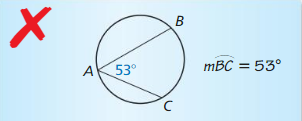
Solution:

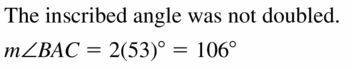
Question 18.
MODELING WITH MATHEMATICS
A carpenter’s square is an L-shaped tool used to draw right angles. You need to cut a circular piece of wood into two semicircles. How can you use the carpenter’s square to draw a diameter on the circular piece of wood?

Solution:
Recall that when a right triangle is inscribed in a circle,
then the hypotenuse is the diameter of the circle.
Simply use the carpenter’s square to inscribe it into the circle.
The hypotenuse formed by both legs of the square should provide a diameter for the circle.

MATHEMATICAL CONNECTIONS
In Exercises 19 – 21, find the values of x and y. Then find the measures of the interior angles of the polygon.

Question 19.

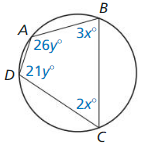
Solution:

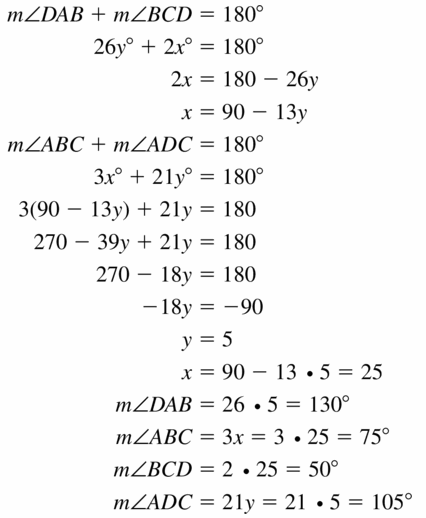
Question 20.

Solution:
∠A = 130.9°, ∠B = 40°, ∠C = 140°, ∠D = 49°

Explanation:
With reference to the given figure,
∠B + ∠C = 180°
14x + 4x = 180°
18x = 180°
x = 10°
∠A + ∠D = 180°
9y + 24y = 180°
33y = 180°
y = 5.45°
∠A = 130.9°, ∠B = 40°, ∠C = 140°, ∠D = 49°

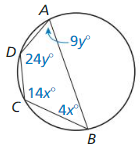
Question 21.

Solution:

Question 22.
MAKING AN ARGUMENT
Your friend claims that ∠PTQ ≅ ∠PSQ ≅ ∠PRQ. Is our friend correct? Explain your reasoning.

Solution:
Yes, my friend is correct.

Explanation:
∠PTQ ≅ ∠PSQ ≅ ∠PRQ is correct according to the inscribed angles of a circle theorem.
According to the inscribed angle theorem,
if an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the circle.

Question 23.
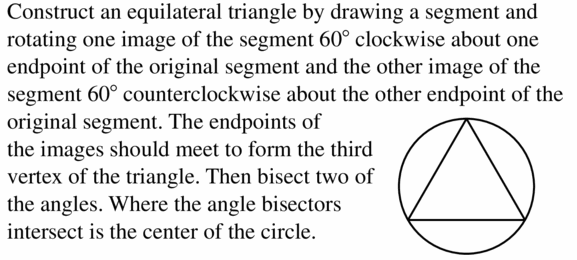
CONSTRUCTION
Construct an equilateral triangle inscribed in a circle.

Solution:

Question 24.
CONSTRUTION
The side length of an inscribed regular hexagon is equal to the radius of the circumscribed circle. Use this fact to construct a regular hexagon inscribed in a circle.

Solution:
As the side length is equal to the radius.
Draw a line representing the radius and draw a chord different chords in the form of hexagons of the radius of the circle.

REASONING
In Exercises 25 – 30, determine whether a quadrilateral of the given type can always be inscribed inside a circle. Explain your reasoning.

Question 25.
Square

Solution:

Question 26.
rectangle

Solution:
yes, angles are right angles.

Explanation:
The opposite angles are always right angles in a rectangle.

Question 27.
parallelogram

Solution:

Question 28.
kite

Solution:
No.

Explanation:
The opposite angles in the kite is not supplementary,
because it is a irregular polygon.

Question 29.
rhombus

Solution:

Question 30.
isosceles trapezoid

Solution:
Yes,

Explanation:
The opposite angles are always supplementary in isosceles trapezoid.

Question 31.
MODELING WITH MATHEMATICS
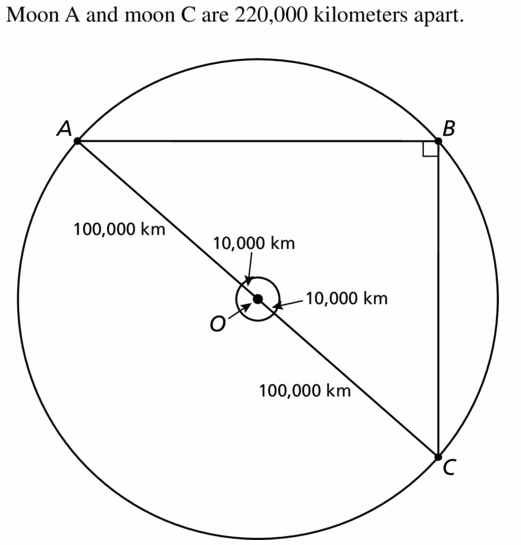
Three moons, A, B, and C, are in the same circular orbit 1,00,000 kilometers above the surface of a planet. The planet is 20,000 kilometers in diameter and m∠ABC = 90°. Draw a diagram of the situation. How far is moon A from moon C?

Solution:

Question 32.
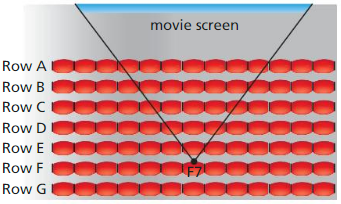
MODELING WITH MATHEMATICS
At the movie theater. you want to choose a seat that has the best viewing angle, so that you can be close to the screen and still see the whole screen without moving your eyes. You previously decided that seat F7 has the best viewing angle, but this time someone else is already sitting there. Where else can you sit so that your seat has the same viewing angle as seat F7? Explain.

Answer:

Question 33.
WRITING
A right triangle is inscribed in a circle, and the radius of the circle is given. Explain how to find the length of the hypotenuse.

Solution:

Question 34.
HOW DO YOU SEE IT?
Let point Y represent your location on the soccer field below. What type of angle is ∠AYB if you stand anywhere on the circle except at point A or point B?

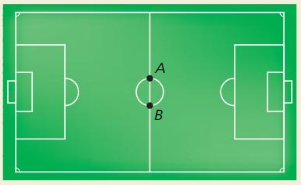
Answer:

Question 35.
WRITING
Explain why the diagonals of a rectangle inscribed in a circle are diameters of the circle.

Solution:

Question 36.
THOUGHT PROVOKING
The figure shows a circle that is circumscribed about ∆ABC. Is it possible to circumscribe a circle about any triangle? Justify your answer.

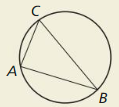
Solution:
Yes.

Explanation:
With reference to the above given triangle in the figure,
we observe that the circumscribed circle is the circle that passes through all three vertices of the triangle. The center of the circumscribed circle is the circumcenter of the triangle.

Question 37.
PROVING A THEOREM
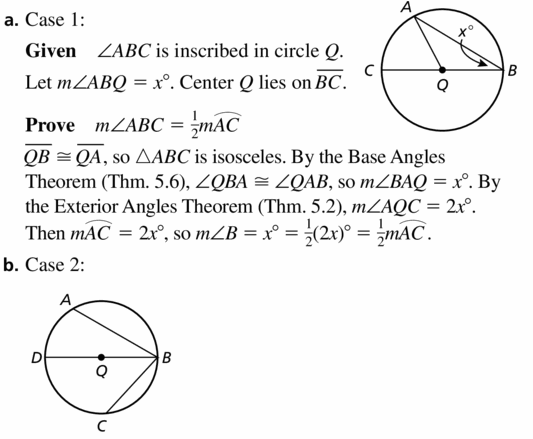
If an angle is inscribed in ⊙Q. the center Q can be on a side of the inscribed angle, inside the inscribed angle, or outside the inscribed angle. Prove each case of the Measure of an Inscribed Angle Theorem (Theorem 10. 10).

a. Case 1
Given ∠ABC is inscribed in ⊙Q
Let m∠B = x°
Center Q lies on \(\overline{B C}\).
Prove m∠ABC = \(\frac{1}{2}\)m\(\widehat{A C}\)
(Hint: Show that ∆AQB is isosceles. Then write m\(\widehat{A C}\) in terms of x.)

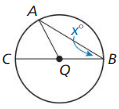
b. Case 2
Use the diagram and auxiliary line to write Given and Prove statements for Case 2. Then write a proof

c. Case 3
Use the diagram and auxiliary line to write Given and Prove statements for Case 3. Then write a proof.

Solution:

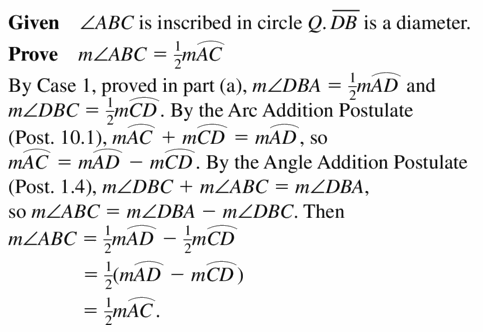
Question 38.
PROVING A THEOREM
Write a paragraph proof of the Inscribed Angles of a Circle Theorem (Theorem 10.11). First, draw a diagram and write Given and Prove statements.
Answer:

Question 39.
PROVING A THEOREM
The Inscribed Right Triangle Theorem (Theorem 10.12) is written as a conditional statement and its converse. Write a plan for proof for each statement.

Solution:

Question 40.
PROVING A THEOREM
Copy and complete the paragraph proof for one part of the Inscribed Quadrilateral Theorem (Theorem 10. 13).
Given ⊙C with inscribed quadrilateral DEFG
Prove m ∠ D + m ∠ F = 180°,
m ∠ E + m ∠ G = 180°

By the Arc Addition Postulate (Postulate 10. 1),
m\(\widehat{E F G}\) + ________ = 360° and m\(\widehat{F G D}\) + m\(\widehat{D E F}\) = 360°.
Using the ___________ Theorem. m\(\widehat{E D G}\) = 2m ∠ F, m\(\widehat{E F G}\) = 2m∠D, m\(\widehat{D E F}\) = 2m∠G, and m\(\widehat{F G D}\) = 2m ∠ E. By the Substitution Property of Equality, 2m∠D + ________ = 360°, So _________ . Similarly, __________ .

Solution:
m\(\widehat{E F G}\) + m\(\widehat{E D F}\) = 360°
m\(\widehat{F G D}\) + m\(\widehat{D E F}\) = 360°.
According to the the measure of an inscribed angle Theorem,
m\(\widehat{E D G}\) = 2m ∠ F,
m\(\widehat{E F G}\) = 2m∠D,
m\(\widehat{D E F}\) = 2m∠G and
m\(\widehat{F G D}\) = 2m ∠ E.
By the Substitution Property of Equality, 2m∠D + 2m∠G = 360°.

Question 41.
CRITICAL THINKING
In the diagram, ∠C is a right angle. If you draw the smallest possible circle through C tangent to \(\overline{A B}\), the circle will intersect \(\overline{A C}\) at J and \(\overline{B C}\) at K. Find the exact length of \(\overline{J K}\).

Solution:

Question 42.
CRITICAL THINKING
You are making a circular cutting board. To begin, you glue eight 1-inch boards together, as shown. Then you draw and cut a circle with an 8-inch diameter from the boards.

a. \(\overline{F H}\) is a diameter of the circular cutting board. Write a proportion relating GJ and JH. State a theorem in to justify your answer.

Solution:
Each board is 1 inch and FJ spans 6 boards.
\(\overline{F H}\) = 6 inches

b. Find FJ, JH, and GJ. What is the length of the cutting board seam labeled \(\overline{G K}\)?

Solution:
FJ = 6, JH = 2, JG = 2√3, GK = 4√3

Explanation:
We know that,
Each board is 1 inch and JH spans 2 boards.
JH = 2 inches
Equation is \(\frac { JH }{ GJ } \) = \(\frac { GJ }{ FJ } \)
\(\frac { 2 }{ GJ } \) = \(\frac { GJ }{ 6 } \)
12 = GJ²
GJ = 2√3
GK = 2(GJ)
GK = 4√3
So, FJ = 6, JH = 2, JG = 2√3, GK = 4√3

Maintaining Mathematical Proficiency

Solve the equation. Check your solution.

Question 43.
3x = 145

Solution:

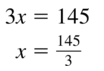
Question 44.
\(\frac{1}{2}\)x = 63

Solution:
x = 126

Explanation:
Given,
\(\frac{1}{2}\)x = 63
x = 63 • 2
x = 126

Question 45.
240 = 2x

Solution:

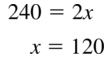
Question 46.
75 = \(\frac{1}{2}\)(x – 30)

Solution:
x = 180

Explanation:
Given,
75 = \(\frac{1}{2}\)(x – 30)
75 • 2 = x – 30
150 + 30 = x
x = 180

10.5 Angle Relationships in Circles

Exploration 1

Angles Formed by a Chord and Tangent Line

Work with a partner: Use dynamic geometry software.

Sample

a. Construct a chord in a circle. At one of the endpoints of the chord. construct a tangent line to the circle.
Answer:

b. Find the measures of the two angles formed by the chord and the tangent line.
Answer:

c. Find the measures of the two circular arcs determined by the chord.
Answer:

d. Repeat parts (a) – (c) several times. Record your results in a table. Then write a conjecture that summarizes the data.
Answer:

Exploration 2

Angles Formed by Intersecting Chords

Work with a partner: Use dynamic geometry software.

sample

a. Construct two chords that intersect inside a circle.
Answer:

b. Find the measure of one of the angles formed by the intersecting chords.
Answer:

c. Find the measures of the arcs intercepted h the angle in part (b) and its vertical angle. What do you observe?
Answer:

d. Repeat parts (a) – (c) several times. Record your results in a table. Then write a conjecture that summarizes the data.

CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to understand and use stated assumptions, definitions, and previously established results.
Answer:

Communicate Your Answer

Question 3.
When a chord intersects a tangent line or another chord, what relationships exist among the angles and arcs formed?
Answer:

Question 4.
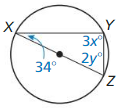
Line m is tangent to the circle in the figure at the left. Find the measure of ∠1.

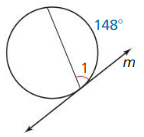
Solution:
m∠1 = 74°

Explanation:
Given,
angle 148°
So, m∠1 = \(\frac { 1 }{ 2 } \) • 148
m∠1 = 74°

Question 5.
Two chords intersect inside a circle to form a pair of vertical angles with measures of 55°. Find the sum of the measures of the arcs intercepted by the two angles.

Solution:
27.5°

Explanation:
Given angle = 55°
The sum of the measures of the arcs intercepted by the two angles = \(\frac { 1 }{ 2 } \) • 55
s = 27.5°

Lesson 10.5 Angle Relationships in Circles

Monitoring Progress

Line m is tangent to the circle. Find the indicated measure.

Question 1.
m ∠ 1

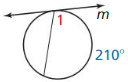
Solution:
m ∠ 1 = 105°

Explanation:
Given angle = 210°
The sum of the measures of the arcs intercepted by the two angles
m ∠ 1 = \(\frac { 1 }{ 2 } \) • 210
m ∠ 1 = 105°

Question 2.
m\(\widehat{R S T}\)

Solution:
m\(\widehat{R S T}\)= 196°

Explanation:
With reference to the data given in the above figure,
m\(\widehat{R S T}\) = 2 • 98
m\(\widehat{R S T}\) = 196°

Question 3.
m\(\widehat{X Y}\)

Solution:
m\(\widehat{X Y}\) = 40°

Explanation:
With reference to the data given in the above figure,
m\(\widehat{X Y}\) = \(\frac { 1 }{ 2 } \) • 80
m\(\widehat{X Y}\) = 40°

Find the value of the variable.

Question 4.

Solution:
y° = 98.5°

Explanation:
With reference to the data given in the above figure,
y° = \(\frac { 1 }{ 2 } \) • (102 + 95)
y° = \(\frac { 1 }{ 2 } \) • 197
y° = 98.5°

Question 5.

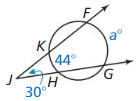
Solution:
a° = 104°

Explanation:
With reference to the data given in the above figure,
a° = 2 • 30° + 44°
a° = 60° + 44°
a° = 104°.

Find the value of x.

Question 6.

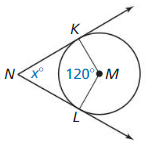
Solution:
x° = 60°

Explanation:
With reference to the data given in the above figure,
We know that sum of the angles = 180°
x° = 180° – 120°
x° = 60°

Question 7.

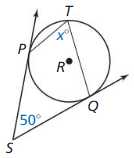
Solution:
x° = 130°

Explanation:
With reference to the data given in the above figure,
We know that sum of the angles = 180°
50° = 180° – x°
x° = 180° – 50°
x° = 130°

Question 8.
You are on top of Mount Rainier on a clear day. You are about 2.73 miles above sea level at point B. Find m\(\widehat{C D}\), which represents the part of Earth that you can see.

Solution:
The part of earth you can see is 31°

Explanation:
With reference to the data given in the above figure,
CB and BD are tangents,
CB is perpendicular to AB and CD is perpendicular to AD by the tangent line to circle theorem.
△ABC is similar to △ABD by the hypotenuese leg congruence theorem.
∠CBA is similar to ∠ABD. So, m∠CBA = 74.5°, m∠CBD = 2 • 74.5° = 149°
m∠CBD = 180° – m∠CAD
m∠CBD = 180° – CD
149° = 180° – CD
CD = 31°

Exercise 10.5 Angle Relationships in Circles

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
Points A, B, C, and D are on a circle, and intersects at point P.
If m∠APC = \(\frac{1}{2}\)(m\(\widehat{B D}\) – m\(\widehat{A C}\)). then point P is _________ the circle.

Solution:

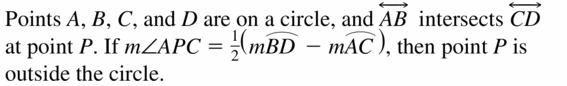
Question 2.
WRITING
Explain how to find the measure of a circumscribed angle.

Solution:
A circumscribed angle is the angle formed by two intersecting tangent lines to a circle.
Draw lines from the circle centre to the point of tangency.
The angle between the radius and tangent line is 90°.
The sum of angles of a quadrilateral is 360°.
Angles between radii and tangent lines is 180°.
The angle at two tangent lines meet is circumscribed angle.

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6, line t is tangent to the circle. Find the indicated measure.

Question 3.
m\(\widehat{A B}\)

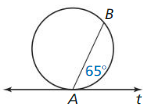
Solution:

Question 4.
m\(\widehat{D E F}\)

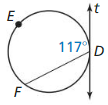
Solution:
m\(\widehat{D E F}\) = 234°

Explanation:
With reference to the data given in the above figure,
m\(\widehat{D E F}\) = 2(117°)
m\(\widehat{D E F}\) = 234°

Question 5.
m < 1

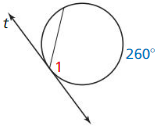
Solution:

Question 6.
m ∠ 3

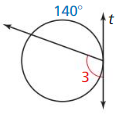
Solution:
m ∠ 3 = 70°

Explanation:
With reference to the data given in the above figure,
m ∠ 3 = ½ • 140
m ∠ 3 = 70°

In Exercises 7 – 14, find the value of x.

Question 7.

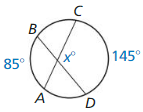
Solution:

Question 8.

Solution:

Question 9.

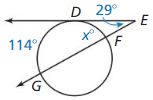
Solution:

Question 10.

Solution:
x° = 38°

Explanation:
With reference to the data given in the above figure,
34° = ½ (3x – 2 – (x + 6))
34° = ½ (3x – 2 – x – 6)
34° = ½ (2x – 8)
34° = x – 4
x° = 34 + 4
x° = 38°

Question 11.

Solution:

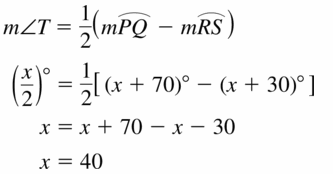
Question 12.

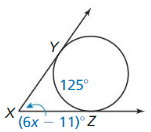
Solution:
x° = 43.5°

Explanation:
With reference to the data given in the above figure,
6x – 11 = 2  • 125
6x = 250 + 11
6x = 261
x° = 216/6
x° = 43.5°

Question 13.

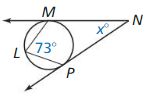
Solution:

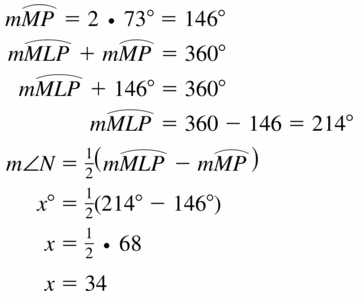
Question 14.

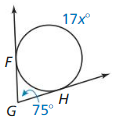
Solution:
x° = 4.41°

Explanation:
With reference to the data given in the above figure,
17x° = 75°
x° = 75/17
x° = 4.41°

ERROR ANALYSIS
In Exercises 15 and 16, describe and correct the error in finding the angle measure.

Question 15.

Solution:

Question 16.

Solution:
m∠1 = 26°

Explanation:
Given,
m∠1 = ½ (122 – 70)
m∠1 = ½ (52)
m∠1 = 26

In Exercises 17 – 22, find the indicated angle measure. justify your answer.

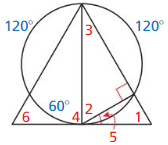
Question 17.
m ∠ 1

Solution:

Question 18.
m ∠ 2

Solution:
m ∠ 2 = 60°

Explanation:
With reference to the above given figure,
m ∠ 3 =30°,
So, m ∠ 2 = 180° – (90° + 30°)
m ∠ 2 = 180° – 120°
m ∠ 2 = 60°

Question 19.
m ∠ 3

Solution:

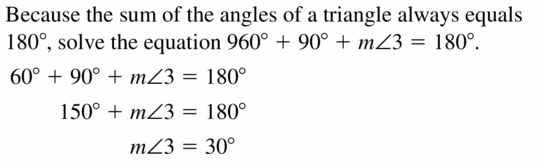
Question 20.
m ∠ 4

Solution:
m ∠ 4 = 90°

Explanation:
With reference to the above given figure,
∠ 4 is a right angle.
So, m∠ 4 = 90°

Question 21.
m ∠ 5

Solution:

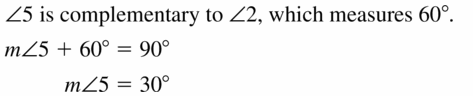
Question 22.
m ∠ 6

Solution:
m ∠ 6 = 60°

Explanation:
With reference to the above given figure,
m ∠ 6 = 180° – (60° + 30° + 30°)
m ∠ 6 = 180° – 120°
m ∠ 6 = 60°

Question 23.
PROBLEM SOLVING
You are flying in a hot air balloon about 1.2 miles above the ground. Find the measure of the arc that represents the part of Earth you can see. The radius of Earth is about 4000 miles.

Solution:

Question 24.
PROBLEM SOLVING
You are watching fireworks over San Diego Bay S as you sail away in a boat. The highest point the fireworks reach F is about 0.2 mile above the bay. Your eyes E are about 0.01 mile above the water. At point B you can no longer see the fireworks because of the curvature of Earth. The radius of Earth is about 4000 miles, and \(\overline{F E}\) is tangent to Earth at point T. Find m\(\widehat{s B}\). Round your answer to the nearest tenth.

Answer:

Question 25.
MATHEMATICAL CONNECTIONS
In the diagram, \(\vec{B}\)A is tangent to ⊙E. Write an algebraic expression for m\(\widehat{C D}\) in terms of x. Then find m\(\widehat{C D}\).

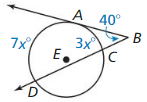
Solution:

Question 26.
MATHEMATICAL CONNECTIONS
The circles in the diagram are concentric. Write an algebraic expression for c in terms of a and b.

Solution:
a° = ½(c° – b°)

Explanation:
Concentric circles are circles with a common center.
The region between two concentric circles of different radii is called an annulus.
An algebraic expression for c in terms of a and b,
a° = ½(c° – b°)

Question 27.
ABSTRACT REASONING
In the diagram. \(\vec{P}\)L is tangent to the circle, and \(\overline{K J}\) is a diameter. What is the range of possible angle measures of ∠LPJ? Explain your reasoning.

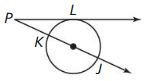
Solution:

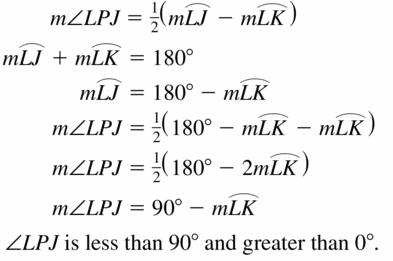
Question 28.
ABSTRACT REASONING
In the diagram, \(\overline{A B}\) is an chord that is not a diameter of the circle. Line in is tangent to the circle at point A. What is the range of possible values of x? Explain your reasoning. (The diagram is not drawn to scale.)

Solution:
The possible values of x are less than 180°

Explanation:
With reference to the above given figure,
\(\overline{A B}\) is an chord that is not a diameter of the circle.
Line in is tangent to the circle at point A.
We know that, if the angle is less than 180 degrees it is known as minor arc.

Question 29.
PROOF
In the diagram and are secant lines that intersect at point L. Prove that m∠JPN > m∠JLN.

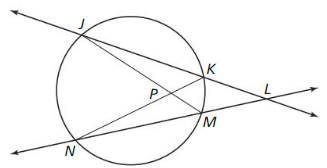
Solution:

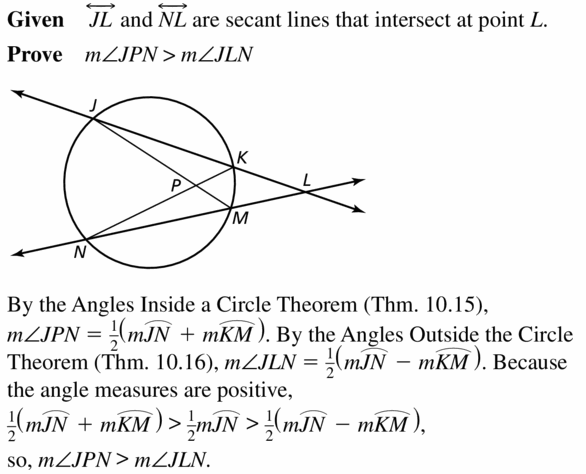
Question 30.
MAKING AN ARGUMENT
Your friend claims that it is possible for a circumscribed angle to have the same measure as its intercepted arc. Is your friend correct? Explain your reasoning.

Solution:
Yes,

Explanation:
when the circumscribed angle measures 90°,
the central angle measures are also 90°.
So, the intercepted arc also measures 90°.

Question 31.
REASONING
Points A and B are on a circle, and t is a tangent line containing A and another point C.
a. Draw two diagrams that illustrate this situation.
b. Write an equation for m\(\widehat{A B}\) in terms of m∠BAC for each diagram.
c. For what measure of ∠BAC can you use either equation to find m\(\widehat{A B}\)? Explain.

Solution:

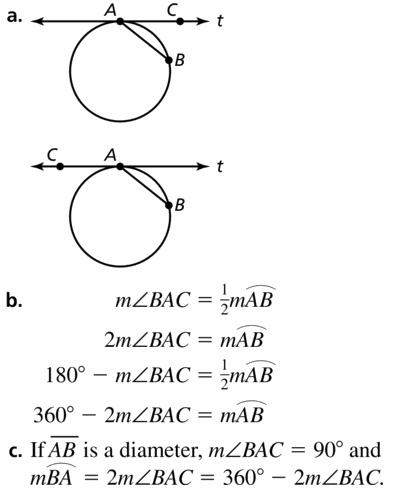
Question 32.
REASONING
∆XYZ is an equilateral triangle inscribed in ⊙P. AB is tangent to ⊙P at point X, \(\overline{B C}\) is tangent to ⊙P at point Y. and \(\overline{A C}\) is tangent to ⊙P at point Z. Draw a diagram that illustrates this situation. Then classify ∆ABC by its angles and sides. Justify your answer.
Answer:

Question 33.
PROVING A THEOREM
To prove the Tangent and Intersected Chord Theorem (Theorem 10. 14), you must prove three cases.
a. The diagram shows the case where \(\overline{A B}\) contains the center of the circle. Use the Tangent Line to Circle Theorem (Theorem 10.1) to write a paragraph proof for this case.

b. Draw a diagram and write a proof for the case where the center of the circle is in the interior of ∠CAB.
c. Draw a diagram and write a proof for the case where the center of the circle is in the exterior of ∠CAB.

Solution:

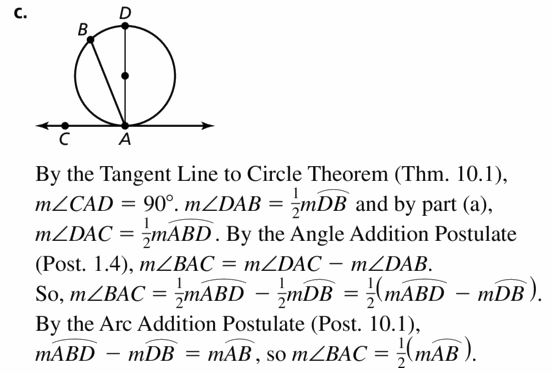
Question 34.
HOW DO YOU SEE IT?
In the diagram, television cameras are Positioned at A and B to record what happens on stage. The stage is an arc of ⊙A. You would like the camera at B to have a 30° view of the stage. Should you move the camera closer or farther away? Explain your reasoning.

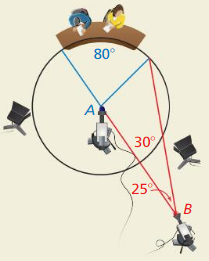
Solution:
Move the camera closer.

Explanation:
With reference to the above given data,
25° = ½(80° – 30°)
25° = ½(50°)
25° = 25°
So, you should move the camera closer.

Question 35.
PROVING A THEOREM
Write a proof of the Angles Inside the Circle Theorem (Theorem 10.15).

Given Chords \(\overline{A C}\) and \(\overline{B D}\) intersect inside a circle.
Prove m ∠ 1 = \(\frac{1}{2}\)(m\(\widehat{D C}\) + m\(\widehat{A B}\))

Solution:

Question 36.
THOUGHT PROVOKING
In the figure, and are tangent to the circle. Point A is any point on the major are formed by the endpoints of the chord \(\overline{B C}\). Label all congruent angles in the figure. Justify your reasoning.

Solution:
m∠CPB = ½(CAB – CB)

Explanation:
With reference to the data given in the above figure,
and are tangent to the circle.
Point A is any point on the major are formed by the endpoints of the chord \(\overline{B C}\).
So, m∠CPB = ½(CAB – CB)

Question 37.
PROVING A THEOREM
Use the diagram below to prove the Angles Outside the Circle Theorem (Theorem 10.16) for the case of a tangent and a secant. Then copy the diagrams for the other two cases on page 563 and draw appropriate auxiliary segments. Use your diagrams to prove each case.

Solution:

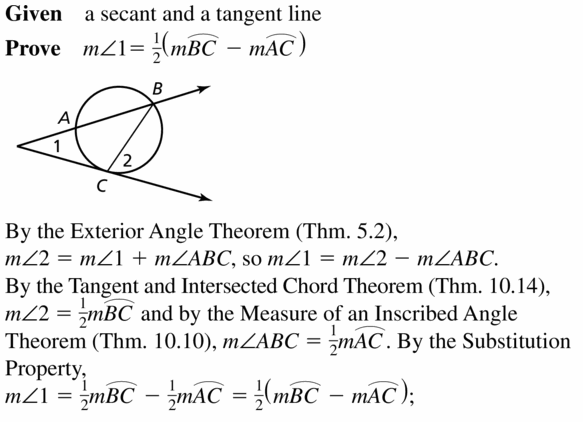
Question 38.
PROVING A THEOREM
Prove that the Circumscribed Angle Theorem (Theorem 10.17) follows from the Angles Outside the Circle Theorem (Theorem 10.16).
Answer:

In Exercises 39 and 40, find the indicated measure(s). justify your answer

Question 39.
Find m ∠ P when m\(\widehat{W Z Y}\) = 200°

Solution:

Question 40.
Find m\(\widehat{A B}\) and m\(\widehat{E D}\)

Solution:
m\(\widehat{A B}\) = 30°
m\(\widehat{E D}\) = 57.5°

Explanation:
With reference to the data given in the above figure,
m\(\widehat{E D}\) = ½ (115°) = 57.5°
m\(\widehat{E D}\) = 57.5°
m\(\widehat{A B}\) = ½ (60°)
m\(\widehat{A B}\) = 30°
∠GJA = 120° – 60°
∠GJA = 30°

Maintaining Mathematical Proficiency

Solve the equation.

Question 41.
x² + x = 12

Solution:

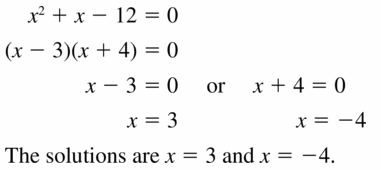
Question 42.
x² = 12x + 35

Solution:
x = \(\frac { 12 ± √284  }{ 2 } \)

Explanation:
x² = 12x + 35
x = \(\frac { 12 ± √(144 + 140)  }{ 2 } \)
x = \(\frac { 12 ± √284  }{ 2 } \)
x = \(\frac { 12 + √284  }{ 2 } \), \(\frac { 12 – √284  }{ 2 } \)

Question 43.
– 3 = x² + 4x

Solution:

10.6 Segment Relationships in Circles

Exploration 1

Segments Formed by Two Intersecting Chords

Work with a partner: Use dynamic geometry software.

Sample

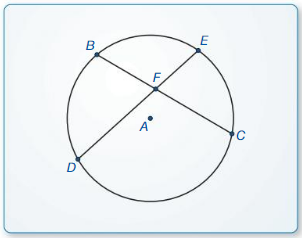
a.
Construct two chords \(\overline{B C}\) and \(\overline{D E}\) that intersect in the interior of a circle at a point F.
Answer:

b.
Find the segment lengths BE, CF, DF, and EF and complete the table. What do you observe?

Answer:

c. Repeat parts (a) and (b) several times. Write a conjecture about your results.
REASONING ABSTRACTLY
To be proficient in math, you need to make sense of quantities and their relationships in problem situations.
Answer:

Exploration 2

Secants Intersecting Outside a Circle

Work with a partner: Use dynamic geometry software.

Sample

a. Construct two secant and that intersect at a point B outside a circle, as shown.
Answer:

b. Find the segment lengths BE, BC, BF, and BD. and complete the table. What do you observe?

Answer:

c. Repeat parts (a) and (b) several times. Write a conjecture about your results.
Answer:

Communicate Your Answer

Question 3.
What relationships exist among the segments formed by two intersecting chords or among segments of two secants that intersect outside a circle?

Question 4.
Find the segment length AF in the figure at the left.

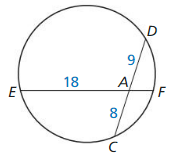
Solution:
AF = 4

Explanation:
With reference to the data given in the above figure,
EA • AF = AD • AC
18 • AF = 9 • 8
18 • AF = 72
AF = 72/18
AF = 4

Lesson 10.6 Segment Relationships in Circles

Monitoring Progress

Find the value of x.

Question 1.

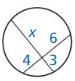
Solution:
x = 8

Explanation:
According to the data given in the above figure,
4 • 6 = 3 • x
3x = 24
x = 24/3
x = 8

Question 2.

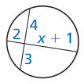
Solution:
x = 5

Explanation:
According to the data given in the above figure,
2 • x + 1 = 4 • 3
2x + 1 = 12
x + 1 = 12/2
x + 1 = 6
x = 6 – 1
x = 5

Question 3.

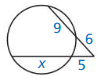
Solution:
x = \(\frac { 54 }{ 5 } \)

Explanation:
According to the data given in the above figure,
6 • 9 = 5 • x
54 = 5x
x = \(\frac { 54 }{ 5 } \)

Question 4.

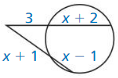
Solution:
x = \(\frac { 3 ± √37 }{ 2 } \)

Explanation:
According to the data given in the above figure,
3 • x + 2 = x + 1 • x – 1
3x + 6 = x² – 1
x² – 3x – 7 = 0
x = \(\frac { 3 ± √(9 + 28) }{ 2 } \)
x = \(\frac { 3 ± √37 }{ 2 } \)

Question 5.

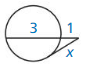
Solution:
x = ±√3

Explanation:
According to the data given in the above figure,
x² = 3 • 1
x² = 3
x = ±√3

Question 6.

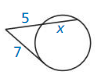
Solution:
x = \(\frac { 49 }{ 5 } \)

Explanation:
According to the data given in the above figure,
7² = 5 • x
49 = 5x
x = \(\frac { 49 }{ 5 } \)

Question 7.

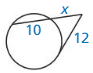
Solution:
x = 14.4

Explanation:
According to the data given in the above figure,
12² = 10x
144 = 10x
x = 144/10
x = 14.4

Question 8.
WHAT IF?
In Example 4, CB = 35 feet and CE = 14 feet. Find the radius of the tank.

Solution:
The radius of the tank is 36.75.

Explanation:
According to the data given in the above figure,
CB² = CE ⋅ CD
Given,
CB = 35 feet and CE = 14 feet.
35² = 14 ⋅ (2r + 14)
1225 = 28r + 196
28r = 1225 – 196
28r = 1029
r = 1029/28
r = 36.75

Exercise 10.6 Segment Relationships in Circles

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
The part of the secant segment that is outside the circle is called a(n) ______________ .

Solution:

Question 2.
WRITING
Explain the difference between a tangent segment and a secant segment.

Solution:
A tangent segment intersects the circle at only one point.
It actually doesn’t go through the circle.
For example;
If a ball is rolling on a table top, then it would be the tangent.
Where as a secant segment intersects the circle in two points.
It goes through the circle. In a tangent, no part is in the interior of the circle.
In a secant, there is a part in the interior called a chord.

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6, find the value of x.

Question 3.

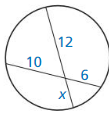
Solution:

Question 4.

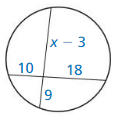
Solution:
x = 23

Explanation:
With reference to the data given in above figure,
10 • 18 = 9 • (x – 3)
180 = x – 3
x – 3 = 180/9
x – 3 = 20
x = 20 + 3
x = 23

Question 5.

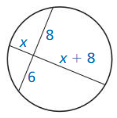
Solution:

Question 6.

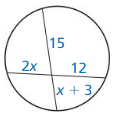
Solution:
x = 5

Explanation:
With reference to the data given in above figure,
2x • 12 = 15 • (x + 3)
24x = 15x + 45
24 x – 15x = 45
9x = 45
x = 45/9
x = 5

In Exercises 7 – 10, find the value of x.

Question 7.

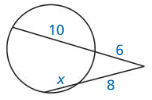
Solution:

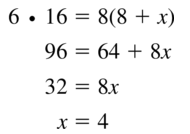
Question 8.

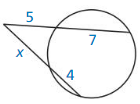
Solution:
x = \(\frac { 35 }{ 4 } \)

Explanation:
With reference to the data given in above figure,
5 • 7 = 4 • x
4x = 35
x = \(\frac { 35 }{ 4 } \)

Question 9.

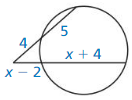
Solution:

Question 10.

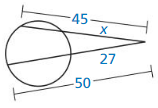
Solution:
x = 30

Explanation:
With reference to the data given in above figure,
45 • x = 50 • 27
45x = 1350
x = 1350/45
x = 30

In Exercises 11 – 14. find the value of x.

Question 11.

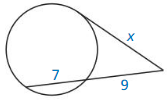
Solution:

Question 12.

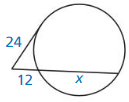
Solution:
x = 48

Explanation:
With reference to the data given in above figure,
24² = 12x
576 = 12x
x = 576/12
x = 48

Question 13.

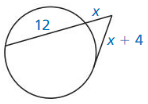
Solution:

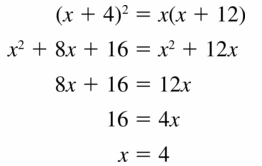
Question 14.

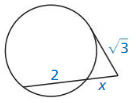
Solution:
x = 1.5

Explanation:
With reference to the data given in above figure,
3 = 2x
x = 3/2
x = 1.5

Question 15.
ERROR ANALYSIS
Describe and correct the error in finding CD.

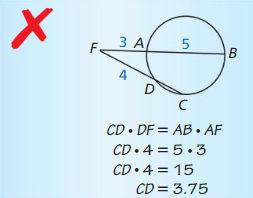
Solution:

Question 16.
MODELING WITH MATHEMATICS
The Cassini spacecraft is on a mission in orbit around Saturn until September 2017. Three of Saturn’s moons. Tethys. Calypso, and Telesto. have nearly circular orbits of radius 2,95,000 kilometers. The diagram shows the positions of the moons and the spacecraft on one of Cassini’s missions. Find the distance DB from Cassini to Tethys when \(\overline{A D}\) is tangent to the circular orbit.

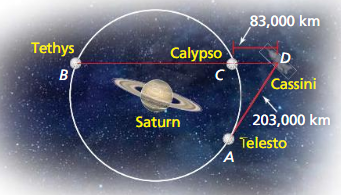
Solution:
BD = 579493 km.

Explanation:
Given,
radius 2,95,000 kilometers.
With reference to the data given in above figure,
AD = the distance between Cassini and Telesto i.e., 203,000km
CD = the distance between Calypso and Cassini i.e., 83000
BD = x
AD² = CD x BD
(203,000)² = 83000x
x = 496493
BC = 496493
BD = 496493 + 83000
BD = 579493km.

Question 17.
MODELING WITH MATHEMATICS
The circular stone mound in Ireland called Newgrange has a diameter of 250 feet. A passage 62 feet long leads toward the center of the mound. Find the perpendicular distance x from the end of the passage to either side of the mound.

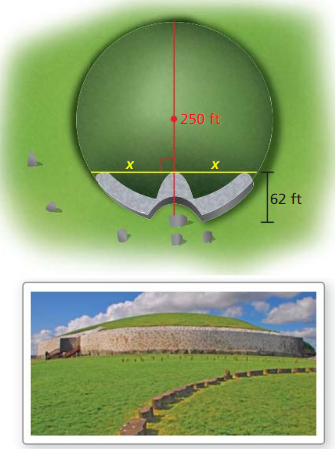
Solution:

Question 18.
MODELING WITH MATHEMATICS
You are designing an animated logo for our website. Sparkles leave point C and move to the Outer circle along the segments shown so that all of the sparkles reach the outer circle at the same time. Sparkles travel from point C to point D at 2 centimeters per second. How fast should sparkles move from point C to point N? Explain.

Solution:
5.33 should sparkles move from point C to point N.

Explanation:
With reference to the data given in the above figure,
4 • 8 = 6 • x
32 = 6x
x = 32/6
x = 5.33

Question 19.
PROVING A THEOREM
Write a two-column proof of the Segments of Chords Theorem (Theorem 10.18).

Plan for Proof:
Use the diagram to draw \(\overline{A C}\) and \(\overline{D B}\). Show that ∆EAC and ∆EDB are similar. Use the fact that corresponding side lengths in similar triangles are proportional.

Solution:

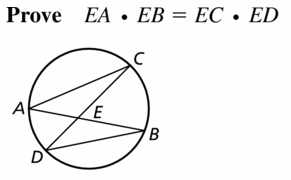
Question 20.
PROVING A THEOREM
Prove the Segments of Secants Theorem (Theorem 10.19). (Hint: Draw a diagram and add auxiliary line segments to form similar triangles.)
Answer:

Question 21.
PROVING A THEOREM
Use the Tangent Line to Circle Theorem (Theorem 10. 1) to prove the Segments of Secants and Tangents Theorem (Theorem 10.20) for the special case when the secant segment Contains the center of the circle.

Solution:

Question 22.
PROVING A THEOREM
Prove the Segments of Secants and Tangents Theorem (Theorem 10.20). (Hint: Draw a diagram and add auxiliary line segments to form similar triangles.)
Answer:

Question 23.
WRITING EQUATIONS
In the diagram of the water well, AB, AD, and DE are known. Write an equation for BC using these three measurements.

Solution:

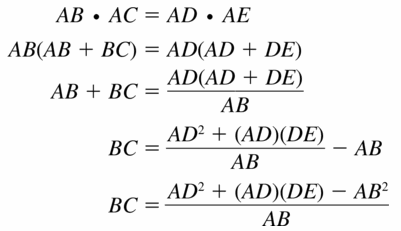
Question 24.
HOW DO YOU SEE IT?
Which two theorems would you need to use to tind PQ? Explain your reasoning.

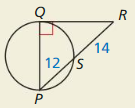
Answer:

Question 25.
CRITICAL THINKING
In the figure, AB = 12, BC = 8, DE = 6, PD = 4, and a is a point of tangency. Find the radius of ⊙P.

Solution:

Question 26.
THOUGHT PROVOKING
Circumscribe a triangle about a circle. Then, using the points of tangency, inscribe a triangle in the circle. Must it be true that the two triangles are similar? Explain your reasoning.

Answer:

Maintaining Mathematical Proficiency

Solve the equation by completing the square.

Question 27.
x² + 4x = 45

Solution:

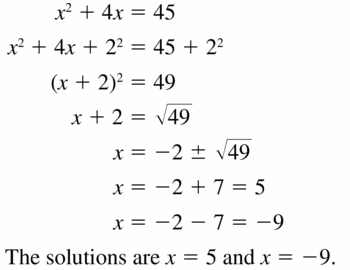
Question 28.
x² – 2x – 1 = 8

Solution:
x = 1 + √10, x = 1 – √10

Explanation:
According to the information given in the above figure,
x² – 2x – 1 = 8
x² – 2x – 9 = 0
x = \(\frac { 2 ± √(4 + 36) }{ 2 } \)
x = \(\frac { 2 ± √40 }{ 2 } \)
x = 1 + √10, x = 1 – √10

Question 29.
2x² + 12x + 20 = 34

Solution:

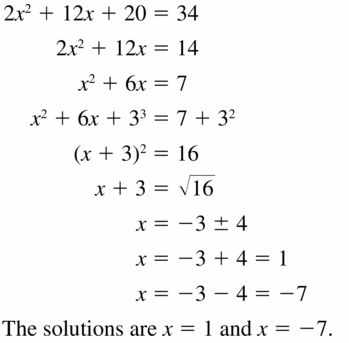
Question 30.
– 4x² + 8x + 44 = 16

Solution:
x = 1 + √8, x = 1 – √8

Explanation:
According to the information given in the above figure,
– 4x² + 8x + 44 = 16
4x² – 8x – 28 =0
x² – 2x – 7 = 0
x = \(\frac { 2 ± √(4 + 28) }{ 2 } \)
x = \(\frac { 2 ± √32 }{ 2 } \)
x = 1 ± √8

10.7 Circles in the Coordinate Plane

Exploration 1

The Equation of a Circle with Center at the Origin

Work with a partner: Use dynamic geometry software to Construct and determine the equations of circles centered at (0, 0) in the coordinate plane, as described below.

a. Complete the first two rows of the table for circles with the given radii. Complete the other rows for circles with radii of your choice.

Solution:

b. Write an equation of a circle with center (0, 0) and radius r.

Solution:
x²  + y²  = r²

Explanation:
According to the information given in the above figure,
(x – 0)² + (y – 0)²  = r²
x²  + y²  = r²

Exploration 2

The Equation of a Circle with Center (h, k)

Work with a partner: Use dynamic geometry software to construct and determine the equations of circles of radius 2 in the coordinate plane, as described below.

a. Complete the first two rows of the table for circles with the given centers. Complete the other rows for circles with centers of your choice.

Solution:

b. Write an equation of a circle with center (h, k) and radius 2.

Solution:
According to the information given in the above figure,
(x – h)² + (y – k)² = 4

c. Write an equation of a circle with center (h, k) and radius r.

Solution:
According to the information given in the above figure,
(x – h)² + (y – k)² = r²

Exploration 3

Deriving the Standard Equation of a Circle

Work with a partner. Consider a circle with radius r and center (h, k).

Write the Distance Formula to represent the distance d between a point (x, y) on the circle and the center (h, k) of the circle. Then square each side of the Distance Formula equation.

How does your result compare with the equation you wrote in part (c) of Exploration 2?

MAKING SENSE OF PROBLEMS
To be proficient in math, you need to explain correspondences between equations and graphs.

Solution:
According to the information given in the above figure,
(x – h)² + (y – k)² = r²

Communicate Your Answer

Question 4.
What is the equation of a circle with center (h, k) and radius r in the coordinate plane?

Solution:
According to the information given in the above figure,
(x – h)² + (y – k)² = r²

Question 5.
Write an equation of the circle with center (4, – 1) and radius 3.

Solution:
x² + y² – 8x + 2y + 8 = 0

Explanation:
According to the information given in the above figure,
(x – 4)² + (y + 1)² = 9
The above equation is in the form of (a – b)² + (a + b)²
x² – 8x + 16 + y² + 2y + 1 = 9
x² + y² – 8x + 2y + 17 – 9 = 0
x² + y² – 8x + 2y + 8 = 0

Lesson 10.7 Circles in the Coordinate Plane

Monitoring Progress

Write the standard equation of the circle with the given center and radius.

Question 1.
center: (0, 0), radius: 2.5

Solution:
x² + y² = 6.25

Explanation:
Given,
center: (0, 0), radius: 2.5
(x – 0)² + (y – 0)² = 2.5²
x² + y² = 6.25

Question 2.
center: (- 2, 5), radius: 7

Solution:
(x + 2)² + (y – 5)² = 49

Explanation:
Given,
center: (- 2, 5), radius: 7
(x + 2)² + (y – 5)² = 7²
(x + 2)² + (y – 5)² = 49

Question 3.
The point (3, 4) is on a circle with center (1, 4). Write the standard equation of the circle.

Solution:
(x – 1)² + (y – 4)² = 4

Explanation:
Given,
The point (3, 4) is on a circle with center (1, 4).
r = √(3 – 1)² + (4 – 4)²
r = √(2)²
r = 2
(x – 1)² + (y – 4)² = 2²
(x – 1)² + (y – 4)² = 4

Question 4.
The equation of a circle is x² + y² – 8x + 6y + 9 = 0. Find the center and the radius of the circle. Then graph the circle.

Solution:
The center of the circle (4, -3) and radius is 4.

Explanation:
Given,
x² + y² – 8x + 6y + 9 = 0
x² – 8x + 16 + y² + 6y + 9 = 16
(x – 4)² + (y + 3)² = 4²
The center of the circle (4, -3) and radius is 4.

Question 5.
Prove or disprove that the point (1, √5) lies on the circle centered at the origin and containing the point (0, 1).

Solution:
Disproved.

Explanation:
Given that the point (1, √5) lies on the circle centerd at the origin and containing the point (0, 1).
Therefore, the radius of the circle r = 1,
let O (0, 0) and B (1, √5).
So the distance between two points is,
OB = √(1 – 0) + (√5 – 0)² = √(1 + 5) = √6
As the radius of the given circle is 1 and distance of the point B from its center is √6,
the point does lie on the given circle.
Hence , it is disproved.

Question 6.
why are three seismographs needed to locate an earthquake’s epicentre?

Answer:

Exercise 10.7 Circles in the Coordinate Plane

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
What is the standard equation of a circle?

Solution:

Question 2.
WRITING
Explain why knowing the location of the center and one point on a circle is enough to graph the circle.

Solution:
If we know the location of the center and one point on the circle,
we can graph a circle because the distance from the center to the point is called the radius.

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 8, write the standard equation of the circle.

Question 3.

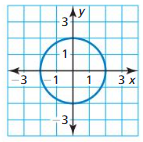
Solution:

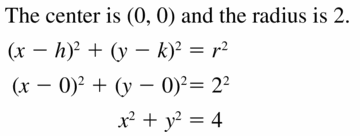
Question 4.

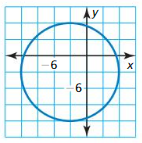
Solution:
x² + y² = 36

Explanation:
With reference to the data given in the above figure,
The center is (0, 0) and the radius is 6.
We know that,
(x – h)² + (y – k)² = r²
(x – 0)² + (y – 0)² = 6²
x² + y² = 36

Question 5.
a circle with center (0, 0) and radius 7

Solution:

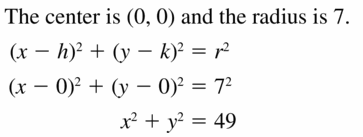
Question 6.
a circle with center (4, 1) and radius 5

Solution:
(x – 4)² + (y – 1)² = 25

Explanation:
Given,
a circle with center (4, 1) and radius 5.
We know that,
(x – h)² + (y – k)² = r²
(x – 4)² + (y – 1)² = 5²
(x – 4)² + (y – 1)² = 25

Question 7.
a circle with center (- 3, 4) and radius 1

Solution:

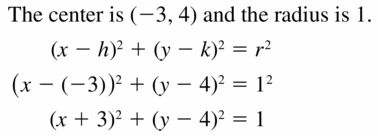
Question 8.
a circle with center (3, – 5) and radius 7

Solution:
(x – 3)² + (y + 5)² = 49

Explanation:
Given,
a circle with center (3, – 5) and radius 7.
We know that,
(x – h)² + (y – k)² = r²
(x – 3)² + (y + 5)² = 7²
(x – 3)² + (y + 5)² = 49

In Exercises 9 – 11, use the given information to write the standard equation of the circle.

Question 9.
The center is (0, 0), and a point on the circle is (0, 6).

Solution:

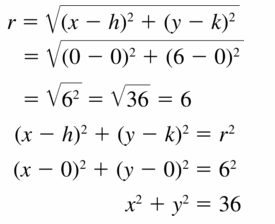
Question 10.
The center is (1, 2), and a point on the circle is (4, 2).

Solution:
x² + y² = 9

Explanation:
Given,
The center is (1, 2), and a point on the circle is (4, 2).
We know that,
r = √(x – h)² + (y – k)²
r = √(4 – 1)² + (2 – 2)²
r = √3²
r = 3
(x – h)² + (y – k)² = r²
(x – 0)² + (y – 0)² = 3²
x² + y² = 9

Question 11.
The center is (0, 0). and a point on the circle is (3, – 7).

Solution:

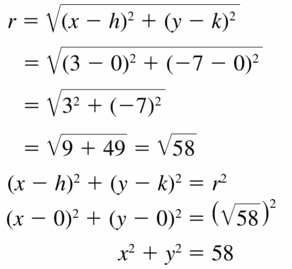
Question 12.
ERROR ANALYSIS
Describe and correct the error in writing the standard equation of a circle.

Solution:
(x + 3)² + (y + 5)² = 9

Explanation:
Given,
the center (-3, -5) and radius is 3.
We know that,
(x – h)² + (y – k)² = r²
(x + 3)² + (y + 5)² = 3²
(x + 3)² + (y + 5)² = 9

In Exercises 13 – 18, find the center and radius of the circle. Then graph the circle.

Question 13.
x² + y² = 49

Solution:

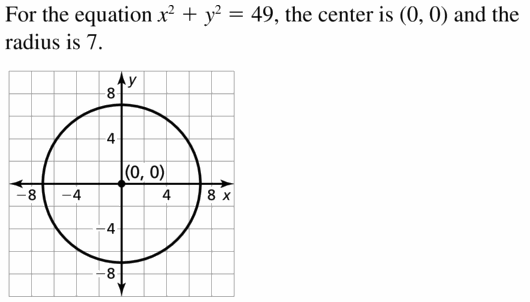
Question 14.
(x + 5)² + (y – 3)² = 9

Solution:
Center is (-5, 3) and radius is 3.

Explanation:
Given,
(x + 5)² + (y – 3)² = 9
x² + 25 + y² – 9 = 9
center is (-5, 3) and radius is 3.

Question 15.
x² + y² – 6x = 7

Solution:

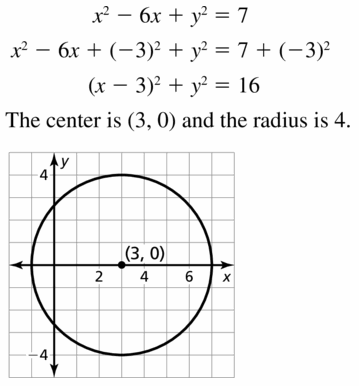
Question 16.
x² + y² + 4y = 32

Solution:
The center is (0, -2) and radius is 6

Explanation:
Given,
x² + y² + 4y = 32
x² + y² + 4y + 4 = 32 + 4
x² + (y + 2)² = 36
(x – 0)² + (y – (-2))² = 6²
The center is (0, -2) and radius is 6

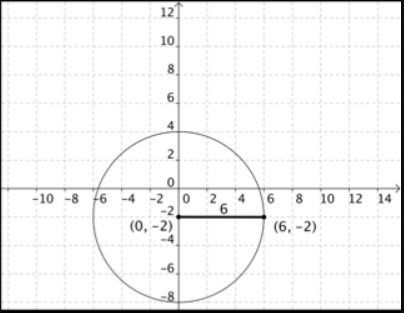
Question 17.
x² + y² – 8x – 2y = – 16

Solution:

Question 18.
x² + y² + 4x + 12y = – 15

Solution:
The center is (-2, -6) and radius is 5.

Explanation:
Given,
x² + y² + 4x + 12y = – 15
x² + 4x + 4 + y² + 12y + 36 = -15 + 36 + 4
(x + 2)² + (y + 6)² = 5²
The center is (-2, -6) and radius is 5

In Exercises 19 – 22, prove or disprove the statement.

Question 19.
The point (2, 3) lies on the circle centered at the origin with radius 8.

Solution:

Question 20.
The point (4, √5) lies on the circle centered at the origin with radius 3.

Solution:
The point (4, √5) does not lie on the circle.

Explanation:
Given,
The point (4, √5) lies on the circle centered at the origin with radius 3.
We know that,
r² = (x – h)² + (y – k)²
3² ______________ (4 – 0)² + (√5 – 0)²
9 ______________ 16 + 5
9 ≠ 21
Because the radius is 3 and the distance between center and the point is more than the radius.
So, the point does not lie on the circle.

Question 21.
The point (√6, 2) lies on the circle centered at the origin and containing the point (3, – 1).

Solution:

Question 22.
The point (√7, 5) lies on the circle centered at the origin and containing the point (5, 2).

Solution:
The point (√7, 5) does not lie on the circle.

Explanation:
Given,
The point (√7, 5) lies on the circle centered at the origin and containing the point (5, 2).

We know that,
r² = (x – h)² + (y – k)²
= (√7 – 0)² + (5 – 0)² = 7 + 25 = 32
r = 5.65
(5.65)² ______________ (5 – 0)² + (2 – 0)²
32 ______________ 25 + 4
32 ≠ 29
Because the radius is 3 and the distance between center and the point is more than the radius.
So, the point does not lie on the circle.

Question 23.
MODELING WITH MATHEMATICS
A City’s commuter system has three zones. Zone I serves people living within 3 miles of the city’s center. Zone 2 serves those between 3 and 7 miles from the center. Zone 3 serves those over 7 miles from the center.

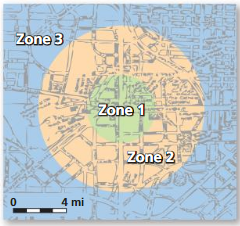
a. Graph this Situation on a coordinate plane where each unit corresponds to 1 mile. Locate the city’s center at the origin.
b. Determine which zone serves people whose homes are represented by the points (3, 4), (6, 5), (1, 2), (0.3). and (1, 6).

Solution:

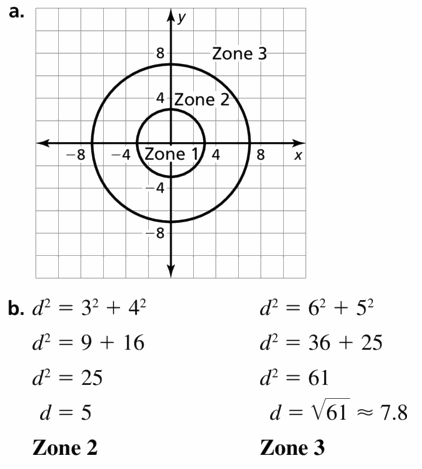
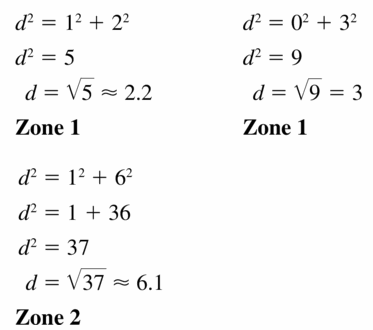
Question 24.
MODELING WITH MATHEMATICS
Telecommunication towers can be used to transmit cellular phone calls. A graph with units measured in kilometers shows towers at points (0, 0), (0, 5), and (6, 3). These towers have a range of about 3 kilometers.
a. Sketch a graph and locate the towers. Are there any locations that may receive calls from more than one tower? Explain your reasoning.
Answer:

b. The center of City A is located at (- 2, 2.5), and the center of City B is located at (5, 4). Each city has a radius of 1.5 kilometers. Which city seems to have better cell phone coverage? Explain your reasoning.

Solution:
There are three towers at points (0, 0), (0, 5) and (6, 3) with range of about 3 km.

a. Let’s sketch the graph to locate towers. Draw the points (0, 0), (0, 5) and (6, 3). Then draw three circles with centers at these points and radii 3.
There are locations that can receive calls from more that one tower because circles with centers (0, 0) and (0, 5) overlap. Locations in their intersection can receive calls from two towers.
The city A has a center located at (-2, 2.5) and city B has a center located at (5, 4).
Both cities have radius 1.5 km
Let’s draw the city A as a circle with center (-2, 2.5) and radius 1.5 and city B with center (5, 4) and radius 1.5.
From the graph we can conclude that the city B has better cell phone coverage because parts of city A do not have coverage.

Question 25.
REASONING
Sketch the graph of the circle whose equation is x² + y² = 16. Then sketch the graph of the circle after the translation (x, y) → (x – 2, y – 4). What is the equation of the image? Make a conjecture about the equation of the image of a circle centered at the origin after a translation m units to the left and n units down.

Solution:

Question 26.
HOW DO YOU SEE IT?
Match each graph with its equation.

a.	A. x2 + (y + 3) 2 = 4
b.	B. (x – 3) 2 + y2 = 4
c.	C. (x + 3) 2 + y2 = 4
d.	D. x2 + (y – 3) 2 = 4

Solution:
a ➝ C,
b ➝ A,
c ➝ D,
d ➝ B

Question 27.
USING STRUCTURE
The vertices of ∆XYZ are X(4, 5), Y(4, 13), and Z(8, 9). Find the equation of the circle circumscribed about ∆XYZ. Justify your answer.

Solution:

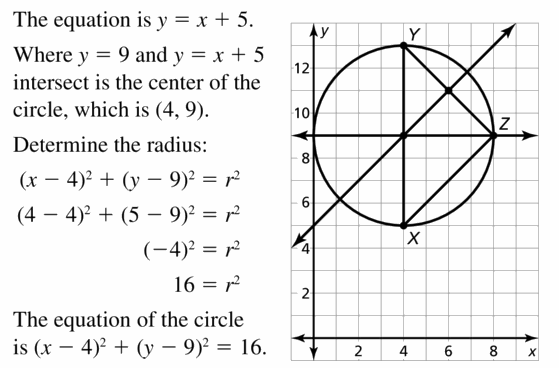
Question 28.
THOUGHT PROVOKING
A circle has center (h, k) and contains point (a, b). Write the equation of the line tangent to the circle at point (a, b).

Solution:
y – b = \(\frac { h – a }{ b – k } \)(x – a)

Explanation:
It is given that a circle with center C(h, k. A circle with point A(a, b).
We have to write the equation of a tangent that intersects the circle at point A.
According to the tangent line to circle theorem, a tangent is perpendicular to the radius.
Two lines are perpendicular if their slopes are negative reciprocals.
So, find the equation of the line AC to know its slope.
The equation of the line which has two points (a, b), (c, d) is y – b = \(\frac { b – c }{ a – d } \)(x – a)
The equation of the line which has two points A(a, b) and C(h, k) is,
y – b = \(\frac { b – k }{ a – h } \)(x – a)
Therefore, the slope of the line through A and C is \(\frac { b – k }{ a – h } \)
Hence, the slope of the tangent is –\(\frac { a – h }{ b – k } \) = \(\frac { h – a }{ b – k } \)
Use the equation of the line y = kx + n through the point (a, b)
y – b = k(x – a) to find the equation of the tangent.
The equation of the tangent with slope \(\frac { h – a }{ b – k } \) and through the point A(a, b) is y – b = \(\frac { h – a }{ b – k } \)(x – a)

MATHEMATICAL CONNECTIONS
In Exercises 29 – 32, use the equations to determine whether the line is a tangent, a secant a secant that contains the diameter, or name of these. Explain your reasoning.

Question 29.
Circle: (x – 4)² + (y – 3)² = 9
Line: y = 6

Solution:

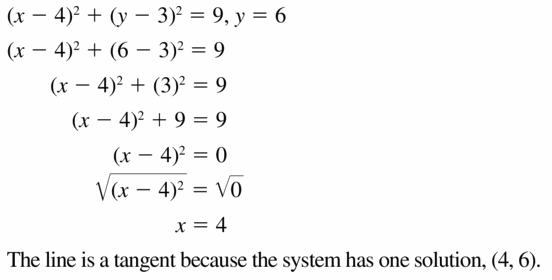
Question 30.
Circle: (x + 2)² + (y – 2)² = 16
Line: y = 2x – 4

Solution:
The line is a secant line.

Explanation:
Given,
Circle: (x + 2)² + (y – 2)² = 16,
Line: y = 2x – 4
(x + 2)² + (2x – 4 – 2)² = 16
x² + 4x + 4 + (2x – 6)² = 16
x² + 4x + 4 + 4x² – 24x + 36 = 16
5x² – 20x + 40 – 16 = 0
5x² – 20x + 24 = 0
x = \(\frac { 20 ±√-80 }{ 10 } \)
x = 2,
y = 2 • 2 – 4
y = 0, (2, 0)
The system has two solutions and point does not lie on the line.
So, the line is a secant line.

Question 31.
Circle: (x – 5)² + (y + 1)² = 4
Line: y = \(\frac{1}{5}\)x – 3\

Solution:

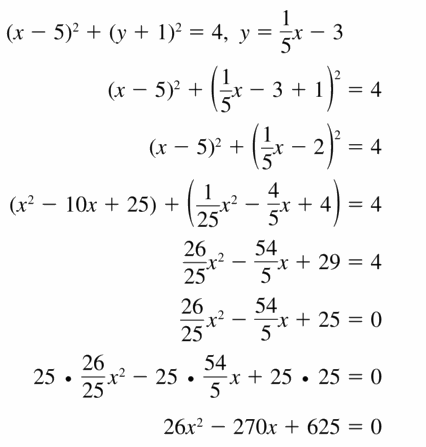
Question 32.
Circle: (x + 3)² + (y – 6)² = 25
Line: y = –\(\frac{4}{3}\)x + 2

Solution:
The line is a secant line.

Explanation:
Given,
Circle: (x + 3)² + (y – 6)² = 25,
Line: y = –\(\frac{4}{3}\)x + 2
(x + 3)² + (-\(\frac{4}{3}\)x + 2 – 6)² = 25
x² + 6x + 9 + \(\frac { 16x² }{ 9 } \) + \(\frac { 32x }{ 3 } \) + 16 = 25
\(\frac { 25x² }{ 9 } \) + \(\frac { 50x }{ 3 } \) = 0
x(25x + 150) = 0
x = 0 or x = -6
y = 2, y = 10
(0, 2) and (-6, 10)
d = √(0 + 6)² + (2 – 10)²
= √(36 + 64)
= 10 ≠ 5
The system has two solutions and point does not lie on the line.
So, the line is a secant line.

MAKING AN ARGUMENT
Question 33.
Your friend claims that the equation of a circle passing through the points (- 1, 0) and (1, 0) is x² – 2yk + y² = 1 with center (0, k). Is your friend correct? Explain your reasoning.

Solution:

Question 34.
REASONING
Four tangent circles are centered on the x-axis. The radius of ⊙A is twice the radius of ⊙O, The radius of ⊙B is three times the radius of ⊙O, The radius of ⊙C is four times the radius of ⊙O, All circles have integer radii, and the point (63, 16) is On ⊙C. What is the equation of ⊙A? Explain your reasoning.

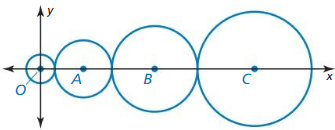
Answer:

Maintaining Mathematical Proficiency

Identify the arc as a major arc, minor arc, or semicircle. Then find the measure of the arc.

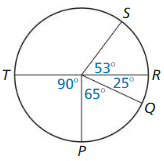
Question 35.
\(\widehat{R S}\)

Solution:

Explanation:
The arc which is less than 180 degrees is known as minor arc.

Question 36.
\(\widehat{P R}\)

Solution:
\(\widehat{P R}\) = 25 + 65 = 90°

Explanation:
With reference to the information given in the above data,
\(\widehat{P R}\) is a right angle.
\(\widehat{P R}\) = 25 + 65 = 90°

Question 37.
\(\widehat{P R T}\)

Solution:

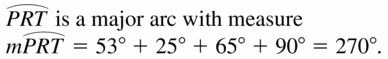
Question 38.
\(\widehat{S T}\)

Solution:
\(\widehat{S T}\) = 127°

Explanation:
With reference to the information given in the above data,
\(\widehat{S T}\) is a major arc.
We know that major arc is greater than 180 degrees.
\(\widehat{S T}\) = 360 – (90 + 65 +25 + 53)
\(\widehat{S T}\) = 127°

Question 39.
\(\widehat{R S T}\)

Solution:

Explanation:
When the arc is equal to 180 degrees is known as semicircle.

Question 40.
\(\widehat{Q S}\)

Solution:
\(\widehat{Q S}\) = 78°

Explanation:
With reference to the information given in the above data,
\(\widehat{Q S}\) is a minor arc.
We know that minor arc is less than 180 degrees.
\(\widehat{Q S}\) = 25 + 53 = 78°
\(\widehat{Q S}\) = 78°

Circles Review

10.1 Lines and Segments That Intersect Circles

Tell whether the line, ray, or segment is best described as a radius, chord, diameter, secant, or tangent of ⊙P.

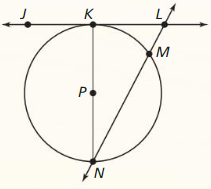
Question 1.
\(\overline{P K}\)

Solution:
\(\overline{P K}\) is radius.

Explanation:
With reference to the information given in the above figure,
\(\overline{P K}\) is radius.
We know that the radius is half the length of the diameter and is joined to the center at one end.

Question 2.
\(\overline{N M}\)

Solution:
\(\overline{N M}\) is chord.

Explanation:
With reference to the information given in the above figure,
\(\overline{N M}\) is chord.
A chord is a straight line inside the circle that touches the circumference at 2 points,
but does not touch the center of a circle.

Question 3.
\(\vec{J}\)L

Solution:
\(\vec{J}\)L is tangent.

Explanation:
With reference to the information given in the above figure,
\(\vec{J}\)L is tangent.
A line that intersects a circle exactly at one point is called a tangent and the point where the intersection occurs is called the point of tangency.
The tangent is always perpendicular to the radius drawn to the point of tangency.

Question 4.
\(\overline{K N}\)

Solution:
\(\overline{K N}\) is diameter.

Explanation:
With reference to the information given in the above figure,
\(\overline{K N}\) is diameter.
We know that,
The diameter is the length of the line through the center that touches two points on the edge of the circle as shown in the above given figure.

Question 5.

Solution:
NL is secant.

Explanation:
We know that,
A secant is a line that intersects a circle in exactly two points.
So, NL is secant.

Question 6.
\(\overline{P N}\)

Solution:
\(\overline{P N}\) is radius.

Explanation:
With reference to the information given in the above figure,
\(\overline{P N}\) is radius.
We know that the radius is half the length of the diameter and is joined to the center at one end.

Tell whether the common tangent is internal or external.

Question 7.

Solution:
Internal common tangent.

Explanation:
We know that the lines are said to be internal tangents,
if they intersect the segment joining the centers of two circles.
So, the above given figure has a common internal tangent.

Question 8.

Solution:
External common tangent.

Explanation:
The lines that do not cross the segment joining the centers of the circles is said to be External tangents.
So, the above given figure has a common external tangent.

Points Y and Z are points of tangency. Find the value of the variable.

Question 9.

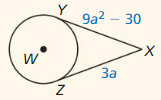
Solution:
a = \(\frac { 3 ± 33 }{ 18 } \)

Explanation:
Given,
Points Y and Z are points of tangency.
With reference to the information given in the above figure,
3a = 9a² – 30
9a² – 3a – 30 = 0
a = \(\frac { 3 ± 33 }{ 18 } \)

Question 10.

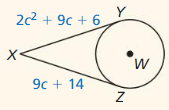
Solution:
c = 2

Explanation:
With reference to the information given in the above figure,
2c² + 9c + 6 = 9c + 14
2c² – 8 = 0
c² – 4 = 0
c = 2

Question 11.

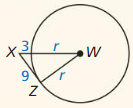
Solution:
r = 12

Explanation:
With reference to the information given in the above figure,
(3 + r)² = r² + 9²
9 + 6r + r² = r² + 81
6r = 72
r = 72/6
r = 12

Question 12.
Tell whether \(\overline{B D}\) is tangent to ⊙C. Explain.

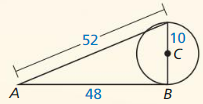
Solution:
\(\overline{B D}\) is not tangent to ⊙C

Explanation:
With reference to the information given in the above figure,
52² = 10² + 48²
2704 = 100 + 2304
2704 = 2404
So, \(\overline{B D}\) is not tangent to ⊙C

10.2 Finding Arc Measures

Use the diagram above to find the measure of the indicated arc.

Question 13.
\(\widehat{K L}\)

Solution:
\(\widehat{K L}\) = 100°

Explanation:
According ot the information given in the above figure,
\(\widehat{K L}\) = ∠KPL = 100°
So, \(\widehat{K L}\) = 100°

Question 14.
\(\widehat{L M}\)

Solution:
\(\widehat{L M}\) = 60°

Explanation:
According ot the information given in the above figure,
\(\widehat{L M}\) = 180° – 120°
\(\widehat{L M}\) = 60°

Question 15.
\(\widehat{K M}\)

Solution:
\(\widehat{K M}\) = 160°

Explanation:
According ot the information given in the above figure,
\(\widehat{K M}\) = 100° + 60°
\(\widehat{K M}\) = 160°

Question 16.
\(\widehat{K N}\)

Solution:
\(\widehat{K N}\) = 80°

Explanation:
According ot the information given in the above figure,
\(\widehat{K N}\) = 360 – (120 + 100 + 60)
\(\widehat{K N}\) = 360 – 280
\(\widehat{K N}\) = 80°

Tell whether the red arcs are congruent. Explain why or why not.

Question 17.

Solution:
\(\widehat{S T}\), \(\widehat{Y Z}\) are not congruent.

Explanation:
We know that,
congruent means exactly equal shape and size.
This shape and size should remain equal, even when we flip, turn, or rotate the shapes.
So, \(\widehat{S T}\), \(\widehat{Y Z}\) are not congruent.
Because both arcs are from different circles and having different radii.

Question 18.

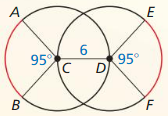
Solution:
\(\widehat{A B}\), \(\widehat{E F}\) are congruent.

Explanation:
We know that,
congruent means exactly equal shape and size.
This shape and size should remain equal, even when we flip, turn, or rotate the shapes.
So,\(\widehat{A B}\), \(\widehat{E F}\) are congruent.
Because those circles have same radii.

10.3 Using Chords

Find the measure of \(\widehat{A B}\).

Question 19.

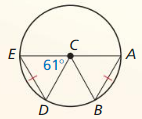
Solution:
\(\widehat{A B}\) = 61°

Explanation:
With reference to the above given figure,
The inscribed triangles are congruent to each other.
\(\widehat{A B}\) = 61°
If ED = AB,
then \(\widehat{A B}\) = \(\widehat{E D}\)

Question 20.

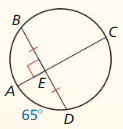
Solution:
\(\widehat{A B}\) = 65°

Explanation:
With reference to the above given figure,
\(\widehat{A B}\) = \(\widehat{A D}\)
So, \(\widehat{A B}\) = 65°

Question 21.

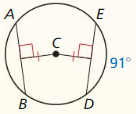
Solution:
\(\widehat{A B}\) = 91°

Explanation:
With reference to the above given figure,
\(\widehat{A B}\) = \(\widehat{E D}\)
So, \(\widehat{A B}\) = 91°

Question 22.
In the diagram. QN = QP = 10, JK = 4x, and LM = 6x – 24. Find the radius of ⊙Q.

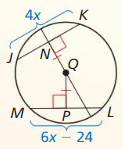
Solution:
The radius of ⊙Q is 26.

Explanation:
With reference to the above given figure,
6x – 24 = 4x
6x – 4x = 24
2x = 24
x = 24/2
x = 12
ML = 6(12) – 24 = 48
JN = \(\frac { 48 }{ 2 } \) = 24
JQ² = JN² + NQ²
JQ² = 24² + 10²
JQ² = 576 + 100
JQ² = 676
JQ = 26
Therefore, the radius of ⊙Q is 26.

10.4 Inscribed Angles and Polygons

Find the value(s) of the variable(s).

Question 23.

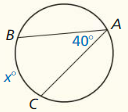
Solution:
x° = 80°

Explanation:
With reference to the data given in the above figure,
x° = 2θ
x° = 2 • 40°
x° = 80°

Question 24.

Solution:
q° = 100°, r° = 20°

Explanation:
With reference to the data given in the above figure,
q° + 80° = 180°
q° = 180° – 80°
q° = 100°
4r° + 100 = 180°
4r° = 180° – 100°
4r° = 80°
r° = 20°

Question 25.

Solution:
d° = 5°

Explanation:
With reference to the data given in the above figure,
14d° = 70°
d° = 70/14
d° = 5°

Question 26.

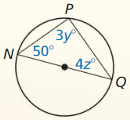
Solution:
y° = 30°, z° = 10°

Explanation:
With reference to the data given in the above figure,
3y° = 90°
y° = 90/3
y° = 30°
50° + 90° + 4z° = 180°
4z° = 180° – 140°
4z° = 40°
z° = 40/4
z° = 10°

Question 27.

Solution:
m° = 44°
n° = 39°

Explanation:
With reference to the data given in the above figure,
m° = 44°
n° = 39°

Question 28.

Solution:
c° = 28°

Explanation:
With reference to the data given in the above figure,
c° = ½ • 56
c° = 28°

10.5 Angle Relationships in Circles

Find the value of x.

Question 29.

Solution:
x° = 250°

Explanation:
With reference to the data given in the above figure,
x° = 250°

Question 30.

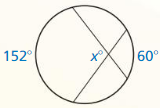
Solution:
x° = 106°

Explanation:
With reference to the data given in the above figure,
x° = ½(152 + 60)
x° = ½(212)
x° = 106°

Question 31.

Solution:
x° = 28°

Explanation:
With reference to the data given in the above figure,
x° = ½(96 – 40)
x° = ½(56)
x° = 28°

Question 32.
Line l is tangent to the circle. Find m\(\widehat{X Y Z}\).

Solution:
m\(\widehat{X Y Z}\) = 240°

Explanation:
Given,
Line l is tangent to the circle.
With reference to the data given in the above figure,
m\(\widehat{X Y Z}\) = 2(120)
m\(\widehat{X Y Z}\) = 240°

10.6 Segment Relationships in Circles

Find the value of x.

Question 33.

Solution:
x = 8

Explanation:
With reference to the data given in the above figure,
3 • x = 4 • 6
x = 24/3
x = 8

Question 34.

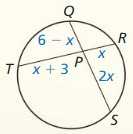
Solution:
x = 3

Explanation:
With reference to the data given in the above figure,
(x + 3) • x = (6 – x) • 2x
(x + 3) • x = 12 – 2x
3x  = 9
x = 9/3
x = 3

Question 35.

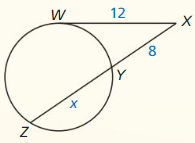
Solution:
x = 18

Explanation:
With reference to the data given in the above figure,
12² = 8 • x
144 = 8x
x = 144/8
x = 18

Question 36.
A local park has a circular ice skating rink. You are standing at point A, about 12 feet from the edge of the rink. The distance from you to a point of tangency on the rink is about 20 feet. Estimate the radius of the rink.

Solution:
Estimated radius of the rink is 10 ft.

Explanation:
Given,
You are standing at point A, about 12 feet from the edge of the rink.
The distance from you to a point of tangency on the rink is about 20 feet.
With reference to the data given in the above figure,
20² = 12 • (2r + 12)
400 = 24r + 144
400 – 144 = 24r
256 = 24r
r = 256/24
r = 10.66
Therefore, estimated radius of the rink is 10 ft.

10.7 Circles in the Coordinate Plane

Write the standard equation of the circle shown.

Question 37.

Solution:
(x – 4)² + (y + 1)² = 12.25

Explanation:
With reference to the data given in the above figure,
(x – 4)² + (y + 1)² = 3.5²
(x – 4)² + (y + 1)² = 12.25

Question 38.

Solution:
(x – 8)² + (y – 5)² = 36

Explanation:
With reference to the data given in the above figure,
(x – 8)² + (y – 5)² = 6²
(x – 8)² + (y – 5)² = 36

Question 39.

Solution:
x² + y² = 4

Explanation:
With reference to the data given in the above figure,
We know that,
(x – h)² + (y – k)² = r²
(x – 0)² + (y – 0)² = 2²
x² + y² = 4

Write the standard equation of the circle with the given center and radius.

Question 40.
center: (0,0), radius: 9

Solution:
x² + y² = 81

Explanation:
Given,
center: (0,0), radius: 9
We know that,
(x – h)² + (y – k)² = r²
(x – 0)² + (y – 0)² = 9²
x² + y² = 81

Question 41.
center: (- 5, 2), radius: 1.3

Solution:
(x + 5)² + (y – 2)² = 1.69

Explanation:
Given,
center: (- 5, 2), radius: 1.3
We know that,
(x – h)² + (y – k)² = r²
(x + 5)² + (y – 2)² = 1.3²
(x + 5)² + (y – 2)² = 1.69

Question 42.
center: (6, 21), radius: 4

Solution:
(x – 6)² + (y – 21)² = 16

Explanation:
Given,
center: (6, 21), radius: 4
We know that,
(x – h)² + (y – k)² = r²
(x – 6)² + (y – 21)² = 4²
(x – 6)² + (y – 21)² = 16

Question 43.
center: (- 3, 2), radius: 16

Solution:
(x + 3)² + (y – 2)² = 256

Explanation:
Given,
center: (- 3, 2), radius: 16
We know that,
(x – h)² + (y – k)² = r²
(x + 3)² + (y – 2)² = 16²
(x + 3)² + (y – 2)² = 256

Question 44.
center: (10, 7), radius: 3.5

Solution:
(x – 10)² + (y – 7)² = 12.25

Explanation:
Given,
center: (10, 7), radius: 3.5
We know that,
(x – h)² + (y – k)² = r²
(x – 10)² + (y – 7)² = 3.5²
(x – 10)² + (y – 7)² = 12.25

Question 45.
center: (0, 0), radius: 5.2

Solution:
x² + y² = 27.04

Explanation:
Given,
center: (0, 0), radius: 5.2
We know that,
(x – h)² + (y – k)² = r²
(x – 0)² + (y – 0)² = 5.2²
x² + y² = 27.04

Question 46.
The point (- 7, 1) is on a circle with center (- 7, 6). Write the standard equation of the circle.

Solution:
(x + 7)² + (y – 6)² = 25

Explanation:
Given,
The point (- 7, 1) is on a circle with center (- 7, 6).
We know that,
(x – h)² + (y – k)² = r²
r² = (-7 + 7)² + (6 – 1)²
r² = 5²
r = 5
So, radius is 5 and center is (-7, 6)
The standard equation of a circle is (x – (-7))² + (y – 6)² = 5²
(x + 7)² + (y – 6)² = 25

Question 47.
The equation of a circle is x² + y² – 12x + 8y + 48 = 0. Find the center and the radius of the circle. Then graph the circle.

Solution:
The radius of the circle is 2, the centre is (6, -4)

Explanation:
Given,
x² + y² – 12x + 8y + 48 = 0
x² – 12x + 36 + y² + 8y + 16 = 4
(x – 6)² + (y + 4)² = 2²
So, the radius of the circle is 2, the centre is (6, -4)

Question 48.
Prove or disprove that the point (4, – 3) lies on the circle centred at the origin and containing
the point (- 5, 0).

Solution:
The point (4, – 3) lies on the circle.

Explanation:
Given that the point (4, – 3) lies on the circle centered at the origin and containing
the point (- 5, 0).
By use the distance formula to find the radius of the circle with center (0, 0) and a point (-5, 0)
r = √(-5 – 0)² + (0 – 0)² = 5
The distance from the point (4, -3) to the center (0, 0)
d = √(4 – 0)² + (-3 – 0)² = √(16 +9) = 5
Since the radius of the circle is 5, the point lies on the circle.

Circles Chapter Test

Find the measure of each numbered angle in ⊙P. Justify your answer.

Question 1.

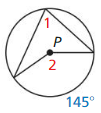
Solution:
m∠1 = 72.5°
m∠2 = 145°

Explanation:
Based on the information given in the above figure,
m∠1 = \(\frac { 145 }{ 2 } \)
m∠1 = 72.5°
m∠2 = 145°

Question 2.

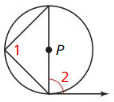
Solution:
m∠1 = 60°, m∠2 = 90°

Explanation:
Based on the information given in the above figure,
A tangent is perpendicular to diameter.
So, m∠2 = 90°
m∠1 = 60°

Question 3.

Solution:
m∠1 = 48°

Explanation:
Based on the information given in the above figure,
m∠1 = \(\frac { 96 }{ 2 } \)
m∠1 = 48°

Question 4.

Answer:

Use the diagram.

Question 5.
AG = 2, GD = 9, and BG = 3. Find GF.

Answer:

Question 6.
CF = 12, CB = 3, and CD = 9. Find CE.

Answer:

Question 7.
BF = 9 and CB = 3. Find CA

Answer:

Question 8.
Sketch a pentagon inscribed in a circle. Label the pentagon ABCDE. Describe the relationship between each pair of angles. Explain your reasoning.

a. ∠CDE and ∠CAE

Answer:

b. ∠CBE and ∠CAE

Answer:

Find the value of the variable. Justify your answer.

Question 9.

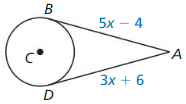
Solution:
x = 5

Explanation:
Based on the information given in the above figure,
5x – 4 = 3x + 6
5x – 3x = 6 + 4
2x = 10
x = 10/2
x = 5

Question 10.

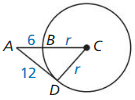
Solution:
r = 9

Explanation:
Based on the information given in the above figure,
(6 + r)² = 12² + r²
(6 + r)² is in the form of (a + b)²
36 + 12r + r² = 144 + r²
12r = 144 – 36
12r = 108
r = 108/12
r = 9

Question 11.
Prove or disprove that the point (2√2, – 1) lies on the circle centered at (0, 2) and containing the point (- 1, 4).

Solution:
Disproved.

Explanation:
Given that the point (2√2, – 1) lies on the circle centered at (0, 2) and containing the point (- 1, 4).
We consider the circle centered at the A(0, 2) and containing the point B(-1, 4).
AB = √(-1 – 0)² + (4 – 2)² = √1 + 4 = √5
The distance between centre A(0, 2) and P(2√2, – 1) is
AP = √(2√2 – 0)² + (-1 – 2)² = √8 + 9 = √17
AB ≠ AP
So, the point (2√2, – 1) dies not lie on the circle.

Prove the given statement.

Question 12.
\(\widehat{S T} \cong \widehat{R Q}\)

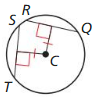
Answer:

Question 13.
\(\widehat{J M} \cong \widehat{L M}\)

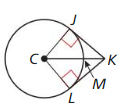
Answer:

Question 14.
\(\widehat{D G} \cong \widehat{F G}\)

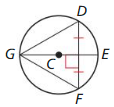
Answer:

Question 15.
A bank of lighting hangs over a stage. Each light illuminates a circular region on the stage. A coordinate plane is used to arrange the lights, using a corner of the stage as the origin. The equation (x – 13)² + (y – 4)² = 16 represents the boundary of the region illuminated by one of the lights. Three actors stand at the points A(11, 4), B(8, 5), and C(15, 5). Graph the given equation. Then determine which actors are illuminated by the light.

Solution:
The actors who stand at points A and C are illuminated by the light.

Explanation:
The equation (x – 13)² + (y – 4)²= 16 represents the standard equation of the circle with center (13, 4) and radius 4.
Graph the circle with center S(13, 4), radius 4.
Then graph the points A(11,4), B (8, 5), C(15,5) which represents the places where the actors stand.

From the graph, we can observe that points A and C inside the circle and point B is outside the circle.
Therefore, actors who stand at points A and C are illuminated by the light.

Question 16.
If a car goes around a turn too quickly, it can leave tracks that form an arc of a circle. By finding the radius of the circle, accident investigators can estimate the speed of the car.
Answer:

a. To find the radius, accident investigators choose points A and B on the tire marks. Then the investigators find the midpoint C of \(\overline{A B}\). Use the diagram to find the radius r of the circle. Explain why this method works.

Solution:
The radius r of the circle = 155.71 ft.

Explanation:
With reference to the above given figure,
AC = 130 ft, CD = 70 ft
CE = (r – 70) ft
r² = a² + b²
r²= 130²+ (r – 70)²
(r – 70)² is in the form of (a – b)²
r² = 16900 + r² – 140r + 4900
140r = 21,800
r = 21800/140
r = 155.71 ft

b. The formula S = 3.87√fr can be used to estimate a car’s speed in miles per hour, where f is the coefficient of friction and r is the radius of the circle in feet. If f = 0.7, estimate the car’s speed in part (a).

Solution:
The estimated car’s speed is 39.67 miles per hour.

Explanation:
Given,
f = 0.7,
With reference to the above given data,
S = 3.87√fr
S = 3.8 √(0.7 x 155.71)
S = 3.8 √108.997
S = 3.8 x 10.44
S = 39.67

Circles Cumulative Assessment

Question 1.
Classify each segment as specifically as possible.

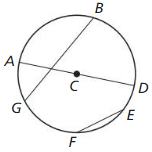
a. \(\overline{B G}\)

Solution:
\(\overline{B G}\) is a chord.

Explanation:
Based on the information given in the above figure,
\(\overline{B G}\) is a chord.
We know that,
The chord is a line segment that joins two points on the circumference of the circle.

b. \(\overline{C D}\)

Solution:
\(\overline{C D}\) is radius.

Explanation:
Based on the information given in the above figure,
\(\overline{C D}\) is radius.
We know that,
Radius of a circle is the distance from the center of the circle to any point on it’s circumference.

c. \(\overline{A D}\)

Solution:
\(\overline{A D}\) is diameter.

Explanation:
Based on the information given in the above figure,
\(\overline{AD}\) is diameter.
We know that,
The diameter is the length of the line through the center that touches two points on the edge of the circle.

d. \(\overline{F E}\)

Solution:
\(\overline{F E}\) is a chord.

Explanation:
Based on the information given in the above figure,
\(\overline{F E}\) is a chord.
We know that,
The chord is a line segment that joins two points on the circumference of the circle.

Question 2.
Copy and complete the paragraph proof.

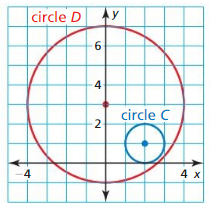
Given Circle C with center (2, 1) and radius 1,
Circle D with center (0, 3) and radius 4
Prove Circle C is similar to Circle D.

Map Circle C to Circle C’ by using the _________ (x, y) → _________ so that Circle C’ and Circle D have the same center at (____, _____). Dilate Circle C’ using a cellIer of dilation (_____, _____) and a scale factor of _____ . Because there is a _________ transformation that maps Circle C to Circle D, Circle C is __________ Circle D.

Solution:
Based on the information given in the above figure,
Map Circle C to Circle C’ by using the scale factor (x, y) → (0, 3)
So, that Circle C’ and Circle D have the same center at (2, 1).
Dilate Circle C’ using a celler of dilation (2, 1) and a scale factor of circles.
Because there is a transformation that maps Circle C to Circle D, Circle C is similar to Circle D.

Question 3.
Use the diagram to write a proof.

Given ∆JPL ≅ ∆NPL
\(\overline{P K}\) is an altitude of ∆JPL
\(\overline{P M}\) is an altitude ∆NPL
Prove ∆PKL ~ ∆NMP

Solution:
∆PKL ~ ∆NMP

Explanation:
With reference to the data given in the above figure,
∆JPL is similar to ∆NPL.
PK is the altitude of ∆JPL and PM is an altitude of ∆NPL.
We know that,
Altitude is a line drawn from one vertex to the opposite site.
It is perpendicular to the side.
So, ∆PKL is similar to ∆NMP.

Question 4.
The equation of a circle is x² + y² + 14x – 16y + 77 = 0. What are the center and radius of the circle?
(A) center: (14, – 16). radius: 8.8
(B) center: (- 7, 8), radius: 6
(C) center (- 14, 16), radius: 8.8
(D) center: (7, – 8), radius: 5.2

Solution:
(B) center: (- 7, 8), radius: 6

Explanation:
With reference to the data given in the above figure,
x² + y² + 14x – 16y + 77 = 0
x² + 14x + 49 + y² – 16y + 64 = 36
(x + 7)² + (y – 8)² = 6²
So, the center is (-7, 8) and radius is 6.

Question 5.
The coordinates of the vertices of a quadrilateral are W(- 7, – 6), X(1, – 2), Y(3, – 6) and Z(- 5, – 10). Prove that quadrilateral WXYZ is a rectangle.

Solution:
Proved.

Explanation:
Given,
The coordinates of the vertices of a quadrilateral are W(- 7, – 6), X(1, – 2), Y(3, – 6) and Z(- 5, – 10).
WY = √(-7 – 3)² + (-6 + 6)² = √(-10)² = 10
ZX = √(1 + 5)² + (-2 + 10)² = √6² + 8² = 10
WY = ZX,
Hence, the diagonals are congruent.
By using the slope formula to find the slopes of diagonals,
Slope of WY = \(\frac { -6 + 6 }{ -7 – 3 } \) = 0
Slope of ZX = \(\frac { -2 + 10 }{ 1 + 5 } \) = \(\frac { 4 }{ 3 } \)
Hence, the product of slopes of diagonals is 0 and the diagonals are not perpendicular.
Therefore, the quadrilateral WXYZ is a rectangle.

Question 6.
Which angles have the same measure as ∠ACB? Select all that apply.
im – 295
∠DEF ∠JGK ∠KGL ∠LGM ∠MGJ
∠QNR ∠STV ∠SWV ∠VWU ∠XYZ

Solution:
∠VWU

Question 7.
Classify each related conditional statement based on the conditional statement
“If you are a soccer player. then you are an athlete.”

a. If you are not a soccer player, then you are not an athlete.

Solution:
False

Explanation:
A statement written in the if-then form is known as conditional statement.
Given,
“If you are a soccer player. then you are an athlete.”
So, If you are not a soccer player, then you are not an athlete condition does not apply.

b. If you are an athlete, then you are a soccer player.

Solution:
False

Explanation:
A statement written in the if-then form is known as conditional statement.
Given,
“If you are a soccer player. then you are an athlete.”
So, If you are an athlete, then you are a soccer player condition does not apply.

c. You are a soccer player if and only if you are an athlete.

Solution:
True

Explanation:
A statement written in the if-then form is known as conditional statement.
Given,
“If you are a soccer player. then you are an athlete.”
So, you are a soccer player if and only if you are an athlete condition apply based on given statement.

d. If you are not an athlete, then you are not a soccer player.

Solution:
False

Explanation:
A statement written in the if-then form is known as conditional statement.
Given,
“If you are a soccer player. then you are an athlete.”
So, If you are not an athlete, then you are not a soccer player condition does not apply.

Question 8.
Your friend claims that the quadrilateral shown can be inscribed in a circle. Is your friend correct? Explain our reasoning.

Solution:
My friend is correct.

Explanation:
We know that,
If the sum of any two angles is 180°, then the quadrilateral is inscribed in a circle.
With reference to the information given in the above figure,
70° + 110° = 180°, 110° + 70°= 180°
So, my friend is correct.