Learn how to solve essential lessons about similarity from Big Ideas Math Geometry Answers Chapter 8 Similarity Guide. Get the pdf link of Big Ideas Math Book Geometry Answer Key Chapter 8 Similarity from this page. Get Big Ideas Math Geometry Answers Chapter 8 Similarity for the lessons, practice questions, Exercises, chapter test, reviews, cumulative assessments, etc. Learn the concepts in depth and try to solve the problems in different and simple methods with the help of BIM Geometry Ch 8 Similarity Solution Key. So, refer to our Big Ideas Math Book Geometry Answer Key Chapter 8 Similarity and score the highest marks in the exams.
Big Ideas Math Book Geometry Answer Key Chapter 8 Similarity
Find step-by-step solutions for all the Questions from BIM Geometry Book Solutions. Learn the subject thoroughly by using BIM Geometry Ch 8 Similarity Answers. Check out the list of the topics covered in Similarity is Similar Polygons, Proving Triangle Similarity by AA, Similarity by SSS, SAS, and Proportionality theorems. All the solutions are prepared by math professionals. Hit the below direct links and refer to the Big Ideas Math Book Geometry Answer Key Chapter 8 Similarity.
- Similarity Maintaining Mathematical Proficiency – Page 415
- Similarity Mathematical Practices – Page 416
- 8.1 Similar Polygons – Page 417
- Lesson 8.1 Similar Polygons – Page (418-426)
- Exercise 8.1 Similar Polygons – Page (423-426)
- 8.2 Proving Triangle Similarity by AA – Page 427
- Lesson 8.2 Proving Triangle Similarity by AA – Page (428-432)
- Exercise 8.2 Proving Triangle Similarity by AA – Page (431-432)
- 8.1 & 8.2 Quiz – Page 434
- 8.3 Proving Triangle Similarity by SSS and SAS – Page 435
- Lesson 8.3 Proving Triangle Similarity by SSS and SAS – Page (436-444)
- Exercise 8.3 Proving Triangle Similarity by SSS and SAS – Page (441-444)
- 8.4 Proportionality Theorems – Page 445
- Lesson 8.4 Proportionality Theorems – Page (446-452)
- Exercise 8.4 Proportionality Theorems – Page (450-452)
- Similarity Chapter Review – Page (454-456)
- Similarity Chapter Test – Page 457
- Similarity Cumulative Assessment – Page (458-459)
Similarity Maintaining Mathematical Proficiency
Tell whether the ratios form a proportion.
Question 1.
\(\frac{5}{3}, \frac{35}{21}\)
Answer:
Yes, the above ratios \(\frac{5}{3}, \frac{35}{21}\) form a proportion.
Explanation:
A proportion means two ratios are equal.
Given, \(\frac{5}{3}, \frac{35}{21}\)
Cross multiply the products of given ratio,
21 x 5 = 105 = 35 x 3
Hence, \(\frac{5}{3}, \frac{35}{21}\) form a proportion.
Question 2.
\(\frac{9}{24}, \frac{24}{64}\)
Answer:
Yes, the above ratios \(\frac{9}{24}, \frac{24}{64}\) form a proportion.
Explanation:
When the product of two ratios are equal, then it forms a proportion.
Given, \(\frac{9}{24}, \frac{24}{64}\)
Cross multiply the products of given ratio,
24 x 24 = 576 = 64 x 9
Therefore, the ratios \(\frac{9}{24}, \frac{24}{64}\) form a proportion.
Question 3.
\(\frac{8}{56}, \frac{6}{28}\)
Answer:
No, the ratios \(\frac{8}{56}, \frac{6}{28}\) do not form a proportion.
Explanation:
When the product of two ratios are equal, then it forms a proportion.
Given, \(\frac{8}{56}, \frac{6}{28}\)
56 x 6 = 336, 28 x 8 = 224
Therefore, the above ratios \(\frac{8}{56}, \frac{6}{28}\) do not form a proportion.
Question 4.
\(\frac{18}{4}, \frac{27}{9}\)
Answer:
No, the ratios \(\frac{18}{4}, \frac{27}{9}\) do not form a proportion.
Explanation:
The cross product of two ratios are equal, then it forms a proportion.
Given, \(\frac{18}{4}, \frac{27}{9}\)
9 x 18 = 162, 27 x 4 = 108
So, the ratios \(\frac{18}{4}, \frac{27}{9}\) do not form a proportion.
Question 5.
\(\frac{15}{21}, \frac{55}{77}\)
Answer:
Yes, the given ratios \(\frac{15}{21}, \frac{55}{77}\) form a proportion.
Explanation:
A proportion means two ratios are equal.
Given, \(\frac{15}{21}, \frac{55}{77}\)
Cross multiply the products of given ratio,
15 x 77 = 1155, 55 x 21 = 1155
Therefore, the ratios \(\frac{15}{21}, \frac{55}{77}\) form a proportion.
Question 6.
\(\frac{26}{8}, \frac{39}{12}\)
Answer:
Yes, the given ratios \(\frac{26}{8}, \frac{39}{12}\) form a proportion.
Explanation:
A proportion means two ratios are equal.
Given, \(\frac{26}{8}, \frac{39}{12}\)
Cross multiply the products of given ratio,
26 x 12 = 312, 39 x 8 = 312
So, the given ratios \(\frac{26}{8}, \frac{39}{12}\) form a proportion.
Find the scale factor of the dilation.
Question 7.
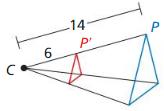
Answer:
k = \(\frac { 3 }{ 7 } \)
Explanation:
Knowing the ratio of the size of the new image to the size of the old image is known as scale factor of dilation.
When we observe the center of dilation is a fixed point in the plane.
So, based on the scale factor and the center of dilation, we decide the dilation transformation.
If the scale factor is more than 1, then the image stretches.
Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
The scale factor k = \(\frac { CP’ }{ CP } \)
= \(\frac { 6 }{ 14 } \)
= \(\frac { 3 }{ 7 } \)
Question 8.
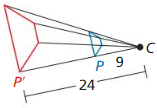
Answer:
k = \(\frac { 3 }{ 8 } \)
Explanation:
Dilation is the process of resizing an object by a certain scale factor.
Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
The scale factor k = \(\frac { CP }{ CP’ } \)
= \(\frac { 9 }{ 24 } \)
= \(\frac { 3 }{ 8 } \)
Question 9.
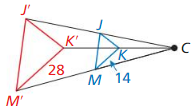
Answer:
k = \(\frac { 1 }{ 2 } \)
Explanation:
Knowing the ratio of the size of the new image to the size of the old image is known as scale factor of dilation.
Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
The scale factor k = \(\frac { MK }{ M’K’ } \)
= \(\frac { 14 }{ 28 } \)
= \(\frac { 1 }{ 2 } \)
Question 10.
ABSTRACT REASONING
If ratio X and ratio Y form a proportion and ratio Y and ratio Z form a proportion, do ratio X and ratio Z form a proportion? Explain our reasoning.
Answer:
Yes, ratio X and ratio Z form a proportion.
Explanation:
If ratios are proportional means they are equal.
Ratio X and ratio Y form a proportion means X = Y
Ratio Y and ratio Z form a proportion means Y = Z
From the above two equations, we can say that X = Z
So, ratio X and ratio Z also form a proportion.
Similarity Mathematical Practices
Monitoring Progress
Question 1.
Find the perimeter and area of the image when the trapezoid is dilated by a scale factor of
(a) 2, (b) 3, and (c) 4.
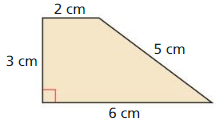
Answer:
(a) Perimeter is 32 centimeter, area is 48 square centimeter.
(b) Perimeter is 48 centimeter, the area is 108 square centimeter.
(c) Perimeter is 64 centimeter, the area is 192 square centimeter.
Explanation:
To find the perimeter of trapezoid add lengths of all four sides.
P = a + b + c + d
The perimeter of trapezoid P = 2 + 5 + 6 + 3 = 16 cm
To find the area of a trapezoid (A) = ½ (a + b) h,
where ‘a’ and ‘b’ are the bases (parallel sides) and ‘h’ is the height.
Area of trapezoid A = \(\frac { (2 + 6)3 }{ 2 } \)
= \(\frac { 3(8) }{ 2 } \)
= \(\frac { 24 }{ 2 } \)
= 12 sq cm
(a) If scale factor k = 2, then
Perimeter = kP
= 2 x 16 = 32 centimeters.
Area = k²A
= 2² x 12
= 4 x 12
= 48 sq cm.
(b) If scale factor k = 3, then,
Perimeter = kP
= 3 x 16 = 48 cm
Area = k²A
= 3² x 12
= 9 x 12
= 108 sq cm.
(c) If scale factor k = 4, then
Perimeter = kP
= 4 x 16
= 64 cm
Area = k²A
= 4² x 12
= 16 x 12
= 192 sq cm.
Question 2.
Find the perimeter and area of the image when the parallelogram is dilated by a scale factor of
(a) 2, (b) 3, and (c) \(\frac{1}{2}\)
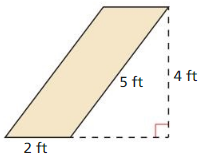
Answer:
(a) Perimeter is 28 ft, area is 32 sq ft
(b) Perimeter is 42 ft, area is 72 sq ft
(c) Perimeter is 7 ft, area is 2 sq ft
Explanation:
Perimeter of parallelogram (P) = 2 x (a + b)
Where ‘b’ is the base and ‘a’ is the side.
Perimeter of parallelogram = 2(2 + 5)
= 7 x 2
= 14 ft
Aera of parallelogram (A) = b x h
Where ‘b’ is the base and ‘h’ is the height.
Area of the parallelogram = 2 x 4
= 8 sq ft
(a) If scale factor k = 2, then
Perimeter = kP
= 2 x 14
= 28 ft
Area = k²A
= 2² x 8
= 4 x 8
= 32 sq ft.
(b) If scale factor k = 3, then
Perimeter = kP
= 3 x 14
= 42 ft
Area = k²A
= 3² x 8
= 72 sq ft
(c) If scale factor k = \(\frac{1}{2}\), then
Perimeter = kP
= \(\frac{1}{2}\) x 14
= 7 ft
Area = k²A
= \(\frac{1}{2²}\) x 8
= \(\frac{1}{4}\) x 8
= 2 sq ft.
Question 3.
A rectangular prism is 3 inches wide, 4 inches long, and 5 inches tall. Find the surface area and volume of the image of the prism when it is dilated by a scale factor of
(a) 2, (b) 3, and (c) 4.
Answer:
(a) Surface area is 376 sq in, volume is 480 cubic in
(b) Surface area is 846 sq in, volume is 1620 cubic in
(c) Surface area is 1504 sq in, volume is 3840 cubic in
Explanation:
The surface area of the rectangular prism (A) = 2 (lh +wh + lw ) Square units.
where ‘l’ is the length, ‘h’ is the height and ‘w’ is the width.
The surface area of the rectangular prism A = 2(3 x 4 + 4 x 5 + 5 x 3)
= 2(12 + 20 + 15)
= 2(47)
= 94 sq in.
Volume of the rectangular prism (V) = l x w x h
where ‘l’ is the length, ‘h’ is the height and ‘w’ is the width.
V = 3 x 4 x 5
= 60 in³
(a) If the scale factor k = 2, then
Surface Area = k²A
= 2² x 94
= 4 x 94
= 376 sq in
Volume = k³V
= 2³ x 60
= 8 x 60
= 480 cubic in.
(b) If the scale factor k = 3, then
Surface Area = k²A
= 3² x 94
= 9 x 94
= 846 sq in.
Volume = k³V
= 3³ x 60
= 27 x 60
= 1620 cu in.
(c) If the scale factor k = 4, then
Surface Area = k²A
= 4² x 94
= 16 x 94
= 1504 sq in.
Volume = k³V
= 4³ x 60
= 64 x 60
= 3840 cu in.
8.1 Similar Polygons
Exploration 1
Comparing Triangles after a Dilation
Work with a partner: Use dynamic geometry software to draw any ∆ABC. Dilate ∆ABC to form a similar ∆A’B’C’ using an scale factor k and an center of dilation.
a. Compare the corresponding angles of ∆A’B’C and ∆ABC.
Answer:
b. Find the ratios of the lengths of the sides of ∆A’B’C’ to the lengths of the corresponding sides of ∆ABC. What do you observe?
Answer:
c. Repeat parts (a) and (b) for several other triangles, scale factors, and centers of dilation. Do you obtain similar results?
Answer:
Exploration 2
Comparing Triangles after a Dilation
Work with a partner: Use dynamic geometry Software to draw any ∆ABC. Dilate ∆ABC to form a similar ∆A’B’C’ using any scale factor k and any center of dilation.
a. Compare the perimeters of ∆A’B’C and ∆ABC. What do you observe?
Answer:
b. Compare the areas of ∆A’B’C’ and ∆ABC. What do you observe?
Answer:
c. Repeat parts (a) and (b) for several other triangles, scale factors, and centers of dilation. Do you obtain similar results?
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:
Communicate Your Answer
Question 3.
How are similar polygons related?
Answer:
if two polygons are similar means they have the same shape, corresponding angles are congruent and the ratios of lengths of their corresponding sides are equal. The common ratio is called the scale factor.
Question 4.
A ∆RST is dilated by a scale factor of 3 to form ∆R’S’T’. The area of ∆RST is 1 square inch. What is the area of ∆R’S’T’?
Answer:
Area of ∆R’S’T’ = 9 sq in.
Explanation:
Given that, ∆RST is dilated by a scale factor of 3 to form ∆R’S’T’
Area of ∆RST = 1 sq inch
Scale factor k = 3
Area of ∆R’S’T’ = k² x Area of ∆RST
= 3² x 1
= 9 x 1
= 9 sq in.
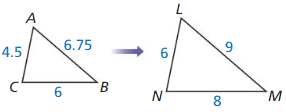
Lesson 8.1 Similar Polygons
Monitoring Progress
Question 1.
In the diagram, ∆JKL ~ ∆PQR. Find the scale factor from ∆JKL to ∆PQR. Then list all pairs of congruent angles and write the ratios of the corresponding side lengths in a statement of proportionality.
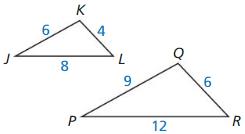
Answer:
The pairs of congruent angles are ∠K = ∠Q; ∠J = ∠P; ∠ L = ∠R
The scale factor is \(\frac { 3 }{ 2 } \)
The ratios of the corresponding side lengths are \(\frac { PQ }{ JK } = \frac { PR }{ JL } = \frac { QR }{ LK } \)
Explanation:
Given that, ∆JKL ~ ∆PQR as shown in the above figure.
Two or more angles that are identical to each other are known as congruent angles.
So, the pairs of congruent angles are ∠K = ∠Q, ∠J = ∠P, ∠ L = ∠R
To find the scale factor,
Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
Scale factor = \(\frac { PQ }{ JK }
= \frac { 9 }{ 6 } \)
= \(\frac { 3 }{ 2 } \),
Scale factor = \(\frac { PR }{ JL }
= [latex]\frac { 12 }{ 8 } \)
= \(\frac { 3 }{ 2 } \),
Scale factor = \(\frac { QR }{ LK }
= [latex]\frac { 6 }{ 4 } \)
= \(\frac { 3 }{ 2 } \)
So, the scale factor is \(\frac { 3 }{ 2 } \)
Question 2.
Find the value of x.
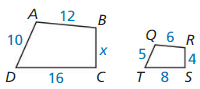
ABCD ~ QRST
Answer:
x = 2
Explanation:
Given, ABCD ~ QRST
When we observe the above figures,
the triangles are similar, so corresponding side lengths are proportional to each other.
\(\frac { RS }{ BC } \) = \(\frac { AB }{ QR } \)
\(\frac { 4 }{ x } \) = \(\frac { 12 }{ 6 } \)
\(\frac { 4 }{ x } \) = 2
4 = 2x
x = 2
Question 3.
Find KM
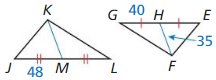
∆JKL ~ ∆EFG
Answer:
KM = 42
Explanation:
From the above given figures, ∆JKL ~ ∆EFG
Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
Scale factor = \(\frac { JM }{ GH } \)
= \(\frac { 48 }{ 40 } \)
= \(\frac { 6 }{ 5 } \)
Because the ratio of the lengths of the altitudes in similar triangles is equal to the scale factor,
the proportion are:
\(\frac { KM }{ HF } \) = \(\frac { 6 }{ 5 } \)
\(\frac { KM }{ 35 } \) = \(\frac { 6 }{ 5 } \)
KM = \(\frac { 6 }{ 5 } \) x 35
KM = 42
Question 4.
The two gazebos shown are similar pentagons. Find the perimeter of Gazebo A.
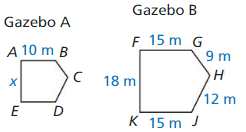
Answer:
Perimeter of Gazebo A = 46 m
Explanation:
Given, two gazebos are similar pentagons as shown above.
Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
Scale factor = \(\frac { AB }{ FG } \)
= \(\frac { 10 }{ 15 } \)
= \(\frac { 2 }{ 3 } \)
So, \(\frac { AE }{ FK } \) = \(\frac { 2 }{ 3 } \)
\(\frac { x }{ 18 } \) = \(\frac { 2 }{ 3 } \)
Cross multiply the products.
3x = 36
x = \(\frac { 36 }{ 2 } \)
x = 12
\(\frac { ED }{ KJ } \) = \(\frac { 2 }{ 3 } \)
\(\frac { ED }{ 15 } \) = \(\frac { 2 }{ 3 } \)
Cross multiply the products.
ED = \(\frac { 30 }{ 3 } \)
ED = 10
\(\frac { DC }{ JH } \) = \(\frac { 2 }{ 3 } \)
\(\frac { DC }{ 12 } \) = \(\frac { 2 }{ 3 } \)
Cross multiply the products.
DC = \(\frac { 24 }{ 3 } \)
DC = 8
\(\frac { BC }{ GH } \) = \(\frac { 2 }{ 3 } \)
\(\frac { BC }{ 9 } \) = \(\frac { 2 }{ 3 } \)
Cross multiply the products.
BC = \(\frac { 18 }{ 3 } \)
BC = 6
Therefore, perimeter = 6 + 8 + 10 + 12 + 10 = 46
Question 5.
In the diagram, GHJK ~ LMNP. Find the area of LMNP.
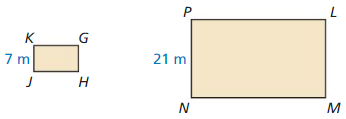
Area of GHJK = 84m2
Answer:
Area of LMNP = 756 m2
Explanation:
Given, GHJK ~ LMNP
As shapes are similar, their corresponding side lengths are proportional to each other.
We know that,
Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
Scale Factor k = \(\frac { NP }{ JK } \)
= \(\frac { 21 }{ 7 } \)
= 3 m
Area of LMNP = k² x Area of GHJK
Given, Area of GHJK = 84m2
= 3² x 84
= 756 m2
Question 6.
Decide whether the hexagons in Tile Design 1 are similar. Explain.
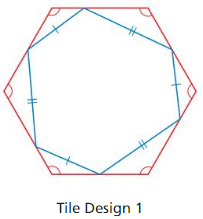
Answer:
Question 7.
Decide whether the hexagons in Tile Design 2 are similar. Explain.
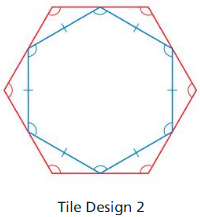
Answer:
Exercise 8.1 Similar Polygons
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
For two figures to be similar, the corresponding angles must be ____________ . and the corresponding side lengths must be _____________ .
Answer:

Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.
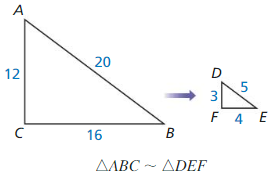
What is the scale factor?
Answer:
\(\frac{1}{4}\)
Explanation:
Given, ∆ABC ~ ∆DEF
We know that,
Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
Scale Factor = \(\frac{image-length}{actual-length}\)
= \(\frac{3}{12}\)= \(\frac{4}{16}\)= \(\frac{5}{20}\)
= \(\frac{1}{4}\)
What is the ratio of their areas?
Answer:
Ratio of the area 1 : 16
Explanation:

What is the ratio of their corresponding side lengths?
Answer:
1 : 4
Explanation:
The ratio of their corresponding side lengths 1 : 4
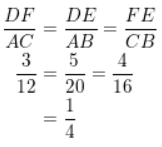
What is the ratio of their perimeters?
Answer:
The ratio of their perimeters 1 : 4
Explanation:

Monitoring Progress and Modeling with Mathematics
In Exercises 3 and 4, find the scale factor. Then list all pairs of congruent angles and write the ratios of the corresponding side lengths in a statement of proportionality.
Question 3.
∆ABC ~ ∆LMN
Answer:
Question 4.
DEFG ~ PQRS
Answer:

In Exercises 5-8, the polygons are similar. Find the value of x.
Question 5.
Answer:
x = 30
Explanation:
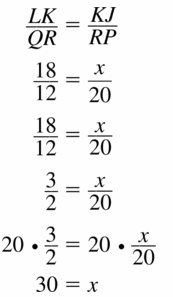
Question 6.
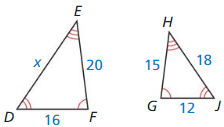
Answer:
x = 20
Explanation:
From the above given figures, both the triangles are similar.
\(\frac { DF }{ GJ } \) = \(\frac { DE }{ GH } \)
\(\frac { 16 }{ 12 } \) = \(\frac { x }{ 15 } \)
x = \(\frac { 16 x 15 }{ 12 } \) = \(\frac { 240 }{ 12 } \)
x = 20
Question 7.
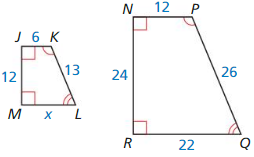
Answer:
x = 11
Explanation:
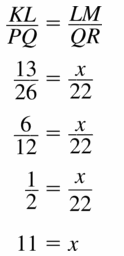
Question 8.
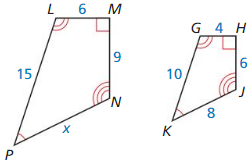
Answer:
x = 12
Explanation:
From the above given figures, both the images are similar.
\(\frac { PN }{ KJ } \) = \(\frac { MN }{ JH } \)
\(\frac { x }{ 8 } \) = \(\frac { 9 }{ 6 } \)
x = \(\frac { 9 x 8 }{ 6 } \) = \(\frac { 72 }{ 6 } \)
x = 12
In Exercises 9 and 10, the black triangles are similar. Identify the type of segment shown in blue and find the value of the variab1e.
Question 9.
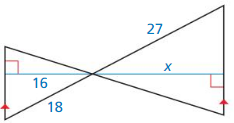
Answer:
x = 24
Explanation:

Question 10.
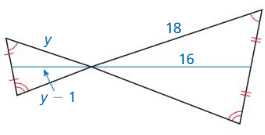
Answer:
y = 9
Explanation:
the ratio of the size of the new image to the size of the old image is known as scale factor dilation.
The center of dilation is a fixed point in the plane as shown above.
\(\frac { y }{ 18 } \) = \(\frac { y – 1 }{ 16 } \)
18(y – 1) = 16y
18y – 18 = 16y
18y – 16y = 18
2y = 18
y = 9
In Exercises 11 and 12, RSTU ~ ABCD. Find the ratio of their perimeters.
Question 11.
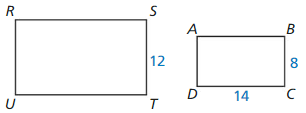
Answer:
The ratio of perimeter is \(\frac { 2 }{ 3 } \).
Explanation:
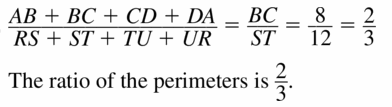
Question 12.
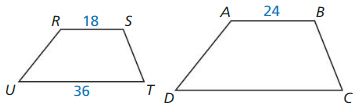
Answer:
The ratio of perimeter is \(\frac { 3 }{ 4 } \).
Explanation:
\(\frac { RS + ST + TU + UR }{ AB + BC + CD + DA } \)
= \(\frac { RS }{ AB } \)
= \(\frac { 18 }{ 24 } \)
The ratio of perimeter is \(\frac { 3 }{ 4 } \).
In Exercises 13-16, two polygons are similar. The perimeter of one polygon and the ratio of the corresponding side lengths are given. Find the perimeter of the other polygon.
Question 13.
perimeter of smaller polygon: 48 cm: ratio: \(\frac{2}{3}\)
Answer:
Perimeter of larger polygon is 72 centimeters.
Explanation:
Given,
perimeter of smaller polygon: 48 cm: ratio: \(\frac{2}{3}\)
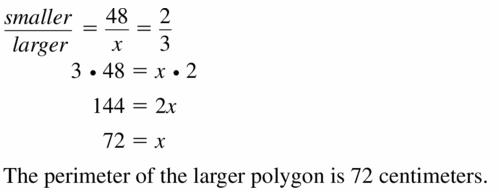
Question 14.
perimeter of smaller polygon: 66 ft: ratio: \(\frac{3}{4}\)
Answer:
The perimeter of smaller polygon is 88 ft.
Explanation:
Given,
perimeter of smaller polygon: 66 ft: ratio: \(\frac{3}{4}\)
\(\frac { smaller }{ larger } \) = \(\frac { 66 }{ x } \)
66 = \(\frac{3}{4}\)
66 x 4 = 3x
3x = 264
x = \(\frac { 264 }{ 3 } \) = 88 ft.
Question 15.
perimeter of larger polygon: 120 yd: ratio: \(\frac{1}{6}\)
Answer:
The perimeter of smaller polygon is 20 yards.
Explanation:
Given,
perimeter of larger polygon: 120 yd: ratio: \(\frac{1}{6}\)
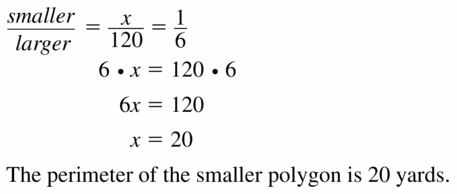
Question 16.
perimeter of larger polygon: 85 m; ratio: \(\frac{2}{5}\)
Answer:
The perimeter of smaller polygon is 34 m.
Explanation:
Given,
perimeter of larger polygon: 85 m; ratio: \(\frac{2}{5}\)
\(\frac { smaller }{ larger } \) = \(\frac { x }{ 85 } \)
85 = \(\frac{2}{5}\)
85 x 2 = 5x
5x = 170
x = \(\frac { 170 }{ 5 } \) = 34m.
Question 17.
MODELING WITH MATHEMATICS
A school gymnasium is being remodeled. The basketball court will be similar to an NCAA basketball court, which has a length of 94 feet and a width of 50 feet. The school plans to make the width of the new court 45 feet. Find the perimeters of ail NCAA court and of the new court in the school.
Answer:
The perimeter of new court is 259.2 ft.
Explanation:
Given,
The basketball court will be similar to an NCAA basketball court, which has a length of 94 feet and a width of 50 feet

Question 18.
MODELING WITH MATHEMATICS
Your family has decided to put a rectangular patio in your backyard. similar to the shape of your backyard. Your backyard has a length of 45 feet and a width of 20 feet. The length of your new patio is 18 feet. Find the perimeters of your backyard and of the patio.
Answer:
Perimeter of the backyard is 130 ft.
Perimeter of patio is 52 ft.
Explanation:
Draw a rectangle to represent the patio and a larger rectangle backyard and its going to similar figures.
Given, backyard has a length of 45 feet and a width of 20 feet.
The length of your new patio is 18 feet.
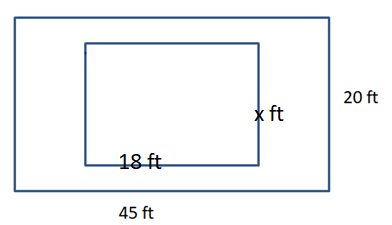
Perimeter of a rectangle = 2 (l + b)
Where ‘l; is the length and ‘b’ is the breadth.
Perimeter of backyard = 2(45 + 20)
= 2 x 65
= 130 ft
Scale factor = \(\frac { 18 }{ 45 } \)
= \(\frac { 2 }{ 5 } \)
So, \(\frac { perimeter of patio }{ perimeter of backyard }\) = \(\frac { 2 }{ 5 } \)
Cross multiply the products of the ratios,
\(\frac { perimeter of patio }{ 130 } \) = \(\frac { 2 }{ 5 } \)
Perimeter of patio = \(\frac { 260 }{ 5 } \)
= 52 ft
In Exercises 19-22, the polygons are similar. The area of one polygon is given. Find the area of the other polygon.
Question 19.
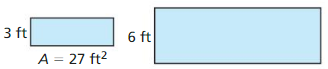
Answer:
108 sq ft.
Explanation:

Question 20.
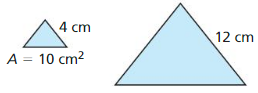
Answer:
Area of the larger triangle is 90 cm²
Explanation:
From the above given figures,
we know that the triangles are similar.
Area of triangle = 1/2 × base × height.
Ratio of the triangles,
\(\frac { 10 }{ A } \) = (\(\frac { 4 }{ 12 } \))²
\(\frac { 10 }{ A } \) = \(\frac { 1 }{ 9 } \)
A = 10 x 9
A = 90
Question 21.
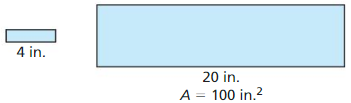
Answer:
4 sq in.
Explanation:
Given, two similar rectangles.

Question 22.
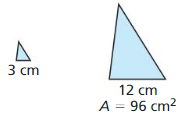
Answer:
Area of smaller triangle = 6 sq cm.
Explanation:
From the above figures, we know that the triangles are similar.
\(\frac { A }{ 96 } \) = (\(\frac { 3 }{ 12 } \))²
\(\frac { A }{ 96 } \) = \(\frac { 1 }{ 16 } \)
16A = 96
A = \(\frac { 96 }{ 16 } \)
A = 6 sq cm.
Question 23.
ERROR ANALYSIS
Describe and correct the error in finding the perimeter of triangle B. The triangles are similar.
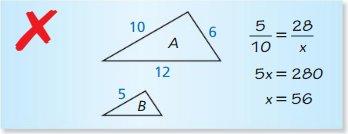
Answer:
x = 14
Explanation:

Question 24.
ERROR ANALYSIS
Describe and correct the error in finding the area of triangle B. The triangles are similar.
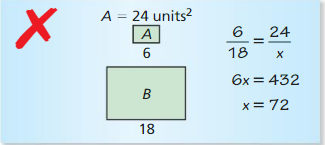
Answer:
x = 216
Explanation:
From the above information,
we observe that the first ratio has a side of A over the side length of B,
the square of the second ratio should have the area of B over the area of A.
\(\frac { 24 }{ x } \) = (\(\frac { 6 }{ 18 } \))²
\(\frac { 24 }{ x } \) = \(\frac { 1 }{ 9 } \)
x = 24 x 9
x = 216
In Exercises 25 and 26, decide whether the red and blue polygons are similar.
Question 25.
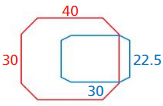
Answer:
No, the given polygons are not similar.
Explanation:
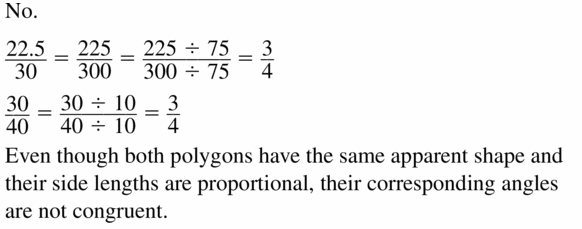
Question 26.
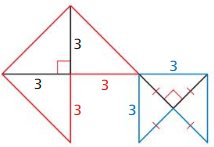
Answer:
Yes, the given polygons are similar.
Explanation:
From the above information,
we observe that both shapes are apparent and their side lengths are proportional to each other.
Even we find that the corresponding angles are also congruent.
Question 27.
REASONING
Triangles ABC and DEF are similar. Which statement is correct? Select all that apply.
(A) \(\frac{B C}{E F}=\frac{A C}{D F}\)
(B) \(\frac{A B}{D E}=\frac{C A}{F E}\)
(C) \(\frac{A B}{E F}=\frac{B C}{D E}\)
(D) \(\frac{C A}{F D}=\frac{B C}{E F}\)
Answer:
![]()
ANALYZING RELATIONSHIPS
In Exercises 28 – 34, JKLM ~ EFGH.
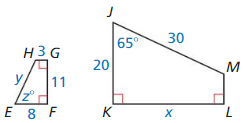
Question 28.
Find the scale factor of JKLM to EFGH.
Answer:
k = \(\frac {2}{5} \)
Explanation:
From the above given figures,
we observe that both the polygons JKLM ~ EFGH.
So, scale factor = \(\frac { EF }{ JK } \) =\(\frac {8}{20} \)
k = \(\frac {2}{5} \)
Question 29.
Find the scale factor of EFGH to JKLM.
Answer:
k = \(\frac {5}{2} \)
Explanation:
From the above given figures,
we observe that both the polygons JKLM ~ EFGH.

Question 30.
Find the values of x, y, and z.
Answer:
x = \(\frac { 55 }{ 2 } \)
y = 12
z = 65°
Explanation:
From the above given figures,
we observe that both the polygons JKLM ~ EFGH.
\(\frac {KL}{GF} \) = \(\frac {x}{11} \) = \(\frac {5}{2} \)
Cross multiply the products of the ratios.
2x = 55
x = \(\frac {55}{2} \)
\(\frac { MJ }{ HE } \) = \(\frac { 30 }{ y } \) = \(\frac { 5 }{ 2 } \)
Cross multiply the products of the ratios.
5y = 60
y = 12
So, z is given in the figure as 65°
Question 31.
Find the perimeter of each polygon.
Answer:
34 units.
Explanation:
To find the perimeter add the lengths of all sides.
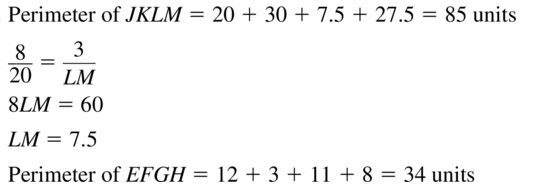
Question 32.
Find the ratio of the perimeters of JKLM to EFGH.
Answer:
The perimeter of JKLM : Perimeter of EFGH = 85 : 34
Explanation:
First find the perimeter of the polygons, then find the ratios.
To find the perimeter add the lengths of all sides.
Perimeter of JKLM = 20 + 30 + 7.5 + 27.5
P = 85 units.
Perimeter of EFGH = 12 + 3 + 11 + 8
P = 34 units.
So, the ratios of JKLM and EFGH are 85 : 34
Question 33.
Find the area of each polygon.
Answer:
Area of EFGH = 60.5 sq units.
Area of JKLM = 378.125 sq units.
Explanation:
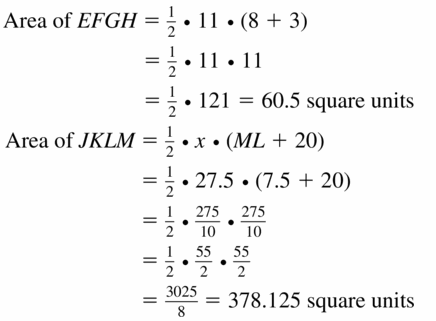
Question 34.
Find the ratio of the areas of JKLM to EFGH.
Answer:
Area of JKLM : Area of EFGH = 378.125 : 60.5 = 25 : 4
Question 35.
USING STRUCTURE
Rectangle A is similar to rectangle B. Rectangle A has side lengths of 6 and 12. Rectangle B has a side length of 18. What are the possible values for the length of the other side of rectangle B? Select all that apply.
(A) 6
(B) 9
(C) 24
(D) 36
Answer:
Option B and D
Explanation:
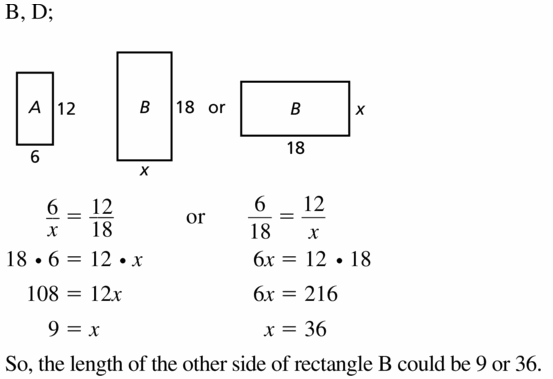
Question 36.
DRAWING CONCLUSIONS
In table tennis, the table is a rectangle 9 feet long and 5 feet wide. A tennis Court is a rectangle 78 feet long and 36 feet wide. Are the two surfaces similar? Explain. If so, find the scale factor of the tennis court to the table.

Answer:
No, the tennis table and the tennis court are not similar.
Explanation:
Given, the tennis table is a rectangle 9 feet long and 5 feet wide.
A tennis Court is a rectangle 78 feet long and 36 feet wide.
We know that, if two figures are similar then their angles are congruent and sides are proportional.
If the tennis court and table are similar then,
\(\frac { length of table }{ length of court } \) = \(\frac { width of table }{ width of court } \)
\(\frac { 9 }{ 78 } \) = \(\frac { 5 }{ 36 } \)
cross multiply the products of the ratio.
9 • 36 = 5 • 78
324 = 390
So, we conclude that the table and court are not similar.
MATHEMATICAL CONNECTIONS
In Exercises 37 and 38, the two polygons are similar. Find the values of x and y.
Question 37.
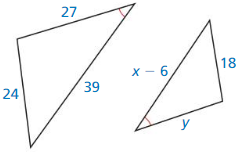
Answer:
x = 35.25 and y = 20.25
Explanation:
From the above given figures,
we know that the two polygons are similar.
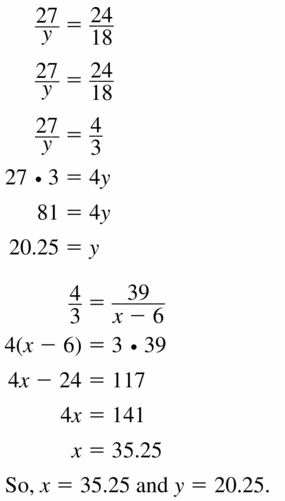
Question 38.
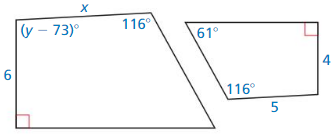
Answer:
x = 7.5
Explanation:
From the above given figures,
we know that the two polygons are similar.
\(\frac { x }{ 5 } \) = \(\frac { 6 }{ 4 } \)
By cross multiplying, we get
x = \(\frac { 30 }{ 4 } \)
x = \(\frac { 15 }{ 2 } \)
x = 7.5
ATTENDING TO PRECISION
In Exercises 39 – 42. the figures are similar. Find the missing corresponding side length.
Question 39.
Figure A has a pen meter of 72 meters and one of the side lengths is 18 meters. Figure B has a perimeter of 120 meters.
Answer:
The corresponding length of figure B is 30 meters.
Explanation:
Given,
Figure A has a pen meter of 72 meters and one of the side lengths is 18 meters.
Figure B has a perimeter of 120 meters.
Ratio of perimeter of both the figures,

Question 40.
Figure A has a perimeter of 24 inches. Figure B has a perimeter of 36 inches and one of the side lengths is 12 inches.
Answer:
The corresponding side length of figure A is 8 in.
Explanation:
Given,
Figure A has a perimeter of 24 inches.
Figure B has a perimeter of 36 inches and one of the side lengths is 12 inches.
Ratio of perimeter of both the figures,
\(\frac { Perimeter of A }{ Perimeter of B } \) = \(\frac { Side length of A }{ Side length of B } \)
\(\frac { 24 }{ 36 } \) = \(\frac { x }{ 12 } \)
\(\frac { 2 }{ 3 } \) = \(\frac { x }{ 12 } \)
12 • 2 = 3x
x = 8
So, the corresponding side length of figure A is 8 in.
Question 41.
Figure A has an area of 48 square feet and one of the side lengths is 6 feet. Figure B has an area of 75 square feet.
Answer:
The corresponding side length of figure B is 7.5 ft.
Explanation:
Given,
Figure A has an area of 48 square feet and one of the side lengths is 6 feet.
Figure B has an area of 75 square feet.
Ratio of perimeter of both the figures,

Question 42.
Figure A has an area of 18 square feet. Figure B has an area of 98 square feet and one of the side lengths is 14 feet.
Answer:
The corresponding side length of figure A is 6 ft.
Explanation:
Given,
Figure A has an area of 18 square feet.
Figure B has an area of 98 square feet and one of the side lengths is 14 feet.
Ratio of perimeter of both the figures,
\(\frac { Area of A }{ Area of B } \) = (\(\frac { Side length of A }{ Side length of B } \))²
\(\frac { 18 }{ 98 } \) = (\(\frac { x }{ 14 } \))²
\(\frac { 9 }{ 49 } \) = \(\frac { x² }{ 196 } \)
x² = 36
x = 6
So, the corresponding side length of figure A is 6 ft.
CRITICAL THINKING
In Exercises 43-48, tell whether the polygons are always, sometimes, or never similar.
Question 43.
two isosceles triangles
Answer:
![]()
Explanation:
Two polygons are said to be similar,
if their corresponding angles are congruent and the corresponding sides have a constant ratio and are identical to each other.
If an angle of one is congruent to the corresponding angle of the other,
then two isosceles triangles are said to be similar.
Question 44.
two isosceles trapezoids
Answer:
Two isosceles trapezoids are sometimes similar.
Explanation:
Two polygons are said to be similar,
if their corresponding angles are congruent and the corresponding sides have a constant ratio and are identical to each other.
If two sides are the same length and the two base angles are the same size as well,
then their corresponding sides have the same ratio.
Then, Two isosceles trapezoids are said to be similar.
Question 45.
two rhombuses
Answer:
![]()
Explanation:
Two polygons are said to be similar,
if their corresponding angles are congruent and the corresponding sides have a constant ratio and are identical to each other.
If all of their corresponding sides are proportional and all of their corresponding angles are congruent,
then it is said to be similar.
Hence, two rhombus are sometimes similar.
Question 46.
two squares
Answer:
Two squares are always similar.
Explanation:
Two polygons are said to be similar,
if their corresponding angles are congruent and the corresponding sides have a constant ratio and are identical to each other.
Squares are similar shapes because they always have four angles and four equal sides,
even if the lengths of their sides differ.
Question 47.
two regular polygons
Answer:
![]()
Explanation:
Two polygons are said to be similar,
If two polygons whose corresponding angles are congruent and the lengths of the corresponding sides are proportional, then they are similar polygons.
So, regular polygons are sometimes similar.
Question 48.
a right triangle and an equilateral triangle
Answer:
A right triangle and an equilateral triangle are never similar.
Explanation:
An equilateral triangle can never be a right triangle because,
In a right – angled triangle one angle is of 90°.
In equilateral triangle the 3 angles are equal to 180 degrees.
60° + 60° + 60° = 180°.
So, a right triangle and an equilateral triangle never be similar.
Question 49.
MAKING AN ARGUMENT
Your sister claims that when the side lengths of two rectangles are proportional, the two rectangles must be similar. Is she correct? Explain your reasoning.
Answer:

Question 50.
HOW DO YOU SEE IT?
You shine a flashlight directly on an object to project its image onto a parallel screen. Will the object and the image be similar? Explain your reasoning.
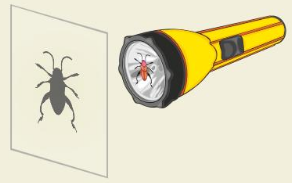
Answer:
The object and image are similar.
Explanation:
At the point where the light from the object converges, a replica of the actual object is created.
This replica is known as the image.
If we shine a flashlight directly on an object to project its image onto a parallel screen,
then the image obtained is similar.
Question 51.
MODELING WITH MATHEMATICS
During a total eclipse of the Sun, the moon is directly in line with the Sun and blocks the Sun’s rays. The distance DA between Earth and the Sun is 93,00,000 miles. the distance DE between Earth and the moon is 2,40,000 miles, and the radius AB of the Sun is 432,5000 miles. Use the diagram and the given measurements to estimate the radius EC of the moon.
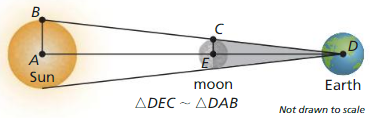
Answer:
EC = 1116 miles.
Explanation:

Question 52.
PROVING A THEOREM
Prove the Perimeters of Similar Polygons Theorem (Theorem 8.1) for similar rectangles. Include a diagram in your proof.
Answer:
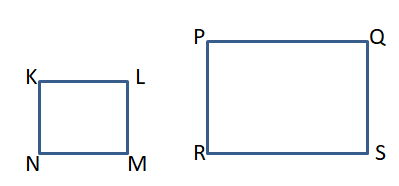
\(\frac{PQ + QR + RS + SP }{KL + LM + MN + NK}\)
\(\frac{PQ}{KL}\) = \(\frac{QR}{LM}\)
\(\frac {RS}{M }\) = \(\frac {SP}{NK}\)
Explanation:
If two polygons are similar, then the ratio of their perimeters is equal to ratios of their corresponding side lengths.
Question 53.
PROVING A THEOREM
Prove the Areas of Similar Polygons Theorem (Theorem 8.2) for similar rectangles. Include a diagram in our proof.
Answer:
If two polygons are similar, then the ratio of their areas is equal to the squares of the ratios of their corresponding
sides.
Explanation:

Question 54.
THOUGHT PROVOKING
The postulates and theorems in this book represent Euclidean geometry. In spherical geometry. all points are points on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. A plane is the surface of the sphere. In spherical geometry, is it possible that two triangles are similar but not congruent? Explain your reasoning.
Answer:
Question 55.
CRITICAL THINKING
In the diagram, PQRS is a square, and PLMS ~ LMRQ. Find the exact value of x. This value is called the golden ratio. Golden rectangles have their length and width in this ratio. Show that the similar rectangles in the diagram are golden rectangles.
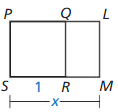
Answer:

Question 56.
MATHEMATICAL CONNECTIONS
The equations of the lines shown are y = \(\frac{4}{3}\)x + 4 and y = \(\frac{4}{3}\)x – 8. Show that ∆AOB ~ ∆COD.
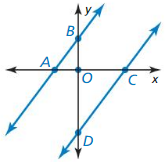
Answer:
The two lines slopes are equal and triangles angles are congruent and side lengths are proportional.
So, triangles are similar.
Explanation:
Given,
y = \(\frac{4}{3}\)x + 4 and y = \(\frac{4}{3}\)x – 8.
for x = 0
y = \(\frac{4}{3}\)(0) + 4 and y’ = \(\frac{4}{3}\)(0) – 8.
y = 4 and y’ = – 8.
for x = 3
y = \(\frac{4}{3}\)(3) + 4 and y’ = \(\frac{4}{3}\)(3) – 8.
y = 8 and y’ = – 4.
(x, y)
Substitute the values in the graph paper.
The center O is shared by both the triangles and the AA similarity criteria,
S, both the angles are same and the sum of the internal angle is also 180 degrees.
Maintaining Mathematical proficiency
Find the value of x.
Question 57.
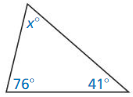
Answer:
x = 63°
Explanation:
Sum of the three angles = 180°
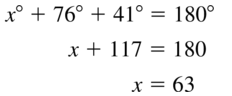
Question 58.
Answer:
x = 66°
Explanation:
Sum of the three angles = 180°
x + 24 + 90 = 180
x + 114 = 180
x = 180 – 114
x = 66
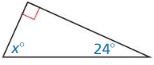
Question 59.
Answer:
x = 64°
Explanation:
Sum of the three angles = 180°
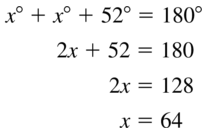
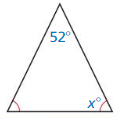
Question 60.
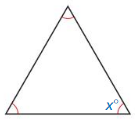
Answer:
x = 60°
Explanation:
Sum of the three angles = 180°
x + x + x = 180
3x = 180
x = 60
8.2 Proving Triangle Similarity by AA
Exploration 1
Comparing Triangles
Work with a partner. Use dynamic geometry software.
a. Construct ∆ABC and ∆DEF So that m∠A = m∠D = 106°, m∠B = m∠E = 31°, and ∆DEF is not congruent to ∆ABC.
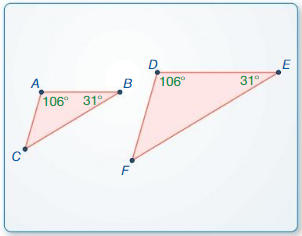
Answer:
m∠C = m∠F
Explanation:
If any two angles of a triangle are equal to any two angles of another triangle,
then the two triangles are similar to each other.
From the figure given above, if ∠ A = ∠D and ∠B = ∠E then ΔABC ~ΔDEF.
From the result obtained, we can easily say that,
\(\frac{AB}{DE}\) = \(\frac{BC}{EF}\) = \(\frac{CA}{FD}\) and ∠C = ∠F
106° + 31° = 137°
180° – 137° = 43°
∠C = ∠F = 43°
b. Find the third angle measure and the side lengths of each triangle. Copy the table below and record our results in column 1.
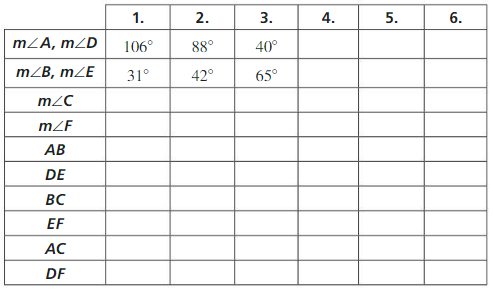
Answer:
c. Are the two triangles similar? Explain.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to understand and use stated assumptions, definitions, and previously established results in constructing arguments.
Answer:
d. Repeat parts (a) – (c) to complete columns 2 and 3 of the table for the given angle measures.
Answer:
e. Complete each remaining column of the table using your own choice of two pairs of equal corresponding angle measures. Can you construct two triangles in this way that are not similar?
Answer:
f. Make a conjecture about any two triangles with two pairs of congruent corresponding angles.
Answer:
Communicate Your Answer
Question 2.
What can you conclude about two triangles when you know that two pairs of corresponding angles are congruent?
Answer:
Question 3.
Find RS in the figure at the left.
Answer:
Lesson 8.2 Proving Triangle Similarity by AA
Monitoring Progress
Show that the triangles are similar. Write a similarity statement.
Question 1.
∆FGH and ∆RQS
Answer:
∆FGH ~ ∆RQS
Explanation:
∆FGH and ∆RQS are similar by the AA similarity theorem.
If the two sides of a triangle are in the same proportion of the two sides of another triangle, then the angle inscribed by the two sides in both the triangles are equal.
Therefore, two triangles are said to be similar.
Question 2.
∆CDF and ∆DEF
Answer:
Question 3.
WHAT IF?
Suppose that \(\overline{S R}\) ![]() \(\overline{T U}\) in Example 2 part (b). Could the triangles still be similar? Explain.
\(\overline{T U}\) in Example 2 part (b). Could the triangles still be similar? Explain.
Answer:
Question 4.
WHAT IF?
A child who is 58 inches tall is standing next to the woman in Example 3. How long is the child’s shadow’?
Answer:
Question 5.
You are standing outside, and you measure the lengths 0f the shadows cast by both you and a tree. Write a proportion showing how you could find the height of the tree.
Answer:
Exercise 8.2 Proving Triangle Similarity by AA
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
If two angles of one triangle are congruent to two angles of another triangle. then the triangles are __________ .
Answer:

Question 2.
WRITING
Can you assume that corresponding sides and corresponding angles of any two similar triangles are congruent? Explain.
Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 3 – 6. determine whether the triangles are similar. If they are, write a similarity statement. Explain your reasoning.
Question 3.
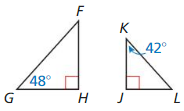
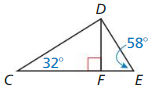
Answer:
∆FHG ~ ∆KJL
Explanation:
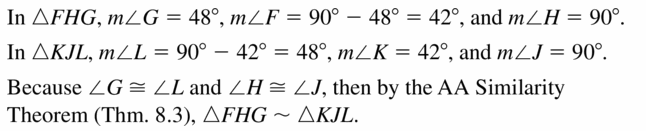
Question 4.
Answer:
Question 5.
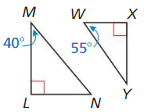
Answer:
∆FGH ≠ ∆YXW
Explanation:
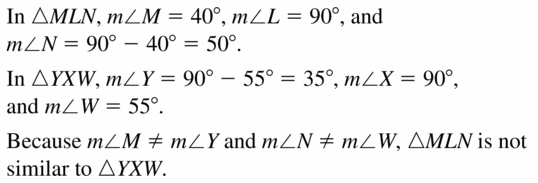
Question 6.
Answer:
In Exercises 7 – 10. show that the two triangles are similar.
Question 7.
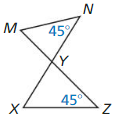
Answer:
∆MYN ~ ∆XYZ
Explanation:
When two lines intersect they form four angles, opposite to each other. 
Question 8.
Answer:
Question 9.
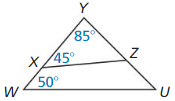
Answer:
∆XYZ ~ ∆UYW
Explanation:
The reflexive property of congruence states that an angle, line segment, or shape is always congruent to itself.

Question 10.
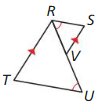
Answer:
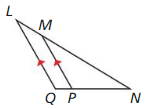
In Exercises 11 – 18, use the diagram to copy and complete the statement.
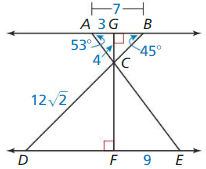
Question 11.
∆CAG ~ _________
Answer:
![]()
Explanation:
If any two angles of a triangle are equal to any two angles of another triangle,
then the two triangles are similar to each other.
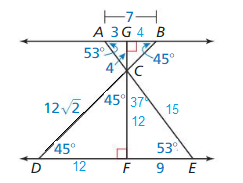
From the figure given above diagram,
if ∠ A = ∠D and ∠B = ∠E then ΔCAG ~ΔCEF.
From the result obtained, we can easily say that,
\(\frac{AG}{EF}\) = \(\frac{GC}{CF}\) = \(\frac{CA}{EC}\) = \(\frac{1}{3}\) and ∠A = ∠E
53° + 90° = 143°
180° – 143° = 37°
∠A = ∠E = 37°
Question 12.
∆DCF ~ _________
Answer:
ΔDCF ~ΔBCG
Explanation:

From the figure given above diagram,
if ∠ A = ∠D and ∠B = ∠E then ΔDCF ~ΔBCG.
Question 13.
∆ACB ~ _________
Answer:
![]()
Explanation:

From the figure given above diagram,
if ∠ A = ∠D and ∠B = ∠E then ΔACF ~ΔECD.
Question 14.
m∠ECF = _________
Answer:
m∠ECF = 37°
Explanation:

From the figure given above diagram,
if ∠ A = ∠D and ∠B = ∠E then ΔACF ~ΔECD.
Question 15.
m∠ECD = _________
Answer:
![]()
Explanation:

From the figure given above diagram,
m∠ECD =∠ DCF + ∠FCE
m∠ECD = 45°+37°= 82°
Question 16.
CF = _________
Answer:
CF = 12
Explanation:

From the figure given above diagram,
CF = 3 x CG
CF = 3 x 4
CF = 12
Question 17.
BC = _________
Answer:
![]()
Explanation:

From the figure given above diagram,
Question 18.
DE = _________
Answer:
4 sqrt 2
Explanation:
BC = CD/3
BC= 12 sqrt 2 /3
BC = 4 sqrt 2
Question 19.
ERROR ANALYSIS
Describe and correct the error in using the AA Similarity Theorem (Theorem 8.3).
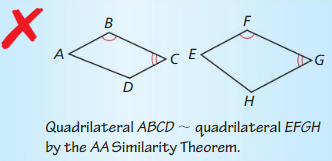
Answer:

Explanation:
AA similarity theorem doesn’t apply to the quadrilaterals.
According to AA similarity theorem, if two angles of one triangle are congruent to two angles of another triangle.
Question 20.
ERROR ANALYSIS
Describe and correct the error in finding the value of x.
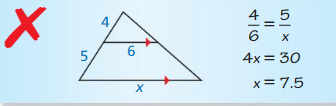
Answer:
Question 21.
MODELING WITH MATHEMATICS
You can measure the width of the lake using a surveying technique, as shown in the diagram. Find the width of the lake, WX. Justify your answer.
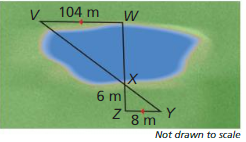
Answer:
WX = 78 meters.
Explanation:
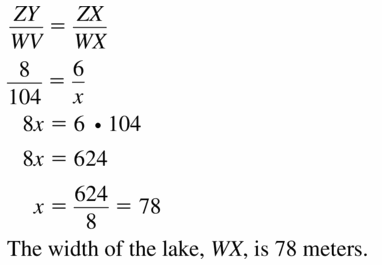
Question 22.
MAKING AN ARGUMENT
You and your cousin are trying to determine the height of a telephone pole. Your cousin tells you to stand in the pole’s shadow so that the tip of your shadow coincides with the tip of the pole’s shadow. Your Cousin claims to be able to use the distance between the tips of the shadows and you, the distance between you and the pole, and your height to estimate the height of the telephone pole. Is this possible? Explain. Include a diagram in your answer.
Answer:
Yes, it is possible to estimate the height of the telephone pole.
Explanation:
We can measure the height of the telephone pole as shown in the below figure.
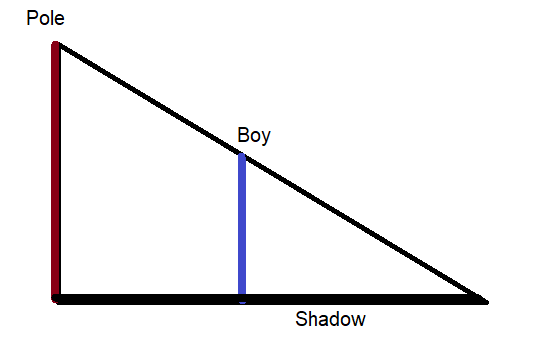
REASONING
In Exercises 23 – 26, is it possible for ∆JKL and ∆XYZ to be similar? Explain your reasoning.
Question 23.
m∠J = 71°, m∠K = 52°, m∠X = 71°, and m∠Z = 57°
Answer:
![]()
Explanation:
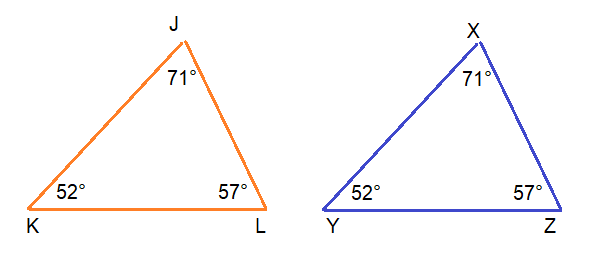
From the figure given above diagram,
if ∠J = ∠X and ∠L= ∠Z then ΔJKL ~ΔXYZ.
Then, ∠K = ∠Y
Question 24.
∆JKL is a right triangle and m∠X + m∠Y= 150°.
Answer:
No
Explanation:
∆JKL is not a right triangle.
If m∠X + m∠Y =150°
Sum of the angles = 180°
So, 180° – 150° = 30°
The third angle should be 30°
Question 25.
m∠L = 87° and m∠Y = 94°
Answer:
![]()
Explanation:
94 + 87 = 181°
The basic property of a triangle is “The sum of the internal angles to 180° ”
m∠J + m∠K + m∠L = 180°
m∠X + m∠Y + m∠Z = 180°
From the figure given above diagram,
Then, ΔJKL ~ΔXYZ.
Question 26.
m∠J + m∠K = 85° and m∠Y + m∠Z = 80°
Answer:
No
Explanation:
Given,
m∠J + m∠K = 85° and m∠Y + m∠Z = 80°
85° + 80° = 165°
165° < 180°
The sum of internal angles of a triangle should be 180°.
m∠J + m∠K = 85° and m∠Y + m∠Z = 80°
will not match or satisfy the m∠J + m∠K + m∠L = 180°
Question 27.
MATHEMATICAL CONNECTIONS
Explain how you can use similar triangles to show that any two points on a line can be used to find its slope.
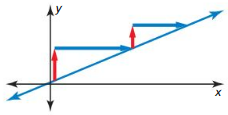
Answer:

Explanation:
In the above given figure,
the triangles are similar and the ratios of the vertical sides to the horizontal sides are equal.
Question 28.
HOW DO YOU SEE IT?
In the diagram, which triangles would you use to find the distance x between the shoreline and the buoy? Explain your reasoning.
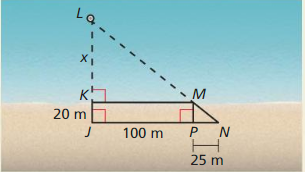
Answer:
ΔKLM and ΔMNP similar triangles are used.
Explanation:
Triangle KLM, with base 100m and height x comparing with triangle MNP
\(\frac{x}{100}\) = \(\frac{20}{25}\)
x = \(\frac{20 x 100}{25}\)
x = 80 m
Question 29.
WRITING
Explain why all equilateral triangles are similar.
Answer:
Explanation:
An equilateral triangle, all the lengths of the sides are equal. The interior angles will have a measure of
Since the angles of an equilateral triangle are the same, it is also known as an equiangular triangle. A property of equilateral triangles includes that all angles are equal to
Question 30.
THOUGHT PROVOKING
Decide whether each is a valid method of showing that two quadrilaterals are similar. Justify your answer.
a. AAA
Answer:
Two quadrilaterals are similar if their corresponding angles are equal and also their corresponding sides must be proportional.
b. AAAA
Answer:
Question 31.
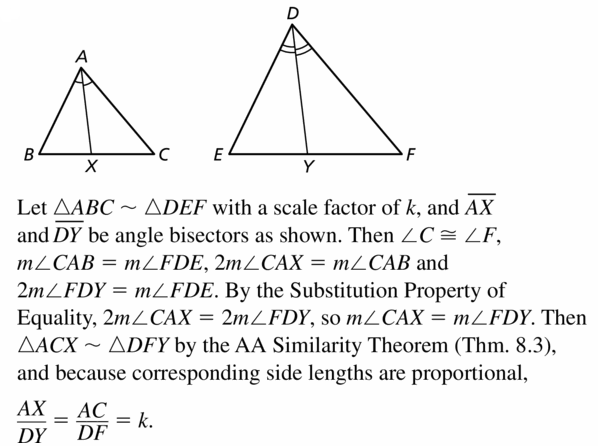
PROOF
Without using corresponding lengths in similar polygons. prove that the ratio of two corresponding angle bisectors in similar triangles is equal to the scale factor.
Answer:
Question 32.
PROOF
Prove that if the lengths of two sides of a triangle are a and b, respectively, then the lengths of the corresponding altitudes to those sides are in the ratio \(\frac{b}{a}\).
Answer:
Question 33.
MODELING WITH MATHEMATICS
A portion of an amusement park ride is shown. Find EF. Justify your answer.
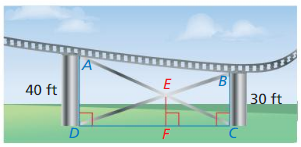
Answer:

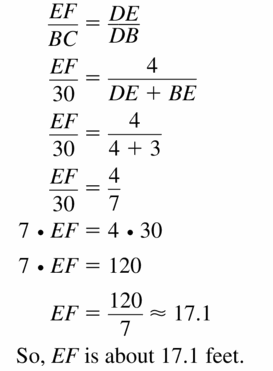
Maintaining Mathematical Practices
Determine whether there is enough information to prove that the triangles are congruent. Explain your reasoning.
Question 34.
Answer:
Question 35.
Answer:
Question 36.
Answer:
8.1 & 8.2 Quiz
List all pairs of congruent angles. Then write the ratios of the corresponding side lengths in a statement of proportionality.
Question 1.
∆BDG ~ ∆MPQ
Answer:
Question 2.
DEFG ~ HJKL
Answer:
The polygons are similar. Find the value of x.
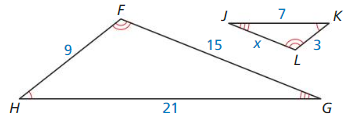
Question 3.
Answer:
Question 4.
Answer:
Determine whether the polygons are similar. If they are, write a similarity statement. Explain your reasoning. (Section 8.1 and Section 8.2)
Question 5.
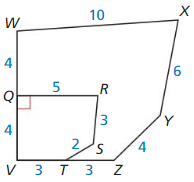
Answer:
Question 6.
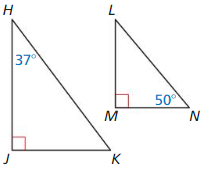
Answer:
Question 7.
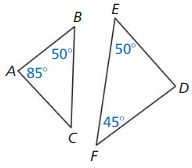
Answer:
Show that the two triangles are similar.
Question 8.
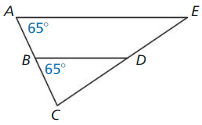
Answer:
Question 9.
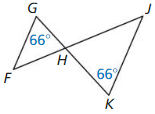
Answer:
Question 10.
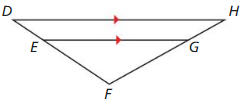
Answer:
Question 11.
The dimensions of an official hockey rink used by the National Hockey League (NHL) are 200 feet by 85 feet. The dimensions of an air hockey table are 96 inches by 408 inches. Assume corresponding angles are congruent. (Section 8.1)
a. Determine whether the two surfaces are similar.
Answer:
b. If the surfaces are similar, find the ratio of their perimeters and the ratio ol their areas. If not, find the dimensions of an air hockey table that are similar to an NHL hockey rink.
Answer:
Question 12.
you and a friend buy camping tents made by the same company but in different sizes and colors. Use the information given in the diagram to decide whether the triangular faces of the tents are similar. Explain your reasoning. (Section 8.2)
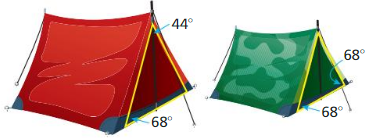
Answer:
8.3 Proving Triangle Similarity by SSS and SAS
Exploration 1
Deciding Whether Triangles Are Similar
Work with a partner: Use dynamic geometry software.
a. Construct ∆ABC and ∆DEF with the side lengths given in column 1 of the table below.
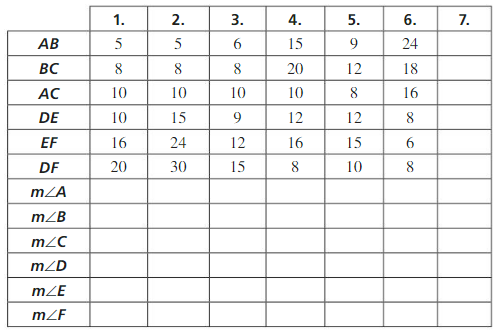
Answer:
b. Copy the table and complete column 1.
Answer:
c. Are the triangles similar? Explain your reasoning.
Answer:
d. Repeat parts (a) – (c) for columns 2 – 6 in the table.
Answer:
e. How are the corresponding side lengths related in each pair of triangles that are similar? Is this true for each pair of triangles that are not similar?
Answer:
f. Make a conjecture about the similarity of two triangles based on their corresponding side lengths.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to analyze situations by breaking them into cases and recognize and use counter examples.
Answer:
g. Use your conjecture to write another set of side lengths of two similar triangles. Use the side lengths to complete column 7 of the table.
Answer:
Exploration 2
Deciding Whether Triangles Are Similar
Work with a partner: Use dynamic geometry software. Construct any ∆ABC.
a. Find AB, AC, and m∠A. Choose any positive rational number k and construct ∆DEF so that DE = k • AB, DF = k • AC, and m∠D = m∠A.
Answer:
b. Is ∆DEF similar to ∆ABC? Explain your reasoning.
Answer:
c. Repeat parts (a) and (b) several times by changing ∆ABC and k. Describe your results.
Answer:
Communicate Your Answer
Question 3.
What are two ways to use corresponding sides of two triangles to determine that the triangles are similar?
Answer:
Lesson 8.3 Proving Triangle Similarity by SSS and SAS
Monitoring progress
Use the diagram.
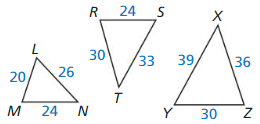
Question 1.
Which of the three triangles are similar? Write a similarity statement.
Answer:
The ratios are equal. So, △LMN, △XYZ are similar.
The ratios are not equal. So △LMN, △RST are not similar.
Explanation:
Compare △LMN, △XYZ by finding the ratios of corresponding side lengths
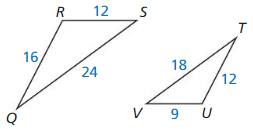
Shortest sides: \(\frac { LM }{ YZ } \) = \(\frac { 20 }{ 30 } \) = \(\frac { 2 }{ 3 } \)
Longest sides: \(\frac { LN }{ XY } \) = \(\frac { 26 }{ 39 } \) = \(\frac { 2 }{ 3 } \)
Remaining sides: \(\frac { MN }{ ZX } \) = \(\frac { 24 }{ 36 } \) = \(\frac { 2 }{ 3 } \)
The ratios are equal. So, △LMN, △XYZ are similar.
Compare △LMN, △RST by finding the ratios of corresponding side lengths
Shortest sides: \(\frac { LM }{ RS } \) = \(\frac { 20 }{ 24 } \) = \(\frac { 5 }{ 6 } \)
Longest sides: \(\frac { LN }{ ST } \) = \(\frac { 26 }{ 33 } \)
Remaining sides: \(\frac { MN }{ RT } \) = \(\frac { 24 }{ 30 } \) = \(\frac { 4 }{ 5 } \)
The ratios are not equal. So △LMN, △RST are not similar.
Question 2.
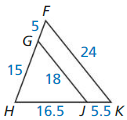
The shortest side of a triangle similar to ∆RST is 12 units long. Find the other side 1enths of the triangle.
Answer:
The other side lengths of the triangle are 15 units, 16.5 units.
Explanation:
The shortest side of a triangle similar to ∆RST is 12 units
Scale factor = \(\frac { 12 }{ 24 } \) = \(\frac { 1 }{ 2 } \)
So, other sides are 33 x \(\frac { 12 }{ 2 } \) = 16.5, 30 x \(\frac { 12 }{ 2 } \) = 15.
Explain how to show that the indicated triangles are similar.
Question 3.
∆SRT ~ ∆PNQ
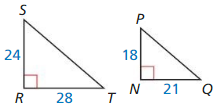
Answer:
Yes, ∆SRT ~ ∆PNQ
Explanation:
The shorter sides: \(\frac { 18 }{ 24 } \) = \(\frac { 3 }{ 4 } \)
Longer sides: \(\frac { 21 }{ 28 } \) = \(\frac { 3 }{ 4 } \)
The side lengths are proportional.
So, ∆SRT ~ ∆PNQ
Question 4.
∆XZW ~ ∆YZX
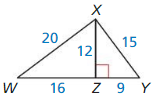
Answer:
∆XZW and ∆YZX are not proportional.
Explanation:
The shorter sides: \(\frac { 9 }{ 16 } \)
Longer sides: \(\frac { 15 }{ 20 } \) = \(\frac { 3 }{ 4 } \)
The side lengths are not proportional. So ∆XZW and ∆YZX are not proportional.
Exercise 8.3 Proving Triangle Similarity by SSS and SAS
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
You plan to show that ∆QRS is similar to ∆XYZ by the SSS Similarity Theorem (Theorem 8.4). Copy and complete the proportion that you will use:
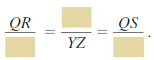
Answer:
Question 2.
WHICH ONE DOESN’T BELONG?
Which triangle does not belong with the other three? Explain your reasoning.

Answer:
Monitoring progress and Modeling with Mathematics
In Exercises 3 and 4, determine whether ∆JKL or ∆RST is similar to ∆ABC.
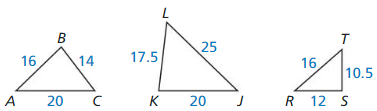
Question 3.
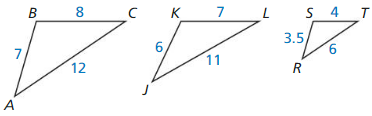
Answer:
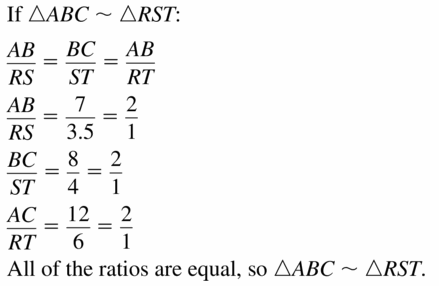
Question 4.
Answer:
In Exercises 5 and 6, find the value of x that makes ∆DEF ~ ∆XYZ.
Question 5.
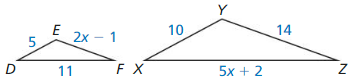
Answer:
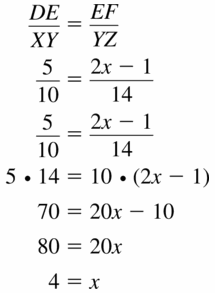
Question 6.
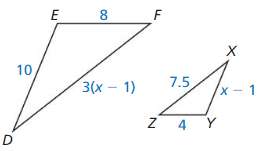
Answer:
In Exercises 7 and 8, verify that ∆ABC ~ ∆DEF Find the scale factor of ∆ABC to ∆DEF
Question 7.
∆ABC: BC = 18, AB = 15, AC = 12
∆DEF: EF = 12, DE = 10, DF = 8
Answer:
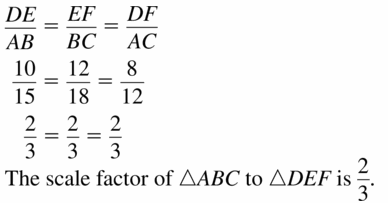
Question 8.
∆ABC: AB = 10, BC = 16, CA = 20
∆DEF: DE = 25, EF = 40, FD =50
Answer:
In Exercises 9 and 10. determine whether the two triangles are similar. If they are similar, write a similarity statement and find the scale factor of triangle B to triangle A.
Question 9.
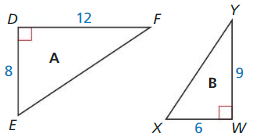
Answer:
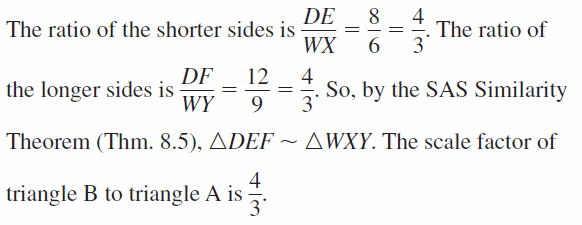
Question 10.
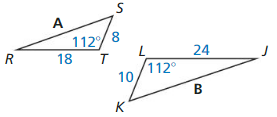
Answer:
In Exercises 11 and 12, sketch the triangles using the given description. Then determine whether the two triangles can be similar.
Question 11.
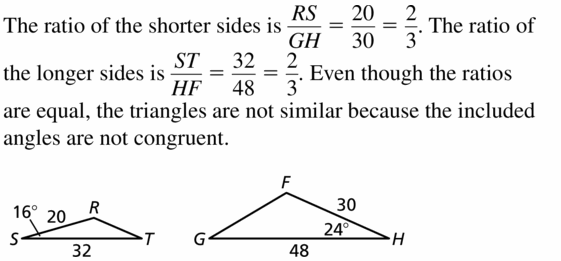
In ∆RST, RS = 20, ST = 32, and m∠S = 16°. In ∆FGH, GH = 30, HF = 48, and m∠H = 24°.
Answer:
Question 12.
The side lengths of ∆ABC are 24, 8x, and 48, and the side lengths of ∆DEF are 15, 25, and 6x.
Answer:
x = 5
Explanation:
Given, the side lengths of ∆ABC are 24, 8x, and 48, and the side lengths of ∆DEF are 15, 25, and 6x.
\(\frac { AB }{ DE } \) = \(\frac { AC }{ DF } \) = \(\frac { BC }{ EF } \)
\(\frac { 24 }{ 15 } \) = \(\frac { 8x }{ 25 } \)
x = 5
In Exercises 13 – 16. show that the triangles are similar and write a similarity statement. Explain your reasoning.
Question 13.
Answer:

Question 14.
Answer:
Question 15.
Answer:

Question 16.
Answer:
In Exercises 17 and 18, use ∆XYZ.
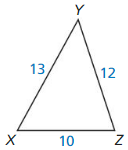
Question 17.
The shortest side of a triangle similar to ∆XYZ is 20 units long. Find the other side lengths of the triangle.
Answer:
Question 18.
The longest side of a triangle similar to ∆XYZ is 39 units long. Find the other side lengths of the triangle.
Answer:
Question 19.
ERROR ANALYSIS
Describe and correct the error in writing a similarity statement.
Answer:
Question 20.
MATHEMATICAL CONNECTIONS
Find the value of n that makes ∆DEF ~ ∆XYZ when DE = 4, EF = 5, XY = 4(n + 1), YZ = 7n – 1, and ∠E ≅ ∠Y. Include a sketch.
Answer:
n = 3
Explanation:
Given, ∆DEF ~ ∆XYZ when DE = 4, EF = 5, XY = 4(n + 1), YZ = 7n – 1, and ∠E ≅ ∠Y.
\(\frac { DE }{ XY } \) = \(\frac { EF }{ YZ } \)
\(\frac { 4 }{ 4(n + 1) } \) = \(\frac { 5 }{ 7n – 1 } \)
cross multiply the fractions.
4(7n – 1) = 20(n + 1)
28n – 4 = 20n + 20
28n – 20n = 20 + 4
8n = 24
n = \(\frac { 24 }{ 8 } \)
n = 3
ATTENDING TO PRECISION
In Exercises 21 – 26, use the diagram to copy and complete the statement.
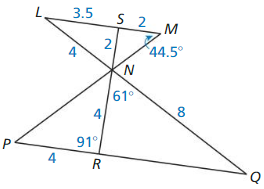
Question 21.
m∠LNS = ___________
Answer:
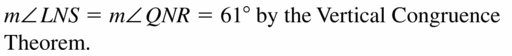
Explanation:
According to the vertical angles theorem states that two opposite vertical angles formed when two lines intersect each other are always congruent to each other.
So, m∠LNS = m∠QNR = 61°
Question 22.
m∠NRQ = ___________
Answer:
m∠NRQ = m∠NRP = 91° by the vertical congruence.
Explanation:
According to the vertical angles theorem states that two opposite vertical angles formed when two lines intersect each other are always congruent to each other.
So, m∠NRQ = m∠NRP = 91°
Question 23.
m∠NQR = ___________
Answer:
m∠NQR = 30°
Explanation:
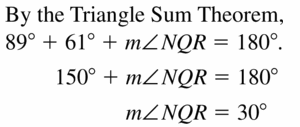
Question 24.
RQ = ___________
Answer:
RQ = 4√3
Explanation:
According to the Pythagorean theorem,
the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse.
a² + b² = c²
NQ² = NR² + RQ²
8² = 4² + RQ²
64 = 16 + RQ²
64 – 16 = RQ²
48 = RQ²
RQ = 4√3
Question 25.
m∠NSM = ___________
Answer:
m∠NSM = 91°
Explanation:
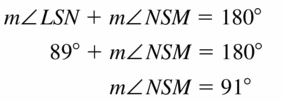
Question 26.
m∠NPR = ___________
Answer:
m∠NPR = 28°
Explanation:
The sum of the angles = 180°
m∠NPR + m∠NRP + m∠RNP = 180°
m∠NPR + 91° + 61° = 180°
m∠NPR + 152° = 180°
m∠NPR = 180° – 152°
m∠NPR = 28°
Question 27.
MAKING AN ARGUMENT
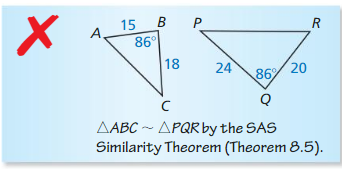
Your friend claims that ∆JKL ~ ∆MNO by the SAS Similarity Theorem (Theorem 8.5) when JK = 18, m∠K = 130° KL = 16, MN = 9, m∠N = 65°, and NO = 8, Do you support your friend’s claim? Explain your reasoning.
Answer:
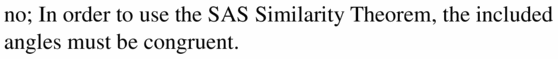
Explanation:
According to SAS similarity theorem, SAS stands for side angle side.
If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are said to be congruent.
Question 28.
ANALYZING RELATIONSHIPS
Certain sections of stained glass are sold in triangular, beveled pieces. Which of the three beveled pieces, if any, are similar?
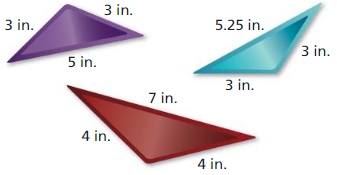
Answer:
Out of three triangles, violet and blue triangles are similar.
Explanation:
Check the similarity of maroon and violet triangles.
From the above given figures we know that,
longest sides: \(\frac { 5 }{ 7 } \)
shortest sides: \(\frac { 3 }{ 4 } \)
remaining sides: \(\frac { 3 }{ 4 } \)
The ratios are not equal.
So those traingles are not similar.
Check the similarity of blue and violet triangles.
longest sides: \(\frac { 5 }{ 5.25 } \) = 1
shortest sides: \(\frac { 3 }{ 3 } \) = 1
remaining sides: \(\frac { 3 }{ 3 } \) = 1
Hence, the ratios are equal.
So, those triangles are similar.
Question 29.
ATTENDING TO PRECISION
In the diagram, \(\frac{M N}{M R}=\frac{M P}{M Q}\) Which of the statements must be true?
Select all that apply. Explain your reasoning.
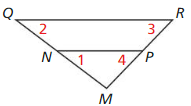
(A) ∠1 ≅∠2
(B) \(\overline{Q R}\) || \(\overline{N P}\)
(C)∠1 ≅ ∠4
(D) ∆MNP ~ ∆MRQ
Answer:
Option (D)
Explanation:
According to the reflexive property of congruence, any geometric figure is congruent to itself.
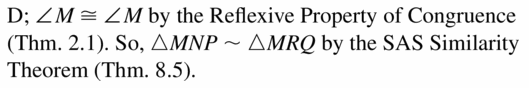
Question 30.
WRITING
Are any two right triangles similar? Explain.
Answer:
Yes, any two right triangles can be similar.
Explanation:
If two right triangles are said to be similar,
then the ratio of their longest, smallest and remaining side lengths must be equal and their angles must be congruent.
Question 31.
MODELING WITH MATHEMATICS
In the portion of the shuffleboard court shown, \(\frac{B C}{A C}=\frac{B D}{A E}\)

a. What additional information do you need to show that ∆BED ~ ∆ACE using the SSS Similarity Theorem (Theorem 8.4)?
b. What additional information do, you need to show that ∆BCD ~ ∆ACE using the SAS Similarity Theorem (Theorem 8.5)?
Answer:
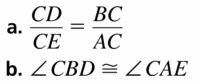
Question 32.
PROOF
Given that ∆BAC is a right triangle and D, E, and F are midpoints. prove that m∠DEF = 90°.
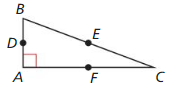
Answer:
By observing the triangle ABC,
m∠BAC = 90°
Join the midpoints of the sides of the triangle.
Then, m∠DEF = 90°
Question 33.
PROVING A THEOREM
Write a two-column proof of the SAS Similarity Theorem (Theorem 8.5).
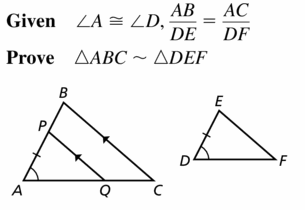
Given ∠A ≅ ∠D, \(\frac{A B}{D E}=\frac{A C}{D F}\)
Prove ∆ABC ~ ∆DEF
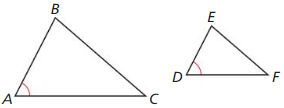
Answer:


Question 34.
CRITICAL THINKING
You are given two right triangles with one pair of corresponding legs and the pair of hypotenuses having the same length ratios.
a. The lengths of the given pair of corresponding legs are 6 and 18, and the lengths of the hypotenuses are 10 and 30. Use the Pythagorean Theorem to find the lengths of the other pair of corresponding legs. Draw a diagram.
Answer:
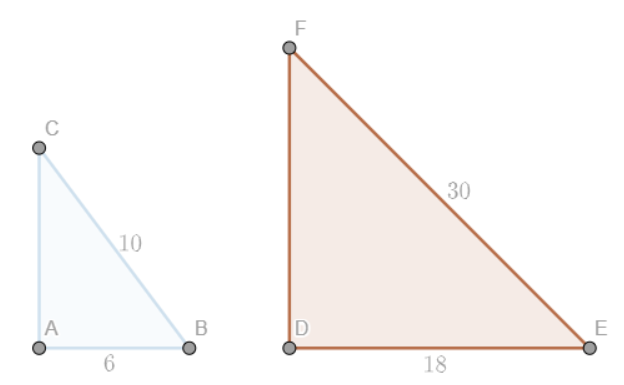
b. Write the ratio of the lengths of the second pair of corresponding legs.
Answer:
8 : 24
Explanation:
First find the length of AC using Pythagorean theorem,
the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse.
AC² + AB² = BC²
AC² + 6² = 10²
AC² + 36 = 100
AC² = 100 – 36
AC² = 64
AC = 8
Find the length of DF using Pythagorean theorem.
DF² + DE² = EF²
DF² + 18² = 30²
DF² + 324 = 900
DF² = 900 – 324
DF² = 576
DF = 24
c. Are these triangles similar? Does this suggest a Hypotenuse-Leg Similarity Theorem for right triangles? Explain.
Answer:
Yes, triangles are similar.
Explanation:
From the above given information and explanations,
k = \(\frac { AC }{ DF } \) = \(\frac { 8 }{ 24 } \) = \(\frac { 1 }{ 3 } \)
k = \(\frac { AB }{ DE } \) = \(\frac { 6 }{ 18 } \) = \(\frac { 1 }{ 3 } \)
So, triangles are similar.
Question 35.
WRITING
Can two triangles have all three ratios of corresponding angle measures equal to a value greater than 1 ? less than 1 ? Explain.
Answer:
No
Explanation:

Question 36.
HOW DO YOU SEE IT?
Which theorem could you use to show that ∆OPQ ~ ∆OMN in the portion of the Ferris wheel shown when PM = QN = 5 feet and MO = NO = 10 feet?

Answer:
The corresponding angle theorem states that ∆OPQ is similar to ∆OMN.
Explanation:
The corresponding angle theorem states that,
when a line intersects two parallel lines, then the corresponding angles in the two regions of intersection are congruent.
Therefore, PM = QN = 5 feet and MO = NO = 10 feet
Question 37.
DRAWING CONCLUSIONS
Explain why it is not necessary to have an Angle-Side-Angle Similarity Theorem.
Answer:

Explanation:
Angle-side-angle theorem states that,
if two angles and a non-included side in one triangle are congruent to two angles and the corresponding non-included side in another triangle, then the triangles are congruent.
Question 38.
THOUGHT PROVOKING
Decide whether each is a valid method of showing that two quadrilaterals are similar. Justify your answer.
a. SASA
Answer:
Two quadrilaterals are said to be similar,
when their corresponding angles are equal and also their corresponding sides must be proportional.
Explanation:
According to SASA or side-angle-side-angle theorem,
If an angle of one triangle is congruent to an angle of a second triangle and the lengths of the sides including these angles are proportional, then the triangles are similar.
b. SASAS
Answer:
If three sides and the included angles of one quadrilateral are congruent to the corresponding three sides and two angles of another quadrilateral, then the quadrilaterals are said to be congruent.
c. SSSS
Answer:
SSSS rule states that,
If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle,
then the two triangles are said to be congruent.
d. SASSS
Answer:
If two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then those two triangles are similar.
Question 39.
MULTIPLE REPRESENTATIONS
Use a diagram to show why there is no Side-Side-Angle Similarity Theorem.
Answer:
Question 40.
MODELING WITH MATHEMATICS
The dimensions of an actual swing set are shown. You want to create a scale model of the swing set for a dollhouse using similar triangles. Sketch a drawing of your swing set and label each side length. Write a similarity statement for each pair of similar triangles. State the scale factor you used to create the scale model.
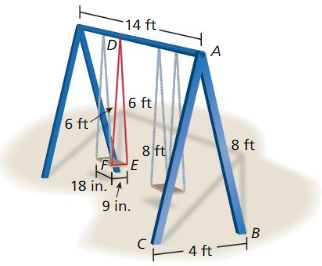
Answer:
∆ABC ~ ∆DEF
Explanation:
According to the similarity statement,
If the measures of the corresponding sides of two triangles are proportional then the triangles are similar.
The scale factor k = \(\frac { AB }{ DE } \)
K = \(\frac { 8 }{ 6 } \)
k = \(\frac { 4 }{ 3 } \)
Hence, △ABC ~ △DEF.
Question 41.
PROVING A THEOREM
Copy and complete the paragraph proot of the second part of the Slopes of Parallel Lines Theorem (Theorern 3. 13) from page 439.
Given ml = mn, l and n are nonvertical.
Prove l || n
You are given that ml = mn. By the definition of slope. ml = \(\frac{B C}{A C}\) and mn = \(\frac{E F}{D F}\) By ____________, \(\frac{B C}{A C}=\frac{E F}{D F}\). Rewriting this proportion yields ___________,
By the Right Angles Congruence Theorem (Thin. 2.3), ___________, So. ∆ABC ~ ∆DEF by ___________ . Because corresponding angles of similar triangles are congruent, ∠BAC ≅∠EDF. By ___________, l || n.
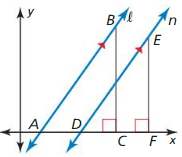
Answer:

Question 42.
PROVING A THEOREM
Copy and complete the two-column proof 0f the second part of the Slopes of Perpendicular Lines Theorem (Theorem 3.14)
Given ml mn = – 1, l and n are nonvertical.
Prove l ⊥ n
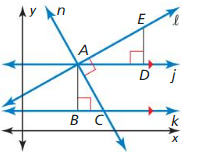
| Statements | Reasons |
| 1. mlmn = – 1 | 1. Given |
| 2. ml = \(\frac{D E}{A D}\), mn = \(\frac{A B}{B C}\) | 2. Definition of slope |
| 3. \(\frac{D E}{A D} \cdot-\frac{A B}{B C}\) = – 1 | 3. ________________________________ |
| 4. \(\frac{D E}{A D}=\frac{B C}{A B}\) | 4. Multiply each side of statement 3 by –\(\frac{B C}{A B}\). |
| 5. \(\frac{D E}{B C}\) = ____________ | 5. Rewrite proportion. |
| 6. ________________________________ | 6. Right Angles Congruence Theorem (Thm. 2.3) |
| 7. ∆ABC ~ ∆ADE | 7. ________________________________ |
| 8. ∠BAC ≅ ∠DAE | 8. Corresponding angles of similar figures are congruent. |
| 9. ∠BCA ≅ ∠CAD | 9. Alternate Interior Angles Theorem (Thm. 3.2) |
| 10. m∠BAC = m∠DAE, m∠BCA = m∠CAD | 10. ________________________________ |
| 11. m∠BAC + m∠BCA + 90° = 180° | 11. ________________________________ |
| 12. ________________________________ | 12. Subtraction Property of Equality |
| 13. m∠CAD + m∠DAE = 90° | 13. Substitution Property of Equality |
| 14. m∠CAE = m∠DAE + m∠CAD | 14. Angle Addition Postulate (Post. 1.4) |
| 15. m∠CAE = 90° | 15. ________________________________ |
| 16. ________________________________ | 16. Definition of perpendicular lines |
Answer:
| Statements | Reasons |
| 1. mlmn = – 1 | 1. Given |
| 2. ml = \(\frac{D E}{A D}\), mn = \(\frac{A B}{B C}\) | 2. Definition of slope |
| 3. \(\frac{D E}{A D} \cdot-\frac{A B}{B C}\) = – 1 | 3. Correspomsding sides are opposite |
| 4. \(\frac{D E}{A D}=\frac{B C}{A B}\) | 4. Multiply each side of statement 3 by –\(\frac{B C}{A B}\). |
| 5. \(\frac{D E}{B C}\) = \(\frac { AB }{ AD } \) | 5. Rewrite proportion. |
| 6. Two right-angled triangles are said to be congruent to each other if the hypotenuse and one side of the right triangle are equal to the hypotenuse and the corresponding side of the other right-angled triangle. | 6. Right Angles Congruence Theorem (Thm. 2.3) |
| 7. ∆ABC ~ ∆ADE | 7. According to the side angle side theorem. |
| 8. ∠BAC ≅ ∠DAE | 8. Corresponding angles of similar figures are congruent. |
| 9. ∠BCA ≅ ∠CAD | 9. Alternate Interior Angles Theorem (Thm. 3.2) |
| 10. m∠BAC = m∠DAE, m∠BCA = m∠CAD | 10. Congruent angles |
| 11. m∠BAC + m∠BCA + 90° = 180° | 11. △ABC is a right-angled triangle |
| 12. m∠CAD + m∠DAE = 90° | 12. Subtraction Property of Equality |
| 13. m∠CAD + m∠DAE = 90° | 13. Substitution Property of Equality |
| 14. m∠CAE = m∠DAE + m∠CAD | 14. Angle Addition Postulate (Post. 1.4) |
| 15. m∠CAE = 90° | 15. Right Angle |
| 16. If two lines meet each other a an angle of 90°, then they are called the perpendicular lines. | 16. Definition of perpendicular lines |
Maintaining Mathematical proficiency
Find the coordinates of point P along the directed line segment AB so that AP to PB is the given ratio.
Question 43.
A(- 3, 6), B(2, 1); 3 to 2
Answer:

Question 44.
A(- 3, – 5), B(9, – 1); 1 to 3
Answer:

Question 45.
A(1, – 2), B(8, 12); 4 to 3
Answer:

8.4 Proportionality Theorems
Exploration 1
Discovering a Proportionality Relationship
Work with a partner. Use dynamic geometry software to draw any ∆ABC.
a. Construct \(\overline{D E}\) parallel to \(\overline{B C}\) with endpoints on \(\overline{A B}\) and \(\overline{A C}\), respectively.
Answer:
b. Compare the ratios of AD to BD and AE to CE.
Answer:
c. Move \(\overline{D E}\) to other locations Parallel to \(\overline{B C}\) with endpoints on \(\overline{A B}\) and \(\overline{A C}\), and repeat part (b).
Answer:
d. Change ∆ABC and repeat parts (a) – (c) several times. Write a conjecture that summarizes your results.
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:
Exploration 2
Discovering a Proportionality Relationship
Work with a partner. Use dynamic geometry software to draw any AABC.
a. Bisect ∆B and plot point D at the intersection of the angle bisector and \(\overline{A C}\).
Answer:
b. Compare the ratios of AD to DC and BA to BC.
Answer:
c. Change ∆ABC and repeat parts (a) and (b) several times. Write a conjecture that summarizes your results.
Answer:
Communicate Your Answer
Question 3.
What proportionality relationships exist in a triangle intersected by an angle bisector or by a line parallel to one of the sides?
Answer:
Question 4.
Use the figure at the right to write a proportion.

Answer:
Lesson 8.4 Proportionality Theorems
Monitoring Progress
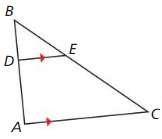
Question 1.
Find the length of \(\overline{Y Z}\).
Answer:
YZ = \(\frac { 315 }{ 11 } \)
Explanation:
According to the triangle property theorem,
The sum of the length of the two sides of a triangle is greater than the length of the third side. In the same way, the difference between the two sides of a triangle is less than the length of the third side.
Triangle property theorem is \(\frac { XW }{ WV } \) = \(\frac { XY }{ YZ } \)
\(\frac { 44 }{ 35 } \) = \(\frac { 36 }{ YZ } \)
cross multiply the fractions
44 • YZ = 36 • 35
44 • YZ = 1260
YZ = \(\frac { 1260 }{ 44 } \)
YZ = \(\frac { 315 }{ 11 } \)
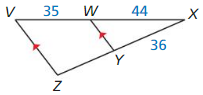
Question 2.
Determine whether \(\overline{P S}\) || \(\overline{Q R}\)
Answer:
Yes, \(\overline{P S}\) || \(\overline{Q R}\)
Explanation:
\(\frac { PQ }{ PN } \) = \(\frac { 50 }{ 90 } \)
\(\frac { PQ }{ PN } \) = \(\frac { 5 }{ 9 } \)
\(\frac { SR }{ SN } \) = \(\frac { 40 }{ 72 } \)
\(\frac { SR }{ SN } \) = \(\frac { 5 }{ 9 } \)
\(\frac { PQ }{ PN } \) = \(\frac { SR }{ SN } \)
So, PS is parallel to QR.
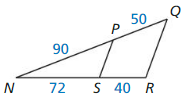
Find the length of the given line segment.
Question 3.
\(\overline{B D}\)
Answer:
\(\overline{B D}\) = 12
Explanation:
All the angles are congruent.
So, \(\overline{A B}\), \(\overline{C D}\), \(\overline{E F}\) are parallel.
According to three parallel lines theorem,
if three or more parallel lines intersect two transversals, then they cut off the transversals proportionally as shown in the above figure.
\(\frac { BD }{ DF } \) = \(\frac { AC }{ CE } \)
\(\frac { [latex]\overline{B D}\) }{ 30 } [/latex] = \(\frac { 16 }{ 40 } \)
\(\overline{B D}\) = \(\frac { 16 }{ 40 } \) • 30
\(\overline{B D}\) = 12
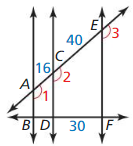
Question 4.
\(\overline{J M}\)
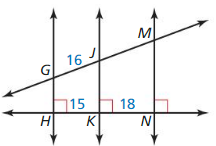
Answer:
\(\overline{J M}\) = \(\frac { 96 }{ 5 } \)
Explanation:
All the angles are congruent.
So, \(\overline{G H}\), \(\overline{J K}\), \(\overline{M N}\) are parallel.
According to three parallel lines theorem,
if three or more parallel lines intersect two transversals, then they cut off the transversals proportionally as shown in the above figure.
\(\frac { HK }{ KN } \) = \(\frac { GJ }{ JM } \)
\(\frac { 15 }{ 18 } \) = \(\frac { 16 }{ [latex]\overline{J M}\) } [/latex]
Cross multiply on both sides.
15 • \(\overline{J M}\) = 16 • 18 = 288
\(\overline{J M}\) = \(\frac { 288 }{ 15 } \)
\(\overline{J M}\) = \(\frac { 96 }{ 5 } \)
Find the value of the variable.
Question 5.
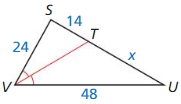
Answer:
x = 28
Explanation:
\(\overline{T V}\) is the angle bisector.
So, \(\frac { ST }{ TU } \) = \(\frac { SV }{ VU } \)
\(\frac { 14 }{ x } \) = \(\frac { 24 }{ 48 } \)
cross multiply on both sides.
24x = 14 • 48 = 672
x = \(\frac { 672 }{ 24 } \)
x = 28
Question 6.
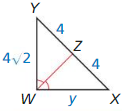
Answer:
x = 4√2
Explanation:
\(\overline{W Z}\) is the angle bisector.
So, \(\frac { YZ }{ ZX } \) = \(\frac { YW }{ WX } \)
\(\frac { 4 }{ 4 } \) = \(\frac { 4√2 }{ x } \)
cross multiply on both sides.
4x = 4 • 4√2 = 16√2
x = 4√2
Exercise 8.4 Proportionality Theorems
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE STATEMENT
If a line divides two sides of a triangle proportionally, then it is ____________ to the third side. This theorem is knon as the ____________ .
Answer:

Question 2.
VOCABULARY
In ∆ABC, point R lies on \(\overline{B C}\) and \(\vec{A}\)R bisects ∆CAB. Write the proportionality statement for the triangle that is based on the Triangle Angle Bisector Theorem (Theorem 8.9).
Answer:
According to the triangle angle bisector theorem \(\frac { CR }{ BR } \) = \(\frac { AC }{ AB } \)
Explanation:
The angle bisector of a triangle theorem states that,
it divides the opposite side into two parts proportional to other two sides of the triangle.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 and 4, find the length of \(\overline{A B}\) .
Question 3.
Answer:
\(\overline{A B}\) = 9 units.
Explanation:

Question 4.
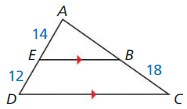
Answer:
\(\overline{A B}\) = 21 units.
Explanation:
From the above given figure,
\(\frac { AE }{ ED } \) = \(\frac { AB }{ BC } \)
\(\frac { 14 }{ 12 } \) = \(\frac { AB }{ 18 } \)
AB = \(\frac { 14 }{ 12 } \) • 18
AB = 21 units.
In Exercises 5 – 8, determine whether \(\overline{K M}\) || \(\overline{J N}\).
Question 5.
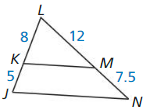
Answer:
Yes, \(\overline{K M}\) || \(\overline{J N}\).
Explanation:
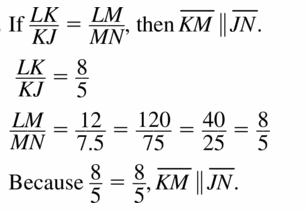
Question 6.
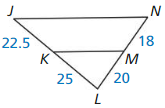
Answer:
Yes, KM || JN
Explanation:
From the above given figure,
If \(\frac { JK }{ KL } \) = \(\frac { NM }{ ML } \),
then KM || JN
\(\frac { JK }{ KL } \) = latex]\frac { 22.5 }{ 25 } [/latex] = latex]\frac { 9 }{ 10 } [/latex]
\(\frac { NM }{ ML } \) = \(\frac { 18 }{ 20 } \) = latex]\frac {9}{10} [/latex]
\(\frac { JK }{ KL } \) = \(\frac { NM }{ ML } \)
Therefore, KM || JN
Question 7.
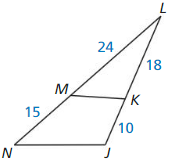
Answer:
No, \(\overline{K M}\) || \(\overline{J N}\).
Explanation:
From the above given figure,

Question 8.
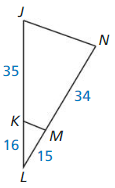
Answer:
No, \(\overline{K M}\) || \(\overline{J N}\).
Explanation:
From the above given figure,
If \(\frac { JK }{ KL } \) = \(\frac { NM }{ ML } \),
then KM || JN
\(\frac { JK }{ KL } \) = latex]\frac {35 }{ 16 } [/latex]
\(\frac { NM }{ ML } \) = \(\frac { 34 }{ 15 } \)
\(\frac { JK }{ KL } \) ≠ \(\frac { NM }{ ML } \)
So, KM is not parallel to JN
CONSTRUCTION
In Exercises 9 – 12, draw a segment with the given length. Construct the point that divides the segment in the given ratio.
Question 9.
3 in.; 1 to 4
Answer:

Question 10.
2 in.; 2 to 3
Answer:
Construct a 2 inch segment and divide the segment into 2 + 3 or 5 congruent pieces.
Point (P) is the point that is \(\frac { 1 }{ 5 } \) of the way from point A to point B.
Question 11.
12 cm; 1 to 3
Answer:
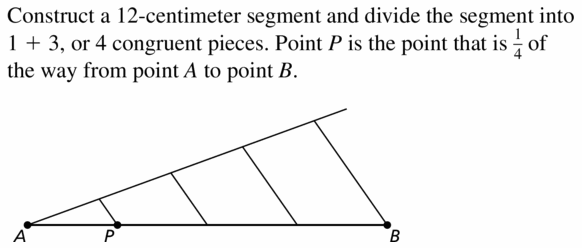
Question 12.
9 cm ; 2 to 5
Answer:
Construct a 9 cm segment and divide the segment into 2 + 5 or 7 congruent pieces.
Point (p) is the point that is \(\frac { 1 }{ 7 } \) of the way from point A to point B.
In Exercises 13 – 16, use the diagram to complete the proportion.
Question 13.
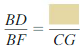
Answer:
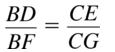
Explanation:
With reference to the basic proportionality theorem (Thales’s theorem),
if three or more parallel lines intersect two transversals,
then they cut off the transversals proportionally.
So, we know that the ratio of the length of BD to that of BF must be equal to the ratio of the length of CE to that of CF.
Question 14.
![]()
Answer:
\(\frac {CG}{EG} \) = \(\frac {BF}{DF} \)
Explanation:
With reference to the basic proportionality theorem (Thales’s theorem),
if three or more parallel lines intersect two transversals,
then they cut off the transversals proportionally.
So, we know that the ratio of the length of BF to that of DF must be equal to the ratio of the length of CG to that of EG.
Question 15.
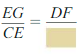
Answer:
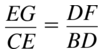
Explanation:
With reference to the basic proportionality theorem (Thales’s theorem),
if three or more parallel lines intersect two transversals,
then they cut off the transversals proportionally.
So, we know that the ratio of the length of EG to that of CE must be equal to the ratio of the length of DF to that of BD.
Question 16.
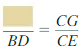
Answer:
\(\frac {BF}{BD} \) = \(\frac {CG}{CE} \)
Explanation:
With reference to the basic proportionality theorem (Thales’s theorem),
if three or more parallel lines intersect two transversals,
then they cut off the transversals proportionally.
So, we know that the ratio of the length of CG to that of CE must be equal to the ratio of the length of BF to that of BD.
In Exercises 17 and 18, find the length of the indicated line segment.
Question 17.
\(\overline{V X}\)
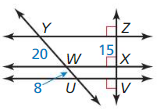
Answer:
\(\overline{V X}\) = 6 units.
Explanation:
From the above given figure,
Question 18.
\(\overline{S U}\)
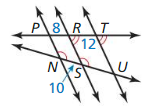
Answer:
\(\overline{S U}\) = 15 units.
Explanation:
From the above given figure,
\(\frac { SU }{ NS } \) = \(\frac { RT }{ PR } \)
\(\frac { SU }{ 10 } \) = \(\frac { 12 }{ 8 } \)
SU = \(\frac { 12 }{ 8 } \) • 10
By simplifying we get,
SU = 15
In Exercises 19 – 22, find the value of the variable.
Question 19.
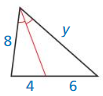
Answer:
y = 12
Explanation:
From the above given figure we know that,
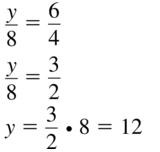
Question 20.
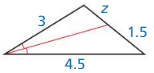
Answer:
z = 1
Explanation:
From the above given figure we know that,
\(\frac { z }{ 1.5 } \) = \(\frac { 3 }{ 4.5 } \)
z = \(\frac { 3 }{ 4.5 } \) • 1.5
z = \(\frac { 3 • 1.5 }{ 4.5 } \)
z = \(\frac { 4.5 }{ 4.5 } \)
z = 1
Question 21.
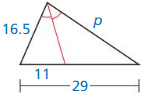
Answer:
p =27
Explanation:
From the above given figure we know that,
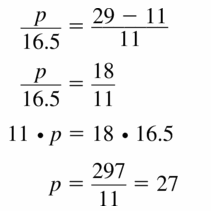
Question 22.
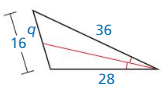
Answer:
q = 9
Explanation:
From the above given figure we know that,
\(\frac { q }{ 16 – q } \) = \(\frac { 36 }{ 28 } \)
28q = 36 (16 – q)
28q = 576 – 36q
28q + 36q = 576
64q = 576
q = 576/64
q = 9
Question 23.
ERROR ANALYSIS
Describe and correct the error in solving for x.
Answer:

Question 24.
ERROR ANALYSIS
Describe and correct the error in the students reasoning.
Answer:
Based on the information in the above figure,
\(\frac { BD }{ CD } \) = \(\frac { AB }{ AC } \)
BD = CD
So, 1 = \(\frac { AB }{ AC } \)
AC = AB
MATHEMATICAL CONNECTIONS
In Exercises 25 and 26, find the value of x for which \(\overline{P Q}\) || \(\overline{R S}\).
Question 25.
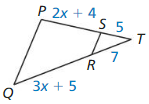
Answer:
x = 3
Explanation:
Based on the information in the above figure,
Question 26.
Answer:
x = 5
Explanation:
Based on the information in the above figure,
\(\frac { PR }{ RT } \) = \(\frac { QS }{ ST } \)
\(\frac { 12 }{ 2x – 2 } \) = \(\frac { 21 }{ 3x – 1 } \)
cross multiply on both sides.
12(3x – 1) = 21(2x – 2)
36x – 12 = 42x – 42
42x – 36x = 42 – 12
6x = 30
x = 30/6
x = 5
Question 27.
PROVING A THEOREM
Prove the Triangle Proportionality Theorem (Theorem 8.6).
Given \(\overline{Q S}\) || \(\overline{T U}\)
Prove \(\frac{Q T}{T R}=\frac{S U}{U R}\)
Answer:


Question 28.
PROVING A THEOREM
Prove the Converse of the Triangle Proportionality Theorem (Theorem 8.7).
Given \(\frac{Z Y}{Y W}=\frac{Z X}{X V}\)
Prove \(\overline{Y X}\) || \(\overline{W V}\)
Answer:
Question 29.
MODELING WITH MATHEMATICS
The real estate term lake frontage refers to the distance along the edge of a piece of property that touches a lake.
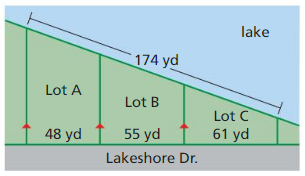
a. Find the lake frontage (to the nearest tenth) of each lot shown.
b. In general, the more lake frontage a lot has, the higher its selling price. Which lot(s) should be listed for the highest price?
c. Suppose that low prices are in the same ratio as lake frontages. If the least expensive lot is $250,000, what are the prices of the other lots? Explain your reasoning.
Answer:
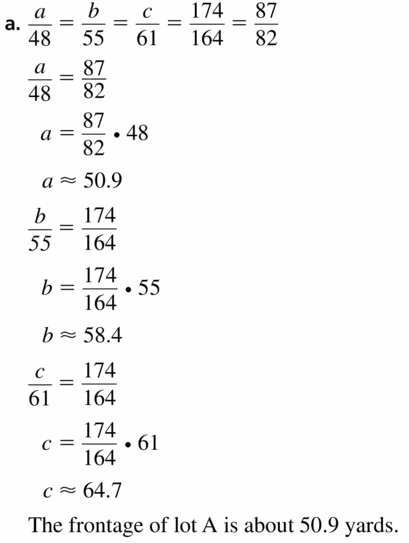

Question 30.
USING STRUCTURE
Use the diagram to find the values of x and y.
Answer:
x = 3.75; y = 2.25
Explanation:
Based on the information in the above figure,
\(\frac { 5 }{ 2 } \) = \(\frac { x }{ 1.5 } \)
x = \(\frac { 5 }{ 2 } \) • 1.5
x = \(\frac { 5 • 1.5 }{ 2 } \)
x = \(\frac { 7.5 }{ 2 } \)
x = 3.75
\(\frac { 3 }{ 7 } \) = \(\frac { y }{ 5.25 } \)
y = \(\frac { 3 }{ 7 } \) • 5.25
y = \(\frac { 3 • 5.25 }{ 7 } \)
y = \(\frac { 15.75 }{ 7 } \)
y = 2.25
Question 31.
REASONING
In the construction on page 447, explain why you can apply the Triangle Proportionality Theorem (Theorem 86) in Step 3.
Answer:
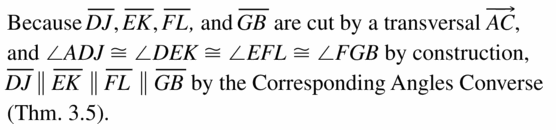
Question 32.
PROVING A THEOREM
Use the diagram with the auxiliary line drawn to write a paragraph proof of the Three Parallel Lines Theorem (Theorem 8.8).
Given K1 || K2 || K3
Prove \(\frac{C B}{B A}=\frac{D E}{E F}\)
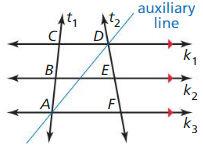
Answer:
Yes, \(\frac{C B}{B A}=\frac{D E}{E F}\)
Explanation:
From the diagram, we observe that K₁ || K₂ || K₃
Those three parallel lines interest two traversals t₁, t₂
So, \(\frac{C B}{B A}=\frac{D E}{E F}\)
Question 33.
CRITICAL THINKING
In ∆LMN, the angle bisector of ∠M also bisects \(\overline{L N}\). Classify ∆LMN as specifically as possible. Justify your answer.
Answer:
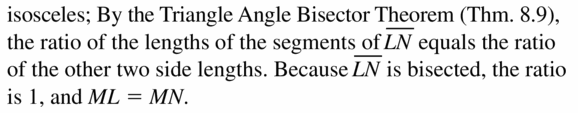
Question 34.
HOW DO YOU SEE IT?
During a football game, the quarterback throws the ball to the receiver. The receiver is between two defensive players, as shown. If Player 1 is closer to the quarterback when the ball is thrown and both defensive players move at the same speed, which player will reach the receiver first? Explain your reasoning.
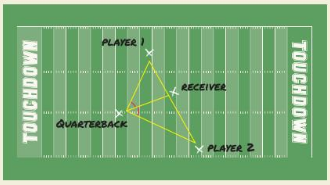
Answer:
As per the image given above,
player 1 is closer to the receiver.
So, player 1 will reach the receiver first.
Question 35.
PROVING A THEOREM
Use the diagram with the auxiliary lines drawn to write a paragraph proof of the Triangle Angle Bisector Theorem (Theorem 8.9).
Given ∠YXW ≅ ∠WXZ
prove \(\frac{Y W}{W Z}=\frac{X Y}{X Z}\)
Answer:

Question 36.
THOUGHT PROVOKING
Write the converse of the Triangle Angle Bisector Theorem (Theorem 8.9). Is the converse true? Justify your answer.
Answer:
Question 37.
REASONING
How is the Triangle Midsegment Theorem (Theorem 6.8) related to the Triangle Proportionality Theorem (Theorem 8.6)? Explain your reasoning.
Answer:

Question 38.
MAKING AN ARGUMENT
Two people leave points A and B at the same time. They intend to meet at point C at the same time. The person who leaves point A walks at a speed of 3 miles per hour. You and a friend are trying to determine how fast the person who leaves point B must walk. Your friend claims you need to know the length of \(\overline{A C}\). Is your friend correct? Explain your reasoning.
Answer:
Yes, my friend is correct.
Explanation:
According to the information given in the above figure,
I started walking from point A with a speed of 3 miles per hour and reaches point C.
My friend starts walking from point B with x speed and reaches point C.
\(\frac { AD }{ DC } \) = \(\frac { BE }{ CE } \)
I have to travel from A to C.
Hence, I need to know distance between AC.
Therefore, my friend is correct.
Question 39.
CONSTRUCTION
Given segments with lengths r, s, and t, construct a segment of length x, such that \(\frac{r}{s}=\frac{t}{x}\)
Answer:

Question 40.
PROOF
Prove Ceva’s Theorem: If P is any point inside ∆ABC, then \(\frac{A Y}{Y C} \cdot \frac{C X}{X B} \cdot \frac{B Z}{Z A}\) = 1
(Hint: Draw segments parallel to \(\overline{B Y}\) through A and C, as shown. Apply the Triangle Proportionality Theorem (Theorem 8.6) to ∆ACM. Show that ∆APN ~ ∆MPC, ∆CXM ~ ∆BXP, and ∆BZP ~ ∆AZN.)
Answer:
Maintaining Mathematical Proficiency
Use the triangle.
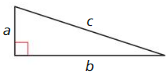
Question 41.
Which sides are the legs?
Answer:
![]()
Question 42.
Which side is the hypotenuse?
Answer:
The leg c is the hypotenuse.
Explanation:
From the above given figure,
the longest side of a right triangle or the side opposite to the right angle is called the hypotenuse.
Solve the equation.
Question 43.
x2 = 121
Answer:
x = ∓ 11
Explanation:
Given,
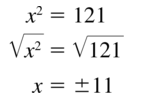
Question 44.
x2 + 16 = 25
Answer:
x = ∓3
Explanation:
Given,
x² + 16 = 25
x² = 25 – 16
x² = 9
x = ∓3
Question 45.
36 + x2 = 85
Answer:
x = ∓7
Explanation:
Given,
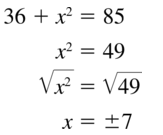
Similarity Review
8.1 Similar Polygons
Find the scale factor. Then list all pairs of congruent angles and write the ratios of the corresponding side lengths in a statement of proportionality.
Question 1.
ABCD ~ EFGH
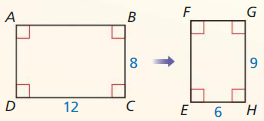
Answer:
According to the information from the above given figure,
\(\frac { BC }{ CD } \) = \(\frac { 8 }{ 12 } \) = \(\frac { 2 }{ 3 } \)
\(\frac { EH }{ GH } \) = \(\frac { 6 }{ 9 } \) = \(\frac { 2 }{ 3 } \)
So, scale factor = \(\frac { 2 }{ 3 } \)
Question 2.
∆XYZ ~ ∆RPQ
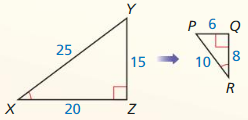
Answer:
According to the information from the above given figure,
longer sides: \(\frac { PR }{ XY } \)
\(\frac { 10 }{ 25 } \) = \(\frac { 2 }{ 5 } \)
shorter sides: \(\frac { PQ }{ YZ } \)
\(\frac { 6 }{ 15 } \) = \(\frac { 2 }{ 5 } \)
remaining sides: \(\frac { QR }{ XZ } \)
\(\frac { 8 }{ 20 } \) = \(\frac { 2 }{ 5 } \)
So, scale factor = \(\frac { 2 }{ 5 } \)
Question 3.
Two similar triangles have a scale factor of 3 : 5. The altitude of the larger triangle is 24 inches. What is the altitude of the smaller triangle?
Answer:
Altitude = 14.4 inches.
Explanation:
Given, Two similar triangles have a scale factor of 3 : 5.
The altitude of the larger triangle is 24 inches.
Scale factor of smaller triangle to larger triangle is \(\frac { 3 }{ 5 } \).
Let x be the smaller triangle altitude,
\(\frac { altitude of smaller triangle }{ altitude of larger triangle } \) = scale factor
\(\frac { x }{ 24 } \) = \(\frac { 3 }{ 5 } \)
x = \(\frac { 3 }{ 5 } \) • 24
x = 14.4
Question 4.
Two similar triangles have a pair of corresponding sides of length 12 meters and 8 meters. The larger triangle has a perimeter of 48 meters and an area of 180 square meters. Find the perimeter and area of the smaller triangle.
Answer:
A = 80 sq mt.
P = 32 m.
Explanation:
The scale factor of smaller to larger triangle = \(\frac { 8 }{ 12 } \)
s = \(\frac { 2 }{ 3 } \)
\(\frac { perimeter of smaller triangle }{ perimeter of larger triangle } \) = scale factor\(\frac { perimeter of smaller triangle }{ 48 } \) = \(\frac { 2 }{ 3 } \)
p = \(\frac { 2 }{ 3 } \) • 48
p = \(\frac { 2 • 48 }{ 3 } \)
p = \(\frac { 96 }{ 3 } \)
p = 32m
\(\frac { Area of smaller triangle }{ Area of larger triangle } \) = (scale factor)²
\(\frac { Area of smaller triangle }{ 180 } \) = ( \(\frac { 2 }{ 3 } \))²
Area of smaller triangle = \(\frac { 4 }{ 9 } \) • 180
A = \(\frac { 4 • 180 }{ 9 } \)
A = \(\frac { 720 }{ 9 } \)
= 80 sq mt.
8.2 Proving Triangle Similarity by AA
Show that the triangles are similar. Write a similarity statement.
Question 5.
Answer:
m∠RQS = m∠UTS = 35°.
△QRS and △STU are similar as per the AA similarity theorem.
Explanation:
According to AA similarity theorem,
If any two angles of a triangle are equal to any two angles of another triangle,
then the two triangles are similar to each other.
Question 6.
Answer:
m∠CAB = 60°, m∠DEF = 30°
△ABC and △DEF are not similar as per the AA similarity theorem.
Explanation:
According to AA similarity theorem,
If any two angles of a triangle are equal to any two angles of another triangle,
then the two triangles are similar to each other.
So, the above given triangles are not similar.
Question 7.
A cellular telephone tower casts a shadow that is 72 feet long, while a nearby tree that is 27 feet tall casts a shadow that is 6 feet long. How tall is the tower?
Answer:
324 ft.
Explanation:
Given, A cellular telephone tower casts a shadow that is 72 feet long,
while a nearby tree that is 27 feet tall casts a shadow that is 6 feet long.
\(\frac { shadow of tree }{ shadow of tower } \) = \(\frac { height of tree }{ height of tower } \)
\(\frac { 6 }{ 72 } \) = \(\frac { 27 }{ x } \)
cross multiply on both sides.
6x = 72 x 27
6x = 1944
x = 1944 ÷ 6
x = 324 ft
So, the height of the tower is 324 ft.
8.3 Proving Triangle Similarity by SSS and SAS
Use the SSS Similarity Theorem (Theorem 8.4) or the SAS Similarity Theorem (Theorem 8.5) to show that the triangles are similar.
Question 8.
Answer:
BD is parallel to AE.
Explanation:
According to the SSS Similarity Theorem,
If all the three sides of a triangle are in proportion to the three sides of another triangle, then the two triangles are similar.
\(\frac { DE }{ CD } \) = \(\frac { 7 }{ 3.5 } \) = 2
\(\frac { AB }{ BC } \) = \(\frac { 8 }{ 4 } \) = 2
\(\frac { DE }{ CD } \) = \(\frac { AB }{ BC } \)
So, BD is parallel to AE.
Question 9.
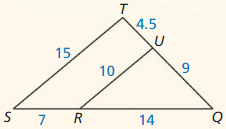
Answer:
ST is parallel to RU.
Explanation:
According to the SSS Similarity Theorem,
If all the three sides of a triangle are in proportion to the three sides of another triangle, then the two triangles are similar.
\(\frac { QU }{ TU } \) = \(\frac { 9 }{ 4.5 } \) = 2
\(\frac { QR }{ SR } \) = \(\frac { 14 }{ 7 } \) = 2
\(\frac { QU }{ TU } \) = \(\frac { QR }{ SR } \)
So, ST is parallel to RU.
Question 10.
Find the value of x that makes ∆ABC ~ ∆DEF
Answer:
x = 4
Explanation:
According to the SSS Similarity Theorem,
If all the three sides of a triangle are in proportion to the three sides of another triangle, then the two triangles are similar.
The information from the above given figure,
\(\frac { 24 }{ 6 } \) = 4
\(\frac { 32 }{ 2x } \) = 4
32 = 8x
x = \(\frac { 32 }{ 8 } \)
x = 4
8.4 Proportionality Theorems
Determine whether \(\overline{A B}\) || \(\overline{C D}\)
Question 11.
Answer:
CD and AB are not parallel.
Explanation:
According to the Proportionality Theorem,
If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio and then the triangles are said to similar to each other.
Based on the information given in the above figure,
\(\frac { DB }{ BE } \) = \(\frac { 10 }{ 16 } \) = \(\frac { 5 }{ 8 } \)
\(\frac { CA }{ AE } \) = \(\frac { 20 }{ 28 } \) = \(\frac { 5 }{ 7 } \)
\(\frac { DB }{ BE } \) ≠ \(\frac { CA }{ AE } \)
So, CD and AB are not parallel.
Question 12.
Answer:
AB and CD are parallel.
Explanation:
According to the Proportionality Theorem,
If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio and then the triangles are said to similar to each other.
Based on the information given in the above figure,
\(\frac { DB }{ BE } \) = \(\frac { 12 }{ 20 } \) = \(\frac { 3 }{ 5 } \)
\(\frac { CA }{ AE } \) = \(\frac { 13.5 }{ 22.5 } \) = \(\frac {3}{5} \)
\(\frac { DB }{ BE } \) = \(\frac { CA }{ AE } \)
So, AB and CD are parallel.
Question 13.
Find the length of \(\overline{Y B}\).
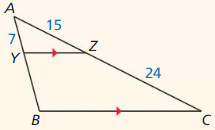
Answer:
\(\overline{Y B}\) is \(\frac { 56 }{ 5 } \)
Explanation:
Based on the information given in the above figure,
\(\frac { ZC }{ AZ } \) = \(\frac { 24 }{ 15 } \) = \(\frac { 8 }{ 5 } \)
\(\frac { YB }{ AY } \) = \(\frac { ZC }{ AZ } \)
\(\frac { YB }{ 7 } \) = \(\frac { 8 }{ 5 } \)
YB = \(\frac { 8 }{ 5 } \) • 7
YB = \(\frac { 56 }{ 5 } \)
The length of \(\overline{Y B}\) is \(\frac { 56 }{ 5 } \)
Find the length of \(\overline{A B}\).
Question 14.
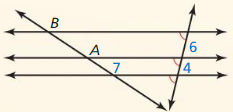
Answer:
\(\overline{A B}\) is \(\frac { 21 }{ 2 } \).
Explanation:
Based on the information given in the above figure,
\(\frac { AB }{ 7 } \) = \(\frac { 6 }{ 4 } \)
\(\overline{A B}\) = \(\frac { 6 }{ 4 } \) • 7
\(\overline{A B}\) = \(\frac { 42 }{ 4 } \)
\(\overline{A B}\) = \(\frac { 21 }{ 2 } \)
The length of \(\overline{A B}\) is \(\frac { 21 }{ 2 } \).
Question 15.
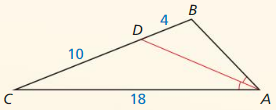
Answer:
AB = \(\frac { 36 }{ 5 } \)
Explanation:
Based on the information given in the above figure,
\(\frac { DB }{ CD } \) = \(\frac { AB }{ AC } \)
\(\frac { 4 }{ 10 } \) = \(\frac { AB }{ 18 } \)
\(\frac { 2 }{ 5 } \) = \(\frac { AB }{ 18 } \)
cross multiply on both sides.
AB = \(\frac { 2 • 18 }{ 5 } \)
AB = \(\frac { 36 }{ 5 } \)
Similarity Test
Determine whether the triangles are similar. If they are, write a similarity statement. Explain your reasoning.
Question 1.
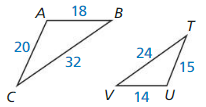
Answer:
△ABC and △TUV are not similar.
Explanation:
Based on the information given in the above figure,
Longer sides: \(\frac { BC }{ TV } \)
\(\frac { 32 }{ 24 } \) = \(\frac { 4 }{ 3 } \)
shorter sides: \(\frac { AB }{ UV } \)
\(\frac { 18 }{ 14 } \) = \(\frac { 9 }{ 7 } \)
remaining sides: \(\frac { AC }{ TU } \)
\(\frac { 20 }{ 15 } \) = \(\frac { 4 }{ 3 } \)
When we observe all the side lengths of a triangle they are not equal.
So, triangles are not similar.
Question 2.
Answer:
△ABC and △JLK are similar.
Explanation:
Based on the information given in the above figure,
\(\frac { AC }{ KJ } \) = \(\frac { 6 }{ 8 } \) = \(\frac { 3 }{ 4 } \)
\(\frac {BC}{JL} \) = \(\frac{24}{32} \) = \(\frac {3}{4} \)
\(\frac { AC }{ KJ } \) = \(\frac { BC }{ JL } \)
So, ∠C = ∠J
Therefore, △ABC and △JLK are similar.
Question 3.
Answer:
\(\frac { XY }{ XW } \) = \(\frac { PZ }{ PW } \)
Therefore, △ABC and △JLK are similar.
Find the value of the variable.
Question 4.
Answer:
w = 3
Explanation:
Based on the information given in the above figure,
\(\frac { 9 }{ w } \) = \(\frac { 15 }{ 5 } \)
\(\frac { 9 }{ w } \) = 3
9 = 3w
w = 3
Question 5.
Answer:
q = \(\frac { 55 }{ 2 } \)
Explanation:
Based on the information given in the above figure,
\(\frac { 17.5 }{ 21 } \) = \(\frac { q }{ 33 } \)
q = \(\frac { 17.5 }{ 21 } \) • 33
q = \(\frac { 55 }{ 2 } \)
Question 6.
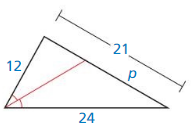
Answer:
p = 14
Explanation:
Based on the information given in the above figure,
\(\frac { 21 – p }{ p } \) = \(\frac { 12 }{ 24 } \)
\(\frac { 21 – p }{ p } \) = \(\frac { 1 }{ 2 } \)
cross multiply on both sides.
2(21 – p) = p
42 – 2p = p
42 = p + 2p
42 = 3p
p = 14
Question 7.
Given ∆QRS ~ ∆MNP, list all pairs of congruent angles, Then write the ratios of the corresponding side lengths in a statement of proportionality.
Answer:
The pairs of congruent angles are:
m∠QRS, m∠RSQ, m∠SQR, m∠MNP, m∠NPM, m∠PMN.
The ratios of side lengths are:
\(\frac { RQ }{ MN } \), \(\frac { QS }{ MP } \), \(\frac {RS}{NP} \)
Use the diagram.
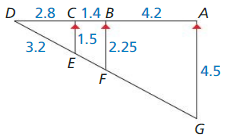
Question 8.
Find the length of \(\overline{E F}\).
Answer:
\(\overline{E F}\) = 1.6
Explanation:
From the above given figure,
\(\frac { DE }{ EF } \) = \(\frac { CD }{ BC } \)
\(\frac { 3.2 }{ EF } \) = \(\frac { 2.8 }{ 1.4 } \)
cross multiply both sides.
EF = \(\frac { 3.2 • 1.4 }{ 2.8 } \)
EF = \(\frac { 4.48 }{ 2.8 } \)
EF = 1.6
So, the length of \(\overline{E F}\) is 1.6
Question 9.
Find the length of \(\overline{F G}\).
Answer:
\(\overline{F G}\) = 4.8
Explanation:
From the above given figure,
\(\frac { EF }{ FG } \) = \(\frac { BC }{ AB } \)
\(\frac { 1.6 }{ FG } \) = \(\frac { 1.4 }{ 4.2 } \)
cross multiply both sides.
FG = \(\frac { 1.6 • 4.2 }{ 1.4 } \)
FG = \(\frac { 6.72 }{ 1.4 } \)
FG = 4.8
So, the length of \(\overline{F G}\) is 4.8
Question 10.
Is quadrilateral FECB similar to quadrilateral GFBA? If so, what is the scale factor of the dilation that maps quadrilateral FECB to quadrilateral GFBA?
Answer:
Yes, quadrilateral FECB similar to quadrilateral GFBA.
According to the scale factor of the dilation,
the ratio of the size of the new image to the size of the old image.
The scale factor of dilation from quadrilateral FECB to quadrilateral GFBA is \(\frac{GF}{FE} \)
Question 11.
You are visiting the Unisphere at Flushing Meadows Corona Park in New York. To estimate the height of the stainless steel model of Earth. you place a mirror on the ground and stand where you can see the top of the model in the mirror. Use the diagram to estimate the height of the model. Explain why this method works.
Answer:
Question 12.
You are making a scale model of a rectangular park for a school project. Your model has a length of 2 feet and a width of 1.4 feet. The actual park is 800 yards long. What are the perimeter and area of the actual park?
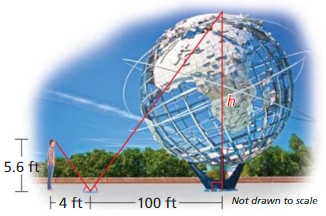
Answer:
A = 1,344,000 sq ft.
P = 5920 ft
Explanation:
Given that, the model has a length of 2 feet and a width of 1.4 feet.
The actual park is 800 yards long.
we know that 1 yard = ft
As per the similarity theorem,
\(\frac { AD }{ EH } \) = \(\frac { AB }{ EF } \)
\(\frac { 2 }{ 800 } \) = \(\frac { 1.4 }{ EF } \)
cross multiply on both sides.
EF = \(\frac { 800 • 1.4 }{ 2 } \)
EF = \(\frac { 1120 }{ 2 } \)
EF = 560
Perimeter of the park P = 2(560 + 2400)
= 2(2960) = 5920 ft
Area of the actual park = 560 • 2400 = 1,344,000 sq ft
Therefore, perimeter of the actual park = 5920 ft
Area of the actual park is 1,344,000 sq ft.
Question 13.
In a Perspective drawing, lines that are parallel in real life must meet at a vanishing point on the horizon. To make the train cars in the drawing appear equal in length, they are drawn so that the lines connecting the opposite corners of each car are parallel. Use the dimensions given and the yellow parallel lines to find the length of the bottom edge of the drawing of Car 2.

Answer:
The length of car 2 is 4.2 cm.
Explanation:
From the above given information,
\(\frac { 5.4 }{ 10.6 } \) = \(\frac { 5.4 + C }{ 19 } \)
C = \(\frac { 45.36 }{ 10.6 } \)
\(\frac { (19 – x – 8.4) }{ (19 – 8.4) } \) = \(\frac { 5.4 }{ 5.4 + c } \)
\(\frac { 19 – 8.4 }{ 19 } \) = \(\frac { c2 + 5.4 }{ c1 + c2 + 5.4 } \)
\(\frac { 19 – 8.4 }{ 19 } \) = \(\frac { 5.4 }{ 5.4 + c2 } \)
c1 = 7.6, c2 = 4.2, x = 4.6
The length of car 2 is 4.2 cm.
Similarity Cumulative Assessment
Question 1.
Use the graph of quadrilaterals ABCD and QRST.
a. Write a composition of transformations that maps quadrilateral ABCD to quadrilateral QRST.
Answer:
According to the scale factor of the dilation,
the ratio of the size of the new image to the size of the old image.
The scale factor = \(\frac { AD }{ QT } \)
k = \(\frac { 2 }{ 1.5 } \)
b. Are the quadrilaterals similar? Explain your reasoning.
Answer:
No.
Explanation:
From the information given above,
\(\frac { AD }{ QT } \) = \(\frac { 2 }{ 1.5 } \)
\(\frac { CD }{ TS } \) = \(\frac { 2.8 }{ 1.4 } \) = 2
So, quadrilaterals are not similar.
Question 2.
In the diagram. ABCD is a parallelogram. Which congruence theorem(s) could you Use to show that ∆AED ≅ ∆CEB? Select all that apply.
SAS Congruence Theorem (Theorem 5.5)
Answer:
According to SAS Congruence Theorem,
It states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent.
SSS Congruence Theorem (Theorem 5.8)
Answer:
According to SSS Congruence Theorem,
If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule.
HL Congruence Theorem (Theorem 5.9)
Answer:
According to HL Congruence Theorem,
In a given set of triangles are congruent if the corresponding lengths of their hypotenuse and one leg are equal.
ASA Congruence Theorem (Theorem 5. 10)
Answer:
According to ASA Congruence Theorem,
If any two angles and the side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.
AAS Congruence Theorem (Theorem 5. 11)
Answer:
According to AAS Congruence Theorem,
AAS stands for Angle-angle-side.
When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle, then the triangles are said to be congruent.
Question 3.
By the Triangle Proportionality Theorem (Theorem 8.6), \(\frac{V W}{W Y}=\frac{V X}{X Z}\) In the diagram, VX > VW and XZ > WY. List three possible values for VX and XZ.
Answer:
From the above given figure,
\(\frac{V W}{W Y}=\frac{V X}{X Z}\)
\(\frac{ 4 }{6}=\frac{V X}{X Z}\)
Therefore the three possible values of VX are greater than 4 means 5, 6, 7, . . .
Therefore the three possible values of XZ are greater than 6 means 7, 8, 9, . .
Question 4.
The slope of line l is – \(\frac{3}{4}\). The slope of line n is \(\frac{4}{3}\) What must be true about lines l and n ?
(A) Lines l and n are parallel.
(B) Lines l and n arc perpendicular.
(C) Lines l and n are skew.
(D) Lines l and n are the same line.
Answer:
Option(B)
Explanation:
Given,
The slope of l = – \(\frac{3}{4}\)
Slope of n = \(\frac{4}{3}\)
lines and slopes are reciprocal and opposite to each other.
So, they are perpendicular.
Question 5.
Enter a statement or reason in each blank to complete the two-column proof.
Given \(\frac{K J}{K L}=\frac{K H}{K M}\)
Prove ∠LMN ≅ ∠JHG
| Statements | Reasons |
| 1. \(\frac{K J}{K L}=\frac{K H}{K M}\) | 1. Given |
| 2. ∠JKH ≅ ∠LKM | 2. ________________________ |
| 3. ∆JKH ~ ∆LKM | 3. ________________________ |
| 4. ∠KHJ ≅∠KML | 4. ________________________ |
| 5. _______________________ | 5. Definition of congruent angles |
| 6. m∠KHJ + m∠JHG = 180° | 6. Linear Pair Postulate (Post. 18) |
| 7. m∠JHG = 180° – m∠KHJ | 7. ________________________ |
| 8. m∠KML + m∠LMN = 180° | 8. ________________________ |
| 9. ________________________ | 9. Subtraction Property of Equality |
| 10. m∠LMN = 180° – m∠KHJ | 10. ________________________ |
| 11. ________________________ | 11. Transitive Property of Equality |
| 12. ∠LMN ≅ ∠JHG | 12. ________________________ |
Answer:
Question 6.
The coordinates of the vertices of ∆DEF are D(- 8, 5), E(- 5, 8), and F(- 1, 4), The coordinates of the vertices of ∆JKL are J(16, – 10), K(10, – 16), and L(2, – 8), ∠D ≅ ∠J. Can you show that ∆DEF ∆JKL by using the AA Similarity Theorem (Theorem 8.3)? If so, do so by listing the congruent corresponding angles and writing a similarity transformation that maps ∆DEF to ∆JKL. If not, explain why not.
Answer:
AA similarity theorem states that ∠D = ∠J.
So, ∆DEF and ∆JKL are similar.
Explanation:
According to AA similarity theorem,
If any two angles of a triangle are equal to any two angles of another triangle,
then the two triangles are similar to each other.
Given,
The coordinates of the vertices of ∆DEF are D(- 8, 5), E(- 5, 8), and F(- 1, 4),
The coordinates of the vertices of ∆JKL are J(16, – 10), K(10, – 16), and L(2, – 8),
∆DEF = ∆JKL
D(- 8, 5), E(- 5, 8), and F(- 1, 4) = J(16, – 10), K(10, – 16), and L(2, – 8)
So, ∠D = ∠J.
Question 7.
Classify the quadrilateral using the most specific name.
rectangle square parallelogram rhombus
Answer:
Question 8.
‘Your friend makes the statement “Quadrilateral PQRS is similar to quadrilateral WXYZ.” Describe the relationships between corresponding angles and between corresponding sides that make this statement true.
Answer:
True.
Explanation:
When 2 figures are similar,
then their corresponding angles and lengths are proportional.
Hence, PQRS is similar to WXYZ.
∠P = ∠W, ∠Q = ∠X, ∠R = ∠Y and ∠S = ∠Z and
\(\frac { PQ }{ WX } \) = \(\frac { QR }{ XY } \)
= \(\frac { RS }{ YZ } \) = \(\frac { PS }{ WZ } \) = k
Here, k is a constant of proportionality.
