Big Ideas Math Geometry Answers Chapter 9 Right Triangles and Trigonometry

If you are wondering how to solve Geometry Questions then the Big Ideas Math Book Geometry Answer Key Chapter 9 Right Triangles and Trigonometry can be of great help. Try to answer the questions from the Big Ideas Math Geometry Answers Chapter 9 Right Triangles and Trigonometry and enhance your overall subject knowledge. Big Ideas Math Geometry Chapter 9 Right Triangles and Trigonometry Solution Key includes questions from the complete textbook and explains them step by step so that it’s easy to understand. Practice the concepts in Big Ideas Math Geometry Answers Chapter 9 Right Triangles and Trigonometry frequently and become proficient in the subject on a deeper level.

Big Ideas Math Book Geometry Answer Key Chapter 9 Right Triangles and Trigonometry

All the answers explained in the Big Ideas Math Geometry Chapter 9 Right Triangles and Trigonometry Solution Key are given by subject experts in accordance with the latest syllabus. Students can learn math concepts efficiently like never before by taking help from the Big Ideas Math Book Geometry Answer Key Chapter 9 Right Triangles and Trigonometry. Score better marks in exams with consistent practice and attempt the exams with utmost confidence. Just click on the quick links listed below to avail the Lesson-wise Big Ideas Math Geometry Answers Chapter 9 Right Triangles and Trigonometry and start preparing right away.

• Right Triangles and Trigonometry Maintaining Mathematical Proficiency
• Right Triangles and Trigonometry Mathematical practices
• 9.1 The Pythagorean Theorem
• Lesson 9.1 The Pythagorean Theorem
• Exercise 9.1 The Pythagorean Theorem
• 9.2 Special Right Triangles
• Lesson 9.2 Special Right Triangles
• Exercise 9.2 Special Right Triangles
• 9.3 Similar Right Triangles
• Lesson 9.3 Similar Right Triangles
• Exercise 9.3 Similar Right Triangles
• 9.1 to 9.3 Quiz
• 9.4 The Tangent Ratio
• Lesson 9.4 The Tangent Ratio
• Exercise 9.4 The Tangent Ratio
• 9.5 The Sine and Cosine Ratios
• Lesson 9.5 The Sine and Cosine Ratios
• Exercise 9.5 The Sine and Cosine Ratios
• 9.6 Solving Right Triangles
• Lesson 9.6 Solving Right Triangles
• Exercise 9.6 Solving Right Triangles
• 9.7 Law of Sines and Law of Cosines
• Lesson 9.7 Law of Sines and Law of Cosines
• Exercise 9.7 Law of Sines and Law of Cosines
• Right Triangles and Trigonometry Review
• Right Triangles and Trigonometry Test
• Right Triangles and Trigonometry Cummulative Assessment

Right Triangles and Trigonometry Maintaining Mathematical Proficiency

Simplify the expression.

Question 1.
√75

Answer:
√75 = 5,625

Explanation:
Given that,
√75
square root of 75 is written as 75 x 75
75 x 75 = 5,625
√75 = 5,625

Question 2.
√270

Answer:
√270 = 72,900

Explanation:
Given that,
√270
square root of 270 is written as 270 x 270
270 x 270 = 72,900
√270 = 72,900

Question 3.
√135

Answer:
√135 = 18,225

Explanation:
Given that,
√135
square root of 135 is written as 135 x 135
135 x 135 = 18,225
√135 = 18,225

Question 4.
\(\frac{2}{\sqrt{7}}\)

Answer:
\(\frac{2}{\sqrt{7}}\) = 0.04

Explanation:
Given that,
\(\frac{2}{\sqrt{7}}\)
square root of 7 is written as, 7 x 7 = 49
\(\frac{2}{\sqrt{7}}\)
So, 2/49 = 0.04

Question 5.
\(\frac{5}{\sqrt{2}}\)

Answer:
\(\frac{5}{\sqrt{2}}\) = 1.25

Explanation:
Given that,
\(\frac{5}{\sqrt{2}}\)
square root of 2 is written as, 2 x 2 = 4
\(\frac{5}{\sqrt{2}}\).
So, 5/4 = 1.25.

Question 6.
\(\frac{12}{\sqrt{6}}\)

Answer:
\(\frac{12}{\sqrt{6}}\) = 0.33

Explanation:
Given that,
\(\frac{12}{\sqrt{6}}\)
square root of 6 is written as, 6 x 6 = 36
\(\frac{12}{\sqrt{6}}\)
\(\frac{12}{36}\)
So, 1/3 = 0.33

Solve the proportion.

Question 7.
\(\frac{x}{12}=\frac{3}{4}\)

Answer:
x = 9

Explanation:
Given that,
\(\frac{x}{12}=\frac{3}{4}\)
x/12 = 3/4
cross multiply on both sides.
4x = 12 x 3
4x = 36
x = \(\frac{36}{4}\)
x = 9

Question 8.
\(\frac{x}{3}=\frac{5}{2}\)

Answer:
x = 7.5

Explanation:
Given that,
\(\frac{x}{3}=\frac{5}{2}\)
x/3 = 5/2
cross multiply on both sides.
2x = 5 x 3
2x = 15
x = 15/2
x = 7.5

Question 9.
\(\frac{4}{x}=\frac{7}{56}\)

Answer:
x = 32

Explanation:
Given that,
\(\frac{4}{x}=\frac{7}{56}\)
4/x = 7/56
cross multiply on both sides.
7x = 56 x 4
7x = 224
x = 224/7
x = 32

Question 10.
\(\frac{10}{23}=\frac{4}{x}\)

Answer:
x = 9.2

Explanation:
Given that,
\(\frac{10}{23}=\frac{4}{x}\)
x/4 = 10/23
cross multiply on both sides.
10x = 23 x 4
10x = 92
x = 92/10
x = 9.2

Question 11.
\(\frac{x+1}{2}=\frac{21}{14}\)

Answer:
x = 135

Explanation:
Given that,
\(\frac{x + 1}{2}=\frac{21}{14}\)
x+12 x 2 = 21×14
cross multiply on both sides.
2x + 24 = 294
2x = 294 – 24
2x = 270
x = 270/2
x = 135

Question 12.
\(\frac{9}{3 x-15}=\frac{3}{12}\)

Answer:
x = 6.33

Explanation:
Given that,
\(\frac{9}{3 x-15}=\frac{3}{12}\)
cross multiply on both sides.
27x – 135 = 3×12
27x = 36 + 135
27x = 171
x = 171/27
x = 6.33

Question 13.
ABSTRACT REASONING
The Product Property of Square Roots allows you to simplify the square root of a product. Are you able to simplify the square root of a sum? of a difference? Explain.

Answer:
Yes, I am able to simplify the square root of a sum.

Explanation:
Given that,
The product property of square roots allows to simplify the square root of a product.
√3 + 1 = √4
√4 = 4 x 4
√4 = 16
√3 – 1 = √2
√2 = 2 x 2
√2 = 4

Right Triangles and Trigonometry Mathematical practices

Monitoring progress

Question 1.
Use dynamic geometry software to construct a right triangle with acute angle measures of 30° and 60° in standard position. What are the exact coordinates of its vertices?

Answer:

Question 2.
Use dynamic geometry software to construct a right triangle with acute angle measures of 20° and 70° in standard position. What are the approximate coordinates of its vertices?
Answer:

9.1 The Pythagorean Theorem

Exploration 1

Proving the Pythagorean Theorem without Words

Work with a partner.

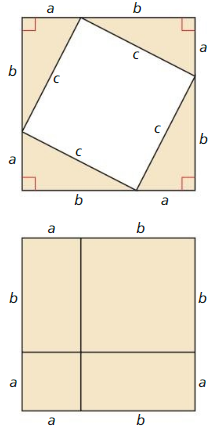
a. Draw and cut out a right triangle with legs a and b, and hypotenuse c.

Answer:

Explanation:
Given that,
proving the Pythagorean theorem without words.
a² + b² = c²

b. Make three copies of your right triangle. Arrange all four triangles to form a large square, as shown.

Answer:
a² + b² = c²

Explanation:
Given that, to make three copies of right triangle.
According to the Pythagorean theorem the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse as shown in the above figure.
a² + b² = c²

c. Find the area of the large square in terms of a, b, and c by summing the areas of the triangles and the small square.

Answer:
The area of the large square = a² x b²

Explanation:
Given that,
Area of the square = l x b
where l = length, and b = breadth
So, the area of the square = a x b
A = a² x b²

d. Copy the large square. Divide it into two smaller squares and two equally-sized rectangles, as shown.
Answer:

e. Find the area of the large square in terms of a and b by summing the areas of the rectangles and the smaller squares.
Answer:

f. Compare your answers to parts (c) and (e). Explain how this proves the Pythagorean Theorem.
Answer:
a² + b² = c²

Explanation:
Given that,
The length of the a and b is equal to the hypotenuse.
According to the Pythagorean theorem,
the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse as shown in the above figure.
a and b are the sides of the length.
So, a² + b² = c²

Exploration 2

Proving the Pythagorean Theorem

Work with a partner:

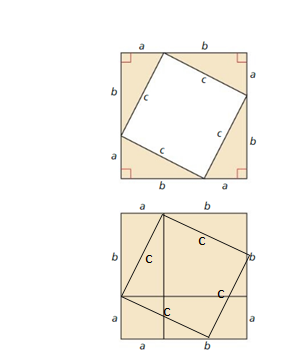
a. Draw a right triangle with legs a and b, and hypotenuse c, as shown. Draw the altitude from C to \(\overline{A B}\) Label the lengths, as shown.

Answer:
a² + b² = c²

Explanation:
Given that,
a² + b² = c²
Pythagorean Theorem states that, the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse as shown in the above figure.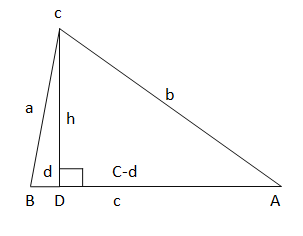

b. Explain why ∆ABC, ∆ACD, and ∆CBD are similar.
Answer:
In a right-angle triangle all the angles are equal.

Explanation:
From the above given figure,
∆ABC, ∆ACD, and ∆CBD are similar.
We know that in a right-angle triangle all the angles are equal.

REASONING ABSTRACTLY
To be proficient in math, you need to know and flexibly use different properties of operations and objects.
Answer:

c. Write a two-column proof using the similar triangles in part (b) to prove that a² + b² = c²

Answer:
a² + b² = c²

Explanation:
Given that,
According to the Pythagorean theorem,
the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse.
Hence, the length of the hypotenuse is equal to the two sides of lengths.
a² + b² = c²

Communicate Your Answer

Question 3.
How can you prove the Pythagorean Theorem?

Answer:
a² + b² = c²

Explanation:
Given that,
In the Pythagorean theorem,
the length of the hypotenuse is equal to the length of the other two sides.
hypotenuse = c
length = a
breadth = b
So, a² + b² = c²

Question 4.
Use the Internet or sonic other resource to find a way to prove the Pythagorean Theorem that is different from Explorations 1 and 2.
Answer:

Lesson 9.1 The Pythagorean Theorem

Monitoring Progress

Find the value of x. Then tell whether the side lengths form a Pythagorean triple.

Question 1.

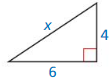
Answer:
x = √52.

Explanation:
Given that,
The side lengths are 6 and 4.
a² + b² = c²
(6 x 6) + (4 x 4) = c²
36 + 16 = c²
52 = c²
c = √52

Question 2.

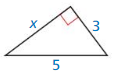
Answer:
x = 4.

Explanation:
Given that,
the side lengths are 3 and 5.
Let a = x
a² + b² = c²
x² + (3 x 3) = (5 x 5)
x² + 9 = 25
x² = 25 – 9
x² = 16
x = 4

Question 3.
An anemometer is a device used to measure wind speed. The anemometer shown is attached to the top of a pole. Support wires are attached to the pole 5 feet above the ground. Each support wire is 6 feet long. How far from the base of the pole is each wire attached to the ground?

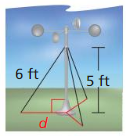
Answer:
x = √11.

Explanation:
Given that,
An anemometer is a device used to measure wind speed.
In the above given figure we observe that,
support wires are attached to the pole 5 feet above the ground.
Each support wire is 6 feet long.
d² + (6 x 6) = (5 x 5)
d² + 36 = 25
d² = 25 – 36
d² = 11
d = √11

Tell whether the triangle is a right triangle.

Question 4.

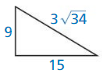
Answer:
Yes, the triangle is a right triangle.

Explanation:
From the above given figure, it is a right angle.
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be right angle.
Given,
hypotenuse = 3 √34 = 5.83 x 3 = 17.49
one side = 15
the other side = 9
15² + 9² = 17.49²
225 + 81 = 306
306 = 306
So, the triangle is a right triangle.

Question 5.

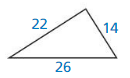
Answer:
Yes, the triangle is a acute triangle.

Explanation:
From the above given figure, it is acute angle.
We know that if the square of the longest side is less than the sum of the squares of two smaller sides then it is said to be acute angle.
a² + b² > c²
Given that,
hypotenuse = 22
one side = 26
the other side = 14
26² + 14² = 22²
676 + 196 = 484
872 = 484
So, the triangle is a acute triangle.

Question 6.
Verify that segments with lengths of 3, 4, and 6 form a triangle. Is the triangle acute, right, or obtuse?
Answer:
Yes, the lengths of the triangle form a acute triangle.

Explanation:
Given that,
the side lengths of 3, 4, and 6 form a triangle.
a² + b² = c²
6 x 6 = 3 x 3 + 4 x 4
36 = 9 + 16
36 = 25
We know that, the square of the longest side is less than the sum of the squares of two smaller sides then it is said to be acute angle.
So, the length of the triangle forms a acute triangle.

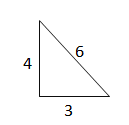
Question 7.
Verify that segments with lengths of 2, 1, 2, 8, and 3.5 form a triangle. Is the triangle acute, right, or obtuse?
Answer:

Exercise 9.1 The Pythagorean Theorem

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
What is a Pythagorean triple?
Answer:

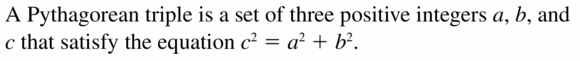
Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

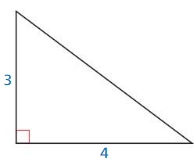
Find the length of the longest side.

Answer:
The length of the longest side = 5

Explanation:
Given that, the side lengths are 3 and 4.
We know that in the Pythagorean theorem, the longest side is equal to the side lengths.
c² = a² + b²
x² = 4² + 3²
x²  = 4 × 4 + 3 × 3
x²  = 16 + 9
x² = 25
X = 5

Find the length of the hypotenuse

Answer:
The length of the hypotenuse = 5.

Explanation:
Given that, the side lengths are 3 and 4.
We know that in the Pythagorean theorem, the longest side is equal to the side lengths.
c² = a² + b²
x² = 4² + 3²
x² = 4 × 4 + 3 × 3
x² = 16 + 9
x² = 25
X = 5

Find the length of the longest leg.

Answer:
The length of the longest leg = 5

Explanation:
Given that, the side lengths are 3 and 4.
We know that in the Pythagorean theorem, the longest side is equal to the side lengths.
c² = a² + b²
x² = 4² + 3²
x² = 4 × 4 + 3 × 3
x² = 16 + 9
x² = 25
X = 5

Find the length of the side opposite the right angle.

Answer:
The length of the side opposite to the right angle = 5

Explanation:
Given that, the side lengths are 3 and 4.
We know that in the Pythagorean theorem, the longest side is equal to the side lengths.
c² = a² + b²
x² = 4² + 3²
x² = 4 × 4 + 3 × 3
x² = 16 + 9
x² = 25
X = 5

Monitoring progress and Modeling with Mathematics

In Exercises 3-6, find the value of x. Then tell whether the side lengths form a Pythagorean triple.

Question 3.

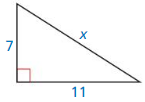
Answer:
x = 13

Explanation:
According to Pythagorean theorem,

Question 4.

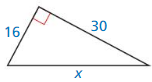
Answer:
The length of the x = 34

Explanation:
Given that, the side lengths are 30 and 16.
We know that in the Pythagorean theorem, the longest side is equal to the side lengths.
c² = a² + b²
x² = 16² + 30²
x² = 16 × 16 + 30 × 30
x²  = 256 + 900
x² = 1156
X = 34

Question 5.

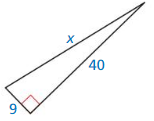
Answer:
x = 41

Explanation:
According to the Pythagorean theorem, the longest side is equal to the side lengths.
Given side lengths are 9 and 40.

Question 6.

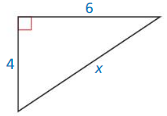
Answer:
The length of the x = 7.2

Explanation:
Given that, the side lengths are 6 and 4.
We know that in the Pythagorean theorem, the longest side is equal to the side lengths.
c² = a² + b²
x² = 6² + 4²
x² = 4 × 4 + 6 × 6
x²  = 16 + 36
x² = 52
X = 7.2

In Exercises 7 – 10, find the value of x. Then tell whether the side lengths form a Pythagorean triple.

Question 7.

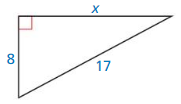
Answer:
x = 15

Explanation:
According to the Pythagorean theorem, the longest side is equal to the side lengths.
Given side lengths are 9 and 40.

Question 8.

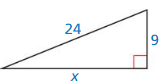
Answer:
The length of the X = 25.6.

Explanation:
Given that, the side lengths are 24 and 9.
We know that in the Pythagorean theorem, the longest side is equal to the side lengths.
c² = a² + b²
x² = 24² + 9²
x² = 24 × 24 + 9 × 9
x²  = 576 + 81
x² = 657
X = 25.6

Question 9.

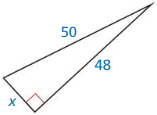
Answer:
x = 14

Explanation:
According to the Pythagorean theorem, the longest side is equal to the side lengths.
Given side lengths are 50 and 48.

Question 10.

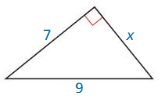
Answer:
The length of the x = 11.4

Explanation:
Given that, the side lengths are 7 and 9.
We know that in the Pythagorean theorem, the longest side is equal to the side lengths.
c² = a² + b²
x² = 7² + 3²
x² = 7 × 7 + 9 × 9.
x² = 49 + 81.
x²  = 130.
X = 11.4.

ERROR ANALYSIS
In Exercises 11 and 12, describe and correct the error in using the Pythagorean Theorem (Theorem 9.1).

Question 11.

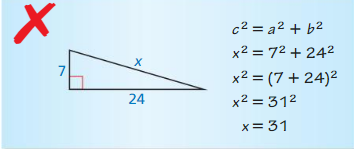
Answer:
x = 25

Explanation:
According to the Pythagorean theorem, the longest side is equal to the side lengths.

Question 12.

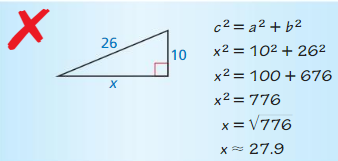
Answer:
x = 24

Explanation:
According to the Pythagorean theorem, the longest side is equal to the side lengths.
Given that, the side lengths are 26 and 10.
c² = a² + b²
26² = a² + 10²
26 × 26 = a² + 10 × 10
676 = a² + 100
676 – 100 = a²
576 = a²
a = 24
So, x = 24

Question 13.
MODELING WITH MATHEMATICS
The fire escape forms a right triangle, as shown. Use the Pythagorean Theorem (Theorem 9. 1) to approximate the distance between the two platforms. (See Example 3.)

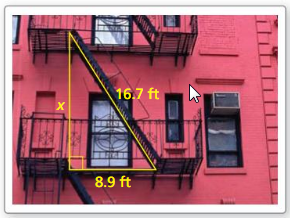
Answer:
x = 14.1 ft

Explanation:
According to the Pythagorean theorem, the longest side is equal to the side lengths.

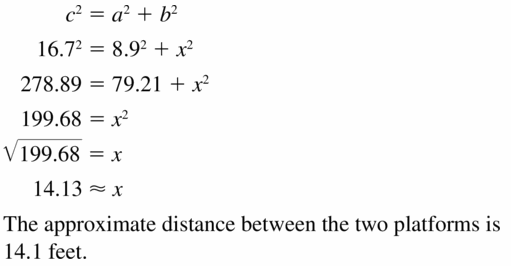
Question 14.
MODELING WITH MATHEMATICS
The backboard of the basketball hoop forms a right triangle with the supporting rods, as shown. Use the Pythagorean Theorem (Theorem 9.1) to approximate the distance between the rods where the meet the backboard.

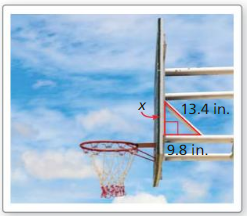
Answer:
x = 9.1.

Explanation:
Given that, the side lengths are 13.4 and 9.8.
According to the Pythagorean Theorem, the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse.
c² = a² + b²
13.4² = x² + 9.8²
13.4 × 13.4 = x² + 9.8 × 9.8.
179.56 = x² + 96.04.
179.56 – 96.04 = x²
83.52 = x²
X = 9.1

In Exercises 15 – 20, tell whether the triangle is a right triangle.

Question 15.

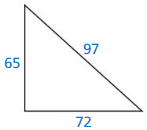
Answer:
Yes, it is a right angle.

Explanation:
From the above given figure, it is a right angle.
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be right angle.
Given,
Hypotheses = 97
Length of the sides are 65 and 72.

Question 16.

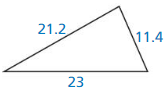
Answer:
No, the triangle is not a right triangle.

Explanation:
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be right angle.
Given, the side lengths are 23 and 11.4 and the hypotenuse is 21.2
c² = a² + b²
21.2² = 23² + 11.4²
21.2 x 21.2 = 23 x 23 + 11.4 x 11.4.
449.44 = 529 + 129.96.
449.44 = 658.96.
449 is not equal to 658.96.
So, the given triangle is not a right triangle.

Question 17.

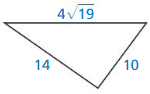
Answer:
No, the triangle is not a right triangle.

Explanation:
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be right angle.
Given, the side lengths are 14 and 10 and the hypotenuse is 4√19

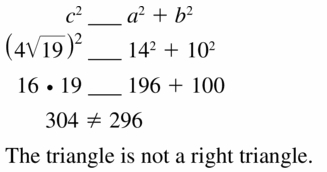
Question 18.

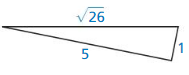
Answer:
No, the triangle is not a right triangle.

Explanation:
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be right angle.
Given, the side lengths are 5 and 1.
hypotenuse = √26
c² = a² + b²
(√26)² = 5² + 1²
26 x 26 = 5 x 5 + 1 x 1
676 = 25 + 1
676 = 26
676 is not equal to 26.
So, the triangle is not a right triangle.

Question 19.

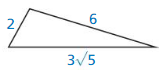
Answer:
No, the triangle is not a right triangle.

Explanation:
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be right angle.
Given, the side lengths are 5 and 1.
hypotenuse = 3√5.

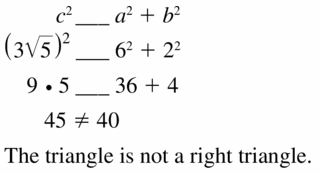
Question 20.

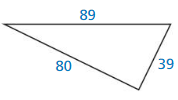
Answer:
Yes, the triangle is a right triangle.

Explanation:
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be a right angle.
Given, the side lengths are 80 and 39.
hypotenuse = 89.
c² = a² + b²
89² = 80² + 39²
89 x 89 = 80 x 80 + 39 x 39
7921 = 6400 + 1521
7921 = 7921
7921 is equal to 7921
So, the triangle forms a right triangle.

In Exercises 21 – 28, verify that the segment lengths form a triangle. Is the triangle acute, right, or obtuse?

Question 21.
10, 11, and 14
Answer:
The line segments 10, 11 and 14 form an acute angle.

Explanation:
We know that if the square of the longest side is less than the sum of the squares of two smaller sides then it is said to be an acute angle.

Question 22.
6, 8, and 10

Answer:
The line segments 6, 8 and 10 form a right triangle.

Explanation:
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be a right angle.
Given that, the side lengths are 8 and 6.
hypotenuse = 10.
c² = a² + b²
10² = 8² + 6²
10 x 10 = 8 x 8 + 6 x 6.
100 = 64 + 36.
100 = 100.
100 is  equal to 100.
So, the triangle is a right triangle.

Question 23.
12, 16, and 20
Answer:
The line segments 10, 11 and 14 form right angle.

Explanation:
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be a right angle.

Question 24.
15, 20, and 36

Answer:
The line segments 15, 20 and 36 form an obtuse triangle.

Explanation:
We know that if the square of the longest side is greater than the sum of the squares of two smaller sides then it is said to be an obtuse angle.
Given that, the side lengths are 15 and 20.
hypotenuse = 36.
c² = a² + b²
36² = 20² + 15²
36 x 36 = 20 x 20 + 15 x 15
1296 = 400 + 225
1296 > 625
1296 is greater than 625
So, the triangle is an obtuse triangle

Question 25.
5.3, 6.7, and 7.8
Answer:
The line segments 5.3, 6.7 and 7.8 form an acute angle.

Explanation:
We know that if the square of the longest side is less than the sum of the squares of two smaller sides then it is said to be an acute angle.

Question 26.
4.1, 8.2, and 12.2

Answer:
The line segments 4.1, 8.2, and 12.2 form an obtuse triangle.

Explanation:
We know that if the square of the longest side is greater than the sum of the squares of two smaller sides then it is said to be an obtuse angle.
Given that, the side lengths are 4.1 and 8.2.
hypotenuse = 12.2.
c² = a² + b²
12.2² = 4.1² + 8.2²
12.2 x 12.2 = 4.1 x 4.1 + 8.2 x 8.2`
148.84 = 16.81 + 67.24
c² > a² + b²
148.84 > 84.05
148.84 is greater than 84.05.
So, the triangle is an obtuse triangle.

Question 27.
24, 30, and 6√43
Answer:
The line segments 24, 30, and 6√43 form an obtuse triangle.

Explanation:
We know that if the square of the longest side is greater than the sum of the squares of two smaller sides then it is said to be an obtuse angle.
Given that, the side lengths are 24 and 30
hypotenuse = 6√43

Question 28.
10, 15 and 5√13

Answer:
The line segments 10, 15, and 5√13 form an acute triangle.

Explanation:
We know that if the square of the longest side is less than the sum of the squares of two smaller sides then it is said to be an acute angle.
the side lengths are 10 and 5√13
the hypotenuse = 15
c² = a² + b²
15² = 10² + (5√13)²
15 x 15 = 10 x 10 + 5√13 x 5√13.
225 = 100 + 34.81.
225 < 134.81.
225 is less than 134.81.
So, the triangle is acute triangle.

Question 29.
MODELING WITH MATHEMATICS
In baseball, the lengths of the paths between consecutive bases are 90 feet, and the paths form right angles. The player on first base tries to steal second base. How far does the ball need to travel from home plate to second base to get the player out?
Answer:
The ball need to travel 127.28 ft from home plate to second base to get the player out.

Explanation:
Given, the baseball lengths of the paths between consecutive bases are 90 feet,
and the paths form right angles.

Question 30.
REASONING
You are making a canvas frame for a painting using stretcher bars. The rectangular painting will be 10 inches long and 8 inches wide. Using a ruler, how can you be certain that the corners of the frame are 90°

Answer:
x = 12.8

Explanation:
According to the Pythagorean theorem the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse as shown in the above figure.
Given that, the side lengths are 10 and 8.
hypotenuse = x
c² = a² + b²
x² = 10² + 8²
x² = 10 x 10 + 8 x 8
X = 100 + 64
X = 12.8

In Exercises 31 – 34, find the area of the isosceles triangle.

Question 31.

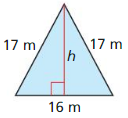
Answer:
Area = 120 sq mt.

Explanation:
We know that the length of the two sides in isosceles triangle are same.

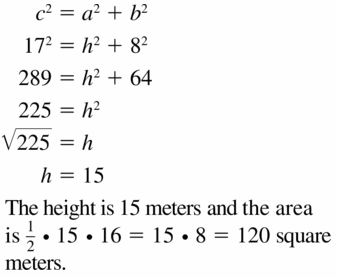
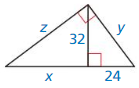
Question 32.

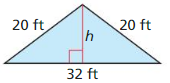
Answer:
Area = 12 ft.

Explanation:
We know that the length of the two sides in isosceles triangle are same.
Given that, base = 32 ft, hypotenuse = 20ft.
a² + b² = c²
h² + 16² = 20²
h² + 16 x 16 = 20 x 20
h² + 256 = 400
h² = 400 – 256
h² = 144
h = 12 ft
So, the area of the isosceles triangle = 12 ft.

Question 33.

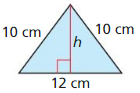
Answer:
Area = 48 sq cm.

Explanation:
We know that the length of the two sides in isosceles triangle are same.

Question 34.

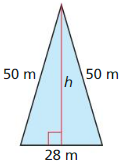
Answer:
Area = 48 sq m.

Explanation:
We know that the length of the two sides in isosceles triangle are same.
Given that, base = 28 m, hypotenuse = 50 m
a² + b² = c²
h² + 14² = 50²
h² + 14 x 14 = 50 x 50
h² + 196 = 2500
h² = 2500 – 196
h² = 2304
h = 48 m
So, the area of the isosceles triangle = 48 m

Question 35.
ANALYZING RELATIONSHIPS
Justify the Distance Formula using the Pythagorean Theorem (Thin. 9. 1).
Answer:

Question 36.
HOW DO YOU SEE IT?
How do you know ∠C is a right angle without using the Pythagorean Theorem (Theorem 9.1) ?

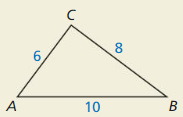
Answer:
Yes, the triangle is a right triangle.

Explanation:
We know that if the square of the longest side is equal the sum of the squares of two smaller sides then it is said to be a right angle.
Given that, the side lengths are 8 and 6.
hypotenuse = 10
10 x 10 = 8 x 8 + 6 x 6.
100 = 64 + 36.
100 = 100.
100 is  equal to 100.
So, the triangle is forming a right triangle.

Question 37.
PROBLEM SOLVING
You are making a kite and need to figure out how much binding to buy. You need the binding for the perimeter of the kite. The binding Comes in packages of two yards. How many packages should you buy?

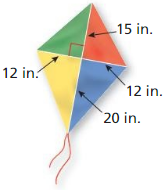
Answer:

Question 38.
PROVING A THEOREM
Use the Pythagorean Theorem (Theorem 9. 1) to prove the Hypotenuse-Leg (HL) Congruence Theorem (Theorem 5.9).

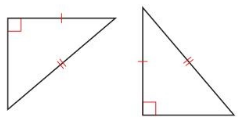
Answer:

Question 39.
PROVING A THEOREM
Prove the Converse of the Pythagorean Theorem (Theorem 9.2). (Hint: Draw ∆ABC with side lengths a, b, and c, where c is the length of the longest side. Then draw a right triangle with side lengths a, b, and x, where x is the length of the hypotenuse. Compare lengths c and x.)
Answer:

Question 40.
THOUGHT PROVOKING
Consider two integers m and n. where m > n. Do the following expressions produce a Pythagorean triple? If yes, prove your answer. If no, give a counterexample.
2mn, m² – n², m² + n²

Answer:

Question 41.
MAKING AN ARGUMENT
Your friend claims 72 and 75 Cannot be part of a Pythagorean triple because 72² + 75² does not equal a positive integer squared. Is your friend correct? Explain your reasoning.
Answer:
No, Friend is not correct.

Explanation:

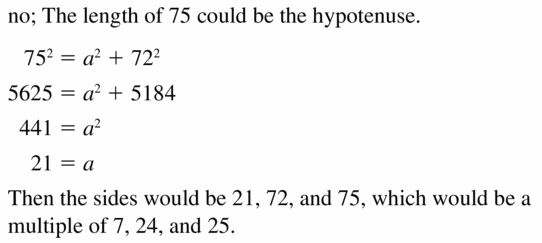
Question 42.
PROVING A THEOREM
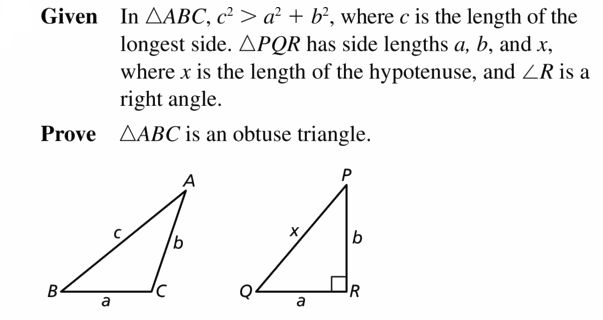
Copy and complete the proof of the Pythagorean Inequalities Theorem (Theorem 9.3) when c² < a² + b².
Given In ∆ABC, c² < a² + b² where c is the length
of the longest side.
∆PQR has side lengths a, b, and x, where x is the length of the hypotenuse, and ∠R is a right angle.
Prove ∆ABC is an acute triangle.

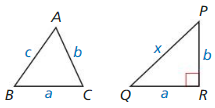
Statements	Reasons
1. In ∆ABC, C2 < (12 + h2, where c is the length of the longest side. ∆PQR has side lengths a, b, and x, where x is the length of the hypotenuse, and ∠R is a right angle.	1. _____________________________
2. a2 + b2 = x2	2. _____________________________
3. c2 < r2	3. _____________________________
4. c < x	4. Take the positive square root of each side.
5. m ∠ R = 90°	5. _____________________________
6. m ∠ C < m ∠ R	6. Converse of the Hinge Theorem (Theorem 6.13)
7. m ∠ C < 90°	7. _____________________________
8. ∠C is an acute angle.	8. _____________________________
9. ∆ABC is an acute triangle.	9. _____________________________

Answer:

Question 43.
PROVING A THEOREM
Prove the Pythagorean Inequalities Theorem (Theorem 9.3) when c² > a² + b². (Hint: Look back at Exercise 42.)
Answer:

Maintaining Mathematical Proficiency

Simplify the expression by rationalizing the denominator.

Question 44.
\(\frac{7}{\sqrt{2}}\)

Answer:
7/√2 = 7√2 /2

Explanation:
Given that,
\(\frac{7}{\sqrt{2}}\) = 7/√2
7/√2 = 7/√2  x √2 /√2
7 √2 /√4
7√2 /2

Question 45.
\(\frac{14}{\sqrt{3}}\)
Answer:

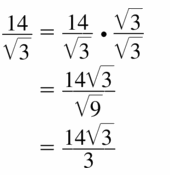
Question 46.
\(\frac{8}{\sqrt{2}}\)

Answer:
8/√2 = 8√2 /2

Explanation:
Given that,
\(\frac{8}{\sqrt{2}}\) = 8/√2
8/√2 = 8/√2  x √2 /√2
8 √2 /√4
8√2 /2

Question 47.
\(\frac{12}{\sqrt{3}}\)
Answer:

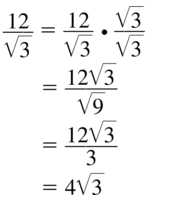
9.2 Special Right Triangles

Exploration 1

Side Ratios of an Isosceles Right Triangle

Work with a partner:

a. Use dynamic geometry software to construct an isosceles right triangle with a leg length of 4 units.
Answer:

b. Find the acute angle measures. Explain why this triangle is called a 45° – 45° – 90° triangle.
Answer:

c. Find the exact ratios of the side lengths (using square roots).
\(\frac{A B}{A C}\) = ____________
\(\frac{A B}{B C}\) = ____________
\(\frac{A B}{B C}\) = ____________

ATTENDING TO PRECISION
To be proficient in math, you need to express numerical answers with a degree of precision appropriate for the problem context.
Answer:

d. Repeat parts (a) and (c) for several other isosceles right triangles. Use your results to write a conjecture about the ratios of the side lengths of an isosceles right triangle.
Answer:

Exploration 2

Work with a partner.

a. Use dynamic geometry software to construct a right triangle with acute angle measures of 30° and 60° (a 30° – 60° – 90° triangle), where the shorter leg length is 3 units.

b. Find the exact ratios of the side lengths (using square roots).
\(\frac{A B}{A C}\) = ____________
\(\frac{A B}{B C}\) = ____________
\(\frac{A B}{B C}\) = ____________

Answer:

C. Repeat parts (a) and (b) for several other 30° – 60° – 90° triangles. Use your results to write a conjecture about the ratios of the side lengths of a 30° – 60° – 90° triangle.
Answer:

Communicate Your Answer

Question 3.
What is the relationship among the side lengths of 45°- 45° – 90° triangles? 30° – 60° – 90° triangles?
Answer:

Lesson 9.2 Special Right Triangles

Monitoring Progress

Find the value of the variable. Write your answer in simplest form.

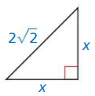
Question 1.

Answer:
x = 4

Explanation:
According to the Pythagorean theorem the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse as shown in the above figure.
Given that, the side lengths are x and x.
hypotenuse = 2√2
c² = a² + b²
(2√2)² = x² + x²
8 = 2x²
x² = 4
x = 4

Question 2.

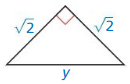
Answer:
y = 2

Explanation:
From the above given figure,
the length of the sides are √2.
c² = a² + b²
y² = (√2)² +(√2)²
y² = 2 + 2
y² = 4
y = 2

Question 3.

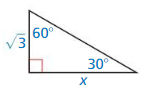
Answer:
x = 3, y = 2√3

Explanation:
Based on the information in the above given figure,
longer leg = shorter leg • √3
Let longer leg be x,
x = √3 • √3
x = 3
Let hypotenuse is y,
hypotenuse = shorter leg • 2
y = √3 • 2
y = 2√3

Question 4

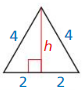
Answer:
h = 2√3

Explanation:
Based on the information in the above given figure,
longer leg = shorter leg • √3
h = 2√3

Question 5.
The logo on a recycling bin resembles an equilateral triangle with side lengths of 6 centimeters. Approximate the area of the logo.
Answer:
Area = \(\frac { 1 }{ 3√3 } \)

Explanation:
Given, the side length of an equilateral triangle is 6 cm.
We know that in equilateral all the sides are equal.
Area = \(\frac { √3 }{ 4 } \) a²
= \(\frac { √3 }{ 4 } \)(6)²
= \(\frac { √3 }{ 4 } \) x 36
= \(\frac { 1 }{ 3√3 } \)

Question 6.
The body of a dump truck is raised to empty a load of sand. How high is the 14-foot-long body from the frame when it is tipped upward by a 60° angle?

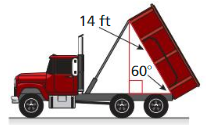
Answer:
\(\frac {28}{3} \) ft .

Explanation:
From the above given information,
Height of body at 90 degrees = 14 ft
Height of body at 1 degree = 14/90
Height of body at 60 degrees = 14 \(\frac {60}{90} \)
= 14 x \(\frac {2}{3} \)
= \(\frac {28}{3} \)  ft

Exercise 9.2 Special Right Triangles

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
Name two special right triangles by their angle measures.
Answer:

Question 2.
WRITING

Explain why the acute angles in an isosceles right triangle always measure 45°.
Answer:
Because the acute angles of a right isosceles triangle must be congruent by the base angles theorem and complementary.
So, their measures must be \(\frac {90°}{2} \) = 45°.

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6, find the value of x. Write your answer in simplest form.

Question 3.

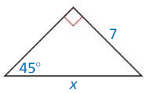
Answer:
x = 7√2

Explanation:
From the above given figure,
the side lengths are 45° and 7.
Let hypotenuse is x.

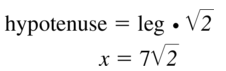
Question 4.

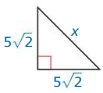
Answer:
x = 10

Explanation:
From the above given figure,
the side lengths are 5√2 and 5√2
Let hypotenuse is x
hypotenuse = leg • √2
x = 5√2 • √2
x = 10

Question 5.

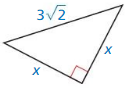
Answer:
x = 3

Explanation:
From the above given figure,
the side lengths are x and x
Let hypotenuse is 3√2

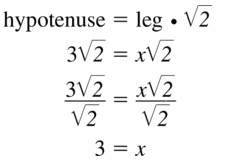
Question 6.

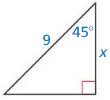
Answer:
x = \(\frac { 9 }{ √2 } \)

Explanation:
From the above given figure,
Let hypotenuse is 9 and angle is 40°
hypotenuse = leg • √2
9 = x • √2
x = \(\frac { 9 }{ √2 } \)

In Exercises 7 – 10, find the values of x and y. Write your answers in simplest form.

Question 7.

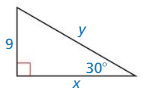
Answer:
x = 9√3 and y = 18

Explanation:
From the above given figure,
the side lengths are x and y.

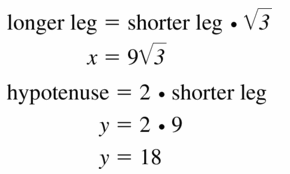
Question 8.

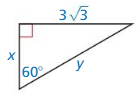
Answer:
x = 3, y = 6

Explanation:
From the above given figure,
longer leg = 3√3
shorter leg = x
hypotenuse = y
hypotenuse = 2 • shorter leg
y = 2 • 3
y = 6
longer leg = √3 • shorter leg
3√3 = √3x
x = 3

Question 9.

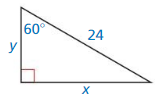
Answer:
y = 12, x = 12√3

Explanation:
Based on the information given in the above figure,
shorter leg = y
hypotenuse = 24
longer leg = x

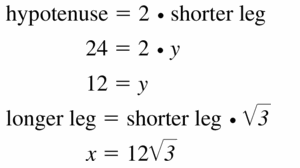
Question 10.

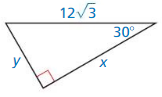
Answer:
x = 18, y = 6√3

Explanation:
Based on the information given in the above figure,
shorter leg = y
hypotenuse = 12√3
longer leg = x
hypotenuse = 2 • shorter leg
12√3 = 2y
y = 6√3
longer leg = √3 • shorter leg
x = √3 . 6√3
x = 18

ERROR ANALYSIS
In Exercises 11 and 12, describe and correct the error in finding the length of the hypotenuse.

Question 11.

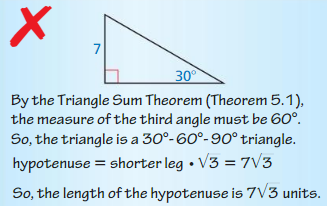
Answer:
Hypotenuse = 14 units

Explanation:

Question 12.

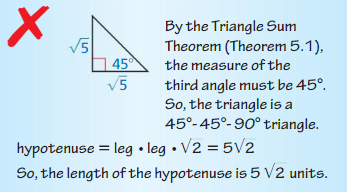
Answer:
Hypotenuse = √10

Explanation:
The hypotenuse of a 45°- 45°- 90° is equal to the shorter leg 2 times.
hypotenuse = leg • √2
x = √5 • √2
x = √10

In Exercises 13 and 14. sketch the figure that is described. Find the indicated length. Round decimal answers to the nearest tenth.

Question 13.
The side length of an equilateral triangle is 5 centimeters. Find the length of an altitude.
Answer:
4.3 centimeters.

Explanation:

Question 14.
The perimeter of a square is 36 inches. Find the length of a diagonal.

Answer:
The length of a diagonal is 9√2.

Explanation:
Given,
The perimeter of a square is 36 inches.
Side of the square = 36/4 = 9
square diagonal = √2a
= √2(9)
= 9√2

In Exercises 15 and 16, find the area of the figure. Round decimal answers to the nearest tenth.

Question 15.

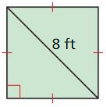
Answer:
Area = 32 sq ft.

Explanation:
Given,
diagonal = 8ft.

Question 16.

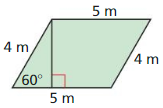
Answer:
Area = 40√(1/3) sq m

Explanation:
From the above given figure,
longer leg = 4m
longer leg = √3 • shorter leg
4 = √3 • shorter leg
shorter leg = 4/√3
h² = 16/3 + 16
h² = 16(4/3)
h = 8√(1/3)
Area of the parallelogram = base x height
= 5(8√(1/3))
= 40√(1/3) sq m

Question 17.
PROBLEM SOLVING
Each half of the drawbridge is about 284 feet long. How high does the drawbridge rise when x is 30°? 45°? 60°?

Answer:
Height = 245.9 ft or 246 ft.

Explanation:

Question 18.
MODELING WITH MATHEMATICS
A nut is shaped like a regular hexagon with side lengths of 1 centimeter. Find the value of x. (Hint: A regular hexagon can be divided into six congruent triangles.)

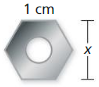
Answer:
x = √3

Explanation:
Given,
Side length = 1cm
We know that a regular hexagon has six equal the side length.
A line drawn from the center to any vertex will have the same length as any side.
This implies the radius is equal to the side length.
As a result, when lines are drawn from the centre to each of the vertexes,
a regular hexagon is said to be made of six equilateral triangles.
From the above diagram given,
x = 2× apothem
Apothem is the distance from the center of a regular polygon to the midpoint of side.
By using Pythagoras theorem, we would get the apothem
Hypotenuse² = opposite² + adjacent²
1² = apothem² + (½)²
Apothem = √(1² -(½)²)
= √(1-¼) = √¾
Apothem = ½√3
x = 2× Apothem = 2 × ½√3
x = √3

Question 19.
PROVING A THEOREM
Write a paragraph proof of the 45°- 45°- 90° Triangle Theorem (Theorem 9.4).
Given ∆DEF is a 45° – 45° – 90° triangle.
Prove The hypotenuse is √2 times as long as each leg.

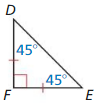
Answer:

Question 20.
HOW DO YOU SEE IT?
The diagram shows part of the wheel of Theodora’s.

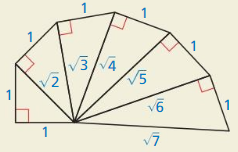
a. Which triangles, if any, are 45° – 45° – 90° triangles?

Answer:

b. Which triangles, if any, are 30° – 60° – 90° triangles?

Answer:

Question 21.
PROVING A THEOREM
Write a paragraph proof of the 30° – 60° – 90° Triangle Theorem (Theorem 9.5).
(Hint: Construct ∆JML congruent to ∆JKL.)
Given ∆JKL is a 30° 60° 9o° triangle.
Prove The hypotenuse is twice as long as the shorter leg, and the longer leg is √3 times as long as the shorter leg.

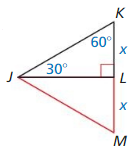
Answer:

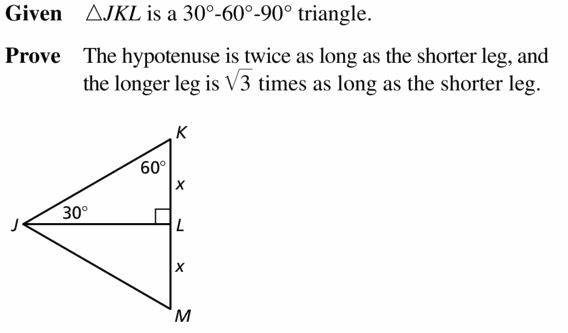
Question 22.
THOUGHT PROVOKING
A special right triangle is a right triangle that has rational angle measures and each side length contains at most one square root. There are only three special right triangles. The diagram below is called the Allies rectangle. Label the sides and angles in the diagram. Describe all three special right triangles.

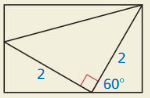
Answer:

Explanation:
According to the Allies rectangle,
It is a rectangle constructed from four right-angled triangles as shown in the above figure.

Question 23.
WRITING
Describe two ways to show that all isosceles right triangles are similar to each other.
Answer:

Question 24.
MAKING AN ARGUMENT
Each triangle in the diagram is a 45° – 45° – 90° triangle. At Stage 0, the legs of the triangle are each 1 unit long. Your brother claims the lengths of the legs of the triangles added are halved at each stage. So, the length of a leg of a triangle added in Stage 8 will be \(\frac{1}{256}\) unit. Is your brother correct? Explain your reasoning.

Answer:

Question 25.
USING STRUCTURE
ΔTUV is a 30° – 60° – 90° triangle. where two vertices are U(3, – 1) and V( – 3, – 1), \(\overline{U V}\) is the hypotenuse. and point T is in Quadrant I. Find the coordinates of T.
Answer:

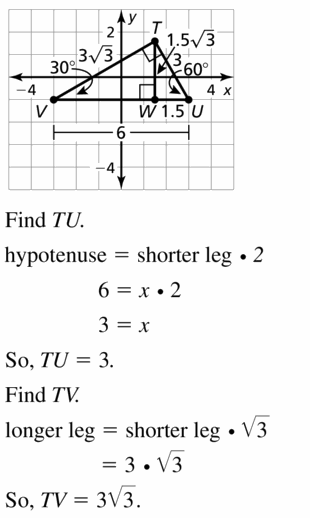
Maintaining Mathematical Proficiency

Find the Value of x.

Question 26.
ΔDEF ~ ΔLMN

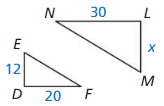
Answer:
x = 18

Explanation:
Given,
ΔDEF ~ ΔLMN
Let LM be x.
\(\frac { DE }{ LM } \) = \(\frac { DF }{ LN } \)
\(\frac { 12 }{ x } \) = \(\frac { 20 }{ 30 } \)
\(\frac { 12 }{ x } \) = \(\frac { 2 }{ 3 } \)
x = 12(\(\frac { 3 }{ 2 } \)) = 18

Question 27.
ΔABC ~ ΔQRS

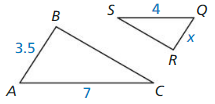
Answer:
x = 2

Explanation:
ΔABC ~ ΔQRS
Let QR be x.

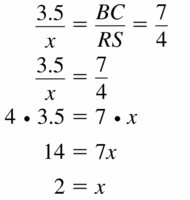
9.3 Similar Right Triangles

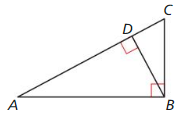
Exploration 1

Writing a Conjecture

a. Use dynamic geometry software to construct right ∆ABC, as shown. Draw \(\overline{C D}\) so that it is an altitude from the right angle to the hypotenuse of ∆ABC.

Answer:

b. The geometric mean of two positive numbers a and b is the positive number x that satisfies
\(\frac{a}{x}=\frac{x}{b}\)
x is the geometric mean of a and b.
Write a proportion involving the side lengths of ∆CBD and ∆ACD so that CD is the geometric mean of two of the other side lengths. Use similar triangles to justify your steps.
Answer:

c. Use the proportion you wrote in part (b) to find CD.
Answer:

d. Generalize the proportion you wrote in part (b). Then write a conjecture about how the geometric mean is related to the altitude from the right angle to the hypotenuse of a right triangle.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to understand and use stated assumptions, definitions, and previously established results in constructing arguments.
Answer:

Exploration 2

Comparing Geometric and Arithmetic Means

Work with a partner:
Use a spreadsheet to find the arithmetic mean and the geometric mean of several pairs of positive numbers. Compare the two means. What do you notice?

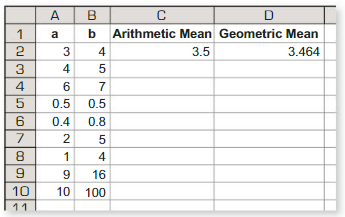
Answer:

Communicate Your Answer

Question 3.
How are altitudes and geometric means of right triangles related?
Answer:

Lesson 9.3 Similar Right Triangles

Monitoring progress

Identify the similar triangles.

Question 1.

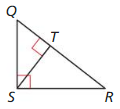
Answer:
△QRS ~ △ QST

Explanation:
The two triangles are said similar,
if they have the same ratio of corresponding sides and equal pair of corresponding angles.
Hence, △QRS and  △ QST are right angle triangles.

Question 2.

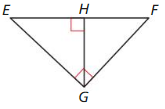
Answer:
△EFG ~ △ EHG

Explanation:
The two triangles are said to be similar,
if they have the same ratio of corresponding sides and equal pair of corresponding angles.
Hence, △EFG and △ EHG are right angle triangles.

Question 3.

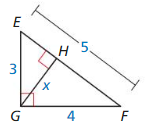
Answer:
△EGH ~ △EFG
\(\frac { EF }{ EG } \) = \(\frac { GF }{ GH } \)
\(\frac { 5 }{ 3 } \) = \(\frac { 4 }{ x } \)
x = 2.4

Explanation:
Area of △EGF = 1/2(GE x GF)
=1/2 x 3 x 4
= 6
Area of △EGH = 1/2(EF x GH)
6 = 1/2 (5x)
12/5 = x
x = 2.4

Question 4.

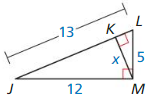
Answer:
x = 4.615

Explanation:
△JLM ~ △LMK
\(\frac { JL }{ LM } \) = \(\frac { JM }{ KM } \)
\(\frac { 13 }{ 5 } \) = \(\frac { 12 }{ x } \)
x = 4.615

Find the geometric mean of the two numbers.

Question 5.
12 and 27

Answer:
x = 18

Explanation:
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
x = √(12 x 27)
x = √324 = 18

Question 6.
18 and 54

Answer:
x = 31.17

Explanation:
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
x = √(18 x 54)
x = √(972)
x = 31.17

Question 7.
16 and 18

Answer:
x = 16.970

Explanation:
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
x = √(16 x 18) = √(288)
x = 16.970

Question 8.
Find the value of x in the triangle at the left.

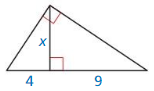
Answer:
x = 6

Explanation:
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
x = √(9 x 4)
x = 6

Question 9.
WHAT IF?
In Example 5, the vertical distance from the ground to your eye is 5.5 feet and the distance from you to the gym wall is 9 feet. Approximate the height of the gym wall.
Answer:
w = 20.22

Explanation:
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
9² = 5.5 x w
81 = 5.5 x w
w = 14.72
The height of the wall = 14.72 + 5.5 = 20.22

Exercise 9.3 Similar Right Triangles

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
If the altitude is drawn to the hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and ____________ .
Answer:

Question 2.
WRITING
In your own words, explain geometric mean.
Answer:
The geometric mean is the average value or mean that signifies the central tendency of set of numbers by finding the product of their values.

Monitoring progress and Modeling with Mathematics

In Exercises 3 and 4, identify the similar triangles.

Question 3.

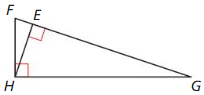
Answer:

△HFE ~ △GHE ~ △GFH

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
Hence, △HFE ~ △GHE ~ △GFH

Question 4.

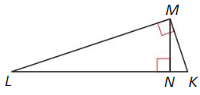
Answer:
△LKM ~ △LMN ~ △MKN

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
Hence, △LKM ~ △LMN ~ △MKN

In Exercises 5 – 10, find the value of x.

Question 5.

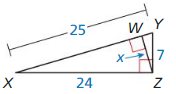
Answer:
x = 6.72

Explanation:
Based on the information in the given figure,

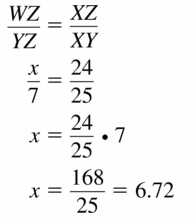
Question 6.

Answer:
x = 9.6

Explanation:
Based on the information in the above given figure,
\(\frac { QR }{ SR } \) = \(\frac { SR }{ TS } \)
\(\frac { 20 }{ 16 } \) = \(\frac { 12 }{ x } \)
cross multiply on both sides.
1.25 = \(\frac { 12 }{ x } \)
x = 9.6

Question 7.

Answer:
x = 13.8

Explanation:
Based on the information in the above given figure,

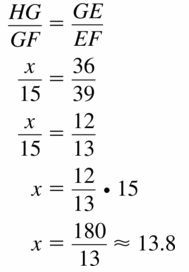
Question 8.

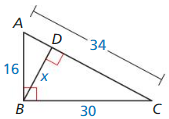
Answer:
x = 14.11

Explanation:
Based on the information in the above given figure,
\(\frac { AB }{ AC } \) = \(\frac { BD }{ BC } \)
\(\frac { 16 }{ 34 } \) = \(\frac { x }{ 30 } \)
x = 14.11

Question 9.

Answer:
x = 11.2 ft

Explanation:
Based on the information in the above given figure,

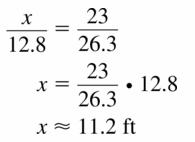
Question 10.

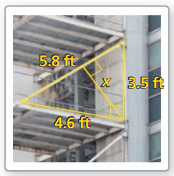
Answer:
x = 2.77

Explanation:
Based on the information in the above given figure,
\(\frac { 5.8 }{ 3.5 } \) = \(\frac { 4.6 }{ x } \)
x = 2.77

In Exercises 11 – 18, find the geometric mean of the two numbers.

Question 11.
8 and 32

Answer:
x = 16

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)

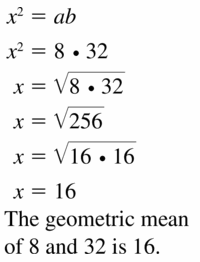
Question 12.
9 and 16

Answer:
x = 12

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
x = √(9 x 16)
x = 12

Question 13.
14 and 20
Answer:
x = 2√70

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)

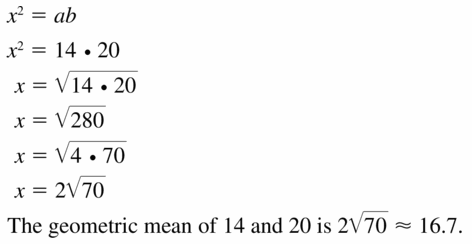
Question 14.
25 and 35

Answer:
x = 29.5

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
x = √(25 x 35)
x = 29.5

Question 15.
16 and 25

Answer:
x = 20

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)

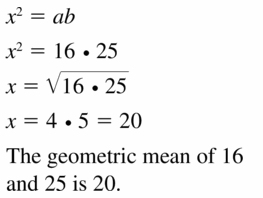
Question 16.
8 and 28

Answer:
x = 14.96

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
x = √(8 x 28)
x = 14.96

Question 17.
17 and 36

Answer:
x =6√17

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)

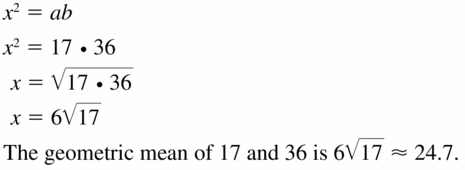
Question 18.
24 and 45

Answer:
x =32.86

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
x = √(24 x 45)
x = 32.86

In Exercises 19 – 26. find the value of the variable.

Question 19.

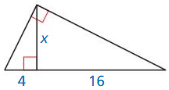
Answer:
x =32.86

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)

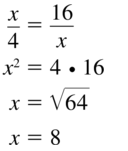
Question 20.

Answer:
x =2√10

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
y = √(5 x 8)
y = √40
y = 2√10

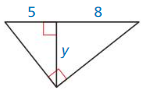
Question 21.

Answer:
y = 27

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
18 x 18 = 12 x  y

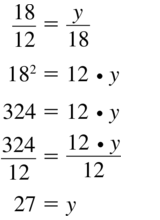
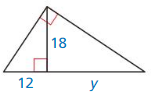
Question 22.

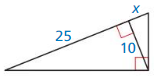
Answer:
x=4

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
10 • 10 = 25 • x
100 = 25x
x = 4

Question 23.

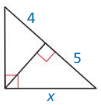
Answer:
x=6.7

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
h = √(4 x 5)
h = 4.47

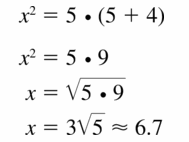
Question 24.

Answer:
b = 18.76

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
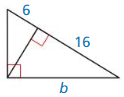
b² = 16(16 + 6)
b² = 16(22) = 352
b = 18.76

Question 25.

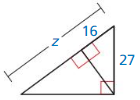
Answer:
z = 45.6

Explanation:
Based on the information in the above given figure,

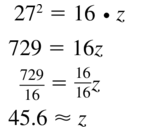
Question 26.

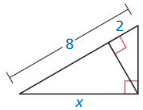
Answer:
x = 8.9

Explanation:
Based on the information in the above given figure,
x² = 8(8 + 2)
x² = 8(10) = 80
x = 8.9

ERROR ANALYSIS
In Exercises 27 and 28, describe and correct the error in writing an equation for the given diagram.

Question 27.

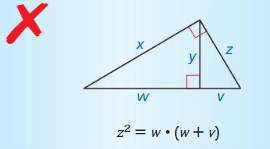
Answer:

Question 28.

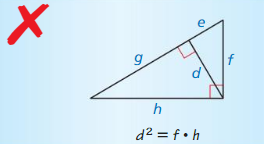
Answer:
d² = g • e

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
h = √(a x b)
d = √(g x e)

MODELING WITH MATHEMATICS
In Exercises 29 and 30, use the diagram.

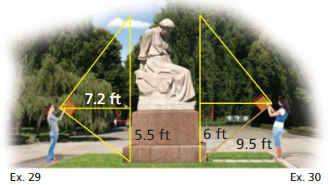
Question 29.
You want to determine the height of a monument at a local park. You use a cardboard square to line up the top and bottom of the monument, as shown at the above left. Your friend measures the vertical distance from the ground to your eye and the horizontal distance from you to the monument. Approximate the height of the monument.
Answer:
h = 14.9 ft

Explanation:
Based on the information in the above given figure,

Question 30.
Your classmate is standing on the other side of the monument. She has a piece of rope staked at the base of the monument. She extends the rope to the cardboard square she is holding lined up to the top and bottom of the monument. Use the information in the diagram above to approximate the height of the monument. Do you get the same answer as in Exercise 29? Explain your reasoning.

Answer:

MATHEMATICAL CONNECTIONS
In Exercises 31 – 34. find the value(s) of the variable(s).

Question 31.

Answer:
a = 3

Explanation:
Based on the information in the above given figure,

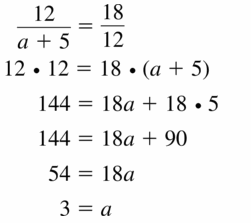
Question 32.

Answer:
b = \(\frac { 3 }{ 2 } \)

Explanation:
Based on the information in the above given figure,
\(\frac { 6 }{ b + 3 } \) = \(\frac { 8 }{ 6 } \)
36 = 8(b + 3)
36 = 8b + 24
8b = 12
b = \(\frac { 3 }{ 2 } \)

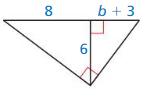
Question 33.

Answer:
x = 9, y = 15 and z = 20

Explanation:
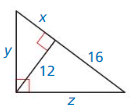
Based on the information in the above given figure,

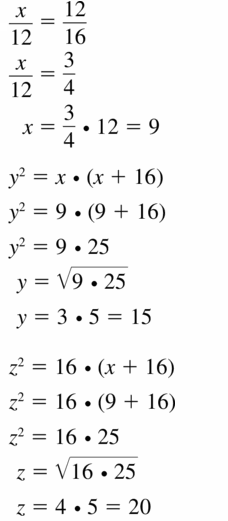
Question 34.

Answer:
x = 42.66, y = 40, z = 53

Explanation:
Based on the information in the above given figure,
\(\frac { 24 }{ 32 } \) = \(\frac { 32 }{ x } \)
0.75 = \(\frac { 32 }{ x } \)
x = 42.66
y = √24² + 32²
y = √576 + 1024 = 40
z = √42.66² + 32² = √1819.87 + 1024 = 53

Question 35.
REASONING
Use the diagram. Decide which proportions are true. Select all that apply.

(A) \(\frac{D B}{D C}=\frac{D A}{D B}\)
(B) \(\frac{B A}{C B}=\frac{C B}{B D}\)
(C) \(\frac{C A}{B \Lambda}=\frac{B A}{C A}\)
(D) \(\frac{D B}{B C}=\frac{D A}{B A}\)
Answer:

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
So, A and D are true.

Question 36.
ANALYZING RELATIONSHIPS
You are designing a diamond-shaped kite. You know that AD = 44.8 centimeters, DC = 72 centimeters, and AC = 84.8 centimeters. You Want to use a straight crossbar \(\overline{B D}\). About how long should it be? Explain your reasoning.

Answer:
BD = 76.12

Explanation:
Based on the information in the above given figure,
AD = 44.8 cm, DC = 72 cm, and AC = 84.8 cm
We know that two disjoint pairs of consecutive sides are congruent.
So, AD = AB = 44.8 cm
DC = BC = 72 cm
The diagonals are perpendicular.
So, AC ⊥ BD
AC = AO + OC
AX = x + y = 84.8 — (i)
Perpendicular bisects the diagonal BD into equal parts let it be z.
BD = BO + OD
BD = z + z
Using Pythagorean theorem
44.8² = x² + z² —- (ii)
72² = y² + z² —– (iii)
Subtract (ii) and (iii)
72² – 44.8² = y²+ z² – x² – z²
5184 – 2007.04 = (x + y) (x – y)
3176.96 = (84.8)(x – y)
37.464 = x – y —- (iv)
Add (i) & (iv)
x + y + x – y = 84.8 + 37.464
2x = 122.264
x = 61.132
x + y = 84.8
61.132 + y = 84.8
y = 23.668
44.8² = x² + z²
z = 38.06
BD = z + z
BD = 76.12

Question 37.
ANALYZING RELATIONSHIPS
Use the Geometric Mean Theorems (Theorems 9.7 and 9.8) to find AC and BD.

Answer:
AC = 25, BD = 12

Explanation:
Based on the information in the above given figure,

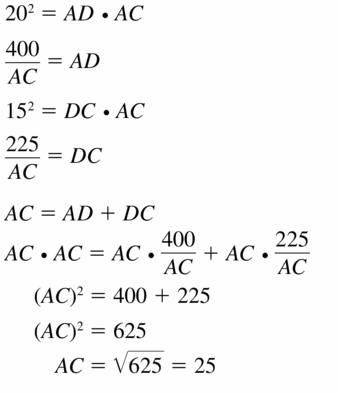
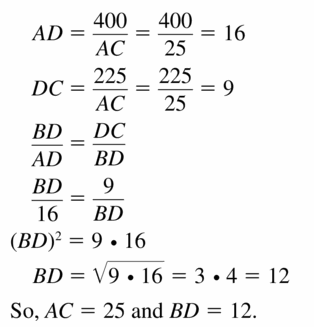
Question 38.
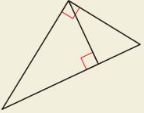
HOW DO YOU SEE IT?
In which of the following triangles does the Geometric Mean (Altitude) Theorem (Theorem 9.7) apply?
(A)

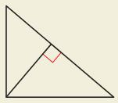
(B)

(C)

(D)

Answer:

Question 39.
PROVING A THEOREM
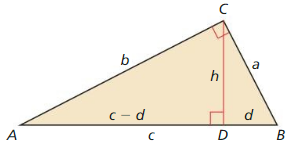
Use the diagram of ∆ABC. Copy and complete the proof of the Pythagorean Theorem (Theorem 9. 1).

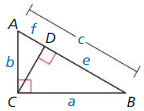
Given In ∆ABC, ∆BCA is a right angle.
Prove c² = a² + b²

Statements	Reasons
1. In ∆ABC, ∠BCA is a right angle.	1. ________________________________
2. Draw a perpendicular segment (altitude) from C to \(\overline{A B}\).	2. Perpendicular Postulate (Postulate 3.2)
3. ce = a2 and cf = b2	3. ________________________________
4. ce + b2 = ___  + b2	4. Addition Property of Equality
5. ce + cf = a2 + b2	5. ________________________________
6. c(e + f) a2 + b2	6. ________________________________
7. e + f = ________	7. Segment Addition Postulate (Postulate 1.2)
8. c  • c = a2 + b2	8. ________________________________
9. c2 = a2 + b2	9. Simplify.

Answer:

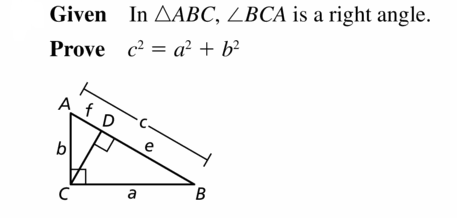
Question 40.
MAKING AN ARGUMENT
Your friend claims the geometric mean of 4 and 9 is 6. and then labels the triangle, as shown. Is your friend correct? Explain your reasoning.

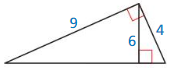
Answer:
My friend is correct.

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
G.M = √(4 x 9)
= √36 = 6

In Exercises 41 and 42, use the given statements to prove the theorem.

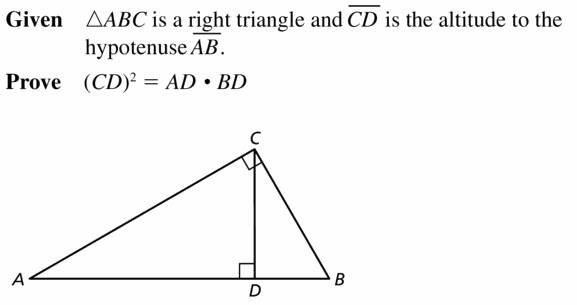
Gein ∆ABC is a right triangle.
Altitude \(\overline{C D}\) is drawn to hypotenuse \(\overline{A B}\).

Question 41.
PROVING A THEOREM
Prove the Geometric Mean (Altitude) Theorem (Theorem 9.7) b showing that CD² = AD • BD.
Answer:

Question 42.
PROVING A THEOREM
Prove the Geometric Mean ( Leg) Theorem (Theorem 9.8) b showing that CB² = DB • AB and AC² = AD • AB.

Answer:

Question 43.
CRITICAL THINKING
Draw a right isosceles triangle and label the two leg lengths x. Then draw the altitude to the hypotenuse and label its length y. Now, use the Right Triangle Similarity Theorem (Theorem 9.6) to draw the three similar triangles from the image and label an side length that is equal to either x or y. What can you conclude about the relationship between the two smaller triangles? Explain your reasoning.
Answer:

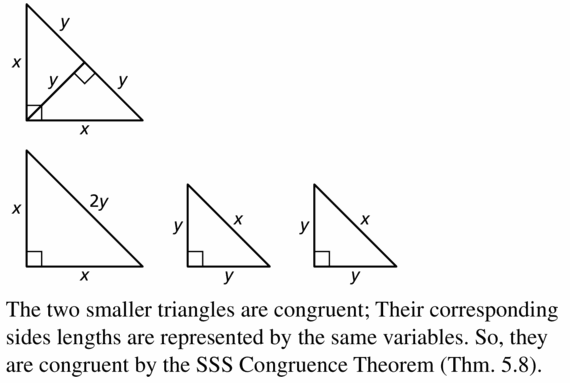
Question 44.
THOUGHT PROVOKING
The arithmetic mean and geometric mean of two nonnegative numbers x and y are shown.
arithmetic mean = \(\frac{x+y}{2}\)
geometric mean = \(\sqrt{x y}\)
Write an inequality that relates these two means. Justify your answer.

Answer:

Question 45.
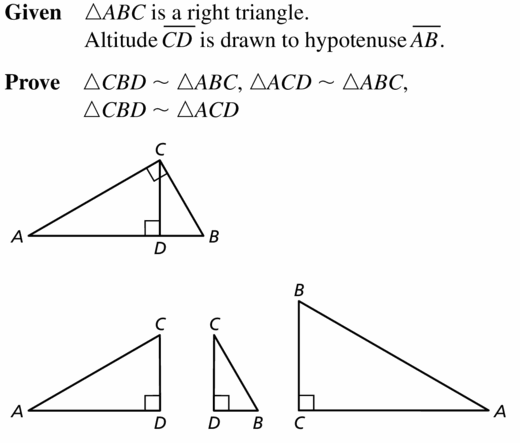
PROVING A THEOREM
Prove the Right Triangle Similarity Theorem (Theorem 9.6) by proving three similarity statements.
Given ∆ABC is a right triangle.
Altitude \(\overline{C D}\) is drawn to hvpotenuse \(\overline{A B}\).
Prove ∆CBD ~ ∆ABC, ∆ACD ~ ∆ABC,
∆CBD ~ ∆ACD
Answer:

Maintaining Mathematical proficiency

Solve the equation for x.

Question 46.
13 = \(\frac{x}{5}\)
Answer:
x = 65

Explanation:
Given,
13 = \(\frac{x}{5}\)
x = 13 x 5
x = 65

Question 47.
29 = \(\frac{x}{4}\)
Answer:
x 116

Explanation:
Given,
29 = \(\frac{x}{4}\)

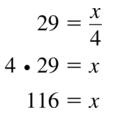
Question 48.
9 = \(\frac{78}{x}\)
Answer:
x = 8.6

Explanation:
Given,
9 = \(\frac{78}{x}\)
9x = 78
x = 8.6

Question 49.
30 = \(\frac{115}{x}\)
Answer:
x = 3.8

Explanation:
Given,
30 = \(\frac{115}{x}\)

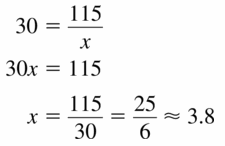
9.1 to 9.3 Quiz

Find the value of x. Tell whether the side lengths form a Pythagorean triple.

Question 1.

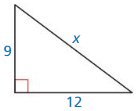
Answer:
x = 15

Explanation:
Based on the information given in the above figure,
A Pythagorean triple consists of three positive integers a, b, and c,
such that a² + b² = c²
Hypothenuse is x, and the length of the sides are 12 and g.
x² = 9² + 12²
x² = 81 + 144
x² = 225
x = 15

Question 2.

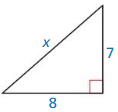
Answer:
x = 10.63

Explanation:
Based on the information given in the above figure,
A Pythagorean triple consists of three positive integers a, b, and c,
such that a² + b² = c²
Hypothenuse is x, and the length of the sides are 7 and 8.
x² = 7² + 8²
x² = 49 + 64
x = √113
x = 10.63

Question 3.

Answer:
x = 4√3

Explanation:
Based on the information given in the above figure,
A Pythagorean triple consists of three positive integers a, b, and c,
such that a² + b² = c²
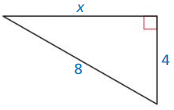
Hypothenuse is 8, and the length of the sides are x and 4.
8² = x² + 4²
64 = x² + 16
x² = 48
x = 4√3

Verify that the segment lengths form a triangle. Is the triangle acute, right, or obtuse?
(Section 9.1)
Question 4.
24, 32, and 40

Answer:
The line segments 24, 32 and 40 form a right angle triangle.

Explanation:
Given that, the side lengths are 24, 32 and 40
We know that if the square of the longest side is equal to the sum of the squares of two smaller sides then it is said to be right angle.
c² = a² + b²
40² = 24² + 32²
1600 = 576 + 1024
1600 = 1600
So, the triangle is a right angle triangle.

Question 5.
7, 9, and 13

Answer:
The line segments 7, 9 and 13 form an obtuse triangle.

Explanation:
Given that, the side lengths are 7, 9 and 13
We know that if the square of the longest side is greater than to the sum of the squares of two smaller sides then it is said to be obtuse angle.
c² = a² + b²
13² = 7² + 9²
169 = 49 + 81
169 = 130
13² > 7² + 9²
So, the triangle is an obtuse triangle.

Question 6.
12, 15, and 10√3

Answer:
The line segments 12, 15 and 10√3 form an acute triangle.

Explanation:
Given that, the side lengths are 12, 15 and 10√3
We know that if the square of the longest side is less than to the sum of the squares of two smaller sides then it is said to be acute angle.
c² = a² + b²
15² = 12² + (10√3)²
225 = 144 + 300
225 = 444
15² < 12² + (10√3)²
So, the triangle is an acute triangle.

Find the values of x and y. Write your answers in the simplest form.

Question 7.

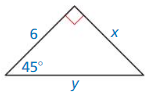
Answer:
x = 6, y = 6√2

Explanation:
Based on the information from the above figure,
x = 6, hypotenuse = leg • √2 and
y = 6√2

Question 8.

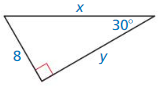
Answer:
y = 8√3, x = 16

Explanation:
Based on the information from the above figure,
Given shorter leg is 8
longer leg = shorter leg • √3
y = 8√3
x² = 8² + (8√3)²
x = 64 + 192
x = 256
x = 16

Question 9.

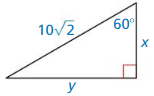
Answer:
x = 5√2, y = 5√6

Explanation:
Based on the information from the above figure,
longer leg = shorter leg • √3
y = x√3, hypotenuse = 10√2, shorter leg = x
hypotenuse = shorter leg • 2
10√2 = 2x
x = 5√2
we know that y = x√2
Substitute the value of x.
y = 5√6

Find the geometric mean of the two numbers.

Question 10.
6 and 12

Answer:
G.M = 6√2

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
G.M = √(a x b)
G.M = √(6 • 12) = 6√2

Question 11.
15 and 20

Answer:
G.M = 10√3

Explanation:
Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
G.M = √(a x b)
G.M = √(15 • 20) = 10√3

Question 12.
18 and 26

Answer:
G.M = 6√13

Based on the information in the above given figure,
Geometric mean is obtained by multiplying all the numbers together and taking the nth root of the product.
G.M = √(a x b)
G.M = √(18 • 26) = 6√13

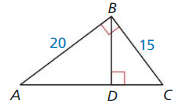
Identify the similar right triangles. Then find the value of the variable.

Question 13.

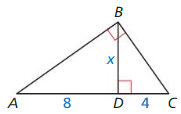
Answer:
x = 4√2

Explanation:
We know that,
If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle, then the triangles are similar.
Based on the information given in the above figure,
x = √(8 • 4)
x = 4√2

Question 14.

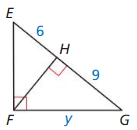
Answer:
y = 3√6

We know that,
If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle, then the triangles are similar.
Based on the information given in the above figure,
y = √(9 • 6)
y = 3√6

Question 15.

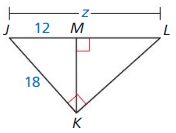
Answer:

Question 16.
Television sizes are measured by the length of their diagonal. You want to purchase a television that is at least 40 inches. Should you purchase the television shown? Explain your reasoning.

Answer:
Yes, I will purchase the television.

Explanation:
Given,
The length of the diagonals 20.25 in and 36 in.
want to purchase a television that is at least 40 inches.
Based on the above information,
x² = 20.25² + 36²
x² = 410.0625 + 1296
x² = 1706.0625
x = 41.30

Question 17.
Each triangle shown below is a right triangle.

a. Are any of the triangles special right triangles? Explain your reasoning.
Answer:
A is a similar triangle.

Explanation:
We know that,
Special right triangles are those right-angled triangles whose interior angles are fixed and whose sides are always in a defined ratio.
Based on the information given in the above figure,
So, A is a special right triangle triangle.

b. List all similar triangles. if any.
Answer:
B, C and D, E are similar triangles.

Explanation:
We know that,
If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle, then the triangles are similar.
Based on the information given in the above figure,
B, C and D, E are similar triangles.

c. Find the lengths of the altitudes of triangles B and C.
Answer:
B altitude = 6
C altitude = 6√3

Explanation:
The altitude of a triangle is a perpendicular that is drawn from the vertex of a triangle to the opposite side.
Hence, the length of the altitudes of triangles B and C.
B altitude = √(9 + 27)
= √36
= 6
C altitude = √(36 + 72)
= √108
= 6√3

9.4 The Tangent Ratio

Exploration 1

Calculating a Tangent Ratio

Work with a partner

a. Construct ∆ABC, as shown. Construct segments perpendicular to \(\overline{A C}\) to form right triangles that share vertex A and arc similar to ∆ABC with vertices, as shown.

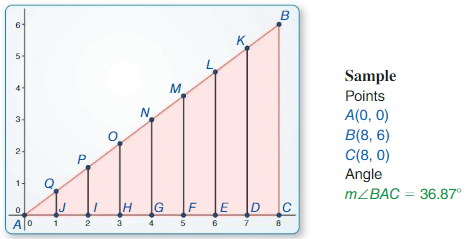
Answer:

b. Calculate each given ratio to complete the table for the decimal value of tan A for each right triangle. What can you Conclude?

Answer:

Exploration 2

Using a calculator

Work with a partner: Use a calculator that has a tangent key to calculate the tangent of 36.87°. Do you get the same result as in Exploration 1? Explain.
ATTENDING TO PRECISION
To be proficient in math, you need to express numerical answers with a degree of precision appropriate for the problem context.
Answer:

Communicate Your Answer

Question 3.
Repeat Exploration 1 for ∆ABC with vertices A(0, 0), B(8, 5), and C(8, 0). Construct the seven perpendicular segments so that not all of them intersect \(\overline{A C}\) at integer values of x. Discuss your results.
Answer:

Question 4.
How is a right triangle used to find the tangent of an acute angle? Is there a unique right triangle that must be used?
Answer:

Lesson 9.4 The Tangent Ratio

Monitoring progress

Find tan J and tan K. Write each answer as a fraction and as a decimal rounded to four places.

Question 1.

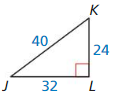
Answer:
tan J = 0.75
tan K = 1.33

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan K = \(\frac { opposite side }{ adjacent side } \)
= \(\frac { JL }{ KL } \)
= \(\frac { 32 }{ 24 } \)
= \(\frac { 4 }{ 3 } \)
= 1.33
tan J = \(\frac { opposite side }{ adjacent side } \)
= \(\frac { KL }{ JL } \)
= \(\frac { 24 }{ 32 } \)
= \(\frac { 3 }{ 4 } \)
= 0.75

Question 2.

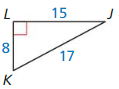
Answer:
tan J = 0.53
tan K = 1.87

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan K = \(\frac { opposite side }{ adjacent side } \)
= \(\frac { LJ }{ LK } \)
= \(\frac { 15 }{ 8 } \)
= 1.87
tan J = \(\frac { opposite side }{ adjacent side } \)
= \(\frac { LK }{ LJ } \)
= \(\frac { 8 }{ 15 } \)
= 0.53

Find the value of x. Round your answer to the nearest tenth.

Question 3.

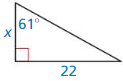
Answer:
x = 12.1951

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan 61 = \(\frac { opposite side }{ adjacent side } \)
tan 61 = \(\frac { 22 }{ x } \)
from the logarithms we know that, tan 61 = 1.804
1.804 = \(\frac { 22 }{ x } \)
x = 12.1951

Question 4.

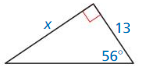
Answer:
x = 19.266

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan 56 = \(\frac { opposite side }{ adjacent side } \)
tan 56 = \(\frac { x }{ 13 } \)
from the logarithms we know that, tan56 = 1.482
1.482 = \(\frac { x }{ 13 } \)
x = 19.266

Question 5.
WHAT IF?
In Example 3, the length of the shorter leg is 5 instead of 1. Show that the tangent of 60° is still equal to √3.

Answer:
Given,
In the above Example 3, the length of the shorter leg is 5 instead of 1.
The tangent of 60° is still equal to √3.
longer leg = shorter leg • √3
= 5√3
Tangent ratio = \(\frac { opposite side }{ adjacent side } \)
tan 60 = \(\frac { 5√3 }{ 5 } \)
= √3
Hence, if we change the length of the shorter leg 5 instead of 1,
there is no change in the tangent of 60° is still equal to √3.

Question 6.
You are measuring the height of a lamppost. You stand 40 inches from the base of the lamppost. You measure the angle of elevation from the ground to the top of the lamppost to be 70°. Find the height h of the lamppost to the nearest inch.

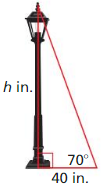
Answer:
h = 109.896 in

Explanation:
Given,
When you stand 40 inches from the base of the lamppost.
You measure the angle of elevation from the ground to the top of the lamppost to be 70°.
Tangent ratio = \(\frac { opposite side }{ adjacent side } \)
tan 70 = \(\frac { h }{ 40 } \)
from the logarithms we know that, tan 70 = 2.7474
2.7474 = \(\frac { h }{ 40 } \)
h = 109.896 in

Exercise 9.4 The Tangent Ratio

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
The tangent ratio compares the length of _________ to the length of ___________ .
Answer:

Question 2.
WRITING
Explain how you know the tangent ratio is constant for a given angle measure.

Answer:
When two triangles are similar, then the corresponding sides are proportional which makes the ratio constant for a given acute angle measurement.

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6, find the tangents of the acute angles in the right triangle. Write each answer as a fraction and as a decimal rounded to four decimal places.

Question 3.

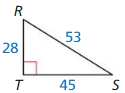
Answer:
tan S = 0.622
tan R = 1.607

Explanation:
From the above given information,
Tangent ratio = \(\frac { opposite side }{ adjacent side } \)

Question 4.

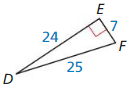
Answer:
tan F = 3.42
tan D = 0.29

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)
tan F = \(\frac { DE }{ EF } \)
= \(\frac { 24 }{ 7 } \)
= 3.42
tan D = \(\frac { EF }{ DE } \)
= \(\frac { 7 }{ 24 } \)
= 0.29

Question 5.

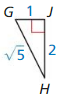
Answer:
tan G = 2
tan H = 0.5

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)

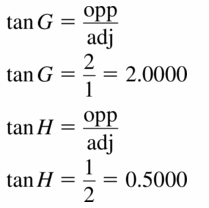
Question 6.

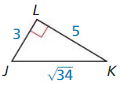
Answer:
tan K = 0.6
tan J = 1.6

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)
tan K = \(\frac { JL }{ LK } \)
= \(\frac { 3 }{ 5 } \)
= 0.6
tan J = \(\frac { LK }{ JL } \)
= \(\frac { 5 }{ 3 } \)
= 1.6

In Exercises 7 – 10, find the value of x. Round your answer to the nearest tenth.

Question 7.

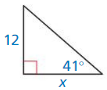
Answer:
x = 13.8

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)

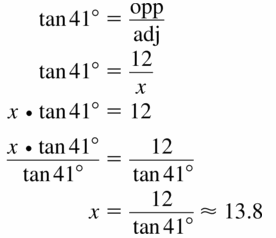
Question 8.

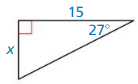
Answer:
x = 7.635

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)
tan 27 = \(\frac { x }{ 15 } \)
from the logarithms we know that, tan 27 = 0.509
0.509 = \(\frac { x }{ 15 } \)
x = 7.635

Question 9.

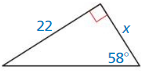
Answer:
x = 13.7

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)

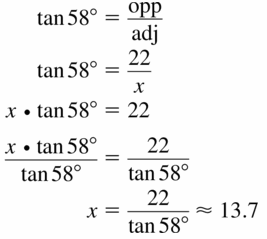
Question 10.

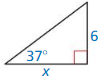
Answer:
x = 7.968

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)
tan 37 = \(\frac { 6 }{ x } \)
According to logarithm tan 37 = 0.753
0.753 = \(\frac { 6 }{ x } \)
x = 7.968

ERROR ANALYSIS
In Exercises 11 and 12, describe the error in the statement of the tangent ratio. Correct the error if possible. Otherwise, write not possible.

Question 11.

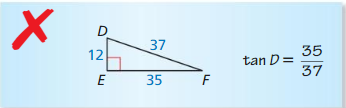
Answer:

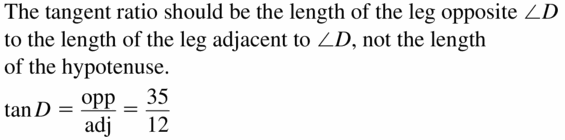
Question 12.

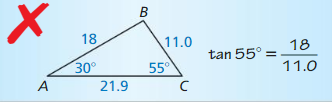
Answer:

In Exercises 13 and 14, use a special right triangle to find the tangent of the given angle measure.

Question 13.
45°
Answer:
tan 45° = 1

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)

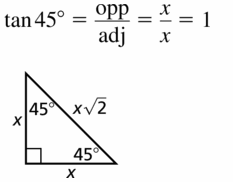
Question 14.
30°

Answer:
tan 30° = \(\frac { 1 }{ √3 } \)

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)
tan 30° = \(\frac { 1 }{ √3 } \)

Question 15.
MODELING WITH MATHEMATICS
A surveyor is standing 118 Feet from the base of the Washington Monument. The surveyor measures the angle of elevation from the ground to the top of the monument to be 78°. Find the height h of the Washington Monument to the nearest foot.

Answer:
h = 555 ft.

Explanation:
Given, A surveyor is standing 118 Feet from the base of the Washington Monument.
The surveyor measures the angle of elevation from the ground to the top of the monument to be 78°.

Question 16.
MODELING WITH MATHEMATICS
Scientists can measure the depths of craters on the moon h looking at photos of shadows. The length of the shadow cast by the edge of a crater is 500 meters. The angle of elevation of the rays of the Sun is 55°. Estimate the depth d of the crater.

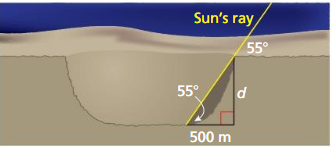
Answer:
Depth = 714 m.

Explanation:
Given, The length of the shadow cast by the edge of a crater is 500 meters.
The angle of elevation of the rays of the Sun is 55°.
tan ratio = \(\frac { opposite side }{ adjacent side } \)
tan 55 = \(\frac { d }{ 500 } \)
1.428 = \(\frac { d }{ 500 } \)
d = 714 m
The depth of the crater is 714 m

Question 17.
USING STRUCTURE
Find the tangent of the smaller acute angle in a right triangle with side lengths 5, 12, and 13.
Answer:

Question 18.
USING STRUCTURE
Find the tangent 0f the larger acute angle in a right triangle with side lengths 3, 4, and 5.

Answer:
tan x = \(\frac { 4 }{ 3 } \)

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information, side lengths 3, 4, and 5.
tan ratio = \(\frac { opposite side }{ adjacent side } \)
tan x = \(\frac { 4 }{ 3 } \)

Question 19.
REASONING
How does the tangent of an acute angle in a right triangle change as the angle measure increases? Justify your answer.
Answer:

Question 20.
CRITICAL THINKING
For what angle measure(s) is the tangent of an acute angle in a right triangle equal to 1? greater than 1? less than 1? Justify your answer.

Answer:
If the tangent of an angle to equal 1, the opposite and adjacent sides of a right triangle must be the same.
This means the right triangle is an isosceles right triangle.
So, the angles are 45 – 45 – 90.
Then the acute angle must be 1.
If the tangent to be greater than 1, the opposite side must be greater than the adjacent side.
This means the angle must be between 45 and 90 degrees.
If the tangent is less than 1, this means the opposite side must be smaller than the adjacent side.
Then the acute angle must be between 0 and 45.

Question 21.
MAKING AN ARGUMENT
Your family room has a sliding-glass door. You want to buy an awning for the door that will be just long enough to keep the Sun out when it is at its highest point in the sky. The angle of elevation of the rays of the Sun at this points is 70°, and the height of the door is 8 feet. Your sister claims you can determine how far the overhang should extend by multiplying 8 by tan 70°. Is your sister correct? Explain.

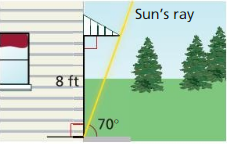
Answer:

Question 22.
HOW DO YOU SEE IT?
Write expressions for the tangent of each acute angle in the right triangle. Explain how the tangent of one acute angle is related to the tangent of the other acute angle. What kind of angle pair is ∠A and ∠B?

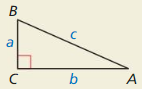
Answer:
∠A and ∠B form complementary angles.

Explanation:
We know that, Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
From the above given information, side lengths 3, 4, and 5.
tan ratio = \(\frac { opposite side }{ adjacent side } \)
tan A = \(\frac { BC }{ AC } \)
= \(\frac { a }{ b } \)
tan B = \(\frac { AC }{ BC } \)
= \(\frac { b }{ a } \)
Hence, the tangents of complementary angles are inverses of each other.
When two lines share a common endpoint called Vertex,
then an angle is formed between these two lines is known as the pair of angles.

Question 23.
REASONING
Explain why it is not possible to find the tangent of a right angle or an obtuse angle.
Answer:

Question 24.
THOUGHT PROVOKING
To create the diagram below. you begin with an isosceles right triangle with legs 1 unit long. Then the hypotenuse of the first triangle becomes the leg of a second triangle, whose remaining leg is 1 unit long. Continue the diagram Until you have constructed an angle whose tangent is \(\frac{1}{\sqrt{6}}\). Approximate the measure of this angle.

Answer:

Question 25.
PROBLEM SOLVING
Your class is having a class picture taken on the lawn. The photographer is positioned 14 feet away from the center of the class. The photographer turns 50° to look at either end of the class.

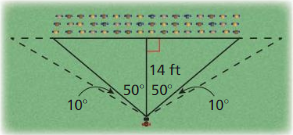
a. What is the distance between the ends of the class?
b. The photographer turns another 10° either way to see the end of the camera range. If each student needs 2 feet of space. about how many more students can fit at the end of each row? Explain.
Answer:

Question 26.
PROBLEM SOLVING
Find the perimeter of the figure. where AC = 26, AD = BF, and D is the midpoint of \(\overline{A C}\).

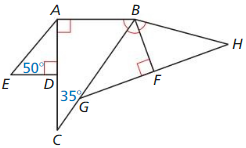
Answer:

Maintaining Mathematical proficiency

Find the value of x.

Question 27.

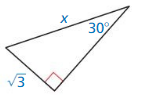
Answer:
x = 3.5

Explanation:
Based on the information given above,

Question 28.

Answer:
x = 4.04

Explanation:
Based on the information given above,
longer side = shorter side • √3
7 = x√3
x = \(\frac { 7 }{ √3 } \)
x = 4.04

Question 29.

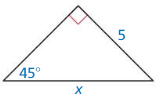
Answer:
x = 7.1

Explanation:
Based on the information given above,

9.5 The Sine and Cosine Ratios

Exploration 1

Work with a partner: Use dynamic geometry software.

a. Construct ∆ABC, as shown. Construct segments perpendicular to \(\overline{A C}\) to form right triangles that share vertex A arid are similar to ∆ABC with vertices, as shown.

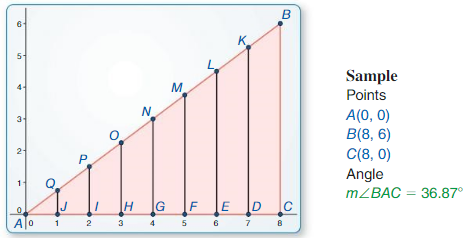
Answer:

b. Calculate each given ratio to complete the table for the decimal values of sin A and cos A for each right triangle. What can you conclude?

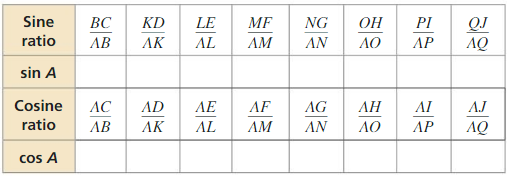
Answer:

Communicate Your Answer

Question 2.
How is a right triangle used to find the sine and cosine of an acute angle? Is there a unique right triangle that must be used?
Answer:

Question 3.
In Exploration 1, what is the relationship between ∠A and ∠B in terms of their measures’? Find sin B and cos B. How are these two values related to sin A and cos A? Explain why these relationships exist.
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:

Lesson 9.5 The Sine and Cosine Ratios

Monitoring Progress

Question 1.
Find sin D, sin F, cos D, and cos F. Write each answer as a fraction and as a decimal rounded to four places.

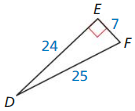
Answer:
sin D = \(\frac { 7 }{ 25 } \) = 0.28
sin F = \(\frac { 24 }{ 25 } \) = 0.96
cos D = \(\frac { 24 }{ 25 } \) = 0.96
cos F = \(\frac { 7 }{ 25 } \) = 0.28

Explanation:
The information given in the above figure states that,
tan ratio = \(\frac { opposite side }{ adjacent side } \)
sin D = \(\frac { EF }{ DF } \)
= \(\frac { 7 }{ 25 } \)
= 0.28
sin F = \(\frac { DE }{ DF } \)
= \(\frac { 24 }{ 25 } \)
= 0.96
cos D = \(\frac { DE }{ DF } \)
= \(\frac { 24 }{ 25 } \)
= 0.96
cos F = \(\frac { EF }{ DF } \)
= \(\frac { 7 }{ 25 } \)
= 0.28

Question 2.
Write cos 23° in terms of sine.

Answer:
cos 23° = sin 67°

Explanation:
cos X = sin(90 – X)
cos 23° = sin (90 – 23)
= sin(67)
So, cos 23° = sin 67°

Question 3.
Find the values of u and t using sine and cosine. Round your answers to the nearest tenth.

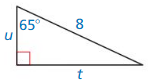
Answer:
t = 7.2, u = 3.3

Explanation:
From the above given information,
tan ratio = \(\frac { opposite side }{ adjacent side } \)
sin 65 = \(\frac { t }{ 8 } \)
we know that sin 65 = 0.906
substitute the value of sin 65 to find t.
0.906 = \(\frac { t }{ 8 } \)
t = 7.2
cos 65 = \(\frac { u }{ 8 } \)
we know that sin 65 = 0.422
substitute the value of cos 65 to find u.
cos 65 = \(\frac { u }{ 8 } \)
0.422 x 8 = u
u = 3.3

Question 4.
Find the sine and cosine of a 60° angle.
Answer:

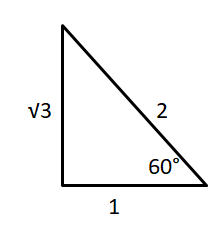
sin 60° = \(\frac { √3 }{ 2 } \)
cos 60° = \(\frac { 1 }{ 2 } \)

Question 5.
WHAT IF?
In Example 6, the angle of depression is 28°. Find the distance x you ski down the mountain to the nearest foot.
Answer:
x = 2558.6

Explanation:
Given, In Example 6, the angle of depression is 28°.
sin 28° = \(\frac { 1200 }{ x } \)
we know that sin 28 = 0.469
substitute the value of sin 28 to find x.
x = \(\frac { 1200 }{ 0.469 } \)
x = 2558.6

Exercise 9.5 The Sine and Cosine Ratios

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
The sine ratio compares the length of ______________ to the length of _____________
Answer:

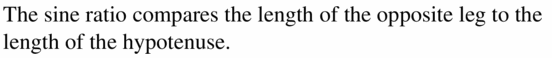
Question 2.
WHICH ONE DOESN’T BELONG?
Which ratio does not belong with the other three? Explain your reasoning.

sin B

Answer:
sin B = \(\frac {AC}{BC} \)
Explanation:

Sin B = \(\frac {Opposite}{Hypotenuse} \)
Sin B = \(\frac {AC}{BC} \)

cos C
Answer:
cos C = \(\frac { AC }{ BC } \)
Explanation:

cos C = \(\frac {Base}{Hypotenuse} \)
cos C = \(\frac {AC}{BC} \)

tan B
Answer:
tan B = \(\frac {AC}{AB} \)
tan B = \(\frac{AC}{BC}\)

Explanation:

tan B = \(\frac {Opposite}{Base} \)
tan B = \(\frac {AC}{AB} \)

Answer:
\(\frac{AC}{BC}\) = sin B

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 8, find sin D, sin E, cos D, and cos E. Write each answer as a Fraction and as a decimal rounded to four places.

Question 3.

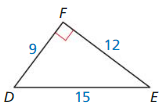
Answer:

Explanation:
To find sin D, sin E, cos D, and cos E

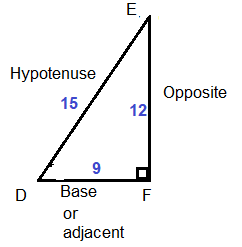
sin D = \(\frac {Opposite}{Hypotenuse} \)
sin D = \(\frac {EF}{ED} \)
sin D = \(\frac {12}{15} \)
sin D = \(\frac {4}{5} \)

sin E = \(\frac {Opposite}{Hypotenuse} \)
sin E = \(\frac {DF}{ED} \)
sin E = \(\frac {9}{15} \)
sin E = \(\frac {3}{5} \)

cos D = \(\frac {adjacent}{Hypotenuse} \)
cos D = \(\frac {DF}{ED} \)
cos D = \(\frac {9}{15} \)
cos D = \(\frac {3}{5} \)

cos E = \(\frac {adjacent}{Hypotenuse} \)
cos E = \(\frac {EF}{ED} \)
cos E = \(\frac {12}{15} \)
cos E = \(\frac {4}{5} \)

Question 4.

Answer:
sin D = \(\frac {35}{37} \)
sin E = \(\frac {12}{37} \)
cos D = \(\frac {12}{37} \)
cos E = \(\frac {35}{37} \)
Explanation:

sin D = \(\frac {Opposite}{Hypotenuse} \)
sin D = \(\frac {EF}{ED} \)
sin D = \(\frac {35}{37} \)

sin E = \(\frac {Opposite}{Hypotenuse} \)
sin E = \(\frac {DF}{ED} \)
sin E = \(\frac {12}{37} \)

cos D = \(\frac {adjacent}{Hypotenuse} \)
cos D = \(\frac {DF}{ED} \)
cos D = \(\frac {12}{37} \)

cos E = \(\frac {adjacent}{Hypotenuse} \)
cos E = \(\frac {EF}{ED} \)
cos E = \(\frac {35}{37} \)

Question 5.

Answer:

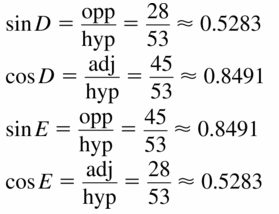
Explanation:

sin D = \(\frac {Opposite}{Hypotenuse} \)
sin D = \(\frac {EF}{ED} \)
sin D = \(\frac {28}{53} \)

sin E = \(\frac {Opposite}{Hypotenuse} \)
sin E = \(\frac {DF}{ED} \)
sin E = \(\frac {45}{53} \)

cos D = \(\frac {adjacent}{Hypotenuse} \)
cos D = \(\frac {DF}{ED} \)
cos D = \(\frac {45}{53} \)

cos E = \(\frac {adjacent}{Hypotenuse} \)
cos E = \(\frac {EF}{ED} \)
cos E = \(\frac {28}{53} \)

Question 6.

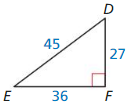
Answer:
sin D = \(\frac { 36 }{ 45 } \)
sin E = \(\frac { 27 }{ 45 } \)
cos D = \(\frac { 27 }{ 45 } \)
cos E = \(\frac { 36 }{ 45 } \)
Explanation:

sin D = \(\frac {Opposite}{Hypotenuse} \)
sin D = \(\frac {EF}{ED} \)
sin D = \(\frac {36}{45} \)

sin E = \(\frac {Opposite}{Hypotenuse} \)
sin E = \(\frac {DF}{ED} \)
sin E = \(\frac {27}{45} \)

cos D = \(\frac {adjacent}{Hypotenuse} \)
cos D = \(\frac {DF}{ED} \)
cos D = \(\frac {27}{45} \)

cos E = \(\frac {adjacent}{Hypotenuse} \)
cos E = \(\frac {EF}{ED} \)
cos E = \(\frac {36}{45} \)

Question 7.

Answer:

Explanation:

sin D = \(\frac {Opposite}{Hypotenuse} \)
sin D = \(\frac {EF}{ED} \)
sin D = \(\frac {13√3}{26} \)

sin E = \(\frac {Opposite}{Hypotenuse} \)
sin E = \(\frac {DF}{ED} \)
sin E = \(\frac {13}{26} \)
sin E = \(\frac {1}{2} \)

cos D = \(\frac {adjacent}{Hypotenuse} \)
cos D = \(\frac {DF}{ED} \)
cos D = \(\frac {13}{26} \)
cos D = \(\frac {1}{2} \)

cos E = \(\frac {adjacent}{Hypotenuse} \)
cos E = \(\frac {EF}{ED} \)
cos E = \(\frac {13√3}{26} \)

Question 8.

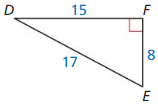
Answer:
sin D = \(\frac { 8 }{ 17 } \)
sin E = \(\frac { 15 }{ 17 } \)
cos D = \(\frac { 15 }{ 17 } \)
cos E = \(\frac { 8 }{ 17 } \)
Explanation:

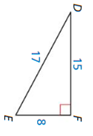
sin D = \(\frac {Opposite}{Hypotenuse} \)
sin D = \(\frac {EF}{ED} \)
sin D = \(\frac {8}{17} \)

sin E = \(\frac {Opposite}{Hypotenuse} \)
sin E = \(\frac {DF}{ED} \)
sin E = \(\frac {15}{17} \)

cos D = \(\frac {adjacent}{Hypotenuse} \)
cos D = \(\frac {DF}{ED} \)
cos D = \(\frac {15}{17} \)

cos E = \(\frac {adjacent}{Hypotenuse} \)
cos E = \(\frac {EF}{ED} \)
cos E = \(\frac {8}{17} \)

In Exercises 9 – 12. write the expression in terms of cosine.

Question 9.
sin 37°

Answer:
sin 37° = cos53°
Explanation:
Given,
sin 37°
sin θ = cos (90 – θ)
sin 37° = cos (90 – 37°) = cos 53°

Question 10.
sin 81°
Answer:
sin 81° = cos9°
Explanation:
Given,
sin 81°
sin θ = cos (90 – θ)
sin 81° = cos (90 – 81°) = cos 9°

Question 11.
sin 29°
Answer:
sin 29° = cos 61°
Explanation:
Given,
sin 29°
sin θ = cos (90 – θ)
sin 29° = cos (90 – 29°) = cos 61°

Question 12.
sin 64°

Answer:
sin 64° = cos 26°
Explanation:
sin 64°
sin θ = cos (90 – θ)
sin 64° = cos(90° – 64°)
sin 64° =  cos 26°

In Exercise 13 – 16, write the expression in terms of sine.

Question 13.
cos 59°
Answer:
cos 59° = sin 31°
Explanation:
Given,
cos 59°
cos θ = sin (90 – θ)
cos 59° = sin (90 – 59°)
cos 59° = sin 31°

Question 14.
cos 42°
Answer:
cos 42° = sin 48°
Explanation:
Given,
cos 42°
cos θ = sin (90 – θ)
cos 42° = sin (90 – 42°)
cos 42° = sin 48°

Question 15.
cos 73°
Answer:
cos 73° = sin17°
Explanation:
Given,
cos 73°
cos θ = sin (90 – θ)
cos 73° = sin (90 – 73°)
cos 73° = sin 17°

Question 16.
cos 18°
Answer:
cos 18° = sin 72°
Explanation:
Given,
cos 18°
cos θ = sin (90 – θ)
cos 18° = sin (90 – 18°)
cos 18° = sin 72°

In Exercises 17 – 22, find the value of each variable using sine and cosine. Round your answers to the nearest tenth.

Question 17.

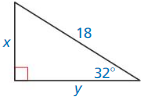
Answer:
x = 9.5, y = 15.3

Explanation:
Based on the information given above,

Question 18.

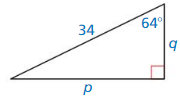
Answer:
p = 30.5, q = 14.8

Explanation:
From the above given information,
sin 64° = \(\frac { p }{34 } \)
p = 0.898 x 34
p = 30.5
cos 64° = \(\frac { q }{ 34 } \)
where as cos 64° = 0.4383
q = 0.4383 x 34
q = 14.8

Question 19.

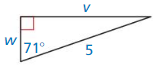
Answer:
w = 1.6, v = 4.7

Explanation:
From the above given above information,

Question 20.

Answer:
s = 17.7, r = 19

Explanation:
From the above given information,
sin 43° = \(\frac { s }{26 } \)
sin 43°  = 0.681
s = 0.681 x 26
s = 17.7
cos 43° = \(\frac { r }{ 26 } \)
r = 0.731 x 26
r = 19

Question 21.

Answer:
a = 14.9, b = 11.1

Explanation:
From the above given information,

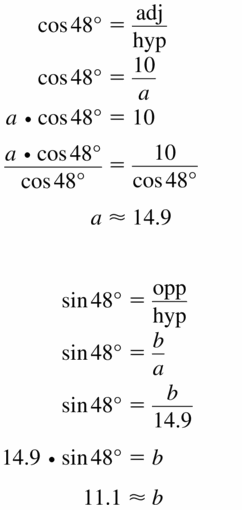
Question 22.

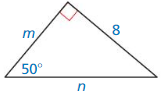
Answer:
m = 6.7, n = 10.44

Explanation:
From the above given information,
sin 50° = \(\frac { 8 }{n } \)
0.766 = \(\frac { 8 }{n } \)
n = 10.44
cos 50° = \(\frac { m }{ n } \)
0.642 = \(\frac { m }{ 10.44 } \)
m = 6.7

Question 23.
REASONING
Which ratios are equal? Select all that apply.

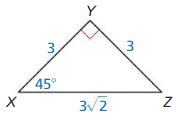
sin X

cos X

sin Z

cos Z
Answer:

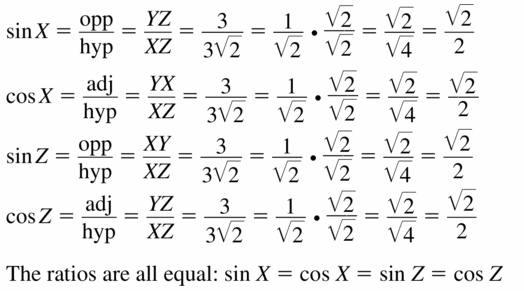
Question 24.
REASONING
Which ratios arc equal to \(\frac{1}{2}\) Select all

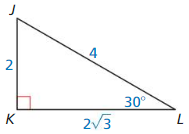
sin L

Answer:
sin L = \(\frac {2}{4} \) = \(\frac { 1 }{ 2 } \)
Explanation:
sin L = \(\frac {Opposite}{Hypotenuse} \)
sin L = \(\frac {2}{4} \)
sin L = \(\frac {1}{2} \)

cos L

Answer:
cos L = \(\frac { 2√3 }{ 4 } \) = \(\frac {√3}{2} \)
Explanation:
cos L = \(\frac {adjacent}{Hypotenuse} \)
cos L = \(\frac {2√3}{4} \)
cos L = \(\frac {√3}{2} \)

sin J

Answer:
sin J = \(\frac { 2√3 }{ 4 } \) = \(\frac {√3}{2} \)
Explanation:
sin L = \(\frac {Opposite}{Hypotenuse} \)
sin J = \(\frac { 2√3 }{ 4 } \)
sin J = \(\frac {√3}{2} \)

cos J

Answer:
cos J = \(\frac {2}{4} \) = \(\frac {1}{2} \)
Explanation:
cos J = \(\frac {adjacent}{Hypotenuse} \)
cos J = \(\frac {2}{4} \)
cos J = \(\frac {1}{2} \)

Question 25.
ERROR ANALYSIS
Describe and correct the error in finding sin A.

Answer:

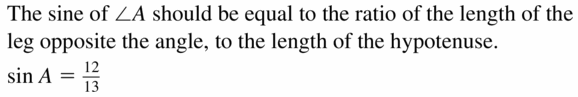
Question 26.
WRITING
Explain how to tell which side of a right triangle is adjacent to an angle and which side is the hypotenuse.
Answer:

Question 27.
MODELING WITH MATHEMATICS
The top of the slide is 12 feet from the ground and has an angle of depression of 53°. What is the length of the slide?

Answer:
x = 15

Explanation:
From the above given information,

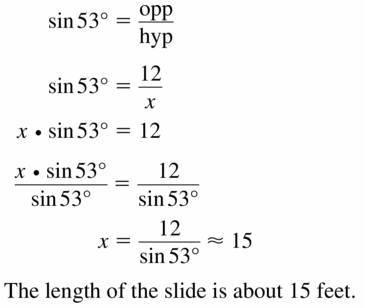
Question 28.
MODELING WITH MATHEMATICS
Find the horizontal distance x the escalator covers.

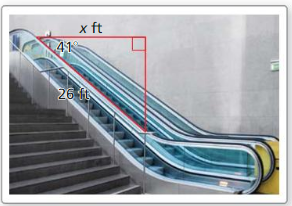
Answer:
x = 19.6 ft

Explanation:
Based on the above information given in the figure,
cos 41 = \(\frac { x }{ 26 } \)
0.754 = \(\frac { x }{ 26 } \)
x = 19.6 ft

Question 29.
PROBLEM SOLVING
You are flying a kite with 20 feet of string extended. The angle of elevation from the spool of string to the kite is 67°.
a. Draw and label a diagram that represents the situation.
b. How far off the ground is the kite if you hold the spool 5 feet off the ground? Describe how the height where you hold the spool affects the height of the kite.
Answer:

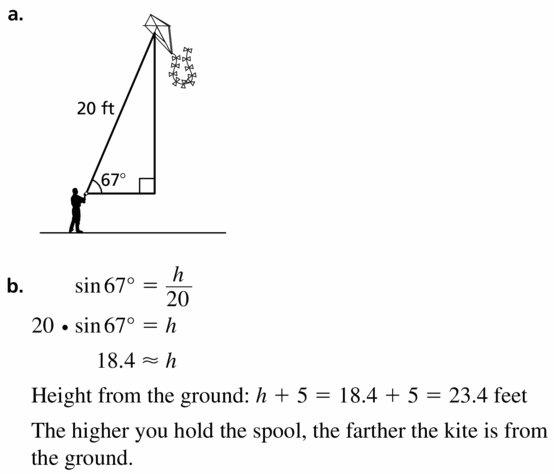
Question 30.
MODELING WITH MATHEMATICS
Planes that fly at high speeds and low elevations have radar s sterns that can determine the range of an obstacle and the angle of elevation to the top of the obstacle. The radar of a plane flying at an altitude of 20,000 feet detects a tower that is 25,000 feet away. with an angle of elevation of 1°

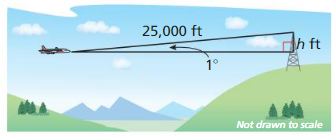
a. How many feet must the plane rise to pass over the tower?
Answer:
h = 425 ft

Explanation:
Given,
The radar of a plane flying at an altitude of 20,000 feet detects a tower that is 25,000 feet away,
with an angle of elevation of 1°
sin 1 = \(\frac { h }{ 25000 } \)
0.017 = \(\frac { h }{ 25000 } \)
h = 425 ft
425 ft the plane rise to pass over the tower.

b. PIanes Caillot come closer than 1000 feet vertically to any object. At what altitude must the plane fly in order to pass over the tower?

Answer:

Question 31.
MAKING AN ARGUMENT
Your friend uses che equation sin 49° = \(\frac{x}{16}\) to find BC. Your cousin uses the equation cos 41° = \(\frac{x}{16}\) to find BC. Who is correct? Explain your reasoning.

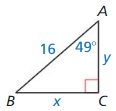
Answer:

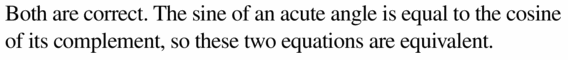
Question 32.
WRITING
Describe what you must know about a triangle in order to use the sine ratio and what you must know about a triangle in order to use the cosine ratio.
Answer:
Sine of an angle is the ratio of the side opposite to that angle to the hypotenuse.
Cosine of an angle is the ratio of the side adjacent to that angle to the hypotenuse.
sin = \(\frac { opposite side }{ hypotenuse } \)
cos = \(\frac { adjacent side }{ hypotenuse } \)

Question 33.
MATHEMATICAL CONNECTIONS
If ∆EQU is equilateral and ∆RGT is a right triangle with RG = 2, RT = 1. and m ∠ T = 90°, show that sin E = cos G.
Answer:

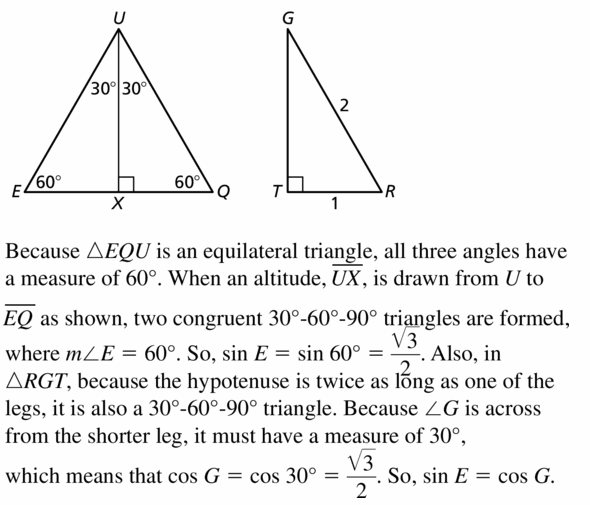
Question 34.
MODELING WITH MATHEMATICS
Submarines use sonar systems, which are similar to radar systems, to detect obstacles, Sonar systems use sound to detect objects under water.

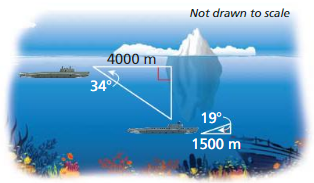
a. You are traveling underwater in a submarine. The sonar system detects an iceberg 4000 meters a head, with an angle of depression of 34° to the bottom of the iceberg. How many meters must the submarine lower to pass under the iceberg?
Answer:
x = 2696

Explanation:
Given,
The sonar system detects an iceberg 4000 meters a head,
with an angle of depression of 34° to the bottom of the iceberg.
tan 34 = \(\frac { x }{ 4000 } \)
.674 = \(\frac { x }{ 4000 } \)
x = 2696

b. The sonar system then detects a sunken ship 1500 meters ahead. with an angle of elevation of 19° to the highest part of the sunken ship. How many meters must the submarine rise to pass over the sunken ship?
Answer:
x = 516 m

Explanation:
Given,
The sonar system then detects a sunken ship 1500 meters ahead,
with an angle of elevation of 19° to the highest part of the sunken ship.
tan 19 = \(\frac { x }{ 1500 } \)
0.344 = \(\frac { x }{ 1500 } \)
x = 516 m

Question 35.
ABSTRACT REASONING
Make a conjecture about how you could use trigonometric ratios to find angle measures in a triangle.
Answer:

Question 36.
HOW DO YOU SEE IT?
Using only the given information, would you use a sine ratio or a cosine ratio to find the length of the hypotenuse? Explain your reasoning.

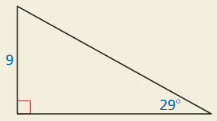
Answer:
x = 18.75

Explanation:
Based on the information given above in the figure,
sin 29 = \(\frac { 9 }{ x } \)
where as sin 29 = 0.48
0.48 = \(\frac { 9 }{ x } \)
x = 18.75
The length of hypotenuse is 18.75

Question 37.
MULTIPLE REPRESENTATIONS
You are standing on a cliff above an ocean. You see a sailboat from your vantage point 30 feet above the ocean.

a. Draw and label a diagram of the situation.
b. Make a table showing the angle of depression and the length of your line of sight. Use the angles 40°, 50°, 60°, 70°, and 80°.
c. Graph the values you found in part (b), with the angle measures on the x-axis.
d. Predict the length of the line of sight when the angle of depression is 30°.
Answer:

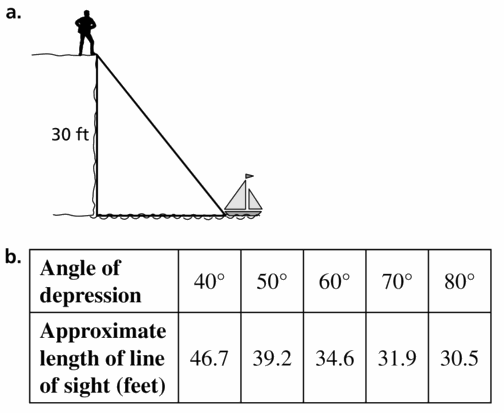
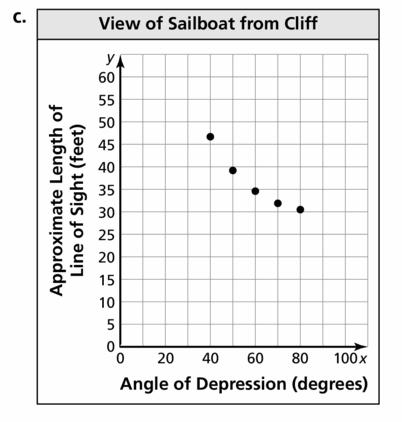
Question 38.
THOUGHT PROVOKING
One of the following infinite series represents sin x and the other one represents cos x (where x is measured in radians). Which is which? Justify your answer. Then use each series to approximate the sine and cosine of \(\frac{\pi}{6}\).
(Hints: π = 180°; 5! = 5 • 4 • 3 • 2 • 1; Find the values that the sine and cosine ratios approach as the angle measure approaches zero).
a.

Answer:
For x = 0
0 – \(\frac { 0³ }{ 3! } \) + \(\frac { 0⁵ }{ 5! } \) – \(\frac { 0⁷ }{ 7! } \) + . . . = 0
sin x = x – \(\frac { x³ }{ 3! } \) + \(\frac { x⁵ }{ 5! } \) – \(\frac { x⁷ }{ 7! } \) + . . .
sin \(\frac { π }{ 6 } \) = 0.5

b.

Answer:
1 – \(\frac { 1² }{ 2! } \) + \(\frac { 1⁴ }{ 4! } \) – \(\frac { 1⁶ }{ 6! } \) + . .  = 1
cos x =x1 – \(\frac { x² }{ 2! } \) + \(\frac { x⁴ }{ 4! } \) – \(\frac { x⁶ }{ 6! } \) + . .
cos \(\frac { π }{ 6 } \) = 0.86

Question 39.
CRITICAL THINKING
Let A be any acute angle of a right triangle. Show that
(a) tan A = \(\frac{\sin A}{\cos A}\) and
(b) (sin A)² + (cos A)² = 1.
Answer:

Question 40.
CRITICAL THINKING
Explain why the area ∆ ABC in the diagram can be found using the formula Area = \(\frac{1}{2}\) ab sin C. Then calculate the area when a = 4, b = 7, and m∠C = 40°:

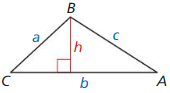
Answer:
a = 8.988

Explanation:
Given,
Area = \(\frac{1}{2}\) ab sin C.
Then calculate the area when a = 4, b = 7, and m∠C = 40°
Area = \(\frac{1}{2}\) ab sin C
= \(\frac{1}{2}\) (4 x 7) sin 40°
= 14 x 0.642
= 8.988

Maintaining Mathematical Proficiency

Find the value of x. Tell whether the side lengths form a Pythagorean triple.

Question 41.

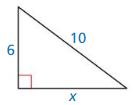
Answer:
x = 8

Explanation:
From the above given information,
By using the Pythagorean triple theorem,

Question 42.

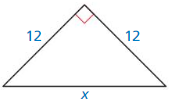
Answer:
x = 12√2

Explanation:
From the above given information,
c² = a² + b²
x² = 12² + 12²
x² = 144 + 144
x² = 288
x = 12√2

Question 43.

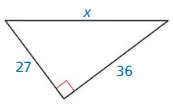
Answer:
x = 45

Explanation:
From the above given information,

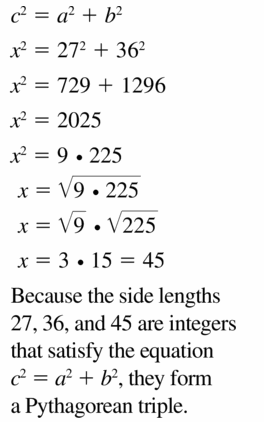
Question 44.

Answer:
x = 6√2

Explanation:
From the above given information,
c² = a² + b²
9² = x² + 3²
81 = x² + 9
x² = 81 – 9
x = 6√2

9.6 Solving Right Triangles

Exploration 1

Solving Special Right Triangles

Work with a partner. Use the figures to find the values of the sine and cosine of ∠A and ∠B. Use these values to find the measures of ∠A and ∠B. Use dynamic geometry software to verify your answers.
a.

Answer:

b.

Answer:

Exploration 2

Solving Right Triangles

Work with a partner: You can use a calculator to find the measure of an angle when you know the value of the sine, cosine, or tangent of the rule. Use the inverse sine, inverse cosine, 0r inverse tangent feature of your calculator to approximate the measures of ∠A and ∠B to the nearest tenth of a degree. Then use dynamic geometry software to verify your answers.
ATTENDING TO PRECISION
To be proficient in math, you need to calculate accurately and efficiently, expressing numerical answers with a degree of precision appropriate for the problem context.
a.

Answer:

b.

Answer:

Communicate Your Answer

Question 3.
When you know the lengths of the sides of a right triangle, how can you find the measures of the two acute angles?
Answer:

Question 4.
A ladder leaning against a building forms a right triangle with the building and the ground. The legs of the right triangle (in meters) form a 5-12-13 Pythagorean triple. Find the measures of the two acute angles to the nearest tenth of a degree.
Answer:

Lesson 9.6 Solving Right Triangles

Determine which of the two acute angles has the given trigonometric ratio.

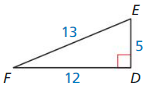
Question 1.
The sine of the angle is \(\frac{12}{13}\).
Answer:
67.3°

Explanation:
Based on the information given,
sine of the angle is \(\frac{12}{13}\)
Sin E = \(\frac{12}{13}\)
m∠E = sin^-1(\(\frac{12}{13}\)) = 67.3°

Question 2.
The tangent of the angle is \(\frac{5}{12}\)
Answer:
22.6°

Explanation:
Based on the information given,
tan F = \(\frac{5}{12}\)
m∠F = tan^-1(\(\frac{5}{12}\)) = 22.6°

Let ∠G, ∠H, and ∠K be acute angles. Use a calculator to approximate the measures of ∠G, ∠H, and ∠K to the nearest tenth of a degree.

Question 3.
tan G = 0.43

Answer:
∠G = inverse tan of 0.43 = 23.3°

Question 4.
sin H = 0.68

Answer:
∠H = inverse sin of 0.68 = 42.8°

Question 5.
cos K = 0.94

Answer:
∠K = inverse cos of 0.94 = 19.9°

Solve the right triangle. Round decimal answers to the nearest tenth.

Question 6.

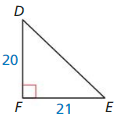
Answer:
DE = 29, ∠D = 46.05°, ∠E = 42.84°

Explanation:
From the information given in the above figure,
c² = a² + b²
x² = 20² + 21²
x² = 400 + 441
x² = 841
x = 29
sin D = \(\frac { 21 }{ 29 } \)
∠D = 46.05
sin E = \(\frac { 20 }{ 29 } \)
∠E = 42.84

Question 7.

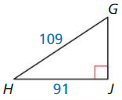
Answer:
GJ = 60, ∠G = 56.09°, ∠H = 33.3°

Explanation:
According to the information given in the above figure,
c² = a² + b²
109² = 91² + x²
x² = 11881 – 8281
x² = 3600
x = 60
sin G = \(\frac { 91 }{ 109 } \)
∠G = 56.09
sin H = \(\frac { 60 }{ 109 } \)
∠H = 33.3

Question 8.
Solve the right triangle. Round decimal answers to the nearest tenth.

Answer:
XY = 13.82, YZ = 6.69, ∠Y = 37.5

Explanation:
From the information given in the above figure,
cos 52 = \(\frac { 8.5 }{ XY } \)
cos 52 = 0.615
0.615 = \(\frac { 8.5 }{ XY } \)
XY = 13.82
sin 52 = \(\frac { YZ }{ XY } \)
sin 52 = 0.788
0.788 = \(\frac { YZ }{ 8.5 } \)
YZ = 6.69
sin Y = \(\frac { 8.5 }{ 13.82 } \)
∠Y = 37.5

Question 9.
WHAT IF?
In Example 5, suppose another raked stage is 20 feet long from front to back with a total rise of 2 feet. Is the raked stage within your desired range?
Answer:
x = 5.7°

Explanation:
Given that,
In Example, suppose another raked stage is 20 feet long from front to back with a total rise of 2 feet.
let the raked stage within your desired range is x.
x = inverse sine of \(\frac { 2 }{ 20 } \)
x = 5.7°

Exercise 9.6 Solving Right Triangles

Question 1.
COMPLETE THE SENTENCE
To solve a right triangle means to find the measures of all its ________ and _______ .
Answer:

Question 2.
WRITING
Explain when you can use a trigonometric ratio to find a side length of a right triangle and when you can use the Pythagorean Theorem (Theorem 9.1 ).
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6. determine which of the two acute angles has the given trigonometric ratio.

Question 3.
The cosine of the angle is \(\frac{4}{5}\)

Answer:
The cosine of the angle is \(\frac{4}{5}\) = ∠C

Explanation:
Based on the above information given in the above figure,

Question 4.
The sine of the angle is \(\frac{5}{11}\)

Answer:
The sine of the angle is \(\frac{5}{11}\) = ∠A

Explanation:
From the above given information,
Sin(angle) = \(\frac { opposite }{ hypo } \)
sin A = \(\frac{5}{11}\)
The acute angle that has a sine of the angle is \(\frac{5}{11}\) is ∠A.

Question 5.
The sine of the angle is 0.95.

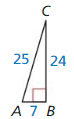
Answer:
The sine of the angle is 0.95 = ∠A.

Explanation:
Based on the information given above ,

Question 6.
The tangent of the angle is 1.5.

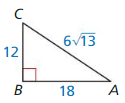
Answer:
The tangent of the angle is 1.5 ∠C.

Explanation:
Based on the information given in the above figure,
tan(angle) = \(\frac { opposite }{ adjacent } \)
1.5 = \(\frac { 18 }{ 12 } \)
tan C = 1.5
The acute angle that has a tangent of the angle is 1.5 ∠C.

In Exercises 7 – 12, let ∠D be an acute angle. Use a calculator to approximate the measure of ∠D to the nearest tenth of a degree.

Question 7.
sin D = 0.75
Answer:
∠D = 48.6°

Explanation:
Given, let ∠D be an acute angle.

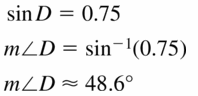
Question 8.
sin D = 0.19
Answer:
∠D = 10.9°

Explanation:
Given,
sin D = 0.19
let ∠D be an acute angle.
∠D = inverse sine of 0.19
∠D = 10.9°

Question 9.
cos D = 0.33
Answer:
∠D = 70.7°

Explanation:
Given, let ∠D be an acute angle.

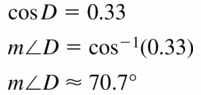
Question 10.
cos D = 0.64
Answer:
∠D = 50.2°

Explanation:
Given,
cos D = 0.64
let ∠D be an acute angle.
∠D = inverse cos of 0.64
∠D = 50.2°

Question 11.
tan D = 0.28
Answer:
∠D = 15.6°

Explanation:
let ∠D be an acute angle.
Given,

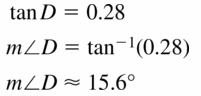
Question 12.
tan D = 0.72
Answer:
∠D = 35.8°

Explanation:
Given,
tan D = 0.72
let ∠D be an acute angle.
∠D = inverse tan of 0.72
∠D = 35.8°

In Exercises 13 – 18. solve the right triangle. Round decimal answers to the nearest tenth.

Question 13.

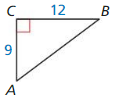
Answer:

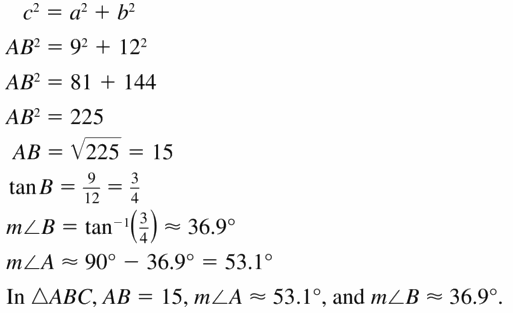
Question 14.

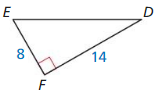
Answer:
ED = 2√65, ∠E = 59.3, ∠D = 29.7

Explanation:
According to the information given in the above figure,
c² = a² + b²
c² = 8² + 14²
x² = 64 + 196
x² = 260
x = 2√65
sin E = \(\frac { 14 }{ 2√65 } \)
∠E = 59.3
sin D = \(\frac { 8 }{ 2√65 } \)
∠D = 29.7

Question 15.

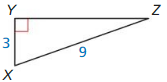
Answer:

Question 16.

Answer:
HJ = 2√15, ∠G = 28.9, ∠J = 61

Explanation:
According to the information given in the above figure,
c² = a² + b²
16² = 14² + x²
x² = 256 – 196
x² = 60
x = 2√15
sin G = \(\frac { 2√15 }{ 16 } \)
∠G = 28.9
sin J = \(\frac { 14 }{ 16 } \)
∠J = 61

Question 17.

Answer:

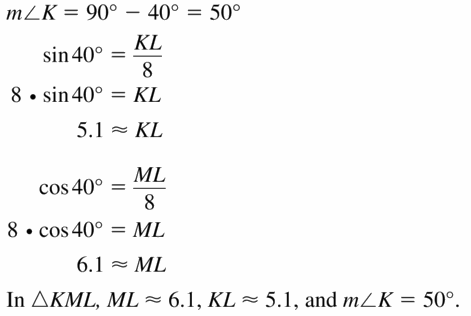
Question 18.

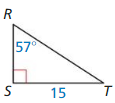
Answer:
RT = 17.8, RS = 9.68, ∠T = 32.8

Explanation:
According to the information given in the above figure,
sin 57 = \(\frac { 15 }{ x } \)
sin 57 = 0.838
0.838 = \(\frac { 15 }{ x } \)
x = 17.899
RT = 17.8
cos 57 = \(\frac { x }{ 17.8 } \)
cos 57 = 0.544
0.544 = \(\frac { x }{ 17.8 } \)
x = 9.68
RS = 9.68
sin T = \(\frac { 9.68 }{ 17.8 } \)
∠T = 32.8

Question 19.
ERROR ANALYSIS
Describe and correct the error in using an inverse trigonometric ratio.

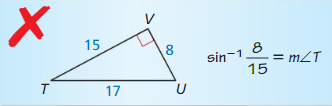
Answer:

Question 20.
PROBLEM SOLVING
In order to unload clay easily. the body of a dump truck must be elevated to at least 45° The body of a dump truck that is 14 feet long has been raised 8 feet. Will the clay pour out easily? Explain your reasoning.
Answer:
No

Explanation:
Given, the body of a dump truck must be elevated to at least 45°.
The body of a dump truck that is 14 feet long has been raised 8 feet.
Angle of elevation: sin x = \(\frac { 8 }{ 14 } \)
x = inverse sine of \(\frac { 8 }{ 14 } \) = 34.9
So, the clay will not pour out easily.

Question 21.
PROBLEM SOLVING
You are standing on a footbridge that is 12 feet above a lake. You look down and see a duck in the water. The duck is 7 feet away from the footbridge. What is the angle of elevation from the duck to you

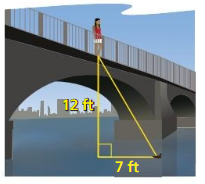
Answer:
x = 59.7°

Explanation:
As shown in the above figure,
You are standing on a footbridge that is 12 feet above a lake.
You look down and see a duck in the water.
The duck is 7 feet away from the footbridge,
then the angle of elevation is..

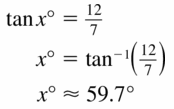
Question 22.
HOW DO YOU SEE IT?
Write three expressions that can be used to approximate the measure of ∠A. Which expression would you choose? Explain your choice.

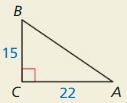
Answer:
Based on the information above in the given figure, the three expressions are:
∠A = inverse tan of (\(\frac { 15 }{ 22 } \)) = 34.2°
∠A = inverse sine of (\(\frac { 15 }{ BA } \))
∠A = inverse cos of (\(\frac { 22 }{ BA } \))

Question 23.
MODELING WITH MATHEMATICS
The Uniform Federal Accessibility Standards specify that awheel chair ramp may not have an incline greater than 4.76. You want to build a ramp with a vertical rise of 8 inches. you want to minimize the horizontal distance taken up by the ramp. Draw a diagram showing the approximate dimensions of your ramp.
Answer:

Question 24.
MODELING WITH MATHEMATICS
The horizontal part of a step is called the tread. The vertical part is called the riser. The recommended riser – to – tread ratio is 7 inches : 11 inches.

a. Find the value of x for stairs built using the recommended riser-to-tread ratio.

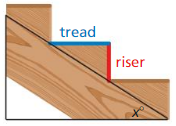
Answer:

b. you want to build stairs that are less steep than the stairs in part (a). Give an example of a riser – to – tread ratio that you could use. Find the value of x for your stairs.
Answer:

Question 25.
USING TOOLS
Find the measure of ∠R without using a protractor. Justify your technique.

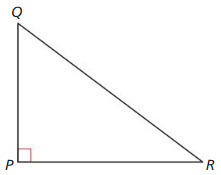
Answer:
∠R = 36.9°

Explanation:
Based on the above figure ∠R,

Question 26.
MAKING AN ARGUMENT
Your friend claims that tan^-1x = \(\frac{1}{\tan x}\). Is your friend correct? Explain your reasoning.
Answer:
No

Explanation:
Given that,
tan^-1x = \(\frac{1}{\tan x}\).
For example;
tan^-1(√3) = 60
\(\frac{1}{\tan √3}\) = 33.1
So, my friend is wrong.

USING STRUCTURE
In Exercises 27 and 28, solve each triangle.

Question 27.
∆JKM and ∆LKM

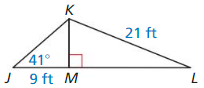
Answer:

Question 28.
∆TUS and ∆VTW

Answer:
TS = 8.2, UT = 7.3, ∠T = 28.6
TV = 13.2, TW = 9.6, ∠V = 46, ∠T = 42.84

Explanation:
Based on the triangles given in the above figure,
tan 64 = \(\frac { TS }{ 4 } \)
Value of tan 64 = 2.05
TS = 2.05 x 4
TS = 8.2
sin 64 = \(\frac { UT }{ 8.2 } \)
value of sin 64 = 0.898
0.898 = \(\frac { UT }{ 8.2 } \)
UT = 7.3
sin T = \(\frac { 4 }{ 8.2 } \)
∠T = 28.6
TV = TS + SV
TV = 8.2 + 5 = 13.2
13.2² = TW² + 9²
TW² = 174.24 – 81
TW = 9.6
sin V = \(\frac { 9.6 }{ 13.2 } \)
∠V = 46
sin T = \(\frac { 9 }{ 13.2 } \)
∠T = 42.84

Question 29.
MATHEMATICAL CONNECTIONS
Write an expression that can be used to find the measure of the acute angle formed by each line and the x-axis. Then approximate the angle measure to the nearest tenth of a degree.
a. y = 3x
b. y = \(\frac{4}{3}\)x + 4
Answer:

Question 30.
THOUGHT PROVOKING
Simplify each expression. Justify your answer.
a. sin^-1 (sin x)

Answer:
sin^-1 (sin x) = x
Explanation:
sin of sin inverse of x is a trigonometric function
denoted as,
sin (sin^–1x) = x

b. tan(tan^-1 y)

Answer:
tan(tan^-1 y) = y
Explanation:
Tan inverse y is the inverse of the tan function.
y = tan y then y = tan^–1(y).
Then here,
tan^–1 is the inverse function of tan.

C. cos(cos^-1 z)

Answer:
cos(cos^-1 z) = z
Explanation:
sin of sin inverse of z is a trigonometric function
denoted as,
cos (cos^–1z) = z

Question 31.
REASONING
Explain why the expression sin^-1 (1.2) does not make sense.
Answer:

Question 32.
USING STRUCTURE
The perimeter of the rectangle ABCD is 16 centimeters. and the ratio of its width to its length is 1 : 3. Segment BD divides the rectangle into two congruent triangles. Find the side lengths and angle measures of these two triangles.
Answer:
Angle measures are ∠ADB = 71; ∠CDB = 19
Side lengths are l = 6, b = 2

Explanation:
Given,
The perimeter of the rectangle ABCD is 16 centimeters.
we know that perimeter = 2(l + b)
2(l + b) = 16
l + b = 8
b : l = 1 : 3
4x = 8
x = 2
l = 6, b = 2
BD = √(6² + 2²) = √40 = 2√10
sin B = \(\frac { AD }{ BD } \) = \(\frac { 2 }{ 2√10 } \)
∠ABD = 18.4
∠CBD = 71.6
sin D = \(\frac { AB }{ BD } \) = \(\frac { 6 }{ 2√10 } \)
∠ADB = 71
∠CDB = 19

Maintaining Mathematical Proficiency

Solve the equation

Question 33.
\(\frac{12}{x}=\frac{3}{2}\)
Answer:
x = 8

Explanation:
Given,
\(\frac{12}{x}=\frac{3}{2}\)

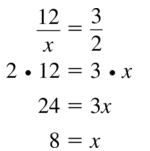
Question 34.
\(\frac{13}{9}=\frac{x}{18}\)
Answer:
x = 26

Explanation:
Given,
\(\frac{13}{9}=\frac{x}{18}\)
By cross multiplying
9x = 13 x 18
x = 26

Question 35.
\(\frac{x}{2.1}=\frac{4.1}{3.5}\)
Answer:
x = 2.46

Explanation:
Given,
\(\frac{x}{2.1}=\frac{4.1}{3.5}\)

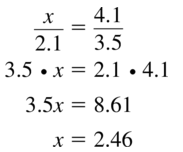
Question 36.
\(\frac{5.6}{12.7}=\frac{4.9}{x}\)

Answer:
x = 11.13

Explanation:
Given,
\(\frac{5.6}{12.7}=\frac{4.9}{x}\)
By cross multiplying
0.44 = 4.9/x
x = 11.13

9.7 Law of Sines and Law of Cosines

Exploration 1

Discovering the Law of Sines

Work with a partner.

a. Copy and complete the table for the triangle shown. What can you conclude?


Answer:

b. Use dynamic geometry software to draw two other triangles. Copy and complete the table in part (a) for each triangle. Use your results to write a conjecture about the relationship between the sines of the angles and the lengths of the sides of a triangle.
USING TOOLS STRATEGICALLY
To be proficient in math, you need to use technology to compare predictions with data.
Answer:

Exploration 2

Discovering the Law of Cosines

Work with a partner:

a. Copy and complete the table for the triangle in Exploration 1 (a). What can you conclude?

Answer:

b. Use dynamic geometry software to draw two other triangles. Copy and complete the table in part (a) for each triangle. Use your results to write a conjecture about what you observe in the completed tables.
Answer:

Communicate Your Answer

Question 3.
What are the Law of Sines and the Law of Cosines?
Answer:

Question 4.
When would you use the Law of Sines to solve a triangle? When would you use the Law of Cosines to solve a triangle?
Answer:

Lesson 9.7 Law of Sines and Law of Cosines

Monitoring Progress

Use a calculator to find the trigonometric ratio. Round your answer to four decimal places.

Question 1.
tan 110°

Answer:
tan 110° = -2.7474

Question 2.
sin 97°

Answer:
sin 97° = 0.9925

Question 3.
cos 165°

Answer:
cos 165° = -0.9659

Find the area of ∆ABC with the given side lengths and included angle. Round your answer to the nearest tenth.

Question 4.
m ∠ B = 60°, a = 19, c = 14
Answer:
Area = 155.18

Explanation:
Given,
m ∠ B = 60°, a = 19, c = 14
Area = \(\frac { 1 }{ 2 } \) ac sin B
= \(\frac { 1 }{ 2 } \) (19 x 14) sin 60°
sin 60° = 0.866
= 133 x 0.866
= 155.18

Question 5.
m ∠ C = 29°, a = 38, b = 31
Answer:
Area = 282.72

Explanation:
Given,
m ∠ C = 29°, a = 38, b = 31
Area = \(\frac { 1 }{ 2 } \) ab sin C
= \(\frac { 1 }{ 2 } \) (38 x 31) sin 29
sin 29 = 0.48
= 598 x 0.48
= 282.72

Solve the triangle. Round decimal answers to the nearest tenth.

Question 6.

Answer:
∠C = 46.6, ∠B = 82.4, AC = 23.57

Explanation:
Using law of sines and the information given above,
\(\frac { c }{ sin C } \) = \(\frac { a }{ sin A } \)
\(\frac { 17 }{ sin C } \) = \(\frac { 18 }{ sin 51 } \)
\(\frac { 17 }{ sin C } \) = \(\frac { 18 }{ 0.77 } \)
By cross multiplying, we get
sin C = 0.7274
∠C = 46.6
∠A + ∠B + ∠C  = 180
51 + 46.6 + ∠B = 180
∠B = 82.4
\(\frac { sin B }{ b } \) = \(\frac { sin A }{ a } \)
\(\frac { 0.99 }{ b } \) = \(\frac { 0.77 }{ 18 } \)
By cross multiplying, we get
b = 23.57

Question 7.

Answer:
∠B = 31.3, ∠C  = 108.7, c = 23.6

Explanation:
According to the information given in the above figure,
\(\frac { sin B }{ b } \) = \(\frac { sin A }{ a } \)
\(\frac { sin B }{ 13 } \) = \(\frac { sin 40 }{ 16 } \)
sin B = \(\frac { .64 }{ 16 } \) x 13
sin B = 0.52
∠B = 31.3
∠A + ∠B + ∠C  = 180
40 + 31.3 + ∠C  = 180
∠C  = 108.7
\(\frac { c }{ sin C } \) = \(\frac { a }{ sin A } \)
\(\frac { c }{ sin 108.7 } \) = \(\frac {16 }{ sin 40 } \)
By cross multiplying, we get
c = \(\frac {16 }{ .64 } \) x 0.947
c = 23.6

Solve the triangle. Round decimal answers to the nearest tenth.

Question 8.

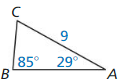
Answer:
∠C = 66, a = 4.36, c = 8.27

Explanation:
According to the information given in the above figure,
∠A + ∠B + ∠C = 180
29 + 85 + ∠C = 180
∠C = 66
\(\frac { a }{ sin A } \) = \(\frac { b }{ sin B } \) = \(\frac { c }{ sin C } \)
\(\frac { a }{ sin 29 } \) = \(\frac { 9 }{ sin 85 } \)
\(\frac { a }{ 0.48 } \) = \(\frac { 9 }{ 0.99 } \)
By cross multiplying and substituting, we get
a = 4.36
\(\frac { b }{ sin B } \) = \(\frac { c }{ sin C } \)
\(\frac { 9 }{ sin 85 } \) = \(\frac { c }{ sin 66 } \)
\(\frac { 9 }{ 0.99 } \) = \(\frac { c }{ 0.91 } \)
By cross multiplying and substituting the values of sin, we get
c = 8.27

Question 9.

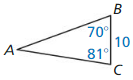
Answer:
∠A = 29, b = 19.37, c = 20.41

Explanation:
According to the information given in the above figure,
∠A + ∠B + ∠C  = 180
∠A + 70 + 81 = 180
∠A = 29
\(\frac { a }{ sin A } \) = \(\frac { b }{ sin B } \) = \(\frac { c }{ sin C } \)
\(\frac { 10 }{ sin 29 } \) = \(\frac { b }{ sin 70 } \)
\(\frac { 10 }{ 0.48 } \) = \(\frac { b }{ 0.93 } \)
By cross multiplying and substituting the values of sin, we get
b = 19.37
\(\frac { a }{ sin A } \) = \(\frac { c }{ sin C } \)
\(\frac { 10 }{ sin 29 } \) = \(\frac { c }{ sin 81 } \)
\(\frac { 10 }{ 0.48 } \) = \(\frac { c }{ 0.98 } \)
By cross multiplying and substituting the values of sin, we get
c = 20.41

Question 10.
WHAT IF?
In Example 5, what would be the length of a bridge from the South Picnic Area to the East Picnic Area?
Answer:
The length of a bridge from the South Picnic Area to the East Picnic Area is 188 m.

Explanation:
Based on the Example 5,
\(\frac { a }{ sin A } \) = \(\frac { b }{ sin B } \) = \(\frac { c }{ sin C } \)
\(\frac { a }{ sin 71 } \) = \(\frac { 150 }{ sin 49 } \)
a = 188

Solve the triangle. Round decimal answers to the nearest tenth.

Question 11.

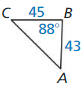
Answer:
b = 61.3, ∠A = 46, ∠C  = 46

Explanation:
According to the information given in the above figure,
b² = a² + c² − 2ac cos B
b² = 45² + 43² – 2(45)(43) cos 88
b² = 2025 + 1849 – 3870 x 0.03 = 3757.9
b = 61.3
\(\frac { sin A }{ a } \) = \(\frac { sin B }{ b } \)
\(\frac { sin A }{ 45 } \) = \(\frac { sin 88 }{ 61.3 } \)
By cross multiplying and substituting the values of sin, we get
sin A = 0.72
∠A = 46
∠A + ∠B + ∠C  = 180
46 + 88 + ∠C  = 180
∠C  = 46

Question 12.

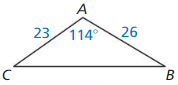
Answer:
a = 41.1, ∠C  = 35.6, ∠B = 30.4

Explanation:
According to the information given in the above figure,
a² = b² + c² − 2bc cos A
a² = 23² + 26² – 2(23)(26) cos 114
a² = 529 + 676 – 1196 x -0.406
a² = 1690.5
a = 41.1
\(\frac { sin 114 }{ 41.1 } \) = \(\frac { sin B }{ 23 } \)
By cross multiplying and substituting the values of sin, we get
0.02 = \(\frac { sin B }{ 23 } \)
sin B = 0.507
∠B = 30.4
∠A + ∠B + ∠C  = 180
114 + 30.4 + ∠C  = 180
∠C  = 35.6

Question 13.

Answer:
∠A = 41.4, ∠B = 81.8, ∠C  = 56.8

Explanation:
According to the information given in the above figure,
a² = b² + c² − 2bc cos A
4² = 6² + 5² – 2(6)(5) cos A
16 = 36 + 25 – 60 cos A
-45 = – 60 cos A
cos A = 0.75
∠A = 41.4
\(\frac { sin 41.4 }{ 4 } \) = \(\frac { sin B }{ 6 } \)
By cross multiplying and substituting the values of sin, we get
0.165 = \(\frac { sin B }{ 6 } \)
sin B = 0.99
∠B = 81.8
∠A + ∠B + ∠C  = 180
41.4 + 81.8 + ∠C  = 180
∠C  = 56.8

Question 14.

Answer:
∠B = 81.8, ∠A = 58.6, ∠C  = 39.6

Explanation:
According to the information given in the above figure,
a² = b² + c² − 2bc cos A
23² = 27² + 16² – 2(27)(16) cos A
529 = 729 + 256 – 864 cos A
456 = 864 cos A
cos A = 0.52
∠A = 58.6
\(\frac { sin 58.6 }{ 23 } \) = \(\frac { sin B }{ 27 } \)
0.03 = \(\frac { sin B }{ 27 } \)
sin B = 0.99
∠B = 81.8
∠A + ∠B + ∠C  = 180
58.6 + 81.8 + ∠C  = 180
∠C  = 39.6

Exercise 9.7 Law of Sines and Law of Cosines

Vocabulary and Core Concept Check

Question 1.
WRITING
What type of triangle would you use the Law of Sines or the Law of Cosines to solve?
Answer:

Question 2.
VOCABULARY
What information do you need to use the Law of Sines?

Answer:

Monitoring progress and Modeling with Mathematics

In Exercises 3 – 8, use a calculator to find the trigonometric ratio, Round your answer to four decimal places.

Question 3.
sin 127°
Answer:

Question 4.
sin 98°

Answer:
sin 98° = 0.9902

Question 5.
cos 139°
Answer:

Question 6.
cos 108°

Answer:
cos 108° = -0.309

Question 7.
tan 165°
Answer:

Question 8.
tan 116°

Answer:
tan 116° = -2.0503

In Exercises 9 – 12, find the area of the triangle. Round your answer to the nearest tenth.

Question 9.

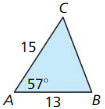
Answer:

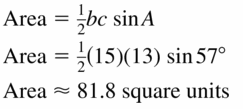
Question 10.

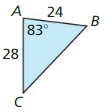
Answer:
Area = 332.64 sq units.

Explanation:
Based on the information given in the above figure,
Area of the triangle = \(\frac{1}{2}\)bc sin A
Area = \(\frac{1}{2}\)(28)(24) sin83
Area = 332.64

Question 11.

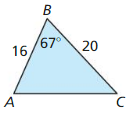
Answer:

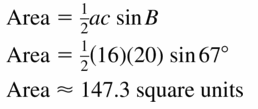
Question 12.

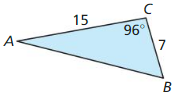
Answer:
Area = 51.9 sq units.

Explanation:
Based on the information given in the above figure,
Area = \(\frac{1}{2}\)ab sin C
Area = \(\frac{1}{2}\)(15)(7) sin 96
Area = 51.9

In Exercises 13 – 18. solve the triangle. Round decimal answers to the nearest tenth.

Question 13.

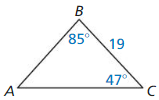
Answer:

Question 14.

Answer:
∠B = 38.3, ∠A = 37.7, a = 15.7

Explanation:
According to the information in the above given figure,
\(\frac { sin B }{16 } \) = \(\frac { sin 104 }{ 25 } \)
cross multiply and substitute the value of sin 104
sin B = 0.62
∠B = 38.3
∠A + ∠B + ∠C = 180
∠A + 38.3 + 104 = 180
∠A = 37.7
\(\frac { sin 37.7 }{ a } \) = \(\frac { sin 104 }{ 25 } \)
cross multiply and substitute the value of sin 37.7
\(\frac { 0.61 }{ a } \) = 0.0388
a = 15.7

Question 15.

Answer:

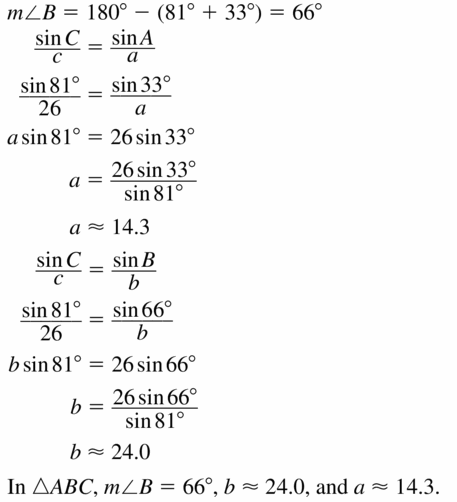
Question 16.

Answer:
∠B = 65, b = 33.55, a = 24.4

Explanation:
According to the information in the above given figure,
∠A + ∠B + ∠C = 180
42 + 73 + ∠B = 180
∠B = 65
\(\frac { sin B }{ b } \) = \(\frac { sin C }{ c } \)
\(\frac { sin 65 }{ b } \) = \(\frac { sin 73 }{ 34 } \)
By cross multiplying,
b = \(\frac { sin 65 × 34 }{ sin 73 } \)
substitute the values of sin 65 and sin73
= 33.55
\(\frac { sin A }{ a } \) = \(\frac { sin C }{ c } \)
\(\frac { sin 42 }{ a } \) = \(\frac { sin 73 }{ 34 } \)
By cross multiplying,
a = \(\frac { sin 42 × 34 }{ 73 } \)
substitute the values of sin 65 and sin73
a = 24.4

Question 17.

Answer:

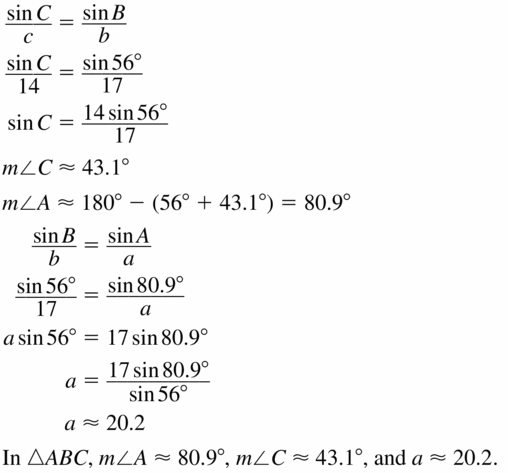
Question 18.

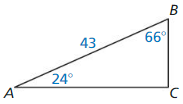
Answer:
∠C = 90, b = 39.56, a = 17.6

Explanation:
According to the information in the above given figure,
∠A + ∠B + ∠C = 180
24 + 66 + ∠C = 180
∠C = 90
\(\frac { sin B }{ b } \) = \(\frac { sin C }{ c } \)
\(\frac { sin 66 }{ b } \) = \(\frac { sin 90 }{ 43 } \)
cross multiply and substitute the values of sin 66 and sin 90.
\(\frac {0.91 }{ b } \) = 0.023
b = 39.56
\(\frac { sin A }{ a } \) = \(\frac { sin C }{ c } \)
\(\frac { sin 24 }{a } \) = \(\frac { sin 90 }{ 43 } \)
cross multiply and substitute the values of sin 24 and sin 90.
\(\frac { 0.406 }{a } \) = 0.023
a = 17.6

In Exercises 19 – 24, solve the triangle. Round decimal answers to the nearest tenth.

Question 19.

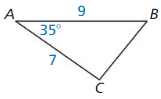
Answer:

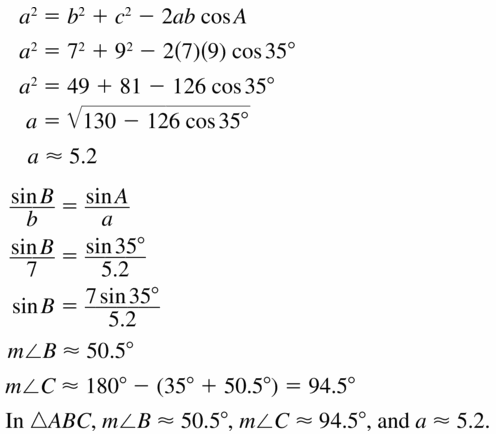
Question 20.

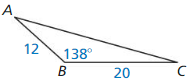
Answer:
b = 29.9, ∠A = 26.1, ∠C = 15.07

Explanation:
According to the information in the above given figure,
b² = a² + c² – 2ac cos B
b² = 20² + 12² – 2(12)(20) cos 138
b² = 400 + 144 – 480 (-0.74)
b² = 899.2
b = 29.9
\(\frac { sin B }{ b } \) = \(\frac { sin A }{ a } \)
\(\frac { sin 138 }{ 29.9 } \) = \(\frac { sin A }{ 20 } \)
cross multiply and substitute the value of sin 138
\(\frac { 0.66 }{ 29.9 } \) = \(\frac { sin A }{ 20 } \)
sin A = 0.44
∠A = 26.1
\(\frac { sin B }{ b } \) = \(\frac { sin C }{ c } \)
\(\frac { sin 138 }{ 29.9 } \) = \(\frac { sin C }{ 12 } \)
cross multiply and substitute the value of sin 138
sin C = 0.26
∠C = 15.07

Question 21.

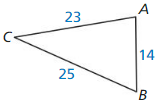
Answer:

Question 22.

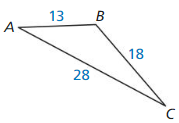
Answer:
∠A = 107.3, ∠B = 51.6, ∠C = 21.1

Explanation:
According to the information in the above given figure,
b² = a² + c² – 2ac cos B
28² = 18² + 13² – 2(18)(13) cos B
784 = 324 + 169 – 468 cos B
291 = 468 cos B
cos B = 0.62
∠B = 51.6
\(\frac { sin C }{ c } \) = \(\frac { sin B }{ b } \)
\(\frac { sin C }{ 13 } \) = \(\frac { sin 51.6 }{ 28 } \)
cross multiply and substitute the value of sin 51.6
sin C = 0.36
∠C = 21.1
∠A + ∠B + ∠C = 180
51.6 + 21.1 + ∠A = 180
∠A = 107.3

Question 23.

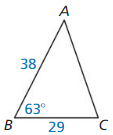
Answer:

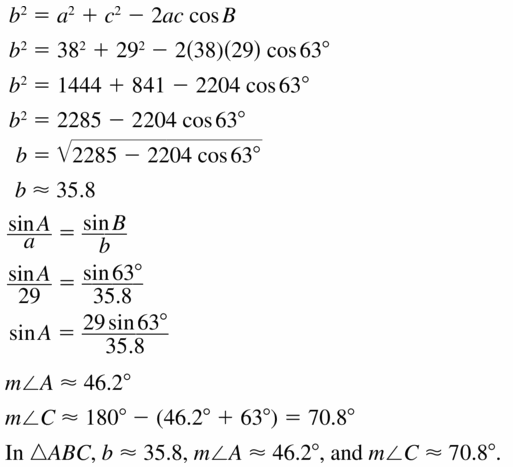
Question 24.

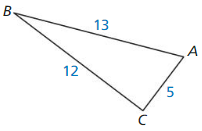
Answer:
∠A = 23, ∠B = 132.1, ∠C = 24.9

Explanation:
According to the information in the above given figure,
b² = a² + c² – 2ac cos B
5² = 12² + 13² – 2(12)(13) cos B
25 = 144 + 169 – 312 cos B
288 = 312 cos B
cos B = 0.92
∠B = 23
\(\frac { sin C }{ c } \) = \(\frac { sin B }{ b } \)
\(\frac { sin C }{ 13 } \) = \(\frac { sin 23 }{ 5 } \)
cross multiply and substitute the value of sin 23
sin C = 1.014
∠C = 24.9
∠A + ∠B + ∠C = 180
23 + 24.9 + ∠B = 180
∠B = 132.1

Question 25.
ERROR ANALYSIS
Describe and correct the error in finding m ∠ C.

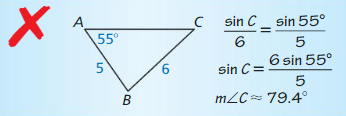
Answer:

Question 26.
ERROR ANALYSIS
Describe and correct the error in finding m ∠ A in ∆ABC when a = 19, b = 21, and c = 11.

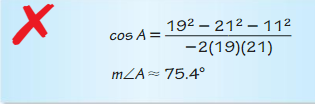
Answer:
∠A = 64.5

Explanation:
According to the information in the above given figure,
a² = b² + c² – 2bc cos A
19² = 21² + 11² – 2(21)(11) cos A
361 = 441 + 121 – 462 cos A
201 = 462 cos A
cos A = 0.43
∠A = 64.5

COMPARING METHODS

In Exercise 27 – 32. tell whether you would use the Law of Sines, the Law of Cosines. or the Pythagorean Theorem (Theorem 9.1) and trigonometric ratios to solve the triangle with the given information. Explain your reasoning. Then solve the triangle.

Question 27.
m ∠ A = 72°, m ∠ B = 44°, b = 14
Answer:

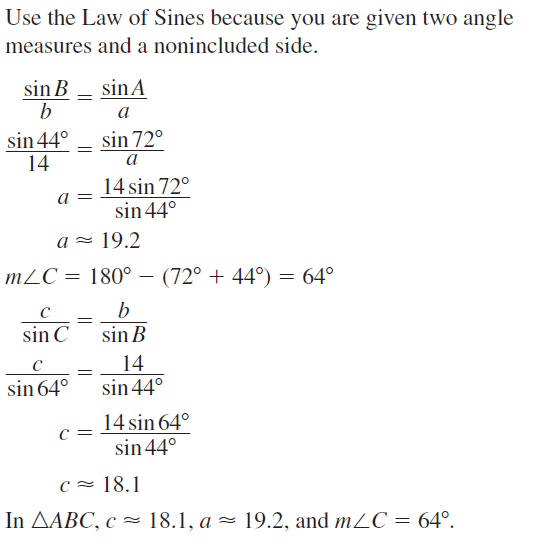
Question 28.
m ∠ B = 98°, m ∠ C = 37°, a = 18
Answer:
∠A = 45, b = 25.38, c = 15.38

Explanation:
Based on the information given in the above figure,
∠A + ∠B + ∠C = 180
∠A + 98 + 37 = 180
∠A = 45
\(\frac { sin B }{ b } \) = \(\frac { sin A }{ a } \)
\(\frac { sin 98 }{ b } \) = \(\frac { sin 45 }{ 18 } \)
cross multiply and substitute the values of sin 98 and sin 45
\(\frac { 0.99 }{ b } \) = 0.039
b = 25.38
\(\frac { sin A }{ a } \) = \(\frac { sin C }{ c } \)
\(\frac { sin 45 }{ 18 } \) = \(\frac { sin 37 }{ c } \)
cross multiply and substitute the values of sin 37 and sin 45
0.039 = \(\frac { sin 37 }{ c } \)
c = 15.38

Question 29.
m ∠ C = 65°, a = 12, b = 21
Answer:

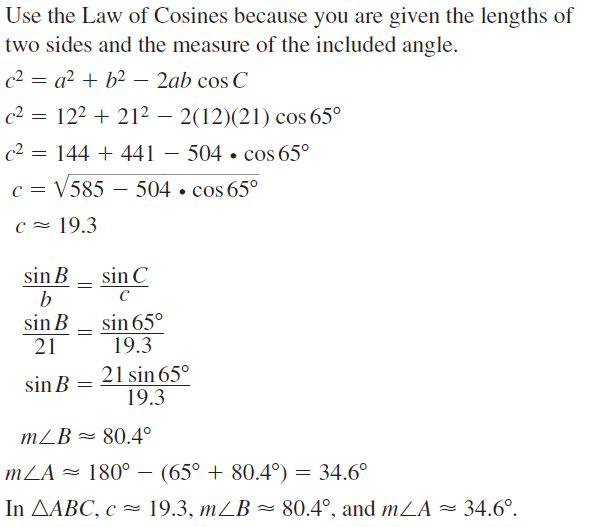
Question 30.
m ∠ B = 90°, a = 15, c = 6

Answer:
b = 3√29, ∠A = 66.9, ∠C = 23.1

Explanation:
According to the information given above,
b² = a² + c²- 2ac cos B
b² = 15² + 6² – 2(15)(6) cos 90
= 225 + 36 – 180(0)
b² = 261
b = 3√29
\(\frac { sin B }{ b } \) = \(\frac { sin A }{ a } \)
\(\frac { sin 90 }{ 3√29 } \) = \(\frac { sin A }{ 15 } \)
cross multiply and substitute the values of sin 90
sin A = 0.92
∠A = 66.9
∠A + ∠B + ∠C = 180
66.9 + 90 + ∠C = 180
∠C = 23.1

Question 31.
m ∠ C = 40°, b = 27, c = 36
Answer:

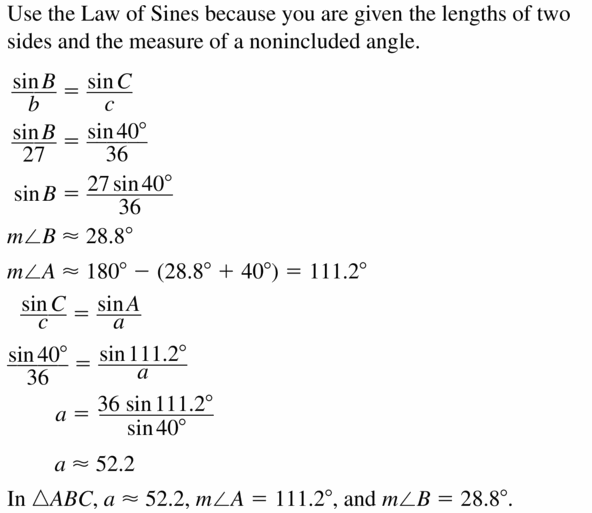
Question 32.
a = 34, b = 19, c = 27

Answer:
∠B = 33.9, ∠A = 78.5, ∠C = 67.6

Explanation:
According to the information in the above given figure,
b² = a² + c²- 2ac cos B
19² = 34² + 27²- 2(34)(27) cos B
361 = 1156 + 729 – 1836 cos B
cos B = 0.83
∠B = 33.9
\(\frac { sin 33.9 }{ 19 } \) = \(\frac { sin A }{ 34 } \)
cross multiply and substitute the values of sin 33.9
sin A = 0.98
∠A = 78.5
∠A + ∠B + ∠C = 180
78.5 + 33.9 + ∠C = 180
∠C = 67.6

Question 33.
MODELING WITH MATHEMATICS
You and your friend are standing on the baseline of a basketball court. You bounce a basketball to your friend, as shown in the diagram. What is the distance between you and your friend?

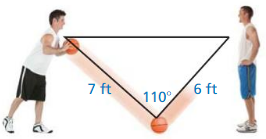
Answer:

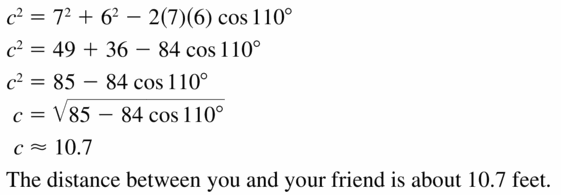
Question 34.
MODELING WITH MATHEMATICS
A zip line is constructed across a valley, as shown in the diagram. What is the width w of the valley?

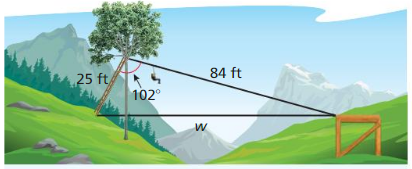
Answer:
w = 92.5 ft

Explanation:
Based on the information given in the diagram,
w² = 25² + 84² – 2(25)(84) cos 102
w² = 7681 – 4200 cos 102
w = 92.5 ft

Question 35.
MODELING WITH MATHEMATICS
You are on the observation deck of the Empire State Building looking at the Chrysler Building. When you turn 145° clockwise, you see the Statue of Liberty. You know that the Chrysler Building and the Empire Slate Building arc about 0.6 mile apart and that the Chrysler Building and the Statue of Liberty are about 5.6 miles apart. Estimate the distance between the Empire State Building and the Statue of Liberty.
Answer:

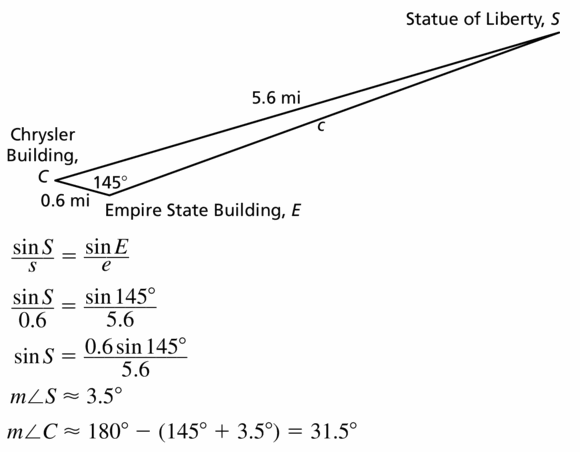
Question 36.
MODELING WITH MATHEMATICS
The Leaning Tower of Pisa in Italy has a height of 183 feet and is 4° off vertical. Find the horizontal distance d that the top of the tower is off vertical.

Answer:

Question 37.
MAKING AN ARGUMENT
Your friend says that the Law of Sines can be used to find JK. Your cousin says that the Law of Cosines can be used to find JK. Who is correct’? Explain your reasoning.

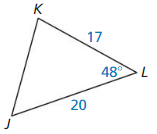
Answer:

Question 38.
REASONING
Use ∆XYZ

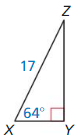
a. Can you use the Law of Sines to solve ∆XYZ ? Explain your reasoning.
Answer:

b. Can you use another method to solve ∆XYZ ? Explain your reasoning.
Answer:

Question 39.
MAKING AN ARGUMENT
Your friend calculates the area of the triangle using the formula A = \(\frac{1}{2}\)qr sin S and says that the area is approximately 208.6 square units. Is your friend correct? Explain your reasoning.

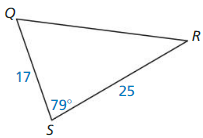
Answer:

Question 40.
MODELING WITH MATHEMATICS
You are fertilizing a triangular garden. One side of the garden is 62 feet long, and another side is 54 feet long. The angle opposite the 62-foot side is 58°.
a. Draw a diagram to represent this situation.
b. Use the Law of Sines to solve the triangle from part (a).
c. One bag of fertilizer covers an area of 200 square feet. How many bags of fertilizer will you need to cover the entire garden?

Answer:
a)

with reference to the Law of Sines:
If A, B, and C are the measurements of the angles are shown in the above triangle,
So, a, b, and c are the lengths of the sides opposite of the corresponding angles,
then the ratios of the a side’s length to the sine of the angle opposite side be the same.
C = 47.6, A = 74.4, a = 70.4
Area of triangle = (1/2) b x h
Area of triangle = (1/2) x 54 x 62 = 1674 sq ft
As, One bag of fertilizer covers an area of 200 square feet.
1674/200 = 8.37
rounding to 9 bags of fertilizer.

Question 41.
MODELING WITH MATHEMATICS
A golfer hits a drive 260 yards on a hole that is 400 yards long. The shot is 15° off target.

a. What is the distance x from the golfer’s ball to the hole?
b. Assume the golfer is able to hit the ball precisely the distance found in part (a). What is the maximum angle θ (theta) by which the ball can be off target in order to land no more than 10 yards fr0m the hole?
Answer:

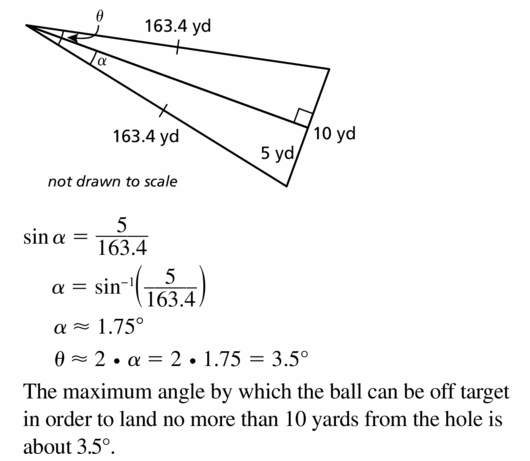
Question 42.
COMPARING METHODS
A building is constructed on top of a cliff that is 300 meters high. A person standing on level ground below the cliff observes that the angle of elevation to the top of the building is 72° and the angle of elevation to the top of the cliff is 63°.
a. How far away is the person from the base of the cliff?
Answer:

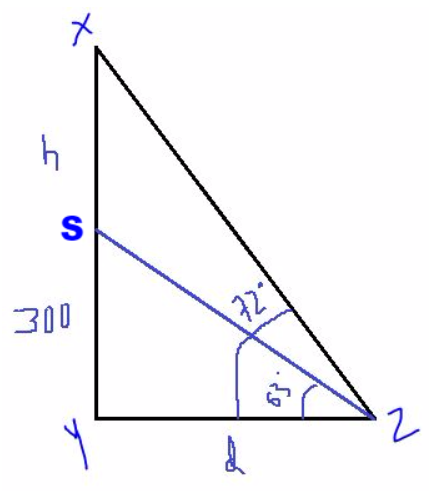
b. Describe two different methods you can use to find the height of the building. Use one of these methods to find the building’s height.
Answer:
h = 170.45

Explanation:
Given that,
A building is constructed on top of a cliff that is 300 meters high.
The angle of elevation to the top of the building is 72° and the angle of elevation to the top of the cliff is 63°.
Consider △SYZ and evaluate d using tangent function.
tan SYZ = \(\frac { 300 }{ d } \)
d = \(\frac { 300 }{ tan 63 } \)
d = 152.86
The person is standing 152.86 m away from the base of the cliff.
Consider △XYS and evaluate h + 300
tan XYZ = \(\frac { h + 300 }{ d } \)
h = 152.86 x tan 72 – 300
h = 170.45
The building is 170.45 m high.

Question 43.
MATHEMATICAL CONNECTIONS
Find the values of x and y.

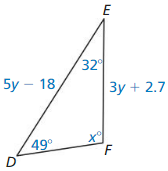
Answer:

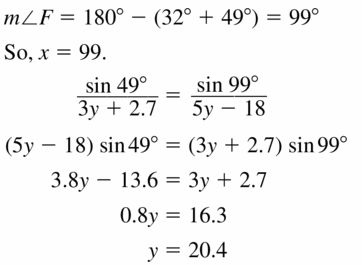
Question 44.
HOW DO YOU SEE IT?
Would you use the Law of Sines or the Law of Cosines to solve the triangle?
Answer:

Question 45.
REWRITING A FORMULA
A Simplify the Law of Cosines for when the given angle is a right angle.
Answer:

Question 46.
THOUGHT PROVOKING
Consider any triangle with side lengths of a, b, and c. Calculate the value of s, which is half the perimeter of the triangle. What measurement of the triangle is represented by \(\sqrt{s(s-a)(s-b)(s-c)} ?\)
Answer:

Question 47.
ANALYZING RELATIONSHIPS
The ambiguous case of the Law of Sines occurs when you are given the measure of one acute angle. the length of one adjacent side, and the length of the side opposite that angle, which is less than the length of the adjacent side. This results in two possible triangles. Using the given information, find two possible solutions for ∆ABC
Draw a diagram for each triangle.
(Hint: The inverse sine function gives only acute angle measures. so consider the acute angle and its supplement for ∠B.)

a. m ∠ A = 40°, a = 13, b = 16
b. m ∠ A = 21°, a = 17, b = 32
Answer:

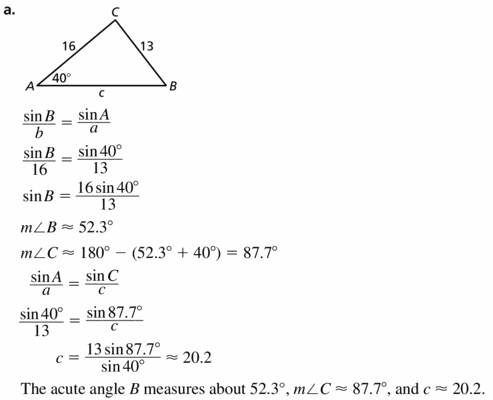
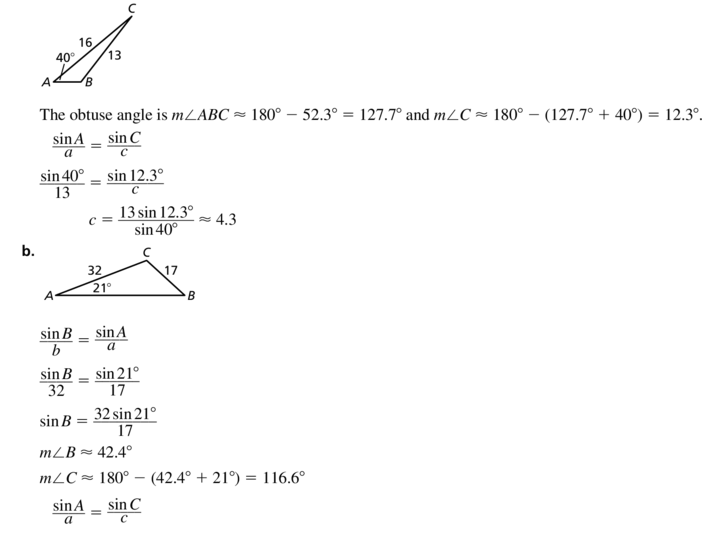
Question 48.
ABSTRACT REASONING
Use the Law of Cosines to show that the measure of each angle of an equilateral triangle is 60°. Explain your reasoning.
Answer:
∠A = 60

Explanation:
Given,
the measure of each angle of an equilateral triangle is 60°.
a² = b² + c²- 2 bc cos A
a² = a² + a² – 2 aa cos A
a² = 2a² cos A
cos A = 1/2
∠A = 60

Question 49.
CRITICAL THINKING
An airplane flies 55° east of north from City A to City B. a distance of 470 miles. Another airplane flies 7° north of east from City A to City C. a distance of 890 miles. What is the distance between Cities B and C?
Answer:

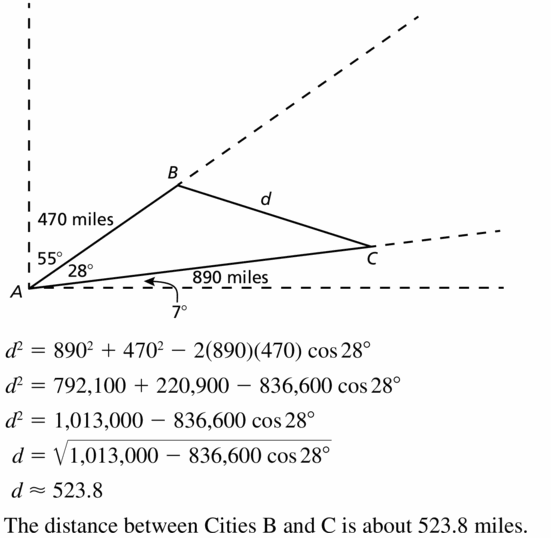
Question 50.
REWRITING A FORMULA
Follow the steps to derive the formula for the area of a triangle.
Area = \(\frac{1}{2}\)ab sin C.

a. Draw the altitude from vertex B to \(\overline{A C}\). Label the altitude as h. Write a formula for the area of the triangle using h.
Answer:

b. Write an equation for sin C
Answer:

c. Use the results of parts (a) and (b) to write a formula for the area of a triangle that does not include h.
Answer:

Question 51.
PROVING A THEOREM
Follow the steps to use the formula for the area of a triangle to prove the Law of Sines (Theorem 9.9).
a. Use the derivation in Exercise 50 to explain how to derive the three related formulas for the area of a triangle.
Area = \(\frac{1}{2}\)bc sin A,
Area = \(\frac{1}{2}\)ac sin B,
Area = \(\frac{1}{2}\)ab sin C
b. why can you use the formulas in part (a) to write the following statement?
\(\frac{1}{2}\)bc sin A = \(\frac{1}{2}\)ac sin B = \(\frac{1}{2}\)ab sin C
c. Show how to rewrite the statement in part (b) to prove the Law of Sines. Justify each step.
Answer:

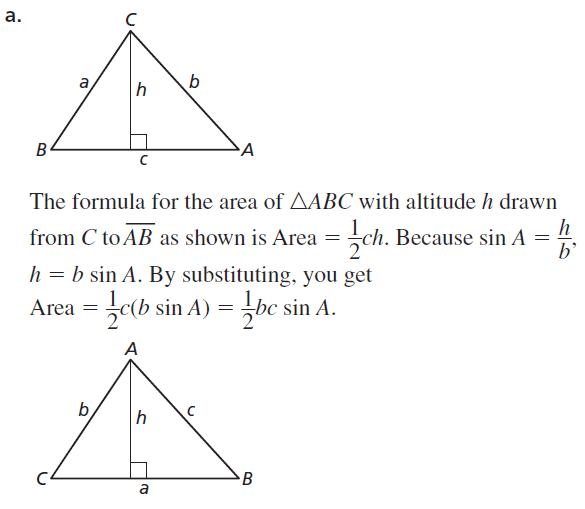
Question 52.
PROVING A THEOREM
Use the given information to complete the two – column proof of the Law of Cosines (Theorem 9.10).

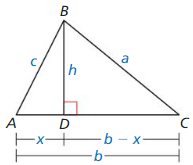
Given \(\overline{B D}\) is an altitude of ∆ABC.
Prove a² = b² + c² – 2bc cos A

Statements	Reasons
1. \(\overline{B D}\) is an altitude of ∆ABC.	1. Given
2. ∆ADB and ∆CDB are right triangles.	2. _______________________
3. a2 = (b – x)2 + h2	3. _______________________
4. _______________________	4. Expand binomial.
5. x2 + h2 = c2	5. _______________________
6. _______________________	6. Substitution Property of Equality
7. cos A = \(\frac{x}{c}\)	7. _______________________
8. x = c cos A	8. _______________________
9. a2 = b2 + c2 – 2bc Cos A	9. _______________________

Answer:

Maintaining Mathematical Proficiency

Find the radius and diameter of the circle.

Question 53.

Answer:

Explanation:
According to the information given in the circle,
diameter = 8 ft.
radius = d/2
r = 8/2
= 4

Question 54.

Answer:
The radius is 10 in and the diameter is 20 in.

Explanation:
According to the information given in the circle,
radius = 10 in
diameter = 2r
d = 2 x 10
d = 20 in

Question 55.

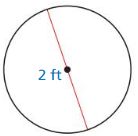
Answer:

Explanation:
According to the information given in the circle,
diameter = 2 ft.
radius = d/2
r = 2/2
r = 1

Question 56.

Answer:
The radius is 50 in and the diameter is 100 in.

Explanation:
According to the information given in the circle,
radius = 50 in
diameter = 2r
d = 2 x 50
d = 100 in

Right Triangles and Trigonometry Review

9.1 The Pythagorean Theorem

Find the value of x. Then tell whether the side lengths form a Pythagorean triple.

Question 1.

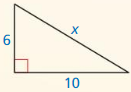
Answer:
x = 2√34
The sides will not form a Pythagorean triple.

Explanation:
Given,
the side lengths are 6 and 10.
let the hypotenuse is x.
x² = 6² + 10²
x²= 36 + 100
x = 2√34

Question 2.

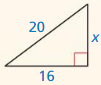
Answer:
x = 12
The sides form a Pythagorean triple.

Explanation:
Given,
the side lengths are 16 and x.
let the hypotenuse is 20.
20² = 16²+ x²
400 = 256 + x²
x² = 144
x = 12

Question 3.

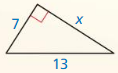
Answer:
x = 2√30
The sides will not form a Pythagorean triple.

Explanation:
Given,
the side lengths are 7 and x.
let the hypotenuse is 13.
13² = 7² + x²
169 = 49 + x²
x = 2√30

Verify that the segments lengths form a triangle. Is the triangle acute, right, or obtuse?

Question 4.
6, 8, and 9

Answer:
Acute triangle.

Explanation:
Given, the line segments as 6, 8, and 9.
c² = a² + b²
9² = 6² + 8²
81 = 36 + 64
81 = 100
9² < 6² + 8²
We know that if the sum of the squares of longer side is lesser than the sum of the squares of the shorter side is said to be an acute angle.
So, the sides of 6, 8, and 9 form a triangle is acute.

Question 5.
10, 2√2, and 6√3

Answer:
Acute triangle.

Explanation:
Given, the line segments as 10, 2√2, and 6√3
c² = a² + b²
10² = 6√3² + 2√2²
100 = 8 + 108
100 = 116
We know that if the sum of the squares of longer side is lesser than the sum of the squares of the shorter side is said to be an acute angle.
So, the sides of 10, 2√2, and 6√3 form a triangle is acute.

Question 6.
13, 18 and 3√55

Answer:
Acute triangle.

Explanation:
Given, the line segments as 13, 18 and 3√55
c² = a² + b²
18² = 13² + (3√55)²
324 =169 + 495
324 = 664
We know that if the sum of the squares of longer side is lesser than the sum of the squares of the shorter side is said to be an acute angle.
So, the sides of 13, 18 and 3√55 form a triangle is acute.

9.2 Special Right Triangles

Find the value of x. Write your answer in simplest form.

Question 7.

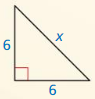
Answer:
x = 6√2

Explanation:
Given, the side lengths 6 and 6
let hypotenuse = x
hypotenuse = leg • √2
x = 6√2

Question 8.

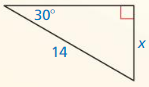
Answer:
x = 8.08

Explanation:
Given, one of the side length is √3 and the other is x
let hypotenuse = 14
longer leg = shorter leg • √3
14 = x • √3
x = 8.08

Question 9.

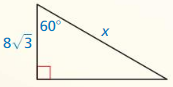
Answer:
x = 24

Explanation:
Given, the side lengths 8√3 and √3
let hypotenuse = x
longer leg = shorter leg • √3
x = 8√3 • √3
x = 24

9.3 Similar Right Triangles

Identify the similar triangles. Then find the value of x.

Question 10.

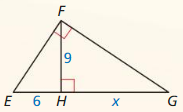
Answer:
x = \(\frac { 27 }{ 2 } \)

Explanation:
From the above given information,
we know that,
If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle then the triangles are similar.
9 = √(6x)
81 = 6x
x = \(\frac { 27 }{ 2 } \)

Question 11.

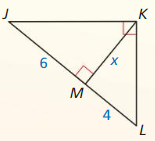
Answer:
x = 2√6

Explanation:
From the above given information,
we know that,
If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle then the triangles are similar.
x = √(6 x 4)
x = 2√6

Question 12.

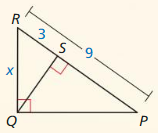
Answer:
x = 3.5

Explanation:
From the above given information,
we know that,
If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle then the triangles are similar.
\(\frac { RP }{ RQ } \) = \(\frac { SP }{ RS } \)
\(\frac { 9 }{ x } \) = \(\frac { 6 }{ 3 } \)
x = 3.5

Question 13.

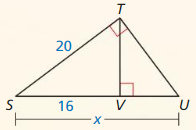
Answer:
x = 16

Explanation:
From the above given information,
we know that,
If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle then the triangles are similar.
\(\frac { SU }{ ST } \) = \(\frac { SV }{ VU } \)
\(\frac { 16 }{ 20 } \) = \(\frac { x }{ (x – 16) } \)
4(x – 16) = 5x
x = 16

Find the geometric mean of the two numbers.

Question 14.
9 and 25

Answer:
GM = 15

Explanation:
Given,
9 and 25
To know the geometric mean of the two numbers,
multiply the given numbers together and take the square root of the result.
mean = √(9 x 25)
= 15

Question 15.
36 and 48

Answer:
GM = 24√3

Explanation:
Given,
36 and 48
To know the geometric mean of the two numbers,
multiply the given numbers together and take the square root of the result.
mean = √(36 x 48)
= 24√3

Question 16.
12 and 42

Answer:
GM = 6√14

Explanation:
Given,
12 and 42
To know the geometric mean of the two numbers,
multiply the given numbers together and take the square root of the result.
mean = √(12 x 42)
= 6√14

9.4 The Tangent Ratio

Find the tangents of the acute angles in the right triangle. Write each answer as a fraction and as a decimal rounded to four decimal places.

Question 17.

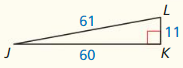
Answer:
tan J = \(\frac { 11 }{ 60 } \) = 0.183
tan L = \(\frac { 60 }{ 11 } \) = 5.45

Explanation:
According to the information given in the above figure,
Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
tan J = \(\frac { Opposite side }{ Adjacent side } \)
tan J = \(\frac { LK }{ JK } \) = \(\frac { 11 }{ 60 } \)
tan L = \(\frac { JK }{ LK } \) = \(\frac { 60 }{ 11 } \)

Question 18.

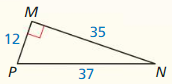
Answer:
tan P = \(\frac { 35 }{ 12 } \) = 2.916
tan N = \(\frac { 12 }{ 35 } \) = 0.342

Explanation:
According to the information given in the above figure,
Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
tan P = \(\frac { MN }{ MP } \) = \(\frac { 35 }{ 12 } \)
tan N = \(\frac { MP }{ MN } \) = \(\frac { 12 }{ 35 } \)

Question 19.

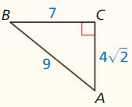
Answer:
tan A = \(\frac { 7 }{ 4√2 } \) = 1.215
tan B = \(\frac { 4√2 }{ 7 } \) = 0.822

Explanation:
According to the information given in the above figure,
Tangent ratio is the ratio of opposite side to adjacent side of a right triangle.
tan A = \(\frac { BC }{ AC } \) = \(\frac { 7 }{ 4√2 } \)
tan B = \(\frac { AC }{ BC } \) = \(\frac { 4√2 }{ 7 } \)

Find the value of x. Round your answer to the nearest tenth.

Question 20.

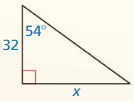
Answer:
x = 43.8

Explanation:
According to the values given in the above figure,
we can write as
tan 54 = \(\frac { x }{ 32 } \)
tan 54 = 1.37
1.37 = \(\frac { x }{ 32 } \)
x = 43.8

Question 21.

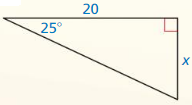
Answer:
x = 9.2

Explanation:
According to the values given in the above figure,
we can write as
tan 25 = \(\frac { x }{ 20 } \)
tan 25 = 0.46
0.46 x 20 = x
x = 9.2

Question 22.

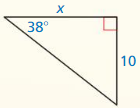
Answer:
x = 12.8

Explanation:
According to the values given in the above figure,
we can write as
tan 38 = \(\frac { 10 }{ x } \)
tan 38 = 0.7813
x = 12.8

Question 23.
The angle between the bottom of a fence and the top of a tree is 75°. The tree is 4 let from the fence. How tall is the tree? Round your answer to the nearest foot.

Answer:
x = 14.92

Explanation:
Given,
The angle between the bottom of a fence and the top of a tree is 75°.
The tree is 4 let from the fence.
tan 75 = \(\frac { x }{ 4 } \)
tan 75 = 3.732
x = 3.732 x 4
x = 14.92

9.5 The Sine and Cosine Ratios

Find sin X, sin Z, cos X, and cos Z. Write each answer as a fraction and as a decimal rounded to four decimal places.

Question 24.

Answer:
sin X = \(\frac { 3 }{ 5 } \)
sin Z = \(\frac { 4 }{ 5 } \)
cos X = \(\frac { 4 }{ 5 } \)
cos Z = \(\frac { 3 }{ 5 } \)
Explanation:

sin X = \(\frac {Opposite}{Hypotenuse} \)
sin X = \(\frac {YZ}{XZ} \)
sin X = \(\frac {3}{5} \)
sin X = 0.6

sin Z = \(\frac {Opposite}{Hypotenuse} \)
sin Z = \(\frac {XY}{XZ} \)
sin Z = \(\frac {4}{5} \)
sin Z = 0.8

cos X = \(\frac {adjacent}{Hypotenuse} \)
cos X = \(\frac {XY}{XZ} \)
cos X = \(\frac {4}{5} \)
cos X = 0.8

cos Z = \(\frac {adjacent}{Hypotenuse} \)
cos Z = \(\frac {YZ}{XZ} \)
cos Z = \(\frac {3}{5} \)
cos Z = 0.6

Question 25.

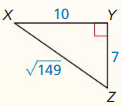
Answer:
sin X = \(\frac { 7 }{ √149 } \) = 0.573
sin Z = \(\frac { 10 }{ √149 } \) = 0.819
cos X = \(\frac { 10 }{ √149 } \) = 0.819
cos Z = \(\frac { 7 }{ √149 } \) = 0.573
Explanation:

sin X = \(\frac {Opposite}{Hypotenuse} \)
sin X = \(\frac {YZ}{XZ} \)
sin X = \(\frac {7}{√149} \)
sin X = 0.573

sin Z = \(\frac {Opposite}{Hypotenuse} \)
sin Z = \(\frac {XY}{XZ} \)
sin Z = \(\frac {10}{√149} \)
sin Z = 0.819

cos X = \(\frac {adjacent}{Hypotenuse} \)
cos X = \(\frac {XY}{XZ} \)
cos X = \(\frac {4}{√149} \)
cos X = 0.819

cos Z = \(\frac {adjacent}{Hypotenuse} \)
cos Z = \(\frac {YZ}{XZ} \)
cos Z = \(\frac {7}{√149} \)
cos Z = 0.573

Question 26.

Answer:
sin X = \(\frac { 55 }{ 73 } \) = 0.7534
sin Z = \(\frac { 48 }{ 73 } \) = 0.6575
cos X = \(\frac { 48 }{ 73 } \) = 0.6575
cos Z = \(\frac { 55 }{ 73 } \) = 0.7534
Explanation:

sin X = \(\frac {Opposite}{Hypotenuse} \)
sin X = \(\frac {YZ}{XZ} \)
sin X = \(\frac {55}{73} \)
sin X = 0.7534

sin Z = \(\frac {Opposite}{Hypotenuse} \)
sin Z = \(\frac {XY}{XZ} \)
sin Z = \(\frac {48}{73} \)
sin Z = 0.6575

cos X = \(\frac {adjacent}{Hypotenuse} \)
cos X = \(\frac {XY}{XZ} \)
cos X = \(\frac {48}{73} \)
cos X = 0.6575

cos Z = \(\frac {adjacent}{Hypotenuse} \)
cos Z = \(\frac {YZ}{XZ} \)
cos Z = \(\frac {55}{73} \)
cos Z = 0.7534

Find the value of each variable using sine and cosine. Round your answers to the nearest tenth.

Question 27.

Answer:
sin 23 = \(\frac { t }{ 34 } \)
t = 13.26
cos 23 = \(\frac { s }{ 34 } \)
s = 31.28

Question 28.

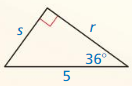
Answer:
sin 36 = \(\frac { s }{ 5 } \)
s = 2.9
cos 36 = \(\frac { r }{ 5 } \)
r = 4

Question 29.

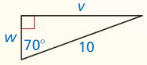
Answer:
sin 70 = \(\frac { v }{ 10 } \)
v = 9.39
cos 70 = \(\frac { w }{ 10 } \)
w = 3.42

Question 30.
Write sin 72° in terms of cosine.

Answer:
sin 72° = cos 18°

Explanation:
Given,
sin 72°
sin 72 = cos(90 – 72)
= cos 18 = 0.95

Question 31.
Write cos 29° in terms of sine.

Answer:
cos 29° = cos 61°

Explanation:
Given,
sin 29°
sin 29 = cos(90 – 29)
= cos 61 = 0.48

9.6 Solving Right Triangles

Let ∠Q be an acute angle. Use a calculator to approximate the measure of ∠Q to the nearest tenth of a degree.

Question 32.
cos Q = 0.32

Answer:
cos Q = 0.32
∠Q = inverse cos of .32
∠Q = 71.3

Question 33.
sin Q = 0.91

Answer:
sin Q = 0.91
∠Q = inverse sin of 0.91
∠Q = 65.5

Question 34.
tan Q = 0.04

Answer:
tan Q = 0.04
∠Q = inverse tan of 0.04
∠Q = 2.29

Solve the right triangle. Round decimal answers to the nearest tenth.

Question 35.

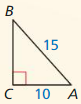
Answer:
a = 5√5, ∠A = 47.7, ∠B = 42.3

Explanation:
c² = a² + b²
15² = a² + 10²
a² = 125
a = 5√5
sin A = \(\frac { 5√5 }{ 15 } \) = 0.74
∠A = 47.7
∠A + ∠B + ∠C = 180
47.7 + ∠B + 90 = 180
∠B = 42.3

Question 36.

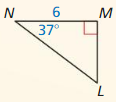
Answer:
NL = 7.59, ∠L = 53, ML = 4.55

Explanation:
cos 37 = \(\frac { 6 }{ NL } \)
NL = 7.59
∠N + ∠M + ∠L = 180
37 + 90 + ∠L = 180
∠L = 53
sin 37 = \(\frac { ML }{ 7.59 } \)
ML = 4.55

Question 37.

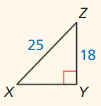
Answer:
XY = 17.34, ∠X = 46, ∠Z = 44

Explanation:
c² = a² + b²
25² = 18²+ b²
b² = 301
b = 17.34
sin X = \(\frac { 18 }{ 25 } \)
∠X = 46
sum of angles = 180
46 + 90 + ∠Z = 180
∠Z = 44

9.7 Law of Sines and Law of Cosines

Find the area of ∆ABC with the given side lengths and included angle.

Question 38.
m ∠ B = 124°, a = 9, c = 11

Answer:
A = 40.59

Explanation:
Given,
m ∠ B = 124°, a = 9, c = 11
Area = \(\frac { 1 }{ 2 } \) ac sin B
= \(\frac { 1 }{ 2 } \) (9 x 11) sin 124
= \(\frac { 1 }{ 2 } \) (99) sin 124
substitute the value of sin 124
= 40.59

Question 39.
m ∠ A = 68°, b = 13, c = 7

Answer:
A = = 41.86

Explanation:
Given,
m ∠ A = 68°, b = 13, c = 7
Area = \(\frac { 1 }{ 2 } \) bc sin A
= \(\frac { 1 }{ 2 } \) (13 x 7) sin 68
= \(\frac { 1 }{ 2 } \) (91) sin 68
substitute the value of sin 68
= 41.86

Question 40.
m ∠ C = 79°, a = 25 b = 17

Answer:
A = 208.25

Explanation:
Given,
m ∠ C = 79°, a = 25 b = 17
Area = \(\frac { 1 }{ 2 } \) ab sin C
= \(\frac { 1 }{ 2 } \) (25 x 17) sin 79
= \(\frac { 1 }{ 2 } \) (425) sin 79
substitute the value of sin 79
= 208.25

Solve ∆ABC. Round decimal answers to the nearest tenth.

Question 41.
m ∠ A = 112°, a = 9, b = 4

Answer:
∠B = 24, ∠C = 44, c = 6.76

Explanation:
Given,
∠B = 24, ∠C = 44, c = 6.76
\(\frac { sin B }{ b } \) = \(\frac { sin A }{ a } \)
\(\frac { sin B }{ 4 } \) = \(\frac { sin 112 }{ 9 } \)
cross multiply
sin B = 0.408
∠B = 24
we know that the sum of the angles is 180 degrees.
∠A + ∠B + ∠C = 180
112 + 24 + ∠C = 180
∠C = 44
\(\frac { sin 112 }{ 9 } \) = \(\frac { sin 44 }{ c } \)
cross multiply
c = 6.76

Question 42.
m ∠ 4 = 28°, m ∠ B = 64°, c = 55

Answer:
∠C = 88, b = 49.4, a = 25.5

Explanation:
Given,
m ∠ 4 = 28°, m ∠ B = 64°, c = 55
we know that the sum of the angles is 180 degrees.
∠A + ∠B + ∠C = 180
28 + 64 + ∠C = 180
∠C = 88
\(\frac { sin B }{ b } \) = \(\frac { sin C }{ c } \)
\(\frac { sin 64 }{ b } \) = \(\frac { sin 88 }{ 55 } \)
cross multiply
\(\frac { sin 64 }{ b } \) = 0.018
b = 49.4
\(\frac { sin 28 }{ a } \) = \(\frac { sin 88 }{ 55 } \)
a = 25.5

Question 43.
m ∠ C = 48°, b = 20, c = 28

Answer:
∠B = 31.3, ∠A = 100.7, a = 37.6

Explanation:
Given,
m ∠ C = 48°, b = 20, c = 28
\(\frac { sin B }{ b } \) = \(\frac { sin C }{ c } \)
\(\frac { sin B }{ 20 } \) = \(\frac { sin 48 }{ 28 } \)
cross multiply
\(\frac { sin B }{ 20 } \) = 0.026
sin B = 0.52
∠B = 31.3
we know that the sum of the angles is 180 degrees.
∠A + ∠B + ∠C = 180
∠A + 31.3 + 48 = 180
∠A = 100.7
\(\frac { sin 100.7 }{ a } \) = \(\frac { sin 48 }{ 28 } \)
cross multiply
a = 37.6

Question 44.
m ∠ B = 25°, a = 8, c = 3

Answer:
b = 5.45, ∠A = 37.5, ∠C = 117.5

Explanation:
Given,
m ∠ B = 25°, a = 8, c = 3
we know that,
b² = a² + c²- 2ac cos B
b² = 8² + 3² – 2(8 x 3) cos 25 = 73 – 43.2 = 29.8
b = 5.45
\(\frac { sin A }{ 8 } \) = \(\frac { sin 25 }{ 5.45 } \)
sin A = 0.61
∠A = 37.5
we know that the sum of the angles is 180 degrees.
∠A + ∠B + ∠C = 180
37.5 + 25 + ∠C = 180
∠C = 117.5

Question 45.
m ∠ B = 102°, m ∠ C = 43°, b = 21

Answer:
∠A = 35, c = 14.72, a = 12.3

Explanation:
Given,
m ∠ B = 102°, m ∠ C = 43°, b = 21
we know that the sum of the angles is 180 degrees.
∠A + ∠B + ∠C = 180
∠A + 102 + 43 = 180
∠A = 35
\(\frac { sin 102 }{ 21 } \) = \(\frac { sin 43 }{ c } \)
cross multiply
0.046 = \(\frac { sin 43 }{ c } \)
c = 14.72
\(\frac { sin 102 }{ 21 } \) = \(\frac { sin 35 }{ a } \)
cross multiply
0.046 = \(\frac { sin 35 }{ a } \)
a = 12.3

Question 46.
a = 10, b = 3, c = 12

Answer:
∠B = 11.7, ∠C = 125.19, ∠A = 43.11

Explanation:
Given,
a = 10, b = 3, c = 12
we know that,
b² = a² + c²- 2ac cos B
3² = 10² + 12²- 2(10 x 12) cos B
9 = 100 + 144 – 240 cos B
cos B = 0.979
∠B = 11.7
a² = b² + c²- 2bc cos A
100 = 9 + 144 – 72 cos A
cos A = 0.73
∠A = 43.11
we know that the sum of the angles is 180 degrees.
∠A + ∠B + ∠C = 180
43.11 + 11.7 + ∠C = 180
∠C = 125.19

Right Triangles and Trigonometry Test

Find the value of each variable. Round your answers to the nearest tenth.

Question 1.

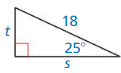
Answer:
s = 16
t = 8

Explanation:
Based on the information given in the figure,
sin 25 = \(\frac { t }{ 18 } \)
t = 7.5 rounded to 8
cos 25 = \(\frac { s }{ 18 } \)
s = 16.2 rounded to 16

Question 2.

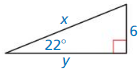
Answer:
x = 16
y = 15

Explanation:
Based on the information given in the figure,
sin 22 = \(\frac { 6 }{ x } \)
x = 16.21 rounded to 16
cos 22 = \(\frac { y }{ 16.21 } \)
y = 14.91 rounded to 15

Question 3.

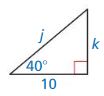
Answer:
k = 8
j = 13

Explanation:
Based on the information given in the figure,
tan 40 = \(\frac { k }{ 10 } \)
k = 8.3
cos 40 = \(\frac { 10 }{ j } \)
j = 13.15

Verity that the segment lengths form a triangle. Is the triangle acute, right, or obtuse?

Question 4.
16, 30, and 34

Answer:
Right angle triangle.

Explanation:
Given,
the line segments of a triangle are 16, 30 and 34.
We know that if the sum of the squares of longer hand is equal to the sum of the shorter hand, then the triangle is said to be right-angled triangle.
c² = a² + b²
34² = 16² + 30²
1156 = 256 + 900
1156 = 1156
So, the triangle is a right-angled triangle.

Question 5.
4, √67, and 9

Answer:
Acute angle.

Explanation:
Given,
the line segments of a triangle are 4, √67, and 9
We know that if the sum of the squares of longer hand is less than the sum of the shorter hand, then the triangle is said to be acute-angled triangle.
c² = a² + b²
9² = 4² + (√67)²
99 = 16 + 67
99 = 83
So, the triangle is acute.

Question 6.
√5., 5. and 5.5

Answer:
Obtuse angle.

Explanation:
Given,
the line segments of a triangle are √5,  5. and 5.5
We know that if the sum of the squares of longer hand is less than the sum of the shorter hand, then the triangle is said to be acute-angled triangle.
c² = a² + b²
5.5² = √5² + 5²
30.25 = 30
So, the triangle is obtuse.

Solve ∆ABC. Round decimal answers to the nearest tenth.

Question 7.

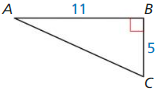
Answer:
c = 12.08, ∠A = 24.22, ∠C = 65.78
when rounded to nearest tenth,
c = 12.1, ∠A = 24.3, ∠C = 65.8

Explanation:
Given ,
the side lengths of a triangle are 5 and 11.
tan A = \(\frac {5}{11} \)
∠A = 24.22
According to Pythagoras theorem , we know that
c² = a² + b²
c² = 11²+ 5²
c² = 121 + 25
c²  = 146
c = 12.08
The sum of the three angles is 180.
substitute the values,
24.22 + 90 + ∠C = 180
114.22 + ∠C = 180∠C = 65.78

Question 8.

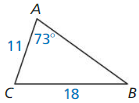
Answer:
∠B = 35.4, ∠C = 71.6, c = 17.9
Estimate: ∠B = 35, ∠C = 72, c = 18

Explanation:
Given,
the side lengths as 11 and 18.
\(\frac { sin 73 }{ 18 } \) = \(\frac { sin B }{ 11 } \)
cross multiply by placing the values of sin
sin B = 0.58
∠B = 35.4
Sum of the angle is 180
73 + 35.4 + ∠C = 180
108.4 + ∠C = 180∠C = 71.6
\(\frac { sin 73 }{ 18 } \) = \(\frac { sin 71.6 }{ c } \)
cross multiply by placing the values of sin
c = 17.9

Question 9.

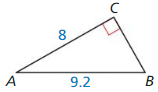
Answer:
BC = 4.54, ∠B = 59.3, ∠A = 30.7
Estimate: BC = 4.6, ∠B = 60, ∠A = 31

Explanation:
Given,
BC = 4.54, ∠B = 59.3, ∠A = 30.7
According to Pythagoras theorem , we know that
c² = a² + b²
9.2² = 8² + x²
84.64 = 64 + x²
x² = 84.64 – 64
x² = 20.611
x = 4.54
\(\frac { sin 90 }{ 9.2 } \) = \(\frac { sin B }{ 8 } \)
sin B = 0.86
∠B = 59.3
Sum of the angles is 180
∠A + 59.3 + 90 = 180
∠A + 149.3 = 180
∠A = 30.7

Question 10.
m ∠ A = 103°, b = 12, c = 24

Answer:
a = 29, ∠B = 53.5

Explanation:
Given,
m ∠ A = 103°, b = 12, c = 24
we know that,
a² = b² + c²- 2bc cos A
a² = 12² + 24²- 2(12 x 24) cos A
a² = 144 + 576 – 2(288) cos 103
a² = (720 – 576) cos 103
a² = 144 cos 103
a = 29
\(\frac { sin B }{ 12 } \) = \(\frac { sin 103 }{ 29 } \)
By cross multiplying, we get
∠B = 23.5
∠C = 180 – (103 + 23.5) = 53.5
∠C = 180 – 126.5
∠C = 53.5

Question 11.
m ∠ A = 26°, m ∠ C = 35°, b = 13

Answer:
∠B = 119, a = 6.42, c = 8.5

Explanation:
Given,
m ∠ A = 26°, m ∠ C = 35°, b = 13
sum of the angles is 180
∠B + 26 + 35 = 180
∠B = 119
\(\frac { sin 119 }{ 13 } \) = \(\frac { sin 26 }{ a } \)
By cross multiplying and subsituting the values, we get
a = 6.42
\(\frac { sin 119 }{ 13 } \) = \(\frac { sin 35 }{ c } \)
c = 8.5

Question 12.
a = 38, b = 31, c = 35

Answer:
∠B=50.2, ∠C = 59.8, ∠A = 70

Explanation:
Given,
a = 38, b = 31, c = 35
We know that,
b² = a² + c²- 2ac cos B
31² = 38²+ 35²- 2(35 x 38) cos B
961 = 1444 + 1225 – 2(1330) cos B
961 = (2699 – 2660) cos B
961 = 39 cos B
cos B = 0.64
∠B=50.2
a² = b² + c²- 2bc cos A
38² = 31²+ 35²- 2(31 x 35) cos A
1330 = 961 + 1225 – 2(1085) cos A
1330 = (2186 – 2170) cos A
1330 = 16 cos A
cos A = 0.341
∠A = 70
∠C = 59.8

Question 13.
Write cos 53° in terms of sine.

Answer:
cos 53° = sin 37°

Explanation:
Given,
cos 53°
cos 53° = sin (90 – 53)
So, cos 53° = sin 37

Find the value of each variable. Write your answers in simplest form.

Question 14.

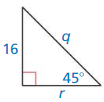
Answer:
r = 16; q = 22.6

Explanation:
Given the side length as 16 and angle is 45 degrees.
we know that, sin and cos are the inverse operations.
sin 45 = \(\frac { 16 }{ q } \)
By cross multiplying, we get
q = 22.6
cos 45 = \(\frac { r }{ q } \)
By cross multiplying, we get
r = 16

Question 15.

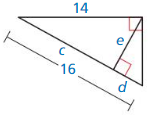
Answer:

Question 16.

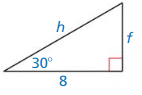
Answer:
h = 9.2; f = 4.6

Explanation:
Given, the side length 8 and angle 30 degrees.
we know that, sin and cos are the inverse operations.
sin 30 = \(\frac { f }{ 9.2 } \)
cross multiply
f = 4.6
cos 30 = \(\frac { 8 }{ h } \)
cross multiply
h = 9.2

Question 17.
In ∆QRS, m ∠ R = 57°, q = 9, and s = 5. Find the area of ∆QRS.

Answer:
A = 18.675

Explanation:
Given,
m ∠ R = 57°, q = 9, and s = 5.
Area = \(\frac { 1 }{ 2 } \) qs sin R
By substitute the values, we get
= \(\frac { 1 }{ 2 } \) (9 x 5) sin 57
= \(\frac { 1 }{ 2 } \) (45) sin 57
= 18.675

Question 18.
You are given the measures of both acute angles of a right triangle. Can you determine the side lengths? Explain.

Answer:
No.

Explanation:
We know that a right triangle has 90 °.
Given the measures of the two acute angles.
It means knowing the measures of all three angles.
If the measurements of all three angles of a triangle doesn’t uniquely determine a triangle. Then we can’t determine the lengths of sides of the triangle.

Question 19.
You are at a parade looking up at a large balloon floating directly above the street. You are 60 feet from a point on the street directly beneath the balloon. To see the top of the balloon, you look up at an angle of 53°. To see the bottom of the balloon, you look up at an angle of 29°. Estimate the height h of the balloon.

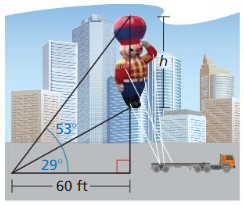
Answer:

Question 20.
You warn to take a picture of a statue on Easter Island, called a moai. The moai is about 13 feet tall. Your camera is on a tripod that is 5 feet tall. The vertical viewing angle of your camera is set at 90°. How far from the moai should you stand so that the entire height of the moai is perfectly framed in the photo?

Answer:

Right Triangles and Trigonometry Cummulative Assessment

Question 1.
The size of a laptop screen is measured by the length of its diagonal. you Want to purchase a laptop with the largest screen possible. Which laptop should you buy?
(A)

(B)

(C)

(D)

Answer:
(B)

Explanation:
From the above given information,
Pythagorean Theorem states that,
c² = a² + b²

(a) d² = √9² + 12²
d² = 81 + 144
d² = = 225
d = 15

(b) d² = √11.25² + 20²
d² = 126.24+ 400
d² = 526.24
d = 22.94
(c) d² = √12² + 6.75²
d² = 144 + 45.56
d² = 189.56
d = 13.76

(d) d² = √8² + 6²
d² = 64 + 36
d² = 100
d = 10

Question 2.
In ∆PQR and ∆SQT, S is between P and Q, T is between R and Q, and \(\) What must be true about \(\overline{S T}\) and \(\overline{P R}\)? Select all that apply.
\(\overline{S T}\) ⊥ \(\overline{P R}\)      \(\overline{S T}\) || \(\overline{P R}\)    ST = PR        ST = \(\frac{1}{2}\)PR
Answer:

Question 3.
In the diagram, ∆JKL ~ ∆QRS. Choose the symbol that makes each statement true.

<      =       >
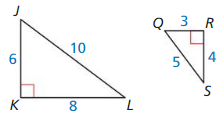
sin J ___________ sin Q                 sin L ___________ cos J                   cos L ___________ tan Q
cos S ___________ cos J                cos J ___________ sin S                 tan J ___________ tan Q
tan L ___________ tan Q               tan S ___________ cos Q                sin Q ___________ cos L
Answer:
sin J = sin Q                 sin L = cos J                   cos L < tan Q
cos S > cos J                  cos J = sin S                 tan J = tan Q
tan L < tan Q               tan S > cos Q                sin Q = cos L

Explanation:
sin J = \(\frac {Opposite}{Hypotenuse} \)
sin J = \(\frac {KL}{JL} \)
sin J = \(\frac {8}{10} \)
sin J = \(\frac {4}{5} \)

sin Q = \(\frac {Opposite}{Hypotenuse} \)
sin Q = \(\frac {RS}{QS} \)
sin Q = \(\frac {4}{5} \)

sin L = \(\frac {Opposite}{Hypotenuse} \)
sin L = \(\frac {KL}{JL} \)
sin L = \(\frac {6}{10} \)
sin L = \(\frac {3}{5} \)

cos J = \(\frac {adjacent}{Hypotenuse} \)
cos J = \(\frac {JK}{JL} \)
cos J = \(\frac {6}{10} \)
cos J = \(\frac {3}{5} \)

cos S = \(\frac {adjacent}{Hypotenuse} \)
cos S = \(\frac {RS}{QS} \)
cos S = \(\frac {4}{5} \)

cos L = \(\frac {adjacent}{Hypotenuse} \)
cos L = \(\frac {KL}{JL} \)
cos L = \(\frac {6}{10} \)
cos L = \(\frac {3}{5} \)

sin J = sin Q
\(\frac {4}{5} \) = \(\frac {4}{5} \)

sin L = cos J
\(\frac {6}{10} \) = \(\frac {6}{10} \)
\(\frac {3}{5} \) = \(\frac {3}{5} \)

cos L < tan Q
\(\frac {8}{10} \) < \(\frac {4}{3} \)
\(\frac {4}{5} \) < \(\frac {4}{3} \)

cos S > cos J
\(\frac {4}{5} \) > \(\frac {6}{10} \)
\(\frac {4}{5} \) > \(\frac {3}{5} \)

cos J = sin S
\(\frac {6}{10} \) = \(\frac {3}{5} \)
\(\frac {3}{5} \) = \(\frac {3}{5} \)

tan J = tan Q
\(\frac {8}{6} \) = \(\frac {4}{3} \)
\(\frac {4}{3} \) = \(\frac {4}{3} \)

tan L < tan Q
\(\frac {6}{8} \) < \(\frac {4}{3} \)
\(\frac {3}{4} \) < \(\frac {4}{3} \)

tan S > cos Q
\(\frac {3}{4} \) = \(\frac {3}{4} \)

sin Q = cos L
\(\frac {4}{5} \) > \(\frac {6}{10} \)
\(\frac {4}{5} \) > \(\frac {3}{5} \)

Question 4.
A surveyor makes the measurements shown. What is the width of the river.

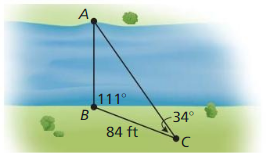
Answer:
tan 34 = \(\frac {AB}{84} \)
AB = 56.28
Explanation:
tan 34 = \(\frac { Opposite }{ Adjacent } \)
tan 34 = \(\frac { AB }{ 84 } \)
AB = tan 34 x 84
AB = 56.28 ft

Question 5.
Create as many true equations as possible.

____________ = ______________

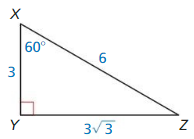
sin X            cos X           tan x           \(\frac{X Y}{X Z}\)           \(\frac{Y Z}{X Z}\)

Sin Z            cos Z           tan Z           \(\frac{X Y}{Y Z}\)           \(\frac{Y Z}{X Y}\)

Answer:
sin X = \(\frac{Y Z}{X Z}\) = cos Z
cos X = \(\frac{X Y}{X Z}\) = sin Z
tan x = \(\frac{Y Z}{X Y}\)
tan Z = \(\frac{X Y}{Y Z}\)

Explanation:
sin X
sin X = \(\frac {Opposite}{Hypotenuse} \)
sin X = \(\frac {YZ}{XZ} \)
sin X = \(\frac {3√3}{6} \)
sin X = \(\frac {√3}{2} \)

cos X
cos X = \(\frac {adjacent}{Hypotenuse} \)
cos X = \(\frac {XY}{XZ} \)
cos X = \(\frac {3}{6} \)
cos X = \(\frac {1}{2} \)

tan X
tan X = \(\frac {Opposite}{adjacent} \)
tan X = \(\frac {YZ}{XY} \)
tan X = \(\frac {3√3}{3} \)
tan X = √3

\(\frac {XY}{XZ}\)
=\(\frac {3}{6}\)
=\(\frac {1}{2}\)

\(\frac {YZ}{XZ}\)
=\(\frac {3√3}{6}\)
=\(\frac {√3}{2}\)

Sin Z
sin Z = \(\frac {Opposite}{Hypotenuse} \)
sin Z = \(\frac {XY}{XZ} \)
sin Z = \(\frac {3}{6} \)
sin Z = \(\frac {1}{2} \)

cos Z
cos Z = \(\frac {adjacent}{Hypotenuse} \)
cos Z = \(\frac {YZ}{XZ} \)
cos Z = \(\frac {3√3}{6} \)
cos Z = \(\frac {√3}{2} \)

tan Z
tan Z = \(\frac {Opposite}{adjacent} \)
tan Z = \(\frac {XY}{YZ} \)
tan Z = \(\frac {3}{3√3} \)

\(\frac{XY}{YZ}\)
= \(\frac{3}{3√3}\)
= \(\frac{1}{√3}\)

\(\frac{YZ}{XY}\)
= \(\frac{3√3}{6}\)
= \(\frac{√3}{2}\)

sin X = \(\frac{Y Z}{X Z}\) = cos Z
cos X = \(\frac{X Y}{X Z}\) = sin Z
tan x = \(\frac{Y Z}{X Y}\)
tan Z = \(\frac{X Y}{Y Z}\)

Question 6.
Prove that quadrilateral DEFG is a kite.
Given \(\overline{H E} \cong \overline{H G}\), \(\overline{E G}\) ⊥ \(\overline{D F}\)
Prove \(\overline{F E} \cong \overline{F G}\), \(\overline{D E} \cong \overline{D G}\)

Answer:

Question 7.
What are the coordinates of the vertices of the image of ∆QRS after the composition of transformations show?

(A) Q’ (1, 2), R'(5, 4), S'(4, -1)
(B) Q'(- 1, – 2), R’ (- 5, – 4), S’ (- 4, 1)
(C) Q'(3, – 2), R’ (- 1, – 4), S’ (0, 1)
(D) Q’ (-2, 1), R'(- 4, 5), S'(1, 4)
Answer:

Question 8.
The Red Pyramid in Egypt has a square base. Each side of the base measures 722 feet. The height of the pyramid is 343 feet.

a. Use the side length of the base, the height of the pyramid, and the Pythagorean Theorem to find the slant height, AB, of the pyramid.

Answer:
h = 635.3

Explanation:
Given that,
The Red Pyramid in Egypt has a square base.
Each side of the base measures 722 feet.
The height of the pyramid is 343 fee.
According to the Pythagorean Theorem,
c² = a² + b²
343² = h² + 722²
117649 = h² + 521284
h² = 403635
h = 635.3

b. Find AC.
Answer:
From the above given information,
AC = 343

c. Name three possible ways of finding m ∠ 1. Then, find m ∠ 1.
Answer:
The three possible ways are:
sin 1, cos 1 and tan 1
tan 1 = \(\frac { 722 }{ 635.3 } \)
∠1 = 48