The centroid is the center point of any object. Today in this article we are going to discuss the centroid of a triangle from Distance and Section Formulae. It is most important to learn centroid, medians from the concept of triangles. It is an important property of a triangle. Let us know what is the definition of a centroid, properties, formula, and examples on the centroid of a triangle.
We know that we can find the centroid of the triangle by dividing the x-coordinates and y-coordinates of the vertices of the given triangle. Check the below sections to know in detail the centroid of a triangle and improve yourself by solving the problems on it.
Also Check:
Centroid of a Triangle – Definition
The centroid of a triangle is a point where three meridians meet. The center point of the triangle is known as the centroid of a triangle. Centroid of a triangle cuts the median into a 2:1 ratio. We can find the centroid of a triangle by taking the average of x-coordinate and y-coordinates of the triangle vertices.
Centroid of a Triangle Properties
The properties of a centroid of a triangle are as follows,
- The centroid is also called the geometric center of the object.
- The centroid of a triangle is within a triangle.
- Centroid is the point of intersection of all the three medians of a triangle.
- The medians of a triangle are divided into a 2:1 ratio by the centroid.
Centroid of a Triangle Formula
- coordinates of the point dividing (x1, y1) and (x2,y2) in the ratio m:n is given by
(m1x1 + m2xx1/m1 + m2 , m1y2 + m2y1/m1 + m2) - Centroid formula =( x1 + x2 + x3/3, y1 + y2 + y3/3)
Centroid of a Triangle Examples
Example 1.
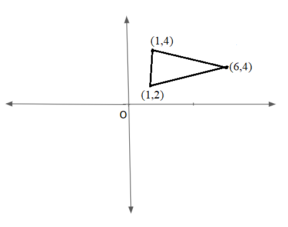
Calculate the coordinates of the centroid of the triangle ABC is A(6,4) B(1,2) C(1,4)
Solution:
Given, the coordinates of the centroid of the triangle ABC is A(6,4) B(1,2) C(1,4)
We know that
Centroid formula =( x1 + x2 + x3/3, y1 + y2 + y3/3)
(6 + 1 + 1 /3 , 4 + 2 + 4 /3)
(8/3, 10/3)
Example 2.
A(3,x), B(4,6) and C( y,2) are the vertices of the triangle ABC whose centroid is the origin and calculate the values of x and y.
Solution:
Given centroid of the triangle ABC is the origin
We know that the coordinates of the point dividing (x1, y1) and (x2,y2) in the ratio m:n is given by
(m1x1 + m2xx1/m1 + m2 , m1y2 + m2y1/m1 + m2)
(m1, m2) = (0,0)
(0,0) = (3 + 6 + y/3, x + 3 + 2 /3)
(0,0) = (9 + y/3, x + 5/3)
0 = 9 + y/3 and 0 = x + 5/3
y = -9 and x = -5
Example 3.
If the centroid of the triangle is at (4,3) and two of its vertices are (3,3) and (5,3) then find the third vertex of the triangle.
Solution:
Let the vertices of a triangle be A(3,2) B(5,2) and c(x3,y3)
The centroid of the triangle is (4,2)
Centroid formula = (x1 + x2 + x3/3 , y1 + y2 + y3/3)
(4,3) = (3 + 5 + x3/3 , 3 + 3 + y3/3)
(4,3) = (8 + x3/3, 6 + y3/3)
8 + x3/3 = 4
8 + x3 = 12
x3 = 12 – 8
x3 = 4.
6 + y3/3 = 3
6 + y3 = 3
y3 = 3-6
y3 = -3
The third vertex is (4,-3)
Example 4.
Find the centroid of the triangle whose vertices are A(1, 3), B(2, 6), and C(4, 10)
Solution:
Given, A(1, 3), B(1, 6), and C(4, 10) are the vertices of a triangle ABC.
By the formula of the centroid we know;
Centroid = ((x1+x2+x3)/3, (y1+y2+y3)/3)
Putting the values, we get;
Centroid = (1+1+4)/3, (3+6+10)/3
=( 6/3, 19/3)
=( 6/3,19/3
= (2,19/3)
Hence, the centroid of the triangle having vertices A(1, 5), B(2, 6), and C(4, 10) is (2,19/3).
Example 5.
Find the centroid of the triangle whose vertices are A(3, 6), B(4, 6), and C(6,15).
Solution:
A(x1, y1) = A(3, 6)
B(x2, y2) = B(4,9)
C(x3, y3) = C(6,15)
We know that the formula to find the centroid of a triangle is = ((x1+x2+x3)/3, (y1+y2+y3)/3)
Now, substitute the given values in the formula
Centroid of a triangle = ((3+4+6)/3, (6+6+15)/3)
= (13/3, 27/3)
= (13/3, 9)
Therefore, the centroid of the triangle for the given vertices A(2, 6), B(4,9), and C(6,15) is (13/3, 9).
FAQs on Centroid of a Triangle
1. What is the centroid of the square?
In the square where the diagonals of the square intersect each other is the centroid of the square. As we know, the square has four sides and all sides are equal. Hence it is easy to locate the centroid in it.
2. What is the Centroid of Triangle and its Properties?
The centroid of a triangle is formed when three medians of a triangle intersect.
The properties of a centroid are
1. The centroid is also called the geometric center of the object.
2. Centroid is the point of intersection of all the three medians of a triangle.
3. The medians are divided into a 2:1 ratio by the centroid.
4. The centroid of a triangle is within a triangle.
3. How many altitudes Can a triangle have?
The triangle has three altitudes.
The three altitudes of a triangle intersect at the orthocenter, which is in the form of an acute triangle inside the triangle.