In trigonometry, the circular system is one of the systems of measuring angles. In this system, the angle is measured in radians. Here radian is a unit for the measurement of angles. Get the statements and proofs of two important theorems on the circular system in the below sections. Check out the solved questions on radian angle measurement.
What is Circular System?
A circular system is a kind of system of measuring trigonometric angles. In higher mathematics angles are measured in a circular system. In this system, a radian is considered as the unit for the measurement of angles. The unit of the circular system depends on the constant relation that exists between the circumference and radius of the circle
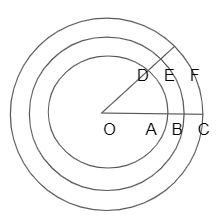
Let us take three concentric circles. Cut an arc AD whose length is equal to the radius of the circle. Join points O, A and O, D. Now, ∠AOD is the angle at the centre subtended by the arc equal in length to the radius of the circle. Extend OA, OD to meet the other two circles at points B, C and E, F. So that BE = CF = radius of the corresponding circles. Here ∠BOE and ∠COF are angles at the centre subtended by arcs equal in length to the respective radii. Hence we say that an arc of any circle equal in length to the radius of the circle subtends at its centre an angle of constant magnitude.
Radian Definition
A radian is defined as an angle subtended at the centre of a circle by an arc whose length is equal to the radius of that circle.
Let OX = r and r be the radius of a circle having a centre at O.
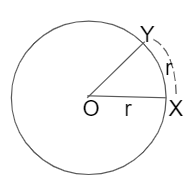
Take an arc XY of the circle so that XY = r and join OY. By definition ∠XOY = one radian = 1c
The circular measure of an angle is the number of radians it contains.
Thus the circular (radian) measure of a right angle is π/2.
Degrees to radians conversion table is given here.
| Degree | Radians |
|---|---|
| 0° | 0 |
| 30° | \(\frac { π }{ 6 } \) |
| 45° | \(\frac { π }{ 4 } \) |
| 60° | \(\frac { π }{ 3 } \) |
| 90° | \(\frac { π }{ 2 } \) |
| 120° | \(\frac { 2π }{ 3 } \) |
| 135° | \(\frac { 3π }{ 4 } \) |
| 150° | \(\frac { 5π }{ 6 } \) |
| 180° | π |
| 270° | \(\frac { 3π }{ 2 } \) |
| 360° | 2π |
More Related Articles:
Theorems of Circular System
In the circular system, the unit of measurement of an angle is the radian.
Theorem 1: Radian is a constant angle.
Proof:
Take a circle with O as centre and r as radius, Take any two points on the circle to mark an arc AP. As per the definition of a radian, the angle formed at the centre is ∠AOP = 1c. Extend AO to meet at B so that ∠AOB = 180 degrees.

Since the angles at the center of a circle is proportional to the arc subtended in it.
\(\frac { ∠AOP }{ ∠AOB } \) = \(\frac { arcAP }{ arcAPB } \)
= \(\frac { r }{ πr } \)
= \(\frac { 1 }{ π } \)
∠AOP = \(\frac { 1 }{ π } \)∠AOB = \(\frac { Straightangle }{ π } \)
1c = \(\frac { Straightangle }{ π } \)
1c = constant
Hence proved.
Theorem 2: The number of radians in an angle subtended by an arc of a circle at the centre is equal to \(\frac { arc }{ radius } \)
Proof:
Let us take a circle with radius r and center O. Draw a diameter having ending A, B. Take any two points P, Q on the circle make an arc AP. Angle formed at the center ∠AOQ = θc. Let us take AP = r, s be the length of AQ.
Thus, ∠AOP = 1c
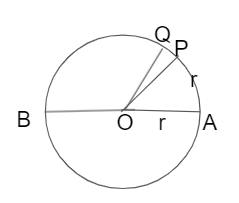
Since the angles at the center of a circle is proportional to the arc subtended in it.
\(\frac { ∠AOQ }{ ∠AOP } \) = \(\frac { arcAQ }{ arcAP } \)
∠AOQ = (\(\frac { AQ }{ AP } \) x 1)c
θ = \(\frac { s }{ r } \) radians.
Hence proved.
Solved Example Questions
Question 1:
In a triangle, the angles are in the ratio 4 : 6 : 5, what is the value of the least angle in radian?
Solution:
Let the angles be 4x, 6x and 5x radians.
So, 4x + 6x + 5x = π
15x = π
x = π/15
The least angle in radian is 4x = 4π/15.
Question 2:
In a triangle, the angles are in the ratio 2 : 3 : 5, what is the value of the greatest angle in radians?
Solution: :
Let the angles be 2x, 3x and 5x radians.
So, 2x + 3x + 5x = π
10x = π
x = π/10
The greatest angle in radian is 5x = 5(π/10) = \(\frac { π }{ 2 } \).
FAQ’s on Circular System
1. What is a circular measure of an angle?
The circular measure of an angle is in radians.
2. What is the circular system?
The unit of the circular system is the radian. It depends on the relationship between the radius and circumference of the circle.
3. What is a radian system?
One radian is the measure of a central angle subtended by an arc that is equal in length to the radius of the circle.