In this article, students can acquire more about the collinear points and the proof of the Collinear Points by Midpoint Theorem. Collinear points are the group of three or more points that lie on the same straight line. These points may exist on different planes but not on different lines. The property of the points being collinear is known as collinearity.
Let us learn the concept of collinear points and see how we construct the theorem to prove the given statement. We hope the information provided on this page will help you all to understand how the points are collinear and proved by the mid-point theorem.
Collinear Points – Definition
The word collinear is a mix of two Latin words ‘col’ and ‘linear’. The word ‘col’ means together and the word ‘linear’ means line. Thus, collinear points mean points together in the same or a single line. In geometry, the set of three or more points that lies on the same straight line is said to be collinear.
You can see many real-world examples of the collinearity name as a group of people or students standing in a straight line, a bunch of oranges kept in a single row, etc. Observe the following figure to get clear knowledge of the collinear points and identify the collinear points and non-collinear points.
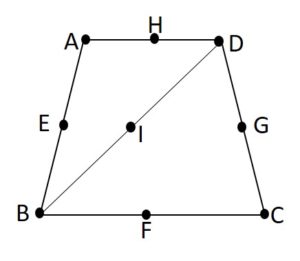
In the above figure, the set of collinear points are {A, E, B}, {B, F, C}, {C, G, D}, {A, H, D}, and {B, I, D}. The set of non-collinear points are {E, G}, {H, F}, and {G, F}, etc.
Collinear Points Proved by Midpoint Theorem Statement and Proof
In ∆ABC, the medians CM and BN are produced to the points P and Q respectively such that CM=MP and BN=NQ. Prove that the points P, A, and Q are collinear and A is the midpoint of PQ.
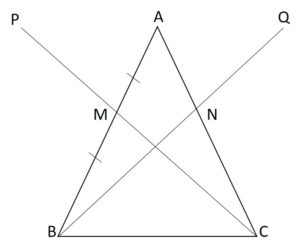
To Prove:
Consider an ∆ABC,
Given, the points M and N are the midpoints of AB and AC respectively. CM and BN are produced to P and Q respectively such that CM=MP and BN=NQ.
Now, we prove that
(i) P, A, and Q are collinear.
(ii) A is the midpoint of PQ.
Construction:
From the above triangle ABC, draw a dotted line to join the points PA, AQ, and MN.
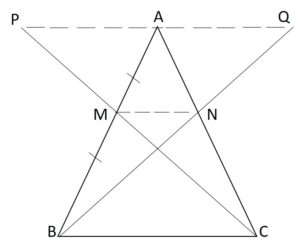
Proof:
In ∆APC, M and N are the midpoints of PC and AC respectively (from given)
Therefore, MN ∥ AP and MN = ½AP (by the midpoint theorem) —-(1)
In ∆ABQ, M and N are the midpoints of AB and BQ respectively (from given)
Therefore, MN ∥ AQ and MN = ½AQ (by the midpoint theorem) —-(2)
Thus, AP ∥ MN and AQ ∥ MN. ( from (1) and (2))
Now, AP and AQ lie in the same straight line because both passes through the same point A and are parallel to the same straight line MN.
∴ The points P, A, and Q are collinear. [(i) proved]
Also, ½AP = ½AQ (from statements (1) and (2)) —-(3)
⇒ AP = AQ (from statement (3))
Therefore, A is the midpoint of PQ. [(ii) proved]
Hence, the given statement is proved and the points are collinear by a midpoint theorem.
Also, refer:
FAQs on How to Prove Points are Collinear using MidPoint Theorem
1. How do you prove the given points are collinear?
Three or more points are on the same straight line are collinear, if the slope of any two pairs of points is the same. For example, we have three points A, B, and C, the pairs formed are AB, BC, and CA respectively. If the slope of AB = Slope of BC = Slope of AC, then the points A, B, and C are collinear points.
2. How do you prove three points are collinear vectors?
Take the three points with position vectors a, b, and c. To prove the vectors are collinear, if and only if the vectors (a-b) and (a-c) are parallel. In other words, to prove the collinearity of the vectors, we need to show (a-b) = k(a-c), where k is a constant.
3. What is the theorem of the midpoint?
The midpoint theorem states that ” The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”