Complementary Angles are the angles with 90°. When we add two angles then the resultant angle should be 90° to call those angles complementary angles. In complementary angles, each angle complements another angle. If an angle is 90 degrees, then it can’t be called a complementary because it doesn’t have any pairs. It consists of only one angle with 90 degrees.
The angles become complementary when the sum of the two angles becomes 90 degrees. Therefore, an angle with 90 degrees cannot be called complementary angles. Find all the Lines and Angles concepts on our website with solved examples.
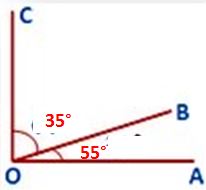
From the above figure, the ∠AOB and ∠BOC are complementary as ∠AOB + ∠BOC = 35° + 55° = 90°. Therefore, they both are Complementary Angles. Also, angles 35 and angle 55 complements each other.
Example 1: If you take a triangle with one angle of 50 degrees and another angle of 40 degrees, the combined angle will become 90 degrees. The two 40 and 50 angles are called complementary angles.
Example 2: If you take a triangle with one angle of 15 degrees and another angle of 75 degrees, the combined angle will become 90 degrees. The two 15 and 75 angles are called complementary angles.
Example 3: If you take a triangle with one angle of 10 degrees and another angle of 80 degrees, the combined angle will become 90 degrees. The two 10 and 80 angles are called complementary angles.
Observations of Complementary Angles
- If two angles complement each other, then each angle must be an acute angle. But any two acute angles need not be complementary.
For example, angles of measures 30° and 40° are not a complement to each other. - Two right angles cannot complement each other.
- Also, two obtuse angles cannot complement each other.
Complementary Angles Examples
1. Find the complement of below angles
(a) 58°
Solution:
To find the complement of 58°, subtract it from 90°
90° – 58° = 32°
Therefore, the complement of 58° is 32°
(b) 37°40′
Solution:
To find the complement of 37°40′, subtract it from 90°
90° – 37°40′
90° = 89°60′
= 89°60′ – 37°40′
= 52°20′
Therefore, the complement of 37°40′ is 52°20′
(c) y + 42°
Solution:
To find the complement of y + 42°, subtract it from 90°
90° – (y + 42°)
= 90° – y – 42°
= 56° – y
Therefore, the complement of y + 42° is 56° – y
2. Find the complement of the angle (20 + x)°
Solution:
To find the complement of (20 + x)°, subtract it from 90°
90° – (20 + x)
= 90° – 20 – x°
= 70° – x° = (70 – x)°
Therefore, the complement of (20 + x)° is (70 – x)°
3. Find the measure of an angle that is 36° less than its complement.
Solution:
Let the unknown angle be y, then measure of its complement = (90° – y)
According to the given question,
(90° – y) – y = 36°
90° – y – y = 36°
90° – 2y = 36°
Subtract 90° from both sides
90° – 90° – 2y = 36° – 90°
-2y = -54°
y = 54/2 = 27°
y = 27°
Therefore, 90 – y (Put the value of y = 27°)
= 90 – 27°
= 63°
Therefore, the pair of complementary angles are 63° and 27°