The basic proportionality theorem or Thales theorem was introduced by a mathematician named Thales. The converse of Thales theorem is also true. Students who have already learnt about the Basic Proportionality Theorem related to similarity can check the statement and proof of the converse of BPT. Get the complete details about the converse of basic proportionality theorem in the following sections.
Statement of Converse of Basic Proportionality Theorem
According to the converse of basic proportionality theorem, if a line segment is drawn to cut two sides of the triangle in equal ratio, then it is parallel to the third side.
For example, in △ABC the line DE cuts the sides AB, AC in equal proportion. Such that DE is parallel to BC.
Also, Check
Converse of Basic Proportionality Theorem Proof
The following is the proof for the statement of the converse of basic proportionality theorem.

Given: In △ABC, the line DE cuts the sides AB, AC in equal proportion. \(\frac { AD }{ BD } \) = \(\frac { AE }{ CE } \)
Construction: In triangle ABC, draw a line that meets AB at point D, AC at point E. Also, draw a line DF.
Proof:
Consider DE is not parallel to the side BC. Hence let us draw another line DF which is parallel to BC.
By applying the basic proportionality theorem, \(\frac { AE }{ CE } \) = \(\frac { AF }{ CF } \)
Add 1 to both sides of the equation.
\(\frac { AE }{ CE } \) + 1 = \(\frac { AF }{ CF } \) + 1
\(\frac { AE + CE }{ CE } \) = \(\frac { AF + CF }{ CF } \)
\(\frac { AC }{ CE } \) = \(\frac { AC }{ CF } \)
Therefore, CE = CF
From the above statement, the points E and F are the same points and they coincide.
Hence the line DE is parallel to BC and it proves the converse of the basic proportionality theorem.
Problems Using Converse of BPT
Problem 1:
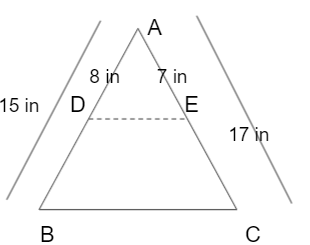
In a triangle ABC, D is a point on the side AB and E is a point on the side AC. And the lengths AB = 15 inches, AC = 17 inches, AD = 8 inches, AE = 7 inches. Is the line DE parallel to BC?
Solution:
For the traingle ABC we have AB = 15 inches, AC = 17 inches, AD = 8 inches, AE = 7 inches
BD = AB – AD = 15 – 8 = 7 inches
CE = AC – AE = 17 – 7 = 10 inches
So, \(\frac { AD }{ BD } \) = \(\frac { 7 }{ 7 } \) = 1 and \(\frac { AE }{ CE } \) = 10/10 = 1. That means \(\frac { AD }{ BD } \) = \(\frac { AE }{ CE } \). Applying the converse of basic proportionality theorem, the line segment DE is parallel to the side BC of the triangle ABC.
∴ DE is parallel to BC
Problem 2:
P and Q are points on sides AB and AC respectively of △ ABC. For each of the following cases, state whether PQ ∥ BC. AP = 4cm, PB = 4.5 cm, AQ = 4 cm, QC = 5 cm.
Solution:
Given that,
AP = 4cm, PB = 4.5 cm, AQ = 4 cm, QC = 5 cm
To find PQ ∥ BC
\(\frac { AP }{ PB } \) = \(\frac { 4 }{ 4.5 } \) = \(\frac { 8 }{ 9 } \)
\(\frac { AQ }{ QC } \) = \(\frac { 4 }{ 5 } \)
\(\frac { AP }{ PB } \) ≠ \(\frac { AQ }{ QC } \)
Basic proportionality theorem states that if a line is drawn parallel to the one side of the triangle the other sides in various points, then the other two sides are divided in the same ratio.
PQ is not parallel to BC.
Problem 3:
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac { AO }{ BO } \) = \(\frac { OC }{ OD } \).
Solution:
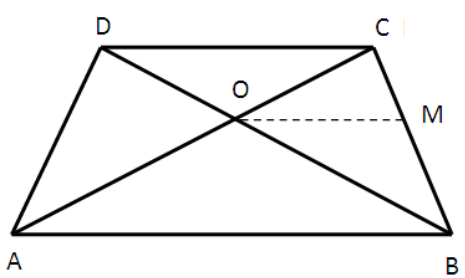
Draw OM parallel to AB meeting BC at point M
In △ACB,
It is given that, OM is parallel to AB
\(\frac { OC }{ OA } \) = \(\frac { CM }{ MB } \) — (i)
In △BDC
OM is parallel to CD
\(\frac { BM }{ MC } \) = \(\frac { OB }{ OD } \)
By taking the reciprocals on both sides
\(\frac { CM }{ MB } \) = \(\frac { OD }{ OB } \) — (ii)
\(\frac { OC }{ OA } \) = \(\frac { OD }{ OB } \)
\(\frac { OC }{ OD } \) = \(\frac { OA }{ OB } \)
Hence proved.
Frequently Asked Question’s
1. What is the meaning of converse of BPT?
The converse of Thales theorem is if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
2. What is the difference between the basic proportion theorem and its converse?
Basic proportionality theorem is a line drawn parallel to one side of a triangle and cuts the other two sides in the same proportion. The converse of BPT is a line drawn to cut two sides of a triangle in the same ratio is parallel to the third side.
3. What is the BPT theorem?
Thales theorem states that a line drawn parallel to one side of a triangle and cutting the other two sides, divides the other two sides in equal proportion.