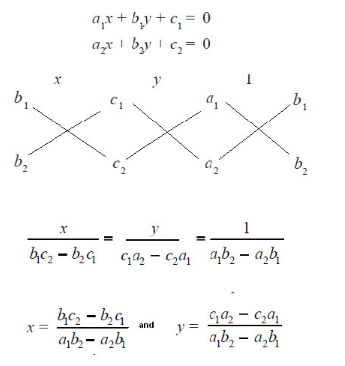
Cross multiplication method is used to solve a pair of simultaneous linear equations in two variables. This method helps you to find the accurate values of variables easily. It is applicable only when we have two linear equations in two variables. Get the steps to solve the system of linear equations with the cross multiplication method in the following sections. Also, check out the solved examples for a better understanding of the concept.
Cross Multiplication Method for Solving Pair of Linear Equations
Follow the easy and simple guidelines listed below while solving Pair of Linear Equations. They are in the following fashion
- Observe the given pair of linear equations and transpose them in the form of ax + by + c = 0
- And represent them as the coefficient constant of term x, the coefficient constant of term y, coefficient of x, and coefficient of y.
- Cross multiply those constants.
- Express the cross multiplicands of x, y, and constants under x, y, and 1.
- Equate them to find the values of x, y.
Check out the derivation to get more details about the Cross-Multiplication Method.
General Solution Using the Method of Cross-Multiplication
Let the pair of linear equations in two variables are
a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0
For solving these linear equations follow the below included steps
Given simultaneous linear equations in two variables are
a₁x + b₁y + c₁ = 0 ——- (i)
a₂x + b₂y + c₂ = 0 ——– (ii)
Multiply equation (i) by b₂ and equation (ii) by b₁.
b₂ (a₁x + b₁y + c₁ = 0)
b₂ (a₁x + b₁y + c₁) = b₂ x 0
a₁b₂x + b₁b₂y + b₂c₁ = 0 ——- (iii)
b₁ (a₂x + b₂y + c₂ = 0)
b₁ (a₂x + b₂y + c₂) = b₁ x 0
a₂b₁x + b₂b₁y + c₂b₁ = 0 —- (iv)
Subtract equation (iv) from equation (iii)
[a₁b₂x + b₁b₂y + b₂c₁ = 0] – [a₂b₁x + b₂b₁y + c₂b₁ = 0]
[a₁b₂x + b₁b₂y + b₂c₁] – [a₂b₁x + b₂b₁y + c₂b₁] = 0
a₁b₂x + b₁b₂y + b₂c₁ – a₂b₁x – b₂b₁y – c₂b₁ = 0
x(a₁b₂ – a₂b₁) + b₂c₁ – c₂b₁ = 0
x(a₁b₂ – a₂b₁) = c₂b₁ – b₂c₁
x = (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁)
Substitute x = (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) in equation (i)
a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) + b₁y + c₁ = 0
b₁y = -a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) – c₁
y = (-a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) – c₁) / b₁
y = (c₁a₂ – c₂a₁) / (b₂a₁ – b₁a₂)
The solution of the equations is
x / (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) = y / (c₁a₂ – c₂a₁) / (b₂a₁ – b₁a₂) = 1/(b₂a₁ – b₁a₂)
The above method is called Cross-Multiplication Methos as it uses cross-multiplication technique.
You can also represent the cross-multiplication as the following diagram.
Cross Multiplication Method Examples
Example 1.
Solve the linear equations x + y = 5, x – y = 3 by using the cross multiplication method?
Solution:
Given system of linear equations are
x + y = 5
x – y = 3
On transposition, we get
x + y – 5 = 0
x – y – 3 = 0
Writing the co-efficient in the following way, we get:
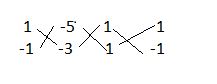
By cross-multiplication method:
x/[(1(-3) – (-1)(-5)] = y/[(-5)1 – 1(-3)] = 1//[1(-1) – 1(1)]
x/(-3 – 5) = y/(-5 + 3) = 1/(-1 – 1)
x/(-8) = y/(-2) = 1/(-2)
x/(-8) = 1/(-2), y/(-2) = 1/(-2)
x/8 = 1/2, y/2 = 1/2
x = 8/2, y = 2/2
x = 4, y = 1
Therefore, required solution is x = 4, y = 1.
Example 2.
Solve the simultaneous linear equations 3x – 4y = 0, 9x – 8y = 12 by the method of cross-multiplication?
Solution:
Given simultaneous equations are,
3x – 4y = 0
9x – 8y = 12
On transposition, we get
3x – 4y = 0 ——– (i)
9x – 8y – 12 = 0 ———- (ii)
Multiply equation (i) by -8 and equation (ii) by -4.
-8(3x – 4y) = 0 x -8
-24x + 32y = 0 —— (iii)
-4(9x – 8y – 12) = 0 x -4
-36x + 32y + 48 = 0 ——- (iv)
Subtract equation (iv) from equation (iii)
[-24x + 32y = 0] – [-36x + 32y + 48 = 0]
-24x + 32y – (-36x + 32y + 48) = 0
-24x + 32y + 36x – 32y – 48 = 0
12x – 48 = 0
12x = 48
x = 48/12
x = 4
Substitute x = 4 in equation (ii)
9(4) – 8y – 12 = 0
36 – 8y – 12 = 0
-8y + 24 = 0
-8y = -24
y = 24/8
y = 3
Therefore, required solution is x = 4, y = 3.
Example 3.
Solve the linear equations 2x + 3y = 5, x – 4y = 8 by using the cross multiplication method?
Solution:
Given linear equations are 2x + 3y = 5, x – 4y = 8
On transposing, we get
2x + 3y – 5 = 0 ——- (i)
x – 4y – 8 = 0 ——- (ii)
Multiply equation (ii) by 2, equation (i) by 1.
From equation (i), we get
2x + 3y – 5 = 0 —– (iii)
From equation (ii), we get
2(x – 4y – 8) = 0
2x – 8y – 16 = 0 —— (iv)
Subtract equation (iii) from equation (iv).
[2x – 8y – 16] – [2x + 3y – 5] = 0
2x – 8y – 16 – 2x – 3y + 5 = 0
-11y – 11 = 0
-11y = 11
y = -11/11
y = -1
Substitute y = -1 in equation (i)
2x + 3(-1) – 5 = 0
2x – 3 – 5 = 0
2x – 8 = 0
2x = 8
x = 8/2
x = 4
Therefore, the required solution is x = 4, y = -1.
Example 4.
Solve the system of linear equations 2x + 5y = 20, x + 2y = 4?
Solution:
Given simultaneous linear equations are 2x + 5y = 20, x + 2y = 4
On transposing, we get
2x + 5y – 20 = 0 —— (i)
x + 2y – 4 = 0 —— (ii)
Multiply equation (i) by 2.
2(2x + 5y – 20) = 2 x 0
4x + 10y – 40 = 0 ——- (iii)
Multiply equation (ii) by 5.
5(x + 2y – 4) = 0 x 5
5x + 10y – 20 = 0 —– (iv)
Subtract equation (iii) from equation (iv)
[5x + 10y – 20] – [4x + 10y – 40] = 0
5x + 10y – 20 – 4x – 10y + 40 = 0
x + 20 = 0
x = -20
Put x = -20 in equation (iii)
4(-20) + 10y – 40 = 0
-80 + 10y – 40 = 0
10y – 120 = 0
10y = 120
y = 120/10
y = 12
Therefore the required solution is x = -20, y = 12.