In geometry, a cylinder is a three dimensional solid figure with parallel faces joined by curved surfaces. In this article, we will know the definition of a cylinder, formulas, volume of a cylinder, and area of a cylinder in depth. With the help of these concepts, the students of grade 9 can solve any type of problems based on the topic cylinder. So, make use of our page and start your preparation and score the highest grades in the exams.
Cylinder – Definition
A cylinder is a 3D shape. The topic view of the cylinder is a circle and the side view of a cylinder is similar to the shape of a rectangle. The shape of a cylinder does not have any vertices. The cylinders are classified into four types they are right circular cylinder, hollow cylinder, elliptical cylinder, oblique cylinder. A cylinder has two bases and one curved surface.
Types of Cylinder
Right Circular Cylinder:
A right circular cylinder is formed by rolling the rectangle. If one of the sides of the rectangle is perpendicular to the radius then it is known as the right circular cylinder. The top view and bottom view of the cylinder are circular in shape and parallel to each other.
Oblique Cylinder:
If the roundabout appearances are not over one another but rather sideways, and the pivot creates a point other than the right point to the bases, then, at that point, it is called an oblique cylinder.
Elliptical Cylinder:
A cylinder that is elliptical in shape bases is known as an elliptical cylinder.
Hollow Cylinder:
A hollow cylinder is a cylinder that is unfilled from within and has a distinction in the external and the inward surface radius of a cylinder. It can have diverse inward lateral surface areas and external lateral surface areas as internal and external radii are not the equivalent.
Also, See:
Properties of Cylinder
We must follow the steps to find the volume, TSA, CSA of the cylinders.
1. The bases of the cylinder are circular in shape thus it is called the right circular cylinder.
2. If the bases are in elliptical shape then it is called an Elliptical cylinder.
3. The bases are congruent and parallel.
4. If the axis forms a right angle with the bases then it is called the right cylinder.
5. Cylinder is similar to the prism it has the same cross-section everywhere.
Cylinder Formulas
- Curved Surface Area: 2Πrh
- Total Surface Area: 2πr (h + r)
- Volume: πr²h
Volume of Cylinder
The volume of the cylinder is the total amount covered in the cylinder container. It is equal to the product of the area of the circle and the height of the cylinder. An example of the volume of a cylinder is gas filled in the cylinder, sand or water filled in the cylinder,
Total Surface Area of Cylinder
The total surface area of the cylinder is the sum of the curved or lateral surface area and the area of two curved bases.
Total surface area = curved surface + area of circular bases
Curved Surface Area of Cylinder
The curved surface area of the means the area measured without the area of the circular base. The curved surface area of the cylinder is the amount contained between the two parallel circular bases. The curved surface area is also known as the lateral surface area. It is double the product of pi, radius, and height.
Examples Problems on Cylinder
Example 1.
Find the lateral surface area of a cylinder whose diameter is 6 cm and height is 15 cm.
Solution:
Given:
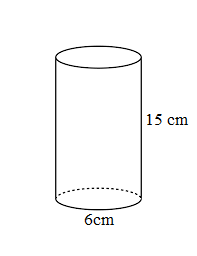
Diameter = 6 cm,
radius, r = d/2 = 6/2 = 3 cm
Height, h = 15 cm
By, the formula
Lateral surface area of a cylinder = 2πrh
= 2 x 3.14 x 3 x 15
= 282.6 cm².
Thus, the lateral surface area of the cylinder is 282.6 cm²
Example 2.
Find the height of a cylinder if its total surface area is 3052 in² and the radius is 8 in.
Solution:
Given that
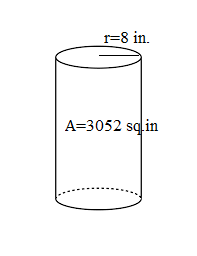
Total surface area = 3052 in²
Radius = r = 8 in.
But total surface area = 2πr (h + r)
3052 = 2 x 3.14 x 8(8 + h)
3052 = 50.24(8 + h)
Divide both sides by 60.74
60.74 = 8 + h
Subtract by on both sides.
h = 52. 74
Hence, the height of the cylinder is 52 in
Example 3.
The cost of painting a cylindrical container is Rs 20 per cm². Find the cost of painting 30 containers of radius, 10 cm, and height, 14 cm.
Solution:
Given that
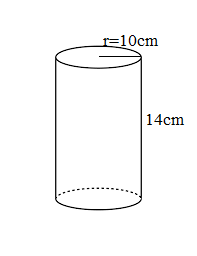
Cost of painting a cylindrical container = rs 20 per cm²
Radius = r = 10
Height = h= 14
First calculate the total surface area of 30 containers.
Total surface area = 2πr (h + r)
= 2 x 3.14 x 10 (14 + 10)
= 62.8 × 24
= 1507.4 cm²
The total surface area of 30 containers =1507.4 × 30 cm²
The cost of painting = cm² x 20 per cm²
= 45,216 cm²
Hence, the cost of painting 30 containers is 45,216 cm²
Example 4.
Find the radius of a cylinder whose total surface area is 2136.56 square feet, and the height is 3 feet.
Solution:
Given that
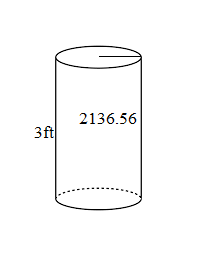
Total surface area = 2136.56 square feet
Height = h = 3 feet
But, total surface area = 2πr (h + r)
2136.56 =2 x 3.14 x r (3 + r)
2136.56 = 6.28r (3 + r)
By using the distributive property of multiplication on the RHS, we have,
2136.56 = 18.84r + 6.28r2
Divide each term by 6.28
340.22 = 3r + r2
r2 + 3r – 340.22 = 0
By solving the equation we get
r = 17
Therefore, the radius of the cylinder is 17 feet.
Example 5.
Find the total surface area of a cylinder whose radius is 6 cm and height is 8 cm.
Solution:
Given that

Radius = r = 6 cm
Height = h = 8 cm
By using formula we know that
Total surface area of a cylinder = 2πr (h + r)
= 2 x 3.14 x 6(8 + 6)
= 37.68 × 14
527.52 cm²
FAQs on Cylinder
1. What are the types of cylinders?
There are four types of cylinders as a right circular cylinder, oblique cylinder, elliptical cylinder, hollow cylinder.
2. What are the formulas for CSA, TSA, and volume of a cylinder?
The formula of the curved surface area of cylinder =2πrh
The formula of the total surface area of cylinder =2πr (h+r)
The formula of volume of cylinder =πr²h
3. How many edges does a cylinder have?
An edge is where two faces meet. A vertex is a corner where edges meet.