Everything cannot be explained with sentences. There are some rotations to represent some words. In maths, there are some notations given for sets of numbers. Learn the Different Notations in Sets and know how to use them while solving problems. We have given Notations of sets of numbers and also their explanation. Also, get a complete grip on notations of numbers. Refer to the entire article to improve your preparation level.
What are Different Notations in Sets?
Check out the different notations insets below.
∈ – Belongs to
∉ – Does not belong to
: or | – Such that
∅ – Null set or empty set
n(A) – Cardinal number of the set A
∪ – Union of two sets
∩ – The intersection of two sets
N – Set of natural numbers = {1, 2, 3, ……}
W – Set of whole numbers = {0, 1, 2, 3, ………}
I or Z – Set of integers = {………, -2, -1, 0, 1, 2, ………}
Z+ – Set of all positive integers
Q – Set of all rational numbers
Q+ – Set of all positive rational numbers
R – Set of all real numbers
R+ – Set of all positive real numbers
C – Set of all complex numbers
The above notations are the various types of problems on sets.
Note:
(i) The pair of curly braces { } denotes a set. All the elements of a set are placed inside the pair of curly braces. Those elements are separated using commas.
(ii) The set always represents a capital letter such as; A, B, C, ………
(iii) The elements of the sets are represented with small letters.
(iv) There is no particular order for elements of a set.
(v) Also, the elements of a set are not repeated.
(vi) The Greek letter Epsilon ‘∈’ is used for the words ‘belongs to’, ‘is an element of’, etc. Therefore, p ∈ S will be read as ‘p belongs to set S’ or ‘p is an element of the set S’.
(vii) The symbol ‘∉’ stands for ‘does not belong to’ also for ‘is not an element of’. Therefore, p ∉ S will read as ‘p does not belong to set S’ or ‘p is not an element of the set S’.
Read Related Articles:
Union
Let A and B be two sets.
Now, we can define the following new set.
A ∪ B = {c | c ∈ A or c ∈ B}
(That is, c may be in A or in B or in both A and B)
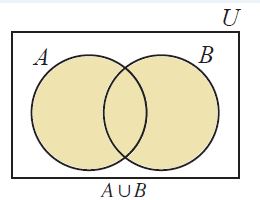
A ∪ B is read as “A union B”
Now that A u B contains all the elements of A and all the elements of B and the figure given below illustrates this.
It is clear that A ⊆ A ∪ B and also B ⊆ A ∪ B.
Intersection
Let A and B be two sets.
Now, we can define the following new set.
A ∩ B = {c | c ∈ A and c ∈ B}
(That is c must be in both A and B)
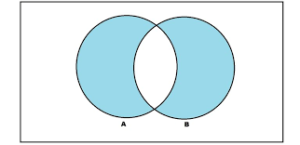
A ∩ B is read as “A intersection B”
Now that A n B contains only those elements which belong to both A and B and the figure given below illustrates this.
It is trivial that A ∩ B ⊆ A and also A ∩ B ⊆ B.
Set Difference
Let A and B be two sets.
Now, we can define the following new set.
A \ B = {c | c ∈ A but c ∉ B}
(That is c must be in A and must not be in B)
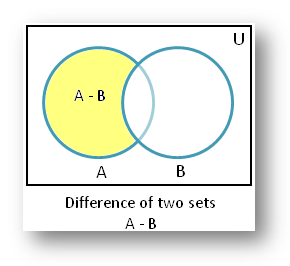
A \ B is read as “A difference B”
Now that A \ B contains only elements of A that are not in B and the figure given below illustrates this. A \ B can also write as A – B
Symmetric Difference
Let A and B be two sets.
Now, we can define the following new set.
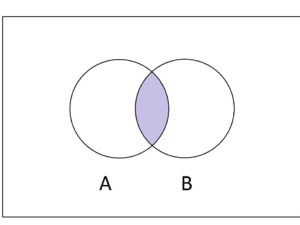
A Δ B = (A \ B) u (B \ A)
A Δ B is read as “A symmetric difference B”
Now that A Δ B contains all elements in A u B which are not in A n B and the figure given below illustrates this.
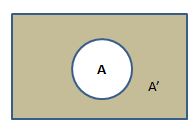
Complement
If A ⊆ U, where U is a universal set, then U \ A is called the complement of A with respect to U. If the underlying universal set is fixed, then we denote U \ A by A’ and it is called the complement of A.
A’ = U \ A
The difference set A \ B can also be viewed as the complement of B with respect to A.
Disjoint Sets
Two sets A and B are said to be disjoint if they do not have any common element. That is, A and B are disjoint if A n B = ᵩ
It is clear that n(A u B) = n(A) + n(B), if A and B are disjoint finite set.
Subset of a Set
A set M is a subset of set N if every element of M is also an element of N.
In symbol, we write m ⊆ n. We can read it as “M is a subset of N” or “M is contained in N”.
Read ⊈ as “M is a not subset of N” or “M is not contained in N”
Proper Subset
A set M is said to be a proper subset of set N if M ⊆ N and M ≠ N.
In symbol, we write M ⊂ N. We can read it as “M is a proper subset of N”
Power Set
The set of all subsets of X is said to be the power set of the set X.
The power set of X is denoted by P(X)
Superset
A set M is said to be a proper subset of set N if M ⊆ N and M ≠ N.
In symbol, we write M ⊂ N. We can read it as N is called superset of M.
Formula to Find Number of Subsets
If M is denoted as the given set and it has n number of elements, then we can find the formula of subsets as
Number of subsets = 2n
Formula to find the number of proper subsets
Number of proper subsets = 2n-1
Null set or Empty set
A set that contains no element is called a null set or an empty set. And it is denoted by { } or ∅. Hence, the cardinal number of a null set is zero.
