The division is the most important and basic arithmetic operation in maths. It is the method of dividing or distributing the number into equal parts. Learn the concept of a two-digit divisor in-depth with the help of examples from here. The operation of Division is exactly opposite to the operation of multiplication. It is a repeated process of subtraction. Know the step-by-step procedure on how to Divide by 2-digit Divisors.
Do Refer:
- Worksheet on Division Problems by 2-Digit Divisors
- Divide by Repeated Subtraction
- Dividing 2-Digit Number by 1-Digit Number
How to Divide with 2 Digit Divisors?
The process to Divide by 2-Digit Divisors is shown in the below section. Read and know the procedure to divide with 2 digit divisors from here.
- Take any number with 3 or more digits as the dividend and then take a two-digit number as the divisor.
- Write the dividend inside the division symbol and the 2-digit divisor outside the symbol.
- First, consider two digits of the dividend from the left.
- Write the quotient and remainder of the two-digit dividend and then take another two-digit dividend and write the quotient and remainder.
- Subtract the result from the digit.
- Repeat the process.
Examples on 2-Digit Divisors with Answers
Let us consider some examples to know how to Divide by 2-Digit Divisors.
Example: 1
Divide 1683 ÷ 99
Solution:
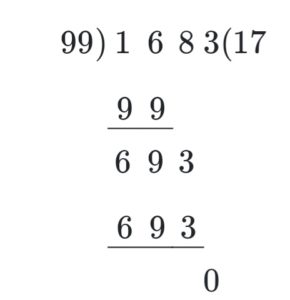
Divisor (99) has two digits. We will divide by 2-digit divisors.
99 > 16
So we will consider 3 digits (168).
99 × 1 = 99
Now subtract 168 – 99 = 69
Write the remainder in the next step.
Now write 3 to the right. It becomes 693.
99 × 7 = 693.
Now subtract 693 and 693 = 0
So, the remainder is 0.
Example: 2
Divide 196 ÷ 12
Solution:

Divisor (12) has two digits. We will divide by 2-digit divisors.
12 < 19
So we will consider 2 digits (19).
12 × 1 = 12
Now subtract 19 – 12 = 7
Write the remainder in the next step.
Now write 6 to the right. It becomes 76.
12 × 6 = 72
Now subtract 76 and 72 = 4
So, the remainder is 4.
Example: 3
Divide 1170 ÷ 10
Solution:

Divisor (10) has two digits. We will divide by 2-digit divisors.
10 < 11
So we will consider 2 digits (11).
10 × 1 = 10
Now subtract 11 – 10 = 1
Write the remainder in the next step.
Now write 7 to the right. It becomes 17.
10 × 1 = 10
Now subtract 17 and 10 = 7
Now take 0 to the right. It becomes 70
10 × 7 = 70
So, the remainder is 0.
Example: 4
Divide 1260 ÷ 12
Solution:

Divisor (12) has two digits. We will divide by 2-digit divisors.
12 = 12
So we will consider 2 digits (11).
12 × 1 = 12
Now subtract 12 – 12 = 0
Write the remainder in the next step.
Now write 6 to the right. It becomes 06.
Write the remainder in the next step.
Now take 0 to the right. It becomes 60
12 × 5 = 60
So, the remainder is 0.
Example: 5
Divide 1792 ÷ 16
Solution:
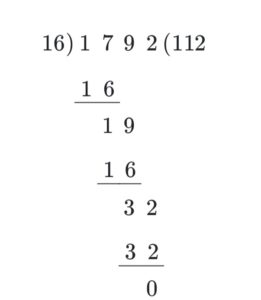
Divisor (16) has two digits. We will divide by 2-digit divisors.
16 < 17
So we will consider 2 digits (17).
16 × 1 = 16
Now subtract 17 – 16 = 1
Write the remainder in the next step.
Now write 9 to the right. It becomes 19.
16 × 1 = 16
Now subtract 19 and 16 = 3
Now take 2 to the right. It becomes 32
16 × 2 = 32
So, the remainder is 0.
FAQs on Divide by 2-Digit Divisors
1. How do you Divide by 2-Digit Divisors?
Take the first digits of the dividend, the same number of digits that the divisor has, and perform the regular division. Continue the Process by bringing down the leftover digits in the dividend until the remainder becomes 0.
2. Which method is preferred for division?
To divide the given numbers, the long division method is preferred.
3. What are the steps while dividing numbers?
Below are the simple steps to keep in mind while dividing numbers. They are as under
- Divide the divisor into the dividend.
- Multiply the quotient times divisor.
- Subtract.
- Bring down if there is nothing to bring down the problem is over.
