In Mathematics there are four basic operations namely Addition, Subtraction, Multiplication, Division. Division Operation is one of the basic arithmetic operations. In Division Process there are two major parts namely Divisor and Dividend. Get to know the definition of each of the parts of the division explained in detail below. Know the Formula to find Dividend When Divisor, Quotient, and Remainer are given.
Dividend Divisor Quotient and Remainder Definitions
Dividend: The number or value that we divide is known as a dividend.
Divisor: The number that divides the dividend is known as a divisor
Quotient: The result obtained from the division process is known as a quotient
Remainder: The number left over after the division process is known as the remainder.
How to find the Dividend? | Dividend Formula
The Formula to Calculate Dividend is given as under
Dividend = Divisor x Quotient + Remainder
Whenever you divide a number with another number you will get the result.
a/b = c
Here “a” is the dividend and “b” is the divisor whereas “c” is the quotient. Thus, we can write it as follows
Dividend = Divisor*Quotient
Rearranging the Terms we can find the other terms if any two are known.
However, if you have a remainder after the division process then the formula is as follows
Dividend = Divisor*Quotient+Remainder
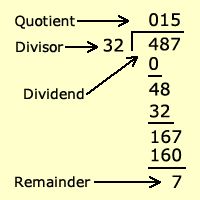
You can verify the same by applying the formula of dividend
We know Dividend = Divisor*Quotient+Remainder
487 = 32*15+7
487 = 480+7
487 = 487
So the answer is correct.
Check out Examples on Division of Integers to learn about the Terms Dividend, Divisor, Quotient, and Remainder in detail. Let us consider few examples to verify the answer of division.
Properties of Division
Below we have listed few division properties explained by considering few examples. Keep these below points in mind you will find the division problems much simple to solve.
Property 1: If you divide zero by a number the quotient is always zero.
Examples:
(i) 0 ÷ 2 = 0
(ii) 0 ÷ 10 = 0
(iii) 0 ÷ 15 = 0
(iv) 0 ÷ 214 = 0
(v) 0 ÷ 320 = 0
(vi) 0 ÷ 6132 = 0
Property 2: The division of a number by zero is not defined.
Example:
34 divided by 0 is not defined
Property 3: If we divide any number with 1 the quotient is always the number itself.
Examples
(i) 22 ÷ 1 = 22
(ii) 658 ÷ 1 = 658
(iii) 3250 ÷ 1 = 3250
(iv) 5483 ÷ 1 = 5483
Property 4: If we divide a non-zero number by itself the quotient is always one.
(i) 40 ÷ 40 = 1
(ii) 92 ÷ 92 = 1
(iii) 2137 ÷ 2137 = 1
(iv) 4130 ÷ 4130 = 1
You can refer to our Properties of Division of Integers to have an idea of more such properties.