Engage NY Eureka Math Algebra 1 Module 1 Mid Module Assessment Answer Key
Eureka Math Algebra 1 Module 1 Mid Module Assessment Task Answer Key
Question 1.
Jacob lives on a street that runs east and west. The grocery store is to the east and the post office is to the west of his house. Both are on the same street as his house. Answer the questions below about the following story:
At 1:00 p.m., Jacob hops in his car and drives at a constant speed of 25 mph for 6 minutes to the post office. After 10 minutes at the post office, he realizes he is late, and drives at a constant speed of 30 mph to the grocery store, arriving at 1:28 p.m. He then spends 20 minutes buying groceries.
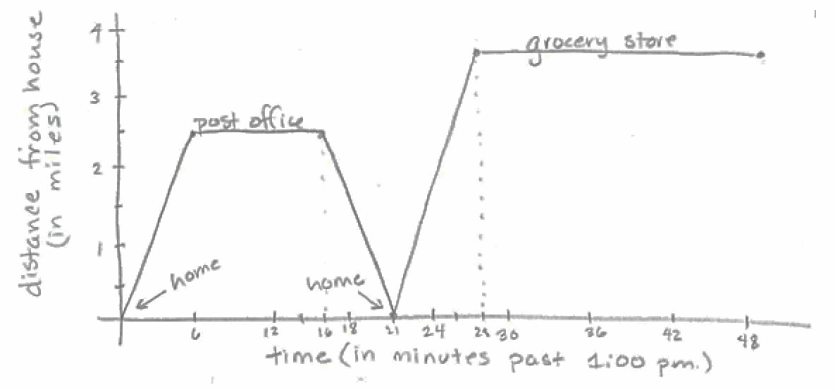
a. Draw a graph that shows the distance Jacob’s car is from his house with respect to time. Remember to label your axes with the units you chose and any important points (home, post office, grocery store).

Answer:
25 \(\frac{miles}{hour}\) × 6 minutes × \(\frac{1hour}{60 minutes}\) = 2.5 miles from house to post office
30 \(\frac{miles}{hour}\) × 12 minutes × \(\frac{1hour}{60 minutes}\) = 6 miles from post office to store
6 miles – 2.5 miles = 3.5 miles from home to store
6 miles in 12 minutes is 1 mile in 2 minutes
so 2.5 miles takes 5 minutes and 3.5 miles takes 7 minutes
b. On the way to the grocery store, Jacob looks down at his watch and notes the time as he passes his house. What time is it when he passes his house? Explain how you found your answer.
Answer:
It is 1:21 p.m. The graph shows the time as 21 minutes past 1:00 p.m. He spent 6 minutes getting to the post office, 10 minutes at the post office, and 5 minutes getting from the post office to the point of passing by his house. You know it took 5 minutes for the last part because he traveled 30 miles per hour and went 2.5 miles. 2.5 miles × \(\frac{60 minutes}{30 miles}\) = 5 minutes
c. If he drives directly back to his house after the grocery story, what was the total distance he traveled to complete his errands? Show how you found your answer.
Answer:

12 miles.
2.5 miles + 6 miles + 3.5 miles = 12 miles
You know it is 2.5 miles from the house to the post office because
25\(\frac{miles}{hour}\) × 6 minutes × \(\frac{1hour}{60 minutes}\) = 2.5 miles.
You know it is 6 miles from the post office to the store because
30\(\frac{miles}{hour}\) × 12 minutes × \(\frac{1hour}{60 minutes}\) = 6 miles.
Question 2.
Jason is collecting data on the rate of water usage in the tallest skyscraper in the world during a typical day. The skyscraper contains both apartments and businesses. The electronic water meter for the building displays the total amount of water used in liters. At noon, Jason looks at the water meter and notes that the digit in the ones place on the water meter display changes too rapidly to read the digit and that the digit in the tens place changes every second or so.
a. Estimate the total number of liters used in the building during one 24-hour day. Take into account the time of day when he made his observation. (Hint: Will water be used at the same rate at
2:00 a.m. as at noon?) Explain how you arrived at your estimate.
Answer:
10 \(\frac{liters}{second}\) × 60\(\frac{seconds}{minute}\) × 60 \(\frac{minutes}{hour}\) × 18 hours = 648 000 liters
Since water is probably only used from about 5:00 a.m. to 11:00 p.m., I did not multiply by 24 hours, but by 18 hours instead.
b. To what level of accuracy can Jason reasonably report a measurement if he takes it at precisely 12:00 p.m.? Explain your answer.
Answer:
It can be reported within ±10 liters, since he can read the 10’s place, but it is changing by a 10 during the second he reads it.
c. The meter will be checked at regular time spans (for example, every minute, every 10 minutes, and every hour). What is the minimum (or smallest) number of checks needed in a 24-hour period to create a reasonably accurate graph of the water usage rate with respect to time? (For example, 24 checks would mean checking the meter every hour; 48 checks would mean checking the meter every half hour.) Defend your choice by describing how the water usage rate might change during the day and how your choice could capture that change.
Answer:
24 checks. Every hour would be good to show the peaks in usage during morning and evening hours from those in the apartments. And it might also show that businesses stop using it after business hours. It would depend on what portion of the building is business vs. apartments.
Question 3.
A publishing company orders black and blue ink in bulk for its two-color printing press. To keep things simple with its ink supplier, each time it places an order for blue ink, it buys B gallons, and each time it places an order for black ink, it buys K gallons. Over a one-month period, the company places m orders of blue ink and n orders of black ink.
a. What quantities could the following expressions represent in terms of the problem context?
m+n
Answer:
Total number of ink orders over a one-month period.
mB+nK
Answer:
Total number of ink orders over a one-month period.
\(\frac{mB+nK}{m+n}\)
Answer:
Total number of ink orders over a one-month period.
b. The company placed twice as many orders for black ink than for blue ink in January. Give interpretations for the following expressions in terms of the orders placed in January, \(\frac{m}{m+n}\) and \(\frac{n}{m+n}\), and explain which expression must be greater using those interpretations.
Answer:
\(\frac{m}{m+n}\) is the fraction of orders that are for blue ink.
\(\frac{n}{m+n}\) is the fraction of orders that are for black ink.
\(\frac{n}{m+n}\) would be bigger, 2 times as big as \(\frac{m}{m+n}\) because they ordered twice as many orders for black ink than for blue ink.
Question 4.
Sam says that he knows a clever set of steps to rewrite the expression
(x+3)(3x+8)-3x(x+3) as a sum of two terms where the steps do not involve multiplying the linear factors first and then collecting like terms. Rewrite the expression as a sum of two terms (where one term is a number and the other is a product of a coefficient and variable) using Sam’s steps if you can.
Answer:
((3x + 8)-3x)∙(x + 3)
8 (x + 3)
8x + 24
Question 5.
Using only the addition and multiplication operations with the numbers 1, 2, 3, and 4 each exactly once, it is possible to build a numeric expression (with parentheses to show the order used to build the expression) that evaluates to 21. For example, 1+((2+3)•4) is one such expression.
a. Build two more numeric expressions that evaluate to 21 using the criteria above. Both must be different from the example given.
Answer:
(1 + 2)∙(3 + 4) = 21
((2 + 4) + 1)∙ 3 = 21
b. In both of your expressions, replace 1 with a, 2 with b, 3 with c, and 4 with d to get two algebraic expressions. For example, a+((b+c)∙d) shows the replacements for the example given.
Answer:
(a + b) ∙ (c + d) = ac + ad + bc + bd
((b + d) + a)∙ c = ac + bc + dc
Are your algebraic expressions equivalent? Circle: Yes No
Answer:

→ If they are equivalent, prove that they are using the properties of operations.
→ If not, provide two examples:
(1) Find four different numbers (other than 0, 1, 2, 3, 4) that when substituted for a, b, c, and d into each expression, the expressions evaluate to different numbers, and
Answer:
a = 5 b = 10 c = 20 d = 30
(5 + 10) ∙ (20 + 30) = 750
((10 + 30) + 5) ∙ 20 = 900
(2) Find four different, nonzero numbers that when substituted into each expression, the expressions evaluate to the same number.
Answer:
5, 6, 11, 7 (ac + ad + bc + bd) needs to equal (ac + bc + dc);
(5 + 6)∙ (11 + 7) = 11 ∙ 18 = 198 so, (ad + bd) needs to equal (dc);
((6 + 7) + 5) ∙ 11 = 18 ∙ 11 = 198 so, (a + b) needs to equal c.
Question 6.
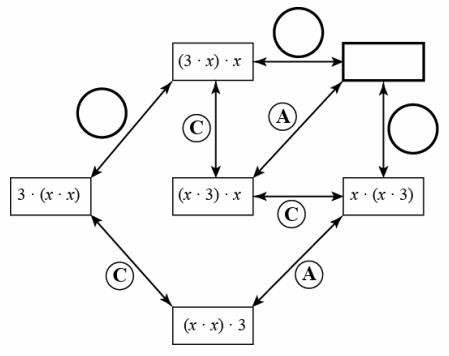
The diagram below, when completed, shows all possible ways to build equivalent expressions of 3x2 using multiplication. The equivalent expressions are connected by labeled segments stating which property of operations, A for associative property and C for commutative property, justifies why the two expressions are equivalent. Answer the following questions about 3x2 and the diagram.
Answer:
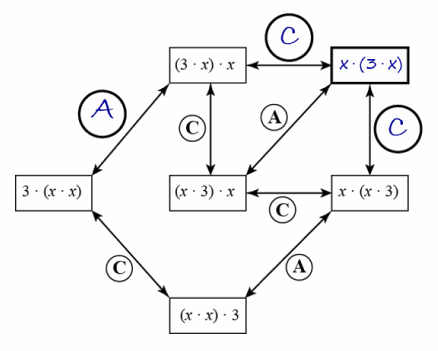
a. Fill in the empty circles with A or C and the empty rectangle with the missing expression to complete the diagram.
b. Using the diagram above to help guide you, give two different proofs that (x∙x)∙3=(3∙x)∙x.
Answer:
1. (x ∙ x) ∙ 3 = x ∙ (x ∙ 3) by associative property
x ∙ (x ∙ 3) = x ∙ (3 ∙ x) by commutative property
x ∙ (3 ∙ x) = (3 ∙ x) ∙ x by commutative property
2. (x ∙ x) ∙ 3 = 3 ∙ (x ∙ x) by commutative property
3 ∙ (x ∙ x) = (3 ∙ x) ∙ x by associative property
Question 7.
Ahmed learned: “To multiply a whole number by ten, just place a zero at the end of the number.” For example, 2813×10, he says, is 28,130. He doesn’t understand why this rule is true.
a. What is the product of the polynomial 2x3+8x2+x+3 times the polynomial x?
Answer:
2x4 + 8 x3 + x2 + 3x
b. Use part (a) as a hint. Explain why the rule Ahmed learned is true.
Answer:
When you multiply by the same number as the base, it creates a new number where each digit in the original number is now one place value higher so that there is nothing left (no numbers) to represent the ones digit, which leads to a trailing “0” in the ones digit.
Question 8.
a. Find the following products:
i. (x-1)(x+1)
Answer:
x2 + x-x-1
x2 – 1
ii. (x-1)(x2+x+1)
Answer:
x3 + x2 + x-x2 -x-1
x3 -1
iii. (x-1)(x3+x2+x+1)
Answer:
x4 + x3 + x2 + x-x3 -x2 -x-1
x4 -1
iv. (x-1)(x4+ x3+x2+x+1)
Answer:
x5 + x4 + x3 + x2 + x-x4 -x3 -x2 -x-1
x5 -1
v. (x-1)(xn+xn-1+……+x3+x2+x+1)
Answer:
xn+1 -1
b. Substitute x=10 into each of the products from parts (i) through (iv) and your answers to show how each of the products appears as a statement in arithmetic.
Answer:
i. (10 -1) ∙ (10 + 1) = (100 -1)
9 ∙ (11) = 99
ii. (10 -1) ∙ (100 + 10 + 1) = (1000 -1)
9 ∙ (111) = 999
iii. (10 -1) ∙ (1000 + 100 + 10 + 1) = (10000 -1)
9 ∙ (1111) = 9,999
iv. (10 -1) ∙ (10000 + 1000 + 100 + 10 + 1) = (100 000 -1)
9 ∙ (11111) = 99,999
c. If we substituted x=10 into the product (x-2)(x7+x6+x5+x4+x3+x2+x+1) and computed the product, what number would result?
Answer:
8 ∙ (11 111 111) = 88 888 888
d. Multiply (x-2) and (x7+x6+x5+x4+x3+x2+x+1) and express your answer in standard form.
Answer:
x8 + x7 + x6 + x5 + x4 + x3 + x2 + x-2 x7 -2 x6 -2 x5 -2 x4 -2 x3 -2 x2 -2x-2
x8 -x7 -x6 -x5 -x4 -x3 -x2 -x-2
Substitute x=10 into your answer and see if you obtain the same result as you obtained in part (c).
Answer:
108 -10 7 -10 6 -10 5 -10 4 -10 3 -102 -10-2 = 88 888 888
Yes,I get the same answer.
e. Francois says (x-9)(x7+x6+x5+x4+x3+x2+x+1) must equal x7+x6+x5+x4+x3+x2+x+1 because when x=10, multiplying by x-9 is the same as multiplying by 1.
i. Multiply (x-9)(x7+x6+x5+x4+x3+x2+x+1).
Answer:
x8 -8 x7 -8 x6 -8 x5 -8x 4 -8x 3 -8x2 -8x-9
ii. Put x=10 into your answer.
Answer:
100 000 000-80 000 000-8 000 000-800 000-80000-8000-800-80-9
100 000 000-88 888 889 = 11 111 111
Is it the same as x7+x6+x5+x4+x3+x2+x+1 with x = 10?
Answer:
Yes.
iii. Was Francois right?
Answer:
No, just because it is true when x is 10, doesn’t make it true for all real x. The two expressions are not algebraically equivalent.