Engage NY Eureka Math Algebra 1 Module 3 Lesson 19 Answer Key
Eureka Math Algebra 1 Module 3 Lesson 19 Exploratory Challenge Answer Key
Exploratory Challenge 1
Let f(x) = x2 and g(x) = f(2x), where x can be any real number.
a. Write the formula for g in terms of x2 (i.e., without using f(x) notation).
Answer:
g(x) = (2x)2
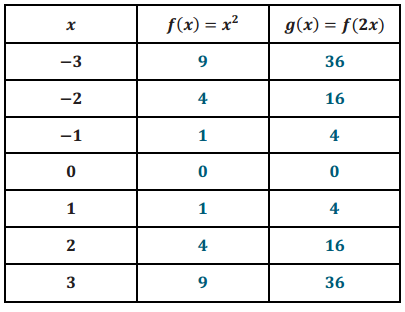
b. Complete the table of values for these functions.
Answer:
c. Graph both equations: y = f(x) and y = f(2x).
Answer:
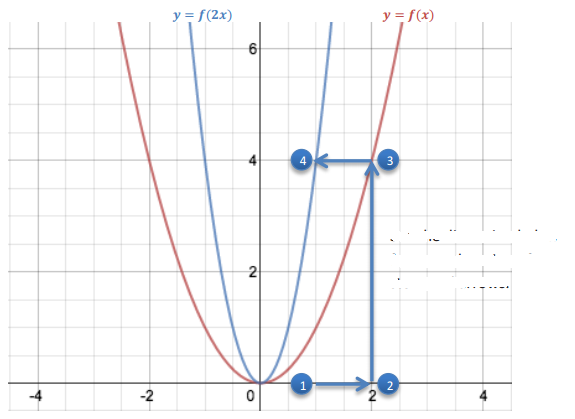
See the discussion below for an explanation of the steps and arrows.
d. How does the graph of y = g(x) relate to the graph of y = f(x)?
Answer:
The corresponding x-value of y = g(x) is half of the corresponding x-value of y = f(x) when g(x) = f(x); the points of the graph of g are \(\frac{1}{2}\) the distance to the y-axis as the corresponding points of the graph of f, which makes the graph of g appear to “shrink horizontally.”
e. How are the values of f related to the values of g?
Answer:
For equal outputs of f and g, the input of g only has to be half as big as the input of f.
Exploratory Challenge 2
Let f(x) = x2 and h(x) = f(\(\frac{1}{2}\) x), where x can be any real number.
a. Rewrite the formula for h in terms of x2 (i.e., without using f(x) notation).
Answer:
h(x) = (\(\frac{1}{2}\) x)2
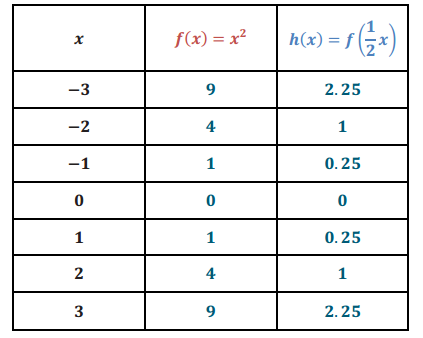
b. Complete the table of values for these functions.
Answer:
c. Graph both equations: y = f(x) and y = f(\(\frac{1}{2}\) x).
Answer:
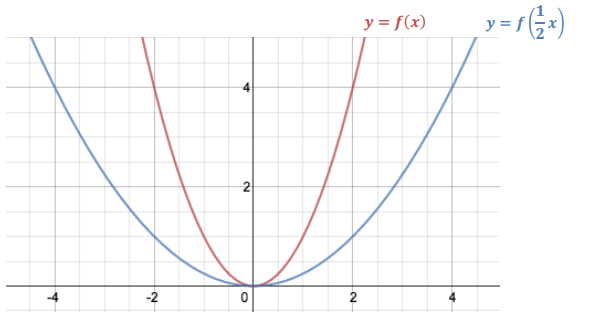
d. How does the graph of y = f(x) relate to the graph of y = h(x)?
Answer:
Since the corresponding x-value of y = h(x) is twice the corresponding x-value of y = f(x) when h(x) = f(x), the points of the graph of h are 2 times the distance to the y-axis as the corresponding points of the graph of f, which makes the graph of h appear to “stretch horizontally.”
e. How are the values of f related to the values of h?
Answer:
To get equal outputs of each function, the input of h has to be twice the input of f.
Exploratory Challenge 3
a. Look at the graph of y = f(x) for the function f(x) = x2 in Exploratory Challenge 1 again. Would we see a difference in the graph of y = g(x) if -2 were used as the scale factor instead of 2? If so, describe the difference. If not, explain why not.
Answer:
There would be no difference. The function involves squaring the value within the parentheses; so, both the graph of y = f(2x) and the graph of y = f(-2x) are the same set as the graph of y = g(x), but both correspond to different transformations: The first is a horizontal scaling with scale factor \(\frac{1}{2}\), and the second is a horizontal scaling with scale factor \(\frac{1}{2}\) and a reflection across the y-axis.
b. A reflection across the y-axis takes the graph of y = f(x) for the function f(x) = x2 back to itself. Such a transformation is called a reflection symmetry. What is the equation for the graph of the reflection symmetry of the graph of y = f(x)?
Answer:
y = f(-x).
c. Deriving the answer to the following question is fairly sophisticated; do this only if you have time. In Lessons 17 and 18, we used the function f(x) = |x| to examine the graphical effects of transformations of a function. In this lesson, we use the function f(x) = x2 to examine the graphical effects of transformations of a function. Based on the observations you made while graphing, why would using f(x) = x2 be a better option than using the function f(x) = |x|?
Answer:
Not all of the effects of multiplying the input of a function are as visible with an absolute function as they are with a quadratic function. For example, the graph of y = 2|x| is the same as y = |2x|. Therefore, it is easier to see the effect of multiplying a value to the input of a function by using a quadratic function than it is by using the absolute value function.
Eureka Math Algebra 1 Module 3 Lesson 19 Exercise Answer Key
Exercise
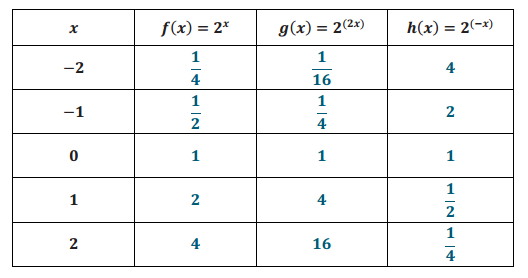
Complete the table of values for the given functions.
a.

Answer:
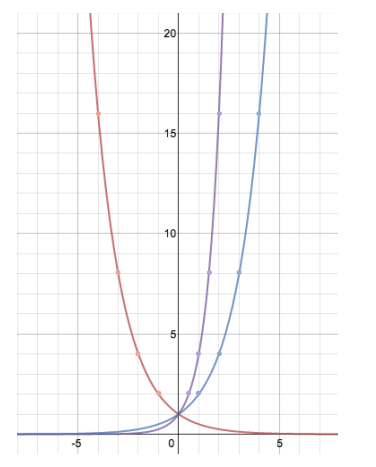
b. Label each of the graphs with the appropriate functions from the table.
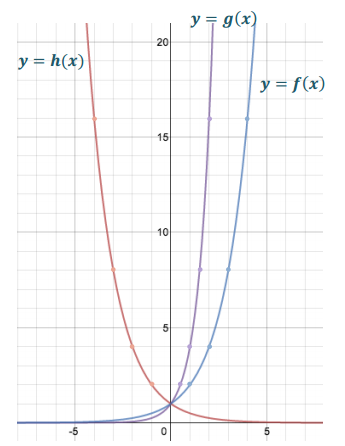
Answer:
c. Describe the transformation that takes the graph of y = f(x) to the graph of y = g(x).
Answer:
The graph of y = g(x) is a horizontal scale with scale factor \(\frac{1}{2}\) of the graph of y = f(x).
d. Consider y = f(x) and y = h(x). What does negating the input do to the graph of f?
Answer:
The graph of h is a reflection over the y-axis of the graph of f.
e. Write the formula of an exponential function whose graph would be a horizontal stretch relative to the graph of g.
Answer:
Answers vary. Example: y = 2(0.5x).
Eureka Math Algebra 1 Module 3 Lesson 19 Problem Set Answer Key
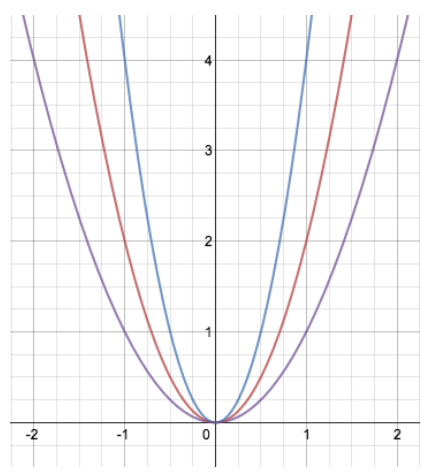
Let f(x) = x2, g(x) = 2x2, and h(x) = (2x)2, where x can be any real number. The graphs above are of the functions y = f(x), y = g(x), and y = h(x).
Question 1.
Label each graph with the appropriate equation.
Answer:
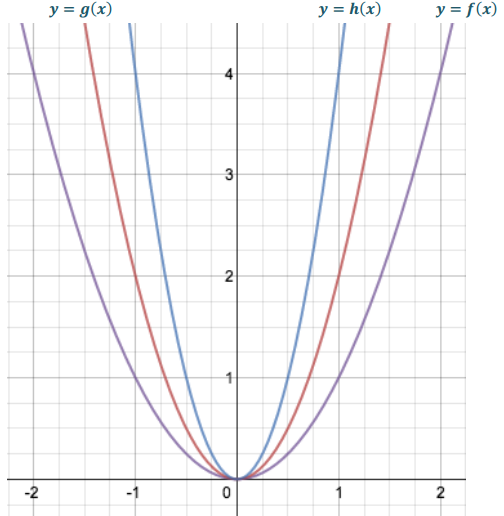
Question 2.
Describe the transformation that takes the graph of y = f(x) to the graph of y = g(x). Use coordinates to illustrate an example of the correspondence.
Answer:
The graph of y = g(x) is a vertical stretch of the graph of y = f(x) by scale factor 2; for a given x-value, the value of g(x) is twice as much as the value of f(x).
OR
The graph of y = g(x) is a horizontal shrink of the graph of y = f(x) by scale factor \(\frac{1}{\sqrt{2}}\). It takes \(\frac{1}{\sqrt{2}}\) times the input for y = g(x) as compared to y = f(x) to yield the same output.
Question 3.
Describe the transformation that takes the graph of y = f(x) to the graph of y = h(x). Use coordinates to illustrate an example of the correspondence.
Answer:
The graph of y = h(x) is a horizontal shrink of the graph of y = f(x) by a scale factor of \(\frac{1}{2}\). It takes \(\frac{1}{2}\) the input for y = h(x), as compared to y = f(x) to yield the same output.
OR
The graph of y = h(x) is a vertical stretch of the graph of y = f(x) by scale factor 4; for a given x-value, the value of h(x) is four times as much as the value of f(x).
Eureka Math Algebra 1 Module 3 Lesson 19 Exit Ticket Answer Key
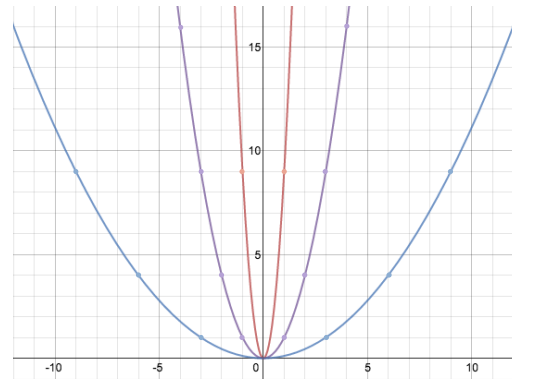
Let f(x) = x2, g(x) = (3x)2, and h(x) = (\(\frac{1}{3}\) x)2, where x can be any real number. The graphs above are of y = f(x), y = g(x), and y = h(x).
Question 1.
Label each graph with the appropriate equation.
Answer:
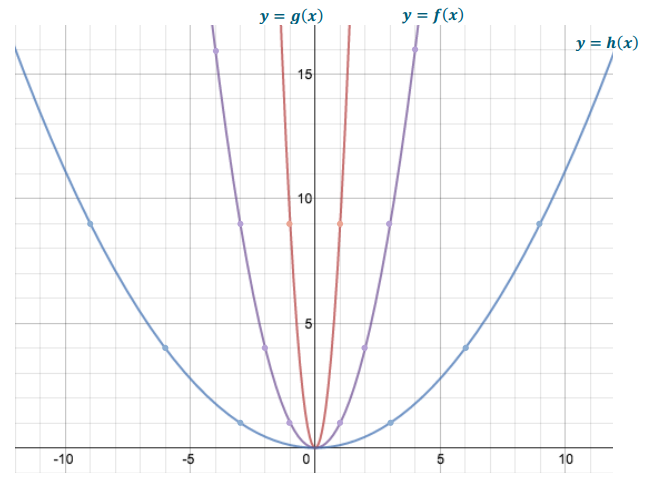
Question 2.
Describe the transformation that takes the graph of y = f(x) to the graph of y = g(x). Use coordinates of each to illustrate an example of the correspondence.
Answer:
The graph of y = g(x) is a horizontal shrink of the graph of y = f(x) with scale factor \(\frac{1}{3}\). The corresponding x-value of y = g(x) is one-third of the corresponding x-value of y = f(x) when g(x) = f(x). This can be illustrated with the coordinate (1, 9) on g(x) and the coordinate (3, 9) on f(x).
Question 3.
Describe the transformation that takes the graph of y = f(x) to the graph of y = h(x). Use coordinates to illustrate an example of the correspondence.
Answer:
The graph of y = h(x) is a horizontal stretch of the graph of y = f(x) with scale factor 3. The corresponding
x-value of y = h(x) is three times the corresponding x-value of y = f(x) when h(x) = f(x). This can be illustrated with the coordinate (1, 1) on y = f(x) and the coordinate (3, 1) on y = h(x).