Engage NY Eureka Math Algebra 1 Module 3 Lesson 23 Answer Key
Eureka Math Algebra 1 Module 3 Lesson 23 Exercise Answer Key
Opening Exercise
A detective is called to the scene of a crime where a dead body has just been found. He arrives at the scene and measures the temperature of the dead body at 9:30 p.m. After investigating the scene, he declares that the person died 10 hours prior, at approximately 11:30 a.m. A crime scene investigator arrives a little later and declares that the detective is wrong. She says that the person died at approximately 6:00 a.m., 15.5 hours prior to the measurement of the body temperature. She claims she can prove it by using Newton’s law of cooling:
T(t) = Ta + (To – Ta )∙2.718(-kt),
where:
T(t) is the temperature of the object after a time of t hours has elapsed,
Ta is the ambient temperature (the temperature of the surroundings), assumed to be constant, not impacted by the cooling process,
To is the initial temperature of the object, and
k is the decay constant.
Using the data collected at the scene, decide who is correct: the detective or the crime scene investigator.
Ta = 68°F (the temperature of the room)
To = 98.6°F (the initial temperature of the body)
k = 0.1335 (13.35% per hour―calculated by the investigator from the data collected)
The temperature of the body at 9:30 p.m. is 72°F.
Answer:
If the person had died 10 hours prior to 9:30 p.m., his body temperature would be approximately 76°F. When you fill in 15.5 hours for t, the temperature is 71.865°F. This is much closer to the measured temperature of 72°F.
Mathematical Modeling Exercise
Two cups of coffee are poured from the same pot. The initial temperature of the coffee is 180°F, and k is 0.2337 (for time in minutes).
Exercise 1.
Suppose both cups are poured at the same time. Cup 1 is left sitting in the room that is 75°F, and Cup 2 is taken outside where it is 42°F.
a. Use Newton’s law of cooling to write equations for the temperature of each cup of coffee after t minutes has elapsed.
Answer:
Cup 1: T1 (t) = 75 + (180 – 75) ∙ 2.718(-0.2337t)
Cup 2: T2 (t) = 42 + (180 – 42) ∙ 2.718(-0.2337t)
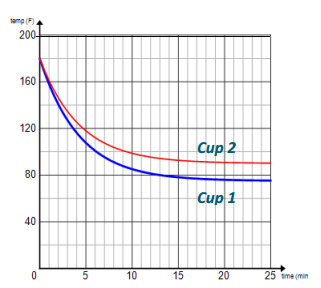
b. Graph and label both on the same coordinate plane, and compare and contrast the two graphs.
Answer:
Both are decreasing exponentially and have the same y-intercept because they have the same initial temperature. The graph for Cup 2 has a larger vertical stretch than Cup 1, but Cup 1 has a larger vertical translation, which is why they both can have the same initial temperature. The y-values of Cup 2 level out lower than the corresponding y-values of Cup 1 because of the lower ambient temperature.
The temperature difference (between the cup and the surroundings) drives the cooling. Larger temperature differences lead to faster cooling. This is why the outdoor cup cools much faster.
c. Coffee is safe to drink when its temperature is below 140°F. Estimate how much time elapses before each cup is safe to drink.
Answer:
Cup 1: Approximately 2 min.
Cup 2: Approximately 1.5 min.
Exercise 2.
Suppose both cups are poured at the same time, and both are left sitting in the room that is 75°F. But this time, milk is immediately poured into Cup 2, cooling it to an initial temperature of 162°F.
a. Use Newton’s law of cooling to write equations for the temperature of each cup of coffee after t minutes has elapsed.
Answer:
Cup 1: T1 (t) = 75 + (180-75)∙2.718(-0.2337t)
Cup 2: T2 (t) = 75 + (162-75)∙2.718(-0.2337t)
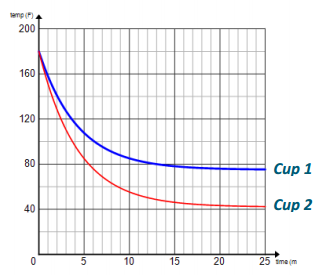
b. Graph and label both on the same coordinate plane, and compare and contrast the two graphs.
Answer:
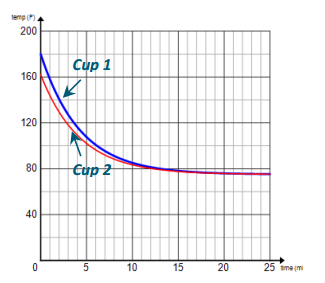
Both are decreasing exponentially, and both appear to level out to approximately the same temperature (the room temperature). The graph for Cup 2 has a smaller vertical stretch than Cup 1 and a smaller y-intercept because of its lower starting temperature.
c. Coffee is safe to drink when its temperature is below 140°F. How much time elapses before each cup is safe to drink?
Answer:
Cup 1: Approximately 2 min.
Cup 2: Approximately 1 min.
Exercise 3.
Suppose Cup 2 is poured 5 minutes after Cup 1 (the pot of coffee is maintained at 180°F over the 5 minutes). Both are left sitting in the room that is 75°F.
a. Use the equation for Cup 1 found in Exercise 1, part (a) to write an equation for Cup 2.
Answer:
Cup 2: T(t) = 75 + (180-75)∙2.718(-0.2337(t-5) )
b. Graph and label both on the same coordinate plane, and describe how to obtain the graph of Cup 2 from the graph of Cup 1.
Answer:
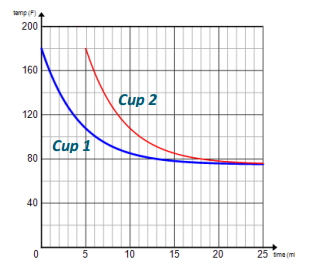
The graph of Cup 2 is the graph of Cup 1 shifted right 5 units.
Eureka Math Algebra 1 Module 3 Lesson 23 Problem Set Answer Key
Use the Coffee Cooling demonstration on Wolfram Alpha to write a short report on the questions that follow. http://demonstrations.wolfram.com/TheCoffeeCoolingProblem/
(Note that Wolfram’s free CDF player needs to be downloaded ahead of time in order to be able to run the demonstration.)
Question 1.
If you want your coffee to become drinkable as quickly as possible, should you add cream immediately after pouring the coffee or wait? Use results from the demonstration to support your claim.
Answer:
Answers will vary, but the results may surprise students. If you want to immediately cool the coffee, you should add cream. But if you are trying to reduce the temperature to 143°F (the temperature where it becomes drinkable according to the demonstration) as quickly as possible, you should wait to add the cream. For example, if you add cream to the first cup immediately and then wait 2 minutes (120 seconds) to add cream to the second cup, the second cup of reaches 143°F almost 30 seconds before the first cup does. Keeping the difference between the temperature of the coffee and the ambient temperature (the temperature of the surrounding air) larger for a longer interval of time causes the coffee to cool more quickly.
Question 2.
If you want your coffee to stay warm longer, should you add cream immediately after pouring the coffee or wait?
Use results from the demonstration to support your claim.
Answer:
It turns out that if you want the coffee to stay hot as long as possible, then you should add the cream immediately. This will initially cool the temperature but then the rate at which the coffee is cooling will be less than the rate would be without the cream. Once the difference between the temperature of the coffee and the ambient temperature is smaller, the rate of cooling is slower, and the coffee stays warmer longer. For example, if you add cream immediately to one cup of coffee and wait 4 minutes (240 seconds) to add cream to the second cup, after 500 seconds the temperature of the first cup of coffee is 2.2°F greater than the temperature of the second cup.
Eureka Math Algebra 1 Module 3 Lesson 23 Exit Ticket Answer Key
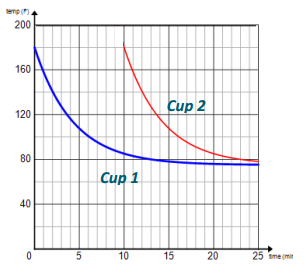
Shown below is the graph of Cup 1 from the exercise completed in class. For each scenario, sketch and label a graph of Cup 2 on the same coordinate plane.
Question 1.
Cup 2 is poured 10 minutes after Cup 1 (the pot of coffee is maintained at 180°F over the 10 minutes).
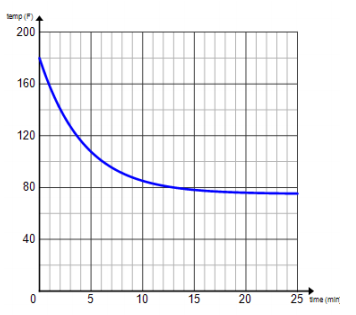
Answer:
Question 2.
Cup 2 is immediately taken outside where the temperature is 90°F.
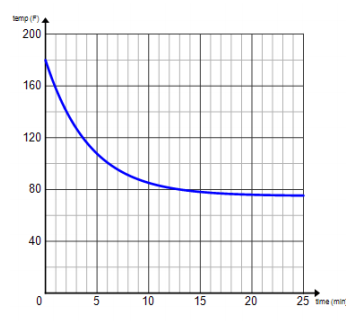
Answer: