Engage NY Eureka Math Algebra 1 Module 4 Lesson 21 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 21 Example Answer Key
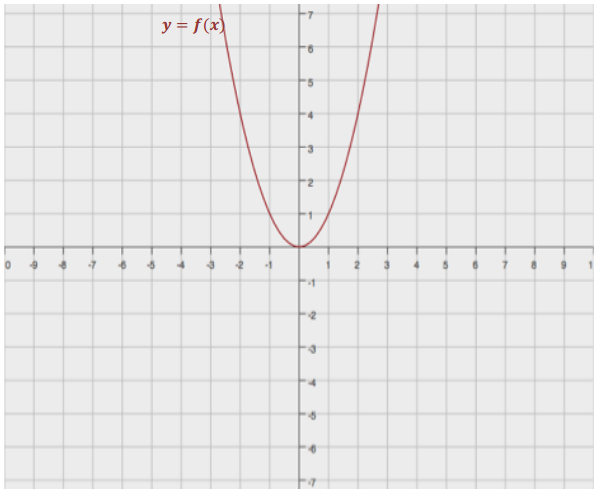
Example 1: Quadratic Expression Representing a Function
a. A quadratic function is defined by g(x) = 2x2 + 12x + 1. Write this in the completed – square (vertex) form and show all the steps.
Answer:
g(x) = 2x2 + 12x + 1
Step 1 = (2x2 + 12x) + 1 Gather variable terms.
Step 2 = 2(x2 + 6x) + 1 Factor out the GCF.
Step 3 = 2(x2 + 6x + 9) + 1 – 18 Complete the square and balance the equality.
Step 4 = 2(x + 3)2 – 17 Factor the perfect square.
g(x) = 2(x + 3)2 – 17
b. Where is the vertex of the graph of this function located?
Answer:
The vertex is at ( – 3, – 17).
c. Look at the completed – square form of the function. Can you name the parent function? How do you know?
Answer:
The parent function is f(x) = x2. The function is quadratic.
d. What transformations have been applied to the parent function to arrive at function g? Be specific.
Answer:
The parent function f(x) = x2 is translated 3 units to the left, stretched vertically by a factor of 2, and translated 17 units down.
e. How does the completed – square form relate to the quadratic parent function f(x) = x2?
Answer:
The completed – square form can be understood through a series of transformations of the quadratic parent function, f.
Example 2.
The graph of a quadratic function f(x) = x2 has been translated 3 units to the right, vertically stretched by a factor of 4, and moved 2 units up. Write the formula for the function that defines the transformed graph.
Answer:
g(x) = 4(x – 3)2 + 2
Eureka Math Algebra 1 Module 4 Lesson 21 Exercise Answer Key
Exercises
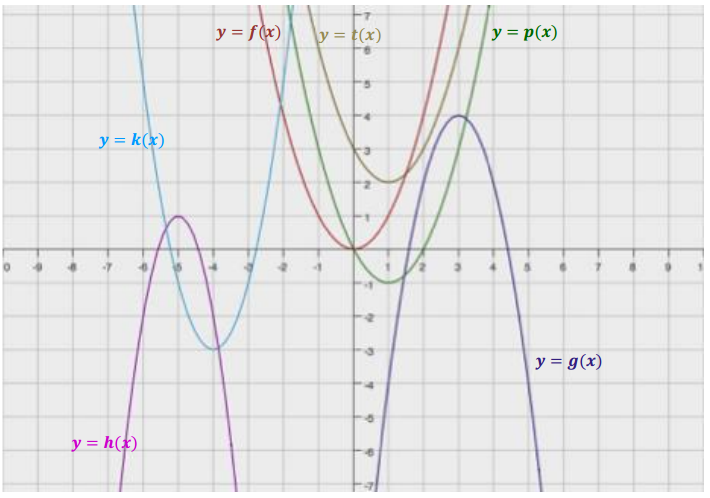
Exercise 1.
Without using a graphing calculator, sketch the graph of the following quadratic functions on the same coordinate plane, using transformations of the graph of the parent function f(x) = x2.
a. g(x) = – 2(x – 3)2 + 4
b. h(x) = – 3(x + 5)2 + 1
c. k(x) = 2(x + 4)2 – 3
d. p(x) = x2 – 2x
e. t(x) = x2 – 2x + 3
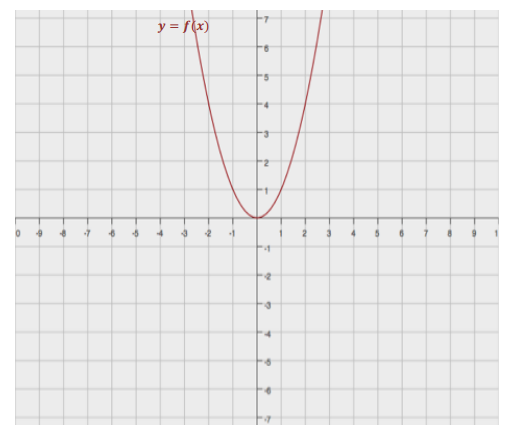
Answer:
Note: By completing the square, we have p(x) = (x – 1)2 – 1 and t(x) = (x – 1)2 + 2.
Exercise 2.
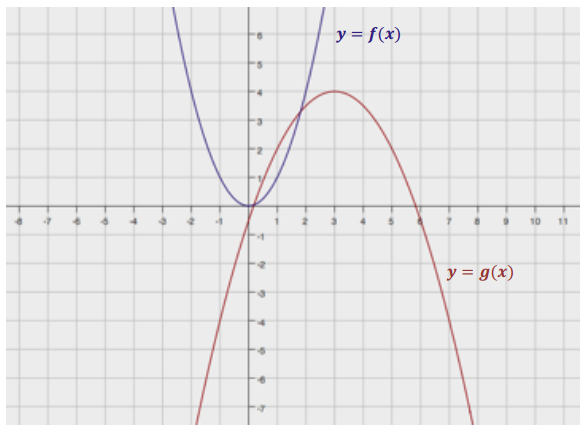
Write a formula for the function that defines the described transformations of the graph of the quadratic parent function f(x) = x2.
a. 3 units shift to the right
b. Vertical shrink by a factor of 0.5
c. Reflection across the x – axis
d. 4 units shift up
Then, graph both the parent and the transformed functions on the same coordinate plane.

Answer:
g(x) = – 0.5(x – 3)2 + 4
Exercise 3.
Describe the transformation of the quadratic parent function f(x) = x2 that results in the quadratic function g(x) = 2x2 + 4x + 1.
Answer:
First, rewrite g(x) into the completed – square form.
g(x) = 2x2 + 4x + 1
= (2x2 + 4x) + 1
= 2(x2 + 2x) + 1
= 2(x2 + 2x + 1) + 1 – 2
= 2(x2 + 2x + 1) – 1
g(x) = 2(x + 1)2 – 1
This means that the graph of f is translated 1 unit to the left, vertically stretched by a factor of 2, and translated 1 unit down.
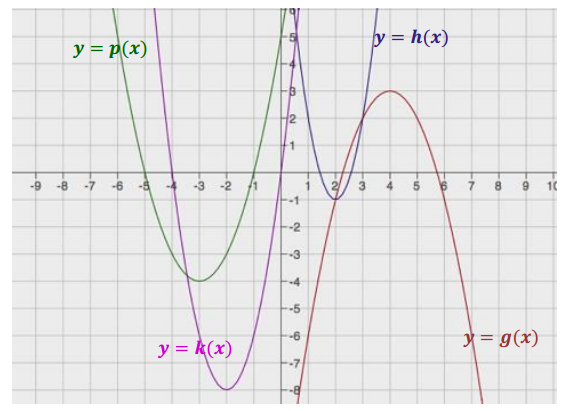
Exercise 4.
Sketch the graphs of the following functions based on the graph of the function f(x) = x2. If necessary, rewrite some of the functions in the vertex (completed – square) form. Label your graphs.
a. g(x) = – (x – 4)2 + 3
b. h(x) = 3(x – 2)2 – 1
c. k(x) = 2x2 + 8x
d. p(x) = x2 + 6x + 5
Answer:
c. k(x) = 2(x + 2)2 – 8
d. p(x) = (x + 3)2 – 4
Eureka Math Algebra 1 Module 4 Lesson 21 Problem Set Answer Key
Question 1.
Write the function g(x) = – 2x2 – 20x – 53 in completed – square form. Describe the transformations of the graph of the parent function f(x) = x2 that result in the graph of g.
Answer:
g(x) = – 2x2 – 20x – 53
= ( – 2x2 – 20x) – 53
= – 2(x2 + 10x) – 53
= – 2(x2 + 10x + 25) – 53 + 50
= – 2(x2 + 10x + 25) – 3
g(x) = – 2(x + 5)2 – 3
The graph of f is translated 5 units to the left, vertically stretched by a factor of 2, and translated 3 units down. The graph of f is facing up, while the graph of g is facing down because of the negative value of a.
Question 2.
Write the formula for the function whose graph is the graph of f(x) = x2 translated 6.25 units to the right, vertically stretched by a factor of 8, and translated 2.5 units up.
Answer:
g(x) = 8(x – 6.25)2 + 2.5
Question 3.
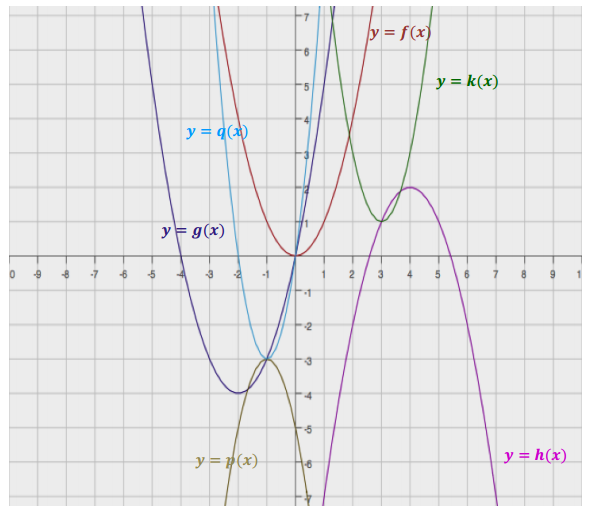
Without using a graphing calculator, sketch the graphs of the functions below based on transformations of the graph of the parent function f(x) = x2. Use your own graph paper, and label your graphs.
a. g(x) = (x + 2)2 – 4
b. h(x) = – (x – 4)2 + 2
c. k(x) = 2x2 – 12x + 19
d. p(x) = – 2x2 – 4x – 5
e. q(x) = 3x2 + 6x
Answer:
c. k(x) = 2(x – 3)2 + 1
d. p(x) = – 2(x + 1)2 – 3
e. q(x) = 3(x + 1)2 – 3
Eureka Math Algebra 1 Module 4 Lesson 21 Exit Ticket Answer Key
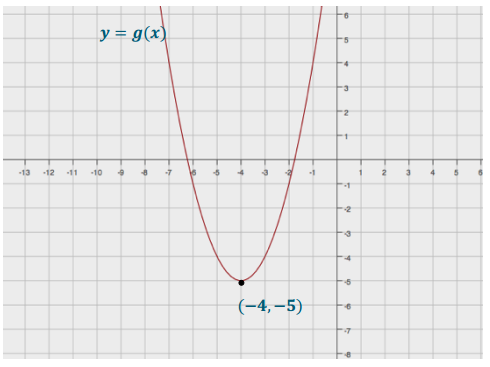
Question 1.
Describe in words the transformations of the graph of the parent function f(x) = x2 that would result in the graph of g(x) = (x + 4)2 – 5. Graph the equation y = g(x).

Answer:
The graph of g is a translation of the graph of f, 4 units to the left and 5 units down.