Engage NY Eureka Math Algebra 2 Module 3 Lesson 24 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 24 Opening Exercise Answer Key
Opening Exercise:
In Lesson 7, we modeled a population of bacteria that doubled every day by the function P(t) = 2t, where t was the time in days. We wanted to know the value of t when there were 10 bacteria. Since we did not know about logarithms at the time, we approximated the value of t numerically, and we found that P(t) = 10 when t ≈ 3.32.
Use your knowledge of logarithms to find an exact value for t when P(t) = 10, and then use your calculator to approximate that value to 4 decimal places.
Answer:
Since P(t) = 2t, we need to solve 2t = 10.
2t = 10
tlog(2) = log(10)
t = \(\frac{1}{\log (2)}\)
t ≈ 3. 3219
Thus, the population will reach 10 bacteria in approximately 3.3219 days.
Eureka Math Algebra 2 Module 3 Lesson 24 Exercise Answer Key
Exercises:
Exercise 1.
Fiona modeled her data from the bean-flipping experiment in Lesson 23 by the function f(t) = 1.263(1.357)t, and Gregor modeled his data with the function g(t) = 0.972(1.629)t.
a. Without doing any calculating, determine which student, Fiona or Gregor, accumulated 100 beans first. Explain how you know.
Answer:
Since the base of the exponentialfunction for Gre gors model, 1.629, is larger than the base of the exponential function for Fionas model, 1.357, Gregor’s model will grow more quickly than Fiona’s, and he will accumulate 100 beans before Fiona does.
b. Using Fiona’s model …
i. How many trials would be needed for her to accumulate 100 beans?
Answer:
We need to solve the equation f(t) = 100 for t.
1.263(1.357)t = 100
1.357t = \(\frac{100}{1.263}\)
t log(1.357) = log(\(\frac{100}{1.263}\))
t log(1.357) = log(100) – log(1.263)
t = \(\frac{2-\log (1.263)}{\log (1.357)}\)
t ≈ 14.32
So, it takes 15 trials for Fiona to accumulate 100 beans.
ii. How many trials would be needed for her to accumulate 1, 000 beans?
Answer:
We need to solve the equation f(t) = 1000 for t.
1. 263(1.357)t = 1000
1.357t = \(\frac{1000}{1.263}\)
t log(1.357) = log(\(\frac{1000}{1.263}\))
t log(1.357) = log(1000) – log(1.263)
t = \(\frac{3-\log (1.263)}{\log (1.357)}\)
t ≈ 21.86
So, it takes 22 trials for Fiona to accumulate 1000 beans.
c. Using Gregor’s model …
i. How many trials would be needed for him to accumulate 100 beans?
Answer:
We need to solve the equation g(t) = 100 for t.
0.972(1.629)t = 100
1.629t = \(\frac{100}{0.972}\)
t log(1.629) = log(\(\frac{100}{0.972}\))
t log(1.629) = log(100) – log(0.972)
t = \(\frac{2-\log (0.972)}{\log (1.629)}\)
t ≈ 9.50
So, it takes 10 trials for Gregor to accumulate 100 beans.
ii. How many trials would be needed for him to accumulate 1000 beans?
Answer:
We need to solve the equation g(t) = 1000 for t.
0.972(1.629))t = 1000
1.629t = \(\frac{1000}{0.972}\)
t log(1.629) = log(\(\frac{1000}{0.972}\))
t log(1.629) = log(1000) – log(0.972)
t = \(\frac{3-\log (0.972)}{\log (1.629)}\)
t ≈ 14.21
So, it takes 15 trials for Gregor to accumulate 1000 beans.
d. Was your prediction in part (a) correct? If not, what was the error in your reasoning?
Answer:
Responses will vary. Either students made the correct prediction, or they did not recognize that the base b determines the growth rate of the exponential function so the larger base 1.629 causes Gregor’s function to grow much more quickly than Fiona’s.
Exercise 2.
Fiona wants to know when her model f(t) = 1.263(1.357)t predicts accumulations of 500, 5,000, and 50,000 beans, but she wants to find a way to figure it out without doing the same calculation three times.
a. Let the positive number c represent the number of beans that Fiona wants to have. Then solve the equation
1.263(1.357)t = c for t.
Answer:
1.263(1.357)t = c
1. 357t = \(\frac{c}{1.263}\)
t log(1.357) = log (\(\frac{c}{1.263}\))
t log(1.357) = log(c) – log(1.263)
t = \(\frac{\log (c)-\log (1.263)}{\log (1.357)}\)
b. Your answer to part (a) can be written as a function M of the number of beans c, where c > 0. Explain what this function represents.
Answer:
The function M(c) = \(\frac{\log (c)-\log (1.263)}{\log (1.357)}\) calculates the number of trials it will take for Fiona to accumulate c beans.
c. When does Fiona’s model predict that she will accumulate …
i. 500 beans?
Answer:
M(500) = \(\frac{\log (500)-\log (1.263)}{\log (1.357)}\) ≈ 19.59
According to her model, it will take Fiona 20 trials to accumulate 500 beans.
ii. 5,000 beans?
Answer:
M(5000) = \(\frac{\log (5000)-\log (1.263)}{\log (1.357)}\) ≈ 27.14
According to her model, it will take Fiona 28 trials to accumulate 5000 beans.
iii. 50,000 beans?
Answer:
M(50000) = \(\frac{\log (50000)-\log (1.263)}{\log (1.357)}\) ≈ 34.68
According to her model, It will take Fiona 35 trials to accumulate 50000 beans.
Exercise 3.
Gregor states that the function g that he found to model his bean-flipping data can be written in the form
g(t) = 0.972(10log(1.629)t). Since log(1.629) ≈ 0.2119, he is using g(t) = 0. 972(100.2119t) as his new model.
a. Is Gregor correct? Is g(t) = 0.972(10log(1.629)t) an equivalent form of his original function? Use properties of exponents and logarithms to explain how you know.
Answer:
Yes, Gregor is correct. Since 10log(1.629) = 1.629, and 10log(1.629)t = (10log(1.629))t≈ 100.2119t, Gregor is right that g(t) = 0.972(100.2119t) is a reasonable model for his data.
b. Gregor also wants to find a function to help him to calculate the number of trials his function g predicts it should take to accumulate 500, 5,000, and 50,000 beans. Let the positive number c represent the number of beans that Gregor wants to have. Solve the equation 0.972(100.2119t) = c for t.
Answer:
0.972(100.2119t) = c
100.2119t = \(\frac{c}{0.972}\)
0.2119t = log (\(\frac{c}{0.972}\))
t = \(\frac{\log (c)-\log (0.972)}{0.2119}\)
c. Your answer to part (b) can be written as a function N of the number of beans C, where c > 0. Explain what this function represents.
Answer:
The function N(c) = \(\frac{\log (c)-\log (0.972)}{0.2119}\) calculates the number of trials it will take for Gregor to accumulate c beans.
d. When does Gregor’s model predict that he will accumulate …
i. 500 beans?
Answer:
N(500) = \(\frac{\log (500)-\log (0.972)}{0.2119}\) ≈ 12.80
According to his model, it will take Gregor 13 trials to accumulate 500 beans.
ii. 5,000 beans?
Answer:
N(5000) = \(\frac{\log (5000)-\log (0.972)}{0.2119}\) ≈ 17.51
According to his model, it will take Gregor 18 trials to accumulate 5,000 beans.
iii. 50,000 beans?
Answer:
N(50000) = \(\frac{\log (50000)-\log (0.972)}{0.2119}\) ≈ 22.23
According to his model, ¡t will take Gregor 23 trials to accumulate 50,000 beans.
Exercise 4.
Helena and Karl each change the rules for the bean experiment. Helena started with four beans in her cup and added one bean for each that landed marked-side up for each trial. Karl started with one bean in his cup but added two beans for each that landed marked-side up for each trial.
a. Helena modeled her data by the function h(t) = 4.127(1.468t). Explain why her values of a = 4.127 and b = 1.468 are reasonable.
Answer:
Since Helena starts with four beans, we should expect that a ≈ 4, so a value a = 4.127 is reasonable. Because she is using the same rule for adding beans fo the cup as we did in Lesson 23, we should expect that b ≈ 1.5. Thus, her value of b = 1.468 is reasonable.
b. Karl modeled his data by the function k(t) = 0.897(1.992t). Explain why his values of a = 0.897 and b = 1.992 are reasonable.
Answer:
Since Karl starts with one bean, we should expect that a ≈ 1, so a value a = 0.897 is reasonable. Because Karl adds two beans to the cup for each that lands marked-side up, we should expect that the number of beans roughly doubles with each trial. That is, we should expect b ≈ 2. Thus, his value of b = 1.992 is reasonable.
c. At what value of t do karl and Helena have the same number of beans?
Answer:
we need to solve the equation h(t) = k(t) for t.
4.127(1.468t) = 0.897(1.992t)
log(4.127(1.468t) = log(0.897(1.992t))
log(4.127) + log(1.468t) = log(0.897) + log(1.992t)
log(4.127) + t log(1.468) = log(0.897) + t log(1.992)
t log(1.992) – t log(1.468) = log(4.127) – log(0.897)
t(log(\(\frac{1.992}{1.468}\))) = log(\(\frac{4.127}{0.897}\))
t(0.13256) ≈ 0.66284
t ≈ 5.0003
d. Use a graphing utility to graph y = h(t) and y = k(t) for 0 < t < 10.
Answer:
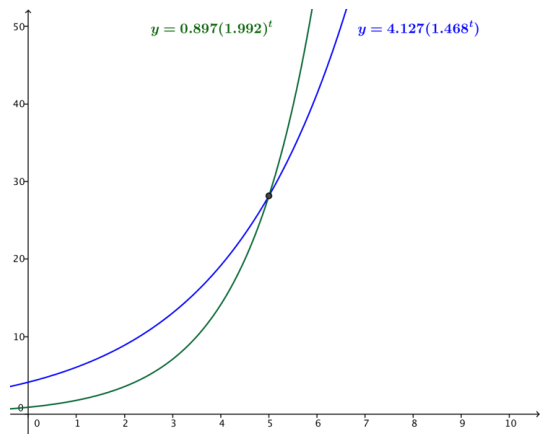
e. Explain the meaning of the intersection point of the two curves y = h(t) and y = k(t) in the context of this problem.
Answer:
The two curves intersect at the t-value where Helena and Karl have the same number of beans. The y-value indicates the number of beans they both have after five trials.
f. Which student reaches 20 beans first? Does the reasoning used in deciding whether Gregor or Fiona would get 100 beans first hold true here? Why or why not?
Answer:
Helena reaches 20 beans first. Although the function modeling Helena’s beans has a smaller base, Karl’s does not catch up to Helena until after five trials. After five trials, Karl’s will always be greater, and he will reach 100 beans first. The logic we applied to comparing Gregor’s model and Fiona’s model does not apply here because Helena and Karl do not start with the same initial number of beans.
For the following functions f and g, solve the equation f(x) = g(x). Express your solutions in terms of logarithms.
Exercise 5.
f(x) = 10(3.7)x + 1, g(x) = 5(7.4)x
Answer:
10(3.7)x + 1 = 5(7.4)x
2(3.7)x + 1 = 7.4x
log(2) + log(3.7x + 1) = log(7.4x)
log(2) + (x + 1) log(3.7) = x log(7.4)
log(2) + x log(3.7) + log(3.7) = x log(7.4)
log(2) + log(3.7) = x(log(7.4) – log(3.7))
log(7.4) = xlog(\(\frac{7.4}{3.7}\))
log(7.4) = xlog(2)
x = \(\frac{\log (7.4)}{\log (2)}\)
Exercise 6.
f(x) = 135(5)3x + 1, g(x) = 75(3)4 – 3x
Answer:
135(5)3x + 1 = 75(3)4 – 3x
9(5)3x + 1 = 5(3)4 – 3x
log(9) + (3x + 1)log(5) = log(5) + (4 – 3x)log(3)
2 log(3) + 3x log(5) + log(5) = log(5) + 4 log(3) – 3x log(3)
3x(log(5) + log(3)) = 4 log(3) – 2 log(3)
3x l(15) = 2 log(3)
x = \(\frac{2 \log (3)}{3 \log (15)}\)
Exercise 7.
f(x) = \(100^{x^{3}+x^{2}-4 x}\), g(x) = \(10^{2 x^{2}-6 x}\)
Answer:
\(100^{x^{3}+x^{2}-4 x}\) = \(10^{2 x^{2}-6 x}\)
\(\left(10^{2}\right)^{x^{3}+x^{2}-4 x}\) = \(10^{2 x^{2}-6 x}\)
2(x3 + x2 – 4x) = 2x2 – 6x
x3 + x2 – 4x = x2 – 3x
x3 – x = 0
x(x2 – 1) = 0
x(x + 1)(x – 1) = 0
x = 0, x = -1, or x = 1
Exercise 8.
f(x) = 48(\(4^{x^{2}+3 x}\)), g(x) = \(8^{x^{2}+4 x+4}\)
Answer:
48(\(4^{x^{2}+3 x}\)) = 3(\(8^{x^{2}+4 x+4}\))
16(\(4^{x^{2}+3 x}\)) = \(8^{x^{2}+4 x+4}\)
\(2^{4}\left(\left(2^{2}\right)^{x^{2}+3 x}\right)\) = \(\left(2^{3}\right)^{x^{2}+4 x+4}\)
\(2^{2 x^{2}+6 x+4}=2^{3 x^{2}+12 x+12}\)
2x2 + 6x + 4 = 3x2 + 12x + 12
x2 + 6x + 8 = 0
(x + 4)(x + 2) = 0
x = -4 or x = -2
Exercise 9.
f(x) = \(e^{\sin ^{2}(x)}\), g(x) = \(e^{\cos ^{2}(x)}\)
Answer:
\(e^{\sin ^{2}(x)}\) = \(e^{\cos ^{2}(x)}\)
sin2(x) = cos2(x)
sin(x) = cos(x) or sin(x) = -cos(x)
x = \(\frac{\pi}{4}\) + kπ or x = \(\frac{3 \pi}{4}\) + kπ for all integers k
Exercise 10.
f(x) = (0.49)cos(x)+sin(x), g(x) = (0.7)2 sin(x)
Answer:
(0.49)cos(x)+sin(x) = (0.7)2 sin(x)
log((0.49)cos(x)+sin(x)) = log(0.7)2 sin(x)
(cos(x) + sin(x))log(0.49) = 2 sin(x)log(0.7)
(cos(x) + sin(x))log(0.72) = 2 sin(x) log(0.7)
2(cos(x) + sin(x))log(0.7) = 2 sin(x) log(0.7)
2 cos(x) + 2 sin(x) = 2 sin(x)
cos(x) = 0
x = \(\frac{\pi}{2}\) + kπ for all integers k
Eureka Math Algebra 2 Module 3 Lesson 24 Problem Set Answer Key
Question 1.
Solve the following equations.
a. 2 . 5x + 3 = 6250
Answer:
5x + 3 = 3125
5x + 3 = 55
x + 3 = 5
x = 2
b. 3 . 62x = 648
Answer:
62x = 216
62x = 63
2x = 3
x = \(\frac{3}{2}\)
c. 5 . 23x + 5 = 10240
Answer:
23x + 5 = 2048
23x + 5 = 211
3x + 5 = 11
3x = 6
x = 2
d. 43x – 1 = 32
Answer:
43x – 1 = 25
22 . (3x – 1) = 25
6x – 2 = 5
6x = 7
x = \(\frac{7}{6}\)
e. 3 . 25x = 216
Answer:
25x = 72
5x . ln(2) = ln(72)
x = \(\frac{\ln (72)}{5 \cdot \ln (2)}\)
x ≈ 1.234
Note:
Students can also use the common logarithm to find the solution.
f. 5 . 113x = 120
Answer:
113x = 24
3x . ln(11) = ln(24)
x = \(\frac{\ln (24)}{3 \cdot \ln (11)}\)
x ≈ 0.442
Note:
Students can also use the common logarithm to find the solution.
g. 7 . 9x = 5405
Answer:
9x = \(\frac{5405}{7}\)
x . ln(9) = ln(\(\frac{5405}{7}\))
x = \(\frac{\ln \left(\frac{5405}{7}\right)}{\ln (9)}\)
x ≈ 3.026
Note:
Students can also use the common logarithm to find the solution.
h. √3 . 3x = 9
Answer:
Solution using poperties of exponents:
3\(\frac{1}{2}\) . 33x = 32
3\(\frac{1}{2}\) + 3x 32
\(\frac{1}{2}\) + 3x = 2
x = \(\frac{1}{2}\)
i. log(400) . 85x = log(160000)
Answer:
85x = \(\frac{\log (160000)}{\log (400)}\)
85x = 2
85x = 8\(\frac{1}{3}\)
5x = \(\frac{1}{3}\)
x = \(\frac{1}{15}\)
Question 2.
Lucy came up with the model f(t) = 0.701(1.382)t for the first bean activity. When does her model predict that she would have 1,000 beans?
Answer:
1000 = 0.701(1.382)t
log(1000) = log(0.701) + t log(1.382)
t = \(\frac{\log (1000)-\log (0.701)}{\log (1.382)}\)
t ≈ 22.45
Lucy’s model predicts that it will take 23 trials to have over 1000 beans.
Question 3.
Jack came up with the model g(t) = 1.033(1.707)t for the first bean activity. When does his model predict that he would have 50,000 beans?
Answer:
50000 = 1.033(1.707)t
log(50000) = log(1.033) + t log(1.707)
t = \(\frac{\log (50000)-\log (1.033)}{\log (1.707)}\)
t ≈ 20.17
Jack’s model predicts that it will take 21 trials to have over 50,000 beans.
Question 4.
If instead of beans in the first bean activity you were using fair pennies, when would you expect to have $1, 000,000?
Answer:
One million dollars is 108 pennies. Using fair pennies, we can model the situation by f(t) = 5t.
108 = 1.5t
8 = tlog(1.5)
t = \(\frac{8}{\log (1.5)}\)
t ≈ 45.43
We should expect it to take 46 trials to reach more than $1 million using fair pennies.
Question 5.
Let f(x) = 2 . 3x and g(x) = 3 . 2x.
a. Which function is growing faster as x increases? Why?
Answer:
The function f is growing faster due to its larger base, even though g(0) > f(0).
b. When will f(x) = g(x)?
Answer:
f(x) = g(x)
2 3x. = 3 . 2x.
ln(2 . 3x.) = ln(3 . 2x.)
ln(2) + x ln(3) = ln(3) + x ln(2)
xln(3) – xln(2) = ln(3) – ln(2)
x ln(\(\frac{3}{2}\)) = ln(\(\frac{3}{2}\))
Note:
Students can also use the common logarithm to find the solution.
Question 6.
The growth of a population of E. coli bacteria can be modeled by the function E(t) = 500(11.547)t, and the growth of a population of Salmonella bacteria can be modeled by the function S(t) = 4000(3.668)t, where t measures time in hours.
a. Graph these two functions on the same set of axes. At which value of t does it appear that the graphs intersect?
Answer:
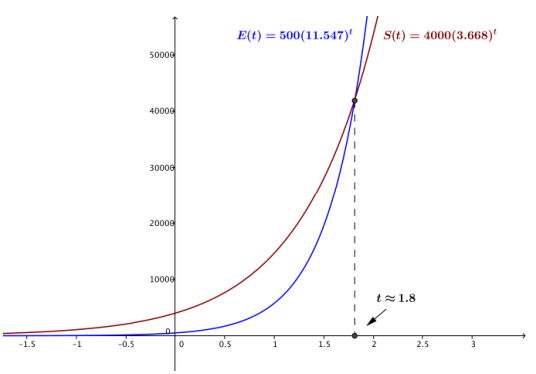
From the graph, it appears that the two curves intersect at t ≈ 1.8
b. Use properties of logarithms to find the time t when these two populations are the same size. Give your answer to two decimal places.
Answer:
E(t) = S(t)
500(11.547)t = 4000(3.668)t
11.547t = 8(3.668)t
t log(11.547) = log(8) + t log(3.668)
t(log(11.547) – log(3. 668)) = log(8)
t = \(\frac{\log (8)}{\log (11.547)-\log (3.668)}\)
t ≈ 1.81 329.
It takes approximately 1.81 hours for the populations to be the same size.
Question 7.
Chain emails contain a message suggesting you will have bad luck if you do not forward the email to others. Suppose a student started a chain email by sending the message to 10 friends and asking those friends to each send the same email to 3 more friends exactly one day after receiving the message.
Assuming that everyone that gets the email participates in the chain, we can model the number of people who receive the email on the th day by the formula E(n) = 10(3n), where n = 0 indicates the day the original email was sent.
a. If we assume the population of the United States is 318 million people and everyone who receives the email sends it to 3 people who have not received it previously, how many days until there are as many emails being sent out as there are people ¡n the United States?
Answer:
318(106) = 10 . 3n
318(105) = 3n
log(318) + log(105) = n . log(3)
log(318) + 5 = n . log(3)
n = \(\frac{5+\log (318)}{\log (3)}\)
n ≈ 15.72
so by 16th day, more than 318 million emails are being sent out.
b. The population of earth is approximately 7.1 billion people. On what day will 7.1 billion emails be sent out?
Answer:
7.1(109) = 10(3n)
7.1(108) = 3n
log(7.1(108)) = n . log(3)
n = \(\frac{8+\log (7.1)}{\log (3)}\)
n ≈ 18.5514
By the 19th day, more than 7.1 billion emails will be sent.
Question 8.
Solve the following exponential equations.
a. 10(3x – 5) = 7x
Answer:
103x – 5 = 7x
3x – 5 = x log(7)
x(3 – log(7)) = 5
x = \(\frac{5}{3-\log (7)}\)
b. 3\(\frac{x}{5}\) = 24x – 2
Answer:
\(\frac{x}{5}\)log(3) = (4x – 2) log(2)
4xlog(2) – x\(\frac{\log (3)}{5}\) = 2 log(2)
x(4 log(2) – \(\frac{\log (3)}{5}\)) = 2 log|(2)
x = \(\frac{2 \log (2)}{4 \log (2)-\frac{\log (3)}{5}}\)
c. 10x2 + 5 = 100x2 + x + 2
Answer:
10x2 + 5 = 100x2 + x + 2
x2 + 5 = (2x2 + x + 2)log(100)
x2 + 5 = 4x2 + 2x + 4
3x2 + 2x – 1 = 0
(3x – 1)(x + 1) = 0
x = \(\frac{1}{3}\) or x = -1
d. \(4^{x^{2}-3 x+4}=2^{5 x-4}\)
Answer:
\(4^{x^{2}-3 x+4}=2^{5 x-4}\)
(x2 – 3x + 4)log2(4) = (5x – 4)log2(2)
2(x2 – 3x + 4) = 5x – 4
2x2 – 6x + 8 = 5x – 4
2x2 – 11x + 12 = 0
(2x – 3)(x – 4) = 0
x = \(\frac{3}{2}\) or x = 4
Question 9.
Solve the following exponential equations.
a. (2x)x = 8x
Answer:
x2log2(2) = x log2(8)
x2 = 3x
x2 – 3x = 0
x(x – 3) = 0
x = 0 or x = 3
b. (3x)x = 12
Answer:
3x2 = 12
x2 log(3) = log(12)
x2 = \(\frac{\log (12)}{\log (3)}\)
x = \(\sqrt{\frac{\log (12)}{\log (3)}}\) or –\(\sqrt{\frac{\log (12)}{\log (3)}}\)
Question 10.
Solve the following exponential equations.
a. 10x + 1 + 10x – 1 = 1287
Answer:
10x + 1 – 10x – 1 = 1287
100(10x – 1) – 10x – 1 = 1287
10x – 1(100 – 1) = 1287
99(10x – 1) = 1287
10x – 1 = 13
x – 1 = log(13)
x = log(13) + 1
b. 2(4x)+ 4x + 1 = 342
Answer:
2(4x) + 4x + 1 = 342
2(4x) + 4(4x) = 342
6(4x) = 342
4x = 57
x = log4(57) = \( = [latex]\frac{1}{2}\)log2(57)
Question 11.
Solve the following exponential equations.
a. (10x)2 – 3(10x) + 2 = 0
Hint: Let u = 10x, and solve for u before solving for x.
Answer:
Let u = 10x. Then
u2 – 3u + 2 = 0
(u – 2)(u – 1) = 0
u = 2 or u = 1
If u = 2, we have 2 = 10x, and then x = log(2).
If u = 1, we have 1 = 10x, and then x = 0.
Thus, the two solutions to this equation are 0 and log(2).
b. (2x)2 3(x) – 4 = 0
Answer:
Let u = 2x.
u2 – 3u – 4 = 0
(u – 4 )(u + 1) = 0
u = 4 or u = -1
If u = 4, we have 2x = 4, and then x = 2.
If u = —1, we have 2x = -1, which has no solution.
Thus, the only solution to this equation is 2.
c. 3(ex)2 – 8(ex) – 3 = 0
Answer:
Let u = ex
3u2 – 8u – 3 = 0
(u – 3)(3u + 1) = 0
u = 3 or u = –\(\frac{1}{3}\)
If u = 3, we have ex = 3, and then x = ln(3).
If u =-\(\frac{1}{3}\), we have ex = –\(\frac{1}{3}\), which has no solution ex > 0 for every value of x.
Thus, the only solution to this equation is ln(3).
d. 4x + 7(2x) + 12 = 0
Answer:
Let u = 2x
(2x)2 + 7(2x) + 12 = 0
u2 + 7u + 12 = 0
(u + 3)(u + 4) = 0
u = -3 or -4
But 2x > 0 for every value of x, thus there are no solutions to this equation.
e. (10x)2 – 2(10x) – 1 = 0
Answer:
Let u = 101x
u2 – 2u – 1 = 0
u = 1 + √2 or u = 1 – √2
If u = 1 + √2, we have 10x = 1 + √2, and then x = log(1 + √2)
If u = 1 – √2, we have 10x = 1 – √2, which has no solution 1 – √2 < 0
Thus, the only solution to this equation is log(1 + √2).
Question 12.
Solve the following systems of equations.
a. 2x + 2y = 8
42x + y = 1
Answer:
2x + 2y = 23
42x + y = 40
x + 2y = 3
2x + y = 0
x + 2y = 3
4x + 2y = 0
y = 2
x = -1
b. 22x + y – 1 = 32
(22)x – 2y = 2
Answer:
22x + y – 1 = 25
4x – 2y = 21
2x + y – 1 = 5
2(x – 2y) = 1
2x + y = 6
2x – 4y = 1
y = 1
x = \(\frac{5}{2}\)
c. 23x = 82y + 1
92y = 33x – 9
Answer:
23x = 82y + 1
(32)2y = 33x – 9
3x = 3(2y + 1)
2(2y) = (3x – 9)
3x – 6y = 3
3x – 4y = 9
y = 3
x = 7
Question 13.
Because f(x) = logb(x) is an increasing function, we know that if p < q, then logb(p) < logb(q). Thus, if we take logarithms of both sides of an inequality, then the inequality is preserved. Use this property to solve the following inequalities.
a. 4x > \(\frac{5}{3}\)
Answer:
4x > \(\frac{5}{3}\)
log(4x) > log(\(\frac{5}{3}\))
x log(4) > log(5) – log(3)
x > \(\frac{\log (5)-\log (3)}{\log (4)}\)
b. (\(\frac{2}{7}\))x > 9
Answer:
(\(\frac{2}{7}\))x > 9
xlog((\(\frac{2}{7}\)) > log(9)
But remember that log(\(\frac{2}{7}\)) < 0, so we need to divide by a negative number. we then have x < \(\frac{\log (9)}{\log (2)-\log (7)}\)
c. 4x > 8x – 1
Answer:
(22)x > (23)x – 1
22x > 23x – 3
2x > 3x – 3
3 > x
d. 3x + 2 > 53 – 2x
Answer:
3x + 2 > 53 – 2x
(x + 2)log(3) > (3 – 2x)log(5)
2x log(5) + x log(3) > 3 log(5) – 2 log(3)
x > \(\frac{3 \log (5)-2 \log (3)}{2 \log (5)+\log (3)}\)
x > \(
e. [latex]\frac{3}{4}\)x > \(\frac{4}{3}\)x + 1
Answer:
\(\frac{3}{4}\)x > \(\frac{4}{3}\)x + 1
x log(\(\frac{3}{4}\) > (x + 1)log(\(\frac{4}{3}\))
x(log\(\frac{3}{4}\)) – log(\(\frac{4}{3}\))) > log(\(\frac{4}{3}\))
But, log(log\(\frac{3}{4}\)) = -log(log\(\frac{4}{3}\)), we have
x(-log(log\(\frac{4}{3}\)) – log((log\(\frac{4}{3}\))) > log(log\(\frac{4}{3}\))
x(-2log(\(\frac{4}{3}\))) > log(\(\frac{4}{3}\))
But, -2log(\(\frac{4}{3}\)) < 0, so we need to divide by a negative number, so we have
x < \(\frac{\log \left(\frac{4}{3}\right)}{-2 \log \left(\frac{4}{3}\right)}\)
x < –\(\frac{1}{2}\)
Eureka Math Algebra 2 Module 3 Lesson 24 Exit Ticket Answer Key
Question 1.
Consider the functions f(x) = 2x + 6 and g(x) = 52x
a. Use properties of logarithms to solve the equation f(x) = g(x). Give your answer as a logarithmic expression, and approximate it to two decimal places.
Answer:
2x + 6 = 52x
(x + 6)log(2) = 2xlog(5)
2xlog(5) – x log(2) = 6 log(2)
x = \(\frac{6 \log (2)}{2 \log (5)-\log (2)}\)
x = \(\frac{\log (64)}{\log (25)-\log (2)}\)
x = \(\frac{\log (64)}{\log \left(\frac{25}{2}\right)}\)
x ≈ 1.65
Any of the final three forms are acceptable, and other correct forms using logarithms with other bases (such as base 2) are possible.
b. Verify your answer by graphing the functions y = f(x) and y = g(x) in the same window on a calculator, and sketch your graphs below. Explain how the graph validates your solution to part (a).
Answer:
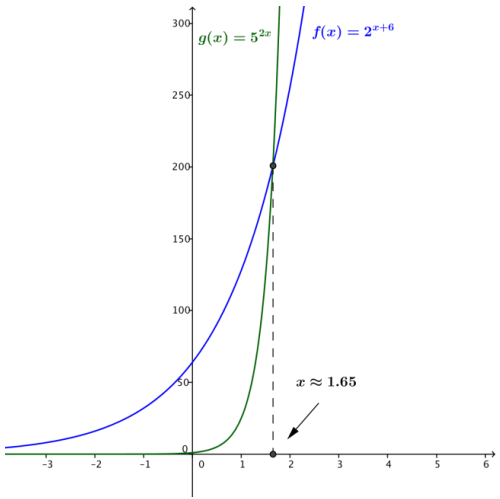
Because the graphs of y = f(x) and y = g(x) intersect when x ≈ 1.65, we know that the equation f(x) = g(x) has a solution at approximately x = 1.65.