Engage NY Eureka Math Algebra 2 Module 3 Lesson 5 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 5 Exercise Answer Key
Exercise 1.
a. Write the following finite decimals as fractions (you do not need to reduce to lowest terms).
1, 1.4, 1.41, 1.414, 1.4142, 1.41421
Answer:
1.4 = \(\frac{14}{10}\)
1.41 = \(\frac{141}{100}\)
1.414 = \(\frac{1414}{1000}\)
1.4142 = \(\frac{14142}{10000}\)
1.41421 = \(\frac{141421}{100000}\)
b. Write 21.4, 21.41 21.414, and 21.4142 in radical form.
Answer:
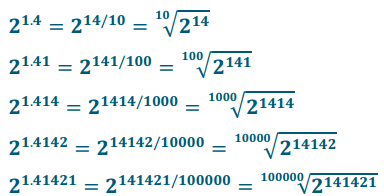
c. Use a calculator to compute decimal approximations of the radical expressions you found in part (b) to 5 decimal places. For each approximation, underline the digits that are also In the previous approximation, starting with 2.00000 done for you below. What do you notice?
21 = 2 = 2.00000
Answer:
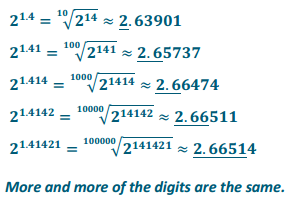
Exercise 2:
a. Write six terms of a sequence that a calculator can use to approximate 2π.
(Hint: π = 3.14159…)
Answer:
{23, 23.1, 23.14, 23.141, 23.1415, 23.14159, ……}
b. Compute 23.14 and 2π on your calculator. In which digit do they start to differ?
Answer:
23.14 = \(\sqrt[100]{2^{314}}\) ≈ 8.81524 ≈ 8.82497
They start to differ in the hundredths place.
c. How could you improve the accuracy of your estimate of 2π?
Answer:
Include more digits of the decimal approximation of π in the exponent.
Eureka Math Algebra 2 Module 3 Lesson 5 Problem Set Answer Key
Question 1.
Is it possible for a number to be both rational and irrational?
Answer:
No. Either the number can be written as \(\frac{p}{q}\) for integers p and q or it cannot. If it can, the number is rational. If it cannot, the number is irrational.
Question 2.
Use properties of exponents to rewrite the following expressions as a number or an exponential expression with only one exponent.
a. \(\left(2^{\sqrt{3}}\right)^{\sqrt{3}}\)
Answer:
8
b. \(\left(\sqrt{2}^{\sqrt{2}}\right)^{\sqrt{2}}\)
Answer:
2
c. \(\left(3^{1+\sqrt{5}}\right)^{1-\sqrt{5}}\)
Answer:
\(\frac{1}{81}\)
d. \(3^{\frac{1+\sqrt{5}}{2}} \cdot 3^{\frac{1-\sqrt{5}}{2}}\)
Answer:
3
e.
\(3^{\frac{1+\sqrt{5}}{2}} \div 3^{\frac{1-\sqrt{5}}{2}}\)
Answer:
\(3^{\sqrt{5}}\)
f. \(3^{2 \cos ^{2}(x)} \cdot 3^{2 \sin ^{2}(x)}\)
Answer:
9
Question 3.
a. Between what two integer powers of 2 does 2 lie?
Answer:
22 < \(2^{\sqrt{5}}\) < 23
b. Between what two integer powers of 3 does 3” lie?
Answer:
33 < \(3^{\sqrt{10}}\) < 34
c. Between what two integer powers of 5 does 5’ lie?
Answer:
51 < \(5^{\sqrt{3}}\) < 52
Question 4.
Use the process outlined in the lesson to approximate the number \(2^{\sqrt{5}}\). Use the approximation √5 ≈ 2.23606798.
a. Find a sequence of five intervals that contain √5 whose endpoints get successively closer to √5.
Answer:
2 < √5 < 3
2.2 < √5 < 2.3
2.23 < √5 < 2.24
2.236 < √5 < 2.237
2.2360 < √5 < 2.2361
b. Find a sequence of five intervals that contain \(2^{\sqrt{5}}\) whose endpoints get successively closer to \(2^{\sqrt{5}}\). Write your intervals in the form 2r < \(2^{\sqrt{5}}\) < 2s for rational numbers r and s.
Answer:
22 <\(2^{\sqrt{5}}\) < 23
22.2 <\(2^{\sqrt{5}}\) < 22.3
22.23 <\(2^{\sqrt{5}}\) < 22.24
22.236 < \(2^{\sqrt{5}}\) < 22.237
22.2360 < \(2^{\sqrt{5}}\) < 22.2361
c. Use your calculator to find approximations to four decimal places of the endpoints of the intervals in part (b).
Answer:
4.0000 < \(2^{\sqrt{5}}\) < 8.0000
4.5948 < \(2^{\sqrt{5}}\) < 4.9246
4.6913 < \(2^{\sqrt{5}}\) < 4.7240
4.7109 < \(2^{\sqrt{5}}\) < 4.7142
4.7109 < \(2^{\sqrt{5}}\) < 4.7112
d. Based on your work in part (c), what is your best estimate of the value of 2?
Answer:
\(2^{\sqrt{5}}\) ≈ 4.711
e. Can we tell if 2 is rational or irrational? Why or why not?
Answer:
No. We do not have enough information to determine whether 2 has a repeated pattern in its decimal representation or not.
Question 5.
Use the process outlined in the lesson to approximate the number \(3^{\sqrt{10}}\). Use the approximation √10 ≈ 3.162 277 7.
a. Find a sequence of five intervals that contain \(3^{\sqrt{10}}\) whose endpoints get successively closer to \(3^{\sqrt{10}}\). Write your intervals in the form 3r < \(3^{\sqrt{10}}\) < 3s for rational numbers r and s.
Answer:
33 < \(3^{\sqrt{10}}\) < 34
33.1 < \(3^{\sqrt{10}}\) < 33.2
33.16 < \(3^{\sqrt{10}}\) < 33.17
33.162 < \(3^{\sqrt{10}}\) < 33.163
33.1622 < \(3^{\sqrt{10}}\) < 33.1623
b. Use your calculator to find approximations to four decimal places of the endpoints of the intervals in part (a).
Answer:
9.0000 < \(3^{\sqrt{10}}\) < 81.0000
30.1353 < \(3^{\sqrt{10}}\) < 33.6347
32.1887 < \(3^{\sqrt{10}}\) < 32. 5443
32.2595 < \(3^{\sqrt{10}}\) < 32.2949
32.2666 < \(3^{\sqrt{10}}\) < 32.2701
c. Based on your work in part (b), what is your best estimate of the value of \(3^{\sqrt{10}}\)?
Answer:
\(3^{\sqrt{10}}\) ≈ 32.27
Question 6.
Use the process outlined in the lesson to approximate the number \(5^{\sqrt{7}}\). Use the approximation √7 ≈ 2.645 751 31.
a. Find a sequence of seven intervals that contain \(5^{\sqrt{7}}\) whose endpoints get successively closer to \(5^{\sqrt{7}}\). Write your intervals in the form 5r < \(5^{\sqrt{7}}\) < 5s for rational numbers r and s.
Answer:
52 < \(5^{\sqrt{7}}\) < 53
52.6 < \(5^{\sqrt{7}}\) < 52.7
52.64 < \(5^{\sqrt{7}}\) < 52.65
52.645 < \(5^{\sqrt{7}}\) < 52.646
52.6457 < \(5^{\sqrt{7}}\) < 52.6458
52.64575 < \(5^{\sqrt{7}}\) < 52.64576
52.645751 < \(5^{\sqrt{7}}\) < 52.645752
b. Use your calculator to find approximations to four decimal places of the endpoints of the intervals in part (a).
Answer:
25.0000 < \(5^{\sqrt{7}}\) < 125.0000
65.6632 < \(5^{\sqrt{7}}\) < 77.1292
70.0295 < \(5^{\sqrt{7}}\) < 71.1657
70.5953 < \(5^{\sqrt{7}}\) < 70.7090
70.6749 < \(5^{\sqrt{7}}\) < 70.6862
70.6805 <\(5^{\sqrt{7}}\) < 70.6817
70.6807 <\(5^{\sqrt{7}}\) < 70. 6808
c. Based on your work in part (b), what is your best estimate of the value of 5?
Answer:
\(5^{\sqrt{7}}\) ≈ 70.681
Question 7.
A rational number raised to a rational power can either be rational or irrational. For example, \(4^{\frac{1}{2}}\) is rational because \(4^{\frac{1}{2}}\) = 2, and \(2^{\frac{1}{4}}\) is irrational because \(2^{\frac{1}{4}}\) = \(\sqrt[4]{2}\). In this problem, you will investigate the possibilities for an irrational number raised to an irrational power.
a. Evaluate \((\sqrt{2})^{(\sqrt{2})^{\sqrt{2}}}\).
Answer:
\((\sqrt{2})^{(\sqrt{2})^{\sqrt{2}}}\) = \((\sqrt{2})^{\sqrt{2} \cdot \sqrt{2}}\) = (√2)2 = 2
b. Can the value of an irrational number raised to an irrational power ever be rational?
Answer:
Yes. For instance, in part (a) above, √2 is irrational, and the number \(\sqrt{2}^{\sqrt{2}}\) is either irrational or rational. If \(\sqrt{2}^{\sqrt{2}}\) is rational, then this is an example of an irrational number raised to an irrational power that is rational. Otherwise, \(\sqrt{2}^{\sqrt{2}}\) is irrational, and part (a) is an example of an irrational number raised to an irrational power that is rational.
Eureka Math Algebra 2 Module 3 Lesson 5 Exit Ticket Answer Key
Question 1.
Use the process outlined in the lesson to approximate the number \(2^{\sqrt{3}}\). Use the approximation √3 ≈ 1. 732 050 8.
a. Find a sequence of five intervals that contain √3 whose endpoints get successively closer to √3.
Answer:
1 < √3 < 2
1.7 < √3 < 1.8
1.73 < √3 < 1.74
1.732 < √3 < 1.733
1.7320 < √3 < 1.7321
b. Find a sequence of five intervals that contain \(2^{\sqrt{3}}\) whose endpoints get successively closer to \(2^{\sqrt{3}}\). Write your intervals in the form 2r < \(2^{\sqrt{3}}\) < 2s for rational numbers r and s.
Answer:
21 <\(2^{\sqrt{3}}\) < 22
21.7 <\(2^{\sqrt{3}}\) < 21.8
21.73 <\(2^{\sqrt{3}}\) < 21.74
21.732 < \(2^{\sqrt{3}}\) < 21.733
21.7320 < \(2^{\sqrt{3}}\) < 21.7321
c. Use your calculator to find approximations to four decimal places of the endpoints of the intervals in part (b).
Answer:
2.0000 < \(2^{\sqrt{3}}\) < 4.0000
3.2490 < \(2^{\sqrt{3}}\) < 3.4822
3. 3173 <\(2^{\sqrt{3}}\) < 3.3404
3.3219 < \(2^{\sqrt{3}}\) < 3.3242
3.3219 < \(2^{\sqrt{3}}\) < 3.3221
d. Based on your work in part (c), what is your best estimate of the value of 2?
Answer:
\(2^{\sqrt{3}}\) ≈ 3.322