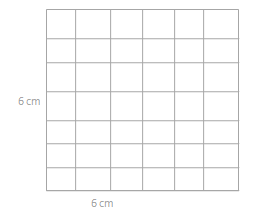
Engage NY Eureka Math 3rd Grade Module 4 Lesson 11 Answer Key
Eureka Math Grade 3 Module 4 Lesson 11 Problem Set Answer Key
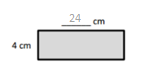
Question 1.
The rectangles below have the same area. Move the parentheses to find the unknown side lengths. Then, solve.
a.
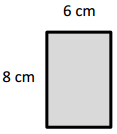
Area: 8 × __6____ = __48____
Area: ___48___ sq cm
Answer:
The area of the rectangle = 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 6 x 8 = 48.
area of the rectangle = 48 sq cm.
b.

Area: 1 × 48 = __( 1_x_6)_x 8
Area: __48____ sq cm
Answer:
The area of the rectangle = 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 48 x 1 = 48.
area of the rectangle = 48 sq cm.
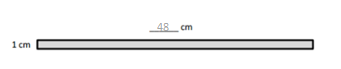
c.
![]()
Area: 8 × 6 = (2 × 4) × 6
= 2 × 4 × 6
= __8____ × __6____
= __48____
Area: __48____ sq cm
Answer:
The area of the rectangle = 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 8 x 6 = 48.
area = 8 x 6 = (2 x 4) x 6.
2 x ( 4 x 6).
2 x 24.
area of the rectangle = 48 sq cm.
d.
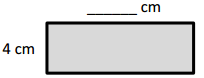
Area: 8 × 6 = (4 × 2) × 6
= 4 × 2 × 6
= ___4___ × ___12___
= __48____
Area: ___48___ sq cm
Answer:
The area of the rectangle = 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 8 x 6 = 48.
area = 8 x 6 = (4 x 2) x 6.
area = 4 x 12.
area of the rectangle = 48 sq cm.
e.
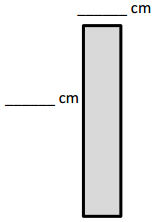
Area: 8 × 6 = 8 × (2 × 3)
= 8 × 2 × 3
= __16____ × ___3__
= ___48___
Area: ___48___ sq cm
Answer:
The area of the rectangle = 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 8 x 6 = 48.
area = 8 x 6 = (8 x 2) x 3.
area = 16 x 3.
area of the rectangle = 48 sq cm.
Question 2.
Does Problem 1 show all the possible whole number side lengths for a rectangle with an area of 48 square centimeters? How do you know?
Answer:
The area of the rectangle = 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 8 x 6 = 48.
area = 8 x 6 = (4 x 2) x 6.
area = 4 x 12.
area of the rectangle = 48 sq cm.
Question 3.
In Problem 1, what happens to the shape of the rectangle as the difference between the side lengths gets smaller?
Answer:
The area of the rectangle also decreases= 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 8 x 6 = 48.
area = 8 x 6 = (4 x 2) x 6.
area = 4 x 12.
area of the rectangle = 48 sq cm.
Question 4.
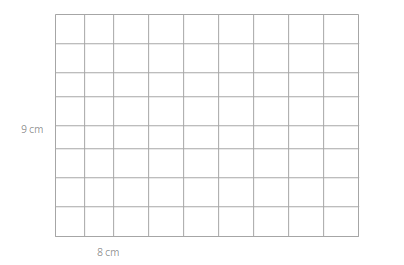
a. Find the area of the rectangle below.
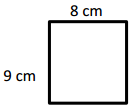
Answer:
The area of the rectangle = 72 sq cm.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length, b = breadth.
l = 8 cm and b = 9 cm given.
area = l x b.
area = 8 x 9.
area = 72 sq cm.
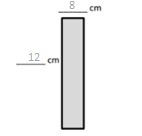
b. Julius says a 4 cm by 18 cm rectangle has the same area as the rectangle in Part (a). Place parentheses in the equation to find the related fact and solve. Is Julius correct? Why or why not?
4 × 18 = 4 × 2 × 9
= 4 × 2 × 9
= ___8___ × __9____
= __72____
Area: __72___ sq cm
Answer:
Yes, Julius was correct.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 4 x 18 = 72.
area = 4 x 18 = (4 x 2) x 9.
area = 8 x 9.
area of the rectangle = 72 sq cm.
c. Use the expression 8 × 9 to find different side lengths for a rectangle that has the same area as the rectangle in Part (a). Show your equations using parentheses. Then, estimate to draw the rectangle and label the side lengths.
Answer:
The area of the rectangle = 72 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 8 x 9 = 72.
area = 8 x 9 = (4 x 2) x 9.
area = 4 x 18.
area of the rectangle = 72 sq cm.
Eureka Math Grade 3 Module 4 Lesson 11 Exit Ticket Answer Key
Question 1.
Find the area of the rectangle.
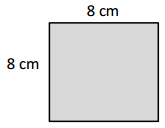
Answer:
The area of the rectangle = 64 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 8 x 8 = 64.
area = 8 x 8 = (4 x 2) x 8.
area = 4 x 16.
area of the rectangle = 64 sq cm.
Question 2.
The rectangle below has the same area as the rectangle in Problem 1. Move the parentheses to find the unknown side lengths. Then, solve.
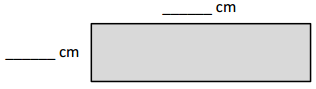
Area: 8 × 8 = (4 × 2) × 8
= 4 × 2 × 8
= __8____ × __8____
= __64____
Area: __64____ sq cm
Answer:
The area of the rectangle = 64 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 8 x 8 = 64.
area = 8 x 8 = (4 x 2) x 8.
area = 4 x 16.
area of the rectangle = 64 sq cm.
Eureka Math Grade 3 Module 4 Lesson 11 Homework Answer Key
Question 1.
The rectangles below have the same area. Move the parentheses to find the unknown side lengths.
Then, solve.
a.
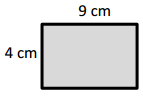
Area: 4 × ___9___ = ___36___
Area: __36____ sq cm
Answer:
The area of the rectangle = 36 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 4 x 9 = 36.
area = 4 x 9 = (4 x 3) x 3.
area = 4 x 9.
area of the rectangle = 36 sq cm.
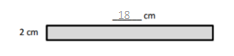
b.

Area: 1 × 36 = __36____
Area: ___36___ sq cm
Answer:
The area of the rectangle = 36 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 1 x 36 = 36.
area = 1 x 36 = (1 x 6) x 6.
area = 6 x 6.
area of the rectangle = 36 sq cm.
c.

Area: 4 × 9 = (2 × 2) × 9
= 2 × 2 × 9
= __4____ × __9____
= ___36___
Area: __36____ sq cm
Answer:
The area of the rectangle = 36 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 4 x 9 = 36.
area = 4 x 9 = (4 x 3) x 3.
area = 12 x 3.
area of the rectangle = 36 sq cm.
d.
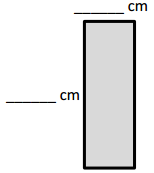
Area: 4 × 9 = 4 × (3 × 3)
= 4 × 3 × 3
= ___12___ × __3____
= ___36___
Area: ___36___ sq cm
Answer:
The area of the rectangle = 36 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 4 x 9 = 36.
area = 4 x 9 = (4 x 3) x 3.
area = 12 x 3.
area of the rectangle = 36 sq cm.
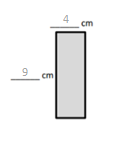
e.
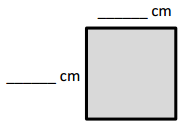
Area: 12 × 3 = (6 × 2) × 3
= 6 × 2 × 3
= ___6___ × __6____
= __36____
Area: ___36___ sq cm
Answer:
The area of the rectangle = 36 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 12 x 3 = 48.
area = 12 x 3 = (6 x 2) x 3.
area = 12 x 3.
area of the rectangle = 36 sq cm.
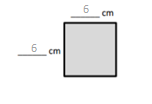
Question 2.
Does Problem 1 show all the possible whole number side lengths for a rectangle with an area of 36 square centimeters? How do you know?
Answer:
The area of the rectangle = 36 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 6 x 6 = 36.
area = 6 x 6 = (6 x 2) x 3.
area = 12 x 3.
area of the rectangle = 36 sq cm.
Question 3.
a. Find the area of the rectangle below.
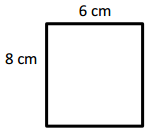
Answer:
The area of the rectangle = 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 6 x 8 = 48.
area of the rectangle = 48 sq cm.
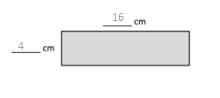
b. Hilda says a 4 cm by 12 cm rectangle has the same area as the rectangle in Part (a). Place parentheses in the equation to find the related fact and solve. Is Hilda correct? Why or why not?
4 × 12 = 4 × 2 × 6
= 4 × 2 × 6
= __8____ × __6____
= ___48___
Area: __48____ sq cm
Answer:
The area of the rectangle = 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 4 x 12 = 48.
area = 4 x 12 = (4 x 2) x 6.
area = 8 x 6.
area of the rectangle = 48 sq cm.
c. Use the expression 8 × 6 to find different side lengths for a rectangle that has the same area as the rectangle in Part (a). Show your equations using parentheses. Then, estimate to draw the rectangle and label the side lengths.
Answer:
The area of the rectangle = 48 sq cm.
Explanation:
In the above-given question,
given that,
The area of the rectangle = l x b.
where l = length, b = breadth.
area = 4 x 12 = 48.
area = 4 x 12 = (4 x 2) x 6.
area = 8 x 6.
area of the rectangle = 48 sq cm.