Eureka Math Grade 3 Module 7 Lesson 20 Answer Key

Engage NY Eureka Math 3rd Grade Module 7 Lesson 20 Answer Key

Eureka Math Grade 3 Module 7 Lesson 20 Sprint Answer Key

A
Multiply or Divide by 2
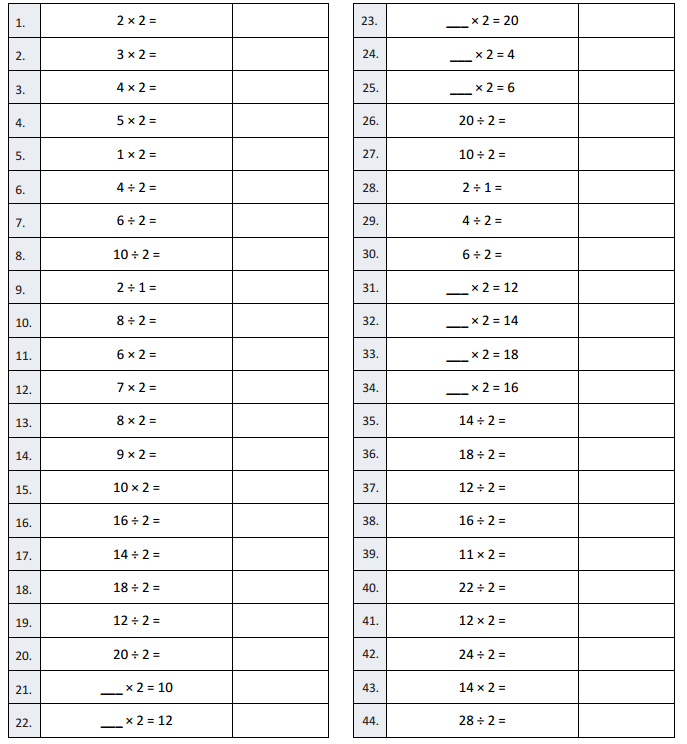
$Engage NY Math 3rd Grade Module 7 Lesson 20 Sprint Answer Key s 1$
Answer:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Sprint Answer Key-A$

Question 1.
2 × 2 =
Answer:
2 × 2 = 4.

Question 2.
3 × 2 =
Answer:
3 × 2 = 6.

Question 3.
4 × 2 =
Answer:
4 × 2 = 8.

Question 4.
5 × 2 =
Answer:
5 × 2 = 10.

Question 5.
1 × 2 =
Answer:
1 × 2 = 2.

Question 6.
4 ÷ 2 =
Answer:
4 ÷ 2 = 2.

Question 7.
6 ÷ 2 =
Answer:
6 ÷ 2 = 3.

Question 8.
10 ÷ 2 =
Answer:
10 ÷ 2 = 5.

Question 9.
2 ÷ 1 =
Answer:
2 ÷ 1 = 2.

Question 10.
8 ÷ 2 =
Answer:
8 ÷ 2 = 4.

Question 11.
6 × 2 =
Answer:
6 × 2 = 12.

Question 12.
7 × 2 =
Answer:
7 × 2 = 14.

Question 13.
8 × 2 =
Answer:
8 × 2 = 16.

Question 14.
9 × 2 =
Answer:
9 × 2 = 18.

Question 15.
10 × 2 =
Answer:
10 × 2 = 20.

Question 16.
16 ÷ 2 =
Answer:
16 ÷ 2 = 8.

Question 17.
14 ÷ 2 =
Answer:
14 ÷ 2 = 7.

Question 18.
18 ÷ 2 =
Answer:
18 ÷ 2 = 9.

Question 19.
12 ÷ 2 =
Answer:
12 ÷ 2 = 6.

Question 20.
20 ÷ 2 =
Answer:
20 ÷ 2 = 10.

Question 21.
___ × 2 = 10
Answer:
5 × 2 = 10.

Question 22.
___ × 2 = 12
Answer:
6 × 2 = 12.

Question 23.
___ × 2 = 20
Answer:
10 × 2 = 20.

Question 24.
___ × 2 = 4
Answer:
2 × 2 = 4.

Question 25.
___ × 2 = 6
Answer:
3 × 2 = 6.

Question 26.
20 ÷ 2 =
Answer:
20 ÷ 2 = 10.

Question 27.
10 ÷ 2 =
Answer:
10 ÷ 2 = 5.

Question 28.
2 ÷ 1 =
Answer:
2 ÷ 1 = 2.

Question 29.
4 ÷ 2 =
Answer:
4 ÷ 2 = 2.

Question 30.
6 ÷ 2 =
Answer:
6 ÷ 2 = 3.

Question 31.
___ × 2 = 12
Answer:
6 × 2 = 12.

Question 32.
___ × 2 = 14
Answer:
7 × 2 = 14.

Question 33.
___ × 2 = 18
Answer:
9 × 2 = 18.

Question 34.
___ × 2 = 16
Answer:
8 × 2 = 16.

Question 35.
14 ÷ 2 =
Answer:
14 ÷ 2 = 7.

Question 36.
18 ÷ 2 =
Answer:
18 ÷ 2 = 9.

Question 37.
12 ÷ 2 =
Answer:
12 ÷ 2 = 6.

Question 38.
16 ÷ 2 =
Answer:
16 ÷ 2 = 8.

Question 39.
11 × 2 =
Answer:
11 × 2 = 22.

Question 40.
22 ÷ 2 =
Answer:
22 ÷ 2 = 11.

Question 41.
12 × 2 =
Answer:
12 × 2 = 24.

Question 42.
24 ÷ 2 =
Answer:
24 ÷ 2 = 12.

Question 43.
14 × 2 =
Answer:
14 × 2 = 28.

Question 44.
28 ÷ 2 =
Answer:
28 ÷ 2 = 14.

B
Multiply or Divide by 2
$Engage NY Math 3rd Grade Module 7 Lesson 20 Sprint Answer Key s 2$
Answer:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Sprint Answer Key-B$
Question 1.
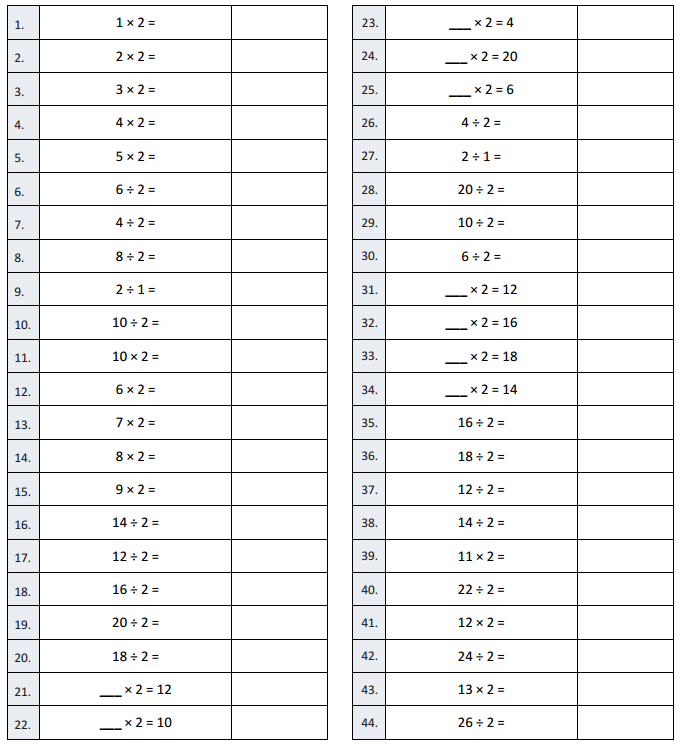
1 × 2 =
Answer:
1 × 2 = 2.

Question 2.
2 × 2 =
Answer:
2 × 2 = 4.

Question 3.
3 × 2 =
Answer:
3 × 2 = 6.

Question 4.
4 × 2 =
Answer:
4 × 2 = 8.

Question 5.
5 × 2 =
Answer:
5 × 2 = 10.

Question 6.
6 ÷ 2 =
Answer:
6 ÷ 2 = 3.

Question 7.
4 ÷ 2 =
Answer:
4 ÷ 2 = 2.

Question 8.
8 ÷ 2 =
Answer:
8 ÷ 2 = 4.

Question 9.
2 ÷ 1 =
Answer:
2 ÷ 1 = 2.

Question 10.
10 ÷ 2 =
Answer:
10 ÷ 2 = 5.

Question 11.
10 × 2 =
Answer:
10 × 2 = 20.

Question 12.
6 × 2 =
Answer:
6 × 2 = 12.

Question 13.
7 × 2 =
Answer:
7 × 2 = 14.

Question 14.
8 × 2 =
Answer:
8 × 2 = 16.

Question 15.
9 × 2 =
Answer:
9 × 2 = 18.

Question 16.
14 ÷ 2 =
Answer:
14 ÷ 2 = 7.

Question 17.
12 ÷ 2 =
Answer:
12 ÷ 2 = 6.

Question 18.
16 ÷ 2 =
Answer:
16 ÷ 2 = 8.

Question 19.
20 ÷ 2 =
Answer:
20 ÷ 2 = 10.

Question 20.
18 ÷ 2 =
Answer:
18 ÷ 2 = 9.

Question 21.
___ × 2 = 12
Answer:
6 × 2 = 12.

Question 22.
___ × 2 = 10
Answer:
5 × 2 = 10.

Question 23.
___ × 2 = 4
Answer:
2 × 2 = 4.

Question 24.
___ × 2 = 20
Answer:
10 × 2 = 20.

Question 25.
___ × 2 = 6
Answer:
3 × 2 = 6.

Question 26.
4 ÷ 2 =
Answer:
4 ÷ 2 = 2.

Question 27.
2 ÷ 1 =
Answer:
2 ÷ 1 = 2.

Question 28.
20 ÷ 2 =
Answer:
20 ÷ 2 = 10.

Question 29.
10 ÷ 2 =
Answer:
10 ÷ 2 = 5.

Question 30.
6 ÷ 2 =
Answer:
6 ÷ 2 = 3.

Question 31.
___ × 2 = 12
Answer:
6 × 2 = 12.

Question 32.
___ × 2 = 16
Answer:
8 × 2 = 16.

Question 33.
___ × 2 = 18
Answer:
9 × 2 = 18.

Question 34.
___ × 2 = 14
Answer:
7 × 2 = 14.

Question 35.
16 ÷ 2 =
Answer:
16 ÷ 2 = 8.

Question 36.
18 ÷ 2 =
Answer:
18 ÷ 2 = 9.

Question 37.
12 ÷ 2 =
Answer:
12 ÷ 2 = 6.

Question 38.
14 ÷ 2 =
Answer:
14 ÷ 2 = 7.

Question 39.
11 × 2 =
Answer:
11 × 2 = 22.

Question 40.
22 ÷ 2 =
Answer:
22 ÷ 2 = 11.

Question 41.
12 × 2 =
Answer:
12 × 2 = 24.

Question 42.
24 ÷ 2 =
Answer:
24 ÷ 2 = 12.

Question 43.
13 × 2 =
Answer:
13 × 2 = 26.

Question 44.
26 ÷ 2 =
Answer:
26 ÷ 2 = 13.

Eureka Math Grade 3 Module 7 Lesson 20 Problem Set Answer Key

Question 1.
Use your square unit tiles to build as many rectangles as you can with a perimeter of 12 units.
a. Estimate to draw your rectangles below. Label the side lengths of each rectangle.
b. Explain your strategy for finding rectangles with a perimeter of 12 units.
c. Find the areas of all the rectangles in part (a) above.
d. The perimeters of all the rectangles are the same. What do you notice about their areas?
Answer:
a.
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Problem Set Answer Key-1a$
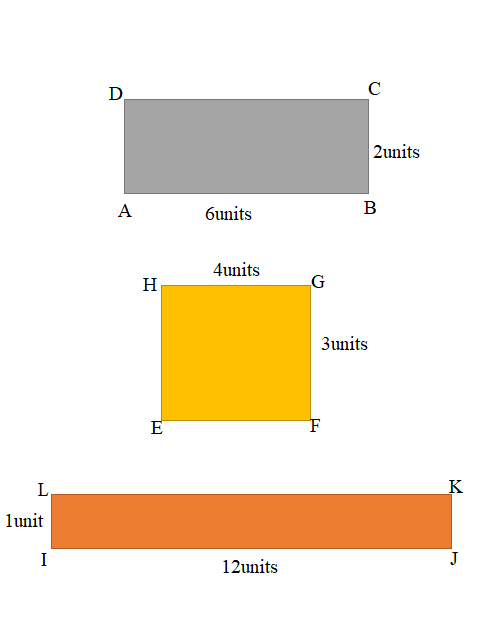
b. Well, I have choose the multiples of 12 to draw the rectangles. Perimeter of the rectangles = 12units.

c. Area of the ABCD rectangle = 12 square units.
Area of the EFGH rectangle = 12 square units.
Area of the IJKL rectangle = 12 square units.

d. Perimeter of ABCD Rectangle = 16units.
Perimeter of EFGH Rectangle = 14units.
Perimeter of IJKL Rectangle = 26units.
Well, areas of all rectangles are same yet their perimeters are completely different to one and the another rectangle.

Explanation:
a.
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Problem Set Answer Key-1a$

b. Perimeter of the rectangles = 12units.
Well, I have choose the multiples of 12 to draw the rectangles.

c.
Figure 1: ABCD Rectangle:
Length of the ABCD rectangle = 6units
Width of the ABCD rectangle = 2units
Area of the ABCD rectangle = Length × Width
= 6units × 2units
= 12 square units.

Figure 2: EFGH Rectangle:
Length of the EFGH rectangle = 4units
Width of the EFGH rectangle = 3units
Area of the EFGH rectangle = Length × Width
= 4units × 3units
= 12 square units.

Figure 3: IJKL Rectangle:
Length of the IJKL rectangle = 12units
Width of the IJKL rectangle = 1units
Area of the IJKL rectangle = Length × Width
= 12units × 1units
= 12 square units.

d.
Figure 1: ABCD Rectangle:
Length of the ABCD rectangle = 6units
Width of the ABCD rectangle = 2units
Perimeter of ABCD Rectangle = 2 ( Length + Width )
= 2 ( 6units + 2units )
= 2 × 8units
= 16 units.

Figure 2: EFGH Rectangle:
Length of the EFGH rectangle = 4units
Width of the EFGH rectangle = 3units
Perimeter of EFGH Rectangle = 2 ( Length + Width )
= 2 ( 4units + 3units )
= 2 × 7units
= 14 units.

Figure 3: IJKL Rectangle:
Length of the IJKL rectangle = 12units
Width of the IJKL rectangle = 1units
Perimeter of IJKL Rectangle = 2 ( Length + Width )
= 2 ( 12units + 1units )
= 2 × 13units
= 26 units.
Well, areas of all rectangles are same yet their perimeters are completely different to one and the another rectangle.

Question 2.
Use your square unit tiles to build as many rectangles as you can with a perimeter of 14 units.
a. Estimate to draw your rectangles below. Label the side lengths of each rectangle.
b. Find the areas of all the rectangles in part (a) above.
c. Given a rectangle’s perimeter, what other information do you need to know about the rectangle to find its area?
Answer:
a. 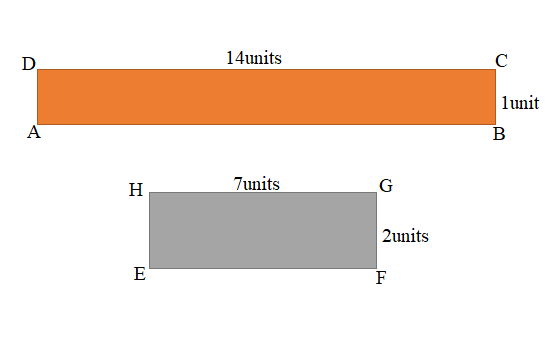$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Problem Set Answer Key-2a$
b. Area of the ABCD rectangle = 30 square units.
Area of the EFGH rectangle = 18 square units.

c. Perimeter of any figure is basically gives the length of the figure. Area of rectangle is the region covered by the rectangle in a two-dimensional plane. Area requires length and width for its calculation.

Explanation:
a.
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Problem Set Answer Key-2a$

b. Figure 1 : ABCD Rectangle:
Length of the ABCD rectangle = 14units
Width of the ABCD rectangle = 1unit
Area of the ABCD rectangle = Length × Width
= 14units × 1units
= 14 square units.

Figure 2 :EFGH Rectangle:
Length of the EFGH rectangle = 7units
Width of the EFGH rectangle = 2unit
Area of the EFGH rectangle = Length × Width
= 7units × 2units
= 14 square units.

Eureka Math Grade 3 Module 7 Lesson 20 Exit Ticket Answer Key

Use your square unit tiles to build as many rectangles as you can with a perimeter of 8 units.
a. Estimate to draw your rectangles below. Label the side lengths of each rectangle.
b. Find the areas of the rectangles in part (a) above.
Answer:
a. 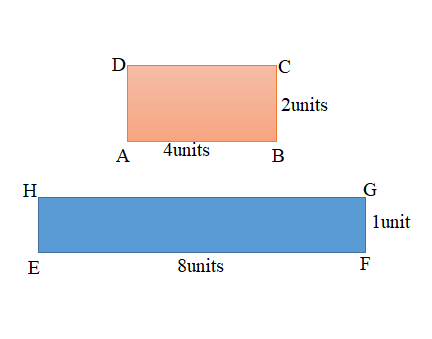$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Exit Ticket Answer Key$

b. Area of the ABCD rectangle = 8 square units.
Area of the EFGH rectangle = 8 square units.

Explanation:
a. $Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Exit Ticket Answer Key$

b. Figure 1 : ABCD Rectangle:
Length of the ABCD rectangle = 4units
Width of the ABCD rectangle = 2unit
Area of the ABCD rectangle = Length × Width
= 4units × 2units
= 8 square units.

Figure 2 : EFGH Rectangle:
Length of the EFGH rectangle = 8units
Width of the EFGH rectangle = 1unit
Area of the EFGH rectangle = Length × Width
= 8units × 1units
= 8 square units.

Eureka Math Grade 3 Module 7 Lesson 20 Homework Answer Key

Question 1.
Cut out the unit squares at the bottom of the page. Then, use them to make as many rectangles as you can with a perimeter of 10 units.
a. Estimate to draw your rectangles below. Label the side lengths of each rectangle.
b. Find the areas of the rectangles in part (a) above.
$Eureka Math Grade 3 Module 7 Lesson 20 Homework Answer Key h 1$
Answer:
a. $Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Homework Answer Key-1a$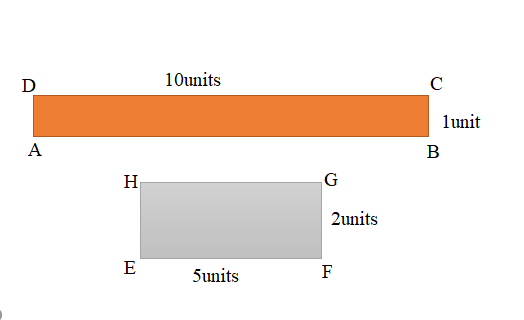

b. Area of the ABCD rectangle = 10 square units.
Area of the EFGH rectangle = 10 square units.

Explanation:
a. $Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Homework Answer Key-1a$

b. Figure 1 : ABCD Rectangle:
Length of the ABCD rectangle = 10units
Width of the ABCD rectangle = 1unit
Area of the ABCD rectangle = Length × Width
= 10units × 1units
= 10 square units.

Figure 2: EFGH Rectangle:
Length of the EFGH rectangle = 5units
Width of the EFGH rectangle = 2units
Area of the EFGH rectangle = Length × Width
= 5units × 2units
= 10 square units.

Question 2.
Gino uses unit square tiles to make rectangles with a perimeter of 14 units. He draws his rectangles as shown below. Using square unit tiles, can Gino make another rectangle that has a perimeter of 14 units? Explain your answer.
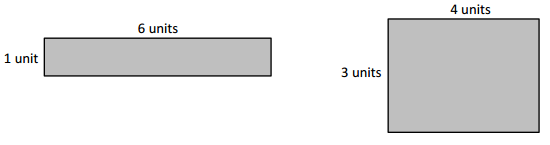
$Eureka Math Grade 3 Module 7 Lesson 20 Homework Answer Key h 2$
Answer:
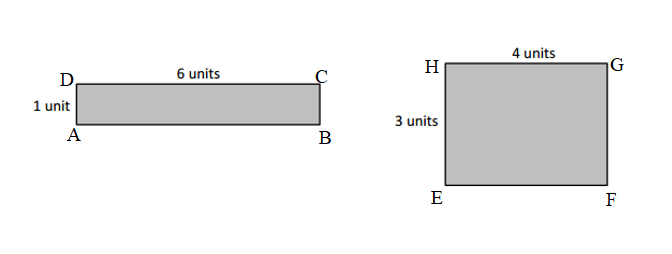
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Exit Ticket Answer Key-2a$

Perimeter of ABCD Rectangle = 14units.
Perimeter of EFGH Rectangle = 14units.

Explanation:
$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Exit Ticket Answer Key-2a$

Figure 1: ABCD Rectangle
Length of the ABCD Rectangle = 6units
Width of the ABCD Rectangle = 1units
Perimeter of ABCD Rectangle = 2 (Length + Width)
= 2 ( 6units + 1unit )
= 2 × 7units
= 14units.

Figure 2: EFGH Rectangle
Length of the EFGH Rectangle = 4units
Width of the EFGH Rectangle = 3units
Perimeter of EFGH Rectangle = 2 (Length + Width)
= 2 ( 4units + 3unit )
= 2 × 7units
= 14units.

Question 3.
Katie draws a square that has a perimeter of 20 centimeters.
a. Estimate to draw Katie’s square below. Label the length and width of the square.
b. Find the area of Katie’s square.
c. Estimate to draw a different rectangle that has the same perimeter as Katie’s square.
d. Which shape has a greater area, Katie’s square or your rectangle?
Answer:
a. 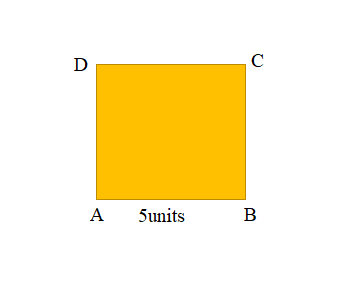$Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Exit Ticket Answer Key-3a$
b. Area of the ABCD Katie’s Square = 25 square units.

c. $Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Exit Ticket Answer Key-3c$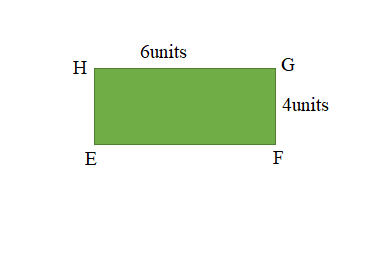

Perimeter of the EFGH Rectangle = 20units.

d. Area of the ABCD Katie’s Square = 25 square units.
Area of the EFGH Rectangle = 24 square units.
Area of the ABCD Katie’s Square is greater than the Area of the EFGH Rectangle.

Explanation:
a. $Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Exit Ticket Answer Key-3a$
b. Length of the side of the ABCD Katie’s Square = 5units
Area of the ABCD Katie’s Square = Side × Side
= 5units × 5units
= 25 square units.

c. $Engage-NY-Eureka-Math-3rd-Grade-Module-7-Lesson-20-Answer-Key-Eureka Math Grade 3 Module 7 Lesson 20 Exit Ticket Answer Key-3c$
Length of the EFGH Rectangle = 6units
Width of the EFGH Rectangle = 4units
Perimeter of the EFGH Rectangle = 2 ( Length + Width )
= 2 ( 6units + 4units )
= 2 × 10units
= 20units.

d. Length of the side of the ABCD Katie’s Square = 5units
Area of the ABCD Katie’s Square = Side × Side
= 5units × 5units
= 25 square units.

Length of the EFGH Rectangle = 6units
Width of the EFGH Rectangle = 4units
Area of the EFGH Rectangle = Length × Width
= 6units × 4units
= 24 square units.

Eureka Math Grade 3 Module 7 Lesson 20 Data Sheet Answer Key

Use the data you gathered from Problem Sets 20 and 21 to complete the charts to show how many rectangles you can create with a given perimeter. You might not use all the spaces in the charts.

Perimeter = 10 units Number of rectangles you made: _2____
Width	Length	Area
1 unit	10 units	10 square units
2 unit	5 units	10 square units

Perimeter = 12 units Number of rectangles you made: __3___
Width	Length	Area
1 units	12 units	12 square units
2 units	6 units	12 square units
3 units	4 units	12 square units

Perimeter = 14 units Number of rectangles you made: _2____
Width	Length	Area
1 units	14 units	14 square units
2 units	7 units	14 square units

Perimeter = 16 units Number of rectangles you made: _2____
Width	Length	Area
1 unit	16 units	16 square units
2 units	8 units	16 square units

Perimeter = 18 units Number of rectangles you made: _2____
Width	Length	Area
1 unit	18 units	18 square units
2 units	9 units	18 square units

Perimeter = 20 units Number of rectangles you made: __2___
Width	Length	Area
1 unit	20 units	20 square units
2 units	10 units	20 square units