Engage NY Eureka Math 4th Grade Module 5 Lesson 14 Answer Key
Eureka Math Grade 4 Module 5 Lesson 14 Problem Set Answer Key
Question 1.
Compare the pairs of fractions by reasoning about the size of the units. Use >, <, or =.
a. 1 fourth _____ 1 fifth
Answer:
1 fourth = 1 fifth.
Explanation:
In the above-given question,
given that,
compare the pairs of fractions by reasoning about the size of the units.
1 fourth = 1/4.
1/4 = 0.25.
1 fifth = 1/5.
1/5 = 0.2.
0.25 = 0.2.
1/4 = 1/5.
b. 3 fourths _____ 3 fifths
Answer:
3 fourths > 3 fifths.
Explanation:
In the above-given question,
given that,
compare the pairs of fractions by reasoning about the size of the units.
3 fourths = 3/4.
3/4 = 0.75.
3 fifths = 3/5.
3/5 = 0.6.
0.75 > 0.6.
3/4 > 3/5.
c. 1 tenth __>___ 1 twelfth
Answer:
1 tenth > 1 twelfth.
Explanation:
In the above-given question,
given that,
compare the pairs of fractions by reasoning about the size of the units.
1 tenth = 1/10.
1/10 = 0.1.
1 twelfth = 1/12.
1/12 = 0.083.
0.1 > 0.08.
1/10 > 1/12.
d. 7 tenths _____ 7 twelfths
Answer:
7 tenths > 7 twelfths
Explanation:
In the above-given question,
given that,
compare the pairs of fractions by reasoning about the size of the units.
7 tenths = 7/10.
7/10 = 0.7.
7 twelfths = 7/12.
7/12 = 0.58.
0.7 > 0.58.
7/10 > 7/12.
Question 2.
Compare by reasoning about the following pairs of fractions with the same or related numerators.
Use >, <, or =. Explain your thinking using words, pictures, or numbers. Problem 2(b) has been done for you.
a. \(\frac{3}{5}\) _____ \(\frac{3}{4}\)
Answer:
\(\frac{3}{5}\) __<___ \(\frac{3}{4}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{5}\).
3/5 = 3 fifths.
3/5 = 0.6.
\(\frac{3}{4}\).
3/4 = 3 fourths.
3/4 = 0.75.
0.6 < 0.75.
3 fifths are less than 3 fourths.
3/5 < 3/4.
b. \(\frac{2}{5}\) < \(\frac{4}{9}\) because \(\frac{2}{5}\) = \(\frac{4}{10}\)
4 tenths is less than 4 ninths because tenths are smaller than ninths.
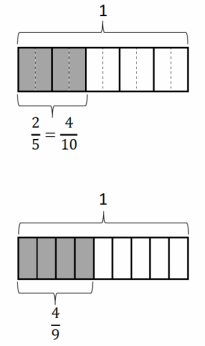
Answer:
\(\frac{2}{5}\) __>___ \(\frac{4}{9}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{5}\).
2/5 = 2 fifths.
2/5 = 0.4.
\(\frac{4}{9}\).
4/9 = 4 ninths.
4/9 = 0.11.
0.4 > 0.11.
2 fifths are greater than 4 ninths.
2/5 > 4/9.
c. \(\frac{7}{11}\) _____ \(\frac{7}{13}\)
Answer:
\(\frac{7}{11}\) __>___ \(\frac{7}{13}\).
Explanation:
In the above-given question,
given that,
\(\frac{7}{11}\).
7/11 = 7 elevenths.
7/11 = 0.63.
\(\frac{7}{13}\).
7/13 = 7 thirteens.
7/13 = 0.53.
0.6 > 0.5.
7 thirteens are less than 7 elevenths.
7/11 > 7/13.
d. \(\frac{6}{7}\) _____ \(\frac{12}{15}\)
Answer:
\(\frac{6}{7}\) __<___ \(\frac{12}{15}\).
Explanation:
In the above-given question,
given that,
\(\frac{6}{7}\).
6/7 = 6 sevenths.
6/7 = 0.85.
\(\frac{2}{15}\).
2/15 = 2 fifteenths.
2/15 = 0.13.
0.8 < 0.13.
6 sevenths are less than 12 fifteenths.
6/7 < 12/15.
Question 3.
Draw two tape diagrams to model each pair of the following fractions with related denominators.
Use >, <, or = to compare.
a. \(\frac{2}{3}\) _____ \(\frac{5}{6}\)
Answer:
\(\frac{2}{3}\) __<___ \(\frac{5}{6}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{3}\).
2/3 = 2 thirds.
2/3 = 0.6.
\(\frac{5}{6}\).
5/6 = 5 sixths.
5/6 = 0.83.
0.6 < 0.83.
2 thirds are less than 5 sixths.
2/3 < 5/6.
b. \(\frac{3}{4}\) _____ \(\frac{7}{8}\)
Answer:
\(\frac{3}{4}\) __<___ \(\frac{7}{8}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{4}\).
3/4 = 3 fourths.
3/4 = 0.6.
\(\frac{7}{8}\).
7/8 = 7 eighths.
7/8 = 0.87.
0.6 < 0.8.
3 fourths are less than 7 eighths.
3/4 < 7/8.
c. 1\(\frac{3}{4}\) _____ 1\(\frac{7}{12}\)
Answer:
1\(\frac{3}{4}\) __>___ 1\(\frac{7}{12}\).
Explanation:
In the above-given question,
given that,
1\(\frac{3}{4}\).
1 (3/4) = 7 fourths.
7/4 = 1.75.
1\(\frac{7}{12}\).
1(7/12) = 19 twelfths.
19/12 = 1.58.
1.75 > 1.58.
3 fourths are greater than 7 twelfths.
3/4 > 7/12.
Question 4.
Draw one number line to model each pair of fractions with related denominators. Use >, <, or = to compare.
a. \(\frac{2}{3}\) _____ \(\frac{5}{6}\)
Answer:
\(\frac{2}{3}\) __<___ \(\frac{5}{6}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{3}\).
2/3 = 2 thirds.
2/3 = 0.6.
\(\frac{5}{6}\).
5/6 = 5 sixths.
5/6 = 0.83.
0.6 < 0.83.
2 thirds are less than 5 sixths.
2/3 < 5/6.
b. \(\frac{3}{8}\) _____ \(\frac{1}{4}\)
Answer:
\(\frac{3}{8}\) __>__ \(\frac{1}{4}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{8}\).
3/8 = 3 eights.
3/8 = 0.37.
\(\frac{1}{4}\).
1/4 = 1 fourths.
1/4 = 0.25.
0.37 > 0.25.
3 eights are greater than 1 fourth.
3/8 > 1/4.
c. \(\frac{2}{6}\) _____ \(\frac{5}{12}\)
Answer:
\(\frac{2}{6}\) __<___ \(\frac{5}{12}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{6}\).
2/6 = 2 sixths.
2/6 = 0.33.
\(\frac{5}{12}\).
5/12 = 5 twelfths.
5/12 = 0.41.
0.33 < 0.41.
2 sixths are less than 5 twelfths.
2/6 < 5/12.
d. \(\frac{8}{9}\) _____ \(\frac{2}{3}\)
Answer:
\(\frac{8}{9}\) __>___ \(\frac{2}{3}\).
Explanation:
In the above-given question,
given that,
\(\frac{8}{9}\).
8/9 = 8 ninths.
8/9 = 0.88.
\(\frac{2}{3}\).
2/3 = 2 thirds.
2/3 = 0.66.
0.88 > 0.66.
8 ninths are greater than 2 thirds.
8/9 > 2/9.
Question 5.
Compare each pair of fractions using >, <, or =. Draw a model if you choose to.
a. \(\frac{3}{4}\) _____ \(\frac{3}{7}\)
Answer:
\(\frac{3}{4}\) __<___ \(\frac{3}{7}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{4}\).
3/4 = 3 fourths.
3/4 = 0.75.
\(\frac{3}{7}\).
3/7 = 3 sevenths.
3/7 = 0.42.
0.75 > 0.42.
3 fourths are greater than 3 sevenths.
3/4 > 3/7.
b. \(\frac{4}{5}\) _____ \(\frac{8}{12}\)
Answer:
\(\frac{4}{5}\) __<___ \(\frac{8}{12}\).
Explanation:
In the above-given question,
given that,
\(\frac{4}{5}\).
4/5 = 4 fifths.
4/5 = 0.8.
\(\frac{8}{12}\).
8/12 = 8 twelfths.
8/12 = 0.66.
0.8 > 0.6.
4 fifths are greater than 8 twelfths.
4/5 > 8/12.
c. \(\frac{3}{10}\) _____ \(\frac{3}{5}\)
Answer:
\(\frac{3}{10}\) __<___ \(\frac{3}{5}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{10}\).
3/10 = 3 tenths.
3/10 = 0.3.
\(\frac{3}{5}\).
3/5 = 3 fifths.
3/5 = 0.6.
0.3 < 0.6.
3 tenths are less than 3 fifths.
3/10 < 3/5.
d. \(\frac{2}{3}\) _____ \(\frac{11}{15}\)
Answer:
\(\frac{2}{3}\) __<___ \(\frac{11}{15}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{3}\).
2/3 = 2 thirds.
2/3 = 0.6.
\(\frac{11}{15}\).
11/15 = 11 fifteenths.
11/15 = 0.73.
0.6 < 0.73.
2 thirds are less than 11 fifteenths.
2/3 < 11/15.
e. \(\frac{3}{4}\) _____ \(\frac{11}{12}\)
Answer:
\(\frac{3}{4}\) __<___ \(\frac{11}{12}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{4}\).
3/4 = 3 fourths.
3/4 = 0.6.
\(\frac{11}{12}\).
11/12 = 11 twelfths.
11/12 = 0.91.
0.6 < 0.91
3 fourths are less than 11 twelths.
3/4 < 11/12.
f. \(\frac{7}{3}\) _____ \(\frac{7}{4}\)
Answer:
\(\frac{7}{3}\) __>___ \(\frac{7}{4}\).
Explanation:
In the above-given question,
given that,
\(\frac{7}{3}\).
7/3 = 7 thirds.
7/3 = 2.33.
\(\frac{7}{4}\).
7/4 = 7 fourths.
7/4 = 1.75.
2.33 > 1.75.
7 thirds are greater than 7 fourths.
7/3 < 7/4.
g. 1\(\frac{1}{3}\) _____ 1\(\frac{2}{9}\)
Answer:
\(\frac{1}{3}\) __<___ \(\frac{2}{9}\).
Explanation:
In the above-given question,
given that,
\(\frac{1}{3}\).
1/3 = 1 thirds.
1/3 = 0.33.
\(\frac{2}{9}\).
2/9 = 2 ninths.
2/9 = 0.22.
0.33 > 0.22.
1 third is greater than 2 ninths.
1/3 > 2/9.
h. 1\(\frac{2}{3}\) _____ 1\(\frac{4}{7}\)
Answer:
1\(\frac{2}{3}\) __>___ 1\(\frac{4}{7}\).
Explanation:
In the above-given question,
given that,
1\(\frac{2}{3}\).
1(2/3) = 5 thirds.
5/3 = 1.66.
1\(\frac{4}{7}\).
1(4/7) = 11 sevenths.
11/7 = 1.57.
1.66 > 1.57.
5 thirds are greater than 11 sevenths.
5/3 > 11/7.
Question 6.
Timmy drew the picture to the right and claimed that \(\frac{2}{3}\) is less than \(\frac{7}{12}\). Evan says he thinks \(\frac{2}{3}\) is greater than \(\frac{7}{12}\). Who is correct? Support your answer with a picture.
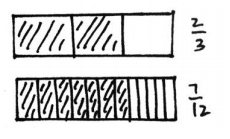
Answer:
Evan is correct.
\(\frac{2}{3}\) __>__ \(\frac{7}{12}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{3}\).
2/3 = 2 thirds.
2/3 = 0.6.
\(\frac{7}{12}\).
7/12 = 7 twelfths.
7/12 = 0.58.
0.6 > 0.58.
2 thirds are greater than 7 twelfths.
2/3 > 7/12.
Eureka Math Grade 4 Module 5 Lesson 14 Exit Ticket Answer Key
Question 1.
Draw tape diagrams to compare the following fractions:
\(\frac{2}{5}\) ________ \(\frac{3}{10}\)
Answer:
\(\frac{2}{5}\) __>___ \(\frac{3}{10}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{5}\).
2/5 = 2 fifths.
2/5 = 0.4.
\(\frac{3}{10}\).
3/10 = 3 tenths.
3/10 = 0.3.
0.4 > 0.3.
2 fifths are greater than 3 tenths.
2/5 > 3/10.
Question 2.
Use a number line to compare the following fractions:
\(\frac{4}{3}\) ________ \(\frac{7}{6}\)
Answer:
\(\frac{4}{3}\) __>___ \(\frac{7}{6}\).
Explanation:
In the above-given question,
given that,
\(\frac{4}{3}\).
4/3 = 4 thirds.
4/3 = 1.33.
\(\frac{7}{6}\).
7/6 = 7 sixths.
7/6 = 1.16.
1.33 > 1.16.
4 thirds are greater than 7 sixths.
4/3 > 7/6.
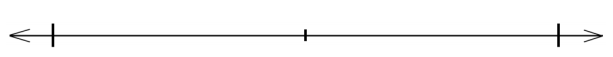
Eureka Math Grade 4 Module 5 Lesson 14 Homework Answer Key
Question 1.
Compare the pairs of fractions by reasoning about the size of the units. Use >, <, or =.
a. 1 third _____ 1 sixth
Answer:
1 third > 1 sixth.
Explanation:
In the above-given question,
given that,
compare the pairs of fractions by reasoning about the size of the units.
1 third = 1/3.
1/3 = 0.33.
1 sixth = 1/6.
1/6 = 0.1.
0.33 > 0.1.
1/3 > 1/6.
b. 2 halves _____ 2 thirds
Answer:
2 halves = 2 thirds.
Explanation:
In the above-given question,
given that,
compare the pairs of fractions by reasoning about the size of the units.
2 halves = 2/2.
2/2 = 1.
2 thirds = 2/3.
2/3 = 0.66
1 > 0.66.
2/2 > 2/3.
c. 2 fourths _____ 2 sixths
Answer:
2 fourths > 2 sixths.
Explanation:
In the above-given question,
given that,
compare the pairs of fractions by reasoning about the size of the units.
2 fourths = 2/4.
2/4 = 0.5.
2 sixths = 2/6.
2/6 = 0.33.
0.5 > 0.33.
2/4 > 2/6.
d. 5 eighths _____ 5 tenths
Answer:
5 eights > 5 tenth.
Explanation:
In the above-given question,
given that,
compare the pairs of fractions by reasoning about the size of the units.
5 eights = 5/8.
5/8 = 0.625.
5 tenths = 5/10.
5/10 = 0.5.
0.625 > 0.5.
5/8 > 5/10.
Question 2.
Compare by reasoning about the following pairs of fractions with the same or related numerators.
Use >, <, or =. Explain your thinking using words, pictures, or numbers. Problem 2(b) has been done for you.
a. \(\frac{3}{6}\) __________ \(\frac{3}{7}\)
Answer:
\(\frac{3}{6}\) __>___ \(\frac{3}{7}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{6}\).
3/6 = 3 sixths.
3/6 = 0.5.
\(\frac{3}{7}\).
3/7 = 3 sevenths.
3/7 = 0.42.
0.5 > 0.42.
3 sixths are greater than 3 sevenths.
3/6 > 3/7.
b. \(\frac{2}{5}\) < \(\frac{4}{9}\) because \(\frac{2}{5}\) = \(\frac{4}{10}\)
4 tenths is less than 4 ninths because tenths are smaller than ninths.

c. \(\frac{3}{11}\) _________ \(\frac{3}{13}\)
Answer:
\(\frac{3}{11}\) __>___ \(\frac{3}{13}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{11}\).
3/11 = 3 elevenths.
3/11 = 0.27.
\(\frac{3}{13}\).
3/13 = 3 elevenths.
3/13 = 0.23.
0.27 > 0.23.
3 elevenths are greater than 3 thirteens.
3/11 > 3/13.
d. \(\frac{5}{7}\) _________ \(\frac{10}{13}\)
Answer:
\(\frac{5}{7}\) __>___ \(\frac{10}{13}\).
Explanation:
In the above-given question,
given that,
\(\frac{5}{7}\).
5/7 = 5 sevenths.
5/7 = 1.33.
\(\frac{10}{13}\).
10/13 = 10 thirteens.
10/13 = 0.769
1.33 > 0.769.
5 sevenths are greater than 10 thirteens.
5/7 > 10/13.
c. \(\frac{3}{11}\) ______ \(\frac{3}{13}\)
Answer:
\(\frac{3}{11}\) __>___ \(\frac{3}{13}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{11}\).
3/11 = 3 elevenths.
3/11 = 0.27.
\(\frac{3}{13}\).
3/13 = 3 elevens.
3/13 = 0.23.
0.27 > 0.23.
3 elevens are greater than 3 thirteens.
3/11 > 3/13.
d. \(\frac{5}{7}\) _______ \(\frac{10}{13}\)
Answer:
\(\frac{5}{7}\) __<___ \(\frac{10}{13}\).
Explanation:
In the above-given question,
given that,
\(\frac{5}{7}\).
5/7 = 5 sevens.
4/3 = 1.33.
\(\frac{10}{13}\).
10/13 = 10 thirteens.
10/13 = 3.33
1.33 < 3.33.
5 sevens are greater than 10 thirteens.
5/7 < 10/13.
Question 3.
Draw two tape diagrams to model each pair of the following fractions with related denominators. Use >, <, or = to compare.
a. \(\frac{3}{4}\) _________ \(\frac{7}{12}\)
Answer:
\(\frac{3}{4}\) __>___ \(\frac{7}{12}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{4}\).
3/4 = 3 fours.
3/4 = 0.75.
\(\frac{7}{12}\).
7/12 = 7 twelves.
7/12 = 0.58.
0.75 > 0.58.
3 fourths are greater than 7 twelves.
3/4 > 7/12.
b. \(\frac{2}{4}\) ___________ \(\frac{1}{8}\)
Answer:
\(\frac{2}{4}\) __>___ \(\frac{1}{8}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{4}\).
2/4 = 2 fourths.
2/4 = 0.5.
\(\frac{1}{8}\).
1/8 = 1 eights.
1/8 = 0.125.
0.5 > 0.125
2 fourths are greater than 1 eights.
2/34 > 1/8.
c. 1\(\frac{4}{10}\) ________ 1\(\frac{3}{5}\)
Answer:
\(\frac{4}{10}\) __<___ \(\frac{3}{5}\).
Explanation:
In the above-given question,
given that,
\(\frac{4}{10}\).
4/10 = 4 tenths.
4/10 = 0.4.
\(\frac{3}{5}\).
3/5 = 3 fifths.
3/5 = 0.6.
0.4 < 0.6.
4 tens are greater than 3 fives.
4/10 < 3/5.
Question 4.
Draw one number line to model each pair of fractions with related denominators. Use >, <, or = to compare.
a. \(\frac{3}{4}\) _________ \(\frac{5}{8}\)
Answer:
\(\frac{3}{4}\) __>___ \(\frac{5}{8}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{4}\).
3/4 = 3 fourths.
3/4 = 0.75
\(\frac{5}{8}\).
5/8 = 5 eights.
5/8 = 0.625.
0.75 > 0.625.
3 fourths are greater than 5 eights.
3/4 > 7/6.
b. \(\frac{11}{12}\) _________ \(\frac{3}{4}\)
Answer:
\(\frac{11}{12}\) __>___ \(\frac{3}{4}\).
Explanation:
In the above-given question,
given that,
\(\frac{11}{12}\).
11/12 = 11 twelves.
11/12 = 0.91.
\(\frac{3}{4}\).
3/4 = 3 fourths.
3/4 = 0.75
0.91 > 0.75.
11 twelves are greater than 3 fourths.
11/12 > 3/4.
c. \(\frac{4}{5}\) _________ \(\frac{7}{10}\)
Answer:
\(\frac{4}{5}\) __>___ \(\frac{7}{10}\).
Explanation:
In the above-given question,
given that,
\(\frac{4}{5}\).
4/5 = 4 fifths.
4/5 = 0.8
\(\frac{7}{10}\).
7/10 = 7 tenths.
7/10 = 0.7.
0.8 > 0.7.
4 fifths are greater than 7 tenths.
4/5 > 7/10.
d. \(\frac{8}{9}\) _________ \(\frac{2}{3}\)
Answer:
\(\frac{8}{9}\) __>___ \(\frac{2}{3}\).
Explanation:
In the above-given question,
given that,
\(\frac{8}{9}\).
8/9 = 8 ninths.
8/9 = 0.88.
\(\frac{2}{3}\).
2/3 = 2 thirds.
2/3 = 0.66.
0.88 > 0.66.
8 ninths are greater than 2 thirds.
8/9 > 2/3.
Question 5.
Compare each pair of fractions using >, <, or =. Draw a model if you choose to.
a. \(\frac{1}{7}\) ________ \(\frac{2}{7}\)
Answer:
\(\frac{1}{7}\) __<___ \(\frac{2}{7}\).
Explanation:
In the above-given question,
given that,
\(\frac{1}{7}\).
1/7 = 1 sevenths.
1/37 = 0.027.
\(\frac{2}{7}\).
2/7 = 2 sevenths.
2/8 = 0.25.
1.33 < 1.16.
1 seventh is less than 2 sevenths.
1/7 < 2/7.
b. \(\frac{5}{7}\) _______ \(\frac{11}{14}\)
Answer:
\(\frac{5}{7}\) __>___ \(\frac{11}{14}\).
Explanation:
In the above-given question,
given that,
\(\frac{5}{7}\).
5/3 = 5 thirds.
5/3 = 1.6.
\(\frac{11}{14}\).
11/14 = 11 fourteens.
11/14 = 2.75.
1.6 < 2.75
5 sevens are less than 11 fourteens.
5/7 < 11/14.
c. \(\frac{7}{10}\) _________ \(\frac{3}{5}\)
Answer:
\(\frac{7}{10}\) __>___ \(\frac{3}{5}\).
Explanation:
In the above-given question,
given that,
\(\frac{7}{10}\).
7/10 = 7 tenths.
7/10 = 0.7.
\(\frac{3}{5}\).
3/5 = 3 fifths.
3/5 = 0.6.
0.7 > 0.6.
7 tenths are greater than 3 fifths.
7/10 > 3/5.
d. \(\frac{2}{3}\) ________ \(\frac{9}{15}\)
Answer:
\(\frac{2}{3}\) __=___ \(\frac{9}{15}\).
Explanation:
In the above-given question,
given that,
\(\frac{2}{3}\).
2/3 = 2 thirds.
2/3 = 0.66.
\(\frac{9}{15}\).
9/15 = 9 fifteens.
9/15 = 0.6.
0.66 = 0.6.
2 thirds is equal to 9 fifteens.
2/3 = 9/15.
e. \(\frac{3}{4}\) _________ \(\frac{9}{12}\)
Answer:
\(\frac{3}{4}\) __>___ \(\frac{9}{12}\).
Explanation:
In the above-given question,
given that,
\(\frac{3}{4}\).
3/4 = 3 fourths.
3/4 = 0.75
\(\frac{9}{12}\).
9/12 = 9 twelfths.
9/12 = 0.75.
0.75 = 0.75.
3 fourths are equal to 9 twelfths.
3/4 = 9/12.
f. \(\frac{5}{3}\) ________ \(\frac{5}{2}\)
Answer:
\(\frac{5}{3}\) __<___ \(\frac{5}{2}\).
Explanation:
In the above-given question,
given that,
\(\frac{5}{3}\).
5/3 = 5 thirds.
5/3 = 1.66.
\(\frac{5}{2}\).
5/2 = 5 twos.
5/2 = 2.5.
1.66 < 2.5.
5 thirds less than 5 twos.
5/3 < 5/2.
Question 6.
Simon claims \(\frac{4}{9}\) is greater than \(\frac{1}{3}\). Ted thinks \(\frac{4}{9}\) is less than \(\frac{1}{3}\). Who is correct? Support your answer with a picture.
Answer:
\(\frac{4}{9}\) __>___ \(\frac{1}{3}\).
Explanation:
In the above-given question,
given that,
\(\frac{4}{9}\).
4/9 = 4 nines.
4/9 = 0.44.
\(\frac{1}{3}\).
1/3 = 1 thirds.
1/3 = 0.33.
0.44 > 0.33.
4 nines are greater than 1 third.
4/9 > 1/3.