Engage NY Eureka Math 4th Grade Module 5 Lesson 17 Answer Key
Eureka Math Grade 4 Module 5 Lesson 17 Problem Set Answer Key
Question 1.
Use the following three fractions to write two subtraction and two addition number sentences.
a. \(\frac{8}{5}\), \(\frac{2}{5}\), \(\frac{10}{5}\)
Answer:
Subtraction sentences = 7/5, 6/5, 1/5, -1/5, 9/5, 8/5.
Addition sentences = 9/5,10/5, 3/5, 4/5, 11/5, 12/5.
Explanation:
In the above-given question,
given that,
8/5, 2/5, 10/5.
8/5 + 1 = 9/5.
9/5 + 1 = 10/5.
2/5 + 1 = 3/5.
3/5 + 1 = 4/5.
10/5 + 1 = 11/5.
11/5 + 1 = 12/5.
8/5 – 1 = 7/5.
7/5 – 1 = 6/5.
2/5 – 1 = 1/5.
1/5 – 1 = -1/5.
10/5 – 1 = 9/5.
9/5 – 1 = 8/5.
b. \(\frac{15}{8}\), \(\frac{7}{8}\), \(\frac{8}{8}\)
Answer:
Subtraction sentences = 14/8, 13/8, 6/8, 5/8, 7/8, 6/8.
Addition sentences = 16/8,17/8, 8/8, 9/8, 9/8, 10/8.
Explanation:
In the above-given question,
given that,
15/8, 7/8, 8/8.
15/8 + 1 = 16/8.
16/8 + 1 = 17/8.
7/8 + 1 = 8/8.
8/8 + 1 = 9/8.
9/8 + 1 = 10/8.
10/8 + 1 = 11/8.
15/8 – 1 = 14/8.
14/8 – 1 = 13/8.
7/8 – 1 = 6/8.
6/8 – 1 = 5/8.
8/8 – 1 = -7/8.
7/8 – 1 = 6/8.
Question 2.
Solve. Model each subtraction problem with a number line, and solve by both counting up and subtracting. Part (a) has been completed for you.
a. 1 – \(\frac{3}{4}\)
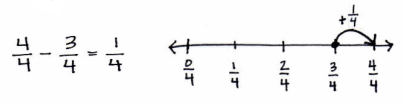
Answer:
1 – 3/4 = 1/4.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 3/4.
4 – 3/4.
1/4.
b. 1 – \(\frac{8}{10}\)
Answer:
1 – 8/10 = 2/10.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 8/10.
10 – 8/10.
2/10.
c. 1 – \(\frac{3}{5}\)
Answer:
1 – 3/5 = 2/5.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 3/5.
5 – 3/5.
2/5.
d. 1 – \(\frac{5}{8}\)
Answer:
1 – 5/8 = 3/8.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 5/8.
8 – 5/8.
3/8.
e. 1\(\frac{2}{10}\) – \(\frac{7}{10}\)
Answer:
1 – 2/10 – 7/10 = 1/10.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 2/10.
10 – 2/10.
8/10 – 7/10.
1/10.
f. 1\(\frac{1}{5}\) – \(\frac{3}{5}\)
Answer:
1 – 1/5 – 3/5 = 1/5.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 1/5.
5 – 1/5.
4/5 – 3/5.
1/5.
Question 3.
Find the difference in two ways. Use number bonds to decompose the total. Part (a) has been completed for you.
a. 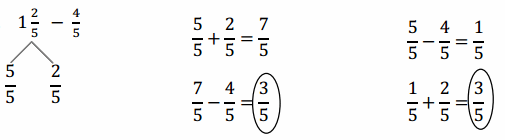
Answer:
5/5 + 2/5 = 7/5.
Explanation:
In the above-given question,
given that,
1(2/5) – 4/5.
7/5 – 4/5 = 3/5.
5/5 + 2/5 = 7/5.
7/5 – 4/5 = 3/5.
5/5 – 4/5 = 1/5.
1/5 + 2/5 = 3/5.
b. 1\(\frac{3}{6}\) – \(\frac{4}{6}\)
Answer:
6/6 + 3/6 = 9/6.
Explanation:
In the above-given question,
given that,
1(3/6) – 4/6.
9/6 – 4/6 = 5/6.
6/6 + 3/6 = 9/6.
9/6 – 4/6 = 5/6.
6/6 – 4/6 = 2/6.
2/6 + 3/6 = 5/6.
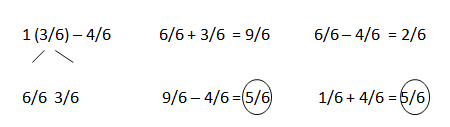
c. 1\(\frac{6}{8}\) – \(\frac{7}{8}\)
Answer:
10/8 + 4/8 = 14/8.
Explanation:
In the above-given question,
given that,
1(6/8) – 7/8.
14/8 – 7/8 = 7/8.
10/8 + 4/8 = 14/8.
14/8 – 7/8 = 7/8.
10/8 – 7/8 = 3/8.
3/8 + 4/8 = 7/8.
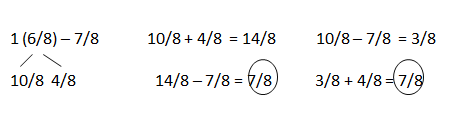
d. 1\(\frac{1}{10}\) – \(\frac{7}{10}\)
Answer:
8/10 + 3/10 = 11/10.
Explanation:
In the above-given question,
given that,
1(1/10) – 7/10.
11/10 – 7/10 = 4/10.
8/10 + 3/10 = 11/10.
11/10 – 7/10 = 4/10.
8/10 – 7/10 = 2/10.
2/10 + 3/10 = 5/10.
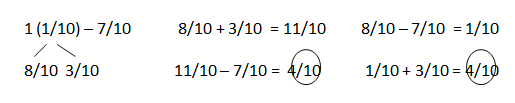
e. 1\(\frac{3}{12}\) – \(\frac{6}{12}\)
Answer:
6/12 + 3/12 = 9/12.
Explanation:
In the above-given question,
given that,
1(3/12) – 9/12.
15/12 – 9/12 = 3/12.
7/12 + 8/12 = 15/12.
9/12 – 6/12 = 3/12.
6/12 – 6/12 = 0.
6/12 + 3/12 = 9/12.
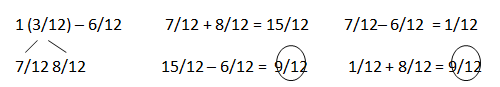
Eureka Math Grade 4 Module 5 Lesson 17 Exit Ticket Answer Key
Question 1.
Solve. Model the problem with a number line, and solve by both counting up and subtracting.
1 – \(\frac{2}{5}\)
Answer:
1 – 2/5 = 3/5.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 2/5.
5 – 2/5.
3/5.
Question 2.
Find the difference in two ways. Use a number bond to show the decomposition.
1\(\frac{2}{7}\) – \(\frac{5}{7}\)
Answer:
5/7 + 4/7 = 9/7.
Explanation:
In the above-given question,
given that,
1(2/7) – 5/7.
9/7 – 5/7 = 4/7.
5/7 + 4/7 = 9/7.
9/7 – 5/7 = 4/7.
5/7 – 4/5 = 1/7.
1/7 + 2/7 = 3/7.
Eureka Math Grade 4 Module 5 Lesson 17 Homework Answer Key
Question 1.
Use the following three fractions to write two subtraction and two addition number sentences.
a. \(\frac{5}{6}\), \(\frac{4}{6}\), \(\frac{9}{6}\)
Answer:
Subtraction sentences = 4/6, 3/6, 3/6, 2/6, 8/6, 7/6.
Addition sentences = 6/6,7/6, 5/6, 6/6, 10/6, 11/6.
Explanation:
In the above-given question,
given that,
5/6, 4/6, 9/6.
5/6 + 1 = 6/6.
6/6 + 1 = 7/6.
4/6 + 1 = 5/6.
5/6 + 1 = 6/6.
9/6 + 1 = 10/6.
10/6 + 1 = 11/6.
5/6 – 1 = 4/6.
4/6 – 1 = 3/6.
4/6 – 1 = 3/6.
3/6 – 1 = 2/6.
9/6 – 1 = -8/6.
8/6 – 1 = 7/6.
b. \(\frac{5}{9}\), \(\frac{13}{9}\), \(\frac{8}{9}\)
Answer:
Subtraction sentences = 4/9, 3/9, 12/9, 11/9, 7/9, 6/9.
Addition sentences = 6/9,7/9, 14/9, 15/9, 9/9, 10/9.
Explanation:
In the above-given question,
given that,
5/9, 13/9, 8/9.
5/9 + 1 = 6/9.
6/9 + 1 = 7/9.
13/9 + 1 = 14/9.
14/9 + 1 = 15/9.
8/9 + 1 = 9/9.
9/9 + 1 = 10/9.
5/9 – 1 = 4/9.
4/9 – 1 = 3/9.
13/9 – 1 = 12/9.
12/9 – 1 = 11/9.
8/9 – 1 = 7/9.
7/9 – 1 = 6/9.
Question 2.
Solve. Model each subtraction problem with a number line, and solve by both counting up and subtracting.
a. 1 – \(\frac{5}{8}\)
Answer:
1 – 5/8 = 3/8.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 5/8.
8 – 5/8.
3/8.
b. 1 – \(\frac{2}{5}\)
Answer:
1 – 2/5 = 3/5.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 2/5.
5 – 2/5.
3/5.
c. 1\(\frac{3}{6}\) – \(\frac{5}{6}\)
Answer:
1 – 3/6 – 5/6 = -2/6.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 3/6.
6 – 3/6.
3/6 – 5/6.
-2/6.
d. 1 – \(\frac{1}{4}\)
Answer:
1 – 1/4 = 3/4.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 1/4.
4 – 1/4.
3/4.
e. 1\(\frac{1}{3}\) – \(\frac{2}{3}\)
Answer:
1 – 1/3 – 2/3 = 0.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 1/3.
3 – 1/3.
2/3 – 2/3.
0
f. 1\(\frac{1}{5}\) – \(\frac{2}{5}\)
Answer:
1 – 1/5 – 2/5 = 2/5.
Explanation:
In the above-given question,
given that,
Model each subtraction problem with a number line.
1 – 1/5.
5 – 1/5.
4/5 – 2/5.
2/5.
Question 3.
Find the difference in two ways. Use number bonds to decompose the total. Part (a) has been completed for you.
a. 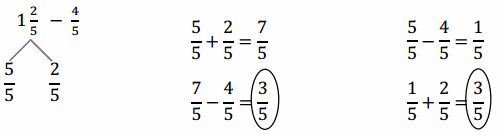
b. 1\(\frac{3}{8}\) – \(\frac{7}{8}\)
Answer:
8/8 + 3/8 = 11/8.
Explanation:
In the above-given question,
given that,
1(3/8) – 7/8.
11/8 – 7/8 = 4/8.
8/8 + 3/8 = 11/8.
11/8 – 7/8 = 4/8.
8/8 – 7/8 = 1/8.
1/8 + 3/8 = 4/8.
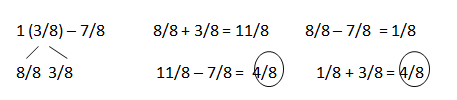
c. 1\(\frac{1}{4}\) – \(\frac{3}{4}\)
Answer:
8/10 + 3/10 = 11/10.
Explanation:
In the above-given question,
given that,
1(1/4) – 3/4.
5/4 – 3/4 = 2/4.
3/4 + 2/4 = 5/4.
5/4 – 3/4 = 2/4.
3/4 – 3/4 = 0.
0 + 2/4 = 2/4.
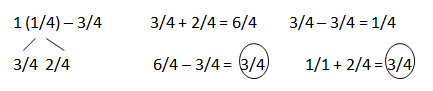
d. 1\(\frac{2}{7}\) – \(\frac{5}{7}\)
Answer:
6/7 + 3/7 = 9/7.
Explanation:
In the above-given question,
given that,
1(2/7) – 5/7.
9/7 – 2/7 = 7/7.
6/7 + 3/7 = 9/7.
9/7 – 2/7 = 7/7.
6/7 – 2/7 = 4/7.
4/7 + 3/7 = 7/7.
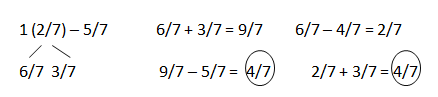
e. 1\(\frac{3}{10}\) – \(\frac{7}{10}\)
Answer:
8/10 + 3/10 = 11/10.
Explanation:
In the above-given question,
given that,
1(3/10) – 7/10.
13/10 – 7/10 = 6/10.
7/10 + 6/10 = 13/10.
13/10 – 7/10 = 6/10.
7/10 – 7/10 = 0.
0 + 6/10 = 6/10.