Engage NY Eureka Math 5th Grade Module 3 Lesson 6 Answer Key
Eureka Math Grade 5 Module 3 Lesson 6 Problem Set Answer Key
Question 1.
For the following problems, draw a picture using the rectangular fraction model and write the answer. Simplify your answer, if possible.
a. 1\(\frac{1}{4}\) – \(\frac{1}{3}\) =
b. 1\(\frac{1}{5}\) – \(\frac{1}{3}\) =
c. 1\(\frac{3}{8}\) – \(\frac{1}{2}\) =
d. 1\(\frac{2}{5}\) – \(\frac{1}{2}\) =
e. 1\(\frac{2}{7}\) – \(\frac{1}{3}\) =
f. 1\(\frac{2}{3}\) – \(\frac{3}{5}\) =
Answer:
a.
1\(\frac{1}{4}\) – \(\frac{1}{3}\) = \(\frac{5}{4}\) – \(\frac{1}{3}\)
lcm of 4 and 3 is 12 .
\(\frac{15}{12}\) – \(\frac{4}{12}\) = \(\frac{11}{12}\).
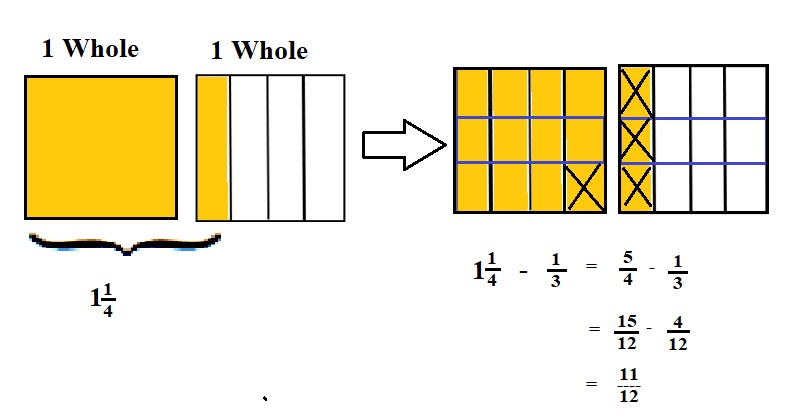
Explanation :
The Rectangle is divided into 4 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{1}{4}\) .
1\(\frac{1}{4}\) and \(\frac{1}{3}\) have lcm 12 so, the rectangle is divided into 12 parts by drawing 2 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts represent the difference of the given fraction to its total parts .
b.
1\(\frac{1}{5}\) – \(\frac{1}{3}\) = \(\frac{6}{5}\) – \(\frac{1}{3}\)
lcm of 5 and 3 is 15 .
\(\frac{18}{15}\) – \(\frac{5}{15}\) = \(\frac{13}{15}\)
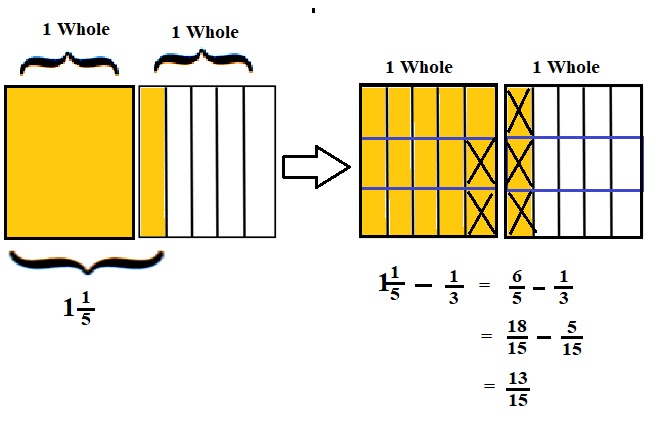
Explanation :
The Rectangle is divided into 5 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{1}{5}\) .
1\(\frac{1}{5}\) and \(\frac{1}{3}\) have lcm 15 so, the rectangle is divided into 15 parts by drawing 2 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts represent the difference of the given fraction to its total parts .
c.
1\(\frac{3}{8}\) – \(\frac{1}{2}\) = \(\frac{11}{8}\) – \(\frac{1}{2}\)
lcm of 8 and 2 is 8 .
\(\frac{11}{8}\) – \(\frac{4}{8}\) =\(\frac{7}{8}\) .
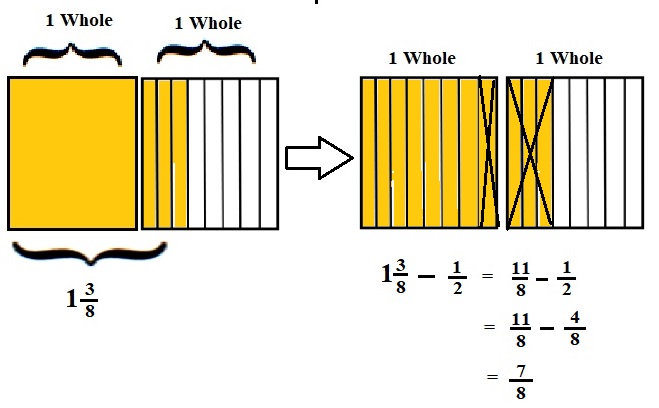
Explanation :
The Rectangle is divided into 8 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{3}{8}\) .
1\(\frac{3}{8}\) and \(\frac{1}{2}\) have lcm 8 so, the rectangle is divided into 8 parts . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts represent the difference of the given fraction to its total parts .
d.
1\(\frac{2}{5}\) – \(\frac{1}{2}\) = \(\frac{7}{5}\) – \(\frac{1}{2}\)
lcm of 5 and 2 is 10.
\(\frac{14}{10}\) – \(\frac{5}{10}\) = \(\frac{9}{10}\)
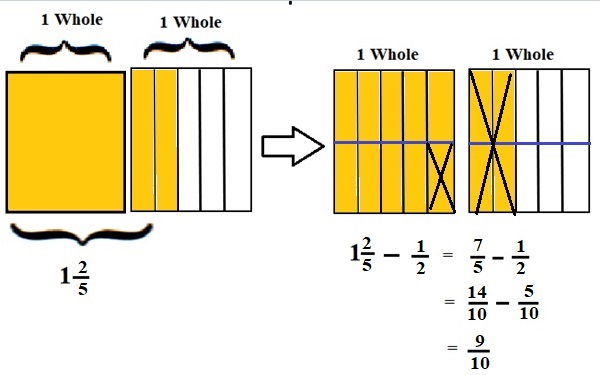
Explanation :
The Rectangle is divided into 5 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{2}{5}\) .
1\(\frac{2}{5}\) and \(\frac{1}{2}\) have lcm 10 so, the rectangle is divided into 10 parts by drawing 1 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts represent the difference of the given fraction to its total parts .
e.
1\(\frac{2}{7}\) – \(\frac{1}{3}\) = \(\frac{9}{7}\) – \(\frac{1}{3}\)
lcm of 7 and 3 is 21 .
\(\frac{27}{21}\) – \(\frac{7}{21}\) = \(\frac{20}{21}\) .
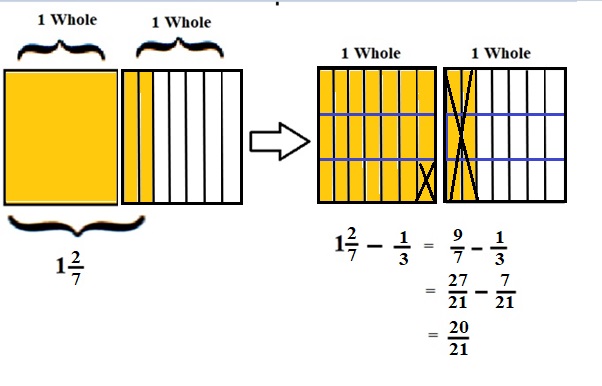
Explanation :
The Rectangle is divided into 7 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{2}{7}\) .
1\(\frac{2}{7}\) and \(\frac{1}{3}\) have lcm 21 so, the rectangle is divided into 21 parts by drawing 2 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts represent the difference of the given fraction to its total parts .
f.
1\(\frac{2}{3}\) – \(\frac{3}{5}\) = \(\frac{5}{3}\) – \(\frac{3}{5}\)
lcm of 3 and 5 is 15 .
\(\frac{25}{15}\) – \(\frac{9}{15}\) = \(\frac{16}{15}\)
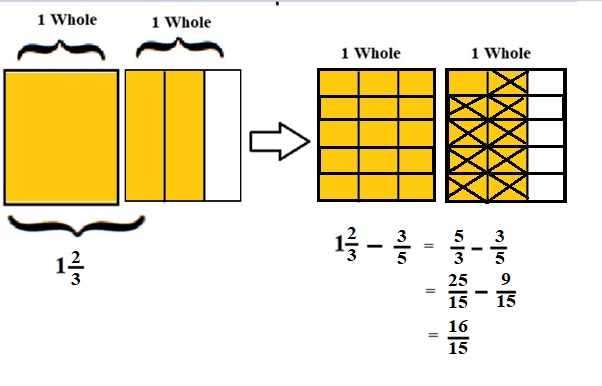
Explanation :
The Rectangle is divided into 5 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{2}{3}\) .
1\(\frac{2}{3}\) and \(\frac{3}{5}\) have lcm 15 so, the rectangle is divided into 15 parts by drawing 4 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts represent the difference of the given fraction to its total parts .
Question 2.
Jean-Luc jogged around the lake in 1\(\frac{1}{4}\) hour. William jogged the same distance in \(\frac{5}{6}\) hour. How much longer did Jean-Luc take than William in hours?
Answer:
Time taken to jog for Jean-Luc = 1\(\frac{1}{4}\) hour .
Time taken to jog for William = \(\frac{5}{6}\) hour .
Time taken by Jean-Luc than William = 1\(\frac{1}{4}\) – \(\frac{5}{6}\) = \(\frac{5}{4}\) – \(\frac{5}{6}\) = \(\frac{30}{24}\) – \(\frac{20}{24}\) = \(\frac{10}{24}\) = \(\frac{5}{12}\) hour .
Question 3.
Is it true that 1\(\frac{2}{5}\) – \(\frac{3}{4}\) = \(\frac{1}{4}\) + \(\frac{2}{5}\)? Prove your answer.
Answer:
Yes , 1\(\frac{2}{5}\) – \(\frac{3}{4}\) = \(\frac{1}{4}\) + \(\frac{2}{5}\)
Explanation :
1\(\frac{2}{5}\) – \(\frac{3}{4}\) = \(\frac{7}{5}\) – \(\frac{3}{4}\) = \(\frac{28}{20}\) – \(\frac{15}{20}\) = \(\frac{13}{20}\) .
\(\frac{1}{4}\) + \(\frac{2}{5}\) = \(\frac{5}{20}\) + \(\frac{8}{20}\) = \(\frac{13}{20}\)
Therefore, 1\(\frac{2}{5}\) – \(\frac{3}{4}\) = \(\frac{1}{4}\) + \(\frac{2}{5}\) = \(\frac{13}{20}\) .
Eureka Math Grade 5 Module 3 Lesson 6 Exit Ticket Answer Key
For the following problems, draw a picture using the rectangular fraction model and write the answer. Simplify your answer, if possible.
a. 1\(\frac{1}{5}\) – \(\frac{1}{2}\) =
b. 1\(\frac{1}{3}\) – \(\frac{5}{6}\) =
Answer:
a.
1\(\frac{1}{5}\) – \(\frac{1}{2}\) = \(\frac{6}{5}\) – \(\frac{1}{2}\)
lcm of 5 and 2 is 10 .
\(\frac{12}{10}\) – \(\frac{5}{10}\) = \(\frac{7}{10}\)
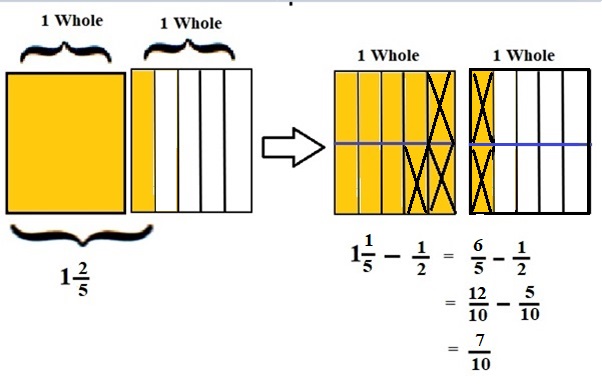
Explanation :
The Rectangle is divided into 5 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{2}{5}\) .
1\(\frac{2}{5}\) and \(\frac{1}{2}\) have lcm 10 so, the rectangle is divided into 10 parts by drawing 1 horizontal line . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts represent the difference of the given fraction to its total parts .
b.
1\(\frac{1}{3}\) – \(\frac{5}{6}\) = \(\frac{4}{3}\) – \(\frac{5}{6}\)
lcm of 3 and 6 is 6 .
\(\frac{8}{6}\) – \(\frac{5}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
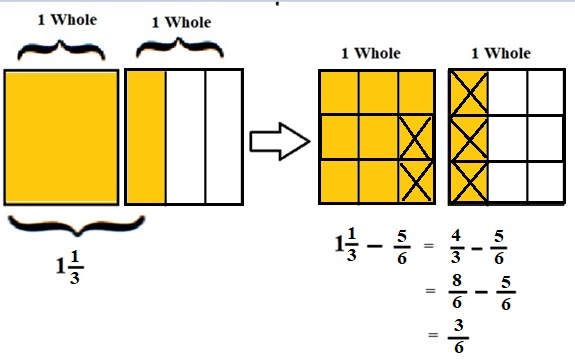
Explanation :
The Rectangle is divided into 3 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{1}{3}\) .
1\(\frac{1}{3}\) and \(\frac{5}{6}\) have lcm 6 so, the rectangle is divided into 6 parts by drawing 2 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts represent the difference of the given fraction to its total parts .
Eureka Math Grade 5 Module 3 Lesson 6 Homework Answer Key
Question 1.
For the following problems, draw a picture using the rectangular fraction model and write the answer. Simplify your answer, if possible.
a. 1 – \(\frac{5}{6}\) =
b. \(\frac{3}{2}\) – \(\frac{5}{6}\) =
c. \(\frac{4}{3}\) – \(\frac{5}{7}\) =
d. 1\(\frac{1}{8}\) – \(\frac{3}{5}\) =
e. 1\(\frac{2}{5}\) – \(\frac{3}{4}\) =
f. 1\(\frac{5}{6}\) – \(\frac{7}{8}\) =
g. \(\frac{9}{7}\) – \(\frac{3}{4}\) =
h. 1\(\frac{3}{12}\) – \(\frac{2}{3}\) =
Answer:
a.
1 – \(\frac{5}{6}\)
lcm of 1 and 6 is 6 .
\(\frac{6}{6}\) – \(\frac{5}{6}\) = \(\frac{1}{6}\) .
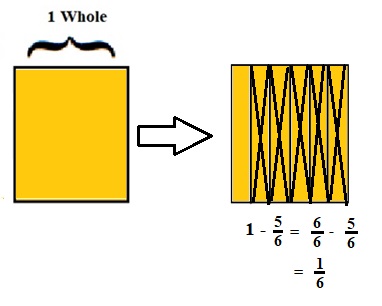
Explanation :
The Rectangle is divided into 6 parts using vertical lines and shaded to represent the fraction \(\frac{6}{6}\) .
1 and \(\frac{5}{6}\) have lcm 6 . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts without x marks represent the difference of the given fraction to its total parts .
b.
\(\frac{3}{2}\) – \(\frac{5}{6}\)
lcm of 2 and 6 is 6 .
\(\frac{9}{6}\) – \(\frac{5}{6}\) = \(\frac{4}{6}\) = \(\frac{2}{3}\)
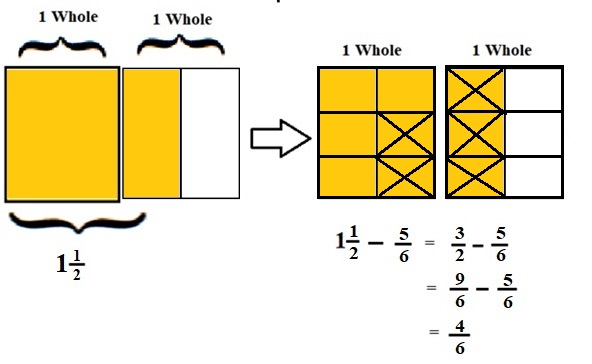
Explanation :
The Rectangle is divided into 2 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{1}{2}\) .
1\(\frac{1}{2}\) and \(\frac{5}{6}\) have lcm 6 so, the rectangle is divided into 6 parts by drawing 2 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts without x marks represent the difference of the given fraction to its total parts .
c.
\(\frac{4}{3}\) – \(\frac{5}{7}\)
lcm of 3 and 7 is 21 .
\(\frac{28}{21}\) – \(\frac{15}{21}\) = \(\frac{13}{21}\)
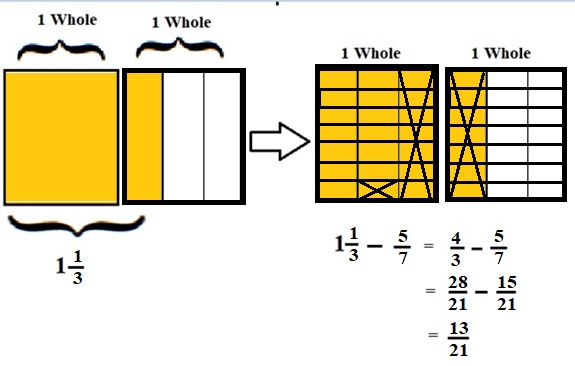
Explanation :
The Rectangle is divided into 3 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{1}{3}\) .
1\(\frac{1}{3}\) and \(\frac{5}{7}\) have lcm 21 so, the rectangle is divided into 21 parts by drawing 6 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts without x marks represent the difference of the given fraction to its total parts .
d.
1\(\frac{1}{8}\) – \(\frac{3}{5}\) = \(\frac{9}{8}\) – \(\frac{3}{5}\)
lcm of 8 and 5 is 40
\(\frac{45}{40}\) – \(\frac{24}{40}\) = \(\frac{21}{40}\)
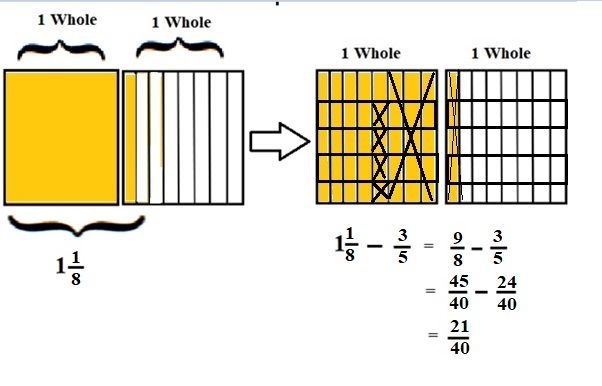
Explanation :
The Rectangle is divided into 8 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{1}{8}\) .
1\(\frac{1}{8}\) and \(\frac{3}{5}\) have lcm 40 so, the rectangle is divided into 40 parts by drawing 4 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts without x marks represent the difference of the given fraction to its total parts .
e.
1\(\frac{2}{5}\) – \(\frac{3}{4}\) = \(\frac{7}{5}\) – \(\frac{3}{4}\)
lcm of 5 and 4 is 20 .
\(\frac{28}{20}\) – \(\frac{15}{20}\) = \(\frac{13}{20}\) .
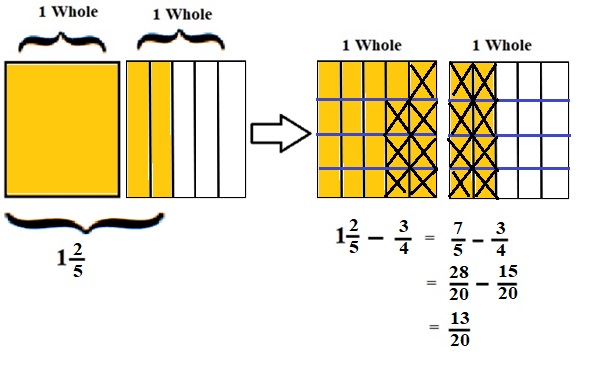
Explanation :
The Rectangle is divided into 5 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{2}{5}\) .
1\(\frac{2}{5}\) and \(\frac{3}{4}\) have lcm 20 so, the rectangle is divided into 20 parts by drawing 3 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts without x marks represent the difference of the given fraction to its total parts .
f.
1\(\frac{5}{6}\) – \(\frac{7}{8}\) = \(\frac{11}{6}\) – \(\frac{7}{8}\)
lcm of 6 and 8 is 24 .
\(\frac{44}{24}\) – \(\frac{21}{24}\) = \(\frac{23}{24}\) .
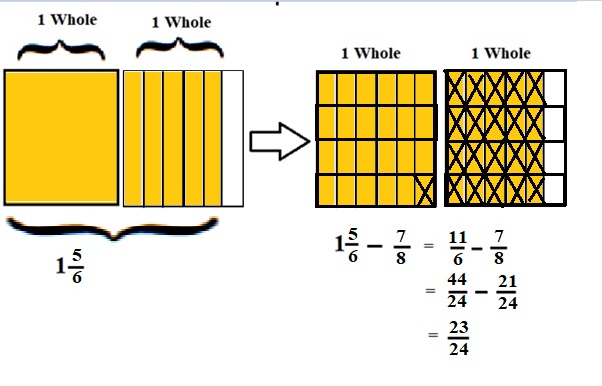
Explanation :
The Rectangle is divided into 6 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{5}{6}\) .
1\(\frac{5}{6}\) and \(\frac{7}{8}\) have lcm 24 so, the rectangle is divided into 24 parts by drawing 3 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts without x marks represent the difference of the given fraction to its total parts .
g.
\(\frac{9}{7}\) – \(\frac{3}{4}\)
lcm of 7 and 4 is 28 .
\(\frac{36}{28}\) – \(\frac{21}{28}\) = \(\frac{15}{28}\)
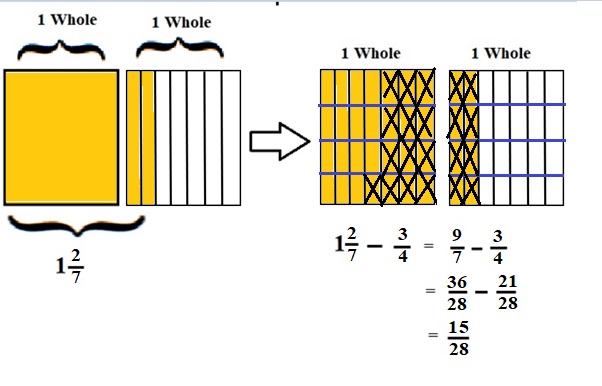
Explanation :
The Rectangle is divided into 7 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{2}{7}\) .
1\(\frac{2}{7}\) and \(\frac{3}{4}\) have lcm 28 so, the rectangle is divided into 28 parts by drawing 3 horizontal lines . after making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts without x marks represent the difference of the given fractions to its total parts .
h.
1\(\frac{3}{12}\) – \(\frac{2}{3}\) = \(\frac{15}{12}\) – \(\frac{2}{3}\)
lcm of 12 and 3 is 12 .
\(\frac{15}{12}\) – \(\frac{8}{12}\) = \(\frac{7}{12}\)
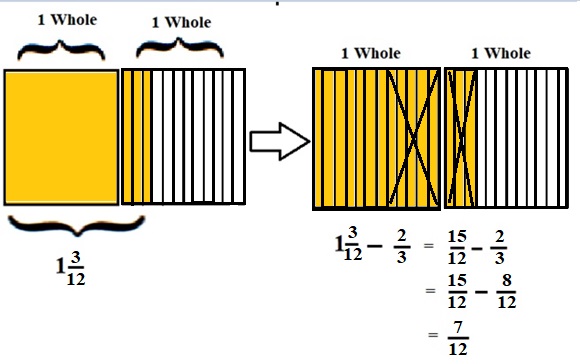
Explanation :
The Rectangle is divided into 12 parts using vertical lines and 2 rectangles are drawn and shaded to represent the fraction 1\(\frac{3}{12}\) .
1\(\frac{3}{12}\) and \(\frac{2}{3}\) have lcm 12 . After making lcm equal then subtraction is done and subtraction is done by showing x-mark on the shaded parts.
The left over shaded parts without x marks represent the difference of the given fractions to its total parts .
Question 2.
Sam had 1\(\frac{1}{2}\) m of rope. He cut off \(\frac{5}{8}\) m and used it for a project. How much rope does Sam have left?
Answer:
Length of Rope with Sam = 1\(\frac{1}{2}\) m
Length of rope used for project = \(\frac{5}{8}\) m
Length of Rope left = 1\(\frac{1}{2}\) – \(\frac{5}{8}\) = \(\frac{3}{2}\) – \(\frac{5}{8}\) =
\(\frac{12}{8}\) – \(\frac{5}{8}\) = \(\frac{7}{8}\) .
Therefore, Length of rope left with sam = \(\frac{7}{8}\) m .
Question 3.
Jackson had 1\(\frac{3}{8}\) kg of fertilizer. He used some to fertilize a flower bed, and he only had \(\frac{2}{3}\) kg left. How much fertilizer was used in the flower bed?
Answer:
Quantity of fertilizers with Jackson = 1\(\frac{3}{8}\) kg
Quantity of fertilizers left = \(\frac{2}{3}\) kg .
Quantity of Fertilizers used for flower bed = 1\(\frac{3}{8}\) kg – \(\frac{2}{3}\) kg = \(\frac{11}{8}\) – \(\frac{2}{3}\) = \(\frac{33}{24}\) – \(\frac{16}{24}\) = \(\frac{17}{24}\) .
Therefore, Quantity of Fertilizers used for flower bed =\(\frac{17}{24}\)