Engage NY Eureka Math 5th Grade Module 3 Lesson 9 Answer Key
Eureka Math Grade 5 Module 3 Lesson 9 Sprint Answer Key
A
Add and Subtract Fractions with Like Units
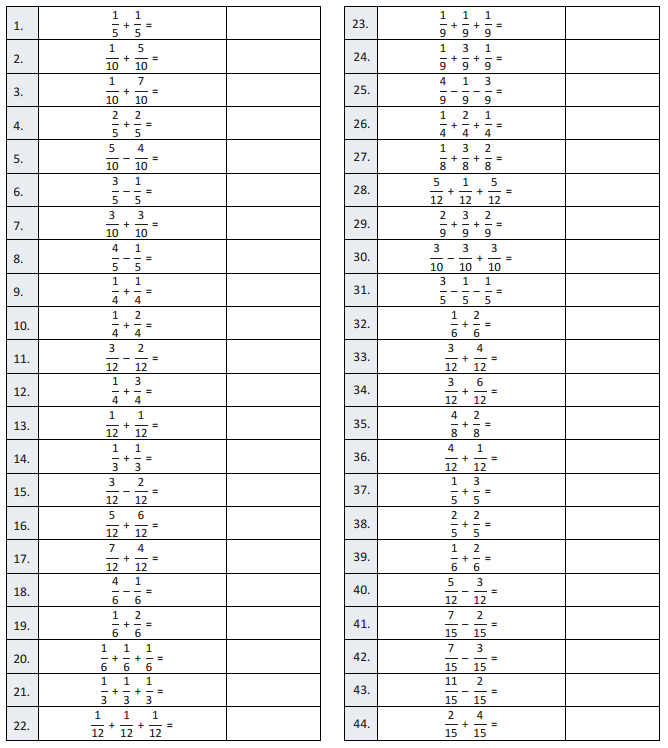
Question 1.
\(\frac{1}{5}\) + \(\frac{1}{5}\) =
Answer:
\(\frac{1}{5}\) + \(\frac{1}{5}\) = \(\frac{2}{5}\)
Question 2.
\(\frac{1}{10}\) + \(\frac{5}{10}\) =
Answer:
\(\frac{1}{10}\) + \(\frac{5}{10}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\)
Question 3.
\(\frac{1}{10}\) + \(\frac{7}{10}\) =
Answer:
\(\frac{1}{10}\) + \(\frac{7}{10}\) = \(\frac{8}{10}\) = \(\frac{4}{5}\)
Question 4.
\(\frac{2}{5}\) + \(\frac{2}{5}\) =
Answer:
\(\frac{2}{5}\) + \(\frac{2}{5}\) = \(\frac{4}{5}\)
Question 5.
\(\frac{5}{10}\) – \(\frac{4}{10}\) =
Answer:
\(\frac{5}{10}\) – \(\frac{4}{10}\) = \(\frac{1}{10}\)
Question 6.
\(\frac{3}{5}\) – \(\frac{1}{5}\) =
Answer:
\(\frac{3}{5}\) – \(\frac{1}{5}\) = \(\frac{2}{5}\)
Question 7.
\(\frac{3}{10}\) + \(\frac{3}{10}\) =
Answer:
\(\frac{3}{10}\) + \(\frac{3}{10}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\)
Question 8.
\(\frac{4}{5}\) – \(\frac{1}{5}\) =
Answer:
\(\frac{4}{5}\) – \(\frac{1}{5}\) = \(\frac{3}{5}\)
Question 9.
\(\frac{1}{4}\) + \(\frac{1}{4}\) =
Answer:
\(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\)
Question 10.
\(\frac{1}{4}\) + \(\frac{2}{4}\) =
Answer:
\(\frac{1}{4}\) + \(\frac{2}{4}\) = \(\frac{3}{4}\)
Question 11.
\(\frac{3}{12}\) – \(\frac{2}{12}\) =
Answer:
\(\frac{3}{12}\) – \(\frac{2}{12}\) = \(\frac{1}{12}\)
Question 12.
\(\frac{1}{4}\) + \(\frac{3}{4}\) =
Answer:
\(\frac{1}{4}\) + \(\frac{3}{4}\) = \(\frac{4}{4}\) = 1
Question 13.
\(\frac{1}{12}\) + \(\frac{1}{12}\) =
Answer:
\(\frac{1}{12}\) + \(\frac{1}{12}\) = \(\frac{2}{12}\) = \(\frac{1}{6}\)
Question 14.
\(\frac{1}{3}\) + \(\frac{1}{3}\) =
Answer:
\(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\)
Question 15.
\(\frac{3}{12}\) – \(\frac{2}{12}\) =
Answer:
\(\frac{3}{12}\) – \(\frac{2}{12}\) = \(\frac{1}{12}\)
Question 16.
\(\frac{5}{12}\) + \(\frac{6}{12}\) =
Answer:
\(\frac{5}{12}\) + \(\frac{6}{12}\) = \(\frac{11}{12}\)
Question 17.
\(\frac{7}{12}\) + \(\frac{4}{12}\) =
Answer:
\(\frac{7}{12}\) + \(\frac{4}{12}\) = \(\frac{11}{12}\)
Question 18.
\(\frac{4}{6}\) – \(\frac{1}{6}\) =
Answer:
\(\frac{4}{6}\) – \(\frac{1}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
Question 19.
\(\frac{1}{6}\) + \(\frac{2}{6}\) =
Answer:
\(\frac{1}{6}\) + \(\frac{2}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
Question 20.
\(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) =
Answer:
\(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
Question 21.
\(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) =
Answer:
\(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{3}{3}\) = 1
Question 22.
\(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) =
Answer:
\(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
Question 23.
\(\frac{1}{9}\) + \(\frac{1}{9}\) + \(\frac{1}{9}\) =
Answer:
\(\frac{1}{9}\) + \(\frac{1}{9}\) + \(\frac{1}{9}\) = \(\frac{3}{9}\) = \(\frac{1}{3}\)
Question 24.
\(\frac{1}{9}\) + \(\frac{3}{9}\) + \(\frac{1}{9}\) =
Answer:
\(\frac{1}{9}\) + \(\frac{3}{9}\) + \(\frac{1}{9}\) = \(\frac{5}{9}\)
Question 25.
\(\frac{4}{9}\) – \(\frac{1}{9}\) – \(\frac{3}{9}\) =
Answer:
\(\frac{4}{9}\) – \(\frac{1}{9}\) – \(\frac{3}{9}\) = \(\frac{8}{9}\)
Question 26.
\(\frac{1}{4}\) + \(\frac{2}{4}\) + \(\frac{1}{4}\) =
Answer:
\(\frac{1}{4}\) + \(\frac{2}{4}\) + \(\frac{1}{4}\) = \(\frac{4}{4}\) = 1
Question 27.
\(\frac{1}{8}\) + \(\frac{3}{8}\) + \(\frac{2}{8}\) =
Answer:
\(\frac{1}{8}\) + \(\frac{3}{8}\) + \(\frac{2}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)
Question 28.
\(\frac{5}{12}\) + \(\frac{1}{12}\) + \(\frac{5}{12}\) =
Answer:
\(\frac{5}{12}\) + \(\frac{1}{12}\) + \(\frac{5}{12}\) = \(\frac{11}{12}\)
Question 29.
\(\frac{2}{9}\) + \(\frac{3}{9}\) + \(\frac{2}{9}\) =
Answer:
\(\frac{2}{9}\) + \(\frac{3}{9}\) + \(\frac{2}{9}\) = \(\frac{7}{9}\)
Question 30.
\(\frac{3}{10}\) – \(\frac{3}{10}\) + \(\frac{3}{10}\) =
Answer:
\(\frac{3}{10}\) – \(\frac{3}{10}\) + \(\frac{3}{10}\) = \(\frac{9}{10}\)
Question 31.
\(\frac{3}{5}\) – \(\frac{1}{5}\) – \(\frac{1}{5}\) =
Answer:
\(\frac{3}{5}\) – \(\frac{1}{5}\) – \(\frac{1}{5}\) = \(\frac{3}{5}\) – \(\frac{2}{5}\) = \(\frac{1}{5}\)
Question 32.
\(\frac{1}{6}\) + \(\frac{2}{6}\) =
Answer:
\(\frac{1}{6}\) + \(\frac{2}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\) =\
Question 33.
\(\frac{3}{12}\) + \(\frac{4}{12}\) =
Answer:
\(\frac{3}{12}\) + \(\frac{4}{12}\) = \(\frac{7}{12}\)
Question 34.
\(\frac{3}{12}\) + \(\frac{6}{12}\) =
Answer:
\(\frac{3}{12}\) + \(\frac{6}{12}\) = \(\frac{9}{12}\) = \(\frac{3}{4}\)
Question 35.
\(\frac{4}{8}\) + \(\frac{2}{8}\) =
Answer:
\(\frac{4}{8}\) + \(\frac{2}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)
Question 36.
\(\frac{4}{12}\) + \(\frac{1}{12}\) =
Answer:
\(\frac{4}{12}\) + \(\frac{1}{12}\) = \(\frac{5}{12}\)
Question 37.
\(\frac{1}{5}\) + \(\frac{3}{5}\) =
Answer:
\(\frac{1}{5}\) + \(\frac{3}{5}\) = \(\frac{4}{5}\)
Question 38.
\(\frac{2}{5}\) + \(\frac{2}{5}\) =
Answer:
\(\frac{2}{5}\) + \(\frac{2}{5}\) = \(\frac{4}{5}\)
Question 39.
\(\frac{1}{6}\) + \(\frac{2}{6}\) =
Answer:
\(\frac{1}{6}\) + \(\frac{2}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
Question 40.
\(\frac{5}{12}\) – \(\frac{3}{12}\) =
Answer:
\(\frac{5}{12}\) – \(\frac{3}{12}\) = \(\frac{2}{12}\) = \(\frac{1}{6}\)
Question 41.
\(\frac{7}{15}\) – \(\frac{2}{15}\) =
Answer:
\(\frac{7}{15}\) – \(\frac{2}{15}\) = \(\frac{5}{15}\) = \(\frac{1}{3}\)
Question 42.
\(\frac{7}{15}\) – \(\frac{3}{15}\) =
Answer:
\(\frac{7}{15}\) – \(\frac{3}{15}\) = \(\frac{4}{15}\)
Question 43.
\(\frac{11}{15}\) – \(\frac{2}{15}\) =
Answer:
\(\frac{11}{15}\) – \(\frac{2}{15}\) = \(\frac{9}{15}\)
Question 44.
\(\frac{2}{15}\) + \(\frac{4}{15}\) =
Answer:
\(\frac{2}{15}\) + \(\frac{4}{15}\) = \(\frac{6}{15}\) = \(\frac{2}{5}\)
B
Add and Subtract Fractions with Like Units
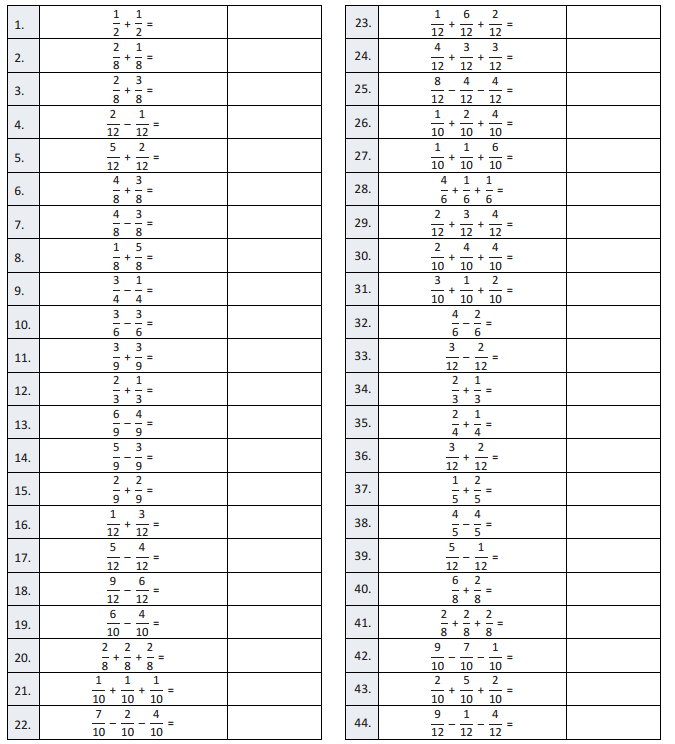
Question 1.
\(\frac{1}{2}\) + \(\frac{1}{2}\) =
Answer:
\(\frac{1}{2}\) + \(\frac{1}{2}\) = \(\frac{2}{2}\) = 1
Question 2.
\(\frac{2}{8}\) + \(\frac{1}{8}\) =
Answer:
\(\frac{2}{8}\) + \(\frac{1}{8}\) = \(\frac{3}{8}\)
Question 3.
\(\frac{2}{8}\) + \(\frac{3}{8}\) =
Answer:
\(\frac{2}{8}\) + \(\frac{3}{8}\) = \(\frac{5}{8}\)
Question 4.
\(\frac{2}{12}\) – \(\frac{1}{12}\) =
Answer:
\(\frac{2}{12}\) – \(\frac{1}{12}\) = \(\frac{1}{12}\)
Question 5.
\(\frac{5}{12}\) + \(\frac{2}{12}\) =
Answer:
\(\frac{5}{12}\) + \(\frac{2}{12}\) = \(\frac{7}{12}\)
Question 6.
\(\frac{4}{8}\) – \(\frac{3}{8}\) =
Answer:
\(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\)
Question 7.
\(\frac{4}{8}\) – \(\frac{3}{8}\) =
Answer:
\(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\)
Question 8.
\(\frac{1}{8}\) + \(\frac{5}{8}\) =
Answer:
\(\frac{1}{8}\) + \(\frac{5}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)
Question 9.
\(\frac{3}{4}\) – \(\frac{1}{4}\) =
Answer:
\(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\)
Question 10.
\(\frac{3}{6}\) – \(\frac{3}{6}\) =
Answer:
\(\frac{3}{6}\) – \(\frac{3}{6}\) = 0
Question 11.
\(\frac{3}{9}\) + \(\frac{3}{9}\) =
Answer:
\(\frac{3}{9}\) + \(\frac{3}{9}\) = \(\frac{6}{9}\) = \(\frac{2}{3}\)
Question 12.
\(\frac{2}{3}\) + \(\frac{1}{3}\) =
Answer:
\(\frac{2}{3}\) + \(\frac{1}{3}\) = \(\frac{3}{3}\) = 1
Question 13.
\(\frac{6}{9}\) – \(\frac{4}{9}\) =
Answer:
\(\frac{6}{9}\) – \(\frac{4}{9}\) = \(\frac{2}{9}\)
Question 14.
\(\frac{5}{9}\) – \(\frac{3}{9}\) =
Answer:
\(\frac{5}{9}\) – \(\frac{3}{9}\) = \(\frac{2}{9}\)
Question 15.
\(\frac{2}{9}\) + \(\frac{2}{9}\) =
Answer:
\(\frac{2}{9}\) + \(\frac{2}{9}\) = \(\frac{4}{9}\)
Question 16.
\(\frac{1}{12}\) + \(\frac{3}{12}\) =
Answer:
\(\frac{1}{12}\) + \(\frac{3}{12}\) = \(\frac{4}{12}\) = \(\frac{1}{4}\)
Question 17.
\(\frac{5}{12}\) – \(\frac{4}{12}\) =
Answer:
\(\frac{5}{12}\) – \(\frac{4}{12}\) = \(\frac{1}{12}\)
Question 18.
\(\frac{9}{12}\) – \(\frac{6}{12}\) =
Answer:
\(\frac{9}{12}\) – \(\frac{6}{12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
Question 19.
\(\frac{6}{10}\) – \(\frac{4}{10}\) =
Answer:
\(\frac{6}{10}\) – \(\frac{4}{10}\) = \(\frac{2}{10}\) = \(\frac{1}{5}\)
Question 20.
\(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{2}{8}\) =
Answer:
\(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{2}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)
Question 21.
\(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) =
Answer:
\(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\) = \(\frac{3}{10}\) +
Question 22.
\(\frac{7}{12}\) – \(\frac{2}{10}\) – \(\frac{4}{10}\) =
Answer:
\(\frac{7}{12}\) – \(\frac{2}{10}\) – \(\frac{4}{10}\) = \(\frac{7}{12}\) – \(\frac{6}{10}\) = \(\frac{1}{10}\)
Question 23.
\(\frac{1}{12}\) + \(\frac{6}{12}\) + \(\frac{2}{12}\) =
Answer:
\(\frac{1}{12}\) + \(\frac{6}{12}\) + \(\frac{2}{12}\) = \(\frac{9}{12}\) = \(\frac{3}{4}\)
Question 24.
\(\frac{4}{12}\) + \(\frac{3}{12}\) + \(\frac{3}{12}\) =
Answer:
\(\frac{4}{12}\) + \(\frac{3}{12}\) + \(\frac{3}{12}\) = \(\frac{10}{12}\) = \(\frac{5}{6}\)
Question 25.
\(\frac{8}{12}\) – \(\frac{4}{12}\) – \(\frac{4}{12}\) =
Answer:
\(\frac{8}{12}\) – \(\frac{4}{12}\) – \(\frac{4}{12}\) = \(\frac{8}{12}\) – \(\frac{8}{12}\) = 0
Question 26.
\(\frac{1}{10}\) + \(\frac{2}{10}\) + \(\frac{4}{10}\) =
Answer:
\(\frac{1}{10}\) + \(\frac{2}{10}\) + \(\frac{4}{10}\) = \(\frac{7}{10}\)
Question 27.
\(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{6}{10}\) =
Answer:
\(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{6}{10}\) = \(\frac{8}{10}\) = \(\frac{4}{5}\)
Question 28.
\(\frac{4}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) =
Answer:
\(\frac{4}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{6}{6}\) = 1
Question 29.
\(\frac{2}{12}\) + \(\frac{3}{12}\) + \(\frac{4}{12}\) =
Answer:
\(\frac{2}{12}\) + \(\frac{3}{12}\) + \(\frac{4}{12}\) = \(\frac{9}{12}\) = \(\frac{3}{4}\)
Question 30.
\(\frac{2}{10}\) + \(\frac{4}{10}\) + \(\frac{4}{10}\) =
Answer:
\(\frac{2}{10}\) + \(\frac{4}{10}\) + \(\frac{4}{10}\) = \(\frac{10}{10}\) = 1
Question 31.
\(\frac{3}{10}\) + \(\frac{1}{10}\) + \(\frac{2}{10}\) =
Answer:
\(\frac{3}{10}\) + \(\frac{1}{10}\) + \(\frac{2}{10}\) = \(\frac{6}{10}\) = \(\frac{3}{5}\)
Question 32.
\(\frac{4}{6}\) – \(\frac{2}{6}\) =
Answer:
\(\frac{4}{6}\) – \(\frac{2}{6}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
Question 33.
\(\frac{3}{12}\) – \(\frac{2}{12}\) =
Answer:
\(\frac{3}{12}\) – \(\frac{2}{12}\) = \(\frac{1}{12}\)
Question 34.
\(\frac{2}{3}\) + \(\frac{1}{3}\) =
Answer:
\(\frac{2}{3}\) + \(\frac{1}{3}\) = \(\frac{3}{3}\) = 1
Question 35.
\(\frac{2}{4}\) + \(\frac{1}{4}\) =
Answer:
\(\frac{2}{4}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\)
Question 36.
\(\frac{3}{12}\) + \(\frac{2}{12}\) =
Answer:
\(\frac{3}{12}\) + \(\frac{2}{12}\) = \(\frac{5}{12}\)
Question 37.
\(\frac{1}{5}\) + \(\frac{2}{5}\) =
Answer:
\(\frac{1}{5}\) + \(\frac{2}{5}\) = \(\frac{3}{5}\)
Question 38.
\(\frac{4}{5}\) – \(\frac{4}{5}\) =
Answer:
\(\frac{4}{5}\) – \(\frac{4}{5}\) = 0
Question 39.
\(\frac{5}{12}\) – \(\frac{1}{12}\) =
Answer:
\(\frac{5}{12}\) – \(\frac{1}{12}\) = \(\frac{4}{12}\) = \(\frac{1}{3}\)
Question 40.
\(\frac{6}{8}\) + \(\frac{2}{8}\) =
Answer:
\(\frac{6}{8}\) + \(\frac{2}{8}\) = \(\frac{8}{8}\) = 1
Question 41.
\(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{2}{8}\) =
Answer:
\(\frac{2}{8}\) + \(\frac{2}{8}\) + \(\frac{2}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)
Question 42.
\(\frac{9}{10}\) – \(\frac{7}{10}\) – \(\frac{1}{10}\) =
Answer:
\(\frac{9}{10}\) – \(\frac{7}{10}\) – \(\frac{1}{10}\) = \(\frac{9}{10}\) – \(\frac{8}{10}\) = \(\frac{1}{10}\) =
Question 43.
\(\frac{2}{10}\) + \(\frac{5}{10}\) + \(\frac{2}{10}\) =
Answer:
\(\frac{2}{10}\) + \(\frac{5}{10}\) + \(\frac{2}{10}\) = \(\frac{9}{10}\)
Question 44.
\(\frac{9}{12}\) – \(\frac{1}{12}\) – \(\frac{4}{12}\) =
Answer:
\(\frac{9}{12}\) – \(\frac{1}{12}\) – \(\frac{4}{12}\) = \(\frac{9}{12}\) – \(\frac{5}{12}\) = \(\frac{4}{12}\) = \(\frac{1}{3}\) .
Eureka Math Grade 5 Module 3 Lesson 9 Problem Set Answer Key
Question 1.
First make like units, and then add.
a. \(\frac{3}{4}\) + \(\frac{1}{7}\) =
b. \(\frac{1}{4}\) + \(\frac{9}{8}\) =
c. \(\frac{3}{8}\) + \(\frac{3}{7}\) =
d. \(\frac{4}{9}\) + \(\frac{4}{7}\) =
e. \(\frac{1}{5}\) + \(\frac{2}{3}\) =
f. \(\frac{3}{4}\) + \(\frac{5}{6}\) =
g. \(\frac{2}{3}\) + \(\frac{1}{11}\) =
h. \(\frac{3}{4}\) + 1\(\frac{1}{10}\) =
Answer:
a.
\(\frac{3}{4}\) + \(\frac{1}{7}\)
lcm of 4 and 7 is 28
=\(\frac{21}{28}\) + \(\frac{4}{28}\) = \(\frac{25}{28}\)
b.
\(\frac{1}{4}\) + \(\frac{9}{8}\)
lcm of 4 and 8 is 8
\(\frac{2}{8}\) + \(\frac{9}{8}\) =\(\frac{11}{8}\) = 1\(\frac{3}{8}\)
c.
\(\frac{3}{8}\) + \(\frac{3}{7}\)
lcm of 8 and 7 is 56
\(\frac{21}{56}\) + \(\frac{24}{56}\) = \(\frac{45}{56}\)
d.
\(\frac{4}{9}\) + \(\frac{4}{7}\)
lcm of 9 and 7 is 63
\(\frac{28}{63}\) + \(\frac{36}{63}\) = \(\frac{64}{63}\) = 1\(\frac{1}{63}\)
e.
\(\frac{1}{5}\) + \(\frac{2}{3}\)
lcm of 5 and 3 is 15 .
\(\frac{3}{15}\) + \(\frac{10}{15}\) = \(\frac{13}{15}\)
f.
\(\frac{3}{4}\) + \(\frac{5}{6}\)
lcm of 4 and 6 is 12.
\(\frac{9}{12}\) + \(\frac{10}{12}\) = \(\frac{19}{12}\) =1 \(\frac{7}{12}\)
g.
\(\frac{2}{3}\) + \(\frac{1}{11}\)
lcm of 3 and 11 is 33
\(\frac{22}{33}\) + \(\frac{3}{33}\) = \(\frac{25}{33}\)
h.
\(\frac{3}{4}\) + 1\(\frac{1}{10}\) = \(\frac{3}{4}\) + \(\frac{11}{10}\)
lcm of 4 and 10 is 20.
\(\frac{15}{20}\) + \(\frac{22}{10}\) = \(\frac{37}{20}\) = 1\(\frac{17}{20}\)
Question 2.
Whitney says that to add fractions with different denominators, you always have to multiply the denominators to find the common unit; for example:
\(\frac{1}{4}+\frac{1}{6}=\frac{6}{24}+\frac{4}{24}\)
Show Whitney how she could have chosen a denominator smaller than 24, and solve the problem.
Answer:
multiples of 4 and 6 are
4 : 4, 8, 12, 16, 20, 24
6: 6, 12, 18, 24, 30 .
12 and 24 are the common multiplies of 4 and 6. smaller than 24 we get 12 multiple .
(\(\frac{1 × 3}{4 × 3}\)) + (\(\frac{1 × 2}{6 × 2}\)) = \(\frac{3}{12}\) + \(\frac{2}{12}\) = \(\frac{5}{12}\)
Question 3.
Jackie brought \(\frac{3}{4}\) of a gallon of iced tea to the party. Bill brought \(\frac{7}{8}\) of a gallon of iced tea to the same party. How much iced tea did Jackie and Bill bring to the party?
Answer:
Fraction of iced tea brought by Jackie = \(\frac{3}{4}\)
Fraction of iced tea brought by Bill = \(\frac{7}{8}\)
Total Fraction of iced tea brought to party = \(\frac{3}{4}\) + \(\frac{7}{8}\) = \(\frac{6}{8}\) + \(\frac{7}{8}\) = \(\frac{13}{8}\) = 1\(\frac{5}{8}\)
Therefore, Total Fraction of iced tea brought to party = \(\frac{13}{8}\) = 1\(\frac{5}{8}\) .
Question 4.
Madame Curie made some radium in her lab. She used \(\frac{2}{5}\) kg of the radium in an experiment and had 1\(\frac{1}{4}\) kg left. How much radium did she have at first? (Extension: If she performed the experiment twice, how much radium would she have left?)
Answer:
Quantity of Radium made by Madam Curie = x kgs
Fraction of Quantity of Radium used by Experiment = \(\frac{2}{5}\) kg
Fraction of Quantity of Radium left = 1\(\frac{1}{4}\) kg = \(\frac{5}{4}\) kg
Quantity of Radium made by Madam Curie = \(\frac{2}{5}\) + \(\frac{5}{4}[/latex
lcm of 5 and 4 is 20 .
[latex]\frac{8}{20}\) + \(\frac{25}{20}\) = \(\frac{33}{20}\) =1\(\frac{13}{20}\) .
Therefore if the experiment is done once the Total Quantity = \(\frac{33}{20}\) =1\(\frac{13}{20}\)
If the Experiment if done twiced .
Total Quantity – Quantity Used for Experiment twice = left Quantity .
\(\frac{33}{20}\) – 2 × \(\frac{2}{5}\) = \(\frac{33}{20}\) – \(\frac{4}{5}\) = \(\frac{33}{20}\) – \(\frac{16}{20}\) = \(\frac{17}{20}\)
Therefore if the experiment is done once the Total Quantity = \(\frac{17}{20}\)
Eureka Math Grade 5 Module 3 Lesson 9 Exit Ticket Answer Key
Make like units, and then add.
a. \(\frac{1}{6}\) + \(\frac{3}{4}\) =
b. 1\(\frac{1}{2}\) + \(\frac{2}{5}\) =
Answer:
a.
\(\frac{1}{6}\) + \(\frac{3}{4}\)
lcm of 6 and 4 is 12
\(\frac{2}{12}\) + \(\frac{9}{12}\) = \(\frac{11}{12}\)
b.
1\(\frac{1}{2}\) + \(\frac{2}{5}\) = \(\frac{3}{2}\) + \(\frac{2}{5}\)
lcm of 2 and 5 is 10.
\(\frac{15}{10}\) + \(\frac{4}{10}\) =\(\frac{19}{10}\) = 1\(\frac{9}{10}\)
Eureka Math Grade 5 Module 3 Lesson 9 Homework Answer Key
Question 1.
Make like units, and then add.
a. \(\frac{3}{5}\) + \(\frac{1}{3}\) =
b. \(\frac{3}{5}\) + \(\frac{1}{11}\) =
c. \(\frac{2}{9}\) + \(\frac{5}{6}\) =
d. \(\frac{2}{5}\) + \(\frac{1}{4}\) + \(\frac{1}{10}\) =
e. \(\frac{1}{3}\) + \(\frac{7}{5}\) =
f. \(\frac{5}{8}\) + \(\frac{7}{12}\) =
g. 1\(\frac{1}{3}\) + \(\frac{3}{4}\) =
h. \(\frac{5}{6}\) + 1\(\frac{1}{4}\) =
Answer:
a.
\(\frac{3}{5}\) + \(\frac{1}{3}\)
lcm of 5 and 3 is 15
\(\frac{9}{15}\) + \(\frac{5}{15}\) = \(\frac{14}{15}\)
b.
\(\frac{3}{5}\) + \(\frac{1}{11}\)
lcm of 5 and 11 is 55
\(\frac{33}{55}\) + \(\frac{5}{55}\) = \(\frac{38}{55}\)
c.
\(\frac{2}{9}\) + \(\frac{5}{6}\)
lcm of 9 and 6 is 18 .
\(\frac{4}{18}\) + \(\frac{15}{18}\) = \(\frac{19}{18}\) = 1 \(\frac{1}{18}\)
d.
\(\frac{2}{5}\) + \(\frac{1}{4}\) + \(\frac{1}{10}\)
lcm of 5 , 4 and 10 is 20 .
\(\frac{8}{20}\) + \(\frac{5}{20}\) + \(\frac{2}{20}\) = \(\frac{15}{20}\)= \(\frac{3}{4}\)
e.
\(\frac{1}{3}\) + \(\frac{7}{5}\)
lcm of 3 and 5 is 15 .
\(\frac{5}{15}\) + \(\frac{21}{15}\) =\(\frac{26}{3}\) =1\(\frac{11}{15}\)
f.
\(\frac{5}{8}\) + \(\frac{7}{12}\)
lcm of 8 and 12 is 24.
\(\frac{15}{24}\) + \(\frac{14}{24}\) = \(\frac{29}{24}\) = 1\(\frac{5}{24}\)
g.
1\(\frac{1}{3}\) + \(\frac{3}{4}\) = \(\frac{4}{3}\) + \(\frac{3}{4}\)
lcm of 3 and 4 is 12
\(\frac{16}{12}\) + \(\frac{9}{12}\) = \(\frac{25}{12}\) = 2 \(\frac{1}{12}\)
h.
\(\frac{5}{6}\) + 1\(\frac{1}{4}\) =\(\frac{5}{6}\) + \(\frac{5}{4}\)
lcm of 4 and 6 is 12 .
\(\frac{10}{12}\) + \(\frac{15}{12}\) = \(\frac{25}{12}\) = 2\(\frac{1}{12}\)
Question 2.
On Monday, Ka practiced guitar for \(\frac{2}{3}\) of one hour. When she finished, she practiced piano for \(\frac{3}{4}\) of one hour. How much time did Ka spend practicing instruments on Monday?
Answer:
Fraction of Time spent in playing guitar of one hour = \(\frac{2}{3}\)
Fraction of Time spent in playing guitar when finished = \(\frac{3}{4}\)
Total Time taken for practicing = \(\frac{2}{3}\) + \(\frac{3}{4}\) = \(\frac{8}{12}\) + \(\frac{9}{12}\) = \(\frac{17}{12}\) = 1\(\frac{5}{12}\) hour .
Therefore, Total Time taken in practicing = \(\frac{17}{12}\) = 1\(\frac{5}{12}\) hour
Question 3.
Ms. How bought a bag of rice for dinner. She used \(\frac{3}{5}\) kg of the rice and still had 2\(\frac{1}{4}\) kg left. How heavy was the bag of rice that Ms. How bought?
Answer:
Fraction of Quantity of rice used = \(\frac{3}{5}\) kg
Fraction of Quantity of rice left = 2\(\frac{1}{4}\) kg
Total Quantity of rice = \(\frac{3}{5}\) + 2\(\frac{1}{4}\) = \(\frac{3}{5}\) + \(\frac{9}{4}\)
= \(\frac{12}{20}\) + \(\frac{45}{20}\) =\(\frac{57}{20}\) = 2\(\frac{17}{20}\)
Therefore, Total Quantity of rice = \(\frac{57}{20}\) = 2\(\frac{17}{20}\) .
Question 4.
Joe spends \(\frac{2}{5}\) of his money on a jacket and \(\frac{3}{8}\) of his money on a shirt. He spends the rest on a pair of pants. What fraction of his money does he use to buy the pants?
Answer:
Money spent on jacket = \(\frac{2}{5}\)
Money spent on a shirt = \(\frac{3}{8}\)
Money spent on pair of pants = x
1 = \(\frac{2}{5}\) + \(\frac{3}{8}\) + x
lcm of 5 and 8 is 40.
\(\frac{40}{40}\) = \(\frac{16}{40}\) + \(\frac{10}{40}\) +x
\(\frac{40}{40}\) = \(\frac{26}{40}\) + x
x = \(\frac{40}{40}\) – \(\frac{13}{40}\)
x = \(\frac{27}{40}\)