Engage NY Eureka Math 5th Grade Module 5 Lesson 13 Answer Key
Eureka Math Grade 5 Module 5 Lesson 13 Problem Set Answer Key
Question 1.
Find the area of the following rectangles. Draw an area model if it helps you.
a. \(\frac{5}{4}\) km × \(\frac{12}{5}\) km
b. 16\(\frac{1}{2}\) m × 4\(\frac{1}{5}\) m
c. 4\(\frac{1}{3}\) yd × 5\(\frac{2}{3}\) yd
d. \(\frac{7}{8}\) mi × 4\(\frac{1}{3}\) mi
Answer:
a.
5/4 x 12/5
= 60/20
= 3
Therefore, 3 square kilometres
b.
16 1/2 x 4 1/5
= (16 x 4) + ( 16 x 1/5) + ( 4 x 1/2) x ( 1/2 x 1/5 )
= 64 + 16/5 + 2 + 1/10
= 66 33/10
= 66 3/10
Therefore, 69 3/10 square metres
c.
4 1/3 x 5 2/3
4 x 5 + 4 x 2/3 + 5 x 1/3 + 1/3 x 2/3
= 20 +8/3 +5/3 +2/9
= 20 41/9
= 24 5/9
Therefore, 24 5/9 square yards
d.7/8 mi x 4 1/3 mi
= (7/8 x 4) + (7/8 x 1/3)
= 84/24 + 7/24
= 91/24
=3 19/24
Therefore, 3 19/24 sq. mi
Question 2.
Julie is cutting rectangles out of fabric to make a quilt. If the rectangles are 2\(\frac{3}{5}\) inches wide and 3\(\frac{2}{3}\) inches long, what is the area of four such rectangles?
Answer:
Given, the measurements of the rectangles =
2 3/5 x 3 2/3
=( 2 x 3 ) + (2 x 2/3) + (3 x 3/5) + ( 3/5 x 2/3)
= 6 + 4/3 + 9/5 + 6/15
=6+53/15
=6 + 3 8/15
= 9 8/15 square inches
Now, number of rectangles = 4
So, 4 x 9 8/15
36 + 32/15
= 36 + 2 2/15
= 38 2/15
Therefore, 38 2/15 square inches.
Question 3.
Mr. Howard’s pool is connected to his pool house by a sidewalk as shown. He wants to buy sod for the lawn, shown in gray. How much sod does he need to buy?
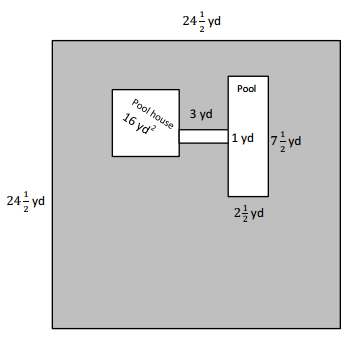
Answer:
Given, the measurements of the lawn = 24 1/2 yd by 24 1/2 yd
The area of the lawn =
24 1/2 x 24 1/2
= (24 x 24 ) + (24 x 1/2 ) + (24 x 1/2) + ( 1/2 x 1/2)
= 576 + 12 +12 +1/4
=600 1/4 square yards
The area of the pool house = 16 square yards
The area of the pool =
7 1/2 yd x 2 1/2 yd
= 14 + 3 1/2 + 1 + 1/4
= 18 3/4
The area of sidewalk = 1 yd x 3 yd = 3 yd
Now, the amount of sod Howard needs to buy =
6001/4 – 16 – 18 3/4 – 3
= 581 1/4 – 18 2/4
= 580 5/4 – 18 3/4
= 562 1/2 square yards
Therefore, Howard need 562 1/2 square yards of sod.
Eureka Math Grade 5 Module 5 Lesson 13 Exit Ticket Answer Key
Find the area of the following rectangles. Draw an area model if it helps you.
Question 1.
\(\frac{7}{2}\) mm × \(\frac{14}{5}\) mm
Answer:
7/2 mm x 4/5 mm
= 7/2 x 4/5
= 98/10
= 9 4/5 square mm
Question 2.
5\(\frac{7}{8}\) km × \(\frac{18}{4}\) km
Answer:
5/8 km x 18/4 km
= 5/8 x 18/4
= 90/32
= 26 7/16 square kilometres.
Eureka Math Grade 5 Module 5 Lesson 13 Homework Answer Key
Question 1.
Find the area of the following rectangles. Draw an area model if it helps you.
a. \(\frac{8}{3}\) cm × \(\frac{24}{4}\) cm
b. \(\frac{32}{5}\) ft × 3\(\frac{3}{8}\) ft
c. 5\(\frac{4}{6}\) in × 4 \(\frac{3}{5}\) in
d. \(\frac{5}{7}\) m × 6\(\frac{3}{5}\) m
Answer:
a.
8/3 cm x 24/4 cm
= 8/3 x 24/4
= 16
Therefore, 16 square centimetres
b.
32/5 feet x 3 3/8
32/5 = 6 2/5
= 18 + 18/8 + 6/5 + 9/40
= 18 + 2 1/4 + 1 1/5 + 9/40
= 21 + 27/40
Therefore, 21 27/40 square feet
c.
5 4/6 feet x 4 3/5 feet
( 5 x 4 ) + ( 5 x 3/5) + (4/6 x 4 ) + ( 4/6 x 3/5)
= 20 + 15/5 + 16/6 + 12/30
=20 + 3 + 8/3 + 2/5
= 25 +20/30 + 12/30
= 26 2/30
= 26 1/15
Therefore, 26 1/15 square inches
d.
5/7 m x 6 3/5 m
= 5/7 x 6 3/5
= 30/7 + 15/35
= 4 2/7 + 3/7
= 4 5/7
Therefore, 4 5/7 square inches
Question 2.
Chris is making a tabletop from some leftover tiles. He has 9 tiles that measure 3\(\frac{1}{8}\) inches long and 2\(\frac{3}{4}\) inches wide. What is the greatest area he can cover with these tiles?
Answer:
Given, the measurements of the tiles =
3 1/8 x 2 3/4
= 6 + 9/4 + 2/8 + 3/32
= 6 +2 1/4 + 1/4 + 3/32
= 8 19/32
Now, the greatest area he can cover with 9 tiles=
= 9 x 8 19/32
= 72 + 191/32
= 72 +5 11/32
= 77 11/32 square inches.
Therefore, the greatest area he can cover = 77 11/32.
Question 3.
A hotel is recarpeting a section of the lobby. Carpet covers the part of the floor as shown below in gray. How many square feet of carpeting will be needed?
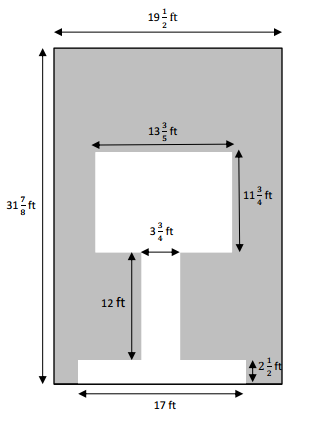
Answer:
a.
31 7/8 x 19 1/2
= ( 31 x 19) + ( 31 x 1/2 ) + (19 x 7/8 ) + ( 7/8 x 1/2)
= 589 + 31/2 + 133/8 + 7/16
= 589 + 15 1/2 + 16 5/8 + 7/16
= 620 + 1/2 + 5/8 + 7/16
= 630 + 8/16 + 10/16 + 7/16
= 620 25/16 square feet.
b. 13 3/5 feet x 11 3/4 feet
= ( 13 x 11) + ( 13 x 3/4 ) + (3/5 x 11 ) + ( 3/5 x 3/4)
= 143 + 9 3/4 + 6 3/5 + 9/20
=158 + 15/20 + 12/20 + 9/20
=158 36/20
= 159 16/20
= 159 4/5 square feet
c.
12 x 3 3/4
= 36 + 36/4
= 45 square feet
d.
17 x 2 1/2
= 34 + 17/2
= 34 + 8 1/2
= 42 1/2 square feet
Now,
159 4/5 + 45 + 42 1/2
= 247 3/10 square feet
So, 621 9/16 – 247 3/10
= 384 21/80
Therefore, 384 21/80 square feet of carpeting is needed.