Engage NY Eureka Math 5th Grade Module 5 Lesson 6 Answer Key
Eureka Math Grade 5 Module 5 Lesson 6 Problem Set Answer Key
Question 1.
Find the total volume of the figures, and record your solution strategy.
a. 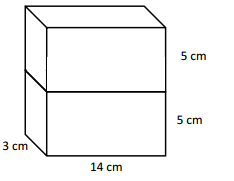
Volume: ______________
Solution Strategy:
Answer:
Volume = length x width x height
V= 14 x 10 x 3
V = 420 cubic centimetres.
Solution strategy :
I added the height of 2 cubes to get 10 cm and applied volume formula
b. 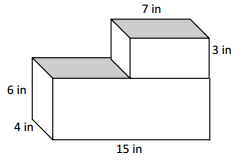
Volume: ______________
Solution Strategy:
1.
Volume = length x width x height
V = 7 x 4 x 3
V = 84 cubic inches
2.
Volume = 15 x 4 x 6
V = 360 cubic inches
Total volume = 84 + 360 = 444 cubic inches
Solution strategy = Calculated volume of each prism individually.
c. 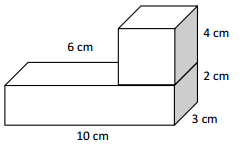
Volume: ______________
Solution Strategy:
1.
Volume = length x width x height
V = 4 x3 x 4
V = 48 cubic centimeters
2.
Volume = 10 x 3 x 2
V = 60 cubic centimeters
Total volume = 48 + 60
V = 108 cubic centimetres.
Solution strategy:
The width of the shape 1 is 10 – 6 = 4 cm ,
Then i calculate dthe volume individually and added them.
.
d. 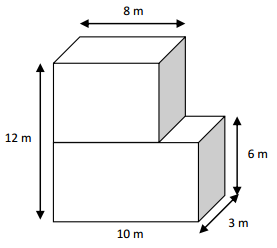
Volume: ______________
Solution Strategy:
Answer:
Volume = length x width x height
1.
V = 8 x 3 x 6
V = 144 cubic centimeters
2.
Volume = 10 X 3 X 6
v = 180 cubic centimeters
Total volume = 144 + 180 = 324 Cubic centimeters
Solution strategy:
The height of the shape 1. is 12 – 6 = 6 cm
Then I caluculated the volume individually and added them together.
Question 2.
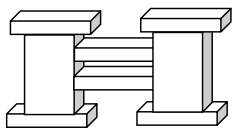
A sculpture (pictured below) is made of two sizes of rectangular prisms. One size measures 13 in by 8 in by 2 in. The other size measures 9 in by 8 in by 18 in. What is the total volume of the sculpture?
Answer:
Let, the small size prisms be A and large sized prisms be B
Given the measurents of prism A =
length = 13, width = 8 and height = 2 inches
Number of A prisms = 6
Now, volume = 13 in x 8 in x 2 in
V = 208 cubic inches
Total volume of 6 prisms(A) =
V = 206 x 6
V = 1248
Also given the measurements of prism B =
Length = 9 in, width = 8 in and height = 18 inches
Volume = 9 in x 8 in x 18 in
V = 1296
Number of prisms B = 2
Now,
Volume = 1296 x 2
V = 2592
Now, the total volume of the sculpture =
Volume of prisms A and volume of prisms B
= 1,248 + 2592
= 3840
Therefore, total volume of sculpture = 3840 cubic inches
Question 3.
The combined volume of two identical cubes is 128 cubic centimeters. What is the side length of each cube?
Answer:
Given the combined volume of two identical cubes = 128 cubic centimetres
So, 128 / 2 = 64
64 can be written as 4 x 4x 4
Therefore, the each side is 4 cm long.
Question 4.
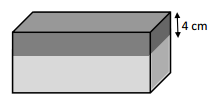
A rectangular tank with a base area of 24 cm2 is filled with water and oil to a depth of 9 cm. The oil and water separate into two layers when the oil rises to the top. If the thickness of the oil layer is 4 cm, what is the volume of the water?
Answer:
Given, the bae area of tank = 24 sq. cm
The depth of water and oil poured into the tank = 9 cm
Given, the thickness of oil poured = 4 cm
So, 9 – 4 = 5
Now, the volume of water =
V = 24 x 5
V = 120
Therefore, the volume of the water = 120 cubic cm.
Question 5.
Two rectangular prisms have a combined volume of 432 cubic feet. Prism A has half the volume of Prism B.
a. What is the volume of Prism A? Prism B?
b. If Prism A has a base area of 24 ft2, what is the height of Prism A?
c. If Prism B’s base is \(\frac{2}{3}\) the area of Prism A’s base, what is the height of Prism B?
Answer:
Given, the combined volume of three prisms = 432 cubic feet,
The prism A has half the volume of prism B
So, 432/3
= 144
So, the volume of prism A = 144 cubic feet and prism B = 288 cubic fet
b.
Given, if the base area of prism A = 24 sq. feet
Now, height of the prism =
Volume / area
144/24
= 6
Therefore, the height of prism A = 6 feet
c.
Given , if the prism B’s base = 2/3 of the prism A’s
Now, the height of prism B =
2/3 X 26
= 16 sq. feet
So, the height of prism B = volume/ area
= 288/16
= 18
Therefore, the height of prism B = 18 feet
Eureka Math Grade 5 Module 5 Lesson 6 Exit Ticket Answer Key
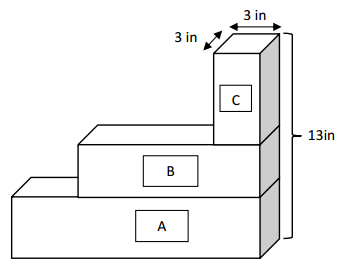
The image below represents three planters that are filled with soil. Find the total volume of soil in the three planters. Planter A is 14 inches by 3 inches by 4 inches. Planter B is 9 inches by 3 inches by 3 inches.
Answer:
Volume of A
= length x width x height
v = 15 X 3 X 3
v = 135 cubic inches
Volume of B =
length x width x height
V = = 9 x 3 x 4
V = 108 cubic inches
Volume of C =
length x width xheight
V = 3 X 3 X 6
V = 54 cubic inches
Total volume = 135 + 108 + 54
V= 297
Therefore, the total volume of planters = 297 cubic inches.
Eureka Math Grade 5 Module 5 Lesson 6 Homework Answer Key
Question 1.
Find the total volume of the figures, and record your solution strategy.
a. 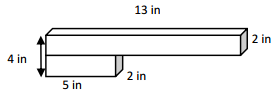
Volume: _________________
Solution Strategy:
Volume = length x width x height
1. V= 13 x 2 x 2
V= 52 cubic inches
2. V = 2 x 2 x 5 = 20 cubic inches
Total volume = 52 + 20 = 72 cubic inches.
Solution strategey = 4/2 = 2 , the heigth of the bottom box = 2 inches
b. 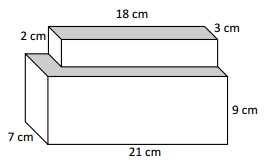
Volume: _________________
Solution Strategy:
Volume = length x width x height
1. 18 x 3 x 2 = 108 cubic centimetres
2. 21 x 9 x 7 = 1326 cubic centimetres
Total volume = 1,431 cubic centimetres.
Solution strategy:
Calculated each shape volume individually.
c. 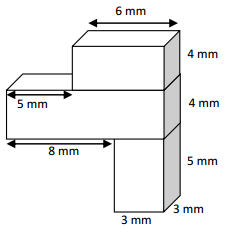
Volume: _________________
Solution Strategy:
Volume = length x width x height
1. 6 x 4 x 3 = 72 cubic mm
2. 11 x 3 x 4 = 132 cubic mm.
3. 3 x 3 x 5 =45 cubic mm.
Total volume =72 + 132 + 45 = 249
Therefore, total volume = 249 cubic mm
Solution strategy :
8 – 5 = 3 So, the width of box is 3 mm
d. 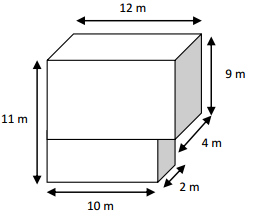
Volume: _________________
Solution Strategy:
Answer:
Volume = length x width x height
1. 12 x 4 x 9 = 432 cubic metres
2. 10 x 2 x 2 = 40 cubic metres
Total volume = 432 + 40 = 472
Therefore, total volume = 472 cubic metres.
Solution strategy:
11 – 9 = 2 , So, the height of the bottom shape is 2 m
Question 2.
The figure below is made of two sizes of rectangular prisms. One type of prism measures 3 inches by 6 inches by 14 inches. The other type measures 15 inches by 5 inches by 10 inches. What is the total volume of this figure?
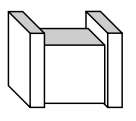
Answer:
1.
Given, the measurement of shape 1 =
3 inches by 6 inches by 14 inches
Now, volume of box 1 =
V = length X width Xheight
v= 3 X 6 X 14
V =252 cubic inches
Now, there are 2 oxes of same shape so,
2 x 252 =504 cubic inches
2. The measurements of box 2 =
15 inches by 5 inches by 10 inches
Volum =- 15 x 5 x 10
V = 750 cubic inches
Now, total volume = 504 cubic in. + 750 cubic in.
V =1,254 cubic inches.
Question 3.
The combined volume of two identical cubes is 250 cubic centimeters. What is the measure of one cube’s edge?
Answer:
Given, the combined volume of indentical cubes = 250 cubic centimetres.
250 / 2 = 125 cubic cm.
125 can be written as 5 x 5 x 5
Therefore, the measurement of one cube’s edge = 5 cm
Question 4.
A fish tank has a base area of 45 cm2 and is filled with water to a depth of 12 cm. If the height of the tank is 25 cm, how much more water will be needed to fill the tank to the brim?
Answer:
Volume = length x width x height
V= area x height
Given, height = 25 cm and area = 45 sq. cm.
V = 45 x 25
V = 1,125 cubic cm.
Given, depth = 12 cm
So, 45 x 12 = 540 cubic cm.
Now, 1125 – 540 = 585
Therefore, 585 millilitre of water is needed to fill the tank
Question 5.
Three rectangular prisms have a combined volume of 518 cubic feet. Prism A has one-third the volume of Prism B, and Prisms B and C have equal volume. What is the volume of each prism?
Answer:
Given,
The total volume of three prisms = 518 cubic feet.
Also given Prism A has one-third the volume of prism B
Now, 518 / 7 = 74 cubic feet
74 x 3 = 222 cubic feet
Therefore, the volume of prism A =74 cubic feet
Volume of prism B and C = 222 cubic feet