Engage NY Eureka Math 5th Grade Module 6 Lesson 11 Answer Key
Eureka Math Grade 5 Module 6 Lesson 11 Sprint Answer Key
A
Round to the Nearest One
Question 1.
3.1 ≈
Answer:
3.1 ≈ 3
Question 2.
3.2 ≈
Answer:
3.2 ≈ 3
Question 3.
3.3 ≈
Answer:
3.3 ≈ 3
Question 4.
3.4 ≈
Answer:
3.4 ≈ 3
Question 5.
3.5 ≈
Answer:
3.5 ≈ 4
Question 6.
3.6 ≈
Answer:
3.6 ≈ 4
Question 7.
3.9 ≈
Answer:
3.9 ≈ 4
Question 8.
13.9 ≈
Answer:
13.9 ≈ 14
Question 9.
13.1 ≈
Answer:
13.1 ≈ 13
Question 10.
13.5 ≈
Answer:
13.5 ≈ 14
Question 11.
7.5 ≈
Answer:
7.5 ≈ 8
Question 12.
8.5 ≈
Answer:
8.5 ≈ 9
Question 13.
9.5 ≈
Answer:
9.5 ≈ 10
Question 14.
19.5 ≈
Answer:
19.5 ≈ 20
Question 15.
29.5 ≈
Answer:
29.5 ≈ 30
Question 16.
89.5 ≈
Answer:
89.5 ≈ 90
Question 17.
2.4 ≈
Answer:
2.4 ≈ 2
Question 18.
2.41 ≈
Answer:
2.41 ≈ 2
Question 19.
2.42 ≈
Answer:
2.42 ≈ 2
Question 20.
2.45 ≈
Answer:
2.45 ≈ 2
Question 21.
2.49 ≈
Answer:
2.49 ≈ 2
Question 22.
2.51 ≈
Answer:
2.51 ≈ 3
Question 23.
12.51 ≈
Answer:
12.51 ≈ 13
Question 24.
16.61 ≈
Answer:
16.61 ≈ 17
Question 25.
17.41 ≈
Answer:
17.41 ≈ 17
Question 26.
11.51 ≈
Answer:
11.51 ≈ 12
Question 27.
11.49 ≈
Answer:
11.49 ≈ 11
Question 28.
13.49 ≈
Answer:
13.49 ≈ 13
Question 29.
13.51 ≈
Answer:
13.51 ≈ 14
Question 30.
15.51 ≈
Answer:
15.51 ≈ 16
Question 31.
15.49 ≈
Answer:
15.49 ≈ 16
Question 32.
6.3 ≈
Answer:
6.3 ≈ 6
Question 33.
7.6 ≈
Answer:
7.6 ≈ 8
Question 34.
49.5 ≈
Answer:
49.5 ≈ 50
Question 35.
3.45 ≈
Answer:
3.45 ≈ 3
Question 36.
17.46 ≈
Answer:
17.46 ≈ 17
Question 37.
11.76 ≈
Answer:
11.76 ≈ 12
Question 38.
5.2 ≈
Answer:
5.2 ≈ 5
Question 39.
12.8 ≈
Answer:
12.8 ≈ 13
Question 40.
59.5 ≈
Answer:
59.5 ≈ 60
Question 41.
5.45 ≈
Answer:
5.45 ≈ 5
Question 42.
19.47 ≈
Answer:
19.47 ≈ 19
Question 43.
19.87 ≈
Answer:
19.87 ≈ 20
Question 44.
69.51 ≈
Answer:
69.51 ≈ 70
B
Round to the Nearest One
Question 1.
4.1 ≈
Answer:
4.1 ≈ 4
Question 2.
4.2 ≈
Answer:
4.2 ≈ 4
Question 3.
4.3 ≈
Answer:
4.3 ≈ 4
Question 4.
4.4 ≈
Answer:
4.4 ≈ 4
Question 5.
4.5 ≈
Answer:
4.5 ≈ 5
Question 6.
4.6 ≈
Answer:
4.6 ≈ 5
Question 7.
4.9 ≈
Answer:
4.9 ≈ 5
Question 8.
14.9 ≈
Answer:
14.9 ≈ 15
Question 9.
14.1 ≈
Answer:
14.1 ≈ 14
Question 10.
14.5 ≈
Answer:
14.5 ≈ 15
Question 11.
7.5 ≈
Answer:
7.5 ≈ 8
Question 12.
8.5 ≈
Answer:
8.5 ≈ 9
Question 13.
9.5 ≈
Answer:
9.5 ≈ 10
Question 14.
19.5 ≈
Answer:
19.5 ≈ 20
Question 15.
29.5 ≈
Answer:
29.5 ≈ 30
Question 16.
79.5 ≈
Answer:
79.5 ≈ 80
Question 17.
3.4 ≈
Answer:
3.4 ≈ 3
Question 18.
3.41 ≈
Answer:
3.41 ≈ 3
Question 19.
3.42 ≈
Answer:
3.42 ≈ 3
Question 20.
3.45 ≈
Answer:
3.45 ≈ 3
Question 21.
3.49 ≈
Answer:
3.49 ≈ 3
Question 22.
3.51 ≈
Answer:
3.51 ≈ 4
Question 23.
13.51 ≈
Answer:
13.51 ≈ 14
Question 24.
17.61 ≈
Answer:
17.61 ≈ 18
Question 25.
18.41 ≈
Answer:
18.41 ≈ 18
Question 26.
12.51 ≈
Answer:
12.51 ≈ 13
Question 27.
12.49 ≈
Answer:
12.49 ≈ 12
Question 28.
14.49 ≈
Answer:
14.49 ≈ 14
Question 29.
14.51 ≈
Answer:
14.51 ≈ 15
Question 30.
16.51 ≈
Answer:
16.51 ≈ 17
Question 31.
16.49 ≈
Answer:
16.49 ≈ 16
Question 32.
7.3 ≈
Answer:
7.3 ≈ 7
Question 33.
8.6 ≈
Answer:
8.6 ≈ 9
Question 34.
39.5 ≈
Answer:
39.5 ≈ 40
Question 35.
4.45 ≈
Answer:
4.45 ≈ 4
Question 36.
18.46 ≈
Answer:
18.46 ≈ 18
Question 37.
12.76 ≈
Answer:
12.76 ≈ 13
Question 38.
6.2 ≈
Answer:
6.2 ≈ 6
Question 39.
13.8 ≈
Answer:
13.8 ≈ 14
Question 40.
49.5 ≈
Answer:
49.5 ≈ 50
Question 41.
6.45 ≈
Answer:
6.45 ≈ 6
Question 42.
19.48 ≈
Answer:
19.48 ≈ 19
Question 43.
19.78 ≈
Answer:
19.78 ≈ 20
Question 44.
59.51 ≈
Answer:
59.51 ≈ 60
Eureka Math Grade 5 Module 6 Lesson 11 Problem Set Answer Key
Question 1.
Complete the tables for the given rules.
Line l
Rule: Double x
| x | y |
(x, y) |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
Line m
Rule: Double x, and then add 1
| x | y |
(x, y) |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule double x, and then subtract 1 would look like. Draw the line on the plane above.
Answer:
Line l
Rule: Double x
y= 2x
| x | y |
(x, y) |
| 0 | 0 | (0, 0) |
| 1 | 2 | (1, 2) |
| 2 | 4 | (2, 4) |
| 3 | 6 | (3, 6) |
Line m
Rule: Double x, and then add 1
y= 2x + 1
| x | y |
(x, y) |
| 0 | 1 | (0, 1) |
| 1 | 3 | (1, 3) |
| 2 | 5 | (2, 5) |
| 3 | 7 | (3, 7) |
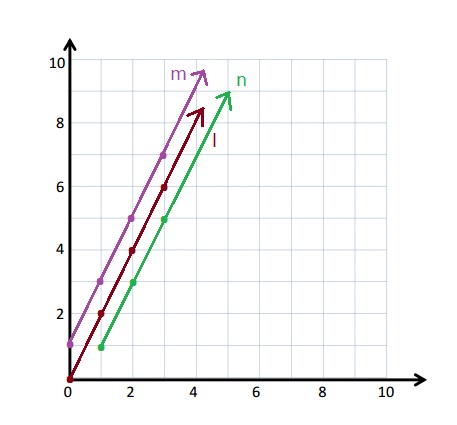
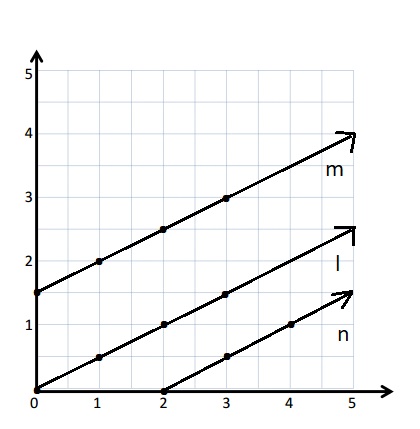
The given points are plotted on the graph .
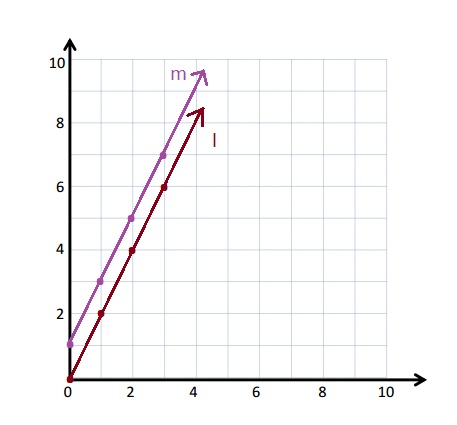
b. The Line l and Line m are parallel to each other.
c.
Line n
Rule: double x, and then subtract 1
y= 2x – 1
| x | y |
(x, y) |
| 1 | 1 | (1, 1) |
| 2 | 3 | (2, 3) |
| 3 | 5 | (3, 5) |
Question 2.
Circle the point(s) that the line for the rule multiply x by \(\frac{1}{3}\), and then add 1 would contain.
(0, \(\frac{1}{3}\))
(2, 1\(\frac{2}{3}\))
(1\(\frac{1}{2}\), 1\(\frac{1}{2}\))
(2\(\frac{1}{4}\), 2\(\frac{1}{4}\))
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:
a.
Rule: multiply x by \(\frac{1}{3}\),
y= x \(\frac{1}{3}\) + 1
| x | y |
(x, y) |
| 0 | 1 | (0, 1) |
| 2 | \(\frac{5}{3}\) | (1, 1\(\frac{2}{3}\)) |
| 1\(\frac{1}{2}\) | \(\frac{3}{2}\) | (1\(\frac{1}{2}\),1\(\frac{1}{2}\)) |
| 2\(\frac{1}{4}\) | \(\frac{7}{4}\) | (2\(\frac{1}{4}\), 1 \(\frac{3}{4}\)) |
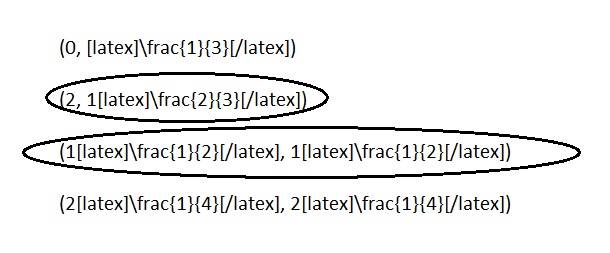
b. Two points that fall on this line are
x = \(\frac{1}{2}\)
y = 1\(\frac{1}{6}\)
Point ( \(\frac{1}{2}\) , 1\(\frac{1}{6}\) )
x = 1
y =1\(\frac{1}{3}\)
Point (1, 1\(\frac{1}{3}\)) .
Question 3.
Complete the tables for the given rules.
Line l
Rule: Halve x
| x | y |
(x, y) |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
Line m
Rule: Halve x, and then add 1\(\frac{1}{2}\)
| x | y |
(x, y) |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule halve x, and then subtract 1 would look like. Draw the line on the plane above.
Answer:
Line l
Rule: Halve x
| x | y |
(x, y) |
| 0 | 0 | (0,0) |
| 1 | \(\frac{1}{2}\) | (1, \(\frac{1}{2}\)) |
| 2 | 1 | (2, 1) |
| 3 | 1\(\frac{1}{2}\) | (3, 1\(\frac{1}{2}\)) |
Line m
Rule: Halve x, and then add 1\(\frac{1}{2}\)
y = \(\frac{x}{2}\) + \(\frac{3}{2}\) = \(\frac{x+3}{2}\)
| x | y |
(x, y) |
| 0 | 1\(\frac{1}{2}\) | (0, 1\(\frac{1}{2}\)) |
| 1 | 2 | (1, 2) |
| 2 | 2\(\frac{1}{2}\) | (2, 2\(\frac{1}{2}\)) |
| 3 | 3 | (3, 3) |
a.
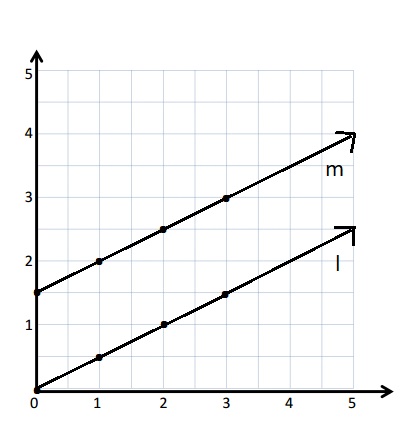
b. Both the lines l and m are parallel to each other.
c.
Line n
Rule: halve x, and then subtract 1
y = \(\frac{x}{2}\) – 1
| x | y |
(x, y) |
| 2 | 0 | (2, 0) |
| 3 | \(\frac{1}{2}\) | (3, \(\frac{1}{2}\)) |
| 4 | 1 | (4, 1) |
| 6 | 2 | (6, 2) |
Question 4.
Circle the point(s) that the line for the rule multiply x by \(\frac{2}{3}\), and then subtract 1 would contain.
(1\(\frac{1}{3}\), \(\frac{1}{9}\))
(2, \(\frac{1}{3}\))
(1\(\frac{3}{2}\), 1\(\frac{1}{2}\))
(3, 1)
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:

Explanation :
Line n
Rule: multiply x by \(\frac{2}{3}\), and then subtract 1
y = \(\frac{2x}{3}\) – 1 = \(\frac{2x – 3 }{3}\)
| x | y |
(x, y) |
| 2 | \(\frac{1}{3}\) | (2, \(\frac{1}{3}\)) |
| 3 | 1 | (3, 1) |
| 1\(\frac{1}{3}\) | \(\frac{1}{9}\) | (1\(\frac{1}{3}\), \(\frac{1}{9}\)) |
| 1\(\frac{3}{2}\) | \(\frac{2}{3}\) | (1\(\frac{3}{2}\),\(\frac{2}{3}\) ) |
b. The other two points that fall on this line are (6 , 3 ) and (9, 5 ) .
Eureka Math Grade 5 Module 6 Lesson 11 Exit Ticket Answer Key
Question 1.
Complete the tables for the given rules.
Line l
Rule: Triple x
| x | y |
(x, y) |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
Line m
Rule: Triple x, and then add 1
| x | y |
(x, y) |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
Answer:
a.
Line l
Rule: Triple x
y = 3x
| x | y |
(x, y) |
| 0 | 0 | (0, 0) |
| 1 | 3 | (1, 3) |
| 2 | 6 | (2, 6) |
| 3 | 9 | (3, 9) |
Line m
Rule: Triple x, and then add 1
y = 3x + 1
| x | y |
(x, y) |
| 0 | 1 | (0, 1) |
| 1 | 4 | (1, 4) |
| 2 | 7 | (2, 7) |
| 3 | 10 | (3, 10) |
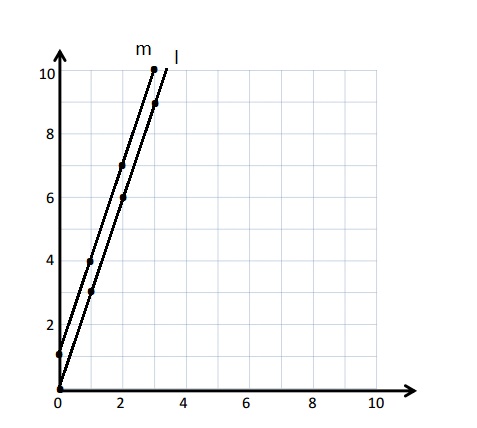
b. Line m is parallel to line m and is shown in above graph .
Question 2.
Circle the point(s) that the line for the rule multiply x by \(\frac{1}{3}\), and then add 1 would contain.
(0, \(\frac{1}{2}\))
(1, 1\(\frac{1}{3}\))
(2, 1\(\frac{2}{3}\))
(3, 2\(\frac{1}{2}\))
Answer:
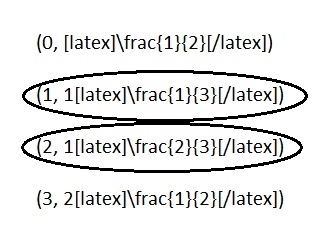
Explanation :
Line n
Rule: x by \(\frac{1}{3}\), and then add 1
y = \(\frac{x}{3}\) + 1 = \(\frac{ x + 3 }{3}\)
| x | y |
(x, y) |
| 0 | 1 | (0, 1) |
| 1 | 1\(\frac{1}{3}\) | (1, 1 \(\frac{1}{3}\)) |
| 2 | 1 \(\frac{2}{3}\) | (2, 1 \(\frac{2}{3}\)) |
| 3 | 2 | (3, 2) |
Eureka Math Grade 5 Module 6 Lesson 11 Homework Answer Key
Question 1.
Complete the tables for the given rules.
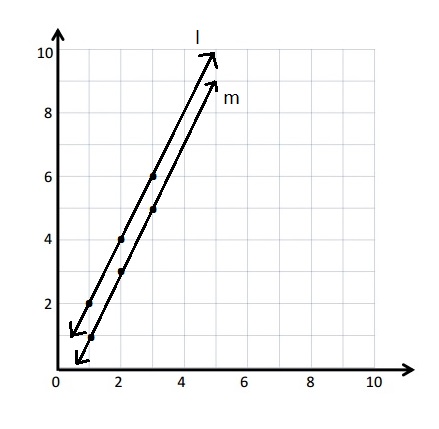
Line l
Rule: Double x
| x | y |
(x, y) |
| 1 | ||
| 2 | ||
| 3 |
Line m
Rule: Double x, and then subtract 1
| x | y |
(x, y) |
| 1 | ||
| 2 | ||
| 3 |
a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule double x, and then add 1 would look like. Draw your prediction on the plane above.
Answer:
a.
Line l
Rule: Double x
y = 2x
| x | y |
(x, y) |
| 1 | 2 | (1, 2) |
| 2 | 4 | (2, 4) |
| 3 | 6 | (3, 6) |
Line m
Rule: Double x, and then subtract 1
y = 2x – 1
| x | y |
(x, y) |
| 1 | 1 | (1, 1) |
| 2 | 3 | (2, 3) |
| 3 | 5 | (3, 5) |
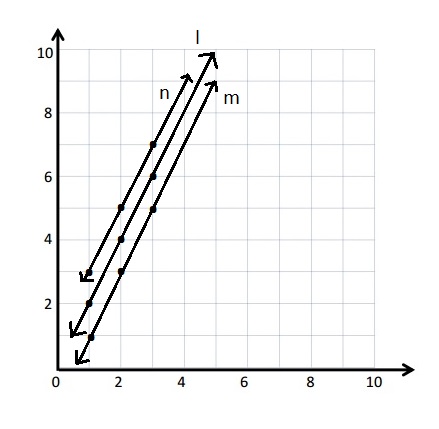
b. The l and m are parallel lines . both lines are parallel to each other .
c.
Line n
Rule: Double x, and then add 1
y = 2x +1
| x | y |
(x, y) |
| 1 | 3 | (1, 3) |
| 2 | 5 | (2, 5) |
| 3 | 7 | (3, 7) |
Question 2.
Circle the point(s) that the line for the rule multiply x by \(\frac{1}{2}\), and then add 1 would contain.
(0, \(\frac{1}{2}\))
(1, 1\(\frac{1}{4}\))
(2, 2)
(3, \(\frac{1}{2}\))
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:
a.
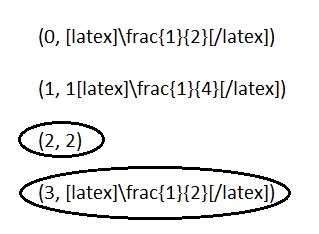
Explanation :
Rule: x by \(\frac{1}{2}\), and then add 1
y = \(\frac{x}{2}\) + 1 = \(\frac{ x + 2 }{2}\)
| x | y |
(x, y) |
| 0 | 1 | (0, 1) |
| 1 | 1\(\frac{1}{2}\) | (1, 1 \(\frac{1}{2}\)) |
| 2 | 2 | (2, 2) |
| 3 | 2\(\frac{1}{2}\) | (3, 2\(\frac{1}{2}\)) |
b. The other two points are (4, 3) and ( 6, 4)
Question 3.
Complete the tables for the given rules.
Line l
Rule: Halve x, and then add 1
| x | y |
(x, y) |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
Line m
Rule: Halve x, and then add 1\(\frac{1}{4}\)
| x | y |
(x, y) |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule halve x, and then subtract 1 would look like. Draw your prediction on the plane above.
Answer:
a.
Line l
Rule: Halve x, and then add 1
y = \(\frac{x}{2}\) + 1 = \(\frac{ x + 2 }{2}\)
| x | y |
(x, y) |
| 0 | 1 | (0, 1) |
| 1 | 1\(\frac{1}{2}\) | (1, 1\(\frac{1}{2}\)) |
| 2 | 2 | (2, 2) |
| 3 | 2\(\frac{1}{2}\) | (3, 2\(\frac{1}{2}\)) |
Line m
Rule: Halve x, and then add 1\(\frac{1}{4}\)
y = \(\frac{x}{2}\) + \(\frac{5}{4}\) = \(\frac{ 2x + 5 }{4}\)
| x | y |
(x, y) |
| 0 | 1\(\frac{1}{4}\) | (0, 1\(\frac{1}{4}\)) |
| 1 | 1\(\frac{3}{4}\) | (1, 1\(\frac{3}{4}\)) |
| 2 | 2\(\frac{1}{4}\) | (2, 2\(\frac{1}{4}\)) |
| 3 | 2\(\frac{3}{4}\) | (3, 2\(\frac{3}{4}\)) |
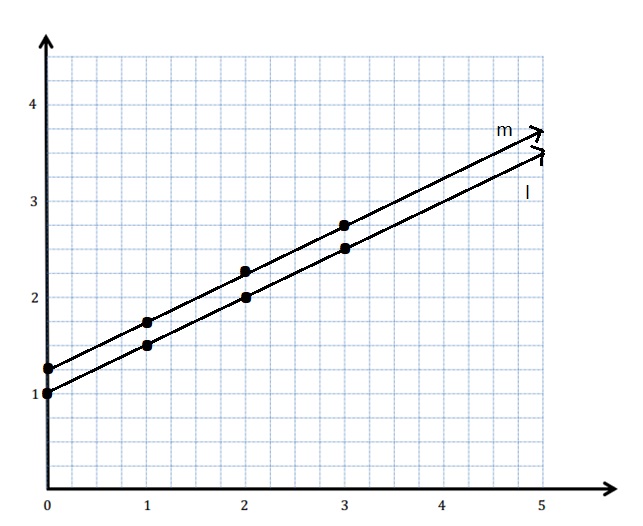
b. Line l and line m are parallel to each other and is shown in above graph .
c.
Line n
Rule: halve x, and then subtract 1
y = \(\frac{x}{2}\) – 1 = \(\frac{ x – 2 }{2}\) .
| x | y |
(x, y) |
| 2 | 0 | (2, 0) |
| 4 | 1 | (4, 1) |
| 6 | 2 | (6, 2) |
| 8 | 3 | (8, 3) |
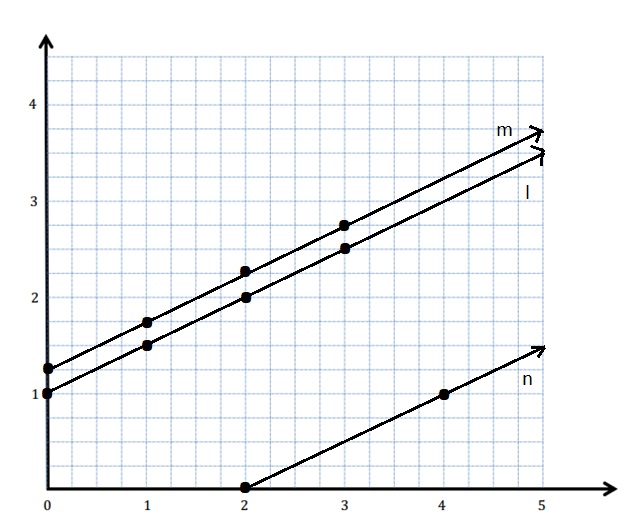
Question 4.
Circle the point(s) that the line for the rule multiply x by \(\frac{3}{4}\), and then subtract \(\frac{1}{2}\) would contain.
(1, \(\frac{1}{4}\))
(2, \(\frac{1}{4}\))
(3, 1\(\frac{3}{4}\))
(3, 1)
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:
a.
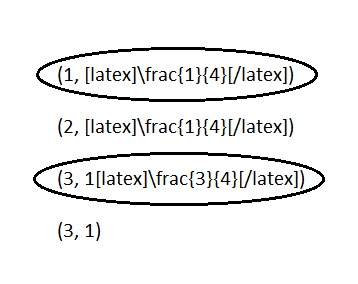
Explanation :
Rule: multiply x by \(\frac{3}{4}\), and then subtract \(\frac{1}{2}\)
y = x\(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{ 3x – 2 }{4}\) .
| x | y |
(x, y) |
| 1 | \(\frac{1}{4}\) | (1, \(\frac{1}{4}\)) |
| 2 | 1 | (2, 1) |
| 3 | 1\(\frac{3}{4}\) | (3, 1\(\frac{3}{4}\)) |
| 4 | 2\(\frac{2}{4}\) | (4, 2\(\frac{2}{4}\)) |
b. The other 2 points that fall on this line are (6, 4) and ( 8, 5\(\frac{ 1 }{2}\))
Explanation :
y = x\(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{ 3x – 2 }{4}\) .
x= 6
y = \(\frac{ 3 x 6 – 2 }{4}\) = 4
and
x = 8
y= \(\frac{ 3 x 8 – 2 }{4}\) = \(\frac{ 22 }{4}\) = \(\frac{ 11 }{2}\) = 5\(\frac{ 1 }{2}\)