Engage NY Eureka Math 5th Grade Module 6 Lesson 12 Answer Key
Eureka Math Grade 5 Module 6 Lesson 12 Sprint Answer Key
A
Subtract Decimals
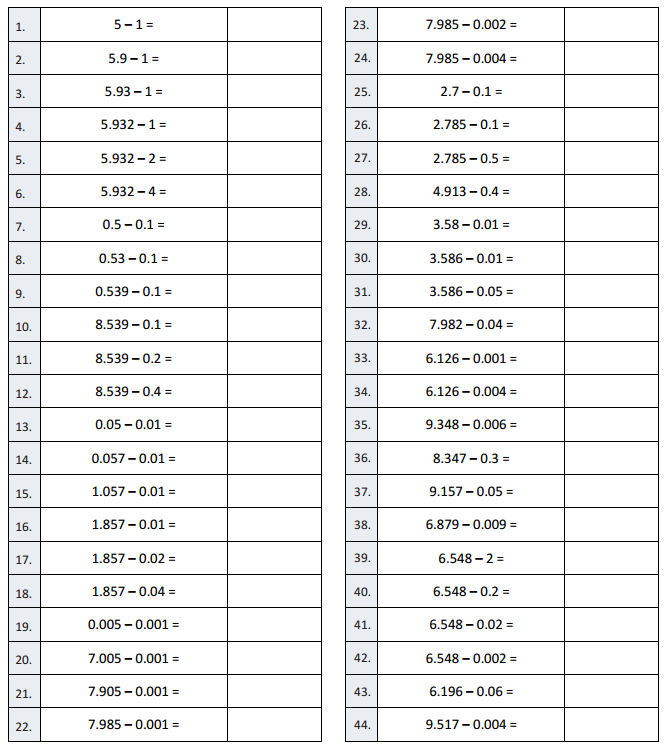
Question 1.
5 – 1 =
Answer:
5 – 1 = 4
Question 2.
5.9 – 1 =
Answer:
5.9 – 1 = 4.9
Explanation :
| Line the decimals up: | 5.9 | ||
| − | 1 | ||
| “Pad” with zeros: | 5.9 | ||
| − | 1.0 | ||
| Subtract: | 5.9 | ||
| 1.0 | |||
| 4.9 |
Question 3.
5.93 – 1 =
Answer:
5.93 – 1 = 4.93
Explanation :
| Line the decimals up: | 5.93 | ||
| − | 1 | ||
| “Pad” with zeros: | 5.93 | ||
| − | 1.00 | ||
| Subtract: | 5.93 | ||
| 1.00 | |||
| 4.93 |
Question 4.
5.932 – 1 =
Answer:
5.932 -1 = 4.932
Explanation :
| Line the decimals up: | 5.932 | ||
| − | 1 | ||
| “Pad” with zeros: | 5.932 | ||
| − | 1.000 | ||
| Subtract: | 5.932 | ||
| 1.000 | |||
| 4.932 |
Question 5.
5.932 – 2 =
Answer:
5.932 – 2 = 3.932
Explanation :
| Line the decimals up: | 5.932 | ||
| − | 2 | ||
| “Pad” with zeros: | 5.932 | ||
| − | 2.000 | ||
| Subtract: | 5.932 | ||
| 2.000 | |||
| 3.932 |
Question 6.
5.932 – 4 =
Answer:
5.932 – 4 = 1.932
Explanation :
| Line the decimals up: | 5.932 | ||
| − | 4 | ||
| “Pad” with zeros: | 5.932 | ||
| − | 4.000 | ||
| Subtract: | 5.932 | ||
| 4.000 | |||
| 1.932 |
Question 7.
0.5 – 0.1 =
Answer:
0.5 – 0.1 = 0.4
Explanation :
| Line the decimals up: | 0.5 | ||
| − | 0.1 | ||
| “Pad” with zeros: | 0.5 | ||
| − | 0.1 | ||
| Subtract: | 0.5 | ||
| 0.1 | |||
| 0.4 |
Question 8.
0.53 – 0.1 =
Answer:
0.53 – 0.1 = 0.43
Explanation :
| Line the decimals up: | 0.53 | ||
| − | 0.1 | ||
| “Pad” with zeros: | 0.53 | ||
| − | 0.10 | ||
| Subtract: | 0.53 | ||
| 0.10 | |||
| 0.43 |
Question 9.
0.539 – 0.1 =
Answer:
0.539 – 0.1 = 0.439
Explanation :
| Line the decimals up: | 0.539 | ||
| − | 0.1 | ||
| “Pad” with zeros: | 0.539 | ||
| − | 0.100 | ||
| Subtract: | 0.539 | ||
| 0.100 | |||
| 0.439 |
Question 10.
8.539 – 0.1 =
Answer:
8.539 – 0.1 = 8.439
Explanation :
| Line the decimals up: | 8.539 | ||
| − | 0.1 | ||
| “Pad” with zeros: | 8.539 | ||
| − | 0.100 | ||
| Subtract: | 8.539 | ||
| 0.100 | |||
| 8.439 |
Question 11.
8.539 – 0.2 =
Answer:
Explanation :
| Line the decimals up: | 8.539 | ||
| − | 0.2 | ||
| “Pad” with zeros: | 8.539 | ||
| − | 0.200 | ||
| Subtract: | 8.539 | ||
| 0.200 | |||
| 8.339 |
Question 12.
8.539 – 0.4 =
Answer:
8.539 – 0.4 = 8.139
Explanation :
| Line the decimals up: | 8.539 | ||
| − | 0.4 | ||
| “Pad” with zeros: | 8.539 | ||
| − | 0.400 | ||
| Subtract: | 8.539 | ||
| 0.400 | |||
| 8.139 |
Question 13.
0.05 – 0.01 =
Answer:
0.05 – 0.01 = 0.04
Explanation :
| Line the decimals up: | 0.05 | ||
| − | 0.01 | ||
| “Pad” with zeros: | 0.05 | ||
| − | 0.01 | ||
| Subtract: | 0.05 | ||
| 0.01 | |||
| 0.04 |
Question 14.
0.057 – 0.01 =
Answer:
0.057 – 0.01 =0.047
Explanation :
| Line the decimals up: | 0.057 | ||
| − | 0.01 | ||
| “Pad” with zeros: | 0.057 | ||
| − | 0.010 | ||
| Subtract: | 0.057 | ||
| 0.010 | |||
| 0.047 |
Question 15.
1.057 – 0.01 =
Answer:
1.057 – 0.01 = 1.047
Explanation :
| Line the decimals up: | 1.057 | ||
| − | 0.01 | ||
| “Pad” with zeros: | 1.057 | ||
| − | 0.010 | ||
| Subtract: | 1.057 | ||
| 0.010 | |||
| 1.047 |
Question 16.
1.857 – 0.01 =
Answer:
1.857 – 0.01 = 1.847
Explanation :
| Line the decimals up: | 1.857 | ||
| − | 0.01 | ||
| “Pad” with zeros: | 1.857 | ||
| − | 0.010 | ||
| Subtract: | 1.857 | ||
| 0.010 | |||
| 1.847 |
Question 17.
1.857 – 0.02 =
Answer:
1.857 – 0.02 = 1.837
Question 18.
1.857 – 0.04 =
Answer:
1.857 – 0.04 = 1.817
Question 19.
0.005 – 0.001 =
Answer:
0.005 – 0.001 = 0.004
Explanation :
| Line the decimals up: | 0.005 | ||
| − | 0.001 | ||
| “Pad” with zeros: | 0.005 | ||
| − | 0.001 | ||
| Subtract: | 0.005 | ||
| 0.001 | |||
| 0.004 |
Question 20.
7.005 – 0.001 =
Answer:
7.005 – 0.001 = 7.004
Explanation :
| Line the decimals up: | 7.005 | ||
| − | 0.001 | ||
| “Pad” with zeros: | 7.005 | ||
| − | 0.001 | ||
| Subtract: | 7.005 | ||
| 0.001 | |||
| 7.004 |
Question 21.
7.905 – 0.001 =
Answer:
7.905 – 0.001 = 7.904
Question 22.
7.985 – 0.001 =
Answer:
7.985 – 0.001 = 7.984
Question 23.
7.985 – 0.002 =
Answer:
7.985 – 0.002 = 7.983
Question 24.
7.985 – 0.004 =
Answer:
7.985 – 0.004 =7.981
Question 25.
2.7 – 0.1 =
Answer:
2.7 – 0.1 = 2.6
Question 26.
2.785 – 0.1 =
Answer:
2.785 – 0.1 = 2.775
Explanation :
| Line the decimals up: | 2.785 | ||
| − | 0.1 | ||
| “Pad” with zeros: | 2.785 | ||
| 0.100 | |||
| Subtract: | 2.785 | ||
| 0.100 | |||
| 2.685 |
Question 27.
2.785 – 0.5 =
Answer:
2.785 – 0.5 = 2.285
Question 28.
4.913 – 0.4 =
Answer:
4.913 – 0.4 = 4.513
Question 29.
3.58 – 0.01 =
Answer:
3.58 – 0.01 = 3.47
Explanation :
| Line the decimals up: | 3.58 | ||
| − | 0.01 | ||
| “Pad” with zeros: | 3.58 | ||
| 0.01 | |||
| Subtract: | 3.58 | ||
| 0.01 | |||
| 3.57 |
Question 30.
3.586 – 0.01 =
Answer:
3.586 – 0.01 = 3.576
Question 31.
3.586 – 0.05 =
Answer:
3.586 – 0.05 = 3.536
Question 32.
7.982 – 0.04 =
Answer:
7.982 – 0.04 = 7.942
Question 33.
6.126 – 0.001 =
Answer:
6.126 – 0.001 = 6.125
Question 34.
6.126 – 0.004 =
Answer:
6.126 – 0.004 = 6.122
Question 35.
9.348 – 0.006 =
Answer:
9.348 – 0.006 = 9.342
Question 36.
8.347 – 0.3 =
Answer:
8.347 – 0.3 = 8.047
Question 37.
9.157 – 0.05 =
Answer:
9.157 – 0.05 = 9.107
Question 38.
6.879 – 0.009 =
Answer:
6.879 – 0.009 = 6.870
Question 39.
6.548 – 2 =
Answer:
6.548 – 2 = 6.348
Question 40.
6.548 – 0.2 =
Answer:
6.548 – 0.2 = 6.348
Question 41.
6.548 – 0.02 =
Answer:
6.548 – 0.02 = 6.528
Question 42.
6.548 – 0.002 =
Answer:
6.548 – 0.002 = 6.546
Question 43.
6.196 – 0.06 =
Answer:
6.196 – 0.06 = 6.136
Question 44.
9.517 – 0.004 =
Answer:
9.517 – 0.004 = 9.513
B
Subtract Decimals
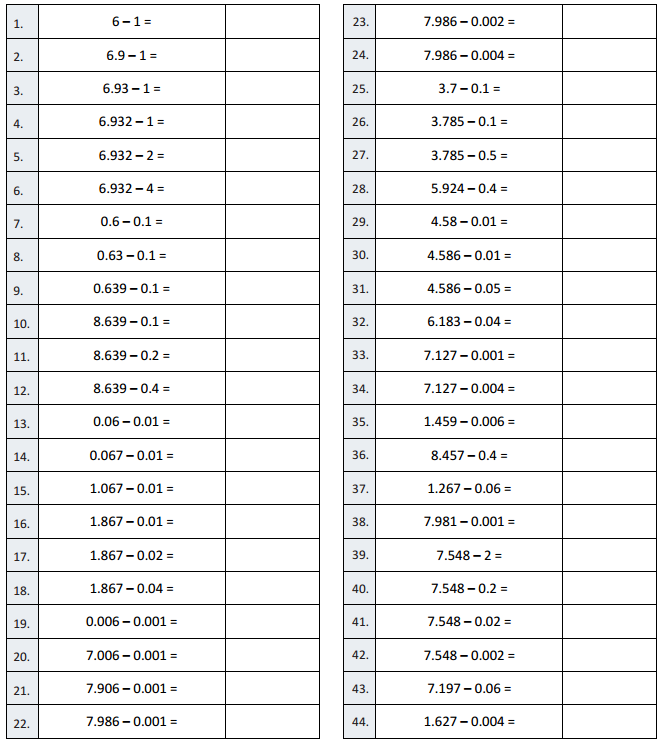
Question 1.
6 – 1 =
Answer:
6 – 1 = 5
Question 2.
6.9 – 1 =
Answer:
6.9 – 1 = 5.9
Question 3.
6.93 – 1 =
Answer:
6.93 – 1 = 5.93
Question 4.
6.932 – 1 =
Answer:
6.932 – 1 = 5.932
Question 5.
6.932 – 2 =
Answer:
6.932 – 2 = 4.932
Question 6.
6.932 – 4 =
Answer:
6.932 – 4 = 2.932
Question 7.
0.6 – 0.1 =
Answer:
0.6 – 0.1 = 0.5
Question 8.
0.63 – 0.1 =
Answer:
0.63 – 0.1 = 0.53
Question 9.
0.639 – 0.1 =
Answer:
0.639 – 0.1 = 0.539
Question 10.
8.639 – 0.1 =
Answer:
8.639 – 0.1 = 8.539
Question 11.
8.639 – 0.2 =
Answer:
8.639 – 0.2 = 8.439
Question 12.
8.639 – 0.4 =
Answer:
8.639 – 0.4 = 8.239
Question 13.
0.06 – 0.01 =
Answer:
0.06 – 0.01 = 0.05
Question 14.
0.067 – 0.01 =
Answer:
0.067 – 0.01 = 0.057
Question 15.
1.067 – 0.01 =
Answer:
1.067 – 0.01 = 1.057
Question 16.
1.867 – 0.01 =
Answer:
1.867 – 0.01 = 1.857
Question 17.
1.867 – 0.02 =
Answer:
1.867 – 0.02 = 1.847
Question 18.
1.867 – 0.04 =
Answer:
1.867 – 0.04 = 1.827
Question 19.
0.006 – 0.001 =
Answer:
0.006 – 0.001 = 0.005
Question 20.
7.006 – 0.001 =
Answer:
7.006 – 0.001 = 7.005
Question 21.
7.906 – 0.001 =
Answer:
7.906 – 0.001 = 7.905
Question 22.
7.986 – 0.001 =
Answer:
7.986 – 0.001 = 7.985
Question 23.
7.986 – 0.002 =
Answer:
7.986 – 0.002 = 7.984
Question 24.
7.986 – 0.004 =
Answer:
7.986 – 0.004 = 7.982
Question 25.
3.7 – 0.1 =
Answer:
3.7 – 0.1 = 3.6
Question 26.
3.785 – 0.1 =
Answer:
3.785 – 0.1 = 3.685
Question 27.
3.785 – 0.5 =
Answer:
3.785 – 0.5 = 3.285
Question 28.
5.924 – 0.4 =
Answer:
5.924 – 0.4 = 5.524
Question 29.
4.58 – 0.01 =
Answer:
4.58 – 0.01 = 4.57
Question 30.
4.586 – 0.01 =
Answer:
4.586 – 0.01 = 4.576
Question 31.
4.586 – 0.05 =
Answer:
4.586 – 0.05 = 4.536
Question 32.
6.183 – 0.04 =
Answer:
6.183 – 0.04 =6.143
Question 33.
7.127 – 0.001 =
Answer:
7.127 – 0.001 = 7.126
Question 34.
7.127 – 0.004 =
Answer:
7.127 – 0.004 = 7.123
Question 35.
1.459 – 0.006 =
Answer:
1.459 – 0.006 = 1.453
Question 36.
8.457 – 0.4 =
Answer:
8.457 – 0.4 = 8.057
Question 37.
1.267 – 0.06 =
Answer:
1.267 – 0.06 = 1.207
Question 38.
7.981 – 0.001 =
Answer:
7.981 – 0.001 = 7.980
Question 39.
7.548 – 2 =
Answer:
7.548 – 2 = 5.548
Question 40.
7.548 – 0.2 =
Answer:
7.548 – 0.2 = 7.348
Question 41.
7.548 – 0.02 =
Answer:
7.548 – 0.02 = 7.528
Question 42.
7.548 – 0.002 =
Answer:
7.548 – 0.002 = 7.546
Question 43.
7.197 – 0.06 =
Answer:
7.197 – 0.06 = 7.191
Question 44.
1.627 – 0.004 =
Answer:
1.627 – 0.004 =1.623
Eureka Math Grade 5 Module 6 Lesson 12 Problem Set Answer Key
Question 1.
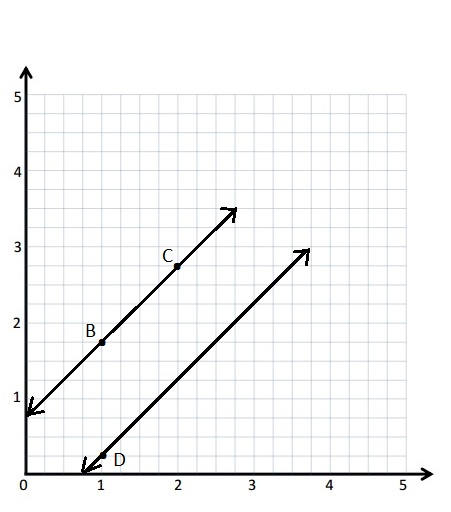
Write a rule for the line that contains the points (0, \(\frac{3}{4}\)) and (2\(\frac{1}{2}\), 3\(\frac{1}{4}\)).
a. Identify 2 more points on this line. Draw the line on the grid below.
|
Point |
x | y |
(x , y) |
| B | |||
| C |
b. Write a rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{4}\)).
Answer:
a.
(0, \(\frac{3}{4}\)) and (2\(\frac{1}{2}\), 3\(\frac{1}{4}\)).
Rule : add \(\frac{3}{4}\) to x .
y = x + add \(\frac{3}{4}\)
|
Point |
x | y |
(x , y) |
| B | 1 | 1\(\frac{3}{4}\) | 1\(\frac{3}{4}\) |
| C | 2 | 2\(\frac{3}{4}\) | 2\(\frac{3}{4}\) |
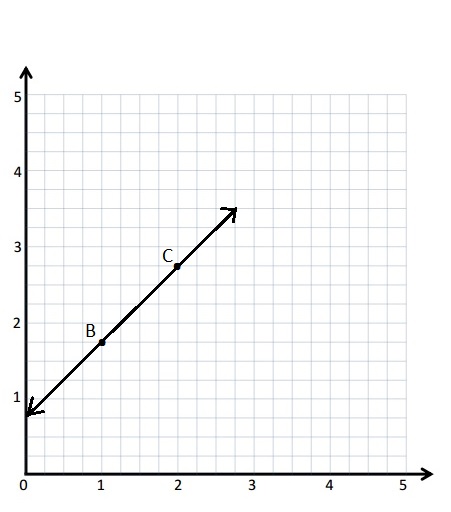
b. A rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{4}\)).
Rule : subtract \(\frac{3}{4}\) from x .
D = (1, \(\frac{1}{4}\)).
Question 2.
Create a rule for the line that contains the points (1, \(\frac{1}{4}\) and (3, \(\frac{3}{4}\)).
a. Identify 2 more points on this line. Draw the line on the grid on the right.
|
Point |
x | y |
(x , y) |
| G | |||
| H |
b. Write a rule for a line that passes through the origin and lies between \(\overleftrightarrow{B C}\) and \(\overleftrightarrow{G H}\).
Answer:
a. Rule :Multiply x by \(\frac{1}{4}\)
(1, \(\frac{1}{4}\) and (3, \(\frac{3}{4}\))
|
Point |
x | y |
(x , y) |
| G | 2 | \(\frac{1}{2}\) | (2, \(\frac{1}{2}\)) |
| H | 4 | 1 | (4, 1) |
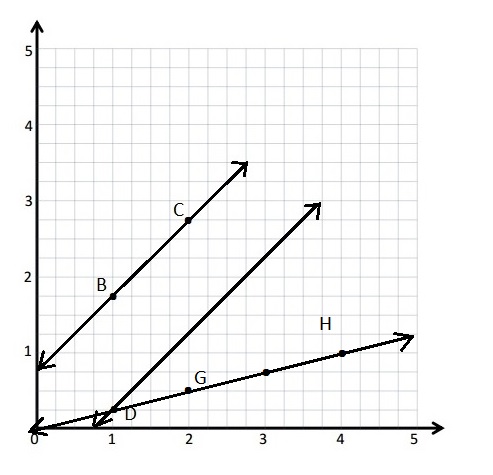
b. Rule :Multiply x by \(\frac{3}{4}\) .
Question 3.
Create a rule for a line that contains the point (\(\frac{1}{4}\), 1\(\frac{1}{4}\)) using the operation or description below. Then, name 2 other points that would fall on each line.
a. Addition: _________
|
Point |
x | y |
(x , y) |
| T | |||
| U |
b. A line parallel to the x-axis: _________
|
Point |
x | y |
(x , y) |
| G | |||
| H |
c. Multiplication: _________
|
Point |
x | y |
(x , y) |
| A | |||
| B |
d. A line parallel to the y-axis: _________
|
Point |
x | y |
(x , y) |
| V | |||
| W |
e. Multiplication with addition: _________
|
Point |
x | y |
(x , y) |
| R | |||
| S |
Answer:
a. Addition: add 1 to x
|
Point |
x | y |
(x , y) |
| T | 2 | 3 | (2, 3) |
| U | 3 | 4 | (3, 4) |
b. A line parallel to the x-axis: y is always 1\(\frac{1}{4}\).
|
Point |
x | y |
(x , y) |
| G | 1 | 1\(\frac{1}{4}\) | ( 1, 1\(\frac{1}{4}\)) |
| H | 2 | 1\(\frac{1}{4}\) | (2, 1\(\frac{1}{4}\)) |
c. Multiplication: multiply x by 5 .
|
Point |
x | y |
(x , y) |
| A | 2 | 10 | (2, 10) |
| B | 3 | 15 | (3, 15) |
d. A line parallel to the y-axis: x coordinate is always 4
|
Point |
x | y |
(x , y) |
| V | 4 | 3 | (4, 3) |
| W | 4 | 4 | (4, 4) |
e. Multiplication with addition: multiply x and add \(\frac{1}{4}\)
|
Point |
x | y |
(x , y) |
| R | \(\frac{1}{2}\) | 2\(\frac{1}{4}\) | (\(\frac{1}{2}\), 2\(\frac{1}{4}\)) |
| S | 2 | 8\(\frac{1}{4}\) | (2, 8\(\frac{1}{4}\)) |
Question 4.
Mrs. Boyd asked her students to give a rule that could describe a line that contains the point (0.6, 1.8). Avi said the rule could be multiply x by 3. Ezra claims this could be a vertical line, and the rule could be x is always 0.6. Erik thinks the rule could be add 1.2 to x. Mrs. Boyd says that all the lines they are describing could describe a line that contains the point she gave. Explain how that is possible, and draw the lines on the coordinate plane to support your response.
Answer:
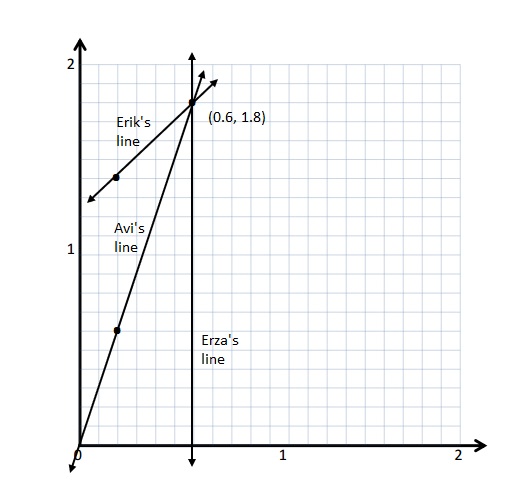
Explanation :
Mrs. Boyd’s gave only one point (0.6, 1.8) on the line .Many lines can be drawn from one point . With 2 points we can say the rule but without 2 points we cannot say the rule.
Question 5.
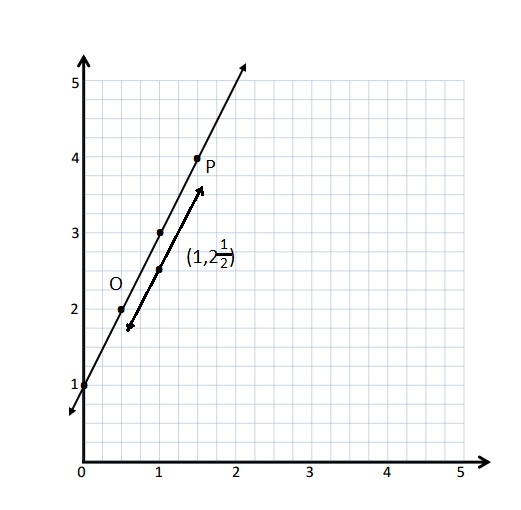
Create a mixed operation rule for the line that contains the points (0, 1) and (1, 3).
a. Identify 2 more points, O and P, on this line. Draw the line on the grid.
|
Point |
x | y |
(x , y) |
| O | |||
| P |
b. Write a rule for a line that is parallel to \(\overleftrightarrow{O P}\) and goes through point (1, 2\(\frac{1}{2}\)).
Answer:
Rule : Multiply x by 2 and add 1 .
a.
|
Point |
x | y |
(x , y) |
| O | \(\frac{1}{2}\) | 2 | (\(\frac{1}{2}\), 2) |
| P | 1\(\frac{1}{2}\) | 4 | (1\(\frac{1}{2}\), 4) |
b. Rule : Multiply by x and add 2.
Eureka Math Grade 5 Module 6 Lesson 12 Exit Ticket Answer Key
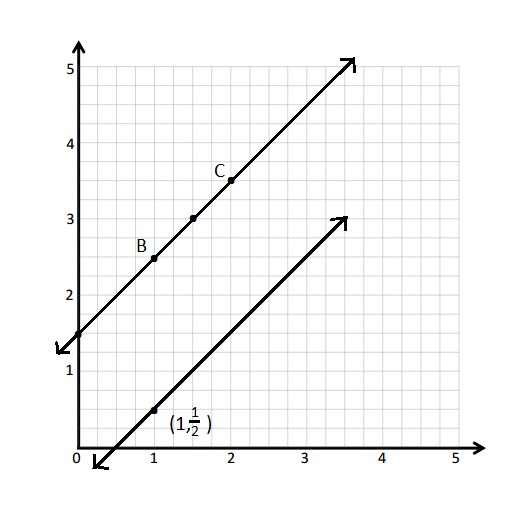
Write the rule for the line that contains the points (0, 1\(\frac{1}{2}\)) and (1\(\frac{1}{2}\), 3).
a. Identify 2 more points on this line. Draw the line on the grid.
|
Point |
x | y |
(x , y) |
| B | |||
| C |
b. Write a rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{2}\)).
Answer:
Rule : add \(\frac{1}{2}\) to x .
|
Point |
x | y |
(x , y) |
| B | 1 | 2\(\frac{1}{2}\) | (1,2\(\frac{1}{2}\)) |
| C | 2 | 3\(\frac{1}{2}\) | (2, 3\(\frac{1}{2}\)) |
b.
The Rule that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{2}\)) is Subtract \(\frac{1}{2}\) from x .
Eureka Math Grade 5 Module 6 Lesson 12 Homework Answer Key
Question 1.
Write a rule for the line that contains the points (0, \(\frac{1}{4}\)) and (2\(\frac{1}{2}\), 2\(\frac{3}{4}\)).
a. Identify 2 more points on this line. Draw the line on the grid below.
|
Point |
x | y |
(x , y) |
| B | |||
| C |
b. Write a rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, 2\(\frac{1}{4}\).
Answer:
Rule : Add \(\frac{1}{4}\) to x .
|
Point |
x | y |
(x , y) |
| B | \(\frac{3}{4}\) | 1 | (\(\frac{3}{4}\), 1) |
| C | 2 | 2\(\frac{1}{4}\) | (2, 2\(\frac{1}{4}\)) |
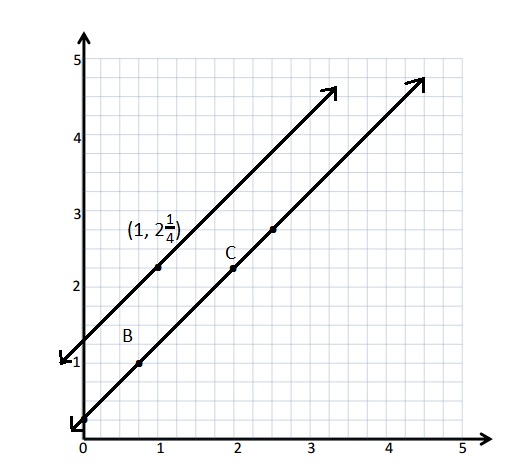
b.
Rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, 2\(\frac{1}{4}\) is add 1\(\frac{1}{4}\) to x .
Question 2.
Give the rule for the line that contains the points (1, 2\(\frac{1}{2}\)) and (2\(\frac{1}{2}\), 2\(\frac{1}{2}\)).
a. Identify 2 more points on this line. Draw the line on the grid above.
|
Point |
x | y |
(x , y) |
| G | |||
| H |
b. Write a rule for a line that is parallel to \(\overleftrightarrow{G H}\).
Answer:
a.
Rule : For all x-coordinates the y- coordinate is 2\(\frac{1}{2}\)
|
Point |
x | y |
(x , y) |
| G | 3 | 2\(\frac{1}{2}\) | (3, 2\(\frac{1}{2}\)) |
| H | 4 | 2\(\frac{1}{2}\) | (4, 2\(\frac{1}{2}\)) |
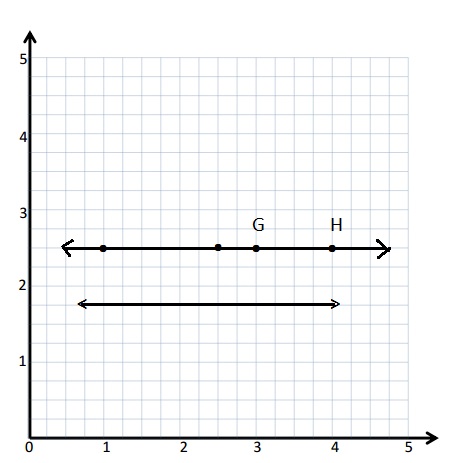
b. A rule for a line that is parallel to \(\overleftrightarrow{G H}\) is
For all x-coordinates the y- coordinate is 1\(\frac{3}{4}\) .
Question 3.
Give the rule for a line that contains the point (\(\frac{3}{4}\), 1\(\frac{1}{2}\)) using the operation or description below. Then, name 2 other points that would fall on each line.
a. Addition: ________________
|
Point |
x | y |
(x , y) |
| T | |||
| U |
b. A line parallel to the x-axis: ________________
|
Point |
x | y |
(x , y) |
| G | |||
| H |
c. Multiplication: ________________
|
Point |
x | y |
(x , y) |
| A | |||
| B |
d. A line parallel to the y-axis: ________________
|
Point |
x | y |
(x , y) |
| V | |||
| W |
e. Multiplication with addition: _____________
|
Point |
x | y |
(x , y) |
| R | |||
| S |
Answer:
a. Addition: add \(\frac{3}{4}\) to x
|
Point |
x | y |
(x , y) |
| T | \(\frac{3}{4}\) | 1\(\frac{1}{2}\) | (\(\frac{3}{4}\), 1\(\frac{1}{2}\)) |
| U | 2 | 2\(\frac{3}{4}\) | (2, 2\(\frac{3}{4}\)) |
b. A line parallel to the x-axis: all x coordinate have y coordinate as 2
|
Point |
x | y |
(x , y) |
| G | 1 | 2 | (1, 2) |
| H | 2 | 2 | (2, 2) |
c. Multiplication: multiply by 2
|
Point |
x | y |
(x , y) |
| A | 1 | 2 | (1, 2) |
| B | 2 | 4 | (2, 4) |
d. A line parallel to the y-axis: All y coordinates have the same x coordinate 2
|
Point |
x | y |
(x , y) |
| V | 3 | 1 | (3, 1) |
| W | 3 | 2 | (3, 2) |
e. Multiplication with addition: multiply by 2 and add 1
|
Point |
x | y |
(x , y) |
| R | 1 | 3 | (1, 3) |
| S | 2 | 5 | (2, 5) |
Question 4.
On the grid, two lines intersect at (1.2, 1.2). If line a passes through the origin and line b contains the point (1.2, 0), write a rule for line a and line b.
Answer:
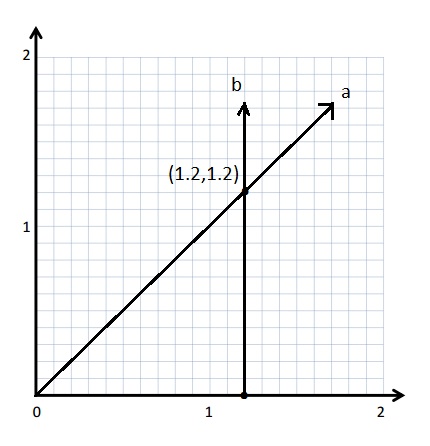
For line a the Rule is x coordinate . The y coordinate is same the x coordinate .
For line b the Rule is All y coordinates have the same x coordinate 1.2 .