Engage NY Eureka Math 5th Grade Module 6 Lesson 21 Answer Key
Eureka Math Grade 5 Module 6 Lesson 21-23 Problem Set Answer Key
Question 1.
Pierre’s Paper
Pierre folded a square piece of paper vertically to make two rectangles. Each rectangle had a perimeter of
39 inches. How long is each side of the original square? What is the area of the original square? What is the area of one of the rectangles?
Answer:
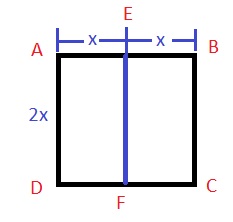
ABCD is a square.
AEFD AND EBCF are two equal rectangles of perimeter 39 inches.
Length of the rectangle = 2x
Breadth of the rectangle = x
Perimeter of a rectangle = 2 (l + b) = 2 (2x +x ) = 6x = 39
x =\(\frac{39}{6}\) =6.5
2x = 13
Area of square ABCD = Side × Side = 2x × 2x = 13 × 13 = 169 sq. inches.
Area of Rectangle AEFD = Area of Rectangle EBCF = length × Breadth = 2x × x = 13 × 6.5 = 84.5 sq inches .
Question 2.
Shopping with Elise
Elise saved $184. She bought a scarf, a necklace, and a notebook. After her purchases, she still had $39.50. The scarf cost three-fifths the cost of the necklace, and the notebook was one-sixth as much as the scarf. What was the cost of each item? How much more did the necklace cost than the notebook?
Answer:
Money with Elisa = $184 .
Money left after shopping = $39.50
Money spent on shopping = $184 = 39.50 = 144.50$
Cost of scarf = \(\frac{3}{5}\) cost of the necklace.
Cost of Note book = \(\frac{1}{6}\) cost of the Scarf . = \(\frac{1}{6}\)\(\frac{3}{5}\) cost of the necklace = \(\frac{1}{10}\) cost of the necklace .
cost of necklace = x
Cost of scarf + notebook + necklace = money spent on shopping
\(\frac{3}{5}\) x + \(\frac{1}{10}\) x + x = 144.50$
\(\frac{6x + 1x +10x }{10}\) = 144.5
17x = 1445
x= \(\frac{1445}{17}\)
x = 85
Cost of Necklace = 85$
Cost of Scarf = \(\frac{3}{5}\) cost of the necklace = \(\frac{3}{5}\) 85 = 39$.
Cost of Notebook = \(\frac{1}{10}\) cost of the necklace = \(\frac{1}{10}\) 85 = 8.5$ .
Money more spent on necklace than the notebook = 85 – 8.5 = 76.5$ .
Question 3.
The Hewitt’s Carpet
The Hewitt family is buying carpet for two rooms. The dining room is a square that measures 12 feet on each side. The den is 9 yards by 5 yards. Mrs. Hewitt has budgeted $2,650 for carpeting both rooms. The green carpet she is considering costs $42.75 per square yard, and the brown carpet’s price is $4.95 per square foot. What are the ways she can carpet the rooms and stay within her budget?
Answer:
Side of dining room = 12 feet
Area of dining square room = Side × Side = 12 × 12 = 144 sq feets .
den is in the shape of rectangle .
Length by breadth = 9 yards by 5 yards
Area of rectangle den = length × Breadth = 9 × 5 = 45 sq yards .
Cost of green carpet = $42.75 per square yard
Cost of green carpet for 45 sqyards = 45 ×$42.75 per square yard = 1923.75 $.
Cost of Brown carpet = $4.95 per square foot
Cost of Brown carpet for 144 sq foot = 144 × $4.95 = 712.8$
Total Cost of Green carpet and Brown carpet = 1923.75 $ + 712.8$ = 2645.55$
Budget for carpeting both rooms = 2650$.
She carpet green carpet to den and Brown carpet to dining Room . Then she can stay within her budget .
Question 4.
AAA Taxi
AAA Taxi charges $1.75 for the first mile and $1.05 for each additional mile. How far could Mrs. Leslie travel for $20 if she tips the cab driver $2.50?
Answer:
Cost of First mile = $1.75
Cost of second mile = $1.75 + $1.05 =$2.8
Cost of Third mile = $1.75 + $1.05 =$2.8
Cost of fourth mile = $1.75 + $1.05 =$2.8 and so on that means cost of second mile is $2.8
Money spent for travel = $20
Tip given for driver = $2.5
Money given to driver for travel = $20 – $ 2.5 = $17.5
x = number of miles traveled after 1st mile
cost of first mile + x cost of second mile = $17.5
1.75 + x (2.8) = 17.5$
2.8x = 17.5 -1.75
2.8x = 15.75 $
x = 5.625 miles
She traveled 5.625 miles
Question 5.
Pumpkins and Squash
Three pumpkins and two squash weigh 27.5 pounds. Four pumpkins and three squash weigh 37.5 pounds. Each pumpkin weighs the same as the other pumpkins, and each squash weighs the same as the other squash. How much does each pumpkin weigh? How much does each squash weigh?
Answer:
all pumpkins weights are equal = p
all Squash weights equal = s
Three pumpkins and two squash weigh 27.5 pounds
3p +2s = 27.5
Four pumpkins and three squash weigh 37.5 pounds.
4p + 3s = 37.5
Taking lcm for 4 and 3 = 12
4(3p +2s = 27.5)
3(4p + 3s = 37.5)
=12p + 8s = 110
12p + 9s = 112.5
= 9s – 8s = 112.5 – 110
s = 2.5
= 3p +2s = 27.5
3p + 2(2.5) = 27.5
3p = 27.5 – 5
p = 22.5 / 3 = 7.5
Weight of Squash =2.5 pounds.
Weight of pumpkin = 7.5 pounds .
Question 6.
Toy Cars and Trucks
Henry had 20 convertibles and 5 trucks in his miniature car collection. After Henry’s aunt bought him some more miniature trucks, Henry found that one-fifth of his collection consisted of convertibles. How many trucks did his aunt buy?
Answer:
Number of convertibles = 20
Number of trucks = 5
Number of trucks bought by Henry’s aunt = One-fifth of his collection consisted of convertibles = \(\frac{1}{5}\) y =20 = y = 100 .
100 – 20 convertibles = 80 .
80 – 5 ( 5 trucks are already with henry ) = 75 trucks .
Question 7.
Pairs of Scouts
Some girls in a Girl Scout troop are pairing up with some boys in a Boy Scout troop to practice square dancing. Two-thirds of the girls are paired with three-fifths of the boys. What fraction of the scouts are square dancing?
(Each pair is one Girl Scout and one Boy Scout. The pairs are only from these two troops.)
Answer:
Two-thirds of the girls are paired with three-fifths of the boys
\(\frac{2}{3}\) girls = \(\frac{3}{5}\) boys
\(\frac{2}{3}\) girls = \(\frac{6}{9}\)
\(\frac{3}{5}\) boys = \(\frac{6}{10}\)
Fraction of the scouts are square dancing = \(\frac{6+ 6}{9 + 10}\) = \(\frac{12}{19}\)
Question 8.
Sandra’s Measuring Cups
Sandra is making cookies that require 5\(\frac{1}{2}\) cups of oatmeal. She has only two measuring cups: a one-half cup and a three-fourths cup. What is the smallest number of scoops that she could make in order to get 5\(\frac{1}{2}\) cups?
Answer:
Measuring cups : a one-half cup and a three-fourths cup.
To make 5\(\frac{1}{2}\) cups with \(\frac{11}{2}\) cups
To make \(\frac{11}{2}\) cups we require 11 scoops .
To make 5\(\frac{1}{2}\) cups with a three-fourths cup. we require 7 Scoops with one fourth left .
So take 6 scoops of \(\frac{3}{4}\) then 1 will left so take 2 \(\frac{1}{2}\) cups.
Then we require 6 \(\frac{3}{4}\) scoops and 2 \(\frac{1}{2}\) cups.
Total fewest scoops are 6 + 2 = 8 scoops .
Question 9.
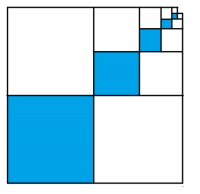
Blue Squares
The dimensions of each successive blue square pictured to the right are half that of the previous blue square. The lower left blue square measures 6 inches by 6 inches.
a. Find the area of the shaded part.
b. Find the total area of the shaded and unshaded parts.
c. What fraction of the figure is shaded?
Answer:
There are 3 sets of squares . 1 out of 3 sets are shaded.
c. Fraction shaded = \(\frac{1}{3}\)
b. Total Area = (12 × 12 ) – ( \(\frac{3}{8}\) \(\frac{3}{8}\))
= 144 – \(\frac{9}{64}\)
= \(\frac{9216 – 9}{64}\)
= 143 \(\frac{55}{64}\) sq inches .
a. Area Shaded = \(\frac{1}{3}\) × 143 \(\frac{55}{64}\) sq inches .
= \(\frac{1}{3}\) \(\frac{9207}{64}\)
= 47 \(\frac{61}{64}\) inches .
Eureka Math Grade 5 Module 6 Lesson 21 Homework Answer Key
Question 1.
Sara travels twice as far as Eli when going to camp. Ashley travels as far as Sara and Eli together. Hazel travels 3 times as far as Sara. In total, all four travel 888 miles to camp. How far does each of them travel?
Answer:
Distance traveled by Eli = x
Distance traveled by Sara = twice as far as Eli = 2x
Distance traveled by Ashley = Sara and Eli together. = x + 2x = 3x
Distance traveled by Hazel = 3 times Sara = 3 ( 2x) = 6x
Total distance traveled by all four = 888 miles
x+ 2x+ 3x+ 6x = 888
12x = 888
3x = 222
x = 74 miles.
Distance traveled by Eli = x = 74 miles
Distance traveled by Sara = twice as far as Eli = 2x = 2(74) = 144 miles
Distance traveled by Ashley = Sara and Eli together. = x + 2x = 3x = 3(74) = 218 miles
Distance traveled by Hazel = 3 times Sara = 3 ( 2x) = 6x = 6(74) = 444 miles
The following problem is a brainteaser for your enjoyment. It is intended to encourage working together and family problem-solving fun. It is not a required element of this homework assignment.
Question 2.
A man wants to take a goat, a bag of cabbage, and a wolf over to an island. His boat will only hold him and one animal or item. If the goat is left with the cabbage, he’ll eat it. If the wolf is left with the goat, he’ll eat it. How can the man transport all three to the island without anything being eaten?

Answer:
The wolf does not eat cabbage, so the crossing can start with the goat.
The man leaves the goat and returns, puts the cabbage in the boat and takes it across. On the other bank, he leaves the cabbage but takes the goat.
He leaves the goat on the first bank and takes the wolf across. He leaves the cabbage with the wolf and rows back alone.
He takes the goat across.