Engage NY Eureka Math 6th Grade Module 1 Lesson 8 Answer Key
Eureka Math Grade 6 Module 1 Lesson 8 Exercise Answer Key
Exercise 1
Circle any equivalent ratios from the list below.
Ratio: 1: 2
Ratio: 5: 10
Ratio: 6: 16
Ratio: 12: 32
Answer:

Revisit this when discussing the value of the equivalent ratios.
Find the value of the following ratios, leaving your answer as a fraction, but rewrite the fraction using the largest possible unit.
Ratio: 1: 2 Value of the Ratio:
Ratio: 5: 10 Value of the Ratio:
Ratio: 6: 16 Value of the Ratio:
Ratio: 12: 32 Value of the Ratio:
Answer:
Ratio: 1: 2 Value of the Ratio: \(\frac{1}{2}\)
Ratio: 5: 10 Value of the Ratio: \(\frac{1}{2}\)
Ratio: 6: 16 Value of the Ratio: \(\frac{3}{8}\)
Ratio: 12: 32 Value of the Ratio: \(\frac{3}{8}\)
What do you notice about the value of the equivalent ratios?
Answer:
The value of the ratio is the same for equivalent ratios.
Exercise 2
Here is a theorem: If A: B with B ≠ 0 and C: D with D ≠ 0 are equivalent, then they have the same value: \(\frac{A}{B}=\frac{C}{D}\). This is essentially stating that if two ratios are equivalent, then their values are the same (when they have values). Can you provide any counterexamples to the theorem above?
Answer:
Allow students to try this in pairs. Observe the progress of students and question students’ counterexamples. Ask for further clarification or proof that the two ratios are equivalent but do not have the same value. If students still think they have discovered a counterexample, share the example with the class and discuss why it is not a counterexample.
Ask entire class if anyone thought of a counterexample. If students share examples, have others explain why they are not counterexamples. Then discuss why there are no possible counterexamples to the given theorem. It is important for students to understand that the theorem is always true, so it is not possible to come up with a counterexample.
Exercise 3
Taivon is training for a duathlon, which is a race that consists of running and cycling. The cycling leg is longer than the running leg of the race, so while Taivon trains, he rides his bike more than he runs. During training, Taivon runs 4 miles for every 14 miles he rides his bike.
a. Identify the ratio associated with this problem and find its value.
Answer:
The ratio of the number of miles he ran to the number of miles he cycled is 4: 14, and the value of the ratio is \(\frac{2}{7}\) The ratio of the number of miles he cycled to the number of miles he ranis 14: 4, and the value of the ratio is \(\frac{7}{2}\).
Use the value of each ratio to solve the following.
b. When Taivon completed all of his training for the duathlon, the ratio of total number of miles he ran to total number of miles he cycled was 80: 280. Is this consistent with Taivon’s training schedule? Explain why or why not.
Answer:
This is consistent because the ratio of the number of miles he ran to the number of miles he cycled, 80: 280, has the value of \(\frac{2}{7}\), which is the same value as the ratio 4: 14.
c. In one training session, Taivon ran 4 miles and cycled 7 miles. Did this training session represent an equivalent ratio of the distance he ran to the distance he cycled? Explain why or why not.
Answer:
This training session does not represent an equivalent ratio of the distance he ran to the distance he cycled because the value of the ratio in this instance is \(\frac{4}{7}\), which is not equal to \(\frac{2}{7}\).
Eureka Math Grade 6 Module 1 Lesson 8 Problem Set Answer Key
Question 1.
The ratio of the number of shaded sections to the number of unshaded sections is 4 to 2. What is the value of the ratio of the number of shaded pieces to the number of unshaded pieces?
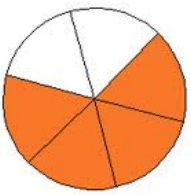
Answer:
\(\frac{4}{2}\) = \(\frac{2}{1}\) or 2
Question 2.
Use the value of the ratio to determine which ratios are equivalent to 7: 15.
a. 21:45
b. 14:45
c. 3:5
d. 63: 135
Answer:
Both (a) and (d) are equivalent to 7: 15.
Question 3.
Sean was at batting practice. He swung 25 times but only hit the ball 15 times.
a. Describe and write more than one ratio related to this situation.
Answer:
Ratio of the number of hits to the total number of swings is 15: 25.
Ratio of the number hits to the number of misses is 15: 10.
Ratio of the number of misses to the number of hits is 10: 15.
Ratio of the number of misses to the total number of swings is 10: 25.
b. For each ratio you oeated, use the value of the ratio to express one quantity as a fraction of the other quantity.
Answer:
The number of hits is \(\frac{15}{25}\) or \(\frac{3}{5}\) of the total number of swh,gs.
The number of hits is \(\frac{15}{10}\) or \(\frac{3}{2}\) the number of misses
The number of misses is \(\frac{10}{15}\) or \(\frac{2}{3}\) the number of hits.
The number of misses is \(\frac{10}{25}\) or \(\frac{2}{5}\) of the total number of swings.
c. Make up a word problem that a student can solve using one of the ratios and its value.
Answer:
If Sean estimates he will take 10 swings in his next game how many hits would he expect to get assuming his ratio of hits-to-swings does not change.
Question 4.
Your middle school has 900 students. \(\frac{1}{3}\) of students bring their lunch instead of buying lunch at school. What is the value of the ratio of the number of students who do bring their lunch to the number of students who do not?
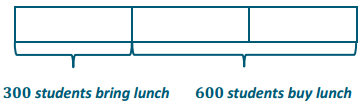
Answer:
First, I created a tape diagram. In the tape diagram, \(\frac{1}{3}\) of students bring their lunch instead of buying lunch at school. I determined that 300 students bring their lunch, leaving 600 students who buy their lunch. One unit of the tape diagram represents 300, and 2 units of the tape diagram represent 600. This creates a ratio of 1: 2. As such, the value of the ratio of the number of students who bring their lunch to the number of students who buy their lunch is \(\frac{1}{2}\)
Eureka Math Grade 6 Module 1 Lesson 8 Exit Ticket Answer Key
Question 1.
You created a new playlist, and 100 of your friends listened to it and shared if they liked the new playlist or not. Nadhii said the ratio of the number of people who liked the playlist to the number of people who did not like the playlist is 75: 25. Dylan said that for every three people who liked the playlist, one person did not.
Do Nadhii and Dy’an agree? Prove your answer using the values of the ratios.
Answer:
Dylan and Nadhii agree. The value of both of their ratios is equivalent, so their ratios are also equivalent.