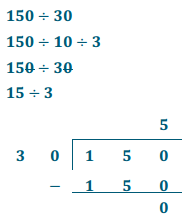Engage NY Eureka Math 6th Grade Module 2 Lesson 12 Answer Key
Eureka Math Grade 6 Module 2 Lesson 12 Example Answer Key
Estimate and apply the division algorithm to evaluate the expression 918 ÷ 27.
Answer:
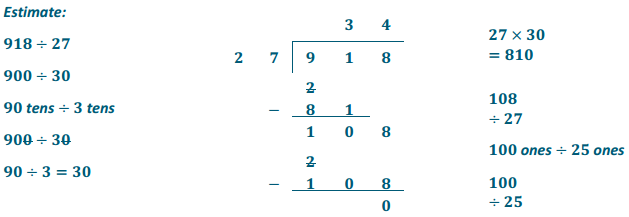
Eureka Math Grade 6 Module 2 Lesson 12 Exercise Answer Key
Round to estimate the quotient. Then, compute the quotient using a calculator, and compare the estimation to the quotient.
Exercise 1.
2,970 ÷ 11
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:
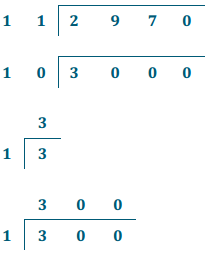
Estimate: 300
b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
2,970 ÷ 11 = 270
The quotient is very close to the estimate.
Exercise 2.
4,752 ÷ 12
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:

Estimate: 500
b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
4,752 ÷ 12 = 396
The quotient is close to the estimate but not as close as the estimate in the first exercise.
Exercise 3.
11,647 ÷ 19
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:
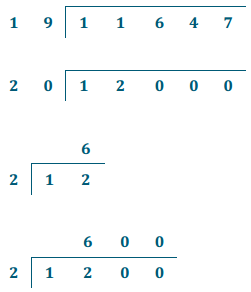
Estimate: 600
b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
11,647 ÷ 19 = 613
The quotient is very close to the estimate.
Exercise 4.
40,644 ÷ 18
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:
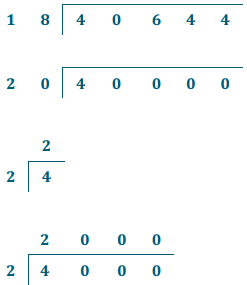
Estimate: 2,000
b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
40,644 ÷ 18 = 2,258
The quotient is close to the estimate but not as close as the estimate in the third exercise.
Exercise 5.
49,170 ÷ 15
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:
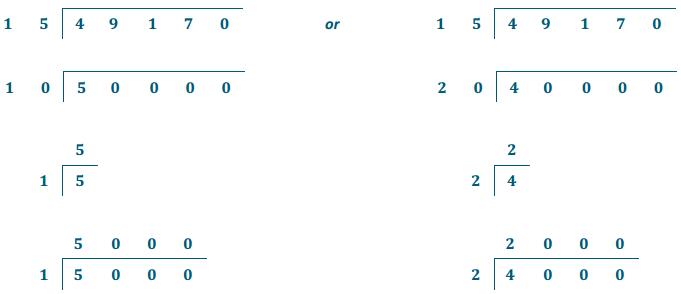
Estimates may vary but could include 5,000 or 2,000.
b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
49,170 ÷ 15 = 3,278
The quotient is somewhat close to the estimate; however, it is not as accurate as previous exercises and examples where the divisors were closer to a multiple of 10.
Eureka Math Grade 6 Module 2 Lesson 12 Problem Set Answer Key
Round to estimate the quotient. Then, compute the quotient using a calculator, and compare the estimate to the quotient.
Estimates may vary.
Question 1.
715 ÷ 11
Answer:
Estimate:. 700 ÷ 10 = 70
Quotient: 715 ÷ 11 = 65
Comparison: Since the dividend is very close to a multiple of ten, the quotient is very close to the estimate.
Question 2.
7,884 ÷ 12
Answer:
Estimate: 8,000 ÷ 10 = 800
Quotient: 7,884 ÷ 12 = 657
Comparison: The dividend is close to a multiple of ten, so the quotient is close to the estimate.
Question 3.
9,646 ÷ 13
Answer:
Estimate: 10,000 ÷ 10 = 1,000
Quotient: 9,646 ÷ 13 = 742
Comparison: The dividend is somewhat close to a multiple of ten, so me quotient is fairly close to the estimate.
Question 4.
11,942 ÷ 14
Answer:
Estimate: 12,000 ÷ 10 = 1,200
Quotient: 11,942 ÷ 14 = 853
Comparison: The dividend is not as close to a multiple of ten, so the quotient is not nearly as close to the estimate as dividends that are closer to a multiple of ten.
Question 5.
48,825 ÷ 15
Answer:
Estimate: 50,000 ÷ 10 = 5,000
Quotient: 48,825 ÷ 15 = 3,255
Comparison: The dividend is midway between multiples often. The quotient is in the same place value but is not as close to the estimate as dividends that are closer to a multiple of ten.
Question 6.
135,296 ÷ 16
Answer:
Estimate: 140,000 ÷ 20 = 7,000
Quotient: 135,296 ÷ 16 = 8,456
Comparison: The dividend is not as close to a multiple of ten, so the quotient is not nearly as close to the estimate as dividends that are closer to a multiple of ten.
Question 7.
199,988 ÷ 17
Answer:
Estimate: 200,000 ÷ 20 = 10,000
Quotient: 199,998 ÷ 17 = 11,764
Comparison: The dividend is somewhat close to a multiple of ten, so the quotient is fairly close to the estimate.
Question 8.
116,478 ÷ 18
Answer:
Estimate: 120,000 ÷ 20 = 6,000
Quotient: 116,478 ÷ 18 = 6,471
Comparison: The dividend is close to a multiple of ten, so the quotient is close to the estimate.
Question 9.
99,066÷ 19
Answer:
Estimate: 100,000 ÷ 20 = 5,000
Quotient: 99,066 ÷ 19 = 5,214
Comparison: Since the dividend is very close to a multiple of ten, the quotient is very close to the estimate.
Question 10.
181,800 ÷ 20
Answer:
Estimate: 180,000 ÷ 20 = 9,000
Quotient: 181,800 ÷ 20 = 9,090
Comparison: Since the divisor is a multiple of ten, the quotient is almost exactly the same as the estimate.
Eureka Math Grade 6 Module 2 Lesson 12 Exit Ticket Answer Key
Round to estimate the quotient. Then, compute the quotient using a calculator, and compare the estimation to the quotient.
Question 1.
4,732 ÷ 13
Answer:
Answers may vary.
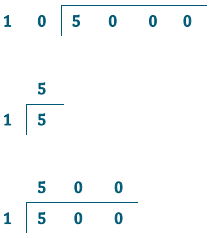
Estimate: 500
4732 ÷ 13 = 364
The quotient 364 is somewhat close to the estimate. Both numbers are in the hundreds. If the divisor was closer to a multiple of 10, the estimate would have been closer to the quotient.
Question 2.
22,752 ÷ 16
Answer:
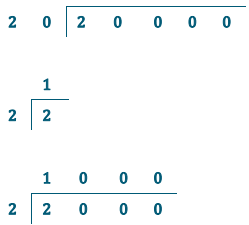
Estimate: 1,000
22,752 ÷ 16 = 1,422
The quotient 1,422 is somewhat close to the estimate. Both numbers are in the thousands place. The quotient is almost 1.5 times the estimate. The estimate would have been much closer to the quotient had the divisor been closer to a multiple of 10.
Eureka Math Grade 6 Module 2 Lesson 12 Discussion Answer Key
Divide 150 by 30.
Answer: