Engage NY Eureka Math 6th Grade Module 2 Lesson 14 Answer Key
Eureka Math Grade 6 Module 2 Lesson 14 Example Answer Key
Evaluate the expression. Use a tape diagram to support your answer.
Example 1.
0.5 ÷ 0.1
Answer:
Rewrite 0. 5 ÷ 0.1 as a fraction.
Answer:
\(\frac{0.5}{0.1}\)
Express the divisor as a whole number.
Answer:
\(\frac{0.5}{0.1} \times \frac{10}{10}=\frac{5}{1}=5\)
Example 2.
Evaluate the expression. First, convert the decimal division expression to a fractional division expression in order to create a whole number divisor.
25.2 ÷ 0.72
Answer:
\(\frac{25.2}{0.72} \times \frac{100}{100}=\frac{2,520}{72}\)
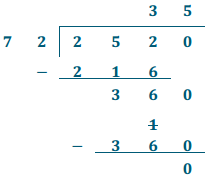
Use the division algorithm to find the quotient.
Answer:
25.2 ÷ 0.72 = 35
Example 3.
A plane travels 3, 625. 26 miles in 6. 9 hours. What is the plane’s unit rate?
Represent this situation with a fraction.
Answer:
\(\frac{3,625.26}{6.9}\)
Represent this situation using the same units.
Answer:
36,252.6 tenths ÷ 69 tenths
Estimate the quotient.
Answer:
35,000 ÷ 70 = 500
Express the divisor as a whole number.
Answer:
\(\frac{3,625.26}{6.9} \times \frac{10}{10}=\frac{36,252.6}{69}\)
Use the division algorithm to find the quotient.
Answer:
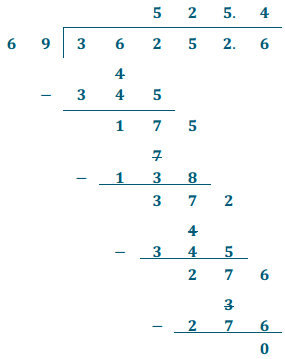
Use multiplication to check your work.
Answer:
525.4 × 69 = 36,252.6
Eureka Math Grade 6 Module 2 Lesson 14 Exercise Answer Key
Convert the decimal division expressions to fractional division expressions in order to create whole number divisors. You do not need to find the quotients. Explain the movement of the decimal point. The first exercise has been completed for you.
Exercise 1.
18.6 ÷ 2.3
Answer:
\(\frac{18.6}{2.3} \times \frac{10}{10}=\frac{186}{23}\)
18.6 ÷ 23
I multiplied both the dividend and the divisor by ten, or by one power of ten, so each decimal point moved one place to the right because they grew larger by ten.
Exercise 2.
14.04 ÷ 4.68
Answer:
\(\frac{14.04}{4.86} \times \frac{100}{100}=\frac{1404}{486}\)
1,404 ÷ 486
I multiplied both the dividend and divisor by one hundred, or by two powers of ten, so each decimal point moved two places to the right because they grew larger by two powers of ten.
Exercise 3.
0.162 ÷ 0036
Answer:
\(\frac{0.162}{0.036} \times \frac{1,000}{1,000}=\frac{162}{36}\)
162 ÷ 36
I multiplied both the dividend and divisor by one thousand, or three powers often, so each decimal point moved three places to the right because they grew larger by three powers of ten.
Convert the decimal division expressions to fractional division expressions in order to create whole number divisors. Compute the quotients using the division algorithm. Check your work with a calculator.
Exercise 4.
2,000 ÷ 3.2
Answer:
\(\frac{2,000}{3.2} \times \frac{10}{10}=\frac{20,000}{32}\)
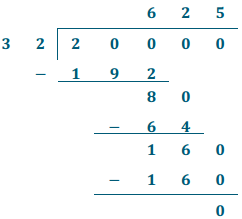
20000 ÷ 32 = 625
625 × 32 = 20000
2,000 ÷ 3.2 = 625
625 × 3.2 = 2,000
Exercise 5.
3,581.9 ÷ 4.9
Answer:
\(\frac{3,581.9}{4.9} \times \frac{10}{10}=\frac{35,819}{49}\)
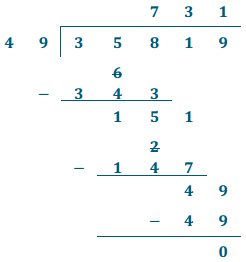
35,819 ÷ 49 = 731
731 × 49 = 35,819
3,581.9 ÷ 4.9 = 731
731 × 4.9 = 3,581.9
Exercise 6.
893.76 ÷ 0.21
Answer:
\(\frac{893.76}{0.21} \times \frac{100}{100}=\frac{89,376}{21}\)
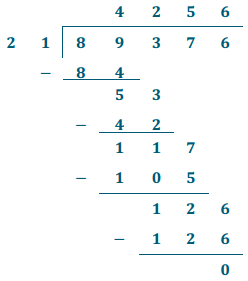
89,376 ÷ 21 = 4,256
4,256 × 21 = 89,376
893.76 ÷ 0.21 = 4,256
4,256 × 0.21 = 893.76
Exercise 7.
6.194 ÷ 0.326
Answer:
\(\frac{6.194}{0.326} \times \frac{1,000}{1,000}=\frac{6,194}{326}\)
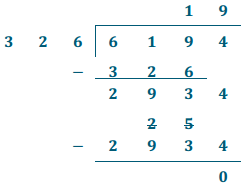
6,194 ÷ 326 = 19
19 × 326 = 6,194
6.194 ÷ 0.326 = 19
19 × 0.326 = 6.194
Eureka Math Grade 6 Module 2 Lesson 14 Problem Set Answer Key
Convert decimal division expressions to fractional division expressions to create whole number divisors.
Question 1.
35.7 ÷ 0.07
Answer:
\(\frac{35.7}{0.07} \times \frac{100}{100}=\frac{3570}{7}\)
Question 2.
486.12 ÷ 0.6
Answer:
\(\frac{486.12}{0.6} \times \frac{10}{10}=\frac{4,861.2}{6}\)
Question 3.
3.43 ÷ 0.035
Answer:
\(\frac{3.43}{0.035} \times \frac{1,000}{1,000}=\frac{3430}{35}\)
Question 4.
5418.54 ÷ 0.009
Answer:
\(\frac{5,418.54}{0.009} \times \frac{1,000}{1,000}=\frac{5,418,540}{9}\)
Question 5.
812.5 ÷ 1.25
Answer:
\(\frac{812.5}{125} \times \frac{100}{100}=\frac{81,250}{125}\)
Question 6.
17.343 ÷ 36.9
Answer:
\(\frac{17.343}{36.9} \times \frac{10}{10}=\frac{173.43}{369}\)
Estimate quotients. Convert decimal division expressions to fractional division expressions to create whole number divisors. Compute the quotients using the division algorithm. Check your work with a calculator and your estimates.
Question 7.
Norman purchased 3. 5 lb. of his favorite mixture of dried fruits to use in a trail mix. The total cost was $16.87. How much does the fruit cost per pound?
Answer:
\(\frac{16.87}{3.5} \times \frac{10}{10}=\frac{168.7}{35}\)
Estimate 16 ÷ 4 = 4
The dried fruit costs $4.82 per pound. This is close to my estimate of 4.
Question 8.
Divide: 994.14÷ 18.9
Answer:
\(\frac{994.14}{18.9} \times \frac{10}{10}=\frac{9,941.4}{189}\)
Estimate: 100 ÷ 2 = 50
The quotient is 52.6. This is close to my estimate of 50.
Question 9.
Daryl spent $4. 68 on each pound of trail mix. He spent a total of $14. 04. How many pounds of trail mix did he purchase?
Answer:
\(\frac{14.04}{4.68} \times \frac{100}{100}=\frac{1,404}{468}\)
Estimate: 15 ÷ 5 = 3
Daryl purchased 3 pounds of trail mix. This is my estimate.
Question 10.
Mamie saved $161. 25. This is 25% of the amount she needs to save. How much money does Mamie need to save?
Answer:
\(\frac{161.25}{0.25} \times \frac{100}{100}=\frac{16,125}{25}\)
Estimate: 1,600 ÷ 2 = 800
Mamie needs to save $645. This Is close to my estimate of 800.
Question 11.
Kareem purchased several packs of gum to place in gift baskets for $1.26 each. He spent a total of $8. 82. How many packs of gum did he buy?
Answer:
\(\frac{8.82}{1.26} \times \frac{100}{100}=\frac{882}{126}\)
Estimate: 9 ÷ 1 = 9
Kareem bought 7 packs of gum. This is close to my estimate of 9.
Question 12.
Jerod is making candles from beeswax. He has 132. 72 ounces of beeswax. If each candle uses 8.4 ounces of beeswax, how many candles can he make? Will there be any wax left over?
Answer:
\(\frac{132.72}{8.4} \times \frac{10}{10}=\frac{1,327.2}{84}\)
Estimate: 120 ÷ 8 = 15
The quotient is 15.8. This means that Jerod can make 15 candles. This is close to my estimate. There will be wax left over.
Question 13.
There are 20. 5 cups of batter in the bowl. This represents 0.4 of the entire amount of batter needed for a recipe. How many cups of batter are needed?
Answer:
\(\frac{20.5}{0.4} \times \frac{10}{10}=\frac{205}{4}\)
Estimate: 200 ÷ 4 = 50
The number of cups of batter needed for the recipe is 51.25. This is close to my estimate.
Question 14.
Divide: 159.12 ÷ 6.8
Answer:
\(\frac{159.12}{6.8} \times \frac{10}{10}=\frac{1,591.2}{68}\)
Estimate: 160 ÷ 8 = 20
The quotient is 23.4. This is close to my estimate.
Question 15.
Divide: 167.67 ÷ 8.1
Answer:
\(\frac{167.67}{8.1} \times \frac{10}{10}=\frac{1,676.7}{81}\)
Estimate: 160 ÷ 8 = 20
The quotient is 20.7. This is close to my estimate.
Eureka Math Grade 6 Module 2 Lesson 14 Exit Ticket Answer Key
Estimate quotients. Convert decimal division expressions to fractional division expressions to create whole number divisor. Compute the quotient using the division algorithm. Check your work with a calculator and your estimate.
Question 1.
Lisa purchased almonds for $3. 50 per pound. She spent a total of $24. 50. How many pounds of almonds did she purchase?
Answer:
\(\frac{24.50}{3.50} \times \frac{100}{100}=\frac{245}{35}\)
Estimate: 270 ÷ 30 = 9
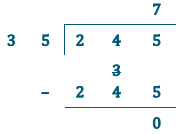
Lisa purchased 7 pounds of almonds. This is close to my estimate of 9.
7 × 35 = 245
7 × 3.5 = 24.5
Question 2.
Divide: 125.01 ÷ 5.4.
Answer:
\(\frac{125.01}{5.4} \times \frac{10}{10}=\frac{1250.1}{54}\)
Estimate: 125 ÷ 5 = 25
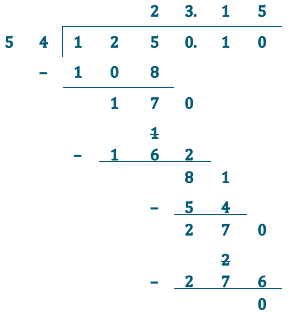
The quotient of 125.01 and 5.4 is 23.15. This is close to my estimate of 25.
23.15 × 54 = 1250.1
23.15 × 5.4 = 125.01
Eureka Math Grade 6 Module 2 Lesson 14 Opening Exercise Answer Key
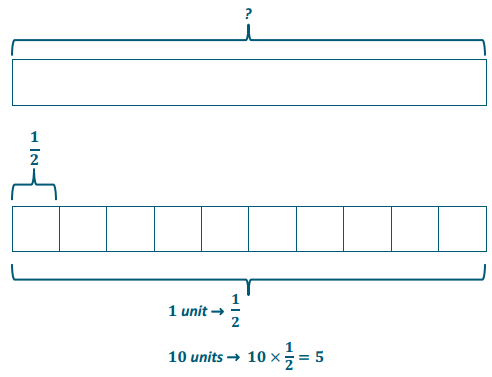
Divide \(\frac{1}{2} \div \frac{1}{10}\) Use a tape diagram to support your reasoning.
Answer:
This question is asking the following: \(\frac{1}{2} \text { is } \frac{1}{10}\) of what number?
Relate the model to the invert and multiply rule.
Answer:
\(\frac{1}{2} \div \frac{1}{10}=\frac{1}{2} \times \frac{10}{1}=\frac{10}{2}=5\)
Another way \(\frac{1}{2} \div \frac{1}{10}\)
Answer:
→ Let’s look at the Opening Exercise another way. We can represent \(\frac{1}{2} \div \frac{1}{10}\) using decimals.
→ We can represent the fractions \(\frac{1}{2}\) and \(\frac{1}{10}\) with which decimals?
One-half can be represented with 0.5, and one-tenth can be represented by 0.1.
→ Display the following:
\(\frac{1}{2} \div \frac{1}{10}\)
0.5 ÷ 0.1
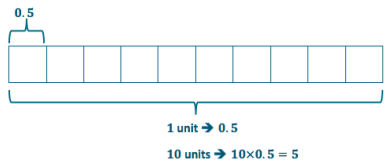
→ This expression can be represented with the same interpretation as the Opening Exercise: 5 tenths is 1 tenth of what number?
→ Let’s model this question with a tape diagram.
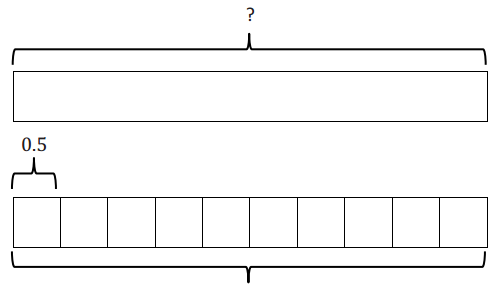
1 unit → 0.5
10 units → 10 × 0.5 = 5
→ What do you notice about the diagram and the quotient?
The diagram is set up exactly the same as in the Opening Exercise with the fraction, and the quotient is the same. Since \(\frac{1}{2}\) is equivalent to 0.5, and \(\frac{1}{10}\) is equivalent to 0.1, the quotients must be the same.
→ Look back at the problem: 0.5 ÷ 0.1. Rewrite this division expression as a fraction.
\(\frac{0.5}{0.1}\)
→ How can we express the divisor as a whole number?
Multiply by a fraction equal to one.
→ Choose a fraction to multiply in order to express the divisor as a whole number.
I could multiply by \(\frac{0.5}{0.1}\) by \(\frac{10}{10}\) to represent the divisor as the whole number 1.
→ Find the Product of \(\frac{0.5}{0.1} \times \frac{10}{10}\)
\(\frac{0.5}{0.1} \times \frac{10}{10}=\frac{5}{1}=5\)
→ What do you notice about the quotient?
It is the same as when we used a tape diagram to determine the quotient.
→ Why do you think the quotients are the same?
They are the same because I multiplied the divisor and the dividend by the same power of ten.
→ What conjecture can you make?
Because the divisor and the dividend both became ten times greater, when we write the numbers as ten times as much, we move the decimal to the right one place.